Size limits of self-assembled colloidal structures made using specific interactions

Significance

Nature uses hierarchical assembly to make complex structures such as biomolecules, virus shells, and microtubules with high fidelity. Today a key challenge is to translate this process to artificial systems, which hinges on understanding the fundamental questions of efficiency and scalability of self-assembly. Although self-assembly has been studied for decades, the principles behind it and its fundamental and practical limits are still largely unknown. In this paper we establish size limitations for assembling structures of controlled size and shape out of colloidal particles with specific interactions. Inspired by simulations of structures with highly variable shapes and sizes, we develop an understanding of yield through a general theory of excited states that compete with the desired structure in assembly.

Abstract

We establish size limitations for assembling structures of controlled size and shape out of colloidal particles with short-ranged interactions. Through simulations we show that structures with highly variable shapes made out of dozens of particles can form with high yield, as long as each particle in the structure binds only to the particles in their local environment. To understand this, we identify the excited states that compete with the ground-state structure and demonstrate that these excited states have a completely topological characterization, valid when the interparticle interactions are short-ranged. This allows complete enumeration of the energy landscape and gives bounds on how large a colloidal structure can assemble with high yield. For large structures the yield can be significant, even with hundreds of particles.

Nature uses hierarchical assembly of complicated building blocks to make highly functional structures such as biomolecules, virus shells, and microtubules without any external influence and with high fidelity. Mimicking this would not only give more insight into biological mechanisms but would also help realize the dream of “bottom-up” assembly that has been a central theme of nanotechnology for many decades (1).

As in biology, the information needed for assembling arbitrary macroscopic structures can be stored in the building blocks through the design of their interactions and interaction rules. Over the years great advances have been made by synthesizing new building blocks differing in geometry, composition, and interactions (2–10), allowing for study of more complex objects. However, basic rules necessary for robust and efficient assembly of a desired structure in a scalable fashion and reasonable time scales are still not understood. A number of schemes for approaching this “inverse” statistical mechanics problem have been proposed (11–13), but a general framework and systematic studies are still missing. One of the essential underlying questions, having both practical and conceptual impact, is whether any desired macroscopic structure can be assembled with a high yield, out of a given set of building blocks. Or are there fundamental constraints limiting the structures that can be effectively built?

In this paper we address these general questions using the model system of DNA-coated particles, itself of considerable recent interest. We consider an isolated system of N spherical colloidal particles, each of which is isotropically coated with DNA strands to control interparticle interactions. At the colloidal scale, such interactions have a range that is much shorter than the size of the particles. The use of DNA labeling to control binding specificity was originally pioneered for assembling nanoparticles (14–17) into infinite crystals (18–24), where recently it was demonstrated that with two species with differing particle radii and DNA linker length a zoo of different crystal morphologies can be created (25). Work at the colloidal scale has begun to bear fruit (13, 17, 26–30). However, the set of possible structures that could be coded is far more general, including structures of any shape and size, both rigid and flexible. For example, the number of clusters that can be assembled out of spherical particles with fixed size increases dramatically with particle number N, so that with only 10 particles there are 223 topologically distinct structures with at least $3N-6=24$ contacts (31–33).

Designing arbitrary complex structures requires using the specificity of interactions to make the desired target the energetic ground state. The most robust way of doing this is to make every particle in the target structure different, with interparticle interactions chosen to favor the desired local configuration in its target structure. The interactions between different particles are coded into an interaction matrix $\widehat{I}$, specifying the interaction energy between every pair of particles.

We begin by asking how high the equilibrium yield can be when $\widehat{I}$ is coded for an arbitrary large structure, using the simplest prescription in which every contact of the desired structure binds specifically and every undesired contact does not bind. In this paper, the yield represents the probability of successful complete assembly of exactly N particles, in contrast to a common definition of yield as the percentage of particles from the bulk that assemble into copies of a desired structure. Numerical simulations using dissipative particle dynamics demonstrate that there is a temperature regime where high-yield (>50%) assembly is possible for a range of complex structures consisting of dozens of particles. This is striking, because as the number of particles grows, the number of competing states grows rapidly with N; such a high yield implies that these states are less competitive than naively expected. To understand why this is the case, we study the yield of an entire family of structures, the set of rigid clusters with $N\le 9$ particles. We design $\widehat{I}$ so each structure is the ground state and numerically calculate the corresponding yield curves. For clusters, the yield degrades quickly with increasing N. However, we use the obtained insights to develop a complete description of the low-energy excited states that compete with the ground state, valid for asymptotically large structures. This description explains the high observed yield for large structures and points to the limits of equilibrium self-assembly with colloidal particles with short-ranged interactions. Finally, we comment on the role and importance of kinetic effects.

Results

Designing Interactions.

We study the assembly yield of arbitrary structures by choosing the interaction energy so that the desired structure is the ground state. This can be done uniquely for an isolated system of N spherical particles with isotropic interactions as follows: Start with the adjacency matrix $\widehat{A}$, which is the $N\times N$ matrix having an element $A_{ij}=1$ if particles i and j are in contact and $A_{ij}=0$ otherwise. We choose $\widehat{I}$ directly from $\widehat{A}$, by mapping nonzero elements of $\widehat{A}$ to favorable interactions in $\widehat{I}$ and zero elements to unfavorable interactions. Every contact in the desired structure has a bond energy $-\mathit{ϵ}$ (favorable), whereas every other interaction has a higher energy ϵ (unfavorable). Setting all favorable interactions to have the same strength and setting all unfavorable interactions to have the same strength has been shown to optimize the equilibrium yield (34). With this interaction matrix the different interactions between different particles are maximally specific. If some particles have identical sets of neighbors their interactions are indistinguishable, so these particles are effectively of the same type. When the interaction matrix is reduced to show the interactions between the different particle types, it is called an alphabet (34), with the maximally specific interactions defining the maximal alphabet.

When a structure has a unique adjacency matrix, this procedure guarantees that the desired structure has the maximal number of contacts and is therefore the unique ground state. However, if a structure has no mirror symmetries, then its “chiral partner,” obtained as the object’s mirror reflection through an arbitrary mirror plane, cannot be made to coincide with the original object through proper rotations or translations. The chiral partners are therefore distinct assemblies of particles, although each particle shares the same neighbors in both (and therefore the chiral partners have the same $\widehat{A}$). When a structure is built out of different types of particles it generically has no mirror symmetries, even if the geometrical shape of the structure does.

Consequently, both chiral partners are ground states, and in this paper we identify both as being the desired structure. For equilibrium yield this difference is not consequential, but we will see at the end of the paper that the simultaneous assembly of both chiral partners can lead to kinetic effects relevant for the yield.

Assembly of Large Structures.

To discover whether it is possible to assemble large structures with high yield we use dissipative particle dynamics (DPD) (35, 36) and measure the equilibrium yield as a function of temperature. Our simulation contains N colloidal spheres of diameter D, with an interaction range of $1.05D$ [this range corresponds roughly to that of a DNA-coated 1-μm particle (37)]. The colloids are immersed into a DPD solvent of smaller particles. Colloids are modeled as 48–96 Lennard-Jones spheres if they interact favorably and with the repulsive part of the Lennard-Jones potential if they interact unfavorably. Simulations are run for a range of temperatures with a volume fraction of colloids ${\varphi }_{coll}=1/30$ and a larger volume fraction of solvent ${\varphi }_{sol}\approx 0.2$. More details are given in SI Text.

The complex structures include (i) a bipyramid with 44 particles, (ii) a bipyramid of 19 particles, (iii) a 19-particle chiral chain structure, and (iv) a 69-particle replica of Big Ben, with a crystalline base and a pyramidal top. Fig. 1A shows snapshots in the time evolution of the Big Ben assembly, starting with randomly distributed and thermalized particles. Assembly into the desired structure occurs with high yield, and this result prevails in most of the complex structures we have studied. Fig. 1B plots yield as a function of temperature $T/\mathit{ϵ}$ for the four previously mentioned structures. Each data point is an ensemble average over ∼100 different initial realizations, run at a fixed temperature T for a fixed time $t_{run}$. The yield is defined as the fraction of runs in the ensemble for which all of the bonds in the complete structure are observed at least once within a short time window ending at time $t_{run}$. This is still a conservative definition of yield, because if the structure with all of the bonds is not observed in the time window, even due to a single particle bond missing, the structure is regarded as a failed assembly (see SI Text for more details).

Fig. 1.

(A) Snapshots in time of DPD simulation of the Big Ben assembly. (B) Absolute yield as a function of temperature $T/\mathit{ϵ}$ for four larger structures described in the main text. Each data point is an ensemble average over 100 different initial condition simulations.

Our simulations exhibit several regimes as a function of temperature T, with a glassy regime at low T and an equilibrium regime at high T (SI Text). At the highest temperatures (at $T/\mathit{ϵ} \mathrm{\gtrsim } 0.16$) the system is in equilibrium, but the bonds between the colloids are short-lived, leading to small absolute yields of the ground states. The most striking feature of the yield curves in Fig. 1B is that the maximum yield is so high, despite the large number of particles in the desired state; this implies that the number of equilibria that are competing with the ground state is relatively small.

Clusters.

To uncover the landscape of equilibria that compete with the ground state we examine a simpler problem, the assembly of small clusters of particles with at least $3N-6$ contacts. Here the complete set of structures is known for $N\le 11$ particles (32, 33). Clusters of identical particles have a degenerate ground state when $6\le N\le 9$ (31, 38), with yields predominantly determined by the rotational entropy, suppressing highly symmetric clusters. Using the prescription for particle interactions ($\widehat{I}$) described above, we simulate the yield as a function of temperature for each cluster with $N\le 9$. Fig. 2 plots yield as a function of temperature $T/\mathit{ϵ}$ for all of the ground state clusters with $N=6$ and 7 particles. As above, each data point is an ensemble average over different initial condition realizations, run at a fixed temperature T for a fixed time $t_{run}$ (SI Text). Using the positions of particles we form an adjacency matrix and use its eigenvalues to uniquely identify the assembled structure at $t_{run}$.

Fig. 2.

Absolute yield as a function of temperature $T/\mathit{ϵ}$ for maximal alphabet vs. identical particles, for all of the clusters with $N=6$ (A and B) and $N=7$ particles (C–G). Matrices next to the panels are the maximal alphabet interaction matrices. When particles in a cluster have identical sets of neighbors, they are effectively of the same type, making the alphabet smaller than N (A, B, C, and F). In general, the yield curves of the clusters with designed interactions outperform the ones with identical interactions. The only exception is the $N=6$ polytetrahedral cluster shown in A. When all of the particles are identical, this cluster appears ∼96% of the time, competing with the highly symmetric octahedron (B) and without any kinetic traps. Although introduction of specific interactions eliminates competition with the second ground state it also introduces multiple kinetic traps that affect the yield in most of the temperature range.

The panels of Fig. 2 compare yield curves of given clusters for identical particles with those when interactions are determined by $\widehat{I}$. The yield improvements are dramatic, with the most enhancement occurring for symmetrical clusters, where the rotational entropy penalty is lifted (Fig. 2 B, F, and G). The yield curves from the clusters simulation exhibit the same phenomenology as those in Fig. 1. By comparing time and ensemble averages we show that the equilibrium regime extends down to $T/\mathit{ϵ}\sim 0.1$. Below $T/\mathit{ϵ}\sim 0.1$, the relaxation time of clusters becomes comparable to $t_{run}$ and the results are strongly influenced by kinetic effects. See SI Text and Figs. S1 and S2 for more details.

Fig. 3A shows how the maximum equilibrium yield $Y_{max}$ (SI Text) depends on N for maximal alphabets of clusters with $6\le N\le 9$ and 26 out of 223 rigid clusters with $N=10$. Fig. 3A also includes all nonmaximal alphabets (SI Text) for $N=6,7,8$. These are alphabets that uniquely encode for a given cluster as the ground state but have a smaller number of different particle types. The maximal alphabets give the highest yield, as previously predicted (34). The maximum yield monotonically decreases with growing N. For each N, the yield is determined by the geometry of the clusters: Fig. 3B shows that the yield of clusters increases with decreasing second moment (i.e., with increasing symmetry).

Fig. 3.

(A) Maximal equilibrium yield $Y_{max}$ extracted from simulations (SI Text) vs. the cluster size N, for all of the alphabets of all of the $N=6,7$ and 8 clusters, for maximal alphabets of all of the $N=9$ clusters, and for maximal alphabets of a subset of the $N=10$ clusters. Big data points correspond to maximal alphabets and small to all of the other alphabet sizes. In general, maximal alphabets give the biggest yield. (B) Maximal equilibrium yield $Y_{max}$ extracted from simulations vs. the anisotropy of the cluster measured by the second moment $M_2$ of the corresponding cluster. $M_2={\displaystyle {\sum }_{i=1}^N{\left|{\mathbf{r}}_i\right|}^2}$, where ${\mathbf{r}}_i$ is the position of i-th particle with respect to center of mass. Only maximal alphabets are included. Color corresponds to the number of particles in a cluster (purple, $N=6$; orange, $N=7$; blue, $N=8$; green, $N=9$; and red, $N=10$).

What Determines the Equilibrium Yield?

Consider N particles with a fixed alphabet that determines the ground-state cluster C. Vibrationally and rotationally excited states of C preserve the cluster’s structure without breaking interparticle bonds. This means that our simulations would identify these states as C too. Hence, the partition function that describes the ground state is $Z_C=\left(1/{\sigma }_C\right)Z_C^0{Z}_C^{vib}{Z}_C^{rot}\equiv \left(1/{\sigma }_C\right)Z_C^0{e}^{S_0/k_B}$, where σ is the symmetry number and $Z_C^{\left(0\right)}$ the partition function given by the potential energy of the geometrical configuration C. $Z_C^{vib}$ and $Z_C^{rot}$ are the vibrational and rotational partition functions, respectively; these are both entropic, with $S_0$ the corresponding total entropy.

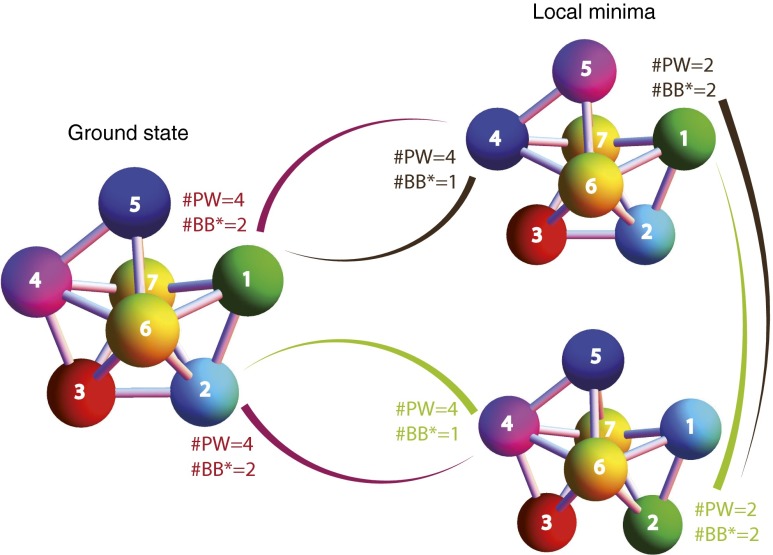
The states that compete for yield with the cluster C are the low-energy excited states. In particular, a local minimum (LM) state is a stable configuration of N particles and must have at least one particle bond less than C. Each LM is characterized by the number of broken bonds compared with C, $B_{LM}$, each bond costing an energy ϵ. As an example, Fig. 4 shows the energy landscape with the two lowest-energy local minima that arise for the maximal alphabet of one of the $N=7$ clusters. Each of these local minima has $B_{LM}=1$. Kinetic landscapes of this type for a few of clusters with $N=6$ and 7 show that both the number of LM and $B_{LM}$ is quite variable between different cluster geometries (Figs. S3–S5).

Fig. 4.

Energy landscape for a $N=7$ cluster designed using maximal alphabet. Only the lowest energy LMs are shown, both missing one bond compared with the ground state. Both can be obtained by permuting two particles in the ground state. $\#B{B}^{\mathrm{\ast }}$ is the minimal number of bonds that need to be broken for transition between different states. $\#PW$ is the number of distinct pathways by which the transition can be achieved. For example, to transition from the ground state to the top local minimum one needs to break at least two bonds. One of the four pathways is to break bonds between particle pairs red–purple and front-yellow–purple and then smoothly exchange positions of purple and blue particles before reconnecting the purple with the front-yellow.

The partition function of the $j^{th}$ local minimum is given by $Z_{LM}^j=\left(1/{\sigma }_{LM}\right)Z_{LM}^{0,j}{e}^{S_j/k_B}$, consisting of energetic and entropic parts, $S_j$ being the entropy. For floppy structures the entropy includes the freedom to explore the entire set of motions consistent with the imposed bond constraints. These entropies can be calculated asymptotically in the limit of vanishing interaction range and identical particles: In this limit they are roughly proportional to the number of missing bonds and depend on the geometry (39).

With a complete enumeration of the set of local minima, the equilibrium yield of the ground-state cluster is given by $Y_C^{eq}=Z_C/(Z_C+{\displaystyle {\sum }_j{Z}_{LM}^j}).$ To go further, we make the simplifying approximation that each of the local minima with the same number of bonds broken has the same entropy, so that $Z_{LM}^j/Z_C\approx \left({\sigma }_C/{\sigma }_{LM}\right)\cdot e^{-B_j\beta \mathit{ϵ}}\cdot f\left(B_j\right)$, with $\beta ={\left(k_{B}T\right)}^{-1}$ and where $f\left(m\right)\equiv \text{exp}\left[\left(S_m-S_0\right)/k_B\right]$ accounts for the entropic free energy lost from breaking m bonds. The partition function then becomes

$$Y_C^{eq}=\frac{1}{1+{\displaystyle {\sum }_{m}f\left(m\right)N_m{e}^{-\beta m\mathit{ϵ}}}},$$ [1]

where $N_m$ is the number of local minima with the number of broken bonds $B_j=m$, and we set the σ factors to 1 temporarily for simplicity of presentation. The maximum yield is determined by the balance between $N_m$ and the exponential penalty of higher m. The dependence of $N_m$ on m is a purely geometrical problem, because the landscape of local minima depends only on the geometry of the structure being assembled.

Note that when a designed cluster C has two chiralities we identify both as desired ground states, thereby doubling $Z_C$ (i.e., introducing factor $1/2$ in the sum over m).

Clusters.

For the clusters, we determine $N_m$ by completely enumerating the local minima for any given alphabet and cluster: We consider all possible arrangements of the particle labels of the given alphabet on a complete list of clusters having the same number of particles as the given cluster and carefully remove any duplicates. With these local minima we can check the correlation between the maximum yield measured in simulations (see SI Text for the definition) and the number and type of local minima. Fig. 5A plots the maximum yield of all alphabets of all $N=\mathrm{6,7,8}$ clusters, as a function of the number of lowest lying local minima; for the clusters the minimum number of bonds broken equals 1 or 2. The yield correlates strongly with the number of lowest-energy LMs. Fig. 5B also considers the LMs with one additional broken bond; the correlation improves only slightly, implying that the yield of these small clusters is determined by the competition between the ground state and the lowest-lying local minima.

Fig. 5.

Maximal equilibrium yield $Y_{max}$ extracted from simulations (SI Text) vs. the theoretical detrimental contribution of low-energy local minima (LMs), which depends on the number ($\#LM$) and energy ($B_{LM}$) of the LMs (see Eq. 1). The factor $\#GS$ accounts for the chirality of ground states by taking values 1 (nonchiral designed cluster) or 2 (chiral pair). All alphabets of all $N=6,7,8$ clusters are shown, with large symbols denoting maximal alphabets. Lines present the upper bound on yield from Eq. 1, which has the LM entropy, assumed equal for all LMs, as single variable parameter f chosen freely here, and we set $\beta \mathit{ϵ}\equiv 1$ to represent the relevant equilibrium regime. (A) Only the lowest LMs are retained in the calculation of the detrimental contribution, having minimal number of broken bonds $B_{LM}$ that takes values 1 or 2 depending on the cluster and alphabet. (Inset) A zoom-in of the main panel. (B) All low-lying LMs up to $B_{LM}=2$ are retained. (Inset) A zoom-in of the main panel.

In these plots we also show the prediction from Eq. 1, with the symmetry number factors reinstated. We used the entropic free-energy loss $f\left(m\right)\equiv const$ (SI Text) as the only free parameter, obtaining a good agreement with data. The value of $\beta \mathit{ϵ}$ in the curves is set to 1, representing the regime of equilibrium with fluctuating bonds, appropriate for the simulation temperatures that gave the maximum yields.

Large structures.

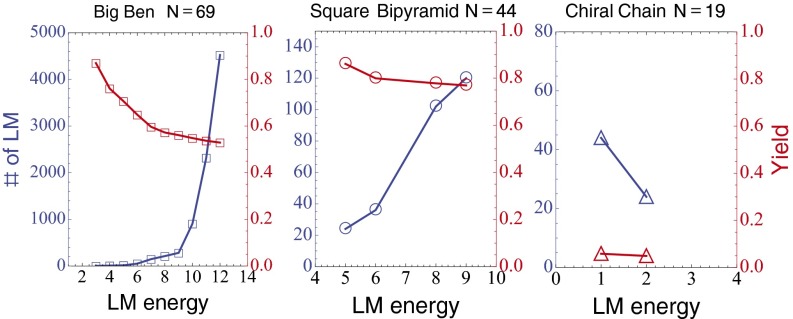
Superficially, the observations of high yields for large structures (Fig. 1) are even more curious in light of the cluster results, because the extrapolated yield from Fig. 3A would correspond to a negligible yield for Fig. 1B. This discrepancy suggests that the dominant low-energy local minima change as N increases. To understand this, we enumerate the local minima for large structures and determine which local minima are competing with the ground state. Within our prescription for specifying $\widehat{I}$, the low-energy local minima have a simple mathematical structure. They are obtained by permuting particles in the structure that share at least one neighbor. Using such permutations we enumerate the LMs for each of the three structures shown in Fig. 1B (SI Text). Fig. 6 shows the rapid increase of number of LMs with growing number of broken bonds m in the large structures. We then compute the predicted yield from Eq. 1 by including only LMs with $m\le M$ and see that the yield quickly converges as M is increased (we fix $\beta \mathit{ϵ}\equiv 1$, whereas $f\left(m\right)\equiv 1$; SI Text). This shows that yield is dominated by low-lying LMs, including some with more than the minimal number of broken bonds. A special case is the chiral chain, which only has $m=\mathrm{1,2}$ LMs owing to its quasi-1D shape.

Fig. 6.

Equilibrium yield and number of local minima for three large structures. The number of local minima (blue) for a fixed LM energy (which equals the number of broken bonds) is calculated by enumerating all possible LMs obtained by permuting nearby particles in the designed structure and counting the number of broken bonds. The equilibrium yield (red) is calculated using Eq. 1, where we include all LMs up to a fixed LM energy on the horizontal axis. In the equation we put for simplicity the entropy factors $f\left(m\right)\equiv 1$ (SI Text) and choose $\beta \mathit{ϵ}\equiv 1$ to represent the equilibrium regime relevant for the simulations throughout this paper.

Local Defects and Asymptotic Yield.

For each of the large-structure examples above the relevant low-lying LMs feature permutations of only nearest-neighbor particles. We note that in case of small clusters all LMs are obtained by permutations of two particles (SI Text and Fig. S6). Considering an arbitrary structure, the interactions given by $\widehat{I}$ imply that the permutation of faraway particles i and j would break all their bonds with the rest of structure.

With these observations, we define a local defect as a permutation of two particles $i,j$ that are in contact or share at least one neighbor. The energy of such a defect is determined by the local environment of particles $i,j$: The number of broken bonds is

$$b_{\text{local\hspace{0.17em}defect}}=\#NN\left(i\right)+\#NN\left(j\right)-2\cdot \#NN\left(i,j\right),$$ [2]

where $\#NN\left(i\right)$ is the number of nearest neighbors to particle i, and $\#NN\left(i,j\right)$ the number of nearest neighbors shared by i and j, including the bond between i and j.

When both $i,j$ are positioned deeply inside the bulk of the structure, we will call it a bulk defect. Bulk defects tend to have high energies as there are many nearest neighbors in the bulk. Surface defects correspond to either or both of $i,j$ on the surface of the structure; these typically have fewer broken bonds and lower energy (Fig. S7). Continuing the classification, the structure might have ridges and sharp apexes, leading to line and point defects, respectively. Any low-energy local minimum is obtained as a configuration of a particular set of local defects. We neglect configurations where defects overlap, because as N grows the number of such configurations is negligible compared with the number of configurations with well-separated defect locations. In this limit, the energy of a configuration of defects is just the sum of the defects’ individual energies.

We can now use these ideas to understand how the yield depends on the size of a structure. As illustrations we consider two particular examples, a cube structure and a chain structure.

Cube.

We consider a cube with face-centered-cubic arrangement of particles and with sides of $L=10$ particles. A bulk local defect costs $b_3=16$ bonds according to Eq. 2. There are $N_3\simeq L^3=\mathrm{1,000}$ positions in the cube where such a defect can be located. Analogously, surface, line, and point defects cost $b_2=10,\hspace{0.17em}{b}_1=6,\hspace{0.17em}{b}_0=3$ bonds, having $N_2\simeq 6L^2=600,\hspace{0.17em}{N}_1\simeq 12L=120,\hspace{0.17em}{N}_0\simeq 8$ positions available in the cube structure, respectively. (We simplify by assuming there is only a single version of every defect type; e.g., all possible surface defects have the same value $b_2$, etc.) Using this input we can find the number of LMs contributing to each term in Eq. 1: For example, LMs with $B_{LM}=9$ can be created out of three point defects, each with $b_0=3$. There are $\left(\begin{array}{c}{N}_0\\ 3\end{array}\right)=56$ such LMs, because the point defects can occur at any three out of eight corners of the cube; also, such a $B_{LM}=9$ LM could consist of one point and one line defect, and there are $\left(\begin{array}{c}{N}_0\\ 1\end{array}\right)\left(\begin{array}{c}{N}_1\\ 1\end{array}\right)=960$ such LMs. In total there are 1,016 LMs, giving a contribution to the denominator of Eq. 1 of $\mathrm{1,016}\cdot e^{-9}=0.13$ (as explained above, we fix $f\left(m\right)\equiv 1$ and $\beta \mathit{ϵ}\equiv 1$). This lowers the yield to $72\text{\%}$. Simple counting shows that LMs with one or two point or line defects dominate and the total yield is about $50\text{\%}$. This is a surprisingly large yield for a 1,000-particle structure.

As structure size increases the yield decreases. The same argument as above implies that if we consider a much larger cube, for example with $L=90$ and $\sim {10}^6$ particles, we find a yield of ∼1%, dominated by surface and line defects. Although both cube examples have large $N\gg 1$, the yield varies between a high value and negligible value.

Linear chain.

For the example of a linear chain with length $L=20$, we would typically have $b_0=1$, $N_0=2$ for (end-)point defect and $b_1=2$ for a line defect having $N_1\simeq L=20$ available positions. Two line defects give the biggest contribution $\left(\begin{array}{c}{N}_1\\ 2\end{array}\right)e^{-2\cdot b_1}$, which lowers yield to $22\text{\%}$, whereas adding contributions from LMs with one or three line defects, with or without one point defect, is enough to converge close to the final, relatively low yield of $5\text{\%}$. This is in accord with our above simulation results showing low chain yield.

Arbitrary structure.

Finally, we consider an arbitrary large structure that has large volume-to-surface, surface-to-edge, and edge-to-corner ratios and abundant contacts so that it is rigid. We call this a “bulky” 3D structure. Then, we can roughly estimate the input data and use the theory to qualitatively distinguish outcomes of considerable yield and negligible yield. Consider a structure of linear dimension L (measured in particles), which has point, line, surface, and bulk defects labeled by the corresponding dimensionality $d=\mathrm{0,1,2,3}$, respectively, each defect type costing $b_d$ broken bonds and, according to spatial dimensionality, having $N_d\simeq L^d$ possible locations.

Consider contributions to the yield from LMs consisting of $x_d$ defects of type d. For simplicity we do not consider LMs that contain different types of defects at the same time. First we demand that the yield stay considerable, that is, the LM contribution to denominator of Eq. 1 stay much smaller than unity, that is, $\left(\begin{array}{c}{N}_d\\ x_d\end{array}\right)\cdot \text{exp}\left(-b_d\right)\ll 1$. This demand leads to

$$\text{exp}\left(b_d\right)\gg L^d,$$ [3]

where we assumed that the defects are dilute, $x_d\ll L^d$, whereas system is large $L^d\gg 1$; with these assumptions the value of $x_d$ drops out. Intuitively, the inequality says that yield stays considerable if the defect cost $b_d$ is high compared with available system size $L^d$, for every defect type d. The high cost of defects is consistent with our assumption of their diluteness in the dominant LMs.

If, however, the defects are energetically cheap compared with system size, that is, the condition in Eq. 3 is violated, the yield is significantly diminished owing to LM contributions. In this case of energetically cheap defects it can also happen that the defect number in relevant LMs becomes large, violating the diluteness assumption. (Notice that this regime can never happen with point defects $d=0$.) Owing to high density of defects our basic approximation of LMs as configurations of noninteracting defects fails, but clearly we can conclude that the yield is negligible.

It is clear that this analysis can be applied to “nonbulky” structures too, because we focused on each defect type separately. For instance, the above example of a chain is representative of quasi-1D structures and is a special case of the arbitrary structure where surface and bulk defects are absent. Additionally, one can consider structures for which the scaling of defect numbers with structure dimension is not trivial; for example, in a planar fractal-like structure the edge length and the number of line defects would scale as a noninteger power of linear system size. Overall, our analysis gives a rough but general and simple understanding of equilibrium yield limitations based on local defects.

Chirality and Kinetic Effects.

Our above theoretical estimates give yields in reasonable quantitative agreement with simulations, in which we indeed observe that LM configurations occur in the assembly process. However, simulations also reveal that some suppression of yield is due to chirality.

In accordance to our analysis of chirality, when separate parts of the assembling structure nucleate independently they randomly acquire one of the two chiralities, leading to an inherent kinetic effect: Formed pieces with opposite chirality can never properly join into the structure. Instead, the pieces can weakly connect, for example along one of their edges (Fig. S8). The detrimental contribution to yield from these effects could dominate the contribution from low-lying LMs, and further analysis of such kinetic effects should be valuable.

Discussion

To summarize, we have demonstrated through numerical simulations that high-yield aggregates of coated colloidal spheres can be created with specific, short-ranged interactions. Strikingly, our simulations indicate that high-yield structures form with dozens of particles. We developed a theoretical framework for understanding this result, based on the fact that the low-energy local minima competing with the designed ground state consist of configurations in which particles in the ground state structure swap places. For example, in bulky (as defined above) structures of hundreds of particles it is the surface defects that are most detrimental to yield. The scalings implied by these calculations indicate that high-yield bulky structures can form from $N\sim \mathrm{1,000}$ particles with specific interactions. This represents a fundamental limit for the complexity of structures that can be robustly built out of purely equilibrium interparticle interactions.

Our focus on maximally specific interactions not only enables the local defect analysis but also prevents transitioning between different structures without breaking any bonds. Still, in nonrigid structures global floppy modes (which do not change the bond network) could influence the yield, and we leave this question for future study.

We note that there are technological challenges with implementing the high-yield DNA-coated colloid schemes outlined here: Our maximal interaction specificity construction requires a different DNA strand to mediate the interaction for every contact (e.g., because a particle in a bulk crystal has of order six nearest neighbors, that many different types of strands per particle are required). Although the practical limit of how many different types of strands per particle can be used is much higher than what we require (40), the density of strands is not high enough yet to avoid kinetic effects (40). Nonetheless, it is possible to implement the basic schemes outlined here with nonmaximal alphabets, in which the number of different strands on each particle is less than the number of contacts. If carefully chosen, a nonmaximal alphabet uniquely identifies a target structure—although having more low-energy excited states, leading to a smaller yield. We have included such nonmaximal alphabets in our simulations of clusters (Fig. 5), and the yields can still be significantly higher than with nonspecific interactions.

There are other opportunities to further increase yield by removing the assumption of equilibrium interactions, which was the basis of our analysis. For example, recent work (41) has shown that in a system with a fixed number of building blocks kinetic effects can be critical for achieving successful assembly. One example of nonequilibrium design that is natural for colloidal assembly is to allow some of the bonds to be irreversible. Any irreversible bond that does not limit pathways out of local minima will increase the yield of the ground state. The assembly of complex systems in biology suggests other ways of beating the equilibrium threshold, including (i) the possibility of using error correction, by allowing energy consuming reactions to bias toward the correctly formed structure, and (ii) including allosteric interactions, in which the binding energy of a particle depends on the set of particles that it binds to. Determining how best to implement these schemes with colloid-mediated DNA interactions is an important topic for future research.

Materials and Methods

A detailed description of our simulations together with one simulation movie (Movie S1) is included in Supporting Information.