Why the proportion of transmission during early-stage HIV infection does not predict the long-term impact of treatment on HIV incidence

Significance

Antiretroviral treatment (ART), which prevents both morbidity and HIV transmission for persons infected with HIV, is now thought to be central to strategies for controlling the spread of HIV. One major concern has been that if a large proportion of HIV transmission occurs early in infection, before persons can be diagnosed and treated, the impact of treatment on reducing new infections will be less. We use a mathematical model to quantify how the proportion of early transmission will affect the impact of intervention strategies, and explain underlying epidemiological mechanisms for this. Model simulations suggest that—counter to expectations—the proportion of early transmission at the start of an ART intervention does not predict the long-term intervention impact.

Abstract

Antiretroviral therapy (ART) reduces the infectiousness of HIV-infected persons, but only after testing, linkage to care, and successful viral suppression. Thus, a large proportion of HIV transmission during a period of high infectiousness in the first few months after infection (“early transmission”) is perceived as a threat to the impact of HIV “treatment-as-prevention” strategies. We created a mathematical model of a heterosexual HIV epidemic to investigate how the proportion of early transmission affects the impact of ART on reducing HIV incidence. The model includes stages of HIV infection, flexible sexual mixing, and changes in risk behavior over the epidemic. The model was calibrated to HIV prevalence data from South Africa using a Bayesian framework. Immediately after ART was introduced, more early transmission was associated with a smaller reduction in HIV incidence rate—consistent with the concern that a large amount of early transmission reduces the impact of treatment on incidence. However, the proportion of early transmission was not strongly related to the long-term reduction in incidence. This was because more early transmission resulted in a shorter generation time, in which case lower values for the basic reproductive number (R₀) are consistent with observed epidemic growth, and R₀ was negatively correlated with long-term intervention impact. The fraction of early transmission depends on biological factors, behavioral patterns, and epidemic stage and alone does not predict long-term intervention impacts. However, early transmission may be an important determinant in the outcome of short-term trials and evaluation of programs.

Recent studies have confirmed that effective antiretroviral therapy (ART) reduces the transmission of HIV among stable heterosexual couples (1–3). This finding has generated interest in understanding the population-level impact of HIV treatment on reducing the rate of new HIV infections in generalized epidemic settings (4). Research, including mathematical modeling (5–10), implementation research (11), and major randomized controlled trials (12–14), are focused on how ART provision might be expanded strategically to maximize its public health benefits (15, 16).

One concern is that if a large fraction of HIV transmission occurs shortly after a person becomes infected, before the person can be diagnosed and initiated on ART, this will limit the potential impact of HIV treatment on reducing HIV incidence (9, 17, 18). Data suggest that persons are more infectious during a short period of “early infection” after becoming infected with HIV (19–22), although there is debate about the extent, duration, and determinants of elevated infectiousness (18, 23). The amount of transmission that occurs also will depend on patterns of sexual behavior and sexual networks (17, 24–27). There have been estimates for the contribution of early infection to transmission from mathematical models (7, 17, 21, 24–26) and phylogenetic analyses (28–31), but these vary widely, from 5% to above 50% (23).

In this study, we use a mathematical model to quantify how the proportion of transmission that comes from persons who have been infected recently affects the impact of treatment scale-up on HIV incidence. The model is calibrated to longitudinal HIV prevalence data from South Africa using a Bayesian framework. Thus, the model accounts for not only the early epidemic growth rate highlighted in previous research (5, 9, 18), but also the heterogeneity and sexual behavior change to explain the peak and decline in HIV incidence observed in sub-Saharan African HIV epidemics (32, 33).

The model calibration allows uncertainty about factors that determine the amount of early transmission, including the relative infectiousness during early infection, heterogeneity in propensity for sexual risk behavior, assortativity in sexual partner selection, reduction in risk propensity over the life course, and population-wide reductions in risk behavior in response to the epidemic (32, 33). This results in multiple combinations of parameter values that are consistent with the observed epidemic and variation in the amount of early transmission. We simulated the impact of a treatment intervention and report how the proportion of early transmission correlates with the reduction in HIV incidence from the intervention over the short- and long-term.

Results

Model Calibration and Transmission During Epidemic Stage.

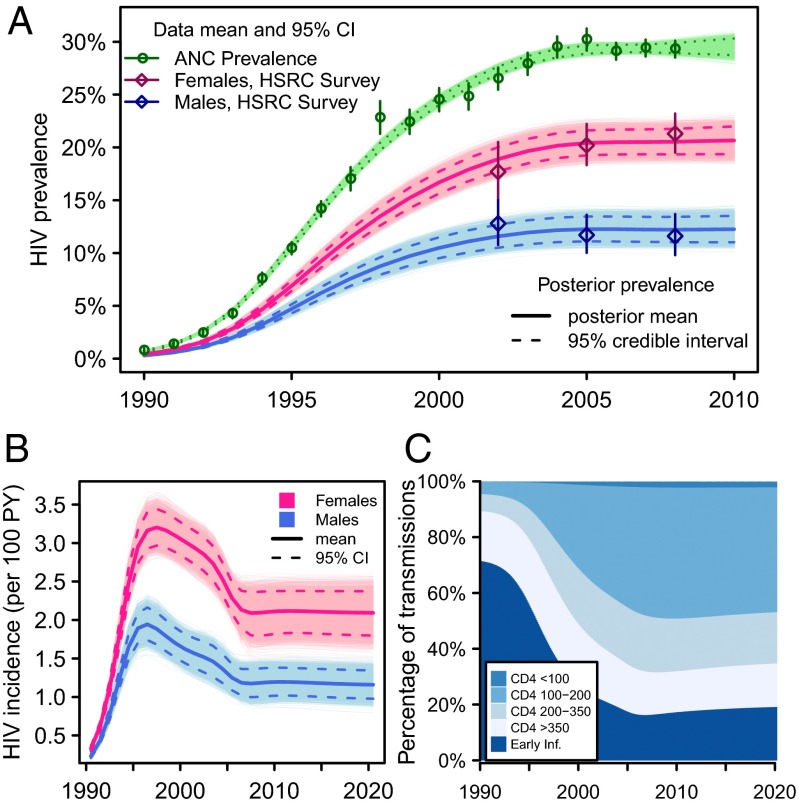
The mathematical model was calibrated to the time series of HIV prevalence among pregnant women in South Africa from 1990 through 2008 (34) and HIV prevalence among adult men and women aged 15–49 y in three national household surveys in 2002, 2005, and 2008 (Fig. 1A). The HIV incidence rate grows rapidly in the early 1990s, peaking in 1997 and declining by around 37% (95% credible interval 30–43) over the next decade (Fig. 1B). The decline in incidence is the result of two factors: infection saturation in the higher-risk groups and a reduction in the unprotected sexual contact rate over time. It is estimated that the contact rate declines by 28% (95% CI, 11–43; parameter posterior distributions in Fig. S1).

Fig. 1.

Epidemiologic outputs for baseline model calibration and projection without ART. (A) Posterior model calibration to adult male and female HIV prevalence and HIV prevalence among pregnant women attending ANC. (B and C) Posterior distribution in counterfactual simulation with no ART provision: (B) HIV incidence rate among adult men and women; (C) mean percentage of transmission from each stage of infection.

The fraction of transmission occurring from individuals in each stage of infection evolves over the course of the epidemic (Fig. 1C). During the early growth phase of the epidemic, most infected persons have been infected recently, and so most new infections result from highly infectious persons in early HIV infection (early transmission). As the epidemic matures, the contribution of early transmission declines whereas the contribution of advanced stages of infection grows.

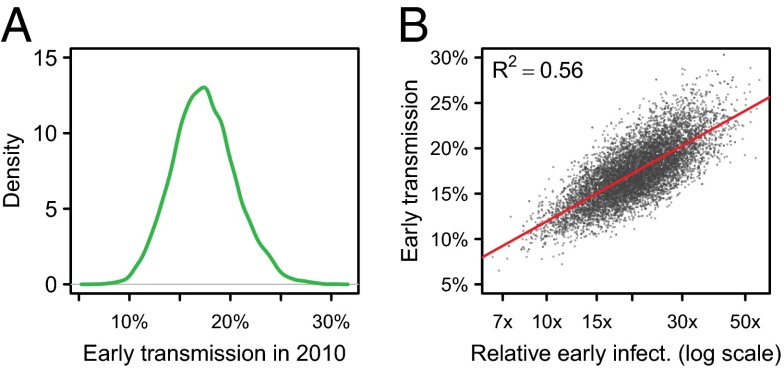
In the absence of ART scale-up, early transmission was estimated to account for 17% (95% CI, 12–24) of all transmission in 2010 (Fig. 2A). Much of the variation in early transmission was explained by the relative infectiousness during early infection compared to chronic infection (R² = 56%; Fig. 2B). Adjusting for the influence of infectiousness during early infection, higher rates of moving from higher- to lower-risk groups resulted in more early transmission because faster movement to low-risk groups results in more transmission occurring early after infection. These two parameters together explained 89% of the variation in early transmission in 2010 (Fig. S2A).

Fig. 2.

(A) Distribution in the percentage of transmission during early infection in 2010. (B) Correlation between the relative infectiousness during early infection (on the log scale) and the proportion of early transmission.

Early Transmission and the Impact of Treatment as Prevention.

We explored how the proportion of early transmission in 2010 affected the impact of ART on reducing HIV incidence. We simulated an intervention in which infected persons are eligible for treatment when their CD4 cell count falls below 350 cells/μL. Eligible persons initiated ART at a rate of 0.23 per year, such that 80% will initiate treatment before death. The intervention was introduced into an ART-naïve epidemic in 2010, and the intervention was simulated for 30 y. We calculated the percentage reduction in incidence rate with reference to the model projection without ART.

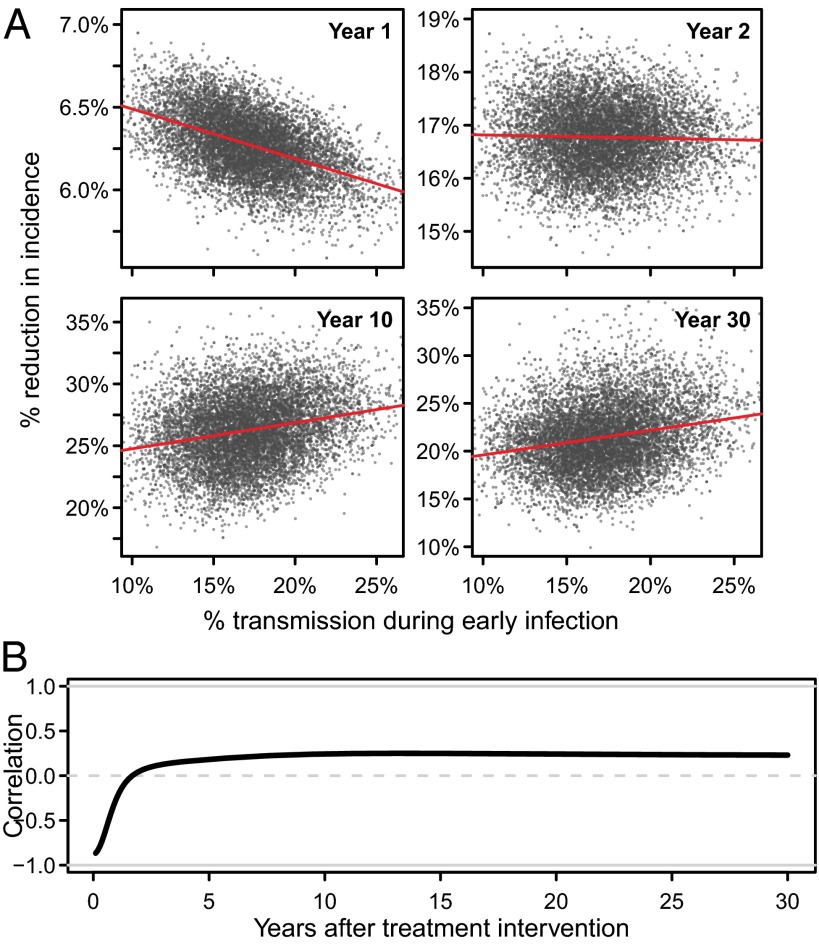
Fig. 3 illustrates the correlation between the proportion of early transmission at the start of the intervention and the reduction in incidence over time. In the first year of the intervention, the reduction in incidence was negatively correlated with the fraction of early transmission (Pearson’s r = −0.49) (Fig. 3A). This is consistent with the conventional wisdom that more early transmission will result in less impact of treatment on reducing incidence.

Fig. 3.

Correlation between percentage of early transmission in 2010 (when ART is introduced) and the reduction in HIV incidence rate over time relative to projected incidence in the absence of ART. (A) Scatter plots comparing the percentage of early transmission in 2010 and the percentage reduction in incidence rate in the first, second, 10th, and 30th years (note: vertical axes are not the same). (B) The Pearson correlation coefficient between early transmission at intervention start and the percentage reduction in incidence rate over time.

However, in the long term, the proportion of early transmission was not strongly predictive of the reduction in incidence, explaining only about 5% of the variation in intervention impact. In fact, after the 10th year, there was a modest positive correlation (r = 0.24; Fig. 3A), which persisted as the epidemic with ART stabilized at a lower equilibrium level (Fig. 3B).

Both the strong negative initial correlation between early transmission and intervention impact and the poor long-term predictive power of early transmission on intervention impact were robust to assumptions about ART eligibility (all HIV+ adults, CD4 ≤350 cells/μL, CD4 ≤200 cells/μL), about treatment coverage (20–95%), and that all treated persons would initiate treatment more rapidly after becoming eligible (Fig. S3).

R₀, Early Transmission, Epidemic Growth, and Intervention Impact.

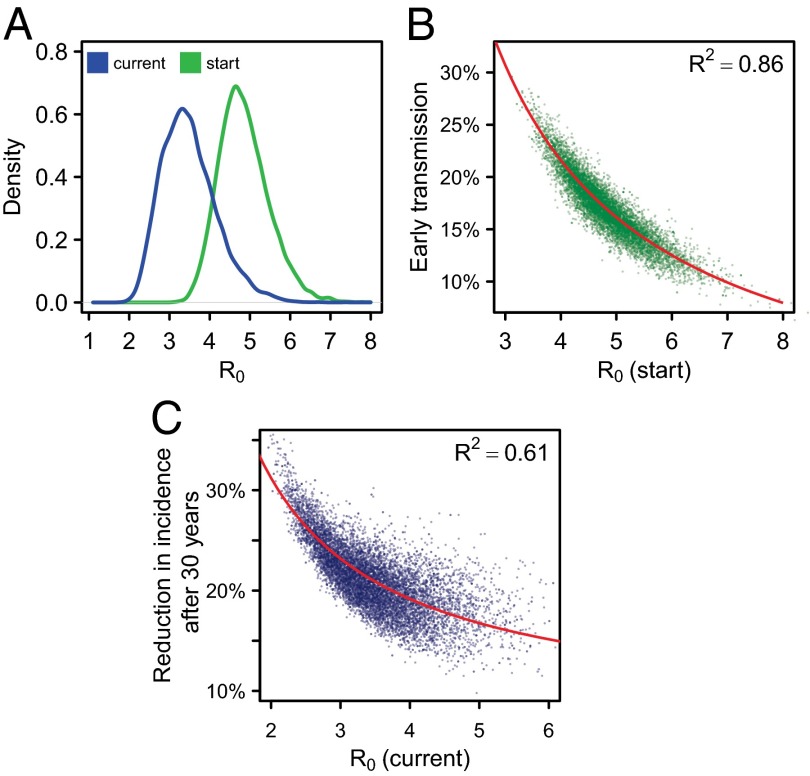
We calculated the basic reproductive number (R₀; the average number of new infections that one infected individual would create in a wholly susceptible population) over the course of the epidemic. The posterior mean for R₀ at the start of the epidemic was 4.9 (95% CI, 3.8–6.2) (Fig. 4A). After the estimated reduction in contact rate, R₀ during the intervention period was 3.5 (2.4–5.0).

Fig. 4.

R₀, early transmission, and reduction in incidence. (A) The distribution of R₀ at the start of the epidemic (green) and during the intervention period (blue), after behavior change. (B) The relationship between R₀ at the start of the epidemic and the percentage of early transmission in 2010, at the start of the intervention. (C) The relationship between R₀ during the intervention period and the reduction in HIV incidence rate after 30 y. Red lines indicate the fitted linear relationship between 1/R₀ and early transmission (B) or reduction in incidence rate (C).

There was a strong negative relationship between the initial R₀ and early transmission in 2010 (Fig. 4B) (9, 18). Eighty-six percent of the variation in the proportion of early transmission is explained by the reciprocal of R₀ (1/R₀; red line in Fig. 4B). This was because when there is more early transmission, on average onward transmissions occur sooner after an individual becomes infected—that is, the “generation time” is shorter. With shorter generation times, the observed rapid epidemic growth rate in HIV prevalence may be achieved with lower values of R₀ (18, 35).

The variation in R₀ at the start of the epidemic is explained predominantly by two parameters—the relative infectiousness during early infection and the rate of risk group movement—which jointly accounted for 92% of the variation (Fig. S2B). The reduction in the contact rate also is an important determinant of R₀ during the intervention period, and together those three parameters accounted for 95% of the variation in R₀ during the intervention period (Fig. S2C).

The lack of association between the proportion of early transmission and the long-term reduction in HIV incidence due to ART therefore may be understood with reference to R₀. If a larger fraction of transmission occurs during early transmission—before individuals receive ART, limiting the impact of ART—then it also will be true that R₀ is lower, which means any intervention may have a greater long-term impact on incidence (Fig. 4C) (36). These two opposing influences appear to counterbalance each other, resulting in the lack of association between early transmission and the long-term impact of treatment interventions on incidence (Fig. 3).

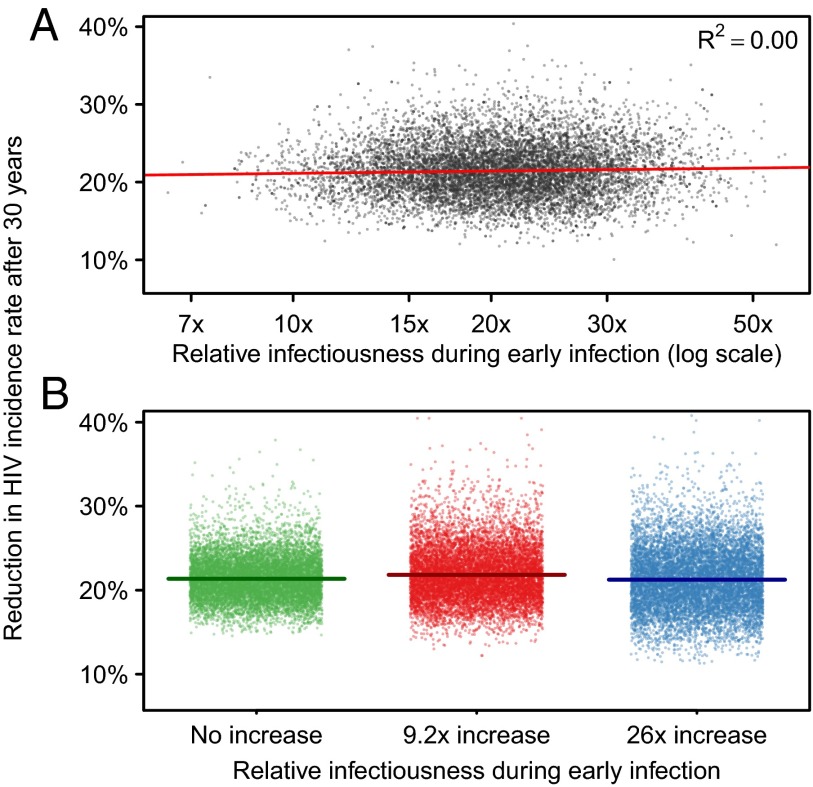
The Influence of Elevated Infectiousness During Early Infection.

The extent to which individuals in early infection are more infectious is highly uncertain. However, we observe no relationship between the parameter determining the increased infectiousness during early infection and the long-term impact on HIV incidence of treatment interventions. (R² = 0%; Fig. 5A). In a secondary analysis, we calibrated model parameters conditional on fixed values of the relative early infectiousness, assuming that persons in early infection were (i) 26 times more infectious (21), (ii) 9.2 times more infectious (37); and (iii) had the same average infectiousness (as assumed by ref. 5) compared with persons with CD4 >350 cells/μL (calibration, Fig. S4; posterior distributions, Fig. S5). These different fixed levels for relative early infectiousness did not affect the impact of the ART intervention on reducing incidence after 30 y (Fig. 5B). The reason is the same as above: higher relative infectiousness resulted in more early transmission in the model and therefore lower R₀ values after calibration to observed epidemic data (Table 1).

Fig. 5.

The relationship between relative infectiousness during early infection and the reduction in HIV incidence rate after 30 y. (A) Results based on sample from posterior distribution of relative infectiousness parameter. (B) Results from calibration of sexual behavior parameters conditional on fixed value of relative infectiousness. In B, horizontal lines represent posterior mean.

Table 1.

Estimates of early transmission, R₀, and intervention impact for fixed values for increased infectiousness during early infection

		R0
Relative infectiousness during early infection	Transmission during early infection when ART is introduced (2010), %	At epidemic start	During intervention period (after behavior change)	Reduction in HIV incidence rate after 31 y from an ART intervention (CD4 ≤350), %
No increase	1.9 (1.3–2.6)	8.2 (6.7–10.5)	4.1 (2.8–6.1)	21.4 (16.9–26.9)
9.2 times	11.4 (8.4–14.5)	5.8 (4.7–7.3)	3.6 (2.5–5.2)	21.8 (16.5–29.0)
26 times	18.8 (14.9–23.3)	4.6 (3.8–5.7)	3.5 (2.4–4.9)	21.2 (14.6–28.9)

Values in parentheses indicate 95% credible intervals.

Discussion

The share of HIV transmission during early infection and the implications for epidemic control have attracted substantial empirical and theoretical attention. Examining these issues within a flexible mathematical model of a heterosexual HIV transmission and calibrating this to the growth, peak, and decline of a well-documented HIV epidemic have illuminated several important concepts.

First, the fraction of transmission during early infection should be considered a quantity that emerges from a complex interaction of behavioral and biological factors rather than a fixed epidemiological characteristic of a given epidemic setting (38). This quantity changes with epidemic stage, epidemiological context, and the stage of the HIV treatment scale-up. Empirical measurement and comparisons of the contribution of early transmission over time and across epidemic settings must be interpreted with these factors in mind.

Second, over the short term, the model predicted that more early transmission would be associated with a smaller reduction in incidence rate following the scale-up of an intervention. Thus, the proportion of new infections arising from early infection may be useful in interpreting the results of community-based trials of treatment, which will measure impact on cumulative incidence over a 2–3-y period.

Third, the proportion of transmission occurring during early infection is surprisingly not predictive of the long-term impact of treatment interventions in model simulations. This is because, through calibration to observed data, epidemiologic parameters that created a larger amount of transmission in early infection also generated lower values of R₀. Lower values of R₀ mean that the same intervention may have a larger impact. This counterbalances the effect that more transmission in early infection interventions weakens interventions that block transmission during chronic infection.

This analysis has focused on whether the proportion of early transmission during the current endemic stage is predictive of the short- and long-term impact of a given intervention strategy in a generalized, predominantly heterosexually transmitted HIV epidemic setting. It did not evaluate what level of intervention would be required to eliminate HIV using treatment, and so our results are not directly comparable to studies that have evaluated thresholds for HIV elimination using ART [e.g., Granich et al. (5), Powers et al. (17), Hontelez et al. (8), Kretzschmar et al. (9)]. The results also may not apply to different epidemiological contexts; for example, concentrated epidemic settings in which transmission occurs primarily among men who have sex with men or persons who inject drugs. In reality, HIV incidence trends during the ART era will depend on many other factors, including changes in risk behavior (39, 40). The abstract representation of sexual risk, mixing, behavior change, and future epidemiologic changes may limit the usefulness of this model for projecting specific intervention impacts and allocating resources in specific settings compared with other models with detailed demographic, spatial, and risk group structures.

Finally, although it is unknown by how much transmission is elevated during early infection, this does not materially add to uncertainty about the impact of treatment on incidence. Uncertainties about other factors (especially sexual behavior and mixing) mean that the observed epidemic may be “explained” in many ways whatever the value for the increased level of infectiousness. It is this latitude that drives uncertainty in estimates. Therefore, further measurement of infectiousness during early-stage infection would not be a priority from the perspective of informing projections of the long-term impact of treatment.

Previous work illustrated how different patterns of heterogeneity in sexual mixing and assumptions about changes in individual risk behavior may give rise to very different endemic prevalence for the same average contact rates or biological assumptions about infectiousness (24, 25, 27, 41–43). This analysis considers similar ideas from a different angle; it treated the prevalence as known and explored consistent combinations of behavioral and biological parameters. Two behavioral parameters—the rate of transition from higher- to lower-risk groups and the population-level reduction in unprotected contact rate over time—were particularly important for simulating the observed prevalence trend in many different ways, as well as determining the intervention impact. There is evidence that reductions in risk have contributed to changes in HIV both in South Africa (8, 33) and elsewhere (32, 44, 45). The value of R₀ during the intervention period was much more predictive of the reduction in incidence than R₀ at the start of the epidemic (Fig. 4). This finding suggests that models that appeal solely to estimates of R₀ based on initial epidemic growth rate to estimate intervention impact or consider only uncertainty about biological determinants of transmission, without accounting for any changes in behaviors required to explain the peak and stabilization of the epidemic, may not provide robust insights about the likely impact of HIV prevention programs today, including ART.

On the other hand, the influence of calibrating the model to the historical epidemic data for identifying plausible combinations of parameter values that were used for projecting the long-term consequences of the intervention suggests that predictions based on models that simulate a plausible current epidemic level but do not simulate a credible epidemic growth (24, 25, 46, 47) should be treated with caution. It is not feasible to measure R₀ directly in an endemic HIV setting, but continued surveillance of all the factors that determine R₀—biological and behavioral determinants of transmission—will be critical for understanding and projecting the implications of control strategies, rather than relying on a single metric, such as the proportion of early transmission.

Conclusion

Modeling illustrated that a large fraction of transmission during early infection resulted in a smaller impact of treatment on HIV incidence in the first few years after the intervention was introduced. However, neither the proportion of early transmission nor the biological level of increased infectiousness was independently predictive of the long-term impact of treatment interventions. Both the long-term intervention impact and the amount of early transmission are dictated by the fundamental drivers of transmission—risk behaviors in the population and how they interact with the pathogen to determine R₀.

Materials and Methods

We developed a mathematical model of heterosexual HIV transmission in a two-sex population by using ordinary differential equations. The model incorporates heterosexual mixing between three sexual risk groups, a realistic representation of the natural history of HIV progression and infectiousness, and the effect of ART on survival and HIV infectiousness. Individuals may move among sexual risk groups, and sexual behavior may change over the course of the epidemic.

The model was calibrated to data about HIV prevalence and ART scale-up in South Africa by varying parameters controlling sexual behavior and infectiousness during early infection in a Bayesian statistical framework. This results in parameter combinations representing different underlying patterns of sexual behavior that are consistent with the observed HIV epidemic, allowing us to investigate how uncertainties about model parameters affect the impact of HIV treatment interventions. Full details and model equations are available in SI Appendix.

Mathematical Model.

Population structure and sexual mixing.

The model simulates a two-sex adult population aged 15 and older (Fig. S6). The population was divided into two age groups: 15–49, presumed to be a sexually active age group, and 50 and older, assumed not to form new sexual contacts but to possibly receive ART. Individuals enter the 15–49 population at a rate α = 0.0226 per year, move to the 50+ age group at a rate ν = 1/35 per year, and experience natural mortality from the age 50+ population at a rate μ = 1/11.45 per year, calibrated to match the composition of the South African population in 1990 and growth over time between 1990–2010 (48).

The sexually active population was divided into three sexual risk groups (termed “low,” “medium,” and “high”). As a crude means of simulating variability in sexual behavior over the life course, individuals may move from higher- to lower-risk groups at an annual rate ψ. Each sexual risk group has a different rate of forming new sexual contacts. A proportion of sexual contacts is reserved to be formed within the same sexual risk group according to an “assortativity” parameter $\epsilon \in (0.2,\hspace{0.17em}0.8)$, and the remaining $1-\epsilon$ proportion of partnerships is formed randomly across the risk groups (49). The sexual contact rate in each risk group changed over time according to the logistic function

$$c_{g,r}\left(t\right)=c_{g,r}\left(0\right)\cdot \left(1-{\mathrm{\Delta }}_c\right)+c_{g,r}\left(0\right)\cdot {\mathrm{\Delta }}_c\cdot \frac{1}{1+exp\left(\frac{t-(t_c+d_c/2)}{d_c/10}\right)},$$

where $c_{g,r}\left(t\right)$ is the contact rate for sex $g$ and risk group $r$ at time $t$, $c_{g,r}\left(0\right)$ is the contact rate at the start of the epidemic, ${\mathrm{\Delta }}_c$ is the overall proportion reduction in contact rate, $t_c$ is the time behavior change begins, and $d_c$ is the duration over which it occurs (Fig. S7). The rate of HIV transmission for contacts between susceptible and infected persons depends on the stage of HIV infection and ART status of the infected partner (see below) and partnership intensity parameter depending on the risk group of each partner. The proportion in each risk group, rate of movement among risk groups, relative contact rates, partnership intensity, and change in contact rate over time were varied in the model calibration.

HIV progression and infectiousness.

HIV infection was divided into fives stages (Fig. S8): early infection (mean 2.9 mo), CD4 >350 cells/μL (4.56 y), CD4 200–350 cells/μL (4.60 y), CD4 100–200 cells/μL (4.17 y), and CD4 ≤100 cells/μL (1.03 y to HIV death) (21, 50). Individuals progressed sequentially through these five stages before experiencing HIV mortality. The baseline HIV transmission rates per 100 person-years for the last four CD4 count stages are 4.4 (CD4 >350), 7.2 (CD4 200–350), 27.1 (CD4 100–200), and 5.1 (CD4 ≤100) (2). For early infection, we defined a lognormal prior distribution for the relative infectiousness during early infection compared with CD4 >350, with a mean of 26.0 times greater infectiousness and 95% prior mass between 12.6 and 47.8 (21).

ART model.

Individuals may initiate ART from any stage of HIV infection. ART is divided into a multistage process (Fig. S9). Upon initiation, all individuals enter a “virally suppressing” stage during which the viral load is not yet fully suppressed [mean of 3 mo (51)]. Infectiousness was assumed to be reduced by half during this stage compared with the CD4 stage from which treatment was initiated (Table S1). Following this stage, a proportion (0.189 for CD4 ≤100, 0.067 for CD4 100–200, 0.025 for CD4 200–350, 0.0 for CD4 >350) moves to a “very sick” stage lasting for a mean of 6.2 mo before death, reflecting elevated early mortality for patients starting treatment with low CD4 cell counts (52). The remainder of patients enter a long period of “effective ART,” during which infectiousness is reduced by 92% compared with untreated individuals with CD4 between 200 and 350 cell/μL (2). Individuals fail treatment (rate 0.03 per year for baseline CD4 ≤200, 0.026 for CD4 200–350, 0.022 for CD4 >350) and enter a viremic stage in which they have the same infectiousness as persons with CD4 100–200 (mean 2.3 y), followed by a very sick stage before HIV death (mean 6.2 mo).

Persons on ART drop out at a rate of 0.12–0.168 per year, increasing with CD4 count at initiation (53) (Table S2), during the first 2 y and a rate of 0.088 thereafter (54). After dropping out from treatment, persons reenter a CD4 stage at or above that at which they initiated treatment, depending on their duration on treatment (Table S3), but progress at twice the rate of a treatment-naïve person. They may reinitiate treatment once. See SI Appendix, section 1.5 for further details.

Statistical Methods.

Data and likelihood.

The model was calibrated to national HIV prevalence data among pregnant women attending antenatal care (ANC) from 1990 through 2008 (34), and HIV prevalence among men and women aged 15–49 y was estimated in nationally representative household surveys in 2002, 2005, and 2008 (55–57) (Fig. 1A). Prevalence from the household surveys was assumed to be an unbiased estimate of true HIV prevalence for adult men and women. The difference between prevalence in women attending ANC and the general female population was described by an antenatal-bias parameter $\gamma$ assumed to be constant over time on the logit scale, that is

$$E\left(\text{logit}\left({\zeta }_{A,t}\right)\right)=\text{logit}\left({\zeta }_{F,t}\right)+\gamma ,$$

where ${\zeta }_{F,t}$ is the HIV prevalence among all women aged 15–49 y at time $t$ and ${\zeta }_{A,t}$ is the prevalence among women attending ANC. The likelihood was specified as a normal distribution around the logit-transformed prevalence estimates with the error variance estimated by the survey SE, accounting for the complex survey design of the ANC and household seroprevalence surveys (58).

The influence of the existing ART scale-up in South Africa on prevalence and incidence was incorporated in the model calibration by simulating the percentage of adults (age 15+ years) on ART at midyear from 2005 through 2010 reported by the South African Department of Health (59) (Fig. S10). During this period, persons with CD4 ≤200 cells/μL were eligible to initiate ART. In the model calibration, persons with CD4 ≤100 cells/μL initiated ART at a rate eight times higher than those with CD4 100–200 cells/μL, and women initiated ART at rate 1.8 times higher than men to capture the median CD4 count and sex differential observed in patients initiating ART (60).

Estimated model parameters and prior distributions.

Seventeen model parameters and the ANC bias parameter $\gamma$ were estimated in the model calibration. Parameters related to the natural history of infection, the effects of ART, and demographics were fixed based on values from the literature as described above (Table S4). Parameters determining sexual behavior and sexual mixing, which are not easily relatable to directly observed measures, were estimated (Table S5). Estimated model parameters included the increased infectiousness during early infection relative to persons with CD4 >350 cells per μL, proportion in each sexual risk group, mean sexual contact rate and relative contact rates for each risk group, degree of assortativity, rate of movement among risk groups, partnership transmission intensities, and start time of the epidemic (Table S5). The prior distribution for the relative infectiousness during early infection was lognormal (3.2, 0.34), resulting in a prior mean of 26.0 times increased infectiousness and 95% of the prior mass between 12.6 and 47.8, based on ref. 21. The assortativity parameter determining the proportion of partnerships formed exclusively within the same sexual risk group was restricted to between 0.2 and 0.8. The joint posterior distribution was estimated by using an incremental mixture importance sample (61). See SI Appendix, section 3.3 for further details; Fig. S1 for the marginal prior and posterior distributions of all parameters; and Table S6 for bivariate correlations between parameters in the posterior distribution.

R₀ Calculation.

We calculated R₀(t) as the spectral radius of the next-generation matrix at time t (62). The next-generation matrix was calculated for a given set of parameter values by using the formalism described for compartmental systems in ref. 63, following which eigenvalues were solved numerically. Because the only time-varying parameter is the change in contact rate $c_{g,r}\left(t\right)$ (described above), the value of R₀ during the intervention period, after behavior change has occurred, may be expressed as R₀ at the start of the epidemic scaled by the proportion reduction in contact rate ${\mathrm{\Delta }}_c$ (see SI Appendix for details):

$${\text{R}}_0^{interv.}={\text{R}}_0^{start}\cdot (1-{\mathrm{\Delta }}_c).$$

The mathematical model was implemented in C++, and statistical calibration was implemented in C by using the GNU Scientific Library (64). Intervention analyses were conducted using R (65). Computer code to reproduce parameter estimation and model analyses is available for download from github.com/jeffeaton/tasp-and-early-infection.