Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2012 Jun 13;32(24):8424–8428. doi: 10.1523/JNEUROSCI.0804-12.2012

Temporal Expectation Improves the Quality of Sensory Information

Gustavo Rohenkohl 1,2,*,✉, André M Cravo 1,2,*, Valentin Wyart 1,2,*, Anna C Nobre 1,2,✉
PMCID: PMC4235252  EMSID: EMS48812  PMID: 22699922

Abstract

It is increasingly clear that we extract patterns of temporal regularity between events to optimize information processing. Whereas some of the mechanisms for facilitating action preparation and execution have been well documented, much less is understood about whether and how temporal expectations influence visual perception. We used a psychophysical paradigm and computational modeling to investigate the mechanisms by which temporal expectation can modulate visual perception. Visual targets appeared in a stream of noise-patches separated by a fixed (400 ms regular condition) or jittered (200/300/400/500/600 ms irregular condition) intervals. Targets were visual gratings tilted 45° clockwise or counter-clockwise, presented at one of seven contrast levels. Human observers were required to perform an orientation discrimination (i.e., left or right). Psychometric functions for contrast sensitivity fitted for the regular and irregular conditions indicated that temporal expectation modulates perceptual processing by enhancing the contrast sensitivity of visual targets. This increase in the signal strength was accompanied by a reduction in reaction times. A diffusion model indicated that rhythmic temporal expectation enhanced the signal-to-noise gain of the sensory evidence upon which decisions were made. These effects support the idea that temporal structure of external events can entrain the attentional focus and psychophysical data, optimizing the processing of relevant sensory information.

Introduction

Our sensory system is consistently being exposed to a rich and rapidly changing scenery. To cope with the overwhelming amount of stimulation, we constantly generate and update expectations about relevant events likely to occur. It is increasingly recognized that anticipatory biases are not restricted to signals about object features and locations, but also extend to the temporal domain. The ability to extract temporal patterns and regularity of events has long been known to improve action preparation and execution (Nobre et al., 2007). However, the effects of temporal expectation on visual perception are not well established, and little is known about how expecting a stimulus in time can enhance its perceptual processing (for discussion, see Nobre et al., 2012).

Traditionally, tasks investigating temporal expectations have tended to emphasize reaction times, not allowing the investigation of the specific psychophysical parameters that may be affected. However, a small number of studies have suggested that fixed temporal intervals between stimuli can lower thresholds for detecting their visual features (Lasley and Cohn, 1981; Westheimer and Ley, 1996) and that temporal cueing can improve stimulus discrimination (Correa et al., 2005). Modulation of early visual potentials (P1) has also been observed when targets appear with high temporal and spatial expectation (Doherty et al., 2005; Rohenkohl and Nobre, 2011), and recordings in animals have shown enhancement of neuronal activity by temporal expectations in visual areas V1 (Shuler and Bear, 2006; Lima et al., 2011), V4 (Ghose and Maunsell, 2002), MT (Ghose and Bearl, 2010), and IT (Anderson and Sheinberg, 2008). Together, these studies suggest that temporal expectations may enhance visual perceptual functions, but leave open the nature of the mediating mechanisms.

Regular, rhythmic stimulation has been shown to induce strong temporal expectation, facilitating processing of events occurring at the predicted beat (Schroeder and Lakatos, 2009; Jones, 2010; Mathewson et al., 2010). Schroeder and colleagues (Lakatos et al., 2008, 2009; Besle et al., 2011) have shown that oscillatory activity in primary perceptual areas (e.g., V1 and A1) becomes entrained to the temporal pattern of relevant events, so that cortical excitability is maximized at predicted moments of subsequent rhythmic events. These findings suggest that temporal expectation—at least when induced by rhythmic patterns—can directly modulate perceptual excitability and influence early visual psychophysical functions. Given the common occurrence of rhythmic streams in the natural environment (Schroeder and Lakatos, 2009), neural entrainment to temporal structures of events could be a central mechanism for attentional biasing.

In the present study, we used rhythmic stimulation as a strong and natural manipulation of temporal expectation combined with parametric variation of the stimulus signal and computational modeling to test how psychophysical functions are modified. Results from behavioral data and computational modeling converge to show that rhythmic temporal expectation enhances visual sensitivity by increasing signal contrast.

Materials and Methods

Participants.

Thirteen right-handed individuals participated in this experiment [mean age, 26.23 years (SD, 3.58 years); 7 females]. Visual acuity was normal or corrected-to-normal. All experimental methods had ethical approval from the Central University Research Ethics Committee of the University of Oxford.

Apparatus.

Stimuli were created on MATLAB v.7.10 (MathWorks) and presented using the Psychtoolbox v.3.0 package for MATLAB (Kleiner et al., 2007). Images were displayed on a 21-inch CRT (CTX Ultra Screen) with a spatial resolution of 1024 by 768 pixels and a vertical refresh rate of 60 Hz, placed 100 cm in front of the participant. A chin rest was used to maintain a constant viewing distance and head position. Responses were collected via a response box (DirectIN High Speed Button; Empirisoft).

Stimuli and task.

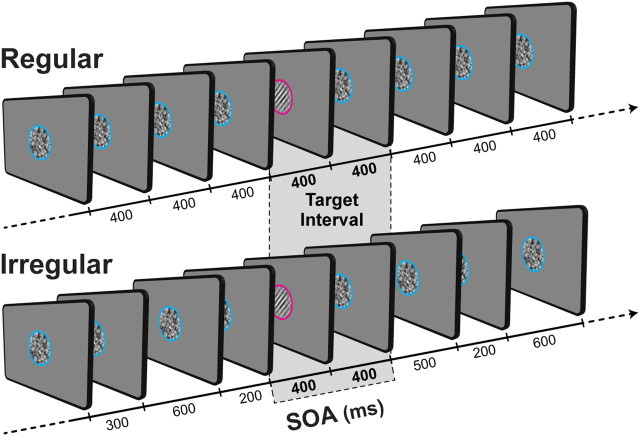
Figure 1 provides a task schematic. Each trial consisted of a stream of 140 foveally presented stimuli (14 targets and 126 standards) with a duration of 50 ms. Stimuli were circular patches (diameter: 4° of visual angle). The standards consisted only of Gaussian noise patches, while targets contained Gabor patches embedded within the noise. Gabor patches were tilted ±45° and their spatial frequency was 2 cycles per degree of visual angle.

Figure 1.

Figure 1.

Open in a new tab

Schematic illustration of the task structure. Each trial consisted of a stream of stimuli presented foveally either with a fixed (regular condition) or jittered (irregular condition) SOA. Notice that the intervals surrounding the targets were exactly the same for the regular and irregular condition. The targets were visual gratings (Gabors) tilted 45° clockwise or counter-clockwise and presented at seven contrast levels to yield a range of performance levels spanning from near chance to near perfect. Participants were asked to respond to the orientation of the target (i.e., left or right) whenever a target was presented. Target presentation was always indicated by a change in the placeholder color to prevent responses to standard stimuli.

Noise stimuli were created by smoothing a pixel-by-pixel Gaussian noise patch using a two-dimensional kernel. The smoothing dimension (0.083°of visual angle) and the root-mean-square contrast of the noise (10%) were fixed across participants and stimuli. Targets were inserted within the stimulus stream in a pseudorandomized order, with 5 to 14 seconds between each target. Task difficulty was adjusted for each participant by titrating the contrast of the Gabor so that orientation discrimination was performed at 75% accuracy. Seven levels of contrast were chosen for target presentation, ranging from −0.3 to +0.3 (in steps of 0.1) on a logarithmic scale, with 0 being the level representing 75% accuracy. Since a large number of targets were presented with a contrast lower than the threshold, isoluminant circles (pink and blue) positioned around the patches signaled the presentation of target versus standard stimuli, thus reducing the number of false alarms.

Temporal expectation was manipulated by varying the regularity of the stimuli-onset asynchrony (SOA) between successive events in a trial. In regular trials, the SOA was fixed at 400 ms, allowing participants to use the temporal regularity of the stimulation to reduce the uncertainty about when stimuli would appear. In irregular trials, the SOA was jittered. Intervals were drawn randomly from 200, 300, 400, 500, and 600 ms. By jittering the SOAs, the trial had an arrhythmic beat, preventing focused temporal expectations about stimulus appearance. Importantly, the intervals immediately preceding and succeeding each target was the same and always fixed in regular and irregular trials (400 ms). This control was introduced to avoid any possible confound related to foreperiod or masking effects caused by the proximity of the standards surrounding the target.

Procedures.

Each participant underwent a calibration session before the experiment using an adaptive psychophysical staircase procedure to estimate the threshold contrast (75% accuracy) for perceiving the Gabor gratings (Kaernbach, 1991). Since we hypothesized that contrast sensitivity should be enhanced by temporal expectations, the calibration was performed on 12 irregular trials. Therefore, any enhancement in contrast sensitivity could not be explained merely by learning effects.

After the calibration session, participants performed 50 trials (25 regular and 25 irregular) presented in a randomized order. Participants were presented with a total of 700 targets (50 at each contrast level within each of the regular and irregular conditions). They were instructed to respond to the orientation of each target with their left or right index finger according to the target orientation. Participants were prompted to respond to targets indicated by the placeholder, even when contrast levels were below their threshold level. The experiment lasted ∼1 h.

The psychometric data from each participant and condition were fitted with sigmoidal Weibull functions, each defined by three parameters: threshold α, slope β, and fixed lapse-rate γ (Wichmann and Hill, 2001). Guess rates were fixed at 0.5 (i.e., chance level) across all subjects and conditions, and the three parameters were fitted separately for each subject and condition (regular or irregular). Threshold was taken as the predicted contrast level corresponding to 75% accuracy. To test for the effect of temporal expectation on target discrimination, fitted threshold and slope values for each participant were submitted to paired t tests. Quality of fit for each subject was assessed by correlating predicted values from the best fitting psychometric function with observed accuracy (mean r-square for group = 0.92, SEM = 0.015; lowest individual r-square = 0.79). The analysis of the psychometric function was performed using the Palamedes toolbox for MATLAB (Prins and Kingdom, 2009).

The diffusion model (Palmer et al., 2005) predicts that the psychometric function for accuracy PC(x) and the chronometric function for the mean response time tT(x) are functions of stimulus strength x according to the two following equations:

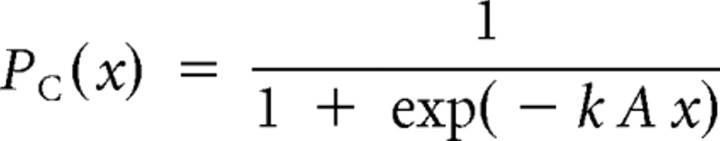graphic file with name zns02412-2069-m01.jpg
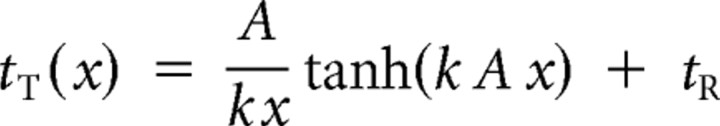graphic file with name zns02412-2069-m02.jpg

where k corresponds to the normalized accumulation rate, A to the normalized decision bound, and tR to the residual time constant. Stimulus strength x follows signal contrast c following a power law whose exponent—which controls the overall slope of both psychometric and chronometric functions as a function of signal contrast—was determined empirically by maximum-likelihood estimation (see below, best-fitting value = 1.97) and fixed across all subjects and conditions.

We performed constrained maximum-likelihood estimation to recover the best-fitting parameter changes for explaining the effect of temporal expectation (i.e., the difference between regular and irregular conditions) on the group-level psychometric and chronometric functions. We used group-level means and standard errors to estimate log-likelihood sums for different sets of parameters, and likelihood-ratio tests to compare between nested models. Finally, we computed the model predictions for the effect of temporal expectation on psychophysical threshold using paired t tests that the observed effect did not differ significantly from model-predicted effects.

Results

Signal enhancement induced by temporal expectation

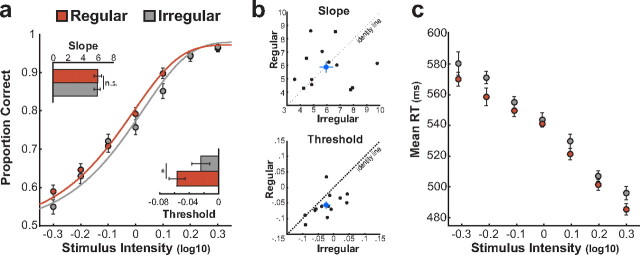
Figure 2a shows the mean psychometric functions in regular and irregular conditions. As expected, performance increased as a function of target contrast in both conditions. Temporal expectation was accompanied by a reduction in threshold (t(12) = 2.95, p = 0.01), but not slope (t(12) = 0.12, p > 0.9) values, indicating that the participants needed less contrast for accurate performance. Figure 2b shows that the vast majority of participants had lower thresholds in regular compared with irregular conditions.

Figure 2.

Figure 2.

Open in a new tab

Behavioral consequences of rhythmic temporal expectation. a, Psychometric functions describing performance on regular (red line) and irregular (gray line) temporal expectation conditions as a function of target contrast. Bar plots show the average values of slope and threshold in the regular and irregular conditions. b, Scatterplots showing the effect of temporal expectation on slope and threshold values for each participant. Blue dots indicate the group average. Points below the identity line indicate a gain effect of temporal expectation. c, Average reaction times for correct responses from the regular and irregular conditions as a function of target contrast. Error bars indicate SEM.

Target discriminability was also measured by means of d ′ (Green and Swets, 1966). The data were submitted to a repeated-measures ANOVA with Temporal Expectation (regular, irregular) and Target Contrast (seven levels) as factors. As expected, this analysis revealed a significant main effect of Target Contrast (F(3.54,42.53) = 139.74; p < 0.001), with higher discriminability for targets with a higher contrast. Additionally, we observed a main effect of Temporal Expectation (F(1,12) = 7.17; p = 0.02) showing larger d ′ for targets in the regular (mean = 1.45, SE = 0.26) than the irregular (mean = 1.35, SE = 0.27) condition. The interaction between the factors was not significant (F(4.11,49.35) = 1.33; p > 0.2).

Effects on reaction time

We compared participants' reaction times (RTs) to targets presented in the regular and irregular conditions. RTs for correct responses from the two conditions (Fig. 2c) were submitted to a repeated-measures ANOVA with Temporal Expectation and Target Contrast as factors. We found a significant main effect of Target Contrast (F(2.26,27.07) = 63.88; p < 0.001), with shorter RTs for targets with a higher contrast. RTs were also shorter for targets in regular versus irregular condition (F(1,12) = 12.41; p < 0.01). The interaction between the factors was not significant (F(3.59,43.09) = 0.40; p > 0.7).

Diffusion model

To determine the component(s) of information processing responsible for the concurrent increase in target discriminability and reaction speed observed between regular and irregular conditions, we fitted simultaneously the group-level psychometric (relationship between target contrast and discriminability) and chronometric (relationship between target contrast and reaction speed) functions using a diffusion model of the decision process (Palmer et al., 2005).

Briefly, this model proposes that simple perceptual decisions, such as the left- versus right-tilt discrimination used in our experiment, are based on the gradual accumulation of noisy sensory evidence favoring either interpretation at an accumulation rate k until a signed decision bound ±A is reached (e.g., +A for a left-tilt decision, or −A for a right-tilt decision). The reaction time for each decision taken by the model corresponds to the decision time required to reach either of the decision bounds. A residual time constant, tR, is also added to account for other nondecision processes such as sensory and motor encoding latencies, whose variability is assumed to be much smaller than the variability in decision time (Ratcliff and Smith, 2004). In this implementation of the diffusion model, the accumulation rate k is defined in signal-to-noise units, so that an increase in k corresponds to a more precise representation of the relevant evidence/signal (here, the tilt of the noisy target). Importantly, k is not merely an amplification of both signal plus noise, which would not change the overall signal-to-noise ratio, but a selective amplification of the signal component. In contrast, a change in A corresponds to a change in the speed–accuracy trade-off (Palmer et al., 2005), without any change in the quality of the relevant evidence.

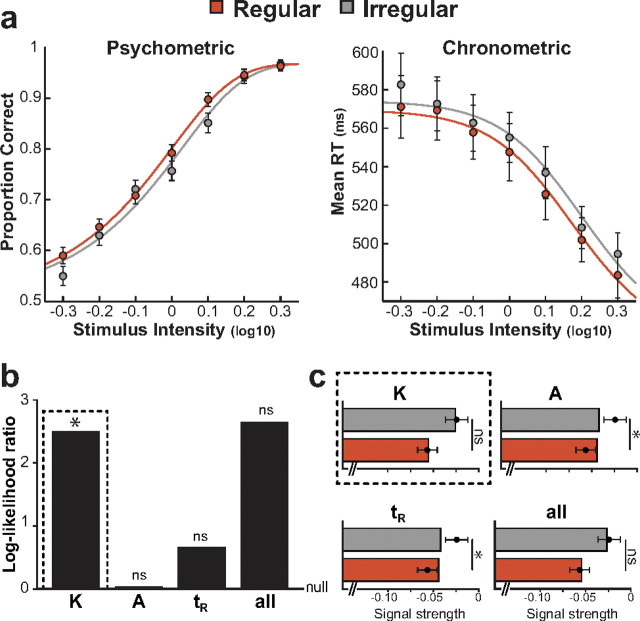
As a first step, we fitted separately, using maximum-likelihood estimation (see Materials and Methods, above), the regular and irregular conditions using the diffusion model with three free parameters for each fit: the accumulation rate k, the decision-bound A, and the residual time constant tR (Fig. 3a). Each set of three parameters was sufficient to describe accurately the group-level psychometric and chronometric functions at the tested target contrasts.

Figure 3.

Figure 3.

Open in a new tab

Comparison between behavioral results and diffusion-model predictions. a, Fitted diffusion model to psychometric and chronometric functions at the target contrasts. All three free parameters were fitted separately for the regular (red) and irregular (gray) conditions using maximum-likelihood estimation. b, Hierarchical model comparing tests between nested models to determine which of the three model parameters (the accumulation rate k, the decision-bound A, and the residual time constant tR) could explain the observed difference between regular and irregular conditions significantly better than a null model for which the three parameters had fixed values across the two conditions. c, Comparison of changes in threshold predicted by each model with the behavioral data. *p < 0.05; ns, nonsignificant effect.

We then asked what subset of these three parameters was best able to explain the effect of temporal expectation (i.e., the difference between regular and irregular conditions) on psychometric and chronometric functions. We used hierarchical model comparison via log-likelihood ratio tests between nested models (see Materials and Methods, above) to determine which of the three model parameters (the accumulation rate k, the decision-bound A, or the residual time constant tR) could explain the observed difference between regular and irregular conditions significantly better than a null model for which the three parameters had fixed values across the two conditions (Fig. 3b). To do so, we fitted simultaneously the regular and irregular conditions using three candidate models with four best-fitting parameter values: two parameters with fixed values across the two conditions, and one parameter allowed to take different values in the two conditions.

An increase in the accumulation rate k explained the observed difference between regular and irregular conditions significantly better than the null model [log-likelihood ratio test (LLR) = 2.51, p = 0.02], whereas changes in either the decision-bound A (LLR = 0.04, p > 0.5) or the residual time constant tR (LLR = 0.67, p > 0.2) were no better than the null model given their extra free parameter. Importantly, the model allowing for all three parameters to change between regular and irregular conditions was also not better than the null model (LLR = 2.64, p = 0.15) given its three extra free parameters. In conclusion, only an increase in the accumulation rate k was able to explain the concurrent effects of temporal expectation on psychometric and chronometric functions.

Finally, we sought to confirm this effect by comparing the changes in threshold predicted by each model with our experimental data (Fig. 3c). To do so, we determined the threshold difference predicted by models allowing for a change either in accumulation rate k, decision-bound A, or residual time constant tR between regular and irregular conditions. We then compared the predicted difference with the group-level results. Consistent with previous analyses, we found that changes in decision-bound A or in residual time constant tR elicited results that are significantly different from our findings (t test between data and model prediction, decision bound: t(12) = 2.8, p = 0.01; residual time constant: t(12) = 2.9, p = 0.01). Changes in accumulation rate k elicited results that were consistent with our results (t(12) = 0.2, p > 0.5). Together, these analyses confirm that only an increased accumulation rate can explain the observed effect of temporal expectation on the speed and accuracy of perceptual decisions.

Discussion

In the present study, we have shown that temporal expectation can modulate the perception of relevant events by an increase of signal contrast. Importantly, we found that this increase in the psychophysical sensitivity was accompanied by a reduction in reaction times. A simple diffusion model indicated that temporal expectation changed the signal-to-noise gain of the sensory evidence upon which decisions were made. Together, our findings support the idea that the entrainment of attentional focus to the temporal structure of external events acts as a central mechanism for the perceptual modulation of relevant sensory information.

Previous studies have also suggested that temporal expectation can improve the detection and discrimination of visual targets (Lasley and Cohn, 1981; Westheimer and Ley, 1996; Correa et al., 2005; Mathewson et al., 2010). While very important, the design or stimulus parameters of these studies limit their interpretation. Early psychophysical studies manipulating temporal certainty (Lasley and Cohn, 1981; Westheimer and Ley, 1996) used other stimuli as temporal markers and did not isolate temporal expectation from temporal order or control for foreperiod effects. More recent studies showing facilitation of d′ in temporal expectation tasks (Correa et al., 2005; Mathewson et al., 2010) used target stimuli defined by one single set of physical parameters, so that it was not possible to test whether and how the signal-to-noise contrast was affected. Changes in d′ are suggestive of perceptual mechanisms occurring in early sensory cortices, but are also compatible with postperceptual mechanisms, such as better pooling of early sensory responses by higher-level regions (Pestilli et al., 2011). By parametrically varying the contrast levels in our task, we derived the effect of temporal expectation on the full psychometric curve. Results revealed an enhancement in perceptual processing via a contrast gain, suggesting that temporal expectation can affect visual perception by increase the quality of sensory representation.

The output of our diffusion model gives further support to this view. An increase in the normalized accumulation rate k, as found for the effect of temporal expectation on decision making, sets a strong constraint on the type of process that can be influenced by temporal expectation in our task. The observed leftward shift of the psychometric function corresponds to a contrast gain—suggesting that temporal expectations act by increasing the effective contrast of the signal, as if the signal was of higher contrast when embedded in a rhythmic stream of stimuli. The alternative explanation that temporal expectations would act by reducing the amount of decision noise does not predict the observed reduction of reaction times. Also, the effect has to occur in signal-selective visual areas because it corresponds of a selective enhancement of the signal component, not an unselective enhancement of both signal and noise, which would not affect the signal-to-noise accumulation rate k.

In this study, temporal expectation was manipulated by varying the regularity of the rhythmic streams in which targets were presented. Recently, it has been proposed that the entrainment of attention to rhythmic events is a fundamental mechanism of sensory selection (Lakatos et al., 2008; Schroeder and Lakatos, 2009; Jones, 2010). In our study, both behavioral data and modeling indicated that perceptual sensitivity to targets was enhanced when the streams were presented rhythmically, supporting the idea that attention can become entrained to external events to enhance perceptual processing.

We are currently investigating the neural mechanisms supporting perceptual facilitation by rhythmic temporal expectation. Schroeder and colleagues (2010) recently proposed a neural mechanism by which low-frequency oscillatory activity in early perceptual areas becomes entrained to the rhythmic input so that task-relevant events are more likely to occur at time points in which the state of excitability of sensory areas is optimal. It is possible that temporal expectation also affects active visual-sensing mechanisms. Recently, the frequency and direction of small fixational eye movements (i.e., microsaccades) have been associated with fluctuations in performance in perception and attention tasks (for review, see Martinez-Conde et al., 2009). It will be interesting to investigate whether temporal expectation modulates the occurrence of microsaccades. Future studies using appropriate visual stimulation and sensitive eye monitoring will be required to address this important question.

Neurophysiological studies in humans have shown that temporal expectation alone can be insufficient to modulate early visual processes (Doherty et al., 2005; Correa and Nobre, 2008; Rohenkohl and Nobre, 2011). Instead, temporal expectation boosts the effect of spatial attention on early visual potentials. These findings led to the hypothesis that temporal expectation influences early visual processing primarily by timing neurons with other relevant receptive field properties (such as spatial location or stimulus feature) (for review, see Nobre et al., 2012). According to this view, temporal information can be used to tune anticipatory activity in neuronal assemblies that are coding other relevant information about the input. In our study, spatial location was always fixed, allowing an association between temporal and spatial expectations, which led to a behavioral an enhancement on signal sensitivity. However, future studies are necessary to investigate whether temporal expectation alone can still facilitate the perceptual processing of relevant events.

We believe that temporal expectations can influence neural processing in a highly flexible manner, controlling local excitability of selected neural populations already engaged by other task attributes. Therefore, the stage of information processing that can be affected by temporal expectations could be greatly dependent on task goals. Finally, our results provide evidence for the behavioral consequences of findings that have been reported by neurophysiological studies, indicating that temporal expectation can boost the perception of relevant events by modulating early stages of visual processing.

Footnotes

This work was funded by the Wellcome Trust (A.C.N.). A.M.C. was supported by Fundação de Amparo à Pesquisa do Estado de São Paulo and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior. V.W. was supported by the Fyssen Foundation. We thank Mark Stokes, Nicholas Myers, and Ian Gould for helpful discussions.

References

  1. Anderson B, Sheinberg DL. Effects of temporal context and temporal expectancy on neural activity in inferior temporal cortex. Neuropsychologia. 2008;46:947–957. doi: 10.1016/j.neuropsychologia.2007.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Besle J, Schevon CA, Mehta AD, Lakatos P, Goodman RR, McKhann GM, Emerson RG, Schroeder CE. Tuning of the human neocortex to the temporal dynamics of attended events. J Neurosci. 2011;31:3176–3185. doi: 10.1523/JNEUROSCI.4518-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Correa A, Nobre AC. Neural modulation by regularity and passage of time. J Neurophysiol. 2008;100:1649–1655. doi: 10.1152/jn.90656.2008. [DOI] [PubMed] [Google Scholar]
  4. Correa A, Lupiáñez J, Tudela P. Attentional preparation based on temporal expectancy modulates processing at the perceptual level. Psychon Bull Rev. 2005;12:328–334. doi: 10.3758/bf03196380. [DOI] [PubMed] [Google Scholar]
  5. Doherty JR, Rao A, Mesulam MM, Nobre AC. Synergistic effect of combined temporal and spatial expectations on visual attention. J Neurosci. 2005;25:8259–8266. doi: 10.1523/JNEUROSCI.1821-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ghose GM, Bearl DW. Attention directed by expectations enhances receptive fields in cortical area MT. Vision Res. 2010;50:441–451. doi: 10.1016/j.visres.2009.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ghose GM, Maunsell JH. Attentional modulation in visual cortex depends on task timing. Nature. 2002;419:616–620. doi: 10.1038/nature01057. [DOI] [PubMed] [Google Scholar]
  8. Green DM, Swets JA. Signal detection theory and psychophysics. New York: Wiley; 1966. [Google Scholar]
  9. Jones MR. Attenting to sound patterns and the role of entrainment. In: Nobre AC, Coull JT, editors. Attention and time. Oxford: Oxford UP; 2010. pp. 137–330. [Google Scholar]
  10. Kaernbach C. Simple adaptive testing with the weighted up-down method. Percept Psychophys. 1991;49:227–229. doi: 10.3758/bf03214307. [DOI] [PubMed] [Google Scholar]
  11. Kleiner M, Brainard D, Pelli D. “What's new in Psychtoolbox-3?”. Perception 36 ECVP Abstract Supplement. 2007 [Google Scholar]
  12. Lakatos P, Karmos G, Mehta AD, Ulbert I, Schroeder CE. Entrainment of neuronal oscillations as a mechanism of attentional selection. Science. 2008;320:110–113. doi: 10.1126/science.1154735. [DOI] [PubMed] [Google Scholar]
  13. Lakatos P, O'Connell MN, Barczak A, Mills A, Javitt DC, Schroeder CE. The leading sense: supramodal control of neurophysiological context by attention. Neuron. 2009;64:419–430. doi: 10.1016/j.neuron.2009.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Lasley DJ, Cohn T. Detection of a luminance increment: effect of temporal uncertainty. J Opt Soc Am. 1981;71:845–850. doi: 10.1364/josa.71.000845. [DOI] [PubMed] [Google Scholar]
  15. Lima B, Singer W, Neuenschwander S. Gamma responses correlate with temporal expectation in monkey primary visual cortex. J Neurosci. 2011;31:15919–15931. doi: 10.1523/JNEUROSCI.0957-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Martinez-Conde S, Macknik SL, Troncoso XG, Hubel DH. Microsaccades: a neurophysiological analysis. Trends Neurosci. 2009;32:463–475. doi: 10.1016/j.tins.2009.05.006. [DOI] [PubMed] [Google Scholar]
  17. Mathewson KE, Fabiani M, Gratton G, Beck DM, Lleras A. Rescuing stimuli from invisibility: inducing a momentary release from visual masking with pre-target entrainment. Cognition. 2010;115:186–191. doi: 10.1016/j.cognition.2009.11.010. [DOI] [PubMed] [Google Scholar]
  18. Nobre A, Correa A, Coull J. The hazards of time. Curr Opin Neurobiol. 2007;17:465–470. doi: 10.1016/j.conb.2007.07.006. [DOI] [PubMed] [Google Scholar]
  19. Nobre AC, Rohenkohl G, Stokes M. Nervous anticipation: top-down biasing across space and time. In: Posner MI, editor. Cognitive neuroscience of attention. 2nd edition. New York: Guilford; 2012. pp. 159–186. [Google Scholar]
  20. Palmer J, Huk AC, Shadlen MN. The effect of stimulus strength on the speed and accuracy of a perceptual decision. J Vis. 2005;5:376–404. doi: 10.1167/5.5.1. [DOI] [PubMed] [Google Scholar]
  21. Pestilli F, Carrasco M, Heeger DJ, Gardner JL. Attentional enhancement via selection and pooling of early sensory responses in human visual cortex. Neuron. 2011;72:832–846. doi: 10.1016/j.neuron.2011.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Prins N, Kingdom FA. Palamedes: Matlab routines for analyzing psychophysical data. 2009. Available at: http://www.palamedestoolbox.org.
  23. Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychol Rev. 2004;111:333–367. doi: 10.1037/0033-295X.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Rohenkohl G, Nobre AC. Alpha oscillations related to anticipatory attention follow temporal expectations. J Neurosci. 2011;31:14076–14084. doi: 10.1523/JNEUROSCI.3387-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Schroeder CE, Lakatos P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 2009;32:9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Schroeder CE, Wilson DA, Radman T, Scharfman H, Lakatos P. Dynamics of active sensing and perceptual selection. Curr Opin Neurobiol. 2010;20:172–176. doi: 10.1016/j.conb.2010.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Shuler MG, Bear MF. Reward timing in the primary visual cortex. Science. 2006;311:1606–1609. doi: 10.1126/science.1123513. [DOI] [PubMed] [Google Scholar]
  28. Westheimer G, Ley E. Temporal uncertainty effects on orientation discrimination and stereoscopic thresholds. J Opt Soc Am A Opt Image Sci Vis. 1996;13:884–886. doi: 10.1364/josaa.13.000884. [DOI] [PubMed] [Google Scholar]
  29. Wichmann FA, Hill NJ. The psychometric function. I. Fitting, sampling, and goodness of fit. Percept Psychophys. 2001;63:1293–1313. doi: 10.3758/bf03194544. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES