Influence of the Disc–Fovea Angle on Limits of RNFL Variability and Glaucoma Discrimination

Abstract

Purpose.

To determine factors affecting the disc–fovea angle (DFA), and to test the hypotheses that adjusting for DFA improves limits of retinal nerve fiber layer (RNFL) variability in normal subjects or enhances performance of RNFL measures for glaucoma detection.

Methods.

Disc–fovea angle was measured on scanning laser ophthalmoscope fundus images from 170 eyes (110 normal and glaucoma subjects). The DFA measurements were repeated in 24 eyes. The relationship between DFA and various anatomic variables was explored. Main outcome measures were changes in 95% RNFL prediction limits or glaucoma discrimination after adjusting for DFA. We also explored the angle between temporal raphe and horizontal meridian in 19 eyes with nasal field defects limited to one hemifield.

Results.

Average mean deviation and DFA were −0.1 (±1.2) dB and −6.6° (±3.4°) and −4.1 (±3.3) dB and −7.9° (±3.9°) in the control and glaucoma groups, respectively (P < 0.001 and = 0.029). The average difference between DFA repeat measurements was 2.0° (±1.8°). Predictors for DFA were female sex (P = 0.004), smaller disc area (P = 0.006), and glaucoma diagnosis (P = 0.019). The absolute change in sectoral RNFL thickness was 6.1 (±3.9) and 4.6 (±3.1) μm in control and glaucoma subjects, respectively. Retinal nerve fiber layer prediction limits improved in 5, 9, and 10 o'clock sectors (P < 0.02). Discrimination ability for the best-performing RNFL sector did not improve (P = 0.936). The average angle between temporal raphe and horizontal meridian was 0.8° (±0.8°).

Conclusions.

Disc–fovea angle measurements demonstrated fair intersession repeatability. While adjusting for DFA improved RNFL prediction limits in some sectors, it did not enhance glaucoma detection.

We report a new approach for correcting RNFL measurements for the disc–fovea angle (DFA). We found that although adjusting for DFA improved RNFL prediction limits in some sectors, it did not enhance detection of glaucoma. We also found that the temporal raphe alignment was very close to horizontal meridian.

Introduction

Measurement of the retinal nerve fiber layer (RNFL) thickness with spectral-domain optical coherence tomography (SD-OCT) has become a useful tool for detection of glaucomatous damage. Creation of normative databases has greatly enhanced our ability to interpret single printouts and to discriminate glaucomatous eyes from normal subjects. However, confounding factors affect the utility of such normative databases. These include patient age, quality of the SD-OCT image, axial length, and, most notably, variability of anatomical structures among normal eyes. The angle between the axis connecting the centroid of the optic disc and the foveal center and the horizon, called the disc–fovea angle (DFA), is an anatomical parameter that has been found to affect the RNFL course toward the optic disc.¹ Currently, one SD-OCT device automatically measures and corrects the RNFL profile (temporal-superior-nasal-inferior-temporal [TSNIT] curve) for DFA. Both head tilt and cyclotorsion have been suggested as a source of variability for RNFL thickness measurements.^2–4 Within-individual variability of DFA has been shown to be smaller than its intersubject variability, suggesting that DFA variations are largely due to true anatomical differences (Botwinick A, et al. IOVS 2013;54:ARVO E-Abstract B0268). However, factors affecting DFA and the effect of adjusting for DFA on RNFL variability and discrimination of glaucoma from normal subjects are not well described in the ophthalmic literature.

We designed a semiautomated technique for estimation of the DFA on registered en face disc cube and scanning laser ophthalmoscope (SLO) fundus images taken with an SD-OCT machine (Cirrus HD-OCT; Carl Zeiss Meditec, Dublin, CA, USA). The goal of this study was to determine anatomical and clinical factors influencing the DFA, to measure the DFA repeatability, and to explore whether adjusting for DFA improves 95% prediction limits for RNFL thickness measurement among normal subjects or its performance for detection of glaucoma. We hypothesized that adjusting for DFA would improve 95% prediction limits for peripapillary RNFL thickness measurements and potentially enhance detection of glaucoma. We also explored the position of the temporal raphe with regard to the horizontal meridian passing through the foveal center in another group of eyes with visual field defects limited to one hemifield.

Methods

Glaucoma patients and normal subjects were prospectively enrolled as part of the UCLA OCT Imaging Study, and those meeting specific inclusion criteria (a total of 170 eyes) were included in this study. A group of 24 eyes from the Advanced Glaucoma Progression Study (AGPS) who had repeat SD-OCT images available within 1 year were also enrolled to assess the repeatability of DFA measurement. A third group of eyes (19 eyes of 17 patients from the AGPS) was chosen to evaluate the location of the anatomical temporal raphe with regard to horizontal meridian. The group of 24 eyes (used to assess the repeatability of DFA) and the group of 19 eyes (used to evaluate the location of temporal raphe) did not overlap. Details of the UCLA OCT Imaging study have been published elsewhere.^5,6 Both studies were approved by the Institutional Review Board at University of California-Los Angeles (UCLA) and were performed in adherence with the Declaration of Helsinki.

Study Subjects

Patients who were diagnosed with open-angle glaucoma by an attending physician at the Stein Eye Institute's Glaucoma Clinic and who met the following criteria were prospectively enrolled in the study: age ≥ 30 years, open angles, visual acuity better than 20/80, visual field mean deviation ≥ −15 dB, refractive error ≤ 8.0 diopters (D), and astigmatism ≤ 3 D. Eyes with evidence of other significant ocular disorders or neurological diseases were excluded. All patients had at least one prior visual field test before being enrolled in the study.

Normal subjects were recruited by advertising on the UCLA campus, placing fliers in clinics, and soliciting spouses or friends of patients seen at the Stein Eye Institute's Glaucoma Clinic. The enrolled normal subjects were required to have open angles, corrected visual acuity of 20/25 or better, a normal eye exam including normal visual fields, and no definitive evidence of glaucomatous damage at the level of the optic nerve head.

All subjects underwent a thorough eye exam on the day of imaging, which included visual acuity, automated refraction, IOP measurement, gonioscopy, slit-lamp exam, dilated fundus exam, and standard achromatic perimetry (SAP) or short wavelength automated perimetry (SWAP) fields. IOLMaster (Carl Zeiss Meditec) was used to measure axial length and keratometry. Central corneal thickness (CCT) was measured with a DGH 55 Pachmate (DGH Technology, Inc., Exton, PA, USA). Stereoscopic optic disc photographs and Optic Disc and Macular Cubes 200 × 200 (Cirrus HD-OCT, model 4000, software version 6.0) were carried out after pupillary dilation. Subjects were asked to fixate on the target, and OCT images were acquired with the patient's forehead and chin stabilized by the headrest. During image acquisition, the subjects were not helped to maintain their head position; however, extra care was taken to make sure the patient's chin and forehead were correctly positioned and did not move during each exam.

Glaucoma was diagnosed if a reproducibly abnormal visual field was present and was consistent with the optic disc findings. An abnormal SAP or SWAP visual field was defined as presence of a Glaucoma Hemifield Test (GHT) outside normal limits and presence of four or more abnormal test locations on the pattern deviation plot with P < 5%, both confirmed at least once.⁷ The Swedish Interactive Thresholding Algorithm [SITA] standard testing strategy was used for both SAP and SWAP tests. Reliable visual fields were defined as those with a false-positive rate ≤ 20%. The visual fields were reviewed to exclude lid or lens artifacts.

All the images were reviewed by one of the investigators, and images with signal strength < 7, lost data on the peripapillary ring, obvious motion artifact, or incorrect segmentation were excluded. The Disc Cube 200 × 200 provides the segmented RNFL thickness for a square area of A-scan measurements centered on the optic nerve head (ONH), which measures 6 × 6 mm in an emmetropic eye (2 mm in depth). A graph of RNFL thickness measurements is provided along a standard measurement circle, 3.46 mm in diameter (12.5° in an emmetropic eye), centered on the ONH centroid. Scanning laser ophthalmoscope fundus images overlaid with macular thickness maps were exported in bmp format. Moreover, en face disc cube OCT images, the corresponding 200 × 200 grid of RNFL measurements for each eye (as segmented by Cirrus HD-OCT), and TSNIT curve values were exported to a personal computer. The RNFL data grid was then superimposed on the en face disc cube image, and RNFL thickness values were retrieved (one measurement per degree or 360 measurements) along a 12.5° measurement circle.⁶ All left eye data were converted to right eye format. After calculation of the DFA and rounding it to the nearest whole degree, the TSNIT RNFL measurements were adjusted, as demonstrated in Figure 1, by the magnitude of the DFA (clockwise for negative angles and counterclockwise for positive angles). The interartery and intervein angles, the disc–fovea distance, and the temporal raphe deviation angle from horizontal meridian were estimated as detailed below.

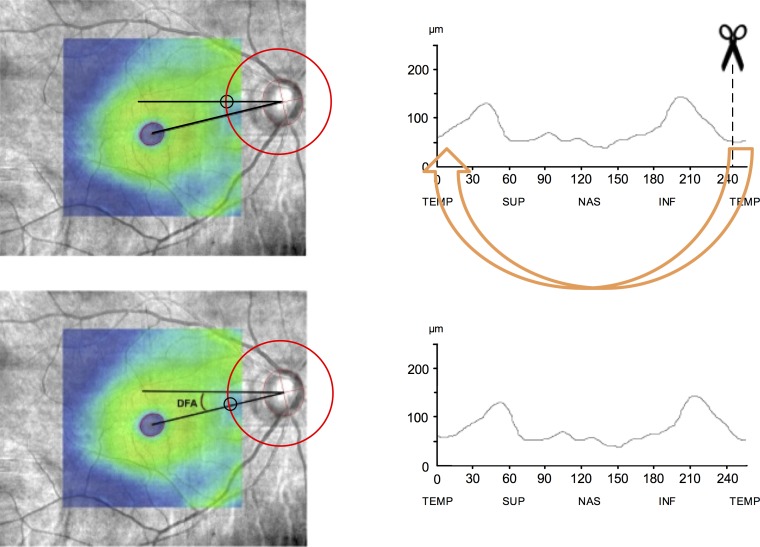
Figure 1.

Calculation of the DFA and compensating for it in RNFL measurements. DFA was calculated on SLO fundus images overlaid with macular thickness maps. Foveal center was found by fitting an ellipse to fovea. To find the disc centroid, the least-squares method was used for fitting an ellipse through a set of eight points identified on the clinical disc margin (left). After calculation of the DFA and rounding it to the nearest whole degree, the TSNIT RNFL measurements were adjusted (right) by the magnitude of the DFA (clockwise for negative angles and counterclockwise for positive angles). More negative DFA values indicate that the fovea is located more inferiorly with respect to the disc. Circles on the left images define the origin of the RNFL TSNIT profile.

Calculation of DFA

A semiautomated, customized MATLAB (ver. 8.1; MathWorks, Cambridge, MA, USA) program was developed to calculate the angle between the horizontal meridian and the line passing through the foveal center and the disc centroid (DFA).

For each eye, the SLO fundus image with the macular color thickness map overlay was used in order to find the foveal center. First, the program converted the thickness map overlay into a binary image through binary search thresholding. The resulting image was inverted so that white regions represented the object of interest, that is, the fovea. The regionprops function was then utilized to fit an ellipse to the fovea. The fitted ellipse could have any angle of tilt. Output parameters included the width and height of the ellipse along with the x- and y-coordinates of its centroid. Next, the optic disc centroid was determined using two different approaches. The first utilizes the centroid of the Bruch's membrane opening (BMO) as defined by Cirrus HD-OCT. The Cirrus HD-OCT automated algorithm identifies the inner termination of Bruch's membrane or BMO as the boundary of the optic disc. Such boundary, as a contour line enclosing the disc, along with its centroid is displayed on Cirrus en face disc cube images. By the use of reference points and visual matching, the en face disc cube image for each eye was overlaid on and aligned with the SLO fundus image. The second approach was to fit an ellipse to points on the clinical disc margin (the inner edge of what has been considered to be the scleral ring) and find its centroid as follows. One of the authors (NC) identified eight points on the clinical disc margin (on SLO fundus images while looking stereoscopically at disc photographs), to which an ellipse was subsequently fitted. The least-squares method was used for fitting the ellipse through the set of points. The calculated parameters of the ellipse, including the coordinates of the center of the disc, were maintained. As shown at the bottom left of Figure 1, the method accounted for the orientation (tilt) of the ellipse.

Once the coordinates of both the center of the fovea and the center of the disc are known, the calculation of the DFA is straightforward. Due to potential inadequate alignment of a number of SLO fundus images and en face disc cube images in the first method, the DFA calculations by the second approach were used in our study. Nevertheless, it should be noted that the numbers achieved by the two approaches were very close (ρ = 0.93, P <0.001). Negative DFA values indicate that the fovea is located inferiorly with respect to the center of the disc.

Calculation of Disc–Fovea Distance

The distance from the fovea to the disc center was measured based on the coordinates of center of the fovea and the center of the disc. The magnification-corrected distance was found by Bennett's formula, which takes into account a magnification factor related to the SD-OCT's camera as well as a magnification factor calculated based on the axial length of the eye to account for the magnification of the eye.⁸ The relationship between the measured disc–fovea distance from SD-OCT's SLO fundus image and the actual distance can be expressed as t = p × q × s, where t is the actual distance, s is the SD-OCT-based measurement, p is the magnification factor related to the SD-OCT's camera, and q is the magnification factor related to the eye. By using the default axial length (AL = 24.46 mm) and refraction (0 D) for a magnification of 1 with the Cirrus HD-OCT system (i.e., t = s), P can be calculated as 1/[0.01306 × (24.46 − 1.82)] = 3.382. The q factor based on AL would be 0.01306 × (AL − 1.82) according to Bennett's formula; therefore, disc–fovea distance measurements obtained from SLO fundus images should be corrected by the following factor: 3.3822 × 0.013062 × (AL − 1.82).⁹

Estimation of the Temporal Raphe Angle

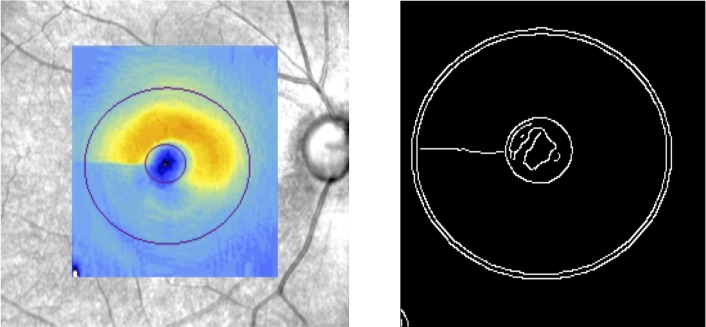
Nineteen eyes (17 patients) from the AGPS with a nasal visual field defect in one hemifield on pattern deviation plot were selected. These eyes had a minimum of three adjacent abnormal points (i.e., a defect at least 12° in width) immediately above or below the horizontal meridian in the nasal quadrants on the visual field test performed on the same day as the SD-OCT image, with no abnormal points in the opposite hemifield. Cirrus macular thickness maps were extracted as colored images, and a Canny edge detector¹⁰ was applied to the thickness maps in order to delineate the boundaries between regions with different color intensities. MATLAB's implementation of the Canny edge detector, which automatically chooses the threshold, was employed. A binary image was produced, where single-pixel-thick line segments show the fraction of pixels identified as edges. A line was fit to the sequence of points found by the Canny edge detector on the nasal side of each macular thickness map (Fig. 2). Angular deviation from the horizontal line was calculated in a custom program in MATLAB.

Figure 2.

Estimation of temporal raphe angle with regard to the horizontal meridian. Macular thickness map of an eye with advanced glaucoma overlaid on its SLO fundus image (left). The visual field pattern deviation probability plot demonstrates a nasal step in only one hemifield. Binary image of the thickness map after applying Canny edge detection (right). The angular deviation of the temporal raphe from the horizontal meridian was 0.5°.

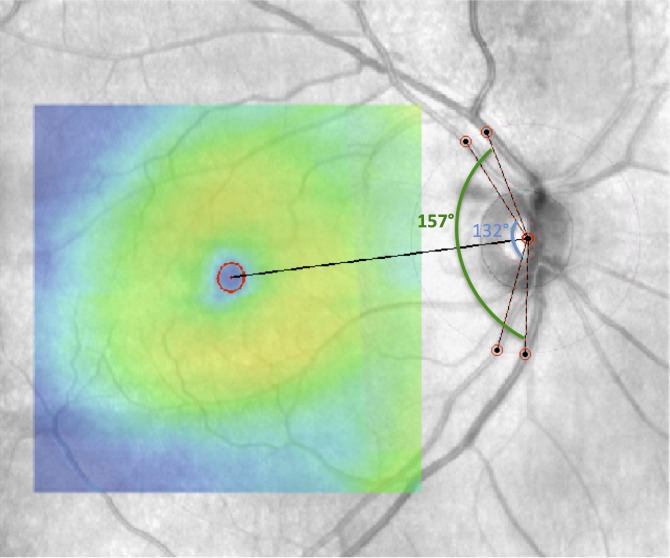
Calculation of Interartery and Intervein Angles

Interartery (vein) angle is the polar angle between the superior temporal artery (vein) and the inferior temporal artery (vein) with the optic disc centroid serving as the vertex (common endpoint) of the angles. A custom MATLAB program was developed to calculate these angles. We used SLO fundus images (with the macular color thickness map overlaid) as inputs to the program. Disc centroid, represented by the centroid of the BMO as defined by Cirrus HD-OCT, was already marked on the overlaid images. As shown in Figure 3, the thickest artery (vein) that extended the farthest on superotemporal and inferotemporal retinal regions (above and below the macula) was selected. The intersection points of the arteries (veins) and the OCT scan circle were selected as the sides of the interartery (vein) angle.^11,12 In cases where a vessel branched out temporally from an artery (vein), the one that followed the original course of the artery (vein) from the optic disc was chosen.

Figure 3.

Measurement of interartery (blue arc) and intervein (green arc) angles on SLO fundus image through a custom program in MATLAB. Interartery (vein) angle is the polar angle between the superior temporal artery (vein) and the inferior temporal artery (vein) with the optic disc centroid as common endpoint of the angles.

Statistical Methods

Bivariate scatter plots were used to explore the relationships between DFA and continuous variables of interest such as axial length, spherical equivalent, and intervascular angle. Continuous variables were compared by unpaired t-test or nonparametric tests depending on the distribution of individual variables. Categorical variables were compared by the χ² test. Factors associated with the DFA or presence of glaucoma were explored in univariate and multivariate regression analyses using a backward entry model keeping variables in the model with P < 0.1.

Comparison of Limits of RNFL Variability

For comparing changes in variability of the RNFL measurements in clock hour sectors in normal eyes, the absolute differences from the mean in the paired groups of data, that is, original unadjusted RNFL thickness measurements and measurements adjusted for DFA, were compared by Wilcoxon signed-rank test. In addition, the significance for the overall change in the 95% limits of RNFL variability was calculated as follows. Since the original (unadjusted) and adjusted RNFL measurements are correlated, RNFL residual errors were first computed through a repeated-measures analysis of variance model with fixed effects for degree and method (original versus adjusted) and a random eye effect. While the RNFL data at any given location may be correlated with values at other locations since they come from the same eye, the eye effect is removed in the residual errors, along with the means by degree level and method, making them independent across the 360° locations. At any degree level, the P value for comparing the two standard deviations (SDs) was computed by first computing the correlation between the difference (original − adjusted) and the sum (original + adjusted) of the two RNFL thickness values. When the two SDs are equal, this correlation is zero. Therefore, the P value for testing that the true correlation is zero is also the P value for comparing the two SDs. This method takes into account the correlation between the data for the two SDs. A separate test was carried out at each degree level (i.e., 360 tests). An overall P value across 360° was computed by the nonparametric signed-rank test on scores, where, for a given degree level, score = +1 if the original SD is significantly greater than the adjusted SD; score = −1 if the original SD is significantly smaller than the adjusted SD; and score = 0 if there is no significant difference. The correlation between the two eyes of the same subjects was taken into account with appropriate statistical tests when applicable. P values < 0.05 were considered significant.

Results

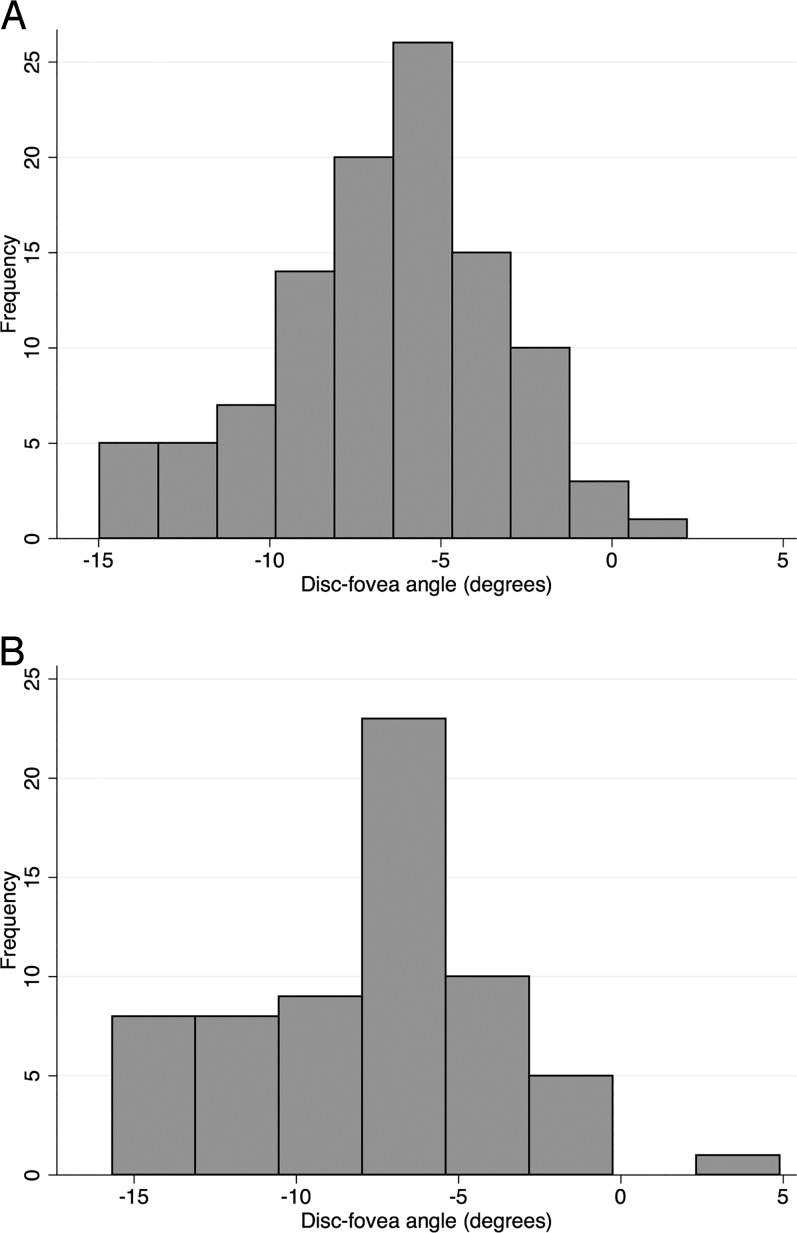
One hundred seventy phakic eyes of 110 subjects (64 eyes of 51 glaucoma patients and 106 eyes of 59 normal subjects) were included in the current study. Table 1 shows the clinical and demographic characteristics of the enrolled subjects. The glaucoma patients were older than the normal subjects (average age of 64.0 ± 6.7 vs. 58.8 ± 9.2 years, respectively; P = 0.001) and had longer axial length (median and interquartile range [IQR]: 24.2 [23.4–25.3] vs. 23.6 [22.9–24.3] mm, respectively; P = 0.002). Average mean deviation and DFA were −0.1 (±1.2) dB and −6.6 (±3.4), and −4.1 (±3.3) and −7.9 (±3.9) in the control and glaucoma groups, respectively (P < 0.001 and = 0.029). Frequency distribution of the DFA in both groups is shown in Figure 4. The DFA was negative in most eyes, which indicates that the fovea is located below the level of the optic disc in a majority of human eyes. The average difference between DFA repeat measurements was 2.0° (±1.8°). In 58% of the eyes, the DFA measurement at the second visit was within 2° of the first-visit value. There was no relationship between the difference between the two DFA measurements and the magnitude of the DFA (P = 0.171).

Table 1.

Demographic and Clinical Characteristics of the Glaucoma and Normal Control Subjects Enrolled in the Study

Demographic Data	Total	Normal	Glaucoma	P Value
Number of eyes (subjects)	170 (110)	106 (59)	64 (51)	-
Age, mean, y (SD)	60.8 (±8.7)	58.8 (±9.2)	64.0 (±6.7)	0.001*
Sex, female/male	70/40	39/20	31/20	0.342†
Spherical equivalent, median, D (IQR)	0 (−2.1 to 1.0)	0 (−1.5 to 1.0)	−0.38 (−3.5 to 1.0)	0.129‡
Axial length, median, mm (IQR)	23.9 (23.2–24.8)	23.6 (22.9–24.3)	24.2 (23.4–25.3)	0.002‡
Mean deviation, median, dB (IQR)	−1.6 (−2.44 to 0.35)	−0.09 (−0.86 to 0.74)	−4.11 (−6.15 to −1.64)	<0.001‡
Disc–fovea distance, mean, mm (IQR)	4.45 (3.97–4.89)	4.46 (3.97–4.88)	4.44 (4.01–4.93)	0.728‡
Interartery angle, mean, deg (IQR)	148.9 (115.5–178.6)	149.1 (114.1–177.5)	148.3 (118.7–178.6)	0.598‡
Intervein angle, mean, deg (IQR)	155.9 (121.1–195.4)	153.1 (120.7–187.7)	160.5 (123.0–201.2)	0.025‡
Disc area, mean, mm2 (IQR)	1.79 (1.30–2.48)	1.79 (1.36–2.38)	1.79 (1.14–2.49)	0.893‡

^* Two-sample t-test.

^† χ² test.

^‡ Wilcoxon rank-sum test.

Figure 4.

(A) Distribution of DFA for the control group (106 eyes of 59 subjects). (B) Distribution of DFA for the glaucoma group (64 eyes of 51 patients).

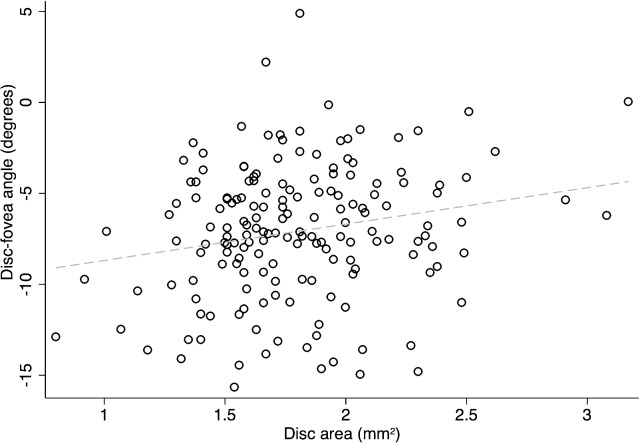
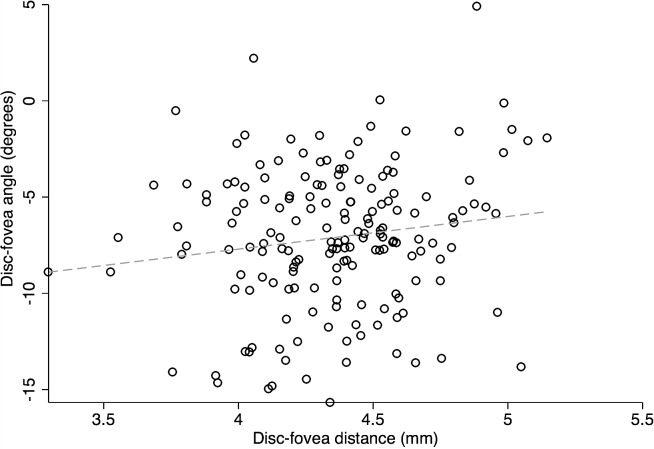
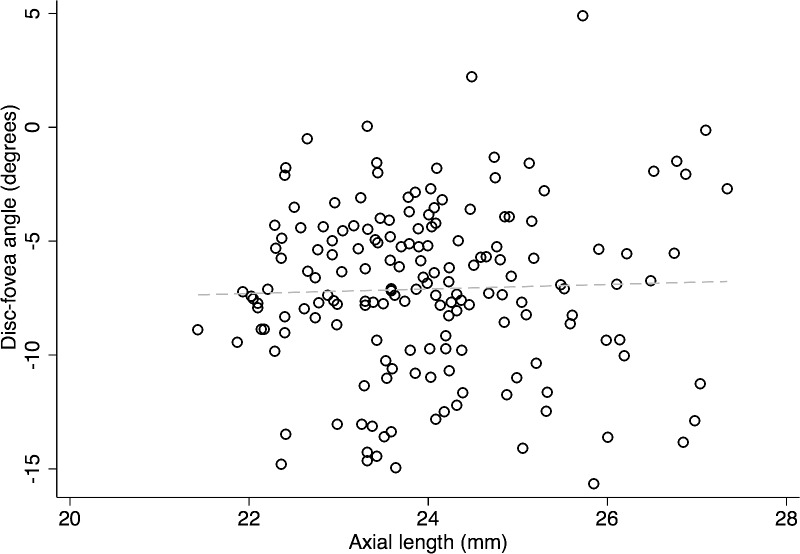
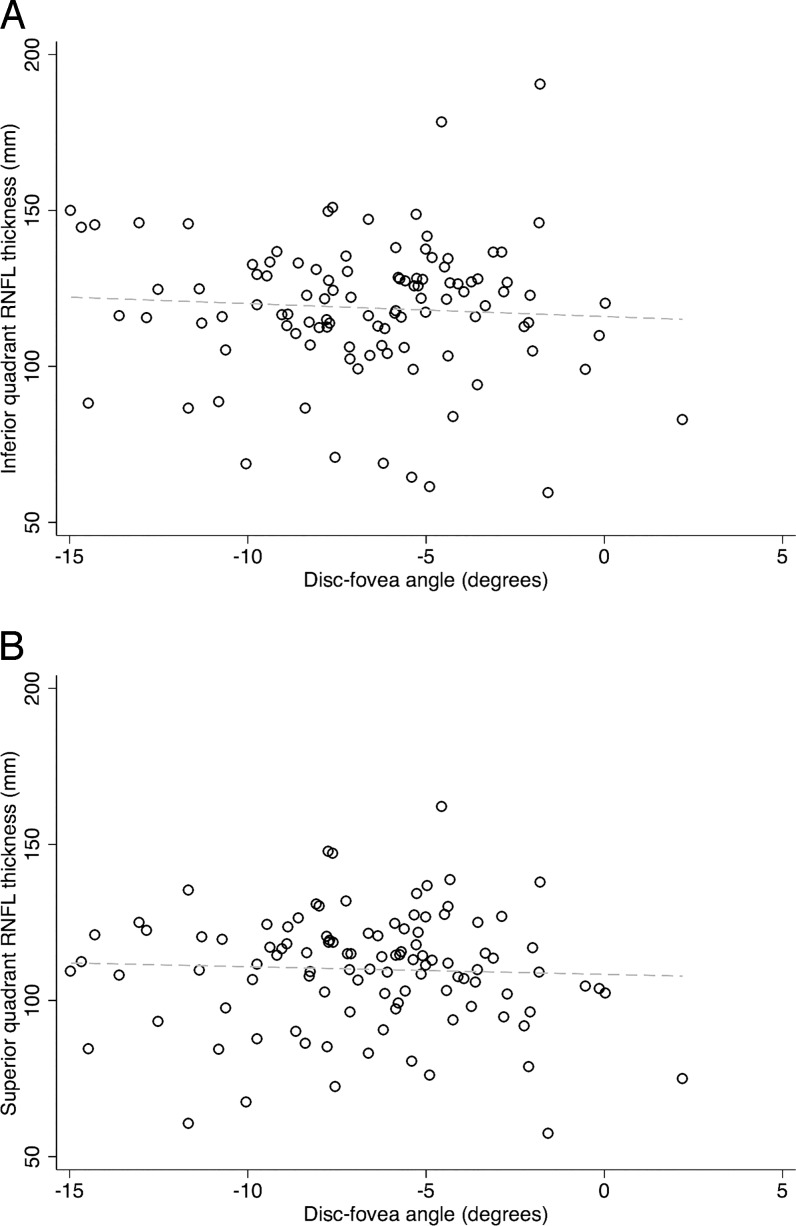
Figures 5 and 6 show scatter plots for DFA against disc area and disc–fovea distance. On univariate analyses, the DFA increased (i.e., became more positive) with larger disc area and longer disc–fovea distance (r = 0.131, P = 0.089; r = 0.206, P = 0.007). In contrast, as shown in Figure 7, there was no correlation between DFA and axial length (r = 0.034, P = 0.660). Among all the potential factors explored, female sex (P = 0.004), smaller disc area (P = 0.006), and diagnosis of glaucoma (P = 0.019) were associated with a more negative DFA in multivariate analyses. The RNFL thickness did not change as a function of DFA (P ≥ 0.51) in any quadrant in 106 normal eyes (of 59 subjects). Figure 8 depicts the scatter plots of RNFL thickness in the inferior and superior quadrants against DFA.

Figure 5.

The relationship between disc area (mm²) and DFA in the entire cohort (r = 0.131, P = 0.089). The DFA became more positive with an increase in the disc area.

Figure 6.

The relationship between disc–fovea distance and the DFA in the entire cohort (r = 0.206, P = 0.007). The DFA became slightly more positive as the disc–fovea distance decreased.

Figure 7.

The relationship between axial length (mm) and DFA in the entire cohort (r = 0.034, P = 0.660).

Figure 8.

Scatter plots demonstrate that there was no correlation between the retinal nerve fiber layer thickness in the superior (A) or inferior quadrant (B) and the DFA (r = −0.010 and 0.003, P = 0.89 and 0.96, respectively).

Multivariate regression analysis was also used to determine whether DFA or other anatomical features predicted presence of glaucoma. Longer axial length (P = 0.001), older age (P = 0.011), more negative DFA (P = 0.030), and larger intervein angle (P = 0.041) were the strongest predictors of glaucoma.

Influence of DFA Adjustment on RNFL Measurements

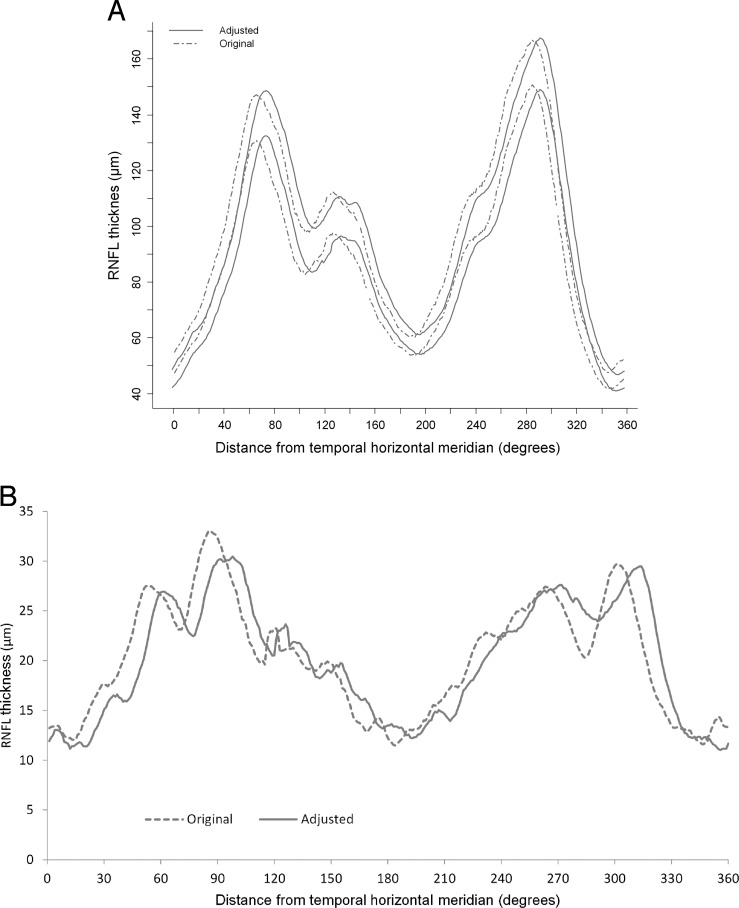
Tables 2 and 3 detail the quadrant and clock hour RNFL measurements before and after adjusting for DFA in the control and glaucoma groups, respectively. The adjusted RNFL measurements were thicker in clock hour sectors 2, 3, 7, 8, and 12 and thinner in the remaining sectors (P < 0.001). Qualitatively, the overall pattern for the 95% prediction limits for the TSNIT curve in normal subjects did not change (Fig. 9A). Variance of RNFL measurements in clock hours and quadrants was analyzed before and after adjusting for DFA in 59 control eyes (the right eyes of all the individuals who had both eyes available were included). A separate comparison was made for the entire TSNIT curve (global comparison). As Figure 9B shows, the change in the global SDs (and thus 95% prediction limits) was not significant after adjusting for DFA (median SD = 20.4 μm before adjusting and = 20.3 μm after adjusting for DFA). However, the 95% prediction limits for sectoral RNFL thickness decreased in clock hour sectors 5, 9, and 10 and increased in the 8 o'clock sector after adjusting for DFA in normal subjects. The median difference from average RNFL (IQR) in clock hour sectors 5, 9, and 10 was 15.5 (8.8–25.4), 6.9 (3.3–12.1), and 12.3 (5.6–19.1) μm, respectively, before adjusting for DFA; it decreased to 11.1 (8.6–19.6), 5.0 (2.7–12.0), and 10.8 (4.0–18.2) μm after adjusting for DFA (P < 0.02 for all comparisons). The median difference from average (IQR) for the RNFL thickness in the 8 o'clock sector increased from 9.1 (4.5–14.8) to 11.6 (5.7–22.7) μm after adjusting for DFA in normal subjects (P < 0.001).

Table 2.

RNFL Measurements in Clock Hour Sectors and Quadrants Before and After Adjusting for the Disc–Fovea Angle in a Group of 106 Eyes of 59 Normal Subjects (P Values Were Adjusted for the Correlation Between the Two Eyes of the Same Subjects)

Outcome Measure	Mean Thickness ± SD Before Adjusting for DFA, μm	Mean Thickness ± SD After Adjusting for DFA, μm	Difference ± SD, μm	P Value
Clock hour 1	101.73 ± 23.68	98.81 ± 24.63	−2.92 ± 8.83	0.001
Clock hour 2	84.81 ± 17.95	91.32 ± 18.85	6.51 ± 6.87	<0.001
Clock hour 3	60.09 ± 11.16	64.02 ± 12.42	3.93 ± 4.50	<0.001
Clock hour 4	65.59 ± 13.18	61.27 ± 12.27	−4.33 ± 4.67	<0.001
Clock hour 5	96.75 ± 22.34	90.12 ± 20.68	−6.64 ± 8.74	<0.001
Clock hour 6	132.04 ± 29.66	122.58 ± 28.81	−9.46 ± 7.82	<0.001
Clock hour 7	128.13 ± 30.78	138.72 ± 31.50	10.59 ± 10.32	<0.001
Clock hour 8	60.04 ± 13.14	71.72 ± 18.44	11.67 ± 9.00	<0.001
Clock hour 9	64.64 ± 9.60	62.18 ± 9.06	−2.46 ± 2.52	<0.001
Clock hour 10	73.71 ± 16.51	66.85 ± 14.26	−6.87 ± 5.33	<0.001
Clock hour 11	121.85 ± 25.00	111.06 ± 25.97	−10.78 ± 8.97	<0.001
Clock hour 12	108.38 ± 29.52	117.41 ± 28.80	9.03 ± 10.51	<0.001
Inferior quadrant	118.73 ± 21.84	117.01 ± 21.54	−1.72 ± 2.93	<0.001
Nasal quadrant	70.33 ± 11.94	72.33 ± 12.10	2.01 ± 2.31	<0.001
Superior quadrant	109.98 ± 18.23	108.81 ± 17.84	−1.17 ± 2.62	<0.001
Temporal quadrant	61.39 ± 11.52	62.36 ± 11.90	0.97 ± 2.15	<0.001

^Pvalues from paired t-test.

Table 3.

RNFL Measurements in Clock Hour Sectors and Quadrants Before and After Adjusting for the Disc–Fovea Angle in a Group of 64 Eyes of 51 Glaucoma Patients (P Values Were Adjusted for the Correlation Between the Two Eyes of the Same Subjects)

Outcome Measure	Mean Thickness ± SD Before Adjusting for DFA, μm	Mean Thickness ± SD After Adjusting for DFA, μm	Difference ± SD, μm	P Value
Clock hour 1	85.68 ± 26.25	81.68 ± 25.64	−4.00 ± 10.45	0.003
Clock hour 2	73.80 ± 15.11	78.64 ± 19.28	4.84 ± 7.55	<0.001
Clock hour 3	58.69 ± 10.75	62.45 ± 11.52	3.77 ± 4.69	<0.001
Clock hour 4	60.97 ± 11.87	57.61 ± 10.65	−3.36 ± 5.53	<0.001
Clock hour 5	76.66 ± 22.68	72.51 ± 18.79	−4.14 ± 8.67	<0.001
Clock hour 6	92.09 ± 33.79	88.12 ± 30.77	−3.97 ± 8.76	<0.001
Clock hour 7	78.88 ± 33.96	87.20 ± 35.31	8.31 ± 11.70	<0.001
Clock hour 8	52.03 ± 14.30	57.71 ± 19.33	5.67 ± 9.67	<0.001
Clock hour 9	57.20 ± 11.49	55.21 ± 10.66	−2.00 ± 2.52	<0.001
Clock hour 10	62.57 ± 19.57	58.00 ± 15.47	−4.57 ± 6.66	<0.001
Clock hour 11	93.20 ± 28.22	83.07 ± 27.33	−10.14 ± 11.64	<0.001
Clock hour 12	88.12 ± 25.72	98.03 ± 26.39	9.91 ± 11.45	<0.001
Inferior quadrant	82.42 ± 24.98	82.55 ± 23.95	0.13 ± 3.19	0.7386
Nasal quadrant	64.55 ± 10.64	66.31 ± 11.25	1.76 ± 2.53	<0.001
Superior quadrant	87.47 ± 22.57	85.89 ± 22.18	−1.58 ± 3.21	<0.001
Temporal quadrant	54.41 ± 13.46	54.06 ± 13.36	−0.35 ± 3.15	0.3712

^Pvalues from paired t-test.

Figure 9.

(A) The 95% prediction limits for distribution of RNFL thickness measurements in normal subjects (59 eyes of 59 subjects) comparing calculated unadjusted TSNIT curves and adjusted TSNIT curves. The overall pattern for the 95% prediction limits for the TSNIT curve in normal subjects did not change. (B) Distribution of the standard deviation for retinal nerve fiber layer measurements in 59 eyes of 59 normal control subjects before and after adjusting for the DFA. The difference between the global standard deviations did not change after adjusting for DFA (median SD = 20.4 μm before adjusting and = 20.3 μm after adjusting for DFA).

To evaluate whether the location or topography of the horizontal raphe is affected by the DFA, 19 eyes (of 17 patients) whose visual field pattern deviation probability plot showed a nasal step in only one hemifield were selected from our advanced glaucoma cohort. The mean angular deviation of the temporal raphe from the horizontal meridian was close to 0° in this subgroup (0.8° ± 0.8°). The deviation of horizontal raphe from horizontal meridian was not related to the DFA in this subgroup of eyes (P = 0.72, Fig. 2).

Performance for Detection of Glaucoma

Receiver-operating characteristic (ROC) curves were used to evaluate the performance of all clock hour sectors and quadrants before and after adjusting for the DFA. The best-performing sectoral parameter for discrimination of glaucoma was RNFL thickness at 7 o'clock (area under ROC curve or AUC = 0.853). However, adjusting for DFA did not improve the performance of this parameter for detection of glaucoma (AUC for adjusted 7 o'clock RNFL thickness = 0.852, P = 0.936 for the difference between adjusted and unadjusted AUC). The best-performing quadrant parameter for discrimination of glaucoma was the RNFL thickness in the inferior quadrant (AUC = 0.854). Similar to RNFL thickness at 7 o'clock, adjusting for DFA did not improve the performance of the RNFL thickness for detection of glaucoma (AUC for adjusted 7 o'clock RNFL thickness = 0.850, P = 0.619). When only early glaucoma eyes (47 eyes with mean deviation better than −6.0 dB) were included, the change in the performance of the RNFL thickness at 8 o'clock after adjusting for DFA was significant (AUC for adjusted 8 o'clock RNFL thickness = 0.715 vs. 0.666 for unadjusted 8 o'clock sector, P = 0.032). For all other sectors the change in the performance for detection of glaucoma after adjusting for DFA was not significant (P > 0.129).

Discussion

It is now believed that the axis connecting the centroid of the optic disc to the foveal center should be considered the reference axis for defining the origin of the RNFL TSNIT profile or that of the newly defined minimum width rim area.^13,14 There is an increasing body of evidence that the clinical disc margin and the neural canal opening may not coincide in an individual eye or in parts of the optic disc in the same eye.^15–18 Given that the termination point of the Bruch's membrane is a more consistent structure than the clinically identified disc margin, the minimum rim width (MRW),^4,19–21 as a new structural outcome measure, has been found to have better diagnostic capability than circumpapillary RNFL thickness.¹⁴

The DFA has become a topic of interest given recent data suggesting that taking it into account may improve performance of MRW and similar structural measures. For example, it has been shown that in eyes with a larger DFA, there was up to a 20% difference in clock hour MRW values when the reference axis was adjusted.²¹ However, there is yet no evidence that accounting for the DFA improves the performance of RNFL thickness or neuroretinal rim area measurements for detection of glaucoma. In this study, we first explored potential factors associated with a more negative (i.e., more tilted) DFA. The eyes enrolled in our study sample, although skewed toward myopia or higher axial lengths, were fairly emmetropic. The average DFA in our study was approximately −7°, consistent with the published literature.^1,21–25 Factors influencing DFA have not been formally explored in these studies. Choi et al.¹ found that a longer disc–fovea distance was associated with a more horizontal DFA in myopic eyes, although no multivariate analyses were performed. There was a trend for the same direct relationship between DFA and disc–fovea distance in univariate analyses in our study sample (P = 0.102). There was no relationship between DFA and the location of main retinal blood vessels. Previous studies have reported that the sectoral RNFL thickness was correlated with the interartery angle.¹² Interestingly, axial length or spherical error was not predictive of a more negative DFA in our study. However, female sex, a smaller disc area, and diagnosis of glaucoma were associated with a more negative DFA, although only a small amount of DFA's total variability was actually explained by these factors (R² = 0.12). The reason for an association between female sex or smaller disc area and DFA is not clear; however, the association of glaucoma with a more negative DFA could have clinical implications. Hood and colleagues^26,27 suggested that because the foveal center is ordinarily below the disc center, the upper and lower macular regions at the optic disc are anatomically asymmetrical, which might be the reason the inferior RNFL is thicker than the superior RNFL at comparable locations close to the disc. As a result, the inferior region of the optic disc may be more vulnerable to glaucomatous damage. Inferior macular damage can manifest as rim loss in the inferior region of the disc in some eyes. It is conceivable that eyes with a more negative DFA, that is, eyes in which the center of fovea is located more inferiorly with respect to the disc, would more likely demonstrate inferior rim loss early in the course of the disease compared to eyes with a less negative DFA. Hence, eyes with a more negative DFA would more likely be diagnosed as glaucomatous, since clinicians tend to look for inferior rim loss as an early sign of glaucoma. This needs to be further investigated in future studies.

Chauhan and Burgoyne²² have suggested that regional data analyses (e.g., MRW or RNFL thickness measurements) consider sector positions with respect to true geometric horizontal and vertical axes of the measurements, thereby adjusting anatomic locations among different subjects.²² The utility of this approach has not been adequately explored. Lee et al.²⁸ hypothesized that the amount of axonal distortion could be different between superior and inferior RNFL bundles. Superotemporal and inferotemporal RNFL bundles pursue different and complex trajectories due to varying spatial relationships between the optic disc and fovea.²⁸ In other words, since the fovea is usually located below the center of the disc, the superotemporally projecting RNFL fibers are projected a bit closer to the vertical midline as opposed to their inferotemporally projecting counterparts.²⁶ In line with these findings, Kim and colleagues²⁹ have noted distinctive interindividual variability in the ganglion cell–inner plexiform layer (GC/IPL) defect pattern, which can partly be attributed to variability in the position of the disc relative to the fovea.

Denniss et al.³⁰ demonstrated that the position of the disc relative to the fovea and axial length play an important role in mapping of the 24-2 visual field locations to the optic disc. Anatomically customized structure–function maps were generated by a computational RNFL model.³¹ In the model, retinal ganglion cell axons first take the shortest path from their retinal origin toward the optic disc; they then curve around the fovea²⁶ and other axons originating closer to the disc, moving their final insertion point at the disc nasally. It has been shown by Lamparter et al.³² that several ocular parameters may impact the layout of the RNFL and hence mapping of the retinal locations (functional loss) to the optic disc. Such parameters consisted of the position of the disc relative to the fovea (i.e., the DFA), spherical equivalent, axial length, disc shape, area, orientation, and tilt in their study.

We examined the intersession repeatability for the DFA in a smaller group of patients who had repeat RNFL and macular images within a year of the index image. Our results showed only fair repeatability, with approximately two-thirds of the repeat DFA measurements within 2° of the baseline measurement. Our findings are consistent with those of Botwinick and colleagues (Botwinick A, et al. IOVS 2013;54:ARVO E-Abstract B0268) as well as those of Choi et al.¹ Patel and associates⁴ developed similar strategies that account for cyclotorsional eye movements when comparing global and local RNFL measurements between different SD-OCT devices.

Another finding of our study was that adjusting for the DFA did not improve the 95% prediction limits globally (P = 0.46); nevertheless, when sectoral 95% prediction limits were explored, some improvements in a few sectors could be observed. Such improvements, however, did not lead to enhanced performance of the sectoral RNFL measures with regard to discrimination of glaucoma from normal eyes. This is in spite of the fact that significant changes in the RNFL thickness measurements could be seen in both normal and glaucoma subjects in our study sample (Tables 2 and 3). When only early glaucoma eyes were included in the analysis (mean deviation better than −6.0 dB), the performance of sectoral RNFL measures for detection of glaucoma did not improve, or slight improvement was achieved in sectors where the AUC values were poor. One limitation of the study concerns the generalizability of the normative data, as all of the normative data were gathered in one center and the sample size was limited. Ideally, the performance of corrections for DFA would need to be validated in a separate group of subjects and across various devices.

One of the available SD-OCT devices (Spectralis; Heidelberg Engineering, Heidelberg, Germany) actually applies a correction factor based on DFA to regionalize the TSNIT RNFL measurements. Our results suggest that a simple approach to compensate for DFA may not be adequate for RNFL measures. Therefore, more sophisticated algorithms to address other confounding factors for the regionalization of TSNIT curves (such as adjusting for location of major peripapillary vessels^11,12,33,34) are likely needed to best address this issue. Adjusting for DFA generally resulted in increased RNFL thickness inferotemporally and decreased RNFL thickness in the superotemporal sectors. Choi and colleagues¹ have emphasized the role of the DFA in the RNFL thickness profile in normal myopic subjects. They compared the circumpapillary RNFL thickness in the superior and inferior quadrants (and the inferior–superior [I−S] difference) of normal myopic eyes as a function of DFA.¹ They found that in eyes with a more negative DFA, the I−S difference increased, with the superior quadrant demonstrating a thinner and the inferior quadrant showing a thicker RNFL profile. Our findings failed to reproduce their results. However, our patient sample was not as myopic as theirs.

The location of the temporal raphe has recently become a topic of interest. Some SD-OCT machines rotate the axis of the entire macular measurement cube as a function of DFA, including the area temporal to the fovea, assuming that the temporal raphe follows the DFA. One interesting finding of our study was that temporal to the fovea, the raphe was practically always aligned with the horizontal meridian in a separate subgroup of patients who were selected based on visual field criteria. This finding has important implications with regard to designing superior-inferior asymmetry algorithms currently used for detecting early glaucoma with macular SD-OCT images. Data in the glaucoma literature on this topic are scarce.³⁵ Recent studies by Hood et al.,²⁶ Le and colleagues,³⁶ and Tanabe and associates (Tanabe F, et al. IOVS 2014;57:ARVO E-Abstract A0309) have suggested that the angle between the temporal raphe and the horizontal meridian is smaller than the DFA. The latter investigators obtained detailed images of the retinal nerve fiber trajectory in the temporal retina through an algorithm called Transverse Section Analysis. Le et al.³⁶ took advantage of the ganglion cell complex (GCC) maps produced by the RTVue frequency-domain OCT system (Optovue, Inc., Fremont, CA, USA).³⁶ They observed a horizontal midline separating the superior and inferior regions temporal to the fovea in maps demonstrating the correspondence between macular GCC loss and visual field deficits. Hood and colleagues²⁶ identified a temporal minimum in RNFL thickness maps of healthy controls produced by the RTVue OCT, which corresponded to the temporal raphe falling approximately along the horizontal meridian. Jansonius et al.³⁷ modeled the course of retinal nerve fibers in 55 normal eyes. By aligning the centers of the fovea and disc, they were able to reduce the intersubject differences in RNFL bundle projections. Although they did not specifically explore the position of the temporal raphe, it could be observed in their model that the temporal raphe would be aligned along the horizontal meridian. However, significant preprocessing of the images to superimpose the centers of the disc in their study could have affected the results.³⁸ More recently, Chauhan and colleagues³⁹ were able to visualize the temporal raphe with a high-density SD-OCT volume scan centered on the fovea. They investigated the orientation of the temporal raphe in 15 healthy subjects and concluded that the temporal raphe is not aligned with the axis connecting the fovea and the center of BMO. Furthermore, they found that the temporal raphe was not horizontal. Nevertheless, it can be inferred from their interindividual variation graphs that for eyes with DFA less than −4° (such eyes comprise majority of eyes in our study and similar studies), the deviation of the horizontal raphe from the horizontal meridian is very close to 0°. This is in agreement with our results. In another recent study, Huang et al.⁴⁰ employed an adaptive optics SLO to image the temporal raphe in 11 healthy young subjects. Similar to the results reported by Chauhan and colleagues,³⁹ they reported that on average, the temporal raphe was above the horizontal midline (deviation of temporal raphe from the horizontal meridian = 1.67 ± 4.8° as opposed to = 2.23 ± 2.4° in the study by Chauhan et al. and = 0.8° ± 0.8° in our study). One caveat regarding our technique is that we actually measured the temporal raphe at the level of GC/IPL; however, there is no reason to believe that the temporal RNFL raphe would not follow the deeper layers.

In summary, we found that the DFA measurement repeatability was fair. There was no relationship between the difference of the two DFA measurements and the magnitude of the DFA. Predictors of a more negative DFA were female sex, smaller disc, and diagnosis of glaucoma in our patient sample. Although significant changes in RNFL thickness measures were observed after adjusting for the DFA, this adjustment improved RNFL prediction limits only in a few sectors in normal subjects. Adjusting for DFA did not enhance performance of the RNFL thickness measures for detection of glaucoma. Utilizing a reference angle, which is more repeatable (e.g., by being independent from the horizontal meridian), may deliver higher performance in detecting glaucoma. We also found that the temporal raphe was mostly horizontal in a subgroup of patients who had visual field defects limited to one nasal hemifield. Future investigations should focus on models or algorithms that incorporate various confounding factors for RNFL measurements to decrease limits of variability for RNFL measurements in normal subjects.