Network Theory Tools for RNA Modeling

Abstract

An introduction into the usage of graph or network theory tools for the study of RNA molecules is presented. By using vertices and edges to define RNA secondary structures as tree and dual graphs, we can enumerate, predict, and design RNA topologies. Graph connectivity and associated Laplacian eigenvalues relate to biological properties of RNA and help understand RNA motifs as well as build, by computational design, various RNA target structures. Importantly, graph theoretical representations of RNAs reduce drastically the conformational space size and therefore simplify modeling and prediction tasks. Ongoing challenges remain regarding general RNA design, representation of RNA pseudoknots, and tertiary structure prediction. Thus, developments in network theory may help advance RNA biology.

“To know what to leave out and what to put in; just where and just how, ah, that is to have been educated in knowledge of simplicity.”

– Frank Lloyd Wright.

1 Introduction

Modeling biological systems involves not only choices of what to approximate and how, as well as what can be neglected, but also selection of appropriate tools, both existing and new, to design and apply to complex problems. Many successes in science can be credited to borrowing tools from seemingly disparate fields and applying them in new ways. Examples include quantum computing using DNA [1], analyzing DNA recombination products using knot theory [91], storing digital information within DNA [15], modeling economic scenarios using game theory [70], and applications of Mandelbrot’s fractal geometry to architecture, financial markets and turbulence [63, 64, 65].

Network or graph theory is a well-established field of mathematics that has been used extensively in a variety of economic, social, biological, and medical contexts. Essentially, foundations of graph the ory can be used to enumerate and analyze combinatorial properties of various systems, such as communication, chemical, and biological networks. Specific examples include chemical structures (e.g., hydrocarbons, drug compounds) [38, 62], genetic and cellular relationship [11, 40, 67, 30, 58], transportation arrays [5], Internet linkages [88], and social media communications [35]. In mathematical terms, an undirected graph G = (V, E) is a discrete object described by a finite set of vertices V and a set E of unordered pair of vertices called edges, where each edge represents a connection between two vertices. If E is composed instead of ordered pairs of vertices (each representing direction of an edge), G is called a directed graph (digraph). In this work, we describe how graphs can be used to model and study RNA structure. See also our recent review [47].

2 RNA Background

RNA has come to the forefront of science with recent discoveries of its regulatory roles [19, 85]. Beyond protein synthesis, RNA can regulate gene expression and modify the genetic message by gene silencing [33], chemical modifications of ribosomal RNAs [2], control of protein stability [90], and changing conformations of ligand-binding sites of messenger RNA [71, 78, 79, 12].

These new discoveries have also opened new avenues for thinking about therapeutic biotechnology applications of RNA, because RNA’s editing, silencing, and other regulatory capabilities can be manipulated to shut off and turn on genes, deliver drugs, diagnose gene activity, and design new materials [80, 31, 13].

Information on RNA structure comes from experimental information (X-ray crystallography, NMR, chemical probing) as well as modeling (e.g., as reviewed in [52]). These structures and their analyses have established RNA’s hierarchical structure, in which building blocks (motifs) combine stepwise to form complex active shapes of RNA [52, 47]: The primary (1D) structure or sequence leads to the seconday (2D) structure – pattern of hydrogen bonding arrangements – which in turn triggers tertiary (3D) structure formation, created by all interactions including long-range contacts between 2D substructures (see, Figure 1). RNA is a single-stranded polymer whose sugar-phosphate backbone contains four standard bases, Adenine (A) and Guanine (G), Uracil (U) and Cytosine (C), and their modified bases in various order. This single-stranded polymer folds upon itself, to form GC, AU, or GU (“wobble”) base pairs which define double-helical regions (“stems”), imperfect with single-stranded regions named “hairpin loops”, “internal loops”, and “junctions”, which have one, two, or more adjacent helical arms, respectively (see 2D structure elements in Figure 2a and Figure 3). When two single-stranded regions flanked by a stem are base-paired, an interwined RNA structure called pseudoknot forms (see Figure 1; top middle, and top right, for the interwining green and red stems). Long-range interactions between secondary structural motifs form complex tertiary network-like structures.

Figure 1.

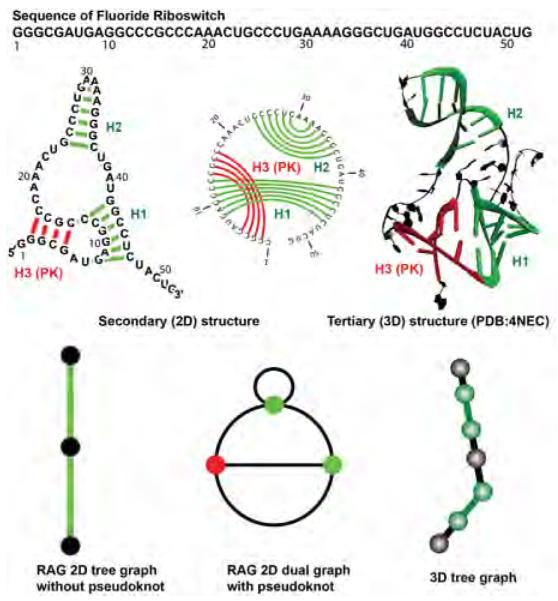
RNA’s hierarchical network-like structures from 1D to 3D. The primary (1D), secondary (2D), and tertiary (3D) structures associated with fluoride riboswitch (PDB:4NEC [81]) are shown. The RAG tree and dual graphs representing its 2D topology without and with pseudoknot, respectively, are also shown. The double-stranded or stem regions are colored green for tree topologies and red for pseudoknot formation.

Figure 2.

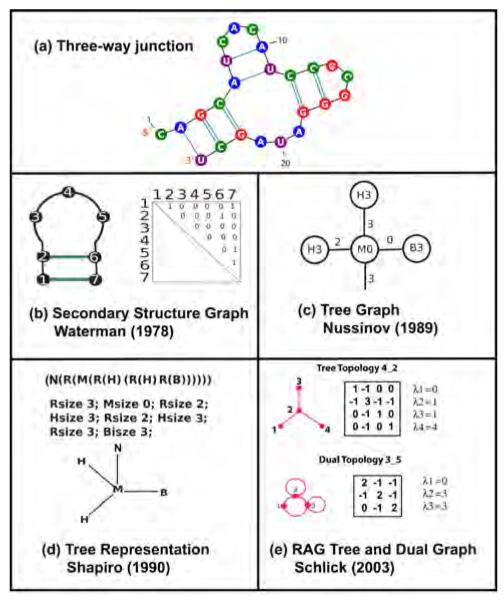
Graph theoretical models of an RNA 2D structure for a three-way junction (a) by Waterman, Nussinov, Shapiro, and Schlick. (b) Waterman (1978): graphs at base-pair level; (c) Nussinov (1989): ordered labeled tree graphs B, I, H, M, and S represent bulge, internal loop, bifurcation loop, and single-stranded region, respectively; (d) Shapiro (1990): simplified tree graphs where R represent a paired region; (e) Schlick (2003): RAG tree and dual graphs.

Figure 3.

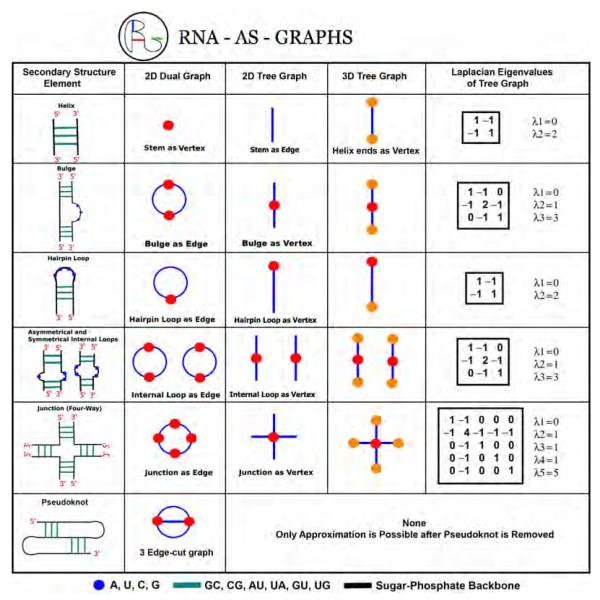
The RAG translation rules of RNA 2D structures as dual, tree, and 3D tree graphs (as developed in our recent work, see text). For each 2D structural element, the associated dual, tree, and 3D tree graphs are shown along with Laplacian of the tree graph. RNAs with pseudoknot structures can only be presented by a dual graph.

These hierarchical, modular, and network-like features of RNA structures invite mathematical and computational approaches to model, analyze, and predict RNA structures (see recent reviews [47, 52]). For example, programs for predicting RNA 2D structures by free energy minimization [95, 82], folding 3D structures of small RNAs [72, 18], and annotating motifs in 2D/3D structures [66, 76] are widely used. Figure 1 shows the abstraction of 2D structures as a tree graph and a knot-like graph (called “dual graph”).

3 Graph Theory Approaches to RNA Structure Modeling

3.1 Early Graph Approaches by Waterman, Nussinov and Shapiro

Pioneering modeling of graphs for RNA began in the late 1970s. Waterman developed graphical representations of RNA in 1978 with the aim of analyzing the secondary structure of tRNA (Figure 2b) [89]. Specifically, he offered the first graph-theoretic definition of secondary structure and classified graphs of RNA secondary structures with the goal of finding stable 2D structures. These planar graphs were analyzed for base pairing using an adjacency matrix. His method allows comparison of two different RNA 2D structures by approximating the free energy based on the adjacency matrix representations. In 1989, Le et al. also developed the ordered labeled tree representation to compare 2D structures of RNA (Figure 2c) [57].

In 1990, Shapiro and coworkers used a tree representation of RNA 2D structures to measure structural similarities (Figure 2d) [83]. They developed an algorithm for analyzing multiple RNA 2D structures by multiple string alignment. In particular, they defined the tree edit distance between two (full) tree 2D structures to quantify the minimum cost (insertion, deletion, and replacement of nodes) along an edit path for converting one tree into another. Morosetti further studied similarities in tree graph representations by using topology connectivity indices known as the Randić index [6]. That is, for a given graph G = (V, E), and d(u) representing the number of edges incident at vertex u of G (i.e., the degree of vertex u), the Randić index, R(G), is defined in term of the degrees of the vertices as R(G) = ∑_(u,v)∈E(d(u) · d(v))^1/2. This index was originally introduced to assess the connectivity in chemical graphs as this measure is sensitive to the shape of a chemical cluster.

3.2 RAG Tree and Dual Graphs

In 2003, Schlick and coworkers introduced tree and dual graphical representations of RNA 2D motifs in a framework called RAG (RNA-As-Graphs) [22, 23, 20, 37] (see Figures 2e, 3 and 4).

Figure 4.

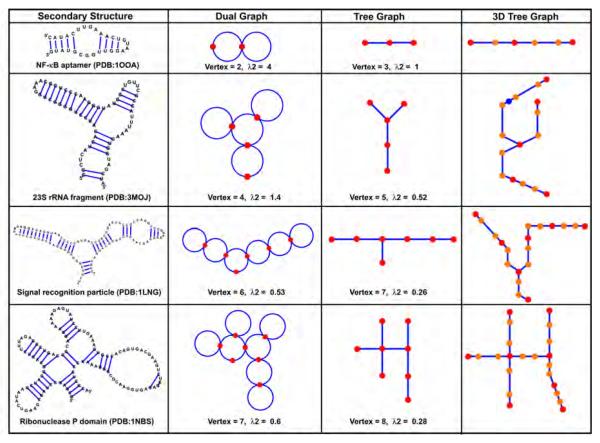
Examples of known RNAs with their RAG represenations: dual, tree, and 3D tree graphs (as developed in our recent work, see text). Each RAG graph is also described by the vertex number and the second smallest Laplacian eigenvalue.

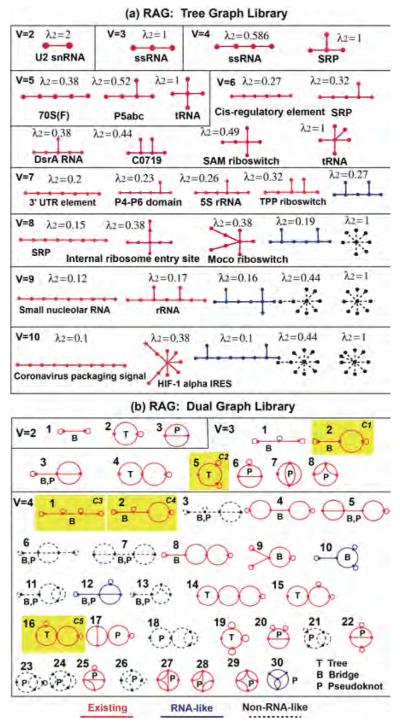
In the RAG tree graphs, RNA 2D structural elements – stems, loops, bulges, and junctions – are converted into 2D graphical objects with the following rules: (1) an edge (−) represents a double-stranded helical stem with more than one base pair; (2) a vertex (●) represents a single strand that occurs in segments connecting secondary structural elements such as bulges, loops, and junctions. Here, a bulge motif is considered to be an internal symmetric or asymmetric loop with more than one unmatched nucleotide or one unstable base pair.

Although RAG tree graphs offer an intuitive description of RNA 2D topologies, they cannot represent pseudoknots. The dual graph representation translates RNA 2D structure into a more abstract graphical model by interchanging the vertices and edges for opposite motifs from the translation rules of RAG tree graphs [22, 20, 23, 37]: (1) a vertex (●) represents a double-stranded helical stem with more than one base pair; (2) an edge (−) represents a single strand that occurs in segments connecting 2D structural elements such as bulges, loops, and junctions where a bulge motif is the same as the translation rules of RAG tree graphs (i.e., asymmetric loop with more than one unmatched nucleotide or one unstable base pair). See Figure 3 for example.

The above definitions can be modified as needed to construct more detailed 2D network models [22, 32, 41]. For example, by adding the flow direction on edges (i.e., labeled vertices), RNA structures with different starting and ending vertices can be differentiated [22, 32, 41]. Currently, in the goal of RNA tertiary structure prediction, Schlick and coworkers are developing 3D tree graph representations for parallel and anti-parallel helical arrangements with the following additions and modification of vertices and edges to RAG tree graphs: (1) additional vertices (●) are set at helix ends; (2) additional edges (−) are set to connect RAG tree vertices representing loops to additional proximal vertices; (3) additional vertices (●) are set to represent bulges for asymmetric loop with one unmatched nucleotide (see Figures 3 and 4). When the geometrical features such as helix lengths and angles are added to 3D tree graphs, we can also represent RNA 3D global geometries intuitively. See end of Section 4.4 for an overview.

3.3 Advantages of the RAG Representation

The graphical representation of RNA secondary structures makes it possible to apply graph theory methods to quantitatively describe topological properties (i.e., topological descriptors) of RNA motifs [20, 43].

Let G = (V, E) be an undirected graph and n = ∣V∣; we define the associated Laplace matrix (called the Laplacian) M = (m_ij) as the n × n matrix where

$$m_{\mathit{ij}}=\{\begin{array}{ccc}d\left(i\right)\hfill & :\hfill & i=j\hfill \\ -w_{\mathit{ij}}\hfill & :\hfill & (i,j)\in E\hfill \\ 0\hfill & :\hfill & (i,j)\notin E,\hfill \end{array}\phantom{\}}$$ (1)

and the value w_ij is the number of edges between vertices i and j. The Laplacian thus decribes the connectivity of a graph (see Figures 2e and 3 and Ref. [20, 43]). The Laplacian eigenvalues λ₁, λ₂, … , λ_n are non-negative and real because M is symmetric, and the smallest eigenvalue λ₁ = 0 [69]; the Laplacian eigenvalues have been extensively studied because they describe combinatorial properties of a topology. As an example, a spanning tree of a graph G is a minimally connected subgraph (i.e., connected and acyclic) containing all the vertices of G. Each RAG tree graph has only one spanning tree, itself, since any removal of an edge makes a graph disconnected. For dual graphs, however, this is not the case; dual graphs can have several spanning trees. An arbitrary spanning tree can be found by an application of Depth First Search [29] under the assumption that G is connected. The number of spanning trees of a graph G on n vertices, t(G), can be evaluated as a function of the Laplacian eigenvalues as $t\left(G\right)=\left({\prod }_{i=2}^n{\lambda }_i\right)∕n$ [7]. An open problem in extremal graph theory, originally proposed in the 1970s [42], is to characterize graphs with maximum number of spanning trees (called t-optimal graphs) among all graphs with e edges and n vertices (see [42, 14, 74, 75]); t-optimal graphs play an important role in the design of reliable communication networks [8, 9] in reliability theory as well as in optimization design theory in statistics [14].

The second smallest eigenvalue, λ₂, and its corresponding eigenvector, μ₂, provide information about topological compactness (i.e., algebraic connectivity) and partition properties of graphs, respectively. The eigenvalue λ₂, also known as the Fiedler eigenvalue [21], increases with the compactness of the structure. For example, λ₂ is smaller in a linear chain than in a branched structure for a family of closely related graphs (see examples in Figure 4). Unlike traditional topological connectivity, algebraic connectivity or compactness depends on the number of vertices and how they are connected.

The eigenvector μ₂ = (v₁, v₂, … , v_n) provides information on how to subdivide a large RNA into smaller fragments by using spectral-graph partitioning methods [77] that minimize dependencies between fragments. A cut C(A, A’) of a graph G = (V, E) is a set of edges that, when removed from G, partitions the set of vertices V into two sets A and A’. The cut-ratio Ω(A, A’) of the cut C(A, A’) is defined as ∣C(A, A’)∣/min(∣A∣, ∣A’∣). The idea of spectral partitioning is to bisect (i.e., split a set into two sets whose cardinalities differ by at most in one) the vertex set V into {i ∈ V : v_i > s} and {i ∈ V : v_i ≤ s} for given value s. Spielman et al. showed that there exists a value s that can be determined in term of the Fiedler eigenvalue, for which the bisection of the Fiedler eigenvector yields the best possible cut-ratio in G [86]. For example, μ₂ corresponding to RAG tree graph 5₂ in Figure 5 is (−0.20, 0.34, −0.42, −0.42, 0.70). When s is the median of the eigenvector components, −0.20, the graph is partitioned into two sets of vertices, {5, 2} and {1, 3, 4}, representing an internal loop and a three-way junction, respectively.

Figure 5.

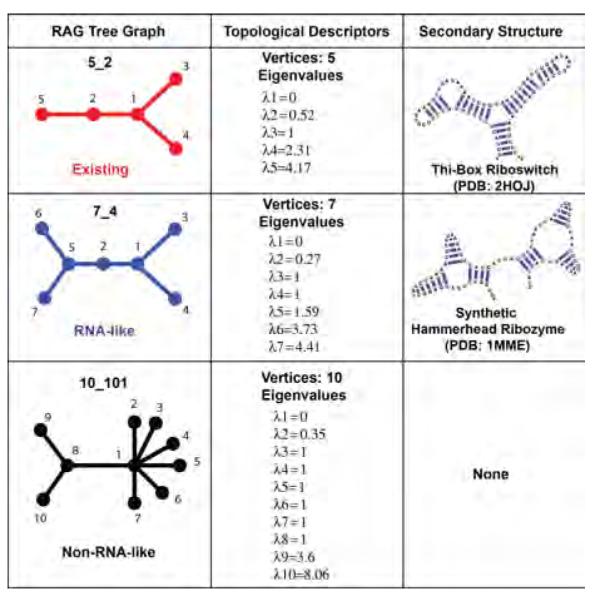
RNA tree graph library segment. Tree graphs are associated with existing RNAs (from the PDB) and classified as RNA-like and non-RNA-like. The eigenvalues of RNA topologies are a measure of structural compactness.

Another important graph-theoretical descriptor is the diameter of a graph G = (V, E) which is defined as the maximum distance (length of the shortest path) between every pair of vertices u, v ∈ V. Intuitively, the diameter represents the maximum possible communication delay between a pair of vertices of a graph. Even though the Fiedler eigenvalue and the diameter assess different structural properties of graphs, the algebraic connectivity is related to the reciprocal of the average distance of a graph. Also 4/(n · λ₂) represents a lower bound for the diameter of a graph G on n vertices [68].

Laplacian eigenvalues [20, 43], graph diameter [25], and spanning trees are examples of topological descriptors widely used to determine properties of graphs. These quantitative measures can be used to compare graphs, subdivide graphs into recurring motifs, and identify subgraphs [43, 73].

In communication applications, graphs with maximum number of spanning trees are useful for reliable network design [74, 75]. Consider a communication network G = (V, E), in which edges fail independently (vertices are perfectly reliable) and each edge x fails with probability ρ_x. The all-terminal reliability, R_V (G), gives the probability that each pair of vertices u, v ∈ V will remain connected via an operational path after deletion of the failed edges. It is not difficult to show that if a graph G₀ has maximum number of spanning trees (i.e., G₀ is t-optimal) among all graphs in a class with equal number of edges e = ∣E∣ and vertices n = ∣V∣, Ωn, e), then when edges are failing (i.e., for each edge x the probability of failure ρ_x approaches 1), G₀ is also the most reliable graph in Ω(n, e). Thus t-optimal graphs play a significant role when characterizing most reliable graphs given a class of graphs Ω(n, e).

Independently from this result in graph theory, Cheng [14] discovered in 1982 that the optimization problem of characterizing t-optimal graphs in a class of graphs Ω(n, e) is equivalent to the optimization problem of characterizing the so-called balanced incomplete-block designs in statistics (i.e., design of network with specific requirements such as the number of objects in each block). We first consider block designs with t treatments to be tested on b blocks of size k with k < t. Each statistical experiment can be mapped to a graph in Ω(n, e), where n = t + b and e = b * k, and the optimal block design is the experiment represented by a t-optimal graph in ω(n, e).

A key advantage of this topological approach is that it reduces the size of RNA space enormously. The RAG framework make it possible to enumerate and generate RNA 2D topologies, opening a new avenue for predicting novel RNA motifs [22, 43]. For RAG unlabeled tree graphs, the number of possible graphs is obtained using the counting polynomial derived by Harary and Prins [22, 34]. To enumerate and construct RAG dual graphs, probabilistic graph-growing techniques are used [43]. These sets of distinct graphs represent libraries of theoretically possible RNA topologies, which include existing and hypothetical (“missing”) RNA motifs.

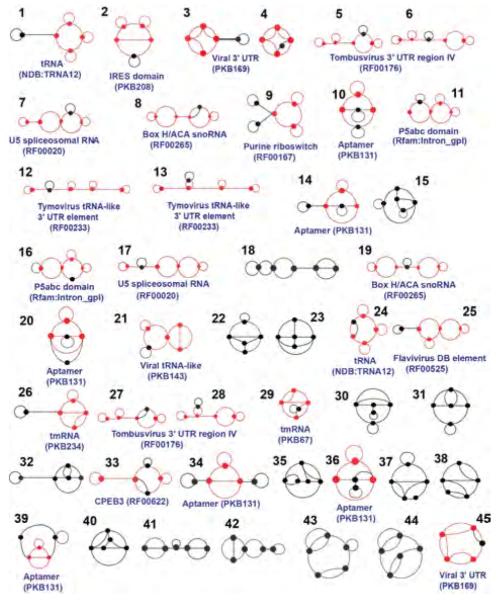
Since not all hypothetical RNA topologies are physically meaningful, Kim et al. predicted motifs, named as “RNA-like” motifs, which are more likely to occur in nature than others by a learning approach based on known RNAs [43]. They clustered RNA graphs into two groups based on topological variables via the transformation of Laplacian eigenvalues and predicted novel candidate RNA-like topologies that possess topological properties similar to existing RNAs [43]. Based on these predictions, RAG catalogued all RNA graphs into existing and RNA-like, and non-RNA-like motifs (http://www.biomath.nyu.edu/rna): see Figures 5–7 for RAG segments. Among the ten RNA-like dual graphs with 3 or 4 vertices predicted in 2004, five motifs (see C1, C2, C3, C4, and C7 in Figure 6b) have been identified in nature with regulatory or catalytic functions [37].

Figure 7.

45 RNA-like topologies with 5 vertices predicted by supervised clustering analysis based on existing RNAs [37]. The submotifs found in nature are colored red.

Figure 6.

RAG tree and dual graphs. (a) The library of topologies of RAG tree graphs between 2 and 10 vertices, with the second smallest Laplacian eigenvalues (λ₂) listed. (b) RAG dual graphs between 2 and 4 vertices, with topological classification (tree, bridge, and pseudoknot). The status of existing, RNA-like, and non-RNA-like topologies is represented by red, blue, and black (dashed), respectively (see text). The motifs in the yellow box indicate the five candidate motifs (C1, C2, C3, C4, and C7) as of 2004 [43] which have been identified as CPEB3, purine riboswitch, tRNA-like, Tombusvirus 3′ UTR region, and Flavivirus, respectively, in the updated RAG as of 2011 [37].

RAG’s systematic catalogue offers a comprehensive search ability and has been used in analyzing, designing, and predicting RNA structures [73, 56, 49]. For example, Pasquiali et al. analyzed modular pseudoknot architectures by dual subgraph-isomorphism searches in large ribosomal RNA [73]. Laserson et al. identified motifs corresponding to antibiotics-binding motifs in genomes by searching tree graphs [56]. Knisley and coworkers applied RAG to predict larger RNA-like structures by merging two small graphs and applying neural network analysis [49]. See also [47] for the impact of RAG on the RNA field.

4 Graph Applications to RNA Structure Prediction

4.1 Motif Analysis

Network analysis applied to RNA structures has identified modular RNA structure which are composed of repetitive motifs, in which patterns appear hierarchically, from 2D to 3D structure levels. Essentially, motifs are recurring structural elements in RNA molecules.

Statistical analysis of 2D networks helped reveal motif distributions of known RNAs and provided improved structural and energetic parameters for 2D structure prediction [94, 24]. Zorn et al. annotated paired and unpaired bases in stems, junctions, hairpin loops, bulges, and internal loops in ribosomal RNAs and discovered that the paired and unpaired bases in structural motifs have characteristic distribution shapes and ranges: the frequency distribution of paired bases in stems declines linearly with the number of bases, whereas, for unpaired bases in junctions, it has a pronounced peak [94]. Gardner et al. correlated structural statistics of hairpins and internal loops to energetic parameters by analyzing sequence alignments and 2D structure data sets to improve the accuracy of RNA 2D prediction [24].

The RNA 3D network plays an important role in RNA 3D folding and provides models of the principles of organization of complex RNA structures [59, 87, 93]. Leontis and Westhof developed the network representation rules to represent 3D structure in 2D (including base pairing, base-stacking, and basebackbone interactions), which facilitates the discrete models and classification of 3D motifs [59]. Using this 3D network representation, they classified base pair interactions into 12 geometric families in terms of base pairing and base-stacking [59], and catalogued by similar base pair interactions that can be substituted by compensatory mutation [87]. Zirbel et al. analyzed and classified 10 base-backbone geometrical families based on their hydrogen bond interaction patterns [93].

The Westhof/Leontis 3D network representation and classifications have been used to define recurrent 3D motifs in known RNA 3D structures [92, 28, 10]. By manual inspection by experts in the field of RNA structure, several 3D motifs have been identified (e.g., coaxial helix, A-minor, ribose zipper, and kissing hairpin, see Ref. [92] for the definition of motifs) and more continue to be discovered. Recently, the Jaeger and Steinberg groups found new 3D motifs found common right-angles, twist-joints and double twist-joints motifs in ribosomal RNAs and other large RNAs, which establish specific helical arrangements [28, 10].

The increased repertoire of RNA motifs has stimulated the development and application of statistical and computational analysis in RNA structures to better understand the network interaction properties of RNA [92, 36]. Xin et al. comprehensively analyzed a data set of 54 high-resolution RNA crystal structures for motif occurrence and correlations. Specifically, they searched seven RNA 3D motifs by various computer programs for motif occurrence and correlations (see the resulting frequencies of motifs at http://www.biomath.nyu.edu/motifs). Pyle and coworkers represented RNA backbone structures using a simplified virtual bond system and reported the pseudo-torsional angles focusing on local RNA backbone geometry [36]. Statistics of RNA 3D motifs provide the groundwork for RNA 3D structure prediction via networks of restraints.

4.2 Junctions Classification and Prediction

RNA junctions are important structural elements that form when two or more helices come together in space in RNA 3D structures associated with 2D structures. The Al-Hashimi, Westhof and Schlick groups performed geometrical analysis and classification of 2-way (or internal loops), 3-way, and 4-way (and higher-order) junctions, respectively [3, 4, 60, 55, 51, 50].

Al-Hashimi and coworkers showed that 2D structure features (e.g., loop size) encode topological constraints on the 3D helical orientations of 2-way junctions and additional long-range contacts serve to stabilize specific helical conformations [3, 4].

Westhof and coworkers classified 3-way junctions to 3 families (called A, B, and C) based on coaxial-stacking and orientation of helices, parallel, diagonal, or anti-parallel [60]. They also developed an algorithm for automatically predicting the topological family of any RNA 3-way junction, from given only 2D structure information, based on the parameters derived from a data set of 3-way junctions taken from known RNAs [55].

Schlick and coworkers focused on 4-way and higher-order junctions [51, 50, 53]. Laing et al. classified 4-way junctions into nine families according to coaxial stacking patterns and helical configurations [51]. They further developed a computational tool, called Junction-Explorer, to predict helical arrangements in 3- and 4-way junctions by a data mining approach, known as random forests, which relies on a set of decision trees trained using length, sequence, and free energy specified for any given junction [53]. The web server Junction-Explorer is freely available at http://bioinformatics.njit.edu/junction. Junction-Explorer can predict the junction family with an accuracy of 85% for 3-way junctions and 74% for 4-way junctions. These studies of RNA junctions help understand the global interaction network of RNAs and thus have great potential for guiding the challenging task of RNA 3D structure prediction.

4.3 In Vitro Selection Modeling In Silico

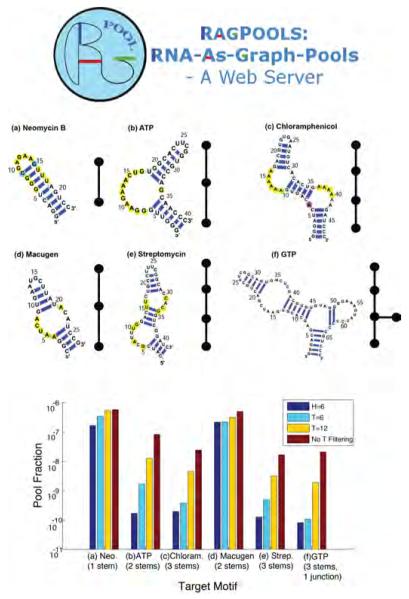
In the laboratory, new RNAs are designed by an experimental procedure called in vitro selection which involves the generation of large random-sequence pools (~10¹⁵) and screening the random pool for molecules that can perform a specific function such as binding to specific targets.

Theoretical analysis of random pools by Gevertz et al. [25] has shown that the random pools are biased towards simple topologies (e.g., see aptamer motifs in Figure 8).

Figure 8.

Pool screening and filtering analysis for 10¹² random-sequence pools for aptamers.

Kim et al. [44, 46] developed a computational framework for modeling the in vitro selection process with specific targets in mind and provided computational tools for analyzing and improving RNA in vitro selection in three ways: by designing structured pools, by generating large sequence pools, and by screening target motifs in large pools. The concept of the “nucleotide transition probability matrix” was introduced to represent the mixing ratios of nucleotides in synthesis ports. This makes it possible to design sequence pools targeting RNA-like topologies that are more likely to be active when produced experimentally.

To assist experimentalists, they made available design tools through a web-server, RAGPOOLS: RNA-As-Graph-Pools at http://rubin2.biomath.nyu.edu [45]. This work represents a first-generation effort to simulate in vitro selection processes in silico and exponentially increases the number of quality samples available to experimentalists. Efficient modeling has extended the approach to pools of up to 10¹⁴ sequences.

Other efforts in this direction include work by Chushak and Stone on generation and screening of 10⁸ random-sequence pools for RNA aptamers for binding specific targets using a 3D folding and docking algorithms [16]. Luo et al. developed computational approaches to generate and evolve DNA pools for five-way junctions [61].

One of main challenges in vitro selection modeling in silico remains 3D structural characterization of the products to complement the 2D motif analysis. Advances in the prediction of RNA 3D structure require more conceptual breakthroughs to address the global positioning of RNA’s 2D structure elements.

4.4 RNA Structure Prediction

RNA’s modular, hierarchical, and network-like properties invite the application of graph approaches to RNA structure prediction. The prediction tools of RNA 2D structures from a given sequence (e.g., Mfold [95]) using energy minimization are already widely used. An alternative approach is the topology-based method, which generates an exhaustive list of all possible topologies, and also uses clustering analysis and shape parameters to narrow down the promising topologies [43]. Once these topologies are identified, the next step is to generate sequences to fold into them. Build-up approaches have been developed for this purpose [43].

The prediction of atomic 3D structure based on a given sequence is an ultimate goal of RNA structure prediction. Several programs predicting all-atom structures for small RNAs have been developed using fragment assembly and energy minimization (FARNA [18]) and modular approach using 4-6 nt building blocks called graph cycles (MC-SYM [72]). NAST [39] and iFold [84] use coarse-grained approach with one-bead or three-beads model, respectively. However, such programs are generally poor at predicting long-range interactions and, for higher prediction accuracy, manual manipulation and expert intuition are required; see recent reviews [52, 17].

The challenge remains for prediction of larger and more complex RNAs. An intermediate step toward 3D atomic structure prediction of any size and shape has been achieved using graphical representation to simplify 3D structures and reduce sampling space [26, 27]. Gillespie et al. represented RNA backbones as polygonal curves on the 3D triangular lattices and simulated the folding of RNA pseudoknots, by considering only the 3D conformations that can realize pseudoknot structures in the 3D space given the base pair restrictions [26]. Gopal et al. predicted and visualized the average structure of 2D/3D topology ensembles of long viral RNAs (with thousands nucleotides) using enumeration of RAG tree graphs and coarse-grained molecular dynamics [27]. Ongoing efforts using graph approaches are aimed at predicting helical arrangements given 1D and 2D information via 3D motif constraints.

Currently, Schlick and coworkers are developing a hierarchical RNA folding approach using RAG 3D tree graphs and the geometrical analyses of RNA junctions and 3D motifs [54, 48]. The approach exploits the advantage of 3D tree graphs to reduce the conformational space for RNA and accelerate global sampling of candidate RNA 3D topologies. From given RNA 2D structures, initial 3D graphs are constructed by a junction family prediction program called Junction-Explorer [54]: Junction-Explorer is based on a data mining study that uses random trees to predict junction topology based on input feature vectors. The algorithm is trained on known RNA junctions. Following initial junction prediction, the Monte Carlo graph sampling is performed where each candidate graph is scored by a statistical potential energy function that guides preferred local and global conformations [48]. This graph-based hierarchical model is being tested on a set of known 3D structures, and shows promise for predicting large RNA structures. The translation of graph predictions to atomic models is also under current development.

5 Concluding Remarks and Open Problems

Network representations of complex RNA structures have been shown to be useful for representing, analyzing, predicting, and designing RNAs. From Waterman’s graph approaches [89] to RAG tree and dual graphs [22], these various mathematical objects offer an efficient way of visualizing, classifying, and predicting RNA structures.

RAG’s tree and dual graphs exploit the network-like nature of RNA 2D topologies [22, 23, 20, 37]. The application of graph theory to RAG representations has been used to measure overall compactness and enumerate all possible 2D topologies [43, 20]. The cataloguing, classification, and clustering of RAG graphs has expanded our understanding of RNAs structural repertoire, and allowed us to predict RNA-like topologies [43, 37, 49]. Graph enumeration and clustering algorithms have been used to explore RNA-like topologies [43, 37], and the graph merge method has been developed to predict larger RNA topologies [49]. The RAG database has been used to perform topology-based approaches which led to prediction of non-coding RNA searches in genomes [56] and submotif searches in larger RNAs [73].

Graph representations in combination with network and geometrical analysis have been applied to RNA structure prediction in multiple ways. By exploring network properties on 2D and 3D levels, recurrent motifs have been searched for and identified in known RNAs, which lays the groundwork for 3D structure prediction [94, 59, 92]. In particular, the 3D geometrical analysis of junction networks are led to topological classification of junction family types [3, 4, 60, 55, 51, 50]. To discover new RNAs with RNA-like topologies, the RAG catalog has been used to analyze, generate, and design targeted RNA structures to ultimately enhance in vitro selection experimental procedures [44, 46, 45]. The substantial reduction in conformational space size can enhance RNA structure prediction [26, 27, 54, 48].

Graph theory is expected to continue to be a useful tool for representing, analyzing, and predicting RNAs; such applications also provide exciting research opportunities in biology for mathematical scientists. We end with three open questions that require collaboration between mathematicians and biologists:

First, can we develop an alternative approach to clustering approaches for predicting RNA-like topologies based on the spectrum of a graph? The clustering analysis used previously by [43, 37] is based on supervised approaches trained on the whole set of all existing RNA topologies. This method has a considerable number of false positives [37]. An alternative approach is to identify in the RAG database those graphs that are non-isomorphic but have the same eigenvalues, determine which are known in nature, and then explore whether a certain spectral pattern lead to a fruitful way to predict novel RNAs. For example, if there are three specific non-isomorphic trees with the same spectrum and only one has been found experimentally, the other two may be RNA-like and good candidates for design. This approach relies on the well-known result in graph theory that two different non-isomorphic trees (for the same number of vertices) can have the same eigenvalues; that is, the vertex number and the eigenvalues alone cannot uniquely identify a topology.

Second, can we extend the RAG database for design of RNAs by build up by systematic identification of RNA submotifs for a target structure and links of submotifs to 1D/3D structures from the PDB? This problem involves rigorously identifying submotifs for a target structure, which can be an automated search of 3D subgraphs based on subgraph isomorphism. Established graph theory properties regarding subgraph isomorphism and maximum number of spanning trees could be appropriate here. Ongoing activity on determining graphs with maximum number of spanning trees (among graphs with the same number of vertices and edges) using the Laplacian eigenvalues and other optimization techniques could be valuable here.

Third, can we expand the repertoire of 3D motifs by applying spectral graph partitioning and the algebraic connectivity? So far, only a limited number of known 3D motifs has been identified and analyzed by manual inspection and computational searches from solved RNAs. The application of spectral graph partitioning could be useful to enumerate all existing 3D motifs by dividing 3D graphs translated from RNA 3D structures. The topological properties of 3D motifs could also be described by the F iedler eigenvalue and related to the diameter of the whole structure.

Unlike Frank Lloyd Wright’s architecture, biological macromolecules cannot be made arbitrarily simple, but perhaps simplified network representations could lead to more innovative and successful approaches for addressing difficult real-life problems in RNA structure prediction and design.