Partial least squares regression as a powerful tool for investigating large combinatorial polymer libraries

Abstract

Partial Least Squares (PLS) regression is an established analytical tool in surface science, particularly for relating multivariate ToF-SIMS data to a univariate surface property. Herein we construct a PLS model using ToF-SIMS and surface energy data from a 496 copolymer micro-patterned library. Using this 496 copolymer library we investigate how changing the number of samples used to construct the PLS model affects the identity of the most influential ions identified in the regression vector. The regression coefficients vary in magnitude, but the general relationship between ion structure and surface energy is maintained. As expected, if copolymers containing monomers with unique chemistries are removed from the training set, secondary ions specific to these copolymers are not present in the regression vector. The use of PLS to obtain quantitative predictions has not been actively explored in the surface analytical field. We investigate whether the PLS model obtained can be used to predict the surface energies of polymers within and outside of the training set. The model systematically underestimated the surface energy of a group of acrylate copolymers synthesised using monomers common to the training set, but in different compositions. The predictions for a group of acrylate copolymers that were synthesised from monomers not used in the training set were very poor. When the model was used to obtain predictions for six commercially available polymers the values obtained were all close to the mean surface energy of the training set. This exercise suggests that PLS may be able to predict the surface energy of polymers synthesised from monomers common to the training set, confirming the importance that the training set reflects the chemistry of the samples to be predicted.

Introduction

During the last decade there has been considerable interest in the preparation of combinatorial libraries with the aim of identifying new polymers with interesting properties.^[1,2] This has been particularly evident in the search for new polymers for use in tissue engineering and drug delivery, in either discrete^{[3 – 6]} or gradient^{[7 – 11]} formats. This research has even progressed to include work involving three-dimensional polymer scaffold libraries.^[12,13] A relatively new development in this field has been the preparation of polymer libraries in microarray format. The first such microarray was synthesised by Anderson et al. who reported a method for the synthesis of nanolitre quantities of novel acrylate copolymers that were polymerised on slide by exposure to UV light in a microarray format. These microarrays were used to screen for polymers that allowed controlled differentiation of human embryonic stem cells.^[14] This approach was then taken further by printing arrays of pre-synthesised polymer libraries from solution.^[15] Such libraries were created by either blending commercially available polymers or de novo synthesis in parallel, which were subsequently used to screen for human mesenchymal stem cells, epithelial and dendritic cell adhesion.^{[15 – 17]} The most recent development in this area has been the preparation of polymer microarrays by sequential inkjet printing of monomers with initiators directly onto a substrate, allowing mixing and polymerisation in situ.^[18]

In the field of combinatorial polymer research there has sometimes been a lack of emphasis on the characterisation of surface properties, probably due to the practical difficulties of analysing large numbers of separate samples. Analysis of the surface properties of combinatorial polymers is important because it is the surface of a material that determines many of its properties. With the advent of polymer microarrays, where the entire library is on one flat support, some of these practical issues are reduced, particularly when combined with automated acquisition. We have recently reported a ‘high throughput’ methodology for the surface analysis of a copolymer microarray on one glass slide by the surface analytical techniques of Time-of-Flight (ToF) SIMS, XPS and water contact angle measurement.^[19] Methods for assessing the polymers’ protein adsorption properties have also been reported.^[20] Once this data has been collected the challenge is to develop the existing statistical data-handling approaches to relate this large amount of surface analytical information to other properties such as wettability, cell adhesion assays and protein adsorption.

High throughput polymer development may take the form of simple identification of ‘hit’ polymers which have a property of interest (e.g. high cell attachment). Alternatively, they may aim for the development of quantitative structure–property relationships which aim to improve our understanding of the key causal factors underlying the properties of ‘hit’, ‘miss’ and intermediate performance polymers. In this case, the surface chemical data (ToF-SIMS and/or XPS) is termed the independent variable, and the data describing the surface property to be predicted is termed the dependent variable. If the independent variable is composed of multiple observations such as spectral data from ToF-SIMS (i.e. it is multivariate in nature), it is necessary to use multivariate regression techniques to identify correlations. These include Multiple Linear Regression (MLR), Principal Component Regression (PCR) and Partial Least Squares (PLS) regression.^[21]

PLS has been previously used in the field of biomaterials to study the relationship between surface chemistry and endothelial cell adhesion on plasma polymer deposits,^[22] and to investigate the relationship between surface chemistry and protein adsorption.^{[23 – 25]} We have recently reported the application of PLS to investigate how different surface functionalities influence wettability, using ToF-SIMS and water contact angle data from a library of 576 novel acrylate copolymers which were printed in microarray format and UV-cured on a poly(2-hydroxyethyl methacrylate) (pHEMA) coated glass slide.^[26] PLS is a multivariate statistical method allowing models to be built that relate a set of multivariate data to a set of univariate data.^[27] Multivariate techniques such as PLS use factors to describe the variance in the dataset, thereby reducing the dimensionality of the data. PLS specifically finds factors (called latent variables) that describe variance in both the independent and dependent variables, i.e. to maximise the covariance described by the model. Covariance is a measure of how closely the independent and dependent variables follow the same trends. The data used to build the PLS model is termed the training set. The predictive ability of a PLS model can be assessed using a test set of samples which have not been included in the training set. This is called validation. An alternative method is cross-validation which does not require a test set, only the original data in the training set. The most common form of cross-validation is the Leave One Out (LOO) method which involves leaving out of the training set one sample at a time, then repeating the PLS model. The error in the predictions of the samples left out can then be determined. LOO cross-validation is commonly used to determine the optimum number of factors used to build a PLS model, i.e. the number which gives a model that adequately describes the variance within the training set data, without including any variance due to noise in the data. Using too many latent variables inevitably leads to a model which over-fits the data.

In ToF-SIMS data analysis, a PLS model assigns each ion with a regression coefficient which quantifies the influence it is having on the model. If an ion has a positive regression coefficient it is positively correlated with the univariate variable and the opposite is true for ions with a negative regression coefficient. Ions with a regression coefficient close to zero do not significantly influence the model. These regression coefficients can be used to build an understanding of the relationship between the two datasets. It is important to emphasise that although PLS can help predict a response, it does not actually explain any underlying relationships between variables. The theory of PLS is described in greater detail elsewhere.^[28,29]

In this paper we investigate how the conclusions reached from this type of PLS model are affected by the number of different samples in the polymer library, and importantly, the chemistry of the monomers making up the polymers included in the training set. We investigate whether the information gained has any predictive application outside the group of copolymers used to build the model, using test copolymers synthesised from the same monomers as the training set and other polymers that are chemically different.

Experimental Details

Polymer microarray synthesis

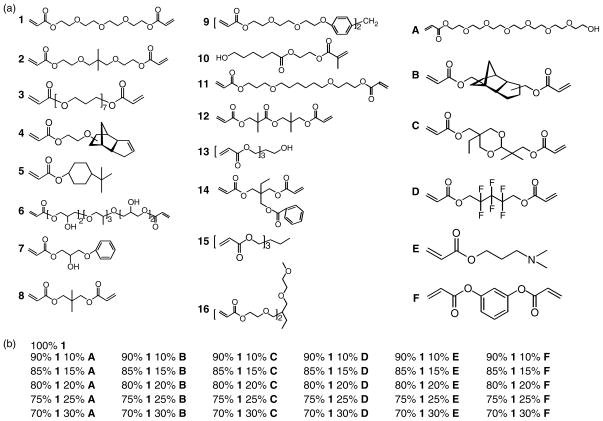
The microarray under investigation was comprised of 496 novel acrylate-based polymers synthesised from 16 major monomers which were mixed pairwise with 6 minor monomers in the following ratios: 100 : 0, 90 : 10, 85 : 15, 80 : 20, 75 : 25 and 70 : 30 (Fig. 1(a)). A radical initiator was added to the monomer mixtures which were then spotted onto a pHEMA-coated glass slide. They were then polymerised with ultraviolet light. Full details of array manufacture can be found elsewhere.^[14] Each polymer is synthesised from two monomers, therefore, to avoid confusion in this paper we will refer to the monomer comprising the majority (90, 85, 80, 75 and 70%) of a polymer as the ‘major monomer’ and the monomer comprising the other 30, 25, 20, 15 or 10% as the ‘minor monomer’. The microarray was printed in triplicate on the slide, therefore, the water contact angle, diiodomethane contact angle and ToF-SIMS measurements were each conducted on one of the three microarrays.

Figure 1.

(a) Structures of the 16 major and 6 minor monomers which were used to create the polymer array; and (b) the ratios of monomers used to create the 31 polymers containing the major monomer 1. The same ratios were used for each of the 16 major monomers to create 496 novel polymers.

Preparation of polymer films

Solutions (1% w/v) of polystyrene (PS) (Mw 100 000), poly(_L-lactic acid) (P_LLA) (Mw 95 000), poly(methyl methacrylate) (PMMA) (Mw 60 000), poly(dimethlsiloxane) (PDMS) (Mw 1000) and poly(2-hydroxyethyl methacrylate) (Mw 20 000) were prepared in chloroform. All polymers were purchased from Sigma Aldrich. Silicon wafers were cleaned using UV light, then sonicated in methanol. The polymer solutions were spin-coated onto the clean silicon wafers at 3000 rpm. The polymer films were left for 24 h before contact angle measurements. The surface of a piece of poly(tetrafluroethylene) (PTFE)(Krüss) was scraped clean before contact angle measurement.

Time-of-Flight Secondary Ion Mass Spectrometry

An ION-TOF ToF-SIMS IV instrument was operated using a monoisotopic ⁶⁹Ga⁺ primary ion source operated at 25 kV and in ‘bunched mode’. A 1 pA primary ion beam was rastered over a 100 × 100 μm area of each polymer spot on the microarray. A 60 s acquisition time was allowed for each polymer sample, ensuring that static conditions were maintained for every spectra acquired. Ion masses were determined using a ToF analyser allowing accurate mass assignment (to typically 40 ppm). The typical mass resolution (at m/z 41) was just over 6000. ToF-SIMS analysis of the microarray was fully automated via the design of a macro using ION-TOF ToF-Bat software, allowing completely unattended operation. ToF-SIMS analysis of polymer microarrays has been described in greater detail elsewhere.^[19] One positive and one negative spectrum were obtained for each polymer on the microarray. The reproducibility of these measurements has been determined previously using principal component analysis and found to be very good.^[26]

Partial least squares regression

The positive and negative ion spectra for all 496 polymers were automatically mass calibrated using ION-TOF ToF-Bat software.^[30] Mean deviations of <40 ppm from true mass for m/z 0–100 were noted after automatic calibration. One peak list each was then created for both positive (344 peaks) and negative (92 peaks) ion spectra using mass spectra taken from a group of polymers from the array containing monomers with widely varying chemistries. This group included polymers synthesised using all the monomers in Fig. 1. This peak list was then applied to all 496 polymers. The peaks were then integrated using ION-SPEC software and peak intensities exported to Origin Pro 7.5. The positive and negative ion intensities for each polymer were separately normalised to the total ion count, to account for normal variation in secondary ion yield between polymers. The positive and negative ion data for all 496 polymers was then arranged into one concatenated data matrix. PLS analysis was carried out using Eigenvector PLS Toolbox 3.5 for Matlab. The ToF-SIMS and surface energy data were mean-centred before analysis. The Root Mean Square Error of Prediction (RMSPE) was calculated to quantify how well each model predicted the training set or test set polymers.^[31]

The SIMPLS algorithm was used for the PLS analysis rather than the other commonly used algorithm NIPALS.^[32] The two algorithms have been shown to give equivalent results when analysing a dataset where the independent variable is multivariate and the dependent variable is univariate.^[33]

Surface energy measurements

Contact angles were determined for each polymer on the array using two liquids: Ultrapure water (18.2 MΩ resistivity at 25 °C) and diiodomethane (≥99% pure) (Aldrich). A DSA100 (Krüss) with a piezo-doser head was used to dispense a 100 pL droplet of each liquid onto the centre of each polymer spot on the array. Data acquisition was automated with the side profile of the back-lit spot being recorded. A dual camera system was used, one to record a profile of the spot and the other to record a bird’s eye view of the spot to ensure that the water droplet was deposited at the centre of each polymer. Data analysis involved following standard contact angle measurement procedures except that due to the small droplet size circle fitting was used instead of Young–Laplace.^[34] Polar and disperse surface energy values were calculated using the Owens and Wendt’s model as described elsewhere.^[35,36] Total surface energy was calculated by the addition of the polar and disperse values. Macros were written to enable rapid calculations for the large dataset. Although more than two probe liquids may be used when using the Owen–Wendt method, the use of only two liquids is common in the literature, and it has been demonstrated that when a polar and non-polar pair of liquids is used accurate surface energy measurements can be obtained.^[36]

Results and Discussion

The use of PLS as a tool in surface analysis is well established, however, the number of samples analysed using this method have been relatively small, with closely related chemistries through the range of samples.^{[22 – 25]} The application of PLS to large polymer libraries containing hundreds of samples of very different chemistries is a new development and the limits of this approach have not yet been systematically investigated. Thus, here we have used a dataset acquired from a 496-member copolymer library printed in microarray format, comprising ToF-SIMS spectra and surface energy values. The positive and negative ToF-SIMS spectra were obtained in an automated fashion using a methodology described previously over an acquisition period of approximately 6 h.^[19] The surface energy values were calculated from water and diiodomethane contact angles measured from picolitre volume droplets over an acquisition period of approximately 24 h. The polar and dispersive components of the surface energy were calculated using the Owen and Wendt’s model, although only the total value is used in this illustrative study.^[37] A PLS model was built using these two datasets with ToF-SIMS ions intensities as the multivariate parameter and total surface energy as the univariate parameter.

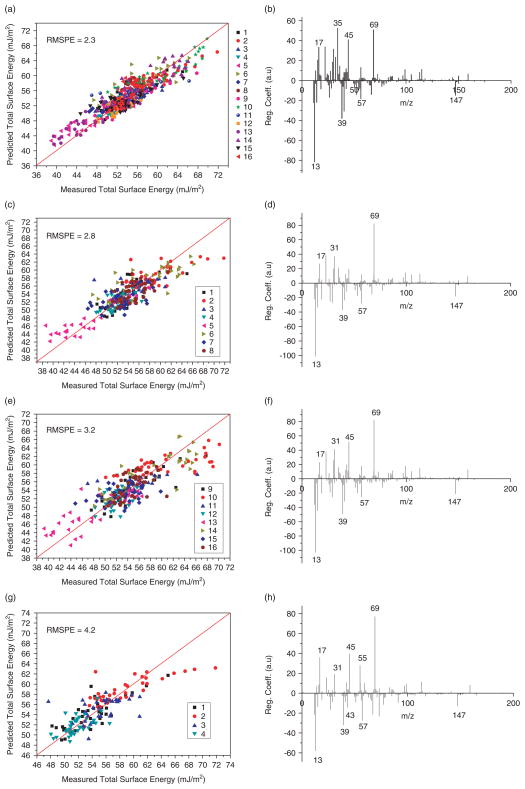
PLS models were constructed using either mean centring, auto-scaling or no pre-processing of the ToF-SIMS and surface energy data. The models constructed using data that was auto-scaled or did not undergo any pre-processing had a very low predictive ability for samples within the training set (RMSPE > 20), therefore, mean-centring was chosen. The model was cross-validated using the LOO method, which indicated that the root mean square error of cross-validation reached a minimum at 5 latent variables. When the experimental values of γ are plotted against those predicted by the PLS model (Fig. 2(a)), a linear relationship with a relatively low RMSPE is observed, suggesting a good predictive ability for the copolymers within the training set (RMSPE = 2.3). Figure 2(b) shows the regression coefficients for the PLS model. It can be seen that the ions with the greatest positive regression coefficients have m/z of 34.992 (Cl⁻), 69.034 (C₄H₅O⁺), 45.034 (C₂H₅O⁺), 22.991 (Na⁺), 17.003 (OH⁻) and 15.996 (O⁻). The ions with the largest negative regression coefficients have m/z of 13.008 (CH⁻), 39.023 (C₃H₃⁺), 41.039 (C₃H₅⁺), 12.000 (C⁻), 15.023 (CH₃⁺) and 57.071 (C₄H₉⁺). The ions positively correlating with γ are predominantly oxygenated hydrocarbons (Table 1). Ions negatively correlating with γ are all hydrocarbons with the exception of C⁻ and Si₂C₅H₁₅O⁺ (Table 1). These results agree with theory concerning the molecular basis of polymer surface energy.^[38] The disperse surface energy of the copolymers in the library is relatively invariant (between ~40 and 50 mJ/m²), therefore, it is changes in the polar component that are responsible for most of the differences in total surface energy.^[37] Oxygenated groups at a polymer surface can form hydrogen bonds, increasing the polar contribution to total surface energy. Attractive forces at surfaces that are predominantly composed of hydrocarbon-containing moieties will mainly be due to dispersive London-van der Waals forces, hence the polar contribution will be very small.

Figure 2.

Measured versus predicted surface energy, and regression coefficient versus m/z are shown for each PLS model. PLS models constructed using (a) and (b) 496 polymers; (c) and (d) 248 polymers (major monomers 1–8); (e) and (f) 248 polymers (major monomers 9–16); and (g) and (h) 124 polymers (major monomers 1–4). X = Y lines are provided to guide the eye. This figure is available in colour online at www.interscience.wiley.com/journal/sia.

Table 1.

Structural assignments for ions with the largest regression coefficients in the PLS model containing all 496 polymers

m/z	Positive regression coefficient	Ion structure	m/z	Negative regression coefficient	Ion structure
15.996	21	O−	12.000	−22	C−
17.003	33	OH−	13.008	−82	CH−
22.991	34	Na+	15.023	−22	CH3+
30.010	19	CH2O+	27.023	−17	C2H3+
31.019	32	CH3O+	39.023	−38	C3H3+
34.992	53	Cl−	41.039	−31	C3H5+
45.034	41	C2H5O+	43.056	−8	C3H7+
57.033	13	C3H5O+	53.038	−14	C4H5+
69.033	51	C4H5O+	55.055	−10	C4H7+
42.031	5	C2H4N+	57.071	−18	C4H9+
42.011	8	C2H2O+	67.050	−14	C5H7+
43.019	12	C2H3O+	147.071	−15	Si2C5H15O+

We investigate two aspects relating to PLS modelling of such a large and varied library of copolymers. Firstly, we will investigate whether the number of the samples in the library influences the ions identified to control the surface energy through assignment of large positive or negative regression coefficients. Secondly, we will investigate the limits of the PLS model in predicting the surface energies of polymers outside the training set.

The Influence of Sample Number on Ions Identified in Regression Vector

To investigate the effect of sample number on the key ions identified in the regression vector, the PLS model of the 496 copolymer dataset above was split in half to produce two new datasets, each one containing 8 major monomer groups (major monomers 1–8 or 9–16, i.e. 248 copolymers each). Each copolymer in the library under investigation contains 1 of 16 monomers as its major constituent (major monomer) and 1 of 6 monomers as a minor constituent (minor monomer). New PLS models were then constructed for each of these two datasets. The number of latent variables used for each new model was again decided by the LOO cross-validation method. When the surface energy values predicted by each of these two new models were plotted against the measured values, the RMSPE were higher (average = 3.0) than the original model (Table 2), indicating a lower predictive ability for polymers within the two smaller training sets (Fig. 2(c) and (e)). Analysis of the regression vectors of these two new models showed that the dominant ions contained in both were the same and were also identical to the original 496 copolymer model (Fig. 2(d) and (f)). The ions positively correlating with surface energy were still predominantly oxygenated hydrocarbons, and those negatively correlating were still hydrocarbons. However, it was noted that there were differences in the relative and absolute magnitude of the regression coefficients of these ions.

Table 2.

Comparison of PLS models with different numbers of samples

Dataset	RMSPE	Number of latent variables
496 polymers (Full)	2.3	5
248 polymers (Major monomers 1–8)	2.8	4
248 polymers (Major monomers 9–16)	3.2	4
124 polymers (Major monomers 1–4)	4.2	5
124 polymers (Major monomer 5–8)	5.9	4
124 polymers (Major monomers 9–12)	5.0	5
124 polymers (Major monomers 13–16)	5.5	5
31 polymers (Major monomer 1)	1.2	5
336 (minus minor monomers E & F)	3.2	5

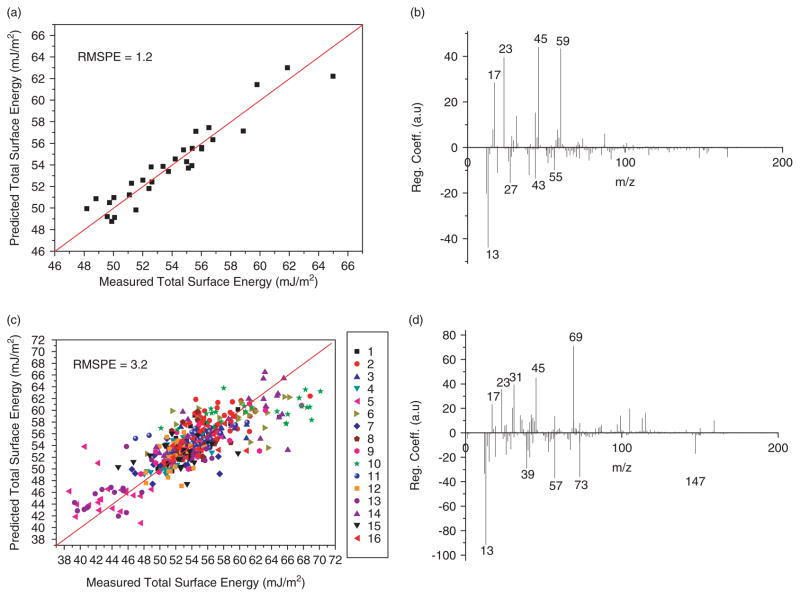
The 496-copolymer dataset was then split into quarters: major monomers 1–4, 5–8, 9–12 and 13–16, each containing 124 copolymers. Each of these groups was then used to build a new PLS model. The RMSPE of the new models (mean = 5.2) are higher than that of the model describing all 496 copolymers (Table 2). Analysis of the regression vector of these models identified the same ions as the full and half datasets; however, there are some subtle differences in the regression vector for major monomers 1–4 (Fig. 2(h)). For example, the ion at m/z 55.055 corresponding to C₄H₇⁺ has a positive regression coefficient, and the ion at m/z 43.019 corresponding to C₂H₃O⁺ has a negative regression coefficient, the inverse of which is observed in the full and half models. There also appears to be a systematic underestimate of predicted surface energies for polymers containing monomer 2 in this model (Fig. 2(g)). This result could suggest that reducing the sample number might lead to anomalies in the regression coefficients obtained due to the more limited range of chemistries in the training set. Therefore, to test this observation the 31 polymers containing major monomer 1 were used to construct a PLS model. The RMSPE value of this model (1.2) is lower than that of the original model (Fig. 3(a)). The regression coefficients of this model are very similar to the model of all 496 copolymers, without the anomalies seen in the model for major monomer 1–4 (Fig. 3(b)). The main difference is the complete absence of the peak at m/z 69.033 corresponding to C₄H₅O⁺. This is combined with the large increase in the positive regression coefficient of the peak at m/z 59.050 corresponding to C₃H₇O⁺. These changes do not contradict the results of the original model and are probably due to the decrease in the variety of surface chemistries included in this model (i.e. only 7 out of 22 monomers). It is also possible that for this group of polymers the peak at m/z 59.050 correlates more strongly with surface energy than the peak at m/z 69.033.

Figure 3.

A–D, measured versus predicted surface energy and regression coefficient versus m/z is shown for each PLS model. PLS models constructed using (a) and (b) 31 polymers (major monomer 1); and (c) and (d) 336 polymers (minor monomers). X = Y lines are provided to guide the eye. This figure is available in colour online at www.interscience.wiley.com/journal/sia.

We postulate that the change in RMSPE values seen above (i.e. a maximum error is observed for intermediate sample numbers in the training set) reflects a changing balance between two competing influences on the PLS models and the number of latent variables used. This balance is between the number of samples included and the chemical diversity of the polymers in the training sets. The model describing all 496 copolymers is very chemically diverse, but this is balanced by the large number of samples included in the training set. Conversely, the model containing 31 polymers has a significantly lower sample number but also much less chemical diversity. Indeed, the high RMSPE value seen in this model is probably the result of using 5 latent variables to describe the variation of only 7 monomers within this group of polymers. The models containing 248 and 124 polymers contain significant diversity, however, have much fewer samples in the training set, and therefore exhibit an increase in the RMSPE values. In summary, changing of sample number influences the auto-predictive capabilities of the PLS models due to the changing balance between the diversity of the training sets and the number of latent variables used to model them.

We can conclude from this exercise that a reduction in sample number does appear to systematically affect the auto-predictive capabilities of the model, i.e. the ability to predict surface energy of polymers within the training set (as judged by the RMSPE value). However, analysis of the regression vectors of the reduced sample models indicate that the same general chemical conclusions can be drawn from regression coefficients of the different models, even though there is a change in the relative magnitude of the regression coefficients for each ion. Unsurprisingly the ions observed in the regression vector are dependent upon the chemistry of the polymers included in the training set.

Investigating the Predictive Ability of the PLS Model outside of the Training Set

The analysis of the PLS models we have obtained has given us further understanding of which ions govern the surface energy of the acrylate copolymers, and therefore, an indication of which surface structures are influential. The fact that the results from this analysis make chemical sense, e.g. hydrocarbon C_nH_n^+/− ions correlate with low surface energy and polar-oxygenated hydrocarbon C_nH_nO_n^+/− ions correlate with high surface energy, gives us confidence in the method. Plotting the measured surface energy values versus those predicted by the PLS model (and calculating RMSPE) has demonstrated the model has good quantitative predictive ability for those polymers within the training set (Fig. 2(a)). However, the model has limited use in predicting surface energy if it is only applicable to polymers within the initial training set. To investigate the extent of the predictive ability of the above PLS model outside the library of acrylate copolymers used in the training set, we used three test sets. The first set contained acrylate copolymers containing the same monomers as the training set, but in different proportions. The second group contained acrylate copolymers synthesised using minor monomers not included in the training set. The third test set comprised six commercially available linear polymers. Hence we investigated predictions using test polymers with varying degrees of similarity to those in the training set.

Acrylate copolymers synthesised using monomers included in the training set

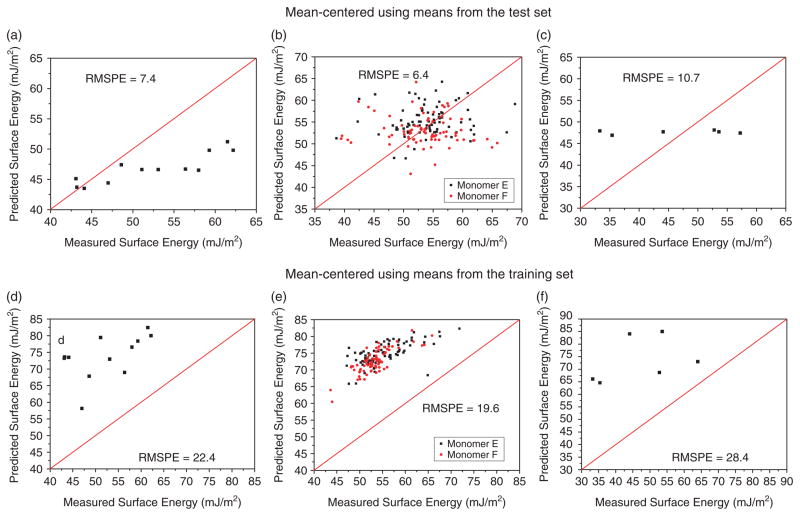
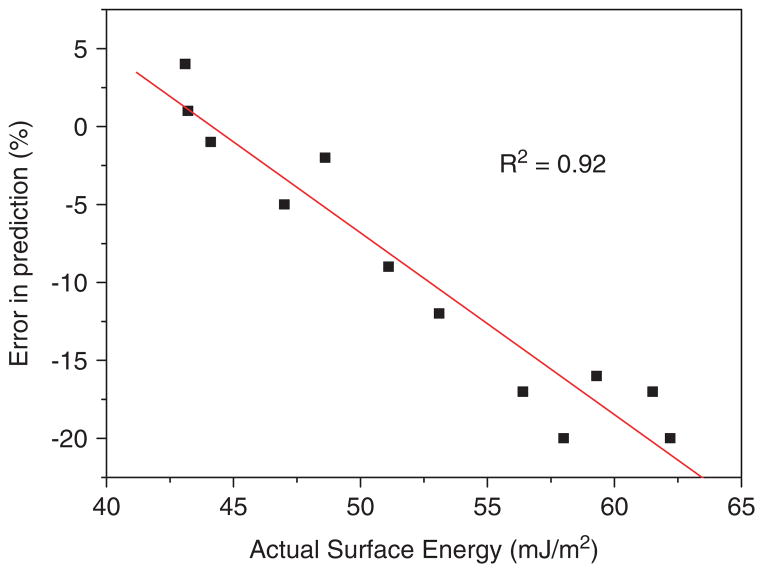
We used the PLS model of the full 496-copolymer dataset to predict the surface energies of 12 acrylate copolymers from a different library. The error in the predictions ranged from ~1 to 20% compared to an error of approximately ±10% in predictions for polymers within the training set (Fig. 2(a)). The error in the predictions for the 12 test polymers appears to be systematic, i.e. the predictions for the polymers with relatively low surface energies is low (<5%), whereas the error increases linearly as polymer surface energy increases (Fig. 5(a)). This is more apparent when the error in prediction is plotted against polymer surface energy (Fig. 4). There are a number of things that could explain this error in surface energy prediction. For example, the error may possibly be due to the pre-processing of the data prior to analysis; both the ToF-SIMS and surface energy data were mean-centreed, which is common prior to multivariate analysis to ensure that numerically larger variables do not unduly influence the statistics.^[39,40] This data transformation sets the origin of the model arbitrarily to the mean of the training set (46.6 mJ/m²), therefore, the model will describe deviations from this mean. However, the mean surface energy of the polymers in the test set is 52.3 mJ/m². To test this theory, the ToF-SIMS ion intensities of the test dataset were mean-centreed using the means from the training set. Predictions were then obtained using these data, and rescaled using the mean of the surface energy values from the training set. This time the model over-estimated the surface energy values of the polymers, with a considerably higher RMSPE (Fig. 5(d)).

Figure 5.

Measured versus predicted surface energy values for (a) & (d) 12 acrylate copolymers synthesised from monomers common to training set; (b) and (e) 160 acrylate copolymers synthesised from monomers not used in training set; (c) & (f) 6 commercially available linear polymers; using data mean-centered using means from both the test and training sets. X = Y lines are provided to guide the eye. This figure is available in colour online at www.interscience.wiley.com/journal/sia.

Figure 4.

Actual surface energy of a polymer versus the error in the predicted surface energy using a PLS model. This figure is available in colour online at www.interscience.wiley.com/journal/sia.

Acrylate copolymers containing minor monomers not included in the training set

Although the 12 polymers used in the test set above were not included in the 496 copolymer training set, they are chemically related, i.e. all monomers used to synthesise the test set polymers are represented in the training set. To test the predictive ability of this approach on copolymers that were more chemically disparate, we proceeded to obtain predictions for acrylate copolymers synthesised from monomers not used in the training set. To achieve this aim a PLS model was constructed using data from the 336 copolymers in the library that were synthesised using minor monomers A–D. The resulting PLS model has an RMSPE value of 3.2 which is greater than the full model generated from all 496 polymers (Table 2). Analysis of the regression vector indicates that again, predominantly, the same ions positively and negatively correlate with surface energy, with the same variation in magnitude of regression coefficients observed in the other reduced sample datasets. However, ions with m/z 29.028 (CH₃N⁺), 42.031 (C₂H₄N⁺) and 58.068 (C₃H₈N⁺) (Fig. 3(d)) are completely absent from the regression vector. These ions can only be formed by cleavage of the tertiary amine group in monomer E; therefore, it is unsurprising that the removal of polymers containing this monomer results in the disappearance of these ions from the regression vector.

This model was then used to predict the surface energies of the remaining 160 copolymers that contain minor monomers E and F (Table 2). Monomer E contains a tertiary amine functionality, and monomer F contains a phenyl group. Therefore, the copolymers in this test set contain monomers not included in the training set. The predicted values for the test set are considerably different from the actual surface energy values (Fig. 5(b)), with a much greater apparently random error than previously obtained. The predictions for the polymers containing either monomers E or F are equally inaccurate. This inaccuracy might be expected for those samples containing monomer E as there are no similar chemical functionalities within the training set. However, monomer F is a phenyl diacrylate, therefore, it might be expected that monomers included in the training set such as 7, 9 and 14 would produce similar secondary ions. This data suggests that it is probable that the model only has a predictive capability for polymers that are chemically related to those in the training set, i.e. contain the same monomers, as noted above.

As shown above, the ToF-SIMS data for these polymers was then mean-centreed using the means from the training set and predictions obtained (Fig. 5(e)). Although the RMSPE is considerably higher than previously, the relatively random error in the predictions has disappeared. Indeed, the predictions appear to differ systematically from the measured values, i.e. approximately 20 mJ/m² higher, which may suggest that the rescaling of the predictions may be at fault.

Polymers which are chemically unrelated to the training set

To investigate if the PLS model has any predictive application in polymers that are chemically unrelated to the test set, the exercise was repeated for six commercially available linear polymers: PS, P_LLA, PMMA, PDMS, poly(2-hydroxyethyl methacrylate) (pHEMA) and PTFE. All the predictions are within 1 mJ/m² of the average surface energy of the training set, suggesting that the model does not have the ability to discriminate between them and returns an estimate based on this average (Fig. 5(c)). It is probable that this is due to the fact that the spectra of these polymers contain secondary ions not found in the training set, which may be equally or more correlated with surface energy for these samples than those modelled above.

When the exercise was repeated using data mean-centreed using means from the training set, the RMSPE was considerably higher (Fig. 5(f)). Although the predictions are no longer approximately identical to the mean of the training set, there is no correlation with the polymers’ measured surface energy values.

The above exercise has helped us to understand the limits of the predictive power of PLS for the type of copolymer dataset tested here. When the model was predicting samples that were synthesised from monomers that were included in the training set, the model gave the best predictions (with an error of 1–20%). When the model was used to predict polymers synthesised from monomers that were not used in training set the predictions were very poor. Unsurprisingly, when the model was used to predict the surface energy of linear polymers with significant chemical differences from the training set, the predictions all approximated to the mean value of the training set because it did not have the information to explain the differences in the test set. Mean-centring using the mean from the training set may help to improve the predictions in some cases; however, more work is needed to investigate the effect of rescaling the data. Indeed changing the pre-processing method for these models has demonstrated just how sensitive these predictions are to the way the data is scaled (Fig. 5).

Therefore we have demonstrated the importance that the training set is chemically related to the samples on which predictions are to be made. More specifically, for this dataset we have demonstrated that it may be possible to use PLS to make predictions for copolymers synthesised from the same monomers as used in the training set. We expect that these predictions may be improved by more sophisticated data pre-processing.

Conclusions

PLS has been shown to be able to identify surface moieties important in controlling surface energy. These are chemically intuitive, with high surface energy coming from moieties that relate to polar surface species while low surface energy correlates with hydrocarbons. We have shown that the results obtained from PLS modelling of large combinatorial polymer libraries are equivalent to those obtained from much smaller datasets, in terms of the ions identified in the regression vector.

We have also demonstrated that removing acrylate copolymers with unique chemistries from the training set does not largely affect the ions identified in the regression vector significantly, although of course secondary ions specific to those polymers are not present. This is consistent with the supposition that PLS can only model information that has been included in the training set. The PLS model underestimated the surface energy values for acrylate copolymers synthesised from monomers used in the training set, probably due to the pre-processing of the data prior to analysis. The predictive error increased substantially when predictions were made for acrylate copolymers that were synthesised from monomers not used in the training set, suggesting that no predictions could be made for these polymers. Finally, when predictions were made for six commercially available polymers that were chemically unrelated to the training set the values obtained were very poor.

Further work could include repeating this study using a polyatomic primary ion beam rather than the Ga⁺ used here. This would likely give more chemical information, particularly at higher mass ranges, which may improve the predictions obtained.