Quantum Mechanics Approaches to Drug Research in the Era of Structural Chemogenomics

Abstract

The rapid growth of the available crystallographic information about proteins and binding pockets creates remarkable opportunities for enriching the drug research pipelines with computational prediction of novel protein-ligand interactions. While ab initio quantum mechanical approaches are known to provide unprecedented accuracy in structure-based binding energy calculations, they are limited to only small systems of dozens of atoms. In the structural chemogenomics era, it is critical that new approaches are developed that enable application of QM methodologies to non-covalent interactions in systems as large as protein-ligand complexes and conformational ensembles. This perspective highlights recent advances towards bridging the gap between high accuracy and high volume computations in drug research.

INTRODUCTION

In the modern age, the success rate of drug discovery efforts is largely dependent on the efficient symbiosis of experimental studies such as X-ray crystallography, medicinal chemistry, classical and reverse pharmacology with computational predictions. Computational methods can now substantially contribute to hit discovery and optimization as well as to multi-target compound profiling for safety, toxicity, or polypharmacology. The rapid growth of available crystallographic information about proteins, binding pockets, and transient protein-ligand interactions dramatically expands the applicability domains of structure-based computational chemistry approaches and prompts the development of faster and more accurate docking and scoring algorithms.

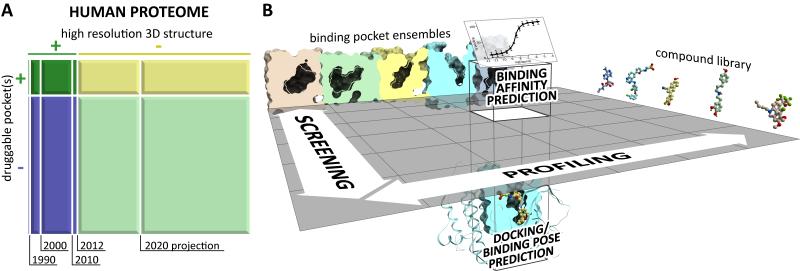
According to different estimates, about 20% of the human proteome may have druggable pockets.¹ This corresponds to about 4,000 proteins in the entire human proteome.^2-4. As of October 2012, more than 18 thousand proteins from the manually curated section of the UniProt knowledgebase⁵ were represented among the 85 thousand Protein Data Bank entries (PDB⁶), with 4.6 thousand of these entries being human proteins. The number of proteins that have been co-crystallized with drug-like small molecules thus far (and are available in the PDB) is around 2,400; of these, approximately 800 are human. In other words, structural information is available for 20% of the potential human pocketome. Several online resources, including Pocketome,¹ PDBSite,⁷ ReliBase,⁸ MSDsite,⁹ sc-PDB,¹⁰ and LigBase¹¹ provide comprehensive structural characterization of the available pockets and their interactions with transient ligands, while other databases (e.g. PDBbind,¹² Binding MOAD,¹³ BindingDB,¹⁴ AutoBind¹⁵) complement it with relevant biochemical information.

The number of unique proteins in the PDB grows constantly with annual increment reaching almost 1000 per year in the years of 2005-07. Although in the recent years, this growth has been gradually slowing down, the structural coverage of the human pocketome is expected to further increase and achieve 50% by the year 2020 (Figure 1A). Pharmaceutical importance and ease of crystallization are among the two main factors that bias this coverage towards certain classes of protein targets. Soluble proteins such as protein kinases, cytochromes P450, or nuclear receptors dominate the structural human pocketome, while membrane proteins are scarcely represented. However, recent breakthroughs in membrane protein crystallization technologies ^16-18 has led to a significant increase in the number of structures of G-protein coupled receptors in 2008-12.

Figure 1.

(A) Retrospective dynamics and projected estimates for the structural coverage of the human proteome and pocketome (B) Main classes of computational drug discovery applications.

21^ST CENTURY PROBLEMS IN STRUCTURE-BASED COMPUTATIONAL CHEMISTRY

The real-life problems addressed by computational chemistry and utilizing crystallographic information about pockets/ligand interactions fall into one of the four classes (Figure 1B): (i) compound docking or pose prediction, (ii) compound screening, (iii) compound profiling, and (iv) compound binding affinity prediction.

Compound binding pose prediction is performed for a single compound and a single binding pocket, although the latter is possibly represented by more than one structure. Solving this problem requires generation of a large number of diverse compound poses with their subsequent scoring and ranking in the pocket structure(s). Real life difficulty arises when none of the pocket structures is a cognate structure (i.e. the structure co-crystallized with the compound in question). Methods for solving the compound pose prediction problem can be efficiently benchmarked if the answer in the form of co-crystallized complex is available but eliminated from the prediction (the so called cross-docking problem). Pose prediction is considered successful if the best ranking compound pose reproduces all essential contacts observed in the co-crystal complex (answer). Root-mean-square deviation (RMSD) of the compound to its crystallographic pose after the superposition of the binding pocket structures is frequently used to evaluate the docking algorithm performance, however, it is not as accurate or informative as the contact-based measures.¹⁹ Notably, the correlation, or even the relative ranking correspondence between the pose accuracy and scoring is not required beyond the best scoring pose being sufficiently accurate according to the selected accuracy evaluation criteria.

In compound screening, different compounds have to be docked and scored in a single binding pocket which is possibly, and preferably, represented by more than one structure. Based on the calculated docking scores, each compound is assigned a level of confidence on the assumption that it binds to the target pocket. The output of a screening algorithm is a “yes” (binder) or “no” (non-binder) prediction for each compound in the screened database, ideally complemented by a numerical indication of prediction confidence in each case. Screening methods can be benchmarked when an answer to the problem is available in the form of a compound set in which some of the compounds are experimentally confirmed binders to the pocket in question while others are not (inactives or decoys). For realistic difficulty, the negative part of the compound answer set must be similar to the active compounds by physico-chemical properties or even by chemical structure.²⁰ The screening prediction is considered successful if the actives are consistently ranked higher by the model than the inactives or decoys. Again, correlation between compound scores and binding affinity is not required, although it may improve screening accuracy.

In compound profiling, a single compound is docked and scored in the binding pockets of multiple proteins, each possibly represented by more than one structure. The output of the profiling procedure is an assignment, for each target pocket, of the likelihood that the compound in question binds to this pocket. As with compound screening, correlation between compound scores and binding affinity is irrelevant. Large scale benchmarking of the profiling problem is hard due to the limited availability of experimental datasets. Authors are aware of only a few initiatives in experimental profiling of large compound sets against a wide panel of targets (e.g. ^21,22). Due to protein-specific shifts in the binding energy that are unaccounted in any of the existing scoring functions, the absolute compound scores are typically calculated in different scales for different target pockets; therefore, normalization and/or parameterization is required in order to achieve comparable scoring between different targets. This is however hard to achieve without overtraining of the models due to the limited availability of benchmarking sets.

Finally in binding affinity prediction: one or more compounds are docked and scored in one binding pocket possibly represented by more than one structure. In this application, the success is defined by the correlation of the predicted binding scores with the experimentally measured compound binding affinities. The methods for binding affinity prediction can be benchmarked although care should be taken to ensure that the experimental affinities in the benchmarking sets come from uniform sources and assays.

The above classification encompasses the majority of the computational drug discovery applications. The fourth task, binding energy prediction, benefits the most from the ab initio methods due to smaller benchmarking sets and high danger of overtraining when empirical or knowledge-based methods are used. For some targets, the computational analysis is bound to go beyond docking and scoring: for example, understanding of potency, specificity and selectivity of covalent inhibitors and transition state analogs requires analysis of reaction paths and reactive intermediates.^23,24 In recent years, covalently acting drugs draw growing interest and attention,^25,26 making this an extremely important field of research, Finally, full characterization of drug candidates includes their interaction not only with their intended or unintended targets, but also with metabolizing most – enzymes importantly, cytochromes P450,^27,28 – i.e. requires tools for understanding of metabolic activation/degradation and formation of reactive metabolites.

PREDICTION METHOD INACCURACIES VS INPUT DATA INACCURACIES

As delineated above, most computational chemistry applications are centered on two critical steps performed for each compound and each pocket structure: conformational sampling and scoring of the obtained poses.²⁹ Conformational searches based on molecular dynamics (MD) or Monte Carlo (MC) simulations, enhanced and modified to dramatically increase the coverage and convergence rate,^30,31 remain the only practical alternatives for sampling; given sufficient sampling time these methods usually produce correct or nearly correct conformations which may or may not be ranked first in the conformation list. Following the conformation generation, the scoring step may be performed in a multitude of ways depending on the specific applications; the arsenal of classical scoring functions includes force-field based, empirical, and knowledge-based functions ³² and it is increasingly enriched by hybrid solutions that involve ligand-centered information (e.g. ^33,34). Molecular mechanics (MM) force-field scoring functions employ energy terms designed to closely approximate ab initio quantum mechanics (QM) calculations (e.g. ^35-37); however, they typically undergo parameterization by fitting the scores to the experimentally observed values (for binding affinity prediction) or by optimizing separation of correct from incorrect poses (for docking) or of binders from non-binders (for screening). As a result, the relative contributions of physics-based terms in the scoring function have empirical nature and reflect, along with the significance of each term, the degree of inevitable numerical inaccuracies and variation in its calculation.

The applicability domain of a force-field-based scoring function is limited to those interactions and atom types that are present in the input set at the design and parameterization stages. Therefore, energy contributions that result from changes in the molecular environment on compound binding cannot be accounted for properly.³⁸ For example, atomic partial charges in the ligand or the binding site may vary from those assigned by the utilized force field due to polarization or charge transfer – the effect that is frequently observed with enzymes and metalloproteins.³⁹ Halogen bonds, CH-π,^40,41 π-π and cation-π interactions are usually not accounted for at sufficient accuracy. In some configurations, London dispersion forces may not be properly approximated by the widely used potentials. Last, but not the least, force fields cannot properly address processes of covalent bond formation or breaking and are therefore inapplicable to simulations of enzyme reactions or covalently acting inhibitors.⁴² Ab initio, force field independent methods that can describe these interactions may therefore lead to more accurate compound activity predictions.

That being said, the inaccuracies in the scoring functions (force-field based or otherwise) are not the main reason for insufficient predictive power of the structure-based computational methods.⁴³ The most important reason lies in the inherently incomplete nature of the input data, i.e. the crystallographic structures. Limited resolution of structure determination techniques creates ambiguities in side-chain placement, orientation, and protonation states, as well as uncertainties in positions and orientations of rotatable polar hydrogens.⁴⁴ Water molecules frequently remain unresolved or ambiguous but may have very pronounced effect on predictive properties of a 3D model in cases when they form stable hydrogen-bonding networks between the ligand and the binding site or on the contrary, are conformationally restricted and therefore unfavorable entropically.^45,46 Finally, crystallographic structures represent only static snapshots of the target pockets, with their shape largely defined by the co-crystallized ligands (the so-called induced fit effect). Even with the current trends in structure determination, experimental coverage of all possible binding site conformations is impossible. These inevitable limitations stress the critical importance of the ability to accurately reconstruct ligand binding poses and interactions when the target pocket is in a sub-optimal conformational or protonation state. The only practical solution to the problem lies in thorough analysis of compositional (e.g. with and without water) or conformational ensembles,³⁴ which greatly increases the amount of 3D information that has to be processed in order to analyze interactions of a single ligand with its target.

QUANTUM MECHANICAL CONTRIBUTIONS TO DRUG RESEARCH: CONQUERING THE COMPUTATIONAL COMPLEXITY

Although quantum mechanics characterization of the interactions between proteins and ligands is not a new approach in computational chemistry,⁴⁷ it has been gaining increasing popularity in the recent years.^38,48,49 QM methods overcome the deficiencies of classical force-field scoring functions by avoiding atom type assignment and parameterization. For a system with defined positions of the nuclei, they provide a reliable foundation for ligand geometry evaluations and energy estimates.

A QM calculation starts with a structure or a model of the complex and, although minor conformation refinement can be achieved in the course of QM-based evaluation, the input model largely defines the result. In this sense, QM is heavily dependent on other methods – crystallography, MM docking/refinement, or molecular dynamics in the question of pose generation. Despite the fact that the accuracy of input conformations is critical for the success of a QM simulation, there is a huge gap in the definition of “accurate” between QM and other applications. For example, in the docking field, ligand pose prediction that lies within 2Å RMSD (heavy atoms only!) from the crystallographic answer is considered a success; a QM simulation requires accuracy of ≤0.5 Å (including all hydrogens).⁵⁰

The QM description of a system is not sufficient for its full characterization because it is (i) static and (ii) in vacuo. It is incapable of accounting for ensemble-mediated conformational entropy or solvation effects. Some publications interpret it as QM providing a description of enthalpy, while entropy must be accounted by other methods; this is not entirely accurate as the aspects accounted for by QM have mixed enthalpy-entropy nature. To completely describe the Gibbs free energy in the system, the conformational entropy effects are added via analysis of MM or MD generated conformational ensembles; to account for solvation, the QM approach must be married to implicit solvation models such as REBEL,⁵¹ polarizable continuum model (PCM), Poisson-Boltzmann/Solvent Accessibility (PB/SA), COSMO, and others (reviewed in ⁵²).

The recent and not so recent theoretical advances allow very accurate QM treatment of covalent and, quite importantly, non-covalent interactions in small systems. For example, with a sufficient level coupled-cluster theory binding energies in non-covalent complexes of rigid small molecules can be calculated with errors not exceeding 1 kcal/mol.⁵³ Due to basis set superposition error (BSSE) accurate calculations of van der Waals interactions require at least avg-cc-pVDZ basis set ⁴⁸. The complexity of these calculations, however, is such that only systems of no more than 70 atoms can be treated. Advancing to larger complex sizes requires lower level theory and leads to immediate loss of “chemical” accuracy. Although in the recent blind assessment of host-guest binding energy predictions (SAMPL3,⁵⁴), QM methods produced the most accurate predictions (R² = 0.94), the obtained RMS errors were as large as 5.9 kcal/mol.

Ab initio QM calculations for most protein-ligand complexes are extremely time-consuming at the present state of computational technology, even for a single frozen position of the nuclei involved (i.e. single point calculation). Therefore, a large number of efforts are devoted to the design of simplified representations and computationally efficient approaches that could make QM methods applicable to real-life-size drug discovery problems. These approaches are based on (i) reducing the size of the system to be treated by QM methods; (ii) use of semiempirical QM (SQM) methods, and (iii) system fragmentation and decomposition.

QM/MM

Methods based on reducing the system size frequently divide the system into QM (usually the ligand and its immediate vicinity) and MM (the rest of the system) parts – the so-called QM/MM approach. The QM part may include ions and parts of the protein, and can be treated at any desired level of theory making the approach very attractive for calculations of metalloenzymes. Burger et al studied interactions of 43 binders and 17 decoys to the Cytochrome c Peroxidase⁵⁰ using B3LYP/6-31G* representation for the ligand and CHARMM22 for the protein. When combined with PCM solvation terms, their calculated QM/MM energy was able to impressively score more than 75% of the binders above all but one of the decoys.

If not only the ligand but also parts of the protein are included in the QM region (i.e. if division occurs across covalent bonds), evaluation of the interaction energy between the two (QM and MM) parts becomes a highly non-trivial task for which several approaches have been designed.⁴² Binding of 28 hydroxamate inhibitors to matrix metalloproteinase 9 was studied by Khandelwal et al⁵⁵ using docking, QM/MM optimization, MD and a single point QM/MM evaluation of the time-averaged complexes. To accurately describe the Zn coordination interactions, the QM region consisted of four protein residues, the inhibitor, and the zinc ion, all represented with DFT functional B3LYP, while the remainder of the protein was treated with MM. The interface between QM and MM regions was mediated by frozen orbitals; the region interaction was described by point charge/wave electrostatic interactions and atom/atom van der Waals interactions. Addition of solvent accessible surface area (SASA) term for ligand desolvation produced excellent agreement (R² = 0.9) with the experimental binding energies.

Semiempirical QM

Unlike QM/MM, SQM methods still represent the entire system quantum mechanically. Calculation speed is gained by reducing the basis set and neglecting or simplifying the most computationally intensive integrals. While giving reasonable results for covalent interactions, these approximations largely lead to loss of information on determinants of non-covalent binding, i.e. hydrogen bonding and dispersion forces, which is corrected by introduction of parameterized force-field based terms.⁵⁶ As with classic QM, entropy and solvation terms are added to obtain the binding energy estimates. For example, in their SQM study of interactions of 29 guests of cucurbit[7]uril (CB7) host using the Mining Minima (M2) method and the PM6-DH+/COSMO energy model, Muddana and Gilson⁵⁷ predicted the binding energies with R² = 0.79. In the publication by Fanfrlik et al.,⁵⁸ interactions of 11 known inhibitors with HIV-1 protease were studied using semiempirical PM6-DH2 formalism. Consistent with the known role of entropy in the binding of these ligands, PM6-DH2 scoring of the MM docked poses produced only a weak positive correlation with the experimental affinities (R = 0.3); however the inclusion of AMBER entropy term, SMD desolvation and combined PM6-DH2/SMD deformation energy helped to achieve significant improvement (R = 0.8). The general applicability of this technology remains questionable, as its performance on 15 inhibitors of CDK2 ⁵⁹ was strikingly different: the PM6-DH2 enthalpic term alone produced a good correlation with experiment (R² = 0.87); inclusion of the desolvation and ligand entropy terms decreased it to R² = 0.77, and incorporation of interaction entropy further decreased it to R² = 0.56.

Because SQM optimization and evaluation still takes several hours for a host-guest system and from several days to several weeks for a protein-ligand system on a single CPU, the methods can hardly be applied to the tasks of large-scale compound screening or optimization. To overcome this barrier, Zhou and Caflisch⁶⁰ developed a clever scheme allowing evaluation of docked poses of millions of compounds. They chose to represent the polar interaction centers in the ATP binding site of EphB4 kinase with tiny QM probes: methanol, acetate, methylammonium, guanidinium ions, water and hydrogen fluoride were chosen to represent the polar groups of Ser/Thr/Tyr, Asp/Glu, Lys, Arg, backbone carbonyl and backbone amide groups, respectively. These probes and the ligand were described in PM6 formalism and SQM energies of the poses were calculated taking <0.5 s for a rigid probe and ~30 s for a flexible probe on a single Opteron 244 2.4GHz. A series of QM-, MM-based and manual hit filtering steps eventually led to selection of 23 compounds for validation in an in vitro enzymatic assay against EphB4; among them, one low micromolar inhibitor was confirmed. Although this success rate is rather low and the confirmed hit is rather weak, the study represents the first promising attempt to employ QM methodologies in high throughput virtual compound screening.

Fragmentation and Decomposition

A revolution in the QM treatment of large systems was brought around by the development of linear scaling algorithms that are based on fragmentation of the system and decomposition of the interactions in a way that takes full account of short distance interactions but simplifies or neglects the effects of spatially distant features. Examples include the divide-and-conquer (DivCon⁶¹) and fragment molecular orbital (FMO⁶²) methodologies. An added bonus of fragmentation methods is that they can be adapted easily for parallel computation which is currently becoming widely accessible to researchers.

Illustrating its potential of describing the complete ligand-protein system, FMO was applied to studies of ligand interaction determinants in nuclear receptors (e.g. estrogen α, progesterone, peroxisome proliferator-activated γ, vitamin D, and retinoid X), FK506 binding protein, metalloenzymes (e.g. farnesyl pyrophosphate synthase⁶³), and multiple viral and bacterial targets.⁶² In the article by Mazanetz et al,⁶⁴ the binding of 28 inhibitors to cyclin-dependent kinase 2 was studied with ab initio FMO; 14 of them were represented by crystallographic poses while for the remaining 14, the poses were modeled by analogy and minimized in MMFF94×. The complexes were evaluated by FMO at MP2/6-31G* theory level which, even in the absence of solvation, produced acceptable agreement with experimental ΔG_bind (R² = 0.68). The addition of PB/SA solvation and PLS of relative weights of the different terms improved the correlation to R² = 0.94 (R² = 0.84 on cross-validation).

The power of divide-and-conquer approach was illustrated in ⁶⁵ where the first large-scale validation of a QM-based protein-ligand complex scoring function (QMScore) was attempted. The benchmarking set contained as many as 165 non-covalent complexes and 40 metalloenzymes. The obtained correlation between predicted and experimental affinities achieved R² = 0.48 without fitting and R² = 0.55 with fitting. For the metalloenzymes, the correlation was R² = 0.68 and R² = 0.70 without and with fitting, respectively. Despite the modest correlation values, this work is a huge step forward from other smaller single target studies, as it validates application of a uniform QM-based methodology across heterogenous target and chemical sets. It also illustrated the fact that in multi-target studies, introduction of target-specific binding energy shifts may be the only practical way to bring all calculated energies to the same scale and to make them uniformly comparable across the set.

QM-based atomic charges

In an alternative approach, QM-based partial atomic charges may be calculated, assigned to atoms in the ligand and the binding site, and used in force-field based scoring and ranking. This new charge assignment is expected to be more accurate, especially for complexes with significant charge transfer or polarization. Among several QM methods for calculation of partial atomic charges,^66-68 the one most relevant to protein-ligand binding calculations is Restrained Electrostatic Potential (RESP ⁶⁸). However, due to the computational complexity of QM charge calculations, much effort in the recent years was devoted to development of faster schemes closely approximating RESP and other QM changes.

In Ref. ⁶⁹ the use of using PM6 partial charges resulted in accurate ligand pose prediction for 42 out of 53 diverse benchmark complexes, while the use of Gasteiger charges resulted in only 28 accurate geometries. However, accuracy of the binding affinity estimation using AutoDock scoring function was not influenced by the partial charge calculation method indicating the inadequateness of the scoring function for this purpose.

The influence of different charge assignment protocols on prediction of binding energy was also analyzed on a set of diverse 161 protein-ligand complexes with known binding mode, using an empirical scoring function with the electrostatic term.^70,71 Correlation coefficients between predicted and experimental binding free energy values were 0.89, 0.90, 0.91, and 0.92 for MMFF, TPACM4, AM1-BCC,⁷² and RESP, respectively: an improvement that is not dramatic, but is nevertheless encouraging due to its consistency with the employed level of theoretical difficulty.

The influence QM/MM ligand charge assignment on performance of MM rigid-receptor docking was investigated for 44 inhibitors of checkpoint kinase 1.⁷³ Compounds were docked in the rigid receptor; the polarizable ligand charges were calculated at the B3LYP/6-31G* level and used in the consequent round of re-docking and re-scoring. The use of QM/MM charges improved the correlation between experimental and calculated inhibitor potencies from R² = 0.622 to R² = 0.766 when solvation-free scoring functions were used. However, further pose optimization and evaluation with MM-GBSA resulted in higher correlation coefficients (R² = 0.85) for both MM and QM/MM charge assignment, largely compensating the beneficial effect of QM charge assignment. This illustrates that in many cases, simulations with force-field based charges are sufficiently accurate, as long as solvation is properly accounted for.

CONCLUSION

The QM and QM-based methods for ligand docking and scoring briefly reviewed above showed promising results in application to individual proteins, as long as very accurate and complete complex models (including all necessary water molecules and hydrogen atoms) are available. In these somewhat idealized situations, QM approaches may provide unprecedented accuracy in ranking the binding poses and, most importantly, predicting binding energies. They also significantly decrease the dependence of inevitable calculation error⁴³ on the system size as compared to MM methods.⁷⁴ Detailed studies of a single target and a small set of ~20-50 compounds are now very amenable to QM methodology, making it a preferred choice for the tasks of binding energy prediction and compound potency optimization.

While the associated computational expenses do not warrant the use of QM for larger scale screening studies, it has proved invaluable for characterization of pockets with polarization and charge transfer (e.g. metalloenzymes), covalent interactions, reactive intermediates and transition state analogs. The logical next step in their development would be systematic benchmarking on large diverse sets of protein structures and chemical compounds. This kind of benchmarking is a widely accepted practice in classical MM methods,^75-77 but is only at the initial stages in the QM field.⁶⁵

Along with software development,⁷⁸ QM calculations take advantage of the new hardware. Both single-processor and supercomputing power increases by Moore’s law. For instance, the 18176 core (Opteron QC 2.2 GHz) Chinook supercomputer used by Odoh and co-workers ⁷⁹ ranked 21st in the Top500 List in November 2008 but only 313rd in November 2012 (http://top500.org/system/176078). Another notable modern trend is massively parallel general-purpose calculations on graphical processing units (GPU), and a GPU-based supercomputer has been recently reported to be used as a web-server for protein-ligand docking that accounts for quantum entanglement contribution.⁸⁰

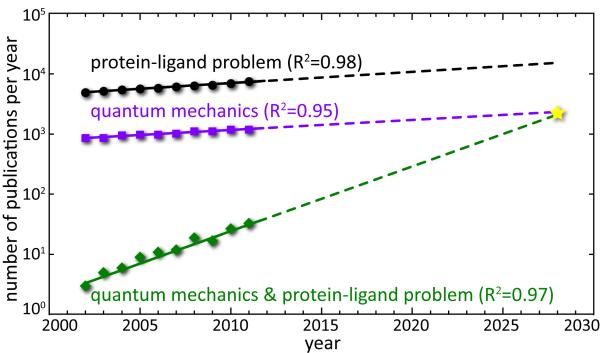
With these advances, QM methods in analysis of protein-ligand interactions become increasingly popular. We analyzed the trends in the field by counting the relevant publications in the Web of Science database (http://thomsonreuters.com/products_services/science/science_products/a-z/web_of_science/) for the last ten years. This analysis shows (Figure 2) that the annual number N_PL of publications devoted to protein-ligand problem grows exponentially with an annual increase of approximately 4%. The same is true for the number N_QM of papers on quantum mechanics. Interestingly, the number N_PL,QM of publications that involve both topics simultaneously grows with the annual increase rate of 28%, illustrating the rapid evolution of this area of research. Quantum mechanics approaches currently constitute less than 1% of all protein-ligand problem publications (i.e. N_PL,QM/N_PL < 1%); however, extrapolation of the present growth trends will result in at least 10-fold increase (up to 5%) of their role in the next decade. If the trends continue, by 2028 virtually all articles on QM will address the protein-ligand problem (N_PL,QM = N_QM) and every seventh published article in the area will use a QM approach.

Figure 2.

Number of articles per year in Web of Science database, returned by search with keywords “(protein AND ligand) OR docking” (protein-ligand problem), “quantum mechanics”, and “quantum mechanics AND ((protein AND ligand) OR docking)” (quantum mechanics in protein-ligand problem), restricted to published in English in the past ten years. Linear fits are calculated and extrapolated to 2028.

While sharing the general optimism on the subject, we have to realize that induced fit and crystallographic errors and ambiguities are a reality. Non-ideal three-dimensional structures dramatically reduce the reliability of QM computations.⁶⁵ Methods that are tolerant to minor structural deviations and are capable of handling diverse conformational ensembles are essential to address this issue. Therefore, rather than seeing QM completely taking over the field, we expect diverse approaches, some working from high-accuracy and others from high volume side of the problem, to slowly converge in their quest of utilizing protein structure for drug research.