Analysis of Chinese hamster ovary cell metabolism through a combined computational and experimental approach

Abstract

Optimization of cell culture processes can benefit from the systematic analysis of experimental data and their organization in mathematical models, which can be used to decipher the effect of individual process variables on multiple outputs of interest. Towards this goal, a kinetic model of cytosolic glucose metabolism coupled with a population-level model of Chinese hamster ovary cells was used to analyse metabolic behavior under batch and fed-batch cell culture conditions. The model was parameterized using experimental data for cell growth dynamics, extracellular and intracellular metabolite profiles. The results highlight significant differences between the two culture conditions in terms of metabolic efficiency and motivate the exploration of lactate as a secondary carbon source. Finally, the application of global sensitivity analysis to the model parameters highlights the need for additional experimental information on cell cycle distribution to complement metabolomic analyses with a view to parameterize kinetic models.

Introduction

Advances in genetic engineering and process development strategies have led to an impressive increase in the recombinant protein titers achieved in mammalian cell culture over the last decade, from a few hundred mg per litre to several grams per litre of broth (Birch and Racher 2006). However, the high demand for such drugs as well as the need for more cost-effective manufacturing dictate that research into improving production titers continues. Metabolomics represent a class of analytical methodologies that aim to detect and quantify intracellular and extracellular metabolites. Such methodologies are increasingly being applied to mammalian cell culture processes to help identify factors critical for cell growth and protein production (Sellick et al. 2011; Ahn and Antoniewicz 2011). Metabolomics are used to detect and analyse a number of metabolites (Sellick et al. 2010), however, the coverage of the entire metabolic map is still limited.

Model-based approaches to cell culture process analysis and optimisation have started to gain ground, with a recent example seeing the application of modelling to analyse the internal metabolic behavior of Chinese hamster ovary (CHO) cells under growth and non-growth phases and identify growth-limiting factors (Selvarasu et al. 2012). Dynamic modeling was also employed in (Nolan and Lee 2011) to analyse the dynamics of nutrient and metabolite transport in CHO cell fed-batch culture, assuming that intracellular metabolic activities were at steady state. Apart from investigating the effect of nutrient addition, which has been addressed in various previous studies (e.g. Kontoravdi et al. 2010), the modeling framework developed by Nolan and Lee provides insight into the impact of temperature shift and seeding density. Such studies demonstrate that reliable model-based approaches can save cost and time when complemented with meaningful experiments.

We have previously presented a kinetic single-cell model of cytosolic glucose metabolism in Saccharomyces cerevisiae and CHO cells informed by published metabolic flux analysis data (Chen et al. 2012). In this article, we build on that work in terms of considering extracellular glucose utilisation and the breakdown of this carbon source to lactate or intermediate metabolites through the TCA cycle, and deduce the provision of energy through central carbon metabolism. We then relate this information to a population level model. Parameter estimation is carried out using experimental data generated by the authors on cell population dynamics, and extracellular and intracellular metabolite concentration profiles. The experiments were carried out in Erlenmeyer flasks under two conditions: batch and fed-batch culture with supplementation of glucose on day 3. Our results and their analysis through the mathematical model highlight differences between these two conditions in terms of metabolic efficiency. The effect of uncertainty in parameter values is ascertained by the application of the Derivative-based Global Sensitivity Measures (DGSM) global sensitivity analysis method (Sobol and Kucherenko 2009). The results provide some insight on crucial measurements for future experiments, which could help reduce uncertainty.

Finally, a computational case study is conducted on lactate metabolism. Given the lower efficiency of glucose utilization during lactate production and the negative impact of high lactate levels on cell growth, it has always been desirable to control lactate accumulation. However, a shift in lactate metabolism from lactate producing in the initial growth phase to lactate consuming from stationary phase onwards has been reported for several CHO cell lines (Luo et al. 2012; Wilkens et al. 2011; Altamirano et al. 2006). Recently, Li et al. (2012) demonstrated that for lactogenic cell lines, lactate depletion in the middle of the culture can lead to high levels of ammonia, which are also undesirable. They further examined the effect of adding lactic acid instead of CO₂ for pH control and as a secondary carbon source together with pyruvate. They observed that lactic acid addition can effectively control the pH while reducing the level of ammonia. Herein, we examine the impact of adding lactate to the medium as a modulator of glucose metabolism and a secondary carbon source using the aforementioned mathematical model and identify its optimal concentration range.

Materials and methods

Cell culture

The GS-CHO cell line Null 8 (Lonza Biologics plc., Slough, UK) was used for this study. The cell line has been transfected with the glutamine synthetase vector but expresses no recombinant protein product. The cells were washed and recovered in CD-CHO medium (Gibco, Life Technologies, Paisley, UK) supplemented with 25 μM methionine sulfoximine (MSX, Sigma-Aldrich, Gillingham, UK), at a seeding concentration of 0.3 × 10⁶ viable cells/mL, in a suitably sized Erlenmeyer flask. Cultures were maintained in an incubator at 37 °C, a humidified atmosphere of 8 % CO₂, on an orbital shaker rotating at 140 rpm. Cells were subcultured on day 3 after revival and on day 4 for all subsequent subcultures, for which a seeding concentration of 0.2 × 10⁶ viable cells/mL was used.

Experiments were conducted under two conditions. First, batch overgrow cultures were carried out in CD-CHO (containing 6.5 g/L glucose) with 25 μM MSX, as described above, in 1L Erlenmeyer flasks with a working volume of 200 mL. Secondly, fed-batch overgrow cultures were conducted in glucose-free CD-CHO media (Gibco, Life Technologies) supplemented with 25 μM MSX and 3 g/L glucose (Sigma-Aldrich) in 1 L Erlenmeyer flasks with a working volume of 200 mL. Glucose (CortecNet, Voisins-Le- Bretonneux, France) was dissolved in glucose-free CD-CHO medium and added to the culture on day 3 to bring the concentration up to its level in full CD-CHO medium.

Cultures were sampled twice per day between days 3 and 6 for the batch experiment, and between days 3 and 9 for the fed-batch experiment, and once daily on the remaining days. The viable cell concentration was determined using the trypan blue (Life Technologies) dye exclusion method under light microscopy (Leica, Milton Keynes, UK). Additionally, 1.5 mL of culture were removed, centrifuged at 100g for 5 min and the supernatant collected and frozen at −20 °C for further analysis.

Following the determination of viable cell concentration, culture samples containing 1 × 10⁷ viable cells were also removed, quenched by adding 5 parts of quenching solution to 1 part of sample, and washed. The quenching solution was ice-cold 0.9 % (w/v) sodium chloride (NaCl, Sigma-Aldrich) dissolved in Milli-Q water. Quenched samples were then resuspended in 2 mL of extraction solution (ice-cold 50 % acetonitrile in Milli-Q water), incubated on ice for 10 min and spun down at 18,000g for 5 min. The supernatant was collected and the pellet was stored at −80 °C for further analysis. The choice of quenching and extraction solutions was based on the work of Dietmair et al. (2010), who compared various methodologies. They concluded that cold NaCl did not damage the cells and was effective in quenching metabolism and that acetonitrile is the most suitable extractant for metabolomic analysis. They further suggested that washing can damage cell pellets, but advised that it was unavoidable when the aim is to quantify metabolites that are present both intracellularly and extracellularly. A washing step was therefore added in our methodology.

Metabolic analysis

Bioprofile analysis

Extracellular samples from batch cultures were analysed using a BioProfile Automated Analyzer 400 (Nova Biomedical, Runcorn, UK), which uses an enzymatic/amperometric method for the analysis of glucose, lactate, glutamine, glutamate, and an ion selective electrode method for the analysis of NH₄, Na⁺ and K⁺.

GC/MS analysis

Extracellular and intracellular samples from the fed-batch cultures were analyzed using GC/MS. In order to accurately detect metabolites of interest, we prepared metabolite standards (all compounds from Sigma-Aldrich) and analysed them in order to build our own library. Analysis involved the following steps. First, samples were transferred into a 2 mL glass vial (Agilent Technologies, Stockport, UK), supplemented with 10 μL of myristic-d₂₇ acid (Sigma-Aldrich) solution (2 mM in water/methanol/isopropanol at a volumetric ratio of 2:5:2) and thoroughly dried at vacuum overnight using a SpeedVac (Eppendorf, Stevenage, UK). Dried samples were resuspended in 10 μL methoxyamine hydrochloride (Sigma-Aldrich) solution [40 mg/mL in anhydrous pyridine (VWR, Lutterworth, UK)] and incubated at 30 °C for 90 min. Samples were then derivatised by the addition of 30 μL N-methy-N-(trimethylsilyl) trifluoroacetamide with 1 % trimethylchlorosilane (MSTFA + 1 % TMCS, Sigma Aldrich), and incubation at 37 °C for 30 min. 10 μL internal standard (2 mM 2-fluorobiphenyl (Fluorochem, Hadfield, UK) in anhydrous pyridine) was then added.

GC/MS analysis was performed on HP 6890 series GC system and HP 5793 Mass select Detector (Hewlett-Packard, Palo Alto, CA, USA) using MSD ChemStation software. Components were separated by chromatography on a HP5MS column (25 m × 0.25 mm × 0.25 μm) using 1.2 mL/min helium as carrier gas. The inlet was held at 250 °C, samples (1 μL) were introduced either by pulsed split (1:10) or pulsed splitless injections. For split injections the GC was programmed to hold at 60 °C for 1 min, then the temperature was steadily increased to 325 °C at a rate of 10 °C/min and held for 10 min. Splitless injections followed the same temperature profile but started at 50 °C. The mass spectrometry results were then identified using the Wiley 275 library and the Mass Bank online mass spectrometry database (http://www.massbank.jp/).

Model development

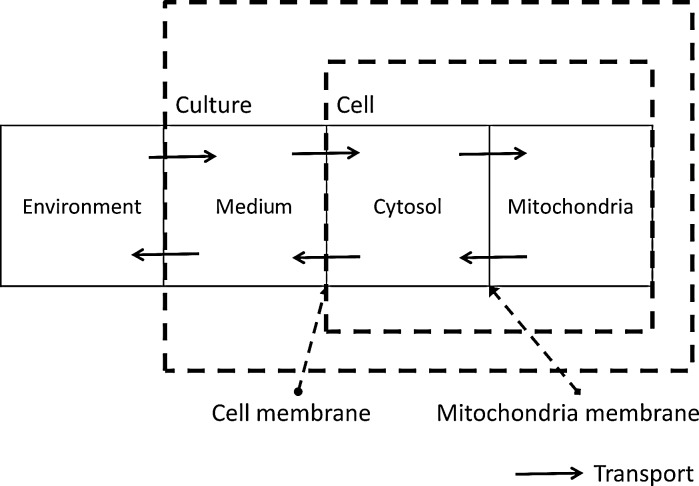
The cell culture model consists of two parts, namely a cell population dynamics model and a single cell model. The single cell model describes glucose metabolism in the cytosol, while the cell growth model connects the single cell model to the extracellular environment and cell population behaviour. Central glucose metabolism includes glycolysis, the pentose-phosphate pathway (PPP) and the tricarboxylic acid (TCA) cycle. In Sanderson et al. (1996) and Sidoli et al. (2005) a method for modularization of the single cell model was introduced, in which the mitochondria were treated as a separate compartment and trans-membrane transport for some metabolites was considered. The TCA cycle is treated separately as it takes place in the mitochondria while glycolysis and pentose-phosphate pathway take place in the cytosol.

Following these studies, we introduced the same compartmentalization into our model, as shown in Fig. 1. The system is divided into four interlinked compartments, which are the environment, medium, cytosol, and mitochondria. The transport between the environment and medium are the inlet and outlet of the reactor. Transport between cell culture medium and the cytosol, and between the cytosol and the mitochondria involves molecules passing through cellular membranes. Each of these four compartments is treated as well-mixed and, thus, homogeneous. Hence, intracellular glucose metabolism is divided into two different stages: the cytosolic stage, which includes glycolysis and the PPP, and the mitochondrial stage, which involves the TCA cycle. However, it should be noted that some reactions of the TCA cycle take place in both the mitochondria and the cytosol (Heiden et al. 2009).

Fig. 1.

Topological model compartmentalization

Cell growth and death

The mass balance around the bioreactor for viable cells is:

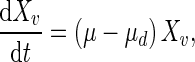1

where μ is the specific cell growth rate (day⁻¹) and μ_d is the specific cell death rate (day⁻¹). Cell death is mainly caused by the accumulation of ammonia in the extracellular environment. The specific cell death rate therefore is:

2

where μ_max and μ_d,max are the maximum specific cell growth and death rate (day⁻¹), respectively, 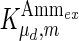is a constant for cell death due to ammonia accumulation (mM), and 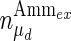is a Hill coefficient (dimensionless). In batch cell culture, no inlet or outlet is considered. Thus the mass balance for extracellular glucose is

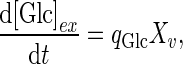3

where

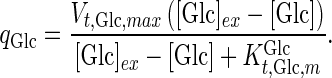4

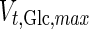is the maximum specific transport rate of glucose (mmol/cell-day), and is the Michaelis–Menten constant for glucose transport into the cell (mM). Glucose transport is facilitated by a family of transporters, some of which are sodium-dependent. In our experiments, we found that the concentration of sodium ions is constant through the culture and have therefore removed this dependency from Eq. 4.

As the cell line used in this study did not produce a recombinant product, the assumption was made that all energy generated through glucose metabolism is used for cell growth. Thus the equation for the specific cell growth rate we put forward is:

5

where 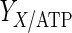is the yield of cells per mol of ATP (cell/mmol), 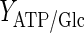and 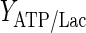are the yields of energy if glucose and lactate are fully degraded through the TCA cycle and converted to ATP (mmol/cell), respectively. For extracellular lactate, the accumulation or consumption can be accounted for by considering its trans-membrane transport. The mass balance for extracellular lactate is:

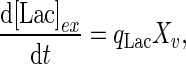6

where the specific lactate accumulation rate 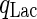is formed based on Michaelis–Menten kinetics:

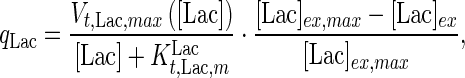7

where 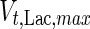is the maximum specific lactate transport rate (mmol/cell-day), 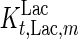is the Michaelis–Menten constant for lactate transport (mM), and 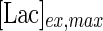is the maximum extracellular lactate concentration (mM). Metabolite transport is usually accompanied by transport of protons or ions, as is the case with lactate. Lactate carriers have a high capacity aimed to support a high rate of lactate secretion or uptake (Poole and Halestrap 1993). This finding along with experimental evidence that the concentration of ions remains stable over the culture time (data not shown) allows us to simplify the mechanism for lactate transport to that shown in Eq. 7.

Extracellular ammonia can be directly link to the cell growth:

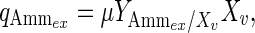8

Cytosolic glucose metabolism

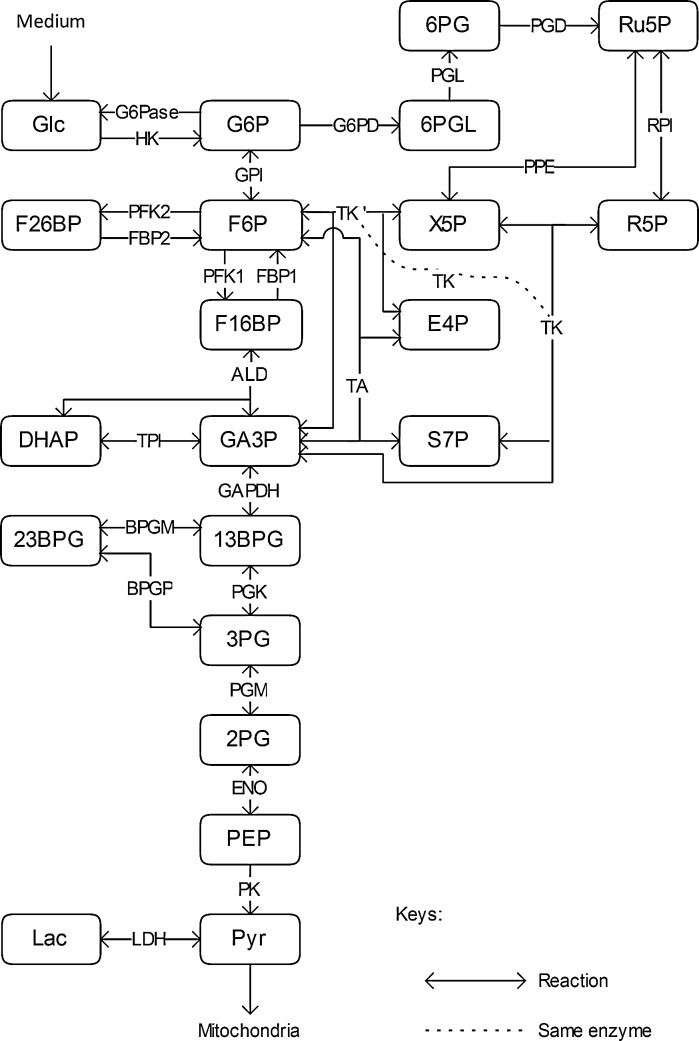
According to the genetic information from the Kyoto Encyclopedia of Genes and Genomes (KEGG), a cytosolic glucose metabolic map for CHO cells based on enzyme availability and expression was built. Since there are no data specifically for CHO cells in KEGG, the closest species, Rattus norvegicus, was chosen instead. The main glucose metabolic pathway in the cytosol is glycolysis, with about 40 % of the glucose flux going through the PPP (Goudar et al. 2010). As there are some minor losses in fluxes throughout glycolysis and the PPP (Goudar et al. 2010), side reactions were also taken into account. The metabolic map developed is shown in Fig. 2. Each reaction is named by the abbreviation of the enzyme that catalyses it. Energy carriers, e.g. ATP, ADP, AMP, NAD⁺, NADP, NADH⁺, NADPH, FAD, FADH₂, etc., CO₂ and H₂O, are not shown on this map.

Fig. 2.

Metabolic map of cytosolic glucose catabolism in CHO cells

One can see from Fig. 1 that transport also contributes to metabolite pools. Although cell growth dilutes the metabolic pools, its effect is much slower than metabolic reaction and transport rates. Therefore, a general mass balance can be written for metabolite i as follows:

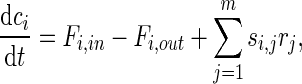9

where 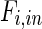and 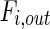denote metabolite i transport rate into and out of the cytosol of a single cell (mmol/day), respectively, which account for nutrient inlet, product/by-product outlet and transport to the mitochondria. The cell growth model and intracellular cytosolic glucose metabolism model are connected through the transmembrane transport of glucose and lactate as follows:

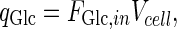10

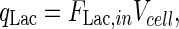11

where the cell volume is

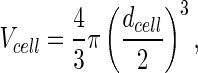12

and the cell diameter (d_cell) is equal to 15 μm (Han et al. 2006). Based on the metabolic map in Fig. 2, enzyme kinetic rates were established as below, which were used to populate the mathematical model. These are described in detail in Chen et al. (2012) and presented in Table 1.

Table 1.

Reaction rate expressions (adapted from Chen et al. 2012)

Reaction	Reaction rate expression
HK
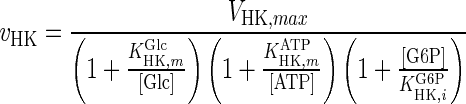
G6Pase
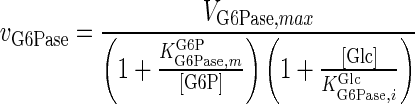
GPI
PFK1
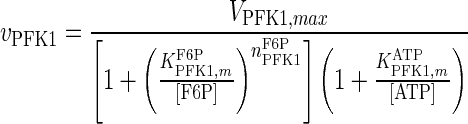
FBP1
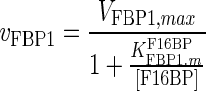
ALD
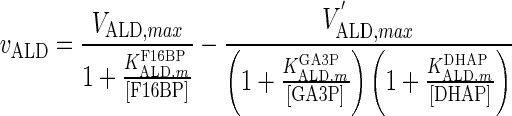
TPI
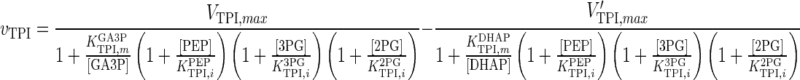
GADPH
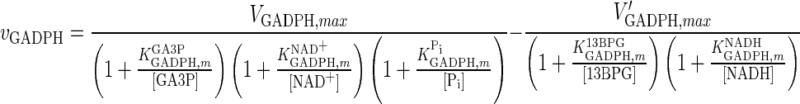
PGK
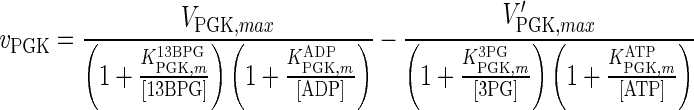
BPGM
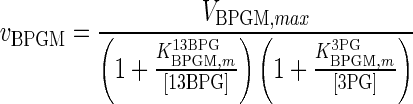
BPGP
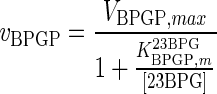
PGM
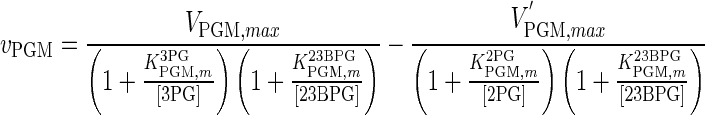
ENO
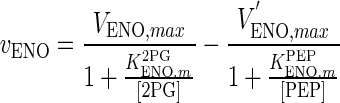
PK
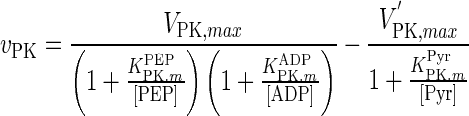
LDH
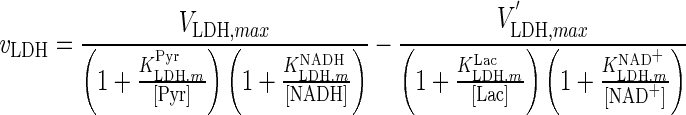
PDH
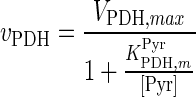
G6PD
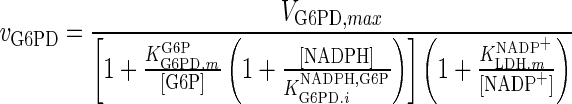
PGL
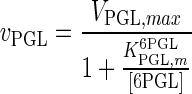
PGD
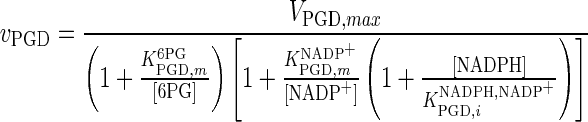
PPE
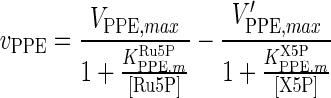
RPI
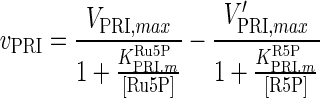
TK
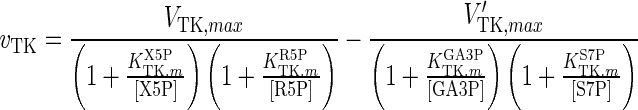
TK′
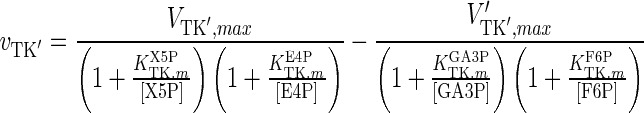
TA

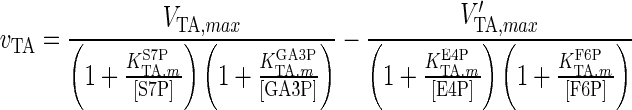
Parameter estimation

The mathematical model for cell growth and cytosolic glucose metabolism was simulated in gPROMS (Process Systems Enterprise ltd., UK). The Braunschweig Enzyme Database (BRENDA) was searched to identify appropriate values for kinetic parameters. However, as for other models of biological process, several kinetic parameters have not been determined experimentally or are not suitable as the experiments in which they were measured were performed under different conditions than those occurring in a living cell. For example, enzyme kinetics reported in literature are mostly deduced from in vitro experiments. It is generally acceptable to use the K_m values from such experiments, which are summarized in Table 2 for the case of the enzymes involved in our metabolic network, but not the v_max values. This is because K_m values only depend on the environment, e.g. pH and temperature, which are typically controlled at physiological levels, but v_max values depend not only on the k_cat but also the enzyme concentration E₀, which is usually arbitrarily set in in vitro experiments and may not be representative of physiological levels.

Table 2.

Parameter values for reaction kinetics

Parameter	Value	Unit	Ref.	Parameter	Value	Unit	Ref.
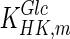
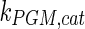
	0.11	mM	Toews (1966)		795	s−1	Mulquiney et al. (1999)
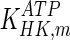
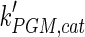
	0.8	mM	Toews (1966)		714	s−1	Mulquiney et al. (1999)
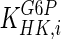
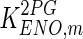
	9.1	mM	Sabate et al. (1995)		0.12	mM	Rider and Taylor (1974)
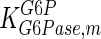
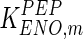
	1.8	mM	Nordlie (1982)		0.37	mM	Rider and Taylor (1974)
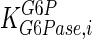
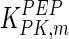
	115	mM	Nordlie (1982)		0.07	mM	Feksa et al. (2005)
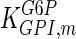
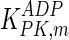
	0.705	mM	Zalitis and Oliver (1967)		1.05	mM	Feksa et al. (2005)
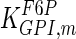
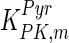
	0.12	mM	Zalitis and Oliver (1967)		0.0204	mM	Jeng et al. (1998)
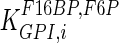
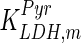
	7.55	mM	Zalitis and Oliver (1967)		0.03	mM	Levan and Goldberg (1991)
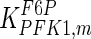
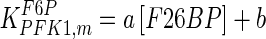
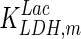
		mM	Uyeda et al. (1981)		1.79	mM	Saad et al. (2006)
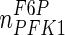
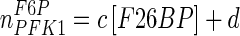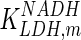
		a = −164.9; b = 1.306; c = −161.7 mM−1; d = 2.964	Uyeda et al. (1981)		0.011	mM	Shoemark et al. (2007)
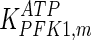
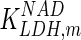
	0.06	mM	Nicolau et al. (2000)		0.18	mM	Nicolau et al. (2000)
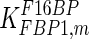
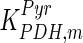
	0.0013	mM	Tashima et al. (1979)		0.0204	mM	Jeng et al. (1998)
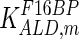
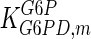
	0.0519	mM	Esposito et al. (2004)		0.329	mM	Corpas et al. (1995)
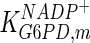
	1	mM	Morse and Horecker (1968)		0.1	mM	Corpas et al. (1995)
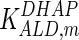
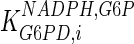
	2	mM	Morse and Horecker (1968)		0.01	mM	Corpas et al. (1995)
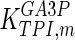
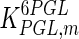
	0.32	mM	Krietsch et al. (1970)		0.08	mM	Schofield and Sols (1976)
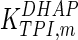
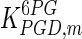
	0.62	mM	Krietsch et al. (1970)		0.157	mM	Corpas et al. (1995)
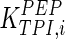
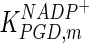
	0.5	mM	Lambeir et al. (1987)		0.258	mM	Corpas et al. (1995)
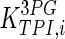
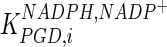
	0.51	mM	Lambeir et al. (1987)		0.021	mM	Corpas et al. (1995)
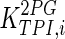
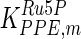
	4.1	mM	Lambeir et al. (1987)		0.19	mM	Wood (1979)
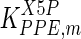
	5.1 × 105	min−1	Lambeir et al. (1987)		0.5	mM	Horecker and Hurwitz (1956)
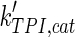
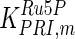
	5.2 × 104	min−1	Lambeir et al. (1987)		0.78	mM	Kiely et al. (1973)
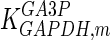
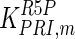
	0.149	mM	Patra et al. (2009)		2.2	mM	Kiely et al. (1973)
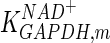
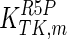
	0.071	mM	Patra et al. (2009)		0.33	mM	Blass et al. (1982)
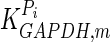
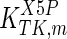
	4	mM	Patra et al. (2009)		0.12	mM	Blass et al. (1982)
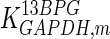
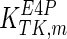
	0.032	mM	Ryzlak and Pietruszko (1988)		0.36	mM	Schenk et al. (1998)
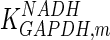
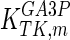
	0.02	mM	Ryzlak and Pietruszko (1988)		4.9	mM	Schenk et al. (1998)
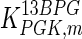
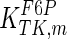
	0.005	mM	Szabo et al. (2008)		7	mM	Schenk et al. (1998)
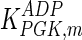
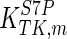
	0.12	mM	Szabo et al. (2008)		4	mM	Sprenger et al. (1995)
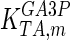
	0.1	mM	Szabo et al. (2008)		0.038	mM	Sprenger et al. (1995)
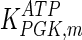
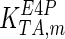
	0.11	mM	Szabo et al. (2008)		0.09	mM	Sprenger et al. (1995)
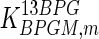
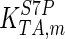
	0.0051	mM	Mulquiney et al. (1999)		0.285	mM	Sprenger et al. (1995)
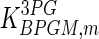
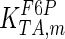
	0.001	mM	Mulquiney et al. (1999)		1.2	mM	Sprenger et al. (1995)
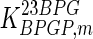
	0.049	mM	Mulquiney et al. (1999)	d	15	μM	Han et al. (2006)
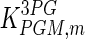
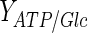
	0.17	mM	Mulquiney et al. (1999)		38	mol ATP/mol glucose	Alberts et al. (2001)
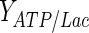
	0.026	mM	Mulquiney et al. (1999)		18	mol ATP/mol lactate	Alberts et al. (2001)
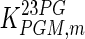
	0.00015	mM	Mulquiney et al. (1999)

Due to insufficient information on parameter values in the relevant literature, certain parameters therefore required estimation. Hence, experiments were performed as described above in order to parameterize the model. An overall parameter calculation/estimation strategy is presented in Fig. 3. Model parameterization was carried out iteratively based on this strategy, as the parameter calculation and estimation affected each other. Hence, the parameterization was not completed until the criterion that the difference between simulated metabolic fluxes and the metabolic fluxes used to calculate the v_max values was less than 5 % was satisfied.

Fig. 3.

Overall strategy for modeling

Quasi-steady state parameter calculation

The cell line used in this study does not produce a recombinant protein product, hence the energy generated through metabolism was assumed to be used for cell growth only. This model therefore focused on analyzing the exponential growth phase, when the specific cell growth rate is high and the intracellular metabolite pools can be assumed to be stable, i.e. the system can be assumed to be in quasi-steady state. At this state, the metabolite concentrations were assumed to be those presented in Table 3, and nutrients are believed to still be in abundance and not limiting cell growth. Adenine nucleotides and oxidized/reduced pyridine coenzymes were assumed to be stable (see Table 3 for details). Due to lack of experimental data, the concentrations of metabolites 13BPG, 23BPG and 6PGL were assumed to be the same as the K_m values of the enzymes for which they act as substrates, while the concentration ratios for NADH, NADP⁺ and NADPH to NAD⁺ were taken from Shin et al. (2008).

Table 3.

Intracellular metabolite concentrations

Metabolite	Concentration (mM)	Ref.	Metabolite	Concentration (mM)	Ref.
13BPG	0.005	Szabo et al. (2008)	GA3P	0.021	Bloch et al. (1971)
23BPG	0.051	Mulquiney et al. (1999)	Glc	2.377	Albe et al. (1990)
2PGA	0.005	Albe et al. (1990)	Lac	2.660–6.700	Albe et al. (1990)
3PGA	0.040–0.048	Albe et al. (1990)	NAD+	0.310	Albe et al. (1990)
6PG	0.018	Sabate et al. (1995)	NADH	0.003	Shin et al. (2008)
6PGL	0.080	Schofield and Sols (1976)	NADP+	0.005	Shin et al. (2008)
ADP	1.059	Albe et al. (1990)	NADPH	0.995	Shin et al. (2008)
ATP	3.075	Albe et al. (1990)	Pi	5.500†	Albe et al. (1990)
DHAP	0.040–0.046	Albe et al. (1990)	PEP	0.008	Albe et al. (1990)
E4P	0.004	Sabate et al. (1995)	Pyr	0.056	Albe et al. (1990)
F16BP	0.046	Albe et al. (1990)	R5P	0.009	Sabate et al. (1995)
F26BP	0–0.070	Uyeda et al. (1981)	Ru5P	0.012	Sabate et al. (1995)
F6P	0.362	Albe et al. (1990)	S7P	0.068	Sabate et al. (1995)
G6P	1.033	Albe et al. (1990)	X5P	0.018	Sabate et al. (1995)

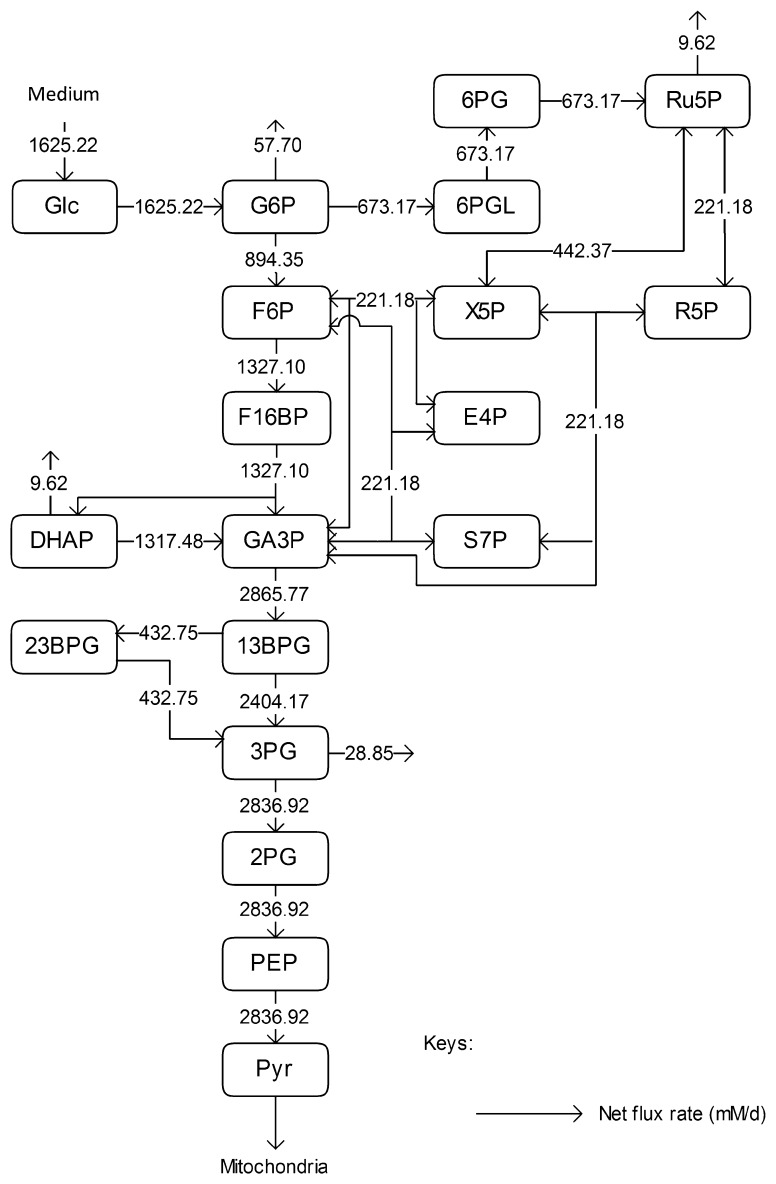
We used the results of a metabolic flux analysis study for CHO cell culture in a perfusion bioreactor (Goudar et al. 2010), in which samples were analysed using 2D ¹³C¹H NMR spectroscopy, to calculate the metabolic fluxes of CHO cells under constant cell growth. For fluxes leading out of the system, the ratios between each outlet flux and its adjacent flux were assumed to be constant. The parameter calculation was performed in MATLAB (MathWorks, UK) and targeted the estimation of V_max values only. It was based on the reaction rate expressions in Table 1, the parameter values in Table 2, metabolite concentrations in Table 3 (assumed to be the concentrations on day 4), and the metabolic flux rates in Fig. 4, which were obtained based on the following assumptions:

1. The calculation of the percentage of metabolic flux towards the PPP and other pathways was based on the results of the metabolic flux analysis study in Goudar et al. (2010), and

2. As the reported fluxes were net fluxes only, the forward reaction rates were assumed to be twice as the backward ones, unless:

   1. There is a reported correlation between the forward and the backward reactions, i.e. experimental values for k_cat for both reactions are available from the same experiment, or
   2. The simulation results for associated metabolite concentrations exceed physiological ranges.

Fig. 4.

Metabolic flux distribution for exponential phase in CHO cells. The open flux from G6P goes toward nucleotide sugar synthesis, that from 3PG toward serine metabolism, the open flux from DHAP goes toward glycerol synthesis, and that from Ru5P goes towards nucleotide synthesis

Dynamic parameter estimation

Dynamic parameter estimation was performed using the parameter estimation entity in gPROMS based on a SRQPD sequential quadratic programming code. The estimation was based on the experimental results of both the batch and the fed-batch cultures, for which parameter values were estimated separately, so that conclusions can be drawn on the differences between cell populations grown under these two conditions in terms of cell growth and metabolism. The dynamic estimation targeted the parameters involved in the cell growth and death expressions, as well as those related to glucose uptake and lactate production and secretion. The dynamic parameter estimation was therefore based on experimental data for cell growth and death, intracellular and extracellular concentrations of glucose, lactate and extracellular concentration of ammonia.

Parameter estimation and model simulation results

The results for the quasi-steady state parameter estimation of v_max values are shown in Table 4. The maximum reaction rates during the earlier steps of glycolysis, i.e. values for HK, G6Pase, GPI, PFK1, FBP1, ALD and TPI, are significantly lower than those for the later stages, i.e. GADPH, PGK, PGM, ENO and PK, with only two exceptions, BPGM and BPGP. These form part of a branch of glycolysis, which suggests that the rate-limiting steps of glycolysis are the earlier reactions up to GA3P. The significant increase in v_max values before and after GA3P in the main glycolysis pathway suggests that the reaction GAPDH is a potential bottleneck for cytosolic glucose metabolism. This finding is in line with previous reports for S. cerevisiae cells (Hauf et al. 2000). For the PPP, only v_max values for G6PD and TA were considerably smaller than for other enzymes. This suggests that the inlet and outlet reactions of the PPP are rate-limiting.

Table 4.

Estimated v_max values

Parameter	Value (mM/d)	Parameter	Value (mM/d)
VALD,max	5,649	V′PGK,max	8,716
V′ALD,max	2,939	VPGL,max	1,346
VBPGM,max	896	VPGM,max	62,370
VBPGP,max	849	V′PGM,max	56,015
VENO,max	141,850	VPK,max	110,170
V′ENO,max	134,040	V′PK,max	3,870
VFBP1,max	1,365	VPPE,max	14,893
VG6Pase,max	4,466	V′PPE,max	12,730
VG6PD,max	36,345	VPRI,max	29,196
VGAPDH,max	162,586	V′PRI,max	54,288
V′GAPDH,max	22,575	VTA,max	6,452
VGPI,max	3,010	V′TA,max	3,102
V′GPI,max	1,428	VTK,max	127,750
VHK,max	4,772	V′TK,max	3.10 × 106
VLDH,max	1,010	VTK′,max	334,061
VPFK1,max	7,710	V′TK′,max	105,410
VPGD,max	16.23 × 106	VTPI,max	21,524
VPGK,max	10,706	V′TPI,max	2,196

The results of the dynamic parameter estimation are shown in Table 5. Certain parameters take comparable values for both experimental conditions. These are the yield of cells on ATP, 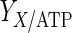, the yield of ammonia on cells, 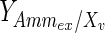, and the maximum specific lactate transport rate, 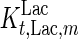. In contrast, the maximum specific cell death rate, μ_d,max, is considerably higher in batch mode, potentially due to the higher degree of metabolic by-product accumulation, while 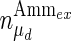, the Hill coefficient for cell death by ammonia, is higher in fed-batch mode. Comparing the values of parameters pertaining to lactate metabolism and export we see that cells cultivated under fed-batch conditions, which include a lower initial glucose concentration, exhibit a more efficient metabolism with lower level of lactate accumulation (10 mM compared to 30 mM in batch) and more efficient glucose utilization. This is particularly evident in the V_max values for PDH, the enzyme that catalyses the conversion of pyruvate to acetyl co-enzyme A (and therefore the maximum rate at which pyruvate enters the TCA cycle), and for LDH, the enzyme that catalyses the conversion of pyruvate to lactate. The former is higher under fed-batch conditions, while the latter is considerably higher under batch cultivation. The high level of accumulation of lactate in batch mode is also reflected in the low value of the Michaelis–Menten constant for lactate transport, 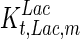, and in the high maximum specific lactate transport rate, 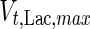. In contrast, certain parameters take considerably different values between batch and fed-batch culture conditions. Along the same lines, the maximum glucose uptake rate in fed-batch is approximately half that at batch conditions, which agrees with the extracellular glucose concentration profiles in Fig. 6.

Table 5.

Estimated parameter values

Parameter	Value
	Batch culture	Fed-batch culture	Unit
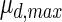
	12.3172	5.46251	1/d
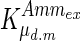
	25	22.1197	mM
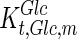
	242.995	371.092	mM
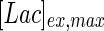
	32.4511	10.0914	mM
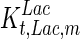
	86.3442	256.955	mM
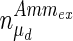
	2.00	2.98651	–
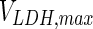
	19,218.7	593.919	mM/d
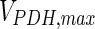
	1,625.66	2,081.08	mM/d
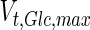
	2.90771 × 10−8	1.71484 × 10−8	mmol/cell d
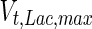
	9.01924 × 10−8	5.40742 × 10−8	mmol/cell d
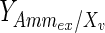
	9.41632 × 10−10	7.29758 × 10−10	mmol/cell
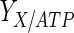
	9.69532 × 106	9.70 × 106	cell/mmol

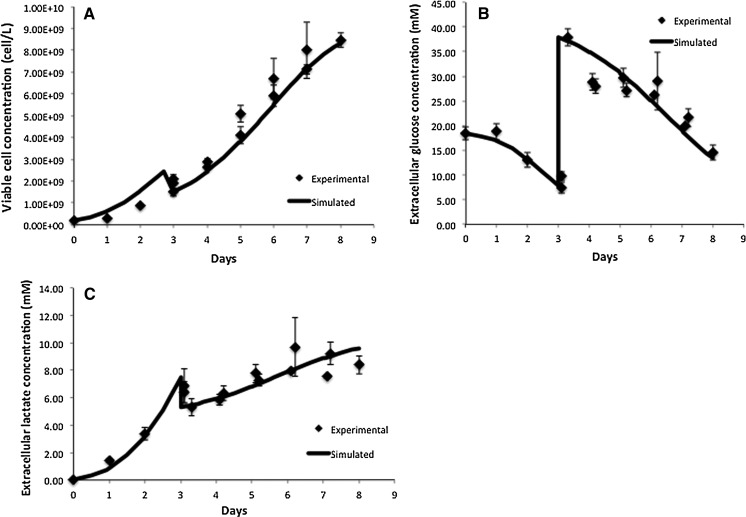
Fig. 6.

Comparison of model simulation results to experimental data for fed-batch cell culture for a viable cell concentration, b Extracellular glucose concentration, c extracellular lactate concentration

Model simulation was performed in gPROMS (Process Systems Enterprise Ltd., London, UK), and the simulation results were compared to experimental findings. Intracellular metabolite concentrations for day 4 are shown in Table 6, where they are compared to values from the literature (sources presented in Table 3). Overall, the results are comparable to reported values, with the exception of glucose, which shows an 81 % deviation. However, the simulated glucose uptake rate is 1,565.22 mM/d, which is 3.7 % smaller than the flux 1,625.22 mM/d used for parameter calculation. Therefore our initial convergence criterion is satisfied. The discrepancy in the value for intracellular glucose concentration may be due to the values of kinetic parameters for the reaction catalysed by hexokinase. Specifically, the value for 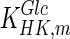used for simulation (0.11 mM) is significantly lower than the reported intracellular glucose concentration of 2.377 mM (Williamson and Brosnan 1971; Albe et al. 1990). There are four different types of hexokinase with different 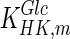values. That for HK IV, also known as glucokinase, is much larger than the rest and if it were used for simulation it would result in a better agreement with previously reported values. Due to the low concentration of glucose predicted by the model, the concentration of glucose-6-phosphate is also lower than the reported one. Furthermore, the concentration of pyruvate is lower than the reported value due to the absence of regulation for the flux entering the TCA cycle.

Table 6.

Simulation results for intracellular metabolite concentrations compared with literature values

Metabolite	Concentration (mM)		Difference (%)
	In literature	Simulation
13BPG	0.005	0.0044	−11.7
23BPG	0.051	0.0447	−12.4
2PGA	0.005	0.0045	−10.0
3PGA	0.040 to 0.048	0.0362	−9.3 to −24.4
6PG	0.018	0.0197	9.4
6PGL	0.080	0.0942	17.8
DHAP	0.040 to 0.046	0.0465	1.1 to 16.25
E4P	0.004	0.0043	6.5
F16BP	0.046	0.0473	2.8
F6P	0.362	0.3532	−2.4
G6P	1.033	0.6964	−32.6
GA3P	0.021	0.0244	16.2
Glc	2.377	0.4525	−81
Lac	2.660 to 6.700	2.9289	−56.3 to 10
PEP	0.008	0.0069	−13.8
Pyr	0.056	0.0303	−45.9
R5P	0.009	0.0095	5.6
Ru5P	0.012	0.0128	6.7
S7P	0.068	0.0645	−5.1
X5P	0.018	0.0188	4.4

It should be noted that the literature values for metabolite concentrations are for a variety of cell lines and types, and, hence, were used as a guide rather than a target that the model or estimation strategy were required to match. Accurate time-course measurements of intermediary species in CHO cell cultures are necessary in order to ascertain the validity of model assumptions and accuracy of estimated parameters. The possibility of regulation of enzyme levels along the pathway would invalidate the assumption of constant V_max values throughout culture duration. In addition, the current model does not consider the effect of pH on cell metabolism. Since the data presented herein are from flask-based studies in which the pH is not controlled, the impact could be considerable as the pH drifts from its initial value due to accumulation of metabolic by-products (Wilkens et al. 2011). A final important assumption of the model is that the levels of energy and electron carriers remain constant. Any modeling approach would benefit from describing their synthesis and consumption in order to capture their dynamic profile (Kochanowski et al. 2006) and its effect on cell metabolism.

Figures 5 and 6 compare the model simulation results to experimental data for the viable cell concentration under both conditions. Figure 6a, which depicts the results for the fed-batch experiment, includes our findings from day 3 of the culture onwards, i.e. from the time of extra glucose addition, so that the profiles are comparable to Fig. 5a. The model closely tracks experimental data, correctly predicting the height and timing of the peak in viable cell concentration. The cells reached a significantly higher maximum viable cell concentration during the fed-batch culture compared to the batch run thanks to the addition of extra glucose and other nutrients present in CD-CHO medium. During the decline phase of the culture the model overpredicts the viable cell concentration because it is based on the assumption that if there is glucose present extracellularly, the cells will grow on it. However, in vivo, the cells have a finite lifetime and once their pro-apoptotic signaling is activated, the presence of nutrients is not sufficient to fuel growth (Mercille et al. 1999).

Fig. 5.

Comparison of model simulation results to experimental data for batch cell culture for a viable cell concentration, b Extracellular glucose concentration, c extracellular ammonia concentration, d extracellular lactate concentration

Figures 5b–d and 6b,c compare the experimental and simulation results for the extracellular glucose and lactate concentrations, respectively. Under both conditions, the extracellular glucose profile is well represented by the model. We can see that glucose is utilized more slowly in the fed-batch culture, which would imply a more efficient metabolism. This is confirmed by the lactate concentration profiles in Figs. 5d and 6c. In batch culture (Fig. 5d) lactate accumulates extracellularly to nearly 30 mM, whereas in fed-batch culture (Fig. 6c) the extracellular lactate accumulation does not exceed 10 mM. Although there is a good overall agreement between the model and experimental data for both modes of operation, the simulation results for the batch culture predict a slower rate of accumulation than that observed experimentally between days 2 and 5 of the batch culture. This may be due to regulation effects in central glucose metabolism that affect the accumulation of lactate intracellularly. A possible regulator is the NAD⁺/NADH ratio, which can be measured in future experiments to confirm this hypothesis. This discrepancy is likely to affect our predictions for intracellular lactate levels under batch conditions, which are possibly higher than simulated. The results for intracellular lactate concentration (Fig. 7b) correctly predict its level under fed-batch conditions. Opposite to lactate, extracellular ammonia concentration is predicted to be higher for the fed-batch experiment (not shown) possibly due to the degradation of added amino acids. Simulations for intracellular glucose and lactate concentrations show reasonable agreement with experimental data as shown in Fig. 7. In this case, we modified the 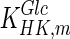for HK IV, to achieve simulation results closer to the experimentally obtained values.

Fig. 7.

Comparison of model simulation results to experimental data for fed-batch cell culture for a intracellular glucose concentration, b intracellular lactate concentration

Overall, the simulation results show good agreement with the available experimental data. The parameterized model has provided a tool for the studies of cell population, extracellular metabolic behavior and intracellular metabolism in CHO cell culture. However, further experimental data on metabolic intermediates are necessary to improve the predictive capability of the model. Dynamic profiles of glycolytic and TCA cycle intermediates and pCO₂ levels in particular would help to better understand the transition from lactate production to lactate consumption, for example, in order to be able to mathematically describe it with accuracy and eventually predict it. Recent studies, which were carried out in parallel to the work presented herein, have successfully quantified the profile of such metabolic intermediates in CHO cell culture and used the results to calculate the intracellular flux distribution in different growth phases (Ahn and Antoniewicz 2011; Carinhas et al. 2013). An additional level of necessary information with respect to kinetic modeling studies would be transcriptomic or proteomic data for the enzymes involved in the reaction network, the concentrations of which can change during culture (e.g. Wong et al. 2010) affecting cell performance considerably.

Sensitivity analysis

The model contains a large number of parameters that require estimation from experimental data. However, time courses of intracellular and extracellular metabolite concentrations are difficult to obtain. Global optimality of parameter values can therefore not be guaranteed. For this reason, a global sensitivity analysis was conducted on model parameters to ascertain the degree of confidence in the model. The derivative based global sensitivity measures (DGSM) method (Sobol and Kucherenko 2009) was applied to the above model to ascertain which parameters exercise the greatest influence over four model outputs of interest, the viable cell concentration, the extracellular concentrations of lactate and glucose, and the intracellular concentration of glucose. The total number of parameters examined is 159 and the parameter space was defined as ±90 %. To reduce the computational expense, the parameters were considered in 3 groups:

1. The first group included parameters of intracellular metabolism, namely all V_max, K_m, and K_i parameters for intracellular reactions, and those intracellular metabolite concentrations that were assumed to remain constant, e.g. [ATP] and [ADP];

2. The second group consisted of parameters pertaining to cell growth and death, e.g. parameters for glucose and lactate transport and maximum cell death rates;

3. The third group included just one parameter, d, which stands for cell diameter. This is a crucial parameter, because cell diameter can vary significantly as the cell goes through the different phases of the cell cycle.

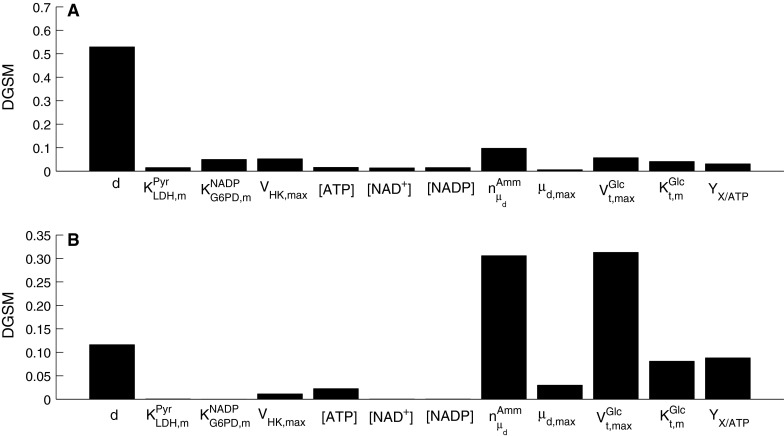
Figure 8 shows the DGSM results (only DGSM values above 0.01 for day 3 or day 6 are shown) when the viable cell concentration is the output of interest. The DGSM value represents the sensitivity index of each parameter and can vary between 0 and 1. The sum of DGSM values for all parameters is equal to 1. The results for day 3 in Fig. 8a highlight the cell diameter as the main contributor to variation in the viable cell concentration. The remaining important parameters relate to glucose uptake and cell metabolism, although their values are below 0.1, i.e. 10 % variation in the output, which is within experimental error. Comparing these results with the sensitivity indices for day 6 in Fig. 8b, we find that the importance of cell diameter is lower, although it remains above 0.1. As expected, when glucose metabolism slows down due to the nutrient being depleted, the indices of parameters directly related to cell growth and glucose uptake increase, while parameters relating to intracellular reactions do not appear to significantly affect the results for Xv.

Fig. 8.

Parameter sensitivity indices for viable cell concentration as the objective function for a day 3, and b day 6 of batch cell culture

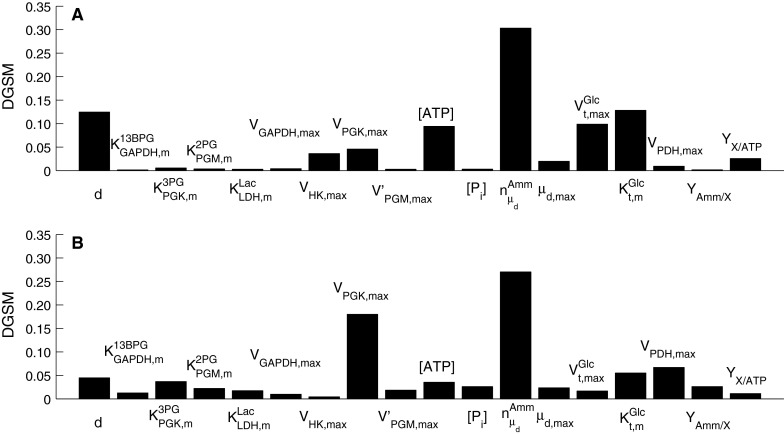
Figures 9 and 10 show the DGSM results for the extracellular glucose and lactate as the target functions. Similarly to the results for the viable cell concentration above, parameters from intracellular metabolism contribute more to these outputs in the exponential cell growth phase than the peak day when metabolism has slowed down. In the early phases of the culture when glucose is abundant, the limiting factor is cell metabolism, whereas in the stationary phase glucose uptake becomes the limiting factor, as also shown by the results of this analysis. However, extracellular lactate concentration was sensitive to intracellular metabolism throughout the culture, since lactate is a by-product of metabolism. Both outputs were found to be sensitive to changes in parameters describing cell growth and death, particularly 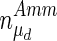, while cell diameter was more important in the case of glucose concentration, as it is critical to deducing the intracellular glucose concentration. This effect is less pronounced in the case of lactate, the dependence of which on cell diameter through the calculation of intracellular glucose concentration is more dilute.

Fig. 9.

Parameter sensitivity indices for extracellular glucose concentration as the objective function for a day 3, and b day 6 of batch cell culture

Fig. 10.

Parameter sensitivity indices for extracellular lactate concentration as the objective function for a day 3, and b day 6 of batch cell culture

For intracellular metabolites, glucose was selected as an example and the results are shown in Fig. 11. These indicate that the cell size was the most important parameter in the model because it significantly influences the inlet and outlet flux of the intracellular metabolic pathways considered in this model. Interestingly, the sensitivity indices for day 3 (Fig. 11a) and day 6 (Fig. 11b) are similar, and besides cell size, the parameters of high importance belong to the enzymatic kinetics of the first glycolytic reactions, which appear to be a bottleneck for the flux through glycolysis.

Fig. 11.

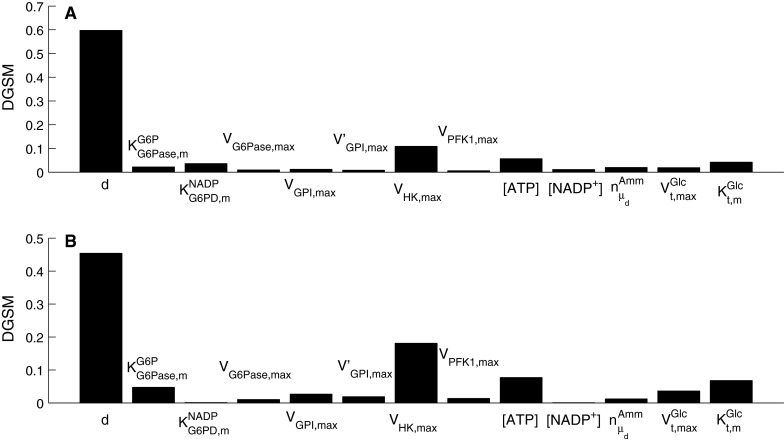
Parameter sensitivity indices for intracellular glucose as the objective function for a day 3, and b day 6 of batch cell culture

Overall, the results highlight the importance of cell diameter on the model outputs. In fact, this corresponds to the mean cell diameter, which is typically used to calculate intracellular metabolite concentrations in kinetic models. However, cell diameter does not remain constant during animal cell culture, it takes a range of values depending on the distribution of the cell population across the cell cycle phases (Han et al. 2006). This finding points to the need of coupling kinetic metabolic models with segregated models, for example population balance (Faraday et al. 2001; Uchiyama and Shioya 1999) or phase transition models (Chen and Hwang 1990; Novak et al. 1998). Metabolomic measurements would also need to be coupled with flow cytometry analysis to parameterise such models.

Case study: lactate feeding

Lactate is generally considered a by-product of glycolysis. Although the constructed model does not include the effect of O₂ or CO₂, it is still possible to provide a different angle to lactate use by the cells. In most cell culture models, the yield of lactate over glucose is considered to be a constant (e.g. Kontoravdi et al. 2010; Ho et al. 2006; Pörtner and Schäfer 1996). Based on our experimental findings, the yield of lactate over glucose

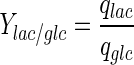has been calculated and was found to be time-dependent, as also shown, for example, in Ahn and Antoniewicz (2011), Martinez et al. (2013). At earlier stages of the cell culture, a larger proportion of the glucose taken up by the cells is metabolized into lactate and the yield is therefore high. When the extracellular lactate concentration increases, q_Lac and, thus, the yield decrease. In the fed-batch experiment, both the glucose utilization rate and the accumulation of lactate are lower than in batch conditions. The yield starts at a value of 1.2 for the batch culture, whereas it never exceeds 0.2 for the fed-batch culture. This suggests that a reasonable concentration of lactate in the medium, at a level that does not inhibit cell growth, could increase the efficiency of glucose utilization.

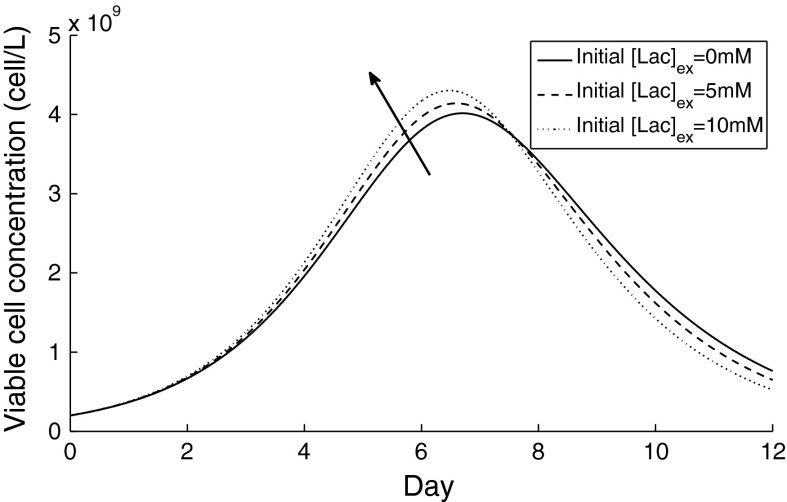
The model was simulated for an initial extracellular lactate concentration of 0, 5 and 10 mM, and the simulation results for the viable cell concentration are compared in Fig. 12. Our findings show that the peak in viable cell concentration can be increased when a reasonable amount of lactate is present in the medium, but that the integral of viable cell concentration with time remains unaltered. However, when the time profile of the corresponding yield of lactate on glucose was examined, this decreased when the initial extracellular lactate concentration was increased, pointing to a more efficient glycolytic metabolic function.

Fig. 12.

Simulation results for viable cell concentration under different initial extracellular lactate concentrations under batch cell culture. The arrow signifies an increasing starting concentration of lactate extracellularly

A recent study (Li et al. 2012) has experimentally shown that other than using lactate-free media, a suitable feeding strategy for lactic acid in CHO cell culture has a positive effect in terms of sustaining cell growth and controlling pH levels. As mentioned above, Li et al. fed pyruvate and lactic acid to CHO cell culture as a pH buffer instead of CO₂ and observed improved culture performance with respect to cell growth and ammonia accumulation compared to fed-batch CHO cell cultures under standard conditions (in which lactate accumulated in the exponential phase and was catabolized in the stationary and decline phases). As in that study, we also observed improved cell growth.

Conclusions

Metabolic networks are complex, intertwined and highly regulated systems. To analyze their behavior, insightful dynamic experiments are necessary. When complimented with meaningful mathematical representations of the underlying systems, the resulting integrated computational/experimental approach can help answer questions about fundamental phenomena but also provide ideas for increasing system efficiency. Herein, we presented a dynamic model of CHO cell population dynamics coupled with a kinetic model for cytosolic glucose metabolism. The model was parameterized using experimental data from batch and fed-batch experiments, the analysis of which highlighted key differences in metabolic function and efficiency under the two operating conditions. Our research suggests that the gradual addition of glucose to the medium increases metabolic efficiency and decreases the yield of lactate on glucose. The model was subjected to a global sensitivity analysis, which pinpointed key parameters that significantly affect measured outputs and helped highlight cell parameter as a key model input that should in future be monitored experimentally to complement metabolomic analysis for populating kinetic models with more informative data. It was further used to examine the effect of adding lactate to the cell culture medium. In line with previous experimental studies, the simulation results suggest that a limited amount of lactate present at the beginning of the culture can increase metabolic efficiency without hindering cell growth.

Abbreviations

CHO

Chinese hamster ovary

PPP

Pentose phosphate pathway

TCA

Tricarboxylic acid cyle

Metabolites

13BPG

1,3-Bisphosphoglycerate

23BPG

2,3-Bisphosphoglycerate

2PGA

2-Phosphoglycerate

3PGA

3-Phosphoglycerate

6PG

6-Phospho-gluconate

6PGL

6-Phospho-glucono-1,5-lactone

ADP

Adenosine diphosphate

ATP

Adenosine triphosphate

DHAP

Dihydroxyacetone phosphate

E4P

Erythrose 4-phosphate

F16BP

Fructose 1,6-bisphosphate

F26BP

Fructose 2,6-bisphosphate

F6P

Fructose 6-phosphate

Fru

Fructose

GA3P

Glyceraldehyde 3-phosphate

Glc

Glucose

Lac

Lactate

NAD⁺

Nicotinamide adenine dinucleotide

NADH

Reduced nicotinamide adenine dinucleotide

NADP⁺

Nicotinamide adenine dinucleotide phosphate

NADPH

Reduced nicotinamide adenine dinucleotide phosphate

P_i

Phosphate

PEP

Phosphoenolpyruvate

Pyr

Pyruvate

R5P

Ribose 5-phosphate

Ru5P

Ribulose 5-phosphate

S7P

Sedoheptulose 7-phosphate

X5P

Xylulose 5-phosphate

Ru5P

Ribulose 5-phosphate

Enzymes

ALD

Fructose-bisphosphate aldolase

BPGM

Biphosphoglycerate mutase

BPGP

Biphosphoglycerate phosphatase

ENO

Phosphopyruvate hydratase

FBP1

Fructose-bisphosphatase

G6PD

Glucose-6-phosphate dehydrogenase

GAPDH

Glyceraldehyde-3-phosphate dehydrogenase

GCK

Glucokinase

G6Pase

Glucose-6-phosphatase

GPI

Glucose-6-phosphate isomerase

HK

Hexokinase

LDH

Lactate dehydrogenase

PDH

Pyruvate dehydrogenase

PFK1

6-Phosphofructokinase

PGD

Phosphogluconate dehydrogenase

PGK

Phosphoglycerate kinase

PGL

6-Phosphogluconolactonase

PGM

Phosphoglycerate mutase

PK

Pyruvate kinase

PPE

Ribulose-phosphate 3-epimerase

RPI

Ribose-5-phosphate isomerase

TA

Transaldolase

TK

Transketolase

TPI

Triose-phosphate isomerase