Conformational Transitions and Stop-and-Go Nanopore Transport of Single Stranded DNA on Charged Graphene

Abstract

Control over interactions with biomolecules holds the key to applications of graphene in biotechnology. One such application is nanopore sequencing, where a DNA molecule is electrophoretically driven through a graphene nanopore. Here, we investigate how interactions of single-stranded DNA and a graphene membrane can be controlled by electrically biasing the membrane. The results of our molecular dynamics simulations suggest that electric charge on graphene can force a DNA homopolymer to adopt a range of strikingly different conformations. The conformational response is sensitive to even very subtle nucleotide modifications, such as DNA methylation. The speed of DNA motion through a graphene nanopore is strongly affected by the graphene charge: a positive charge accelerates the motion whereas a negative charge arrests it. As a possible application of the effect, we demonstrate stop-and-go transport of DNA controlled by the charge of graphene. Such on-demand transport of DNA is essential for realizing nanopore sequencing.

Control over the interactions between biomolecules and carbon-based materials may hold the key to unlocking potential of nanotechnology for biomedical applications.¹ One such application is nanopore sequencing of DNA, which may enable ultra-rapid sequencing of human genomes at a fraction of the cost of current generation DNA sequencing methods.^2–4 In nanopore sequencing, single-stranded DNA (ssDNA) is electrophoretically driven through a nanopore embedded in a nanometer thin membrane.⁵ As ssDNA transits the nanopore, individual DNA nucleotides affect the ability of dissolved ions to pass through the nanopore. Thus, a measurement of nanopore ionic current can provide, in principle, real-time readout of the DNA nucleotide sequence. Among the advantages of nanopore sequencing are the potentially limitless read lengths, minimal requirements for consumable reagents, the ability to read native DNA and re-read the same fragment of a DNA molecule multiple times.^6,7

Graphene, a single layer of hexagonally arranged carbon atoms,⁸ harbors unique electrical and physical properties conducive to nanopore-based DNA sequencing. The atomically thin structure of graphene and its straightforward layerability allows the membrane thickness to be precisely controlled at the scale comparable to the distance between neighboring nucleotides in a DNA strand. Recent advances in transmission electron microscopy,⁹ developing lithography¹⁰ and bottom-up growth techniques^11–13 have enabled atomic-scale manufacturing of graphene-based nanostructures. Furthermore, the unique electrical properties of graphene offer, at least in theory, several plausible methods for DNA sequence detection,¹⁴ including ionic current readout,^15,16 nanoribbon conductance,^17–20 and transverse tunneling.^21–23

Several experimental groups have reported measurements of ionic current signals produced by interactions of double-stranded DNA with graphene nanopores.^24–26 Alternative means of DNA sequence readout has been experimentally explored, including measurements of the electrochemical current off the edge of graphene²⁷ and graphene nanoribbon conductance.²⁸ Experiments using ssDNA have proven to be more difficult^29–31 and required exquisite control over the properties of the graphene membrane.

Using the all-atom molecular dynamics (MD) method,³² we have previously shown that molecules of ssDNA adhere to the surface of graphene and, when driven by an external electric field, translocate through a nanopore in discrete, often single-nucleotide steps.¹⁶ Our atomic-resolution Brownian dynamics simulations³³ predicted a measurable dependence of the nanopore ionic current on the type of DNA nucleotides confined within a graphene nanopore.¹⁶ Thus, a graphene nanopore system appears to have all the features that have made DNA sequencing using biological nanopores possible.^34,35 However, just as when a biological enzyme is used to thread a DNA strand through a nanopore, the stepwise motion of ssDNA through a graphene nanopore is stochastic. A deterministic trap-and-release control over DNA transport through a nanopore³⁶ can considerably reduce the stochastic variation in the duration of individual translocation steps and thereby increase fidelity of DNA sequence detection.

Here, we report the effect that electric charge on graphene has on the conformation of adsorbed ssDNA and on the velocity of electrophoretic motion of ssDNA through a graphene nanopore. Surprisingly, we find the conformation of ssDNA to depend sensitively on both the sign and magnitude of the graphene charge and on the nucleotide composition of the DNA strand. We also show that the charge of a graphene membrane can be used to regulate the velocity of nanopore transport. Our results open new avenues for using graphene in biosensing, in particular, nanopore sequencing of nucleic acids.

Results

Study setting

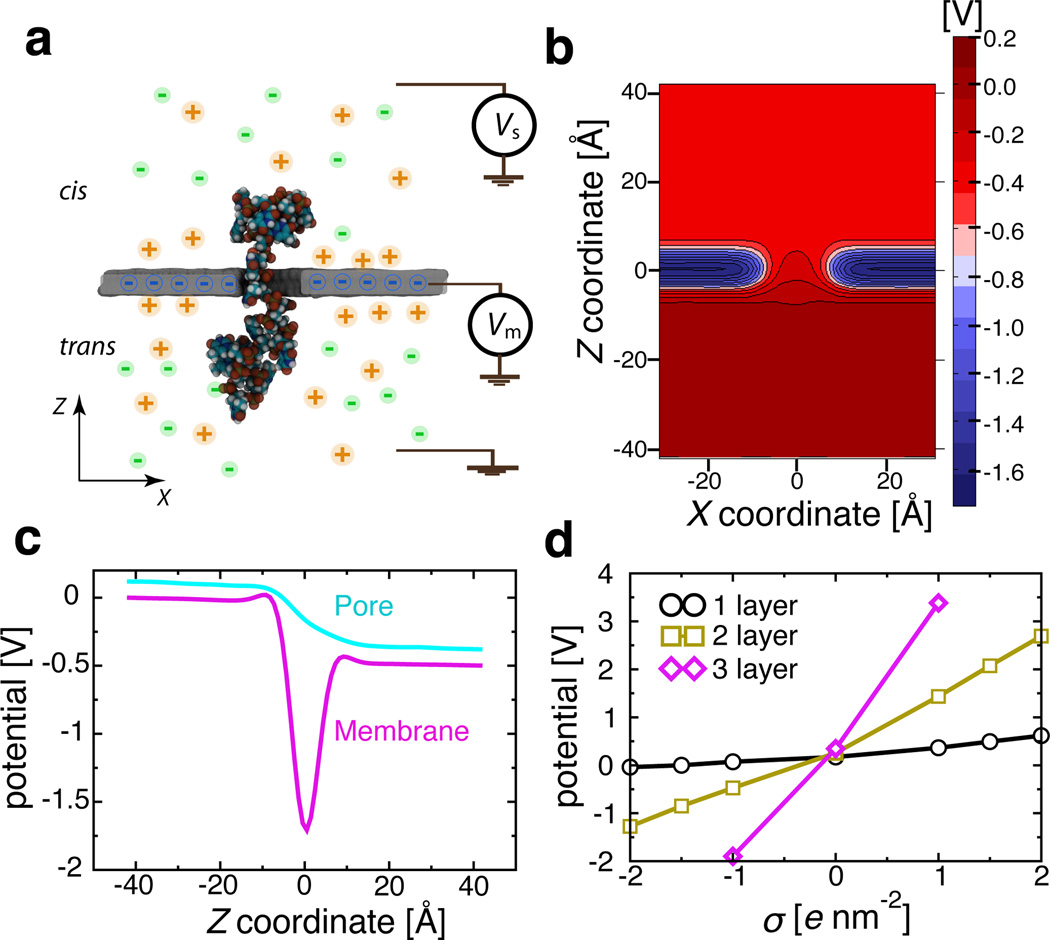
Figure 1a illustrates a typical system considered in this work. A graphene membrane containing a single 1.6 nm-diameter nanopore is submerged in 1 M KCl solution; a DNA molecule is threaded half-way through the nanopore. An external electric field is applied to produce a transmembrane gradient of electrostatic potential V_s.³² Carbon atoms comprising the graphene membrane are assigned partial charges to electrostatically bias the graphene membrane with respect to solution. Figure 1b illustrates the distribution of the electrostatic potential in a typical simulation system. The electrostatic potential drops monotonically along the nanopore axis but attains elevated values within the graphene membrane, Figure 1c. An approximate relationship between the membrane charge density σ and the membrane potential V_m can be determined by computing the average change in the electrostatic potential of the graphene membrane upon the assignment of the membrane charge density σ. A more precise characterization of the relationship would require a multiscale approach^23,37 to take the electronic structure of graphene into account. The surface charge densities considered in this work are rather realistic; for example, the charge density of a silica surface can vary between 0 and 5 e nm⁻², depending on the fabrication procedures.³⁸

Figure 1.

MD simulations of ssDNA on charged graphene. (a) Schematic of a typical system considered in this work. A DNA strand is threaded half-way through the nanopore in a two-layer graphene membrane, surrounded by 1 M aqueous solution of KCl. The DNA is drawn using vdW spheres colored according to the atom type (carbon-cyan, nitrogen-blue, oxygen-red, hydrogen-white and phosphorus-gold). The graphene membrane is shown as a cut-away molecular surface to reveal the presence of a nanopore. An electric potential V_s biases the solution at the one side of the membrane (cis) relative to the solution at the other (trans) side, which is grounded. The graphene membrane is electrically biased relative to the trans side with a potential difference V_m. The latter is modeled implicitly by assigning partial charges to the atoms of the graphene membrane (see panel d). (b) Typical distribution of the electrostatic potential in an MD simulation of a charged graphene membrane. The electrostatic potential map was obtained by averaging instantaneous distributions of electrostaticic potentials over the frames of the MD trajectory. The charge density of the membrane featured in the map is −2.0 e nm⁻², the transmembrane bias V_s = 500 mV. (c) Variation of the electrostatic potential with the distance from the membrane along the nanopore axis (blue) and away from the nanopore (purple) for the system featured in panel b. The latter profile was obtained by averaging the electrostatic potential 9 Å away from the nanopore axis. (d) The average difference between the electrostatic potentials of the graphene membrane and the trans side solution in equilibrium (V_s = 0 mV) MD simulations as a function of the membrane’s charge density σ. The difference approximately reports on the membrane potential V_m. Lines are guides to the eyes.

Effect of graphene charge on the conformation of adhered DNA

The charge of a graphene membrane can dramatically alter the conformation of adhered ssDNA. Figure 2 illustrates the results of MD simulations performed in the absence of an external electric field (V_s = 0), a poly(dT)₂₀ strand, a two-layer membrane and the surface charge density of 0, −2 and +2 e nm⁻². On charge-neutral graphene (σ = 0), the bases of ssDNA adhere to the surface of the membrane as the phosphate groups of the DNA backbone remain un-bound from the surface, Figure 2 a,b. Changing the membrane charge density from 0 to −2 e nm⁻² was observed to unbind ssDNA from graphene, Figure 2c, indicating the dominance of electrostatic repulsion between the electronegative phosphate groups of DNA and the negatively charged graphene surface over the attractive, hydrophobic ssDNA–graphene forces. The charge-induced unbinding of ssDNA is reversible: upon changing the membrane charge density back to zero, the poly(dT)₂₀ strand was observed to rebind to the graphene surface. Figure 2d and Supplementary Movie 1 illustrate an MD trajectory where the DNA binding-unbinding cycle was repeated six times. While unbinding of ssDNA was observed to occur almost instantaneously (within 1 ns), rebinding of all the bases onto a charge-neutral membrane required considerably longer time intervals (≈ 50 ns). The rebinding time scale is determined by the diffusive motion of ssDNA and spontaneous disruption of the non-specific secondary structure formed by the unbound fragments of ssDNA.

Figure 2.

The charge of graphene alters the conformation of ssDNA. (a) Typical conformation of a poly(dT)₂₀ strand near a charge-neutral graphene membrane (water and ions are not shown). (b) Close-up view of poly(dT)₂₀ near charge-neutral graphene. The bases of DNA are parallel to the surface of the graphene membrane, forming direct contacts with the latter. The phosphate groups of the DNA backbone are detached from the surface. This conformation is referred to as at. (c) Typical conformation of a poly(dT)₂₀ strand near a two-layer graphene membrane charged at −2.0 e nm⁻². The DNA strand does not make direct contacts with the membrane except near the nanopore. (d) Reversible modulation of poly(dT)₂₀ conformation by the charge of the graphene membrane. Changes in the charge density σ of the membrane produce reversible binding/unbinding of the DNA strand. The conformations of ssDNA are quantitatively characterized by plotting the number of bases that are bound at to the graphene surface, N_flat (panel b), unbound from the graphene surface, N_unbound (panel c), and bound but tilted with respect to the membrane, N_tilted (panel f). (e) Typical conformation of a poly(dT)₂₀ strand near a two-layer graphene membrane charged at +2.0 e nm⁻². (f) Close-up view of the poly(dT)₂₀ strand shown in panel e. The bases of ssDNA are tilted with respect to the membrane; only a fraction of the base atoms make direct contacts with the membrane. The phosphate group of the backbone is bound to the surface of graphene. This conformation is referred to as tilted. (g) Reversible tilting/attening of the DNA bases stimulated by the changes of the membrane charge density σ.

Figures 2e,f illustrate the effect of a positive membrane charge (σ = +2 e nm⁻²) on the conformation of ssDNA. Although the bases of ssDNA remain bound to the membrane, they are no longer parallel to the membrane and tilt at a ~47 degree angle. At the same time, the phosphate groups of the backbone attach to the membrane surface, Figure 2f. The at (σ = 0 e nm⁻²) and tilted (σ = +2 e nm⁻²) conformations can be easily distinguished from one another by computing the distances between the graphene membrane and the centers of mass of the base and phosphate groups, Figure 3a,b. The force driving ssDNA into the tilted conformation is electrostatic: the negatively charged backbone is attracted toward the positively charged membrane while the base tilts to minimize the electrostatic energy of its dipole moment. The methyl groups’ exposure to water is minimized by the base stacking of the tilted nucleotides, Figure 2f. The change between at and tilted conformations is reversible and occurs in less than 10 ns. Figure 2g and Supplementary Movie 2 illustrate an MD trajectory where the at-tilt cycle was repeated six times. In the tilted conformation, the DNA strand remains mobile on the graphene surface, diffusing around the nanopore.

Figure 3.

Conformations of poly(dT)₂₀ on charged graphene. (a) A representative conformation of ssDNA near a graphene membrane. The yellow and green arrows illustrate the nearest distances between the graphene membrane and the center of mass of a nucleotide’s base and between the graphene membrane and the center of mass of a nucleotide’s phosphate, respectively. The yellow and green spheres indicate the locations of the center of mass of the bases and phosphates, respectively. (b) A representative normalized histogram characterizing an ensemble of conformations adopted by a DNA strand during a typical MD simulation. The nearest distances between the graphene and the base and backbone groups of the nucleotides are used as independent parameters. The snapshots illustrate typical conformations of bound nucleotides classified as (clockwise) at, tilted, backbone phosphate bound, and unbound. This particular data set features a poly(dT)₂₀ strand interacting with a two-layer graphene membrane charged at 1.5 e nm⁻². (c) Ensemble of conformations adopted by a DNA strand versus the charge density of the graphene membrane. Twenty nucleotides of a poly(dT)₂₀ strand were assigned to one of the following conformations: at, tilted, backbone bound, unbound and confined to a nanopore. For a given value of the graphene charge density σ, the number of nucleotides in a particular conformation was averaged over the last 40 ns of the 60 ns equilibration trajectory. Examples of typical conformations are shown in panel b. Lines are guides to the eyes.

Figure 3c specifies the range of conformations adopted by a poly(dT)₂₀ strand on a two-layer charged graphene membrane. Regardless of the graphene surface charge density, about two out of twenty nucleotides reside within the nanopore, on average. For |σ|≤ 1 e nm⁻² the remaining bases are bound at to the surface of graphene as shown in Figure 3b. The number of unbound nucleotides increases as σ decreases from −1 to −2 e nm⁻². Conversely, for the charge density exceeding +1 e nm⁻², the number of nucleotides adopting a tilted conformation increases with the charge density, Figure 3b. However, even at high charge densities a number of nucleotides remains bound at to the surface. At σ = +2.25 e nm⁻², a new population of nucleotide conformation (backbone bound) emerges: the nucleotides can have both their base and backbone bound to the membrane, Figure 3b.

Conformations of DNA homopolymers on charged graphene

The unique atomic structure of DNA nucleotides makes the conformational response of a DNA strand to a change in the graphene charge dependent on the nucleotide composition of the DNA strand. Specifically, we found homopolymers of thymine, guanine, cytosine, methylated cytosine and adenine nucleotides to adopt statistically different conformations at a graphene surface of the same charge density, Figure 4. On charge-neutral graphene, DNA nucleotides of all types adopt the same at conformations, similar to that shown in Figure 2a,b. A negative charge on a graphene surface repels the negatively charged phosphate group of a DNA backbone. For a poly(dT) strand, this repulsion produces unbinding of the strand from the graphene surface at σ < −1.5 e nm⁻². However, several factors can influence the energetics of the surface charge-induced unbinding: the strength of hydrophobic base-graphene interactions, the distribution of partial charges on the nucleotides and the ionic strength of the solution. For example, we found the conformational response of ssDNA to graphene charging in vacuum to be qualitatively different from that in ionic solution, see Supplementary Figure 1.

Figure 4.

Nucleotide type-specific conformational changes of ssDNA on charged graphene. In panels a,c,d,f,h,k,l, and o, the sequence of snapshots illustrates conformational dynamics observed during an MD simulation of a DNA homopolymer in proximity of a charged two-layer graphene membrane. The simulations characterized in panels (a–f) and (h–o) correspond to the membrane charge density σ of −2.0 and +2.0 e nm⁻², respectively. The type of DNA nucleotides comprising each homopolymer is indicated in each panel. Close-up views are provided for some simulation trajectories. Supplementary Movies 3–10 illustrate each simulation featured in this figure. Diagrams (g) and (p) characterize the ensemble of conformations adopted by each DNA homopolymer at −2 and +2 e nm⁻², respectively. Each point on the diagram specifies the relative abundance of the three conformations among nucleotides comprising the corresponding DNA homopolymer: at, N_flat, upright, N_upright and unbound, N_unbound, for σ = −2 e nm⁻² and at, N_flat, tilted, N_tilted and unbound, N_unbound, for σ = +2 e nm⁻². The number of nucleotides adopting a particular conformation was obtained by averaging over the last 40 ns of the corresponding 60 ns equilibration trajectory. Examples of typical conformations can be found in panels e (upright), i (tilted) and n (at and unbound).

Unlike poly(dT), poly(dC) remains partially bound to the graphene surface at σ = −2.0 e nm⁻², Figure 4a; the unbound cytosine bases form a base-stacking pattern near the pore opening, see Supplementary Movie 3. Compared to poly(dC), a homopolymer of methylated cytosines, poly(d^mC), exhibits a more pronounced unbinding, albeit having more bases bound to the surface than poly(dT), Figure 4b,c. The nucleotides of poly(d^mC) adopt a variety of conformations, including at, unbound and upright. In the latter case, the nucleotides make contact with the graphene surface through their amine and methyl groups, see Supplementary Movie 4. On the other hand, the majority of nucleotides of a poly(dA) strand unbind from the graphene surface at σ = −2.0 e nm⁻², Figure 4d. The unbound adenine bases can form a tight base-stacked structure over the opening of the pore, see Supplementary Movie 5. Strikingly, the majority of nucleotides in a poly(dG) strand adopt an upright conformation, Figure 4e,f, in which the backbone of a DNA strand is detached from graphene while the amine groups of each dG base remain in contact with the graphene surface (see Supplementary Movie 6). The upright conformation of dG is seen only at σ = −2.0 e nm⁻²; at lower magnitude negative charges, dG bases remain partially adhered to graphene. Because of the relatively short duration of our simulations, the homopolymer of guanines was not expected to form a G-quadruplex.³⁹ Figure 4g quantitatively describes the ensemble of conformations sampled by each homopolymer at σ = −2.0 e nm⁻². With the exception of poly(dA) and poly(dT), each homopolymer has a unique conformation.

At σ = +2.0 e nm⁻², the phosphate groups of the backbone generally adhere to the membrane whereas the DNA bases either tilt or unbind from the membrane, Figure 4h–o. There are, however, considerable differences in the behavior of DNA homopolymers. In a poly(dC) strand, the majority of DNA bases remain bound to the membrane, although a few bases tilt to varying angles, see Supplementary Movie 7. Under the same conditions, a considerable fraction of nucleotides from the poly(d^mC) strand have their bases completely detached from the graphene surface, Supplementary Movie 8. In a poly(dA) strand, the majority of nucleotides have their bases detached from the membrane, Supplementary Movie 9. A poly(dG) strand contains a mixture of tilted, unbound and bound at bases, Supplementary Movie 10. Overall, poly(dA) has the greatest number of unbound bases, followed by poly(dG) and poly(d^mC). Figure 4p quantitatively describes the ensemble of conformations observed for each homopolymer at σ = +2.0 e nm⁻². On average, each homopolymer adopts a distinct conformation.

To estimate the effect of graphene charging on the conformation of a random-sequence DNA strand, it is useful to note that the interactions of nucleotides with graphene is short-range because of both exponentially decreasing base-stacking⁴⁰ and screened electrostatic interactions. Neglecting secondary structure formation, the conformational effects should be local, about 1 nm in range, which correspond to the nearest neighbors in the DNA sequence space. The local, additive nature of the interaction can permit, in principle, extraction of some information about the DNA sequence from the conformational transformations upon charging, such as the percentage of nucleotides of certain types, single nucleotide polymorphism or degree of methylation. In the presence of a competing secondary structure, one can expect to observe a rather complex conformation behavior. Solvent additives, such as urea, or temperature can be used to suppress secondary structure formation and make the conformational response of a heterogeneous-sequence DNA more predictable.

Graphene charge controls nanopore transport of ssDNA

The charge of a graphene membrane can have a pronounced effect on the electrophoretic velocity of ssDNA in a nanopore, Figure 5a. The initial conformations for each of the seven simulations shown in the figure were obtained from a ~60 ns equilibration (V_s = 0) at the target charge density. A transmembrane bias of ±500 mV was applied in each simulation. For several systems, the sign of the bias was switched during the simulation to prevent ssDNA from escaping the nanopore.

Figure 5.

The charge of graphene controls the velocity of nanopore translocation. (a) The number of DNA nucleotides at the trans side of the membrane versus simulations time. A transmembrane bias V_s = ±500 mV applied in each simulation; the charge of the graphene membrane σ varied from −2.0 to +2.0 e nm⁻². To prevent DNA from escaping the nanopore, the sign of the transmembane bias was reversed when either the 3rd or 17th nucleotide reached the pore. (b) The average translocation velocity of a poly(dT)₂₀ strand versus graphene charge density. The average velocity was computed by splitting the corresponding MD trajectory into 10 ns fragments and averaging the translocation velocity of the fragments. If the sign of the bias was changed during the simulation, the ratio was computed for every constant-bias fragment and averaged over all fragments. The error bars represent the standard deviation of the velocity among the 10 ns fragments. (c) Same as in panel b but for ssDNA homopolymers comprising of twenty dA, dG, ^mC, and dA nucleotides. Translocation traces for individual trajectories are shown in Supplementary Figure 2. In all simulations reported in this figure the graphene membrane had two carbon layers.

Figure 5b shows the average translocation velocity as a function of the membrane charge density. For a charge-neutral membrane, the average translocation velocity is 0.06 nt ns⁻¹. The translocation velocity increases with the charge density, reaching 0.25 nt ns⁻¹ at +1 e nm⁻². Despite the increase, the DNA translocation may still occasionally halt. The translocation velocity drops by at least two orders of magnitude at σ ≤ −1.0 e nm⁻², regardless of whether the strand remains partially bound to (−1.0 and −1.5 e nm⁻²) or completely unbound from (−2.0 e nm⁻²) the graphene surface. Similar dependence of the translocation velocity on the membrane charge density was observed for DNA homopolymers consisting of A, C, ^mC and G nucleotides, Figure 5c and Supplementary Figure 2. The effect appears to depend on the number of carbon layers: the three-layer graphene membrane has shown the most reliable control over DNA transport whereas transport of ssDNA occurred at all charge densities studied for single-layer graphene, Supplementary Figure 3.

The highly non-linear dependence of the DNA translocation velocity on the graphene charge density can be used to control the velocity of DNA transport without altering the transmembrane bias. Figure 6 illustrates a proof-of-principle simulation of such velocity control. At the beginning of the simulation, the three-layer membrane was positively charged (σ = +1.5 e nm⁻²), which was expected to promote translocation of ssDNA. Indeed, under a +500 mV bias, ssDNA was observed to move by ~7 nucleotides through the nanopore until the membrane charge density was switched to −1.5 e nm⁻², which arrested the translocation. Then, the sign of the transmembrane bias was reversed; the transport of ssDNA remained arrested by the negative charge density of the membrane. The charge of the membrane was then switched to +1.5 e nm⁻², which restarted the translocation of ssDNA, and then back to −1.5 e nm⁻², which arrested the transport. The sign of the transmembrane bias was reversed; the stop-and-go motion of ssDNA was produced again by switching the membrane’s charge density. In total, two cycles of stop-and-go motion of ssDNA strand were demonstrated within this 860 ns simulation. Supplementary Movie 11 illustrates this simulation trajectory. Similar control over DNA motion was observed in our simulations of a two-layer membrane system, Supplementary Figure 4. In the latter case, the stop-and-go motion was less robust than in the three-layer system, which may be explained by weaker interactions of DNA with the nanopore. The presence of DNA in the nanopore introduced minor perturbations in the distribution of the electrostatic potential along the nanopore axis, Supplementary Figure 5.

Figure 6.

Stop-and-go nanopore translocation of ssDNA. (a–c) The graphene charge density (a), the transmembrane bias (b) and the number of DNA nucleotides at the trans side of the membrane (c) versus simulation time. The sign of the transmembrane bias was switched several times to prevent ssDNA escaping the nanopore. At constant bias, changing the charge density from +1.5 to −1.5 e nm⁻² halts ssDNA translocation whereas changing the charge density from −1.5 to +1.5 e nm⁻² restarts ssDNA translocation. The snapshots in panel b illustrate the conformations of the DNA strand at the moments of switching the sign of the transmembrane bias. The simulation featured in this figure was performed using a poly(dT)₂₀ strand and a three-layer graphene membrane.

For a random-sequence DNA strand, one can expect to observe the same kind of stop-and-go motion as along as its secondary structure does not prevent its bases from adhering to the graphene membrane. For a DNA strand adhered to a graphene membrane, the interaction of the strand with the graphene membrane can be approximated as a superposition of interactions between individual nucleotides and the membrane. Hence, the transport rate modulations observed for the DNA homopolymers (Figure 5b,c) will determine the transport rate of a random-sequence DNA polymer. The possibility of transporting ssDNA in on-demand discrete steps may facilitate DNA sequencing if combined with a rapid DNA sequence detection method, such as a transverse conductance measurement.^17–23

In this study, we have considered an idealized system of a single nanopore made in a defect-free graphene sheet having a uniform distribution of the charge along its surface. However, the charge distribution near the edge of graphene can differ from that in the rest of the membrane. To prove that our results still hold even if the charge distribution is altered we simulated a system that had the annulus of the pore neutralized. The results of these simulations are shown in Supplementary Figures 6 and 7. Even in such a partially neutralized system, the structural response of DNA to charging of the graphene and the modulations of the DNA translocation velocity were found to be very similar in magnitude to those observed in the case of a uniformly charged graphene membrane. It may also be possible that adsorption of ssDNA to graphene can alter the charge distribution within graphene. However, our analysis of the charge distribution in MD simulations performed with and without a DNA strand, Supplementary Figure 8, indicates that the effect of the DNA charge on the membrane potential is rather minor (< 25 mV) and can be neglected for the graphene charge densities considered.

In summary, electrical charging of a graphene membrane was found to alter the conformations of ssDNA homopolymers bound to the membrane in a manner dependent on the nucleotide composition of ssDNA. The charge of a graphene membrane was shown to regulate the velocity of nanopore transport of ssDNA. Furthermore, switching of the graphene charge density under constant transmembrane bias was shown to produce stop-and-go motion of ssDNA, which is highly desirable for DNA sequencing applications. The described effects can be observed for other atomically smooth hydrophobic surfaces that can alter their electric charge density and biopolymers containing charged and hydrophobic groups, such as unfolded proteins. While electrochemical effects can limit applicability of certain materials for practical realization of the conformation and transport control principle, properties of the solution can be adjusted to fine-tune the balance of hydrophobic and electrostatic forces and thereby achieve the desirable control over the conformation and transport of biopolymers.

Methods

General MD protocols

All MD simulations were performed using the program NAMD,⁴¹ a 2 fs integration time step, 2-2-6 multiple time-stepping, CHARMM27 parameter set, a 7–8 Å cutoff for van der Walls and short-range electrostatic forces, the particle mesh Ewald (PME) method for long-range electrostatics⁴² computed over a 1.1 Å grid and periodic boundary conditions. Simulations in the NPT ensemble (constant number of particles N, pressure P, and temperature T) were performed using a Lowe-Andersen thermostat,⁴³ and Nosé-Hoover langeivn piston pressure control⁴⁴ set at 295 K and 1 atm, respectively. Visualization and analysis were performed using VMD.⁴⁵

MD simulations of graphene-DNA systems

All models of graphene sheets were generated using the Inorganic Builder plugin⁴⁶ of VMD.⁴⁵ Carbon atoms in the graphene sheets were modeled as type CA atoms of the CHARMM force field.^16,47 Nanopores in graphene were generated by removing carbon atoms whose x,y coordinates fulfilled the condition x² + y² < r², where r was the radius of the pore. After removing the initial selection of carbon atoms, singly bonded carbon atoms at the edge of the pore were removed as well. The graphene membranes considered in this study contained either one, two or three carbon layers and had a single circular pore 8 Å in radius. It was previously determined that nanopores of such dimensions facilitate stepwise translocation of ssDNA.¹⁶

To model the effect of electrical bias applied to the graphene membrane, atoms of graphene were assigned partial charges to produce charge densities ranging from −2 to +2 e nm⁻². The distribution of partial charges among carbon atoms comprising the membranes depended on the number of carbon layers. For a single sheet of carbons, the charge was evenly distributed among all carbon atoms. For two-layer systems, each carbon atom was assigned the same partial charge to produce the charge density in each of the two carbon layers equal to the half of the target charge density. For example, to model a two-layer graphene membrane charged at 1.0 e nm⁻², carbon atoms in each layer were assigned a partial charge of 0.0144 e so that the charge density in each layer was 0.5 e nm⁻². For a three-layer membrane, the charge was assigned only to the top and bottom layers of the membrane; the interior layer remained uncharged.

Each graphene nanopore system was combined with an all-atom model of ssDNA that was threaded halfway through the membrane. The initial conformation of ssDNA was that of a single strand of B-form duplex DNA. Each system was solvated using the Solvate Plugin of VMD. Potassium and chloride atoms were added to produce an electrically neutral 1.0 M solution of KCl using the Autoionize Plugin of VMD.

With the exception of the poly(dT) systems, each final system was a hexagonal prism 71.3 Å on side and 91.4 Åin height and contained approximately 43,200 atoms; hexagonal periodic boundary conditions were applied in the xy-plane. The system used for simulations of poly(dT) was smaller and measured 46.7 Åon the side and 92.1 Å in the direction normal to the membrane. The systems were minimized for 480 steps using the conjugate gradient method, followed by a 50 to 60 ns equilibration in the NPT ensemble during which only the dimension normal to the membrane was allowed to change.

All production simulations of ssDNA translocation were performed in the NVT ensemble (constant number of particles N, volume V, and temperature T) by applying an external electric field in the z direction. The electric fields are reported in terms of a trans-membrane voltage difference V_s = − EL_z, where E is the strength of the electric field and L_z is the length of the simulation system in the z direction. Taking the periodic boundary conditions into account, our simulations correspond to an infinite system of graphene membrane/electrolyte layers having a prescribed drop of the electrostatic potential per layer. To prevent membrane layers from drifting, harmonic restraints were applied to the outermost carbon atoms at the edges of the period cell; the spring constant of each harmonic restraint was 40 kcal mol⁻¹ Å⁻².

To adjust the charge of a graphene membrane during a stop-and-go simulation, the course of the simulation was interrupted; the latest atomic coordinates were used to build a new system featuring identical conformations of DNA and graphene but modified partial charges of the carbon atoms in the graphene membrane. To preserve the overall electrical neutrality of the system, a small number of potassium ions (less than 10% of the total number of ions) were randomly added to or removed from the system. A short (500 ps) NPT equilibration immediately followed each charge modification. The conformation of ssDNA was harmonically restrained during the 500-ps equilibration while ions and water rearranged, screening the charge of the DNA and membrane. After the 500-ps equilibration, constraints were removed from ssDNA and the production simulation in the NVT ensemble continued.

Calculation of the electrostatic potential

To visualize the distributions of the electrostatic potential in our systems, we averaged the instantaneous distributions of the electrostatic potential over the MD trajectory using the PMEpot Plugin⁴⁸ of VMD. Each atom of the system was approximated by a spherical Gaussian

$${\rho }_i(\mathbf{r})=q_i{\left(\frac{\beta }{\sqrt{\pi }}\right)}^3{e}^{-\beta {|\mathbf{r}-{\mathbf{r}}_i|}^2},$$ (1)

where σ was the Gaussians’ width. The instantaneous distribution of the electrostatic potential corresponding to the instantaneous charge configuration was obtained by solving the Poisson equation

$${\nabla }^2\varphi (\mathbf{r})=4\pi \sum _i{\rho }_i(\mathbf{r}).$$ (2)

To obtain the average distribution of the potential in a given MD simulation, instantaneous distributions of the potential were averaged over the entire MD trajectory. The electrostatic potential maps were obtained by averaging 20–30 ns fragments of MD trajectories; σ= 0.1 A⁻¹ was used for these calculations. One-dimensional profiles of the electrostatic potential across the graphene membranes or through the nanopores were obtained by averaging the corresponding regions of the three-dimensional electrostatic potential maps.

Classification of DNA conformations

The conformations of DNA nucleotides were characterized by computing the nearest distances from the nucleotides’ base and phosphate groups to the graphene surface, as illustrated in Figure 3a. For a given MD trajectory, normalized two-dimensional histograms were constructed using the graphene-base and graphene-phosphate distances as independent parameters. An example of such a histogram is shown in Figure 3b. The histograms were constructed for all nucleotides in a DNA strand using the last 40 ns of a 60 ns equilibration trajectory. Typically, the histograms contained several distinct peaks that could be associated with the particular conformations of individual nucleotides with the exception of nucleotides not bound to the surface, which were characterized as such using a distance cutoff of ~7.6 Å for the base and ~5.6 Å for the backbone. To quantitatively characterize the number of nucleotides bound in a particular conformation, a least-squares fit was used to approximate the normalized histograms as a set of Gaussian distributions. The average number of nucleotides adopting a particular conformation was determined by computing the volume of the respective distribution.

The triangle diagrams (Figures 4g and 4p) were created by averaging the number of nucleotides categorized to adopt one of the three specific conformations during the last 40 ns of the corresponding equilibration trajectories. The average numbers were normalized by the total number of nucleotides located outside of the nanopore (17.5 on average) and multiplied by 100 to obtain the percentage makeup. The conformations were categorized as follows. In the at conformation, the base of a nucleotide is bound to the membrane (as defined above). Figure 2b shows an example of such conformation. For the negative charge density, unbound describes a conformation where both backbone and base are detached, as depicted in Figure 2c. For the positive charge density, the unbound conformation describes nucleotides that have their backbones bound to and bases detached from the graphene membrane, Figure 4n. In the tilted conformation, the center of mass of the base is located 5.6 to 7.4 Å away from the graphene, Figure 2f. In the upright conformation, the backbone of a DNA nucleotide is detached from graphene while the amine groups of the base are in contact with graphene, Figure 4e.

Calculation of the number of permeated nucleotides

To quantitatively characterize the process of DNA translocation, the number of DNA atoms located at the trans, grounded side of the membrane was counted for each microscopic state recored in the MD trajectory. That number was divided by the number of atoms in one nucleotide to give the number of nucleotides located at the trans side of the membrane. A change in that number reported on the progress of DNA translocation.