Navigation by environmental geometry: the use of zebrafish as a model

SUMMARY

Sensitivity to environmental shape in spatial navigation has been found, at both behavioural and neural levels, in virtually every species tested, starting early in development. Moreover, evidence that genetic deletions can cause selective deficits in such navigation behaviours suggests a genetic basis to navigation by environmental geometry. Nevertheless, the geometric computations underlying navigation have not been specified in any species. The present study teases apart the geometric components within the traditionally used rectangular enclosure and finds that zebrafish selectively represent distance and directional relationships between extended boundary surfaces. Similar behavioural results in geometric navigation tasks with human children provide prima facie evidence for similar underlying cognitive computations and open new doors for probing the genetic foundations that give rise to these computations.

INTRODUCTION

The rapid development of the field of genomics holds promise for transforming our understanding of the nature and development of human cognition and its disorders. Yet, the greatest advances in genomic analyses thus far have occurred on animals that are distantly related to humans (e.g. Dubnau and Tully, 1998; Guo, 2004; Garrison et al., 2012); furthermore, these analyses focus on simple perceptual, motivational or learning processes. To leverage research on such animals for purposes of investigating the genetic bases of our cognitive capacities, it is crucial to specify and characterize cognitive mechanisms that may be shared between humans and nonhuman animals.

Spatial navigation is an area of cognition that has been studied over many decades, across many species, at both neural and behavioural levels, and with many task variations. One process underlying navigation behaviour is the use of geometric properties of the environment for location memory and orientation. This geometric orientation capacity has been shown to guide navigation in virtually every species tested (Cheng and Newcombe, 2005; Tommasi et al., 2012; Gallistel and Matzel, 2013), making it a potential candidate for a cognitive process that is shared across distantly related species, but the metric representations involved in such computations have not yet been specified.

Recent studies of children begin to address this limit by testing for sensitivity to different geometric properties in fragmented surface arrays. When 2-year-old children see a goal in one corner of a continuous rectangular arena, and then are disoriented by turning around slowly after the goal is hidden or removed, they subsequently search for the goal in both the correct corner and the geometrically identical, rotationally symmetric corner. This type of behaviour, shown by a wide range of animals, is generally taken as evidence for navigation by geometry, but specifically which geometric relationships are represented: length and direction (encoding the goal as ‘left of the longer wall’), distance and direction (encode the goal as ‘left of the closer wall’), or both?

Because distance and length are intimately related in a single, connected polygon, a recent study of children's navigation tested each of these properties in isolation using fragmented corners and wall surfaces, embedded within a larger, circular space (Lee, Sovrano, and Spelke, 2012). Results showed that children's reorientation is based on the computation of distances, but not lengths, between extended three-dimensional surface layouts. Moreover, disoriented children also fail to encode angle relationships between surfaces, and they encode distance relationships between wall-like surfaces but not between freestanding objects or fragmented corners (Gouteux and Spelke, 2001; Lee and Spelke, 2008; Lee and Spelke, 2010; Lee and Spelke, 2011; Lee et al., 2012a). Importantly, children use these geometric properties not only to solve the navigation problems faced by other animals, but also to solve the uniquely human problem of navigating by a map (Huang and Spelke, 2013).

Given that the geometric reorientation capacity is so widely observed across distantly related species, it is reasonable to wonder whether the similarities in behaviour translate to similarities in the underlying computations that guide behaviour. Furthermore, if such similarities can be found in a species conducive to behavioural genomics research, it may take us one step closer to research concerning the genetic bases of such cognitive processes.

One of the challenges to making comparisons between tests of navigation across species is the wide range of methods employed to test navigation capacity. For example, while children in most reorientation studies perform the task without any training, through simple verbal instructions, many studies of reorientation in nonhuman animals have used repetitive trial-and-error training sessions, followed by a transformation of the environment during test trials (for reviews, see Cheng and Newcombe, 2005; Vallortigara, 2009).

The effect of training on behaviour is an important factor to take into account, as revealed by the earliest investigations of reorientation in rats. Although untrained rats ignore room features such as odours, wall colours and landmark patterns when they search for food after disorientation, trained rats use both geometric and featural properties to guide their search in symmetrical environments (e.g. Cheng, 1986; Pearce et al., 2001). For example, rats trained to find a goal location within a rectangular pool and tested within a kite-shaped pool will search for the goal with respect to local geometric cues provided by the walls of different length (McGregor et al., 2006; Pearce et al., 2004); however, it is not clear whether wall length is learned through association and reinforcement, like other landmarks or featural properties (Cheng, 1986), or whether, like children, the rats' representation of length is dissociable from the representation of distance in a spontaneous reorientation task. Moreover, trained domestic chicks also learn to navigate by an array of freestanding objects (Pecchia and Vallortigara, 2010; Pecchia and Vallortigara, 2012) whereas untrained chicks do not (Lee et al., 2012b), and trained fish navigate by featural landmarks (Sovrano et al., 2003) but do not spontaneously reorient by them (Lee et al., 2012c). Training may implicate general learning mechanisms in addition to spontaneous navigational or environmental representations; in order to compare animals' use of distance and length with that of children, therefore, it is important to use species and tasks for which search behaviour can be tested without training.

The purpose of the present experiments is to specify the nature of the geometric representations underlying navigation in a species reported to be sensitive to environmental shape – the zebrafish. Like many other animals, including human children (e.g. Hermer and Spelke, 1994; Wang et al., 1999), zebrafish spontaneously reorient by the environmental shape of a rectangular arena, but fail to reorient by a distinctively coloured wall, even in the absence of competing geometric cues. Given these similarities, a further test of geometric specificity in the zebrafish may provide some insight as to a potential comparison between the computations underlying navigation behaviour in these two distantly related species.

Following a spontaneous, unreinforced navigation task previously developed for zebrafish and redtail splitfins (Fig. 1) (Lee et al., 2012c), we used the logic of isolating the geometrically informative parts of a rectangular arena (Fig. 2) by testing zebrafish in fragmented arrays, each providing differences in surface length, surface distance or corner distance.

Fig. 1.

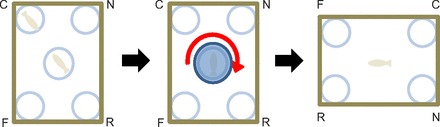
The spontaneous spatial reorientation task developed for zebrafish (Lee et al., 2012c). The subject observes a conspecific in the goal location (C), is covered and rotated slowly for disorientation, and is then released into the empty tank to navigate freely. Approaches within 1 cm to a corner jar are coded as choices. Choosing the correct corner and its rotationally geometric twin (R) over the near (N) and far (F) errors indicates successful use of the rectangular shape of the arena.

Fig. 2.

Photographs of the experimental arenas used in Experiments 1–5, consisting of opaque and transparent surfaces centred within a rectangular or square transparent tank that was embedded in a larger cylindrical enclosure.

MATERIALS AND METHODS

Subjects

Zebrafish [Danio rerio (Hamilton 1822)] are an active shoaling species that live in groups of around 15. The innate shoaling tendency is observable soon after hatching and occurs even in captivity, where fish reared in isolation quickly form shoals when placed together (Kerr, 1963). Subjects in the present study were reared in captivity, housed in groups of eight to nine in transparent 20 l tanks, kept constantly at 23°C, and exposed to artificial lighting for 8 h day⁻¹. Each home tank was equipped with a filter, gravel and vegetation.

A total of 112 zebrafish were tested: 24 in each of Experiments 1, 3, 4 and 5, and 16 in Experiment 2. In every experiment, equal numbers of males and females were tested at each of the four corner locations. All subjects were naïve to the experiment: each fish was tested in only one condition and was given no experience or training prior to testing. The fish were never given any reinforcement for a response during the entirety of the task.

Apparatus

All experiments were performed within a circular outer tank (diameter 175 cm) with a crimson base and black walls (height 30 cm) that blocked the use of external cues. The water level in the tank was kept constant around 4.5 cm, as zebrafish tend to swim near the surface both in their natural habitat and in their home tanks. Monochromatic crimson gravel covered with a transparent Plexiglas surface provided a flat, uniform ground surface throughout the tank. At the centre of the outer circular tank was the experimental tank, which was either rectangular (30×20 cm) or square (24.5 cm sides), depending on the experimental condition (see below). At each corner of the experimental tank was a transparent glass jar (5 cm diameter, 5 cm height) filled with water to the same level as the experimental tank (4.5 cm).

A lamp (60 W) was placed centrally above the tank to maintain uniform lighting, and other lights in the room were extinguished. A digital camera was used to record the test trials and was fixed above the tank but without casting any shadows onto the apparatus.

Design

Each fish was tested in a single session consisting of 12 consecutive trials with a constant but unreinforced goal. Approaches within 1 cm to the four corner jars were coded as choices. In the coding phase we used the subsequent corner denomination: correct (C), rotationally symmetric (R), near error (N) to the geometrically incorrect corner along the short/near side of C, and far error (F) to the geometrically incorrect corner along the long/far side of C. The use of geometric information, therefore, is evidenced by significantly higher choices at C+R over N+F, or, in the case of proportions, relative to chance (50%). To ensure successful disorientation and the absence of uncontrolled asymmetries, C must not be significantly higher than R.

Two behavioural measures were taken for each trial: the first corner approached and the total number of approaches to each corner over a 10-s period following release.

General procedures

The procedures involved a spontaneous navigation task which did not provide subjects with any experience or training prior to the test session.

After its removal from the home tank, the subject fish was released into the experimental tank for 2 min of familiarisation. Then the fish was captured and placed in an opaque, covered container, while a female conspecific was placed in one of four transparent corner jars in the test environment. The subject was placed in a transparent circular chamber (3.5 cm diameter) in the centre of the apparatus for a 2-min observation period, during which the fish could see but not swim to the conspecific in the target corner. The chamber containing the subject was again covered, gently removed from the tank, and rotated slowly on a turntable (at least 360 deg clockwise and 360 deg counter-clockwise) for disorientation. Meanwhile, the jar containing the conspecific was replaced with an otherwise empty water-filled jar, and the whole apparatus, including the circular outer tank, was rotated 90 deg clockwise to eliminate possible influences of uncontrolled external cues. Finally, the subject was transferred into a clear cylinder at the centre of the tank, and the cylinder was gently lifted upward to release the fish. The subject's behaviour was recorded for 10 s after release. After 2 min, the subject was placed back in the observation chamber, with the conspecific in the target corner for the start of the next trial.

All experiments were conducted in accordance with the Italian and European regulations on animal research. Data are presented as means ± s.e.m.

Experiment 1

The purpose of Experiment 1 was to show successful spontaneous reorientation by geometry in a rectangular arena with opaque walls. The experimental setup consisted of a transparent Plexiglas rectangular arena (30×20×10 cm, length × width × height), whose walls were covered with white plastic, to create a continuous opaque rectangle.

Experiment 2

The purpose of this control condition was to verify whether fish are able to use an array of transparent surfaces, as well as any extra-maze cues to reorient in the absence of distinctive environmental geometry provided by opaque extended surfaces.

The apparatus consisted of a transparent Plexiglas rectangular arena (without opaque covering) with the same dimensions as that used in Experiment 1.

Experiment 3

Experiment 3 tested the geometric property of distance while equating for length, by providing zebrafish with a rectangular array of four fragmented, opaque surfaces of identical length (15 cm), fixed to the centre of each of the walls of the transparent rectangular arena (from Experiment 2; Fig. 2). The purpose of the transparent arena was to create a fixed area for navigation that is controlled across all experiments (600 cm²).

Experiment 4

To test for amodal completion in fish navigation, and to probe further the similarities or dissimilarities between the navigation performance of children and zebrafish, Experiment 4 investigated whether zebrafish spontaneously reorient using a geometrically informative arrangement of opaque surfaces at the four corners of the transparent, rectangular array used in the previous experiments. We truncated the four corners of the rectangle so as to present the same area of opaque surfaces specifying the same rectangular configuration (Fig. 2).

The experimental setup consisted of the transparent rectangular arena (from Experiments 2 and 3), with the corners covered with L-shaped white, opaque plastic, 7.5-cm-long on each side (resulting in a total of 60 cm of opaque surface in this condition, as in the previous experiment).

Experiment 5

While spontaneous navigation by environmental geometry is supported by visual representation of distance relationships between extended surfaces (Experiment 3), and not by the corners at which they intersect (Experiment 4), it does not yet preclude the possibility that zebrafish also reorient by differences in surface length, contrary to the findings of previous experiments with children (Lee et al., 2012a). Experiment 5 tested for this ability with arrays like those presented to children, consisting of two pairs of opaque surfaces whose length differed by a 2:1 ratio, standing at equal distances within a geometrically uninformative enclosure arena.

The experimental setup consisted of a transparent square arena with the same total area as the rectangular arena in the first two experiments (24.5 cm sides, 10 cm height). Attached to the centre of each wall of this arena were four fragmented opaque surfaces of two different lengths (10 and 20 cm) made of white plastic and arranged such that opposite walls presented surfaces of the same length. The total length of the opaque surfaces in the apparatus (60 cm) and the total area of the experimental tank were equal to those of Experiments 3 and 4.

RESULTS

Experiment 1

Zebrafish made their first approaches in Experiment 1 according to geometry for 57.3±2.4% of trials (Fig. 3A), which was significantly greater than a chance value of 50% (t₂₃=3.097, P<0.005; because all tests of geometric sensitivity are directional, one-tailed significance levels are reported, unless otherwise specified). Geometric first searches in the present experiment were comparable to those reported previously (Lee et al., 2012c) for zebrafish (61.0±3.3%). Taking this effect size into account, a Bayesian analysis (see Gallistel, 2009) was performed in each experiment to compare the odds of a geometrically correct search between 50 and 70% with the odds of the null hypothesis (50% chance). The resulting Bayes factor for geometrically correct choice in Experiment 1 was 11.96, with corresponding odds of the null hypothesis at 0.08, providing support for successful use of geometry.

Fig. 3.

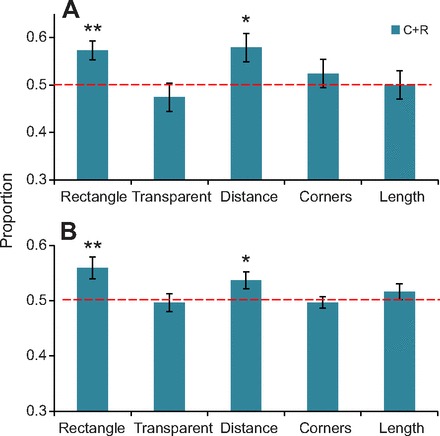
Proportions of (A) first approaches and (B) total approaches in 10 s to the geometrically correct (C+R) corners (Experiments 1–5, from left to right). *P<0.05; **P<0.01 (one-tailed t-tests against chance of 0.5).

Because the present experiment administered 12 trials at a consistent goal location, we compared the first choice performance of the first four trials with that of the last four trials and found no significant difference (t<1, P>0.05). There was no preference for the correct corner over its geometric twin, the rotational corner (t<1, P>0.05), indicating that the higher number of choices to the geometrically correct corners is not driven by the discrimination of the goal location as a result of either the lack of disorientation or an asymmetry in the apparatus.

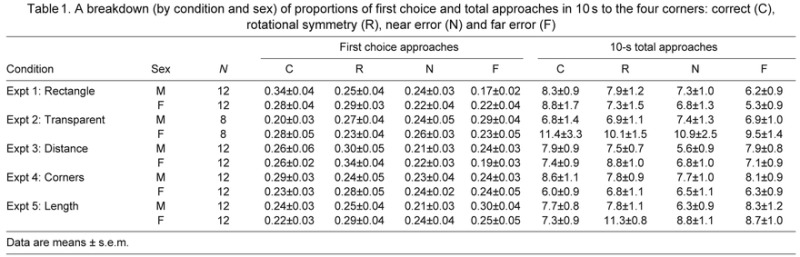
Similar results were found in the analyses of total corner approaches (Fig. 3B). Over a 10-s period following their release, the fish made a mean of 16.17±1.23 geometrically correct approaches, a significantly greater number than their total approaches to the geometrically incorrect corners, 12.79±1.08 (t₂₃=4.136, P<0.001). Because the total number of corner approaches within a given time period was variable across individuals, we also analyzed the data using search proportions rather than raw numbers, and again found a preference for geometrically correct corners in the 10-s period following release (t₂₃=3.510, P<0.001). Each of the above t-tests was checked using the nonparametric Wilcoxon signed rank test; all tests confirmed the results obtained with t-tests. Finally, there were no significant sex differences in the geometric accuracy across all measures (all F<1, P>0.05). Table 1 provides a breakdown of the data, separately for males and females.

Table 1.

A breakdown (by condition and sex) of proportions of first choice and total approaches in 10 s to the four corners: correct (C), rotational symmetry (R), near error (N) and far error (F)

The first experiment confirmed use of environmental shape by zebrafish. In a unitary, opaque rectangular arena, such as those used in past studies and Experiment 1, distance and length information are confounded. To isolate and separately test each geometric component using fragmented parts of the rectangle, while providing a controlled search area for the purposes of reliable coding, we designed the fragmented arrays of opaque surfaces to be tested within transparent Plexiglas arenas (see Fig. 2). In the following experiment, we first verified that spontaneous geometric encoding does not take place with respect to the transparent arena itself, by repeating the method of Experiment 1 after removing all of the opaque covering on the walls (Experiment 2, Fig. 2).

Experiment 2

In Experiment 2, first approaches were made according to geometry for 49.0±3.0% of the trials, which was not statistically different from a chance value of 50% (t₁₅=−0.752, P=0.232; Fig. 3). The Bayes factor for geometrically correct choice (as described in Experiment 1) was 0.003, with corresponding odds of the null hypothesis at 313.27, providing overwhelming support in favour of the null hypothesis. The correct corner was not distinguished from its geometric twin (t<1, P>0.05), and performance in the first four trials did not differ from that in the last four trials (t<1, P>0.05).

Looking at the total approach measures, there were no differences between the mean number of approaches in 10 s to the geometrically correct corners (17.56±2.33) and that in the geometrically incorrect corners (17.31±1.84; t₁₅=0.156, P=0.439). There were no sex differences in the geometric accuracy across all measures (all F<1, P>0.05). However, there was a marginal difference between the total number of corner approaches made overall, showing a tendency for females to be slightly more active than the males (see Table 1) in this transparent arena condition (F_1,14=3.882, P=0.069). Nevertheless, when we converted these data into proportions, we again found that there was no difference between the proportion of approaches to the geometrically correct versus incorrect locations over the 10-s period after release (t₁₅=−0.156, P=0.439).

A comparison between the proportions of geometric searches in Experiments 1 and 2 showed that the opaque rectangular surfaces in Experiment 1 indeed provided fish with crucial visual information about the shape of the environmental arena (first choice: t₃₈=2.196, P=0.017; 10-s period: t₂₈=2.248, P=0.015). Each of the above t-tests was checked and confirmed using the nonparametric Wilcoxon signed rank test.

The randomly distributed approaches in this condition provided evidence that the zebrafish do not spontaneously reorient using the transparent surfaces, and that there were no uncontrolled visual cues in the circular outer tank.

Experiment 3

In Experiment 3, first approaches were made according to geometry for 57.9±3.3% of trials, which was significantly greater than a chance value of 50% (t₂₃=2.373, P=0.013; Fig. 3). The resulting Bayes factor for geometrically correct choice (see Experiment 1) was 39.46, with corresponding odds of the null hypothesis at 0.03, providing strong support for geometric navigation.

First choice accuracy in the first four trials was not statistically different from that in the last four trials (t<1, P>0.05), showing that performance did not change significantly over the course of the experimental session. Furthermore, there was no preference for the correct corner over its geometric twin (t<1, P>0.05), indicating that success was not driven by a lack of disorientation or other uncontrolled cues. In the 10-s period following their release, the fish made a mean of 15.83±0.82 geometrically correct approaches, a significantly greater number than the total approaches to the geometrically incorrect corners (13.67±0.78; t₂₃=3.090, P=0.003). This successful use of geometry was confirmed by analyses of the proportions of geometrically correct versus incorrect approaches (t₂₃=2.355, P=0.014). There were no sex differences across all measures (all F<1, P>0.05). Each of the above t-tests was checked and found to be consistent with results from nonparametric Wilcoxon signed rank tests.

Zebrafish used the distance information provided by the array of equal-length surfaces to the same degree as they did in a fully connected rectangular arena in Experiment 1 (all t<1.1, P>0.05). These findings suggest that fragmentation per se does not impair the performance of fish in this task, and that fish, like children, reorient by distance information. Nevertheless, it is possible that fish and children benefited from surface distance for different reasons. In particular, it is possible that the fish successfully inferred the full rectangular form in this condition by a perceptual process of amodal completion (Sovrano and Bisazza, 2008). Children were shown not to engage amodal completion processes in experiments using these arrays, because they failed to reorient by the shape of a fragmented rectangular array when they were presented with surfaces at the array corners and gaps at the centres of its walls, even though the total amount of opaque surface contour was the same in this condition as in the condition presenting four fragmented walls (Lee et al., 2012a). Because amodal completion is more effective with information at corners than with information at the centres of lines or surfaces (Biederman and Cooper, 1991), these findings suggest that children do not engage shape completion processes in these experiments. Further evidence against amodal completion processes guiding navigation comes from other experiments on children (Gouteux and Spelke, 2001; Lee et al., 2012a). Experiment 4 investigated whether the same conclusion applies to fish.

Experiment 4

In Experiment 4, first approaches were made according to geometry for 52.4±3.0% of the trials, which was not statistically different from chance (t₂₃=0.802, P=0.215; Fig. 3). The resulting Bayes factor for geometrically correct choice (see Experiment 1) was 0.04, with corresponding odds of the null hypothesis at 23.21, providing strong support in favour of the null hypothesis (Gallistel, 2009).

There were no differences between the correct corner and its geometric twin (t<1, P>0.05), nor between performance in the first four trials and that in the last four trials (t<1, P>0.05). Moreover, there was no added advantage provided by the array of opaque corners, compared with the completely transparent arena of Experiment 2 (t<1, P>0.05). The fish also showed no differences between the geometrically correct versus incorrect approaches within the 10-s period (14.58±1.21 versus 14.21±0.95; t₂₃=0.481, P=0.318). Each of the above t-tests was checked and found to be consistent with results from nonparametric Wilcoxon signed rank tests.

Further analyses revealed no sex differences in geometric accuracy (all F<1, P>0.05), but there was a weak difference between the total number of corner approaches made overall (see Table 1), indicating a non-significant trend for males to be slightly more active than the females (F_1,22=2.838, P=0.106, two-tailed). Nevertheless, the null results for geometric accuracy held, even with the use of proportions of geometrically correct versus incorrect approaches within the 10-s period (t<1, P>0.05). The causes for these marginal differences in activity found in the present experiment and Experiment 2 (in which females were slightly more active) are not known; given that they are only marginal, and that the geometric analyses of each experiment are the same with the use of proportions, we do not address these differences further.

The results showed that zebrafish failed to use a rectangular array of freestanding corners to reorient, providing evidence for a second similarity between the reorientation performance of zebrafish and children in their failure to navigate spontaneously by a geometric representation of freestanding objects that are separated from any extended surface layout.

Experiment 5

In Experiment 5, first approaches showed no difference between geometrically correct (50.1±3.4%) and chance performance (t₂₃=0.028, P=0.489). The resulting Bayes factor for geometrically correct choice (see Experiment 1) was 0.02, with corresponding odds of the null hypothesis at 40.25, providing support for the null hypothesis.

There were no differences between the correct location and its geometric twin (t<1, P>0.05), nor between performance in the first four trials and that in the last four trials (t<1, P>0.05). Failure to use the surface length differences was found for comparisons between geometrically correct versus incorrect responses within the 10-s window (17.00±1.11 versus 16.08±1.13; t₂₃=1.297, P=0.104). These results were confirmed using proportions of approaches made within the 10-s period (t<1.3, P>0.05). No significant sex differences were found (all F<1, P>0.05).

Zebrafish failed to reorient by the length relationships presented in this experiment, despite the fact that the lengths of the opaque surfaces differed by 10 cm in absolute length and by a 2:1 ratio (20 cm versus 10 cm; Fig. 2). Thus, Experiment 5 provides evidence for a further specificity of the geometric representations that underlie spontaneous, disoriented navigation.

To test the hypothesis that distance relationships between surfaces had precedence in a rectangular environment, we compared the proportions of searches to the geometrically correct corners in an array consisting of only surface distance (Experiment 3) with that in arrays consisting of the other geometric elements of the rectangle – corners and lengths (Experiments 4 and 5) – across both the first choice and 10-s measures. Preferential approach to the geometrically correct locations was indeed significantly greater for arrays containing distance relationships between extended surfaces (first choice: t₇₀=1.670, P=0.049; 10-s period: t₇₀=1.780, P=0.039). Each of these differences remained significant when tested by nonparametric Wilcoxon signed rank tests.

DISCUSSION

The results of the present experiments support a view of spontaneous navigation involving mechanisms by which relative directions and positions are computed with respect to the distance relationships among extended visible three-dimensional surfaces. Like human children, zebrafish failed to use either an equidistant array of walls of different lengths or a rectangular array of fragmented corners to guide their search for a hidden goal. These striking similarities in the spontaneous navigation of humans and fish suggest the possibility of a domain-specific, evolutionarily ancient computation of surface distance and direction in navigation.

Given the specificity of the geometric reorientation capacity, it may be possible to gain insight into gene–behaviour relationships in geometric navigation using zebrafish as model organisms. This hypothesis is further motivated by reports of a specific navigational deficit in Williams syndrome individuals, who are born with a genetic deletion in chromosome 7. On many cognitive tasks, including most tests of spatial cognition that recruit attention to objects or other landmarks, adults with Williams syndrome perform like young children, showing overall deficits but abilities qualitatively similar to those found early in human development. On tests of spontaneous reorientation, in contrast, adults with Williams syndrome show no sensitivity to surface layout geometry and perform far worse than normally developing toddlers (Lakusta et al., 2010). Through genetic variations of model species such as zebrafish, it may be possible to investigate the role of specific genes in the emergence of specific spatial cognitive abilities, as well as their neural correlates.

Neurophysiological studies of the rat hippocampal formation suggest the existence of neural correlates of this specific sensitivity to three-dimensional surfaces. Studies of spatial representations in the rodents provide evidence for cells in the subiculum (Lever et al., 2009) and medial entorhinal cortex (Solstad et al., 2008) that are specifically attuned to extended surfaces. These cells interact with hippocampal place cells and may provide animals with information about environmental boundaries at various distances and directions (Barry et al., 2006). While further research must be carried out to provide a clearer picture of the neurobiological and genetic bases of boundary geometry representations, zebrafish may provide a useful model organism linking research from multiple fields to the study of spatial representations supporting navigation behaviour – a basic cognitive system that may serve as a building block to human geometric knowledge (Spelke and Lee, 2012).