Membrane potential-dependent integration of synaptic inputs in entorhinal stellate neurons

Abstract

Stellate cells (SCs) of the medial entorhinal cortex exhibit robust spontaneous membrane-potential oscillations (MPOs) in the theta (4–12 Hz) frequency band as well as theta-frequency resonance in their membrane impedance spectra. Past experimental and modeling work suggests that these features may contribute to the phase-locking of SCs to the entorhinal theta rhythm and may be important for forming the hexagonally tiled grid cell place fields exhibited by these neurons in vivo. Among the major biophysical mechanisms contributing to MPOs is a population of persistent (non-inactivating or slowly inactivating) sodium channels. The resulting persistent sodium conductance (G_NaP) gives rise to an apparent increase in input resistance as the cell approaches threshold. In this study, we used dynamic clamp to test the hypothesis that this increased input resistance gives rise to voltage-dependent, and thus MPO phase-dependent, changes in the amplitude of excitatory and inhibitory post-synaptic potential (PSP) amplitudes. We find that PSP amplitude depends on membrane potential, exhibiting a 5–10% increase in amplitude per mV depolarization. The effect is larger than—and sums quasi-linearly with—the effect of the synaptic driving force, V – E_syn. Given that input-driven MPOs 10 mV in amplitude are commonly observed in MEC stellate cells in vivo, this voltage- and phase-dependent synaptic gain is large enough to modulate PSP amplitude by over 50% during theta-frequency MPOs. Phase-dependent synaptic gain may therefore impact the phase locking and phase precession of grid cells in vivo to ongoing network oscillations.

Introduction

The 4–12 Hz theta rhythm is the dominant electrical signal recorded extracellularly in the rodent hippocampal formation during a variety of behavioral states (Buzsáki, 2002; Kramis et al., 1975; Mitchell and Ranck, 1980; Vanderwolf, 1969) and has been observed concurrently in the medial septum, nucleus accumbens, amygdala, prefrontal cortex, and many parts of the olfactory system (Bland and Oddie, 2001; Seidenbecher et al., 2003; Siapas et al., 2005). Brain functions as diverse as memory formation, synaptic plasticity, spatial navigation, and sensorimotor integration have been suggested to be reliant upon the theta rhythm for temporal coordination (Bland and Oddie, 2001; Buzsáki, 2002; Huerta and Lisman, 1993; Lisman, 2010). Additionally, the theta rhythm has been hypothesized to play a critical role in the formation of the grid-like spatial firing patterns of neurons in the superficial entorhinal cortex (Brandon et al., 2011; Giocomo et al., 2007; Hafting et al., 2005; Koenig et al., 2011), although recent evidence points to other models (Couey et al., 2013; Domnisoru et al., 2013; Harvey et al., 2009; Pastoll et al., 2013; Remme et al., 2010; Schmidt-Hieber and Häusser, 2013; Stensola et al., 2012; Yartsev et al., 2011). Several factors have been suggested to contribute to the hippocampal theta rhythm, including cellular and synaptic properties within the hippocampus and medial entorhinal cortex (Alonso and Llinás, 1989; Gillies et al., 2002; Gloveli et al., 2005a, 2005b; Goldin et al., 2007; Goutagny et al., 2008; Haas et al., 2007; Heys et al., 2013; Pastoll et al., 2012; Tort et al., 2007; White et al., 2000) and uni- or bi-directional interactions of these structures with the medial septum (Bland and Bland, 1986; Freund and Antal, 1988; Hangya et al., 2009; Manseau et al., 2008; Stewart and Fox, 1990; Wang, 2002).

Stellate neurons of the medial entorhinal cortex (MEC) layer II exhibit pronounced narrow-band, though non-periodic, membrane potential oscillations (MPOs) in the theta band. In vitro, MPOs occur spontaneously through an interplay of intrinsic ionic currents near spike threshold (Alonso and Llinás, 1989; Burton et al., 2008; Dickson et al., 2000; Dorval and White, 2005; Pastoll et al., 2012; White et al., 1998) and typically have a peak-to-peak amplitude of 1–5 mV. Furthermore, stellate neurons exhibit a resonant peak in the subthreshold membrane impedance spectrum at theta frequencies (Burton et al., 2008; Erchova et al., 2004; Fernandez and White, 2008; Garden et al., 2008; Haas and White, 2002; Nolan et al., 2007), indicating that synaptic inputs modulated at theta frequencies may be preferentially amplified. While this effect is present in stellate cells in vitro, these intrinsic MPOs are not observed in vivo either at rest, where synaptic input may be dampening such oscillations, or during movement, where theta oscillations are synaptically driven (Schmidt-Hieber and Häusser, 2013). During movement in vivo, ~10 mV MPOs have been observed concomitantly with population-level local field potential oscillations at theta frequencies (Domnisoru et al., 2013; Harvey et al., 2009; Quilichini et al., 2010; Schmidt-Hieber and Häusser, 2013), presumably reflecting resonant responses to coherent synaptic input. It is currently unknown if and how the intrinsic rhythmicity of stellate neurons contributes to population-level oscillations. However, the ability of these cells to spontaneously produce theta-frequency MPOs and the observation of a theta generator in the superficial MEC (Alonso and García-Austt, 1987; Kocsis et al., 1999; Mitchell and Ranck, 1980) have prompted the suggestion that the intrinsic electrophysiological rhythmicity of stellate cells could be responsible for the production or strengthening of this rhythm (Hasselmo et al., 2000).

Here, we demonstrate that a slowly inactivating, TTX-sensitive conductance, primarily represented by the persistent sodium conductance (G_NaP) (Magistretti and Alonso, 1999), is responsible for a highly nonlinear subthreshold membrane mechanism. Our results are consistent with those from other brain areas (Stuart and Sakmann, 1994). The inward current generated by G_NaP gives rise to an apparent depolarization-induced increase in input resistance, an effect known in the literature as negative slope conductance (Stafstrom et al., 1982). Using the dynamic clamp technique, we show that a non-inactivating, TTX-sensitive conductance leads to highly nonlinear, membrane potential- and phase-dependent integration of synaptic inputs in the membrane potential range of ongoing oscillations—both intrinsic and synaptically-driven—near spike threshold. This nonlinearity has a profound impact on the integrative properties of stellate cells and may contribute to the selective amplification of synaptic input arriving coherently as a result of population-level, input-driven theta oscillations in vivo.

Materials and Methods

Electrophysiology

All experiments were conducted as approved by the University of Utah Institutional Animal Care and Use Committee. Measurements from stellate cells of the medial entorhinal cortex were made from Long-Evans rats, 18–32 days old. These animals were anesthetized with isoflurane and decapitated. The brain was removed and chilled in ACSF (in mM, 125 NaCl, 2.5 KCl, 1.25 NaH2PO4, 10 MgCl2, 25 NaHCO3, 25 Glucose, 2 CaCl2) and slices were cut in the horizontal plane using a vibrating microtome (Vibratome 1000+; Vibratome, St. Louis, MO) to 400 µm thickness. After letting slices recover for at least one hour in a holding chamber at room temperature, they were transferred to a heated (32–34°C) chamber (Warner Instruments), mounted on an upright microscope stage (AxioSkop FS2; Carl Zeiss, Thornwood, NY). Slices were perfused with heated ACSF and bubbled continuously with 95/5 percent O₂/CO₂. Neurons were visualized using infrared differential interference contrast video microscopy (CCD 100; Dage/MTI, Michigan City, IN). Whole-cell patch clamp recordings were obtained using patch pipettes (2–5 MΩ) fabricated from borosilicate glass (1.0 O.D. 0.5 I.D.; Sutter Instruments, Novato, CA) and filled with (in mM), 120 K-Gluconate, 5 MgCl2, 0.2 EGTA, 10 HEPES, 20 KCl, 7 di(tris) phosphocreatine, 4 Na2ATP, 0.3 Tris-GTP. Presented data were not corrected for the junction potential, presumed to be 10–12 mV. Entorhinal stellate cells were identified electrophysiologically by their prominent sag potentials following hyperpolarization and the presence of MPOs near threshold (Alonso and Klink, 1993). Stellate cells were anatomically identified by their location in layer II of the MEC, their large cell body and the absence of an apical dendrite. In a small number of experiments, the recording pipette contained 0.6% biocytin (Invitrogen, Carlsbad, CA) and recorded cells were processed for post-hoc visualization using established techniques (Kispersky et al., 2012). This aided post-hoc anatomical identification of stellate and pyramidal cells. Control trials using tetrodotoxin (TTX) used ACSF that with 0.5 µM of TTX; those using ZD7288 used concentrations of 20 µM in ACSF. All reagents were obtained from Sigma-Aldrich (St. Louis, MO), unless otherwise noted.

Stimulation protocols

Stimuli for calculating subthreshold impedance were frozen noise current waveforms with white frequency spectra up to 250 Hz. Current waveforms were either 10 sec in duration and repeated 8 times, or 50 sec long and applied in a single trial. Trials in which action potentials were generated were omitted from further analysis.

In comparisons with pyramidal neurons and stellate neurons in TTX, artificial MPOs were elicited by injecting a small-amplitude current waveform constructed in the frequency domain. These stimuli had Gaussian power spectra with a standard deviation of 4 Hz, centered at 3.5 Hz, and truncated at 0Hz. The phases of individual frequency components were uniformly distributed between 0 and 2π. This stimulus was constructed in the frequency domain to resemble spontaneous MPOs and adjusted to generate 3–5 mV peak-to-peak fluctuations in the membrane potential of each neuron.

Synaptic conductances were simulated using dynamic clamp software (Bettencourt et al., 2008; www.rtxi.org; Dorval et al., 2001; Lin et al., 2010) on a Pentium 4 computer running Linux with a patched version of the real-time application interface (RTAI) kernel and equipped with an analog-to-digital converter card (National Instruments, Atlanta GA). Voltage was measured and a control signal applied using a MultiClamp 700B amplifier (Axon Instruments, Union City, CA).

Conductances were implemented according to:

$${\mathrm{I}}_{\text{syn}}(\mathrm{t})={\mathrm{g}}_{\text{max}}\cdot \mathrm{s}(\mathrm{t})(\mathrm{V}-{\mathrm{E}}_{\text{syn}}),$$ (1)

where g_max is maximal conductance, V is membrane voltage, E_syn is the reversal potential of the synapse (−75 mV for inhibitory, 0 mV for excitatory), and s(t) is the difference of two exponentials with time constants of T_rise = 1 ms and T_fall = 3 ms. Artificial post-synaptic conductances (PSGs) were elicited as above using a modified homogeneous Poisson process at an average rate of 0.5 Hz with the additional constraint that events were separated by at least 500 ms. PSGs occurring within 250 ms of an action potential were disregarded during further analysis.

Data analysis

Data analyses were performed using custom scripts written in MATLAB (The Mathworks, Natick, MA). Impedance-frequency plots were calculated by dividing the amplitude of the Fourier transform of the membrane voltage by the transform of input current waveforms. Post-synaptic potential amplitudes were calculated as the difference between the maximum (minimum) voltage within 15 ms of stimulation in response to excitatory (inhibitory) inputs and the voltage immediately prior to stimulation. Given that the implemented synaptic inputs include a driving-force term, the amplitude of applied synaptic currents varied with membrane potential. To correct this driving force effect, in the analysis PSP amplitudes were divided by the integral of the input current (total electric charge) driving that PSP. In order to compare across trials, PSP amplitudes were also normalized by dividing PSP amplitudes by the mean PSP amplitude of that trial. PSP modulation values are thus presented as percent differences per mV of depolarizations, rather than mV (in amplitude) differences per mV of depolarization. When determining significant difference to zero, reported p values were calculated using a one-sample t-test. When comparing among groups, reported p values were calculated using a one-way ANOVA with a Tukey test for means when comparing groups assuming equal variance, except when otherwise noted. P values reported for correlation coefficients were calculated with the 'corrcoef' function in MATLAB and represent the probability that a correlation coefficient as large as or larger than the reported value would be obtained by chance.

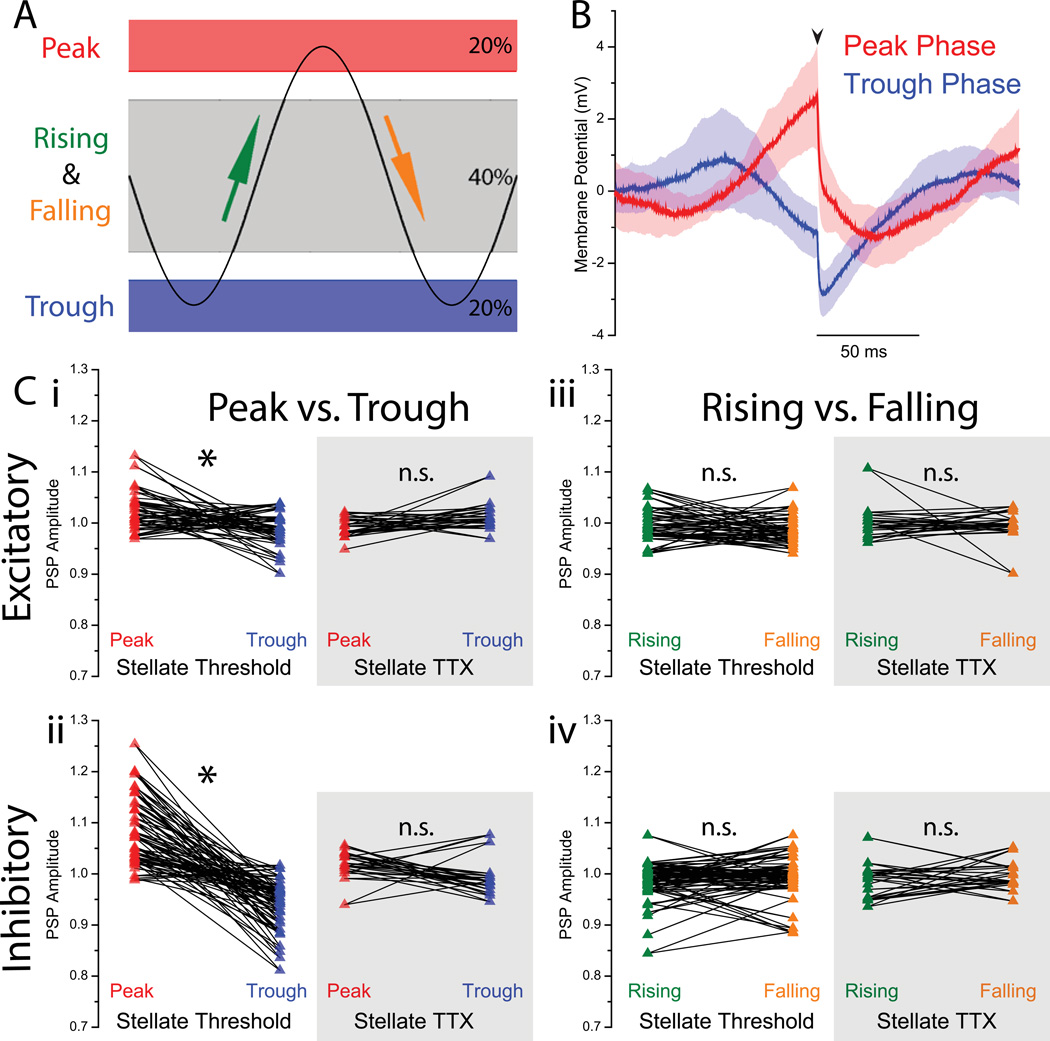
To evaluate the effect of peak vs. trough and rising vs. falling phase on the amplitude of PSPs, traces were detrended using a 4^th order highpass Butterworth filter with a cutoff frequency of 1 Hz. Using this detrended trace, the PSPs within the band of 20% most depolarized potentials were labelled “peak phase” PSPs; the PSPs within the band of 20% most hyperpolarized potentials were labelled “trough phase” PSPs. The middle 40% membrane potential band was used to calculate the rising and falling phase PSPs. Within this band, PSPs that were preceded by 25 ms of an overall increase in membrane potential were labeled “rising phase” PSPs, whereas those preceded by 25 ms of an overall decrease in membrane potential were labeled “falling phase” PSPs. When comparing PSP amplitudes between a) peak and trough phase PSPs and b) rising and falling phase PSPs, the reported p values were calculated using a two sample paired t-test assuming equal variance.

Results

Voltage dependence of subthreshold impedance

Below spike threshold, stellate neurons of the medial entorhinal cortex express substantial quantities of a non-inactivating, “persistent” sodium conductance, G_NaP (Alonso and Klink, 1993; Burton et al., 2008; Fig. 1C; Magistretti and Alonso, 1999; White et al., 1998). Somewhat paradoxically, activation of G_NaP leads to an increase in the apparent input resistance of stellate neurons, as the slope of the current-voltage relationship of the channel is negative (Stafstrom et al., 1982). The presence of G_NaP necessarily contributes a nonlinearity to the subthreshold response properties of these neurons: membrane impedance is thus a function of membrane voltage, increasing as a neuron is depolarized towards spike threshold. Here, our results are consistent with prior findings showing the characteristic membrane impedance spectrum of entorhinal stellate cells (Erchova et al., 2004; Nolan et al., 2007) and the role of TTX-sensitive currents in the impedance spectrum (Boehlen et al., 2013).

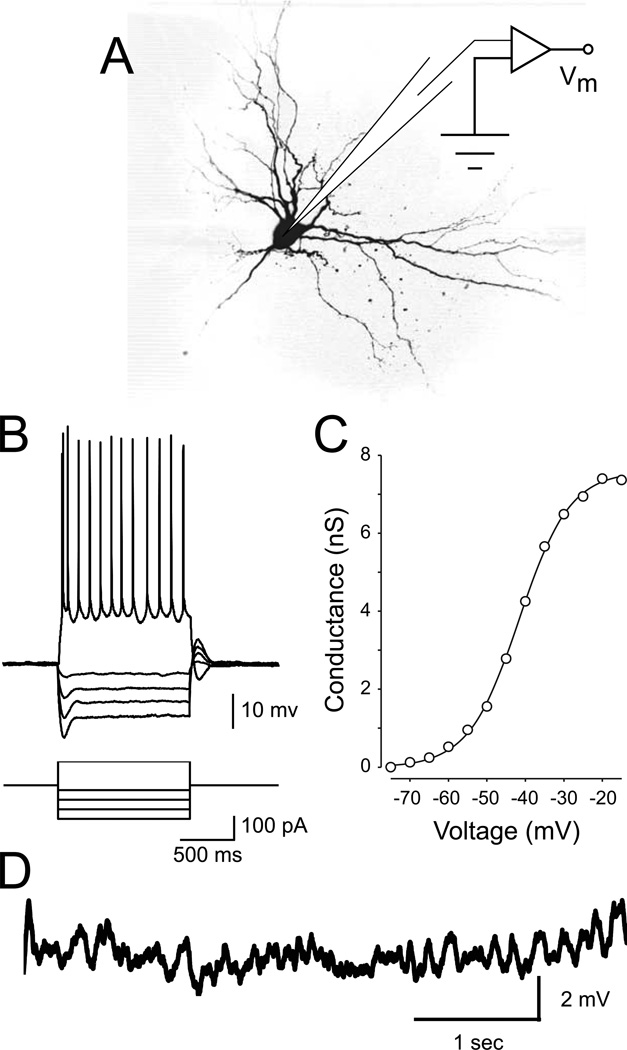
Figure 1. Stellate neuron morphology and electrophysiology.

A Schematic of the recording setup and morphology of a representative stellate neuron. B Stellate neurons display a pronounced inward rectification (sag) in response to hyperpolarizing current steps. In response to a step of depolarizing current, stellate neurons respond with a short burst of action potentials followed by tonic spiking. C Average activation curve of persistent sodium conductance (G_NaP) across a population of stellate cells (modified from Burton et al., 2008). D Spontaneous subthreshold oscillations appear as the neuron is depolarized to a just below spike threshold.

To quantify the voltage dependence of the subthreshold impedance in entorhinal stellate cells, we recorded from these cells in the current-clamp configuration (Fig. 1). Stellate neurons were easily identifiable by established criteria (Alonso and Klink, 1993), including their location in superficial layer II of the medial entorhinal cortex, the presence of a prominent sag in response to hyperpolarizing current steps (Fig 1B), and the presence of spontaneous MPOs near spike threshold (Fig. 1D). In a subset of experiments, the recording pipette contained 0.6% biocytin and stellate morphology was confirmed following post-hoc staining with a fluorescent molecule (Fig. 1A).

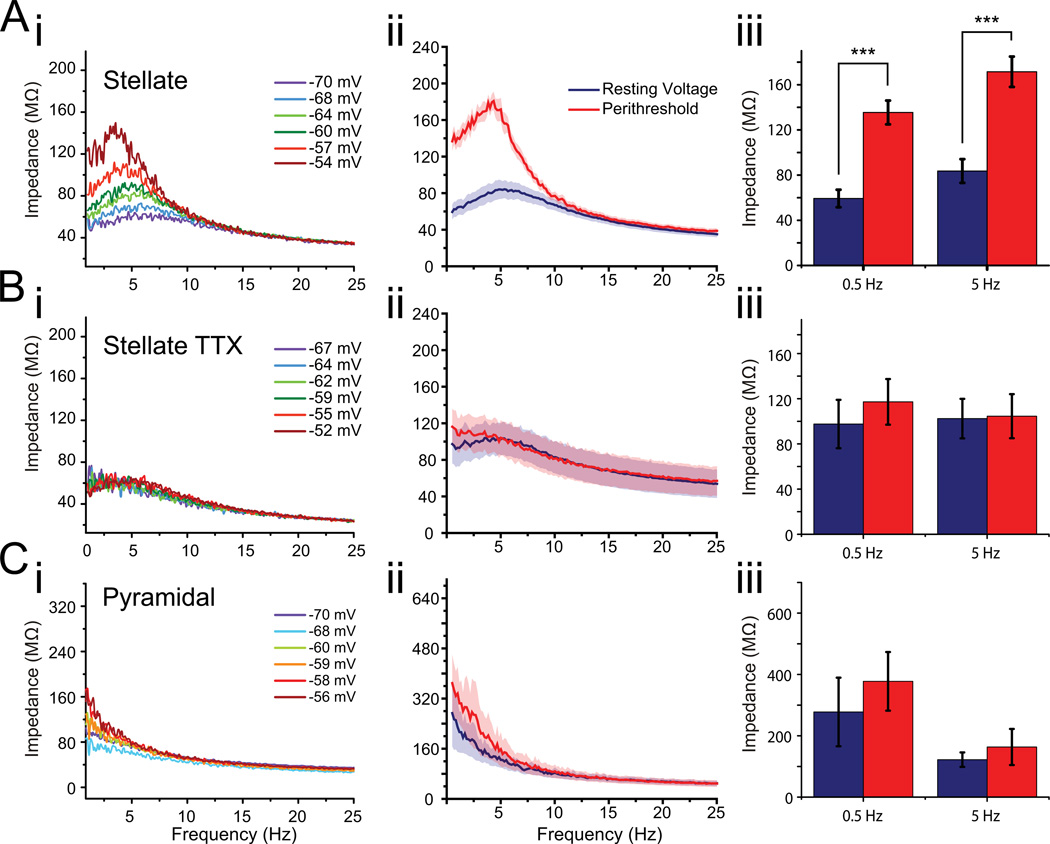
In addition to displaying the characteristic resonance peak at theta frequencies resulting from the presence of the hyperpolarization-activated cation current, I_h, (Burton et al., 2008; Nolan et al., 2007), the membrane impedance of entorhinal stellate cells was found to be exquisitely sensitive to membrane potential (Fig. 2A). Specifically, the impedance increased at all frequencies below the membrane's intrinsic cutoff frequency (~10 Hz) as the membrane potential was depolarized towards spike threshold (Fig. 2A). We observed a particularly large increase at the resonant frequency, where the impedance reaches a maximum, although the Q-value (ratio of peak impedance to impedance at 0.1 Hz) was statistically unchanged (Fig. 2Aiii; Q_rest = 1.30 ± 0.09; Q_thresh = 1.42 ± 0.11; p = 0.45). Additionally, the sensitivity of impedance to voltage became greater as threshold was approached. Across all stellate cells studied, the impedance at 5 Hz increased from 83.6 ± 10.5 MΩ at resting potential to 171.5 ± 13.4 MΩ near threshold (p < 10⁻³). Similarly, at 0.5 Hz, impedance increased from 59.3 ± 7.7 MΩ at rest to 135.4 ± 10.5 MΩ near threshold (p < 10⁻³; n = 9). For the preceding comparisons, the mean voltage in the resting condition was −68.0 mV ± 0.6 mV compared to −54.8 ± 1.1 near threshold, reflecting the presumed biologically relevant range of subthreshold voltages for these neurons. It is worth noting that slices were held at a temperature of 32–34°C, lower than the physiological 37°C, in order to preserve the health of the brain slices. At this lower temperature, the resonance frequency in hippocampal pyramidal cells has been shown to decrease from approximately 8 Hz to 4 Hz (Hu et al., 2002). As such, it is possible that using lower-than-physiological holding temperatures may have lowered the resonance frequency of the stellate cells in this study.

Figure 2. Stellate cells exhibit nonlinear impedance.

Ai Membrane impedance as a function of frequency for a stellate cell at different mean voltages (as indicated). ii,iii Average ± SEM impedance of stellate neurons (n=10) at their resting potentials and near threshold. Bi Impedance measurements in the same cell as in (Ai) in 0.5 µM tetrodotoxin (TTX). ii,iii Average ± SEM impedance across all stellate neurons recorded in TTX (n=8) at resting and threshold potentials. Ci Impedance of a putative entorhinal layer II/III pyramidal neuron at a range of mean voltages. ii,iii Average ± SEM impedance of putative pyramidal neurons (n = 5) at resting and threshold potentials. Impedance is sensitive to voltage in stellate neurons under control conditions (A) but not in TTX (B) or in nearby pyramidal neurons (C).

To confirm that the observed voltage dependency of impedance was indeed a product of persistent sodium channels, we repeated these measurements in the presence of 0.5 µM tetrodotoxin to block voltage-gated sodium channels (TTX; Fig. 2B). In TTX, the voltage dependence of the membrane impedance was abolished and the impedance spectrum closely matched the spectrum measured at the resting membrane potential in control ACSF (Fig. 2B; threshold impedance in TTX at 5 Hz: 104.6 ± 19.5 MΩ, hyperpolarized impedance in control: 102.4 ± 17.5 MΩ; p = 0.94; n = 9). Averaged data (Fig. 2Bii) show a hint of resonance near resting potential, probably due to the effects of I_h. This effect is small, and thus hard to see in many individual examples (e.g., Fig. 2Bi). The observation that impedance in TTX was similar to that measured at the resting potential of the cell in the control condition (p = 0.36) is consistent with the interpretation that voltage-sensitive input resistance is mediated by G_NaP, as the persistent sodium conductance is nearly completely deactivated at rest (Fig. 1C). Furthermore, nearby pyramidal neurons did not display a voltage-dependent impedance profile (5 Hz: 122.2 ± 23.6 MΩ at rest vs. 163.6 ± 58.8 MΩ near threshold; p = 0.54; n = 4), which suggests that G_NaP-mediated increase in impedance near threshold in pyramidal cells is either small or non-existing. Although TTX also blocks the transient sodium current, I_NaT, responsible for the upstroke of the action potential, this channel population comprises only a small (approximately 10%) of the total sodium current at this membrane potential range (Magistretti and Alonso, 1999). Since G_NaP represents the overwhelming majority of the sodium current in this voltage range, G_NaP is used here to refer to the slowly inactivating, TTX-sensitive conductance responsible for this effect.

Membrane potential variations within the physiological range affect synaptic integration

The observations of voltage-dependent membrane impedance and theta-rhythmic membrane potential oscillations led us to hypothesize that synaptic inputs might be integrated with variable efficacy within the range of membrane potentials where subthreshold oscillations occur. We tested this hypothesis by depolarizing cells to perithreshold potentials, at which MPOs were spontaneously and robustly generated, and applying artificial synaptic conductances via dynamic clamp (Fig. 3A). Test artificial excitatory and inhibitory postsynaptic conductances (PSGs) with constant amplitude were applied randomly in time at low rates (see Materials and Methods). PSG amplitudes were set to elicit 0.5–3.0 mV voltage deflections (Fig. 3B), which are small enough as to not alter either the steady state conductance of the cell or the amplitude/frequency of the theta-frequency subthreshold oscillations (as was done in Fernandez and White, 2008 and Schmidt-Hieber and Häusser, 2013). Interestingly, even these small artificial PSPs appear to reset the phase of MPOs (Fig. 3B).

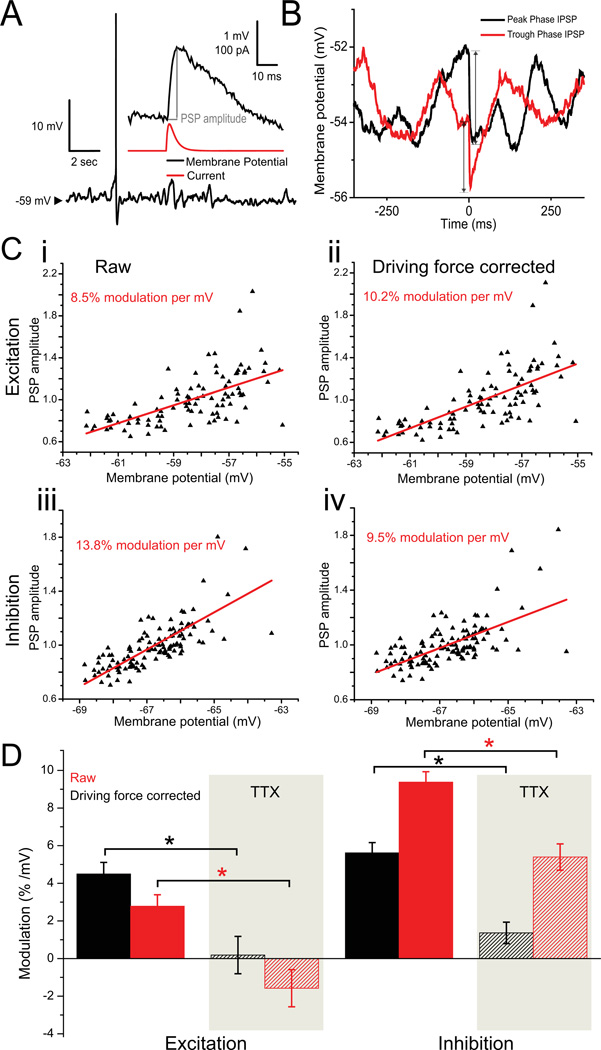
Figure 3. Combined effects of driving force and impedance on PSP amplitude.

A Post-synaptic potentials (PSPs) induced via dynamic clamp in a stellate cell depolarized to the peri-threshold region. At this level of depolarization, membrane potential oscillations are pronounced. PSPs of amplitude 0.5–3 mV were induced randomly in time to quantify modulation of PSP amplitudes by fluctuations in membrane potential. B Single IPSP samples were measured from moment of initiation (time = 0) to their peak, as illustrated by the arrows. The IPSP occurring at the more depolarized membrane potential (peak phase of the oscillation) is greater in amplitude than the IPSP in the more hyperpolarized membrane potential (trough phase of the oscillation). C Examples of the relationship between PSP amplitude and membrane potential for excitatory (i,ii) and inhibitory (iii, iv) PSPs amplitudes excluding a driving force correction (i,iii) and including the driving force correction (ii, iv). As expected, excitatory PSPs are somewhat attenuated with depolarization by the decreasing driving force (compare i and ii), while inhibitory PSPs are further amplified by the increasing driving force (compare iii and iv). D Population averages (stellates near threshold, n = 29 in 24 cells for excitatory, n = 41 in 26 cells for inhibitory; stellates in TTX, n = 15 in 11 cells for excitatory, n = 15 in 10 cells for inhibitory) for the modulation of PSP amplitude by membrane potential for the four cases illustrated in A (solid bars) and when the same measurements were repeated in TTX (shaded bars). The modulation effect is maintained in both uncorrected and driving force corrected conditions.

The resulting relationship between postsynaptic potential (PSP) amplitude and the membrane potential at the time of PSG onset is illustrated for a single, representative stellate neuron in Fig. 3C. Here, driving force corrected data are also shown along with raw, non-corrected data. Since the magnitude of postsynaptic current waveforms in the intact brain—introduced here via dynamic clamp—also depend on membrane potential, the synaptic driving force changes with changing membrane potential. For this reason, a simple calculation would predict that excitatory PSP amplitudes would decrease by approximately 2% per mV depolarization near threshold if the reversal potential of an 2-amino-3-(5-methyl-3-oxo-1,2- oxazol-4-yl)propanoic acid (AMPA) channel is taken to be 0 mV and the perithreshold region is assumed to be −55 to −50 mV. In contrast, inhibitory PSPs would be expected to increase in magnitude by 4–5% per mV depolarization for ionotropic γ–aminobutyric acid (GABA) synapses in the absence of any membrane nonlinearity if the reversal potential of these channels was taken to be −75 mV. When referring to driving force corrected data, PSP amplitudes have been divided by the integral of the input current (total electric charge) injected during that PSP.

In Figure 3C, both excitatory and inhibitory PSP representative samples are plotted versus membrane potential, in both non-corrected and driving force corrected form. The corresponding PSP amplitude modulatory effect is shown using the calculated correlation coefficient. As expected, with the driving force correction the modulation of PSP amplitude becomes larger for excitatory synapses and smaller for inhibitory synapses (Fig. 3D; compare solid red and black bars). The net effect of these two factors is that raw (non-corrected) inhibitory PSPs are dramatically increased in magnitude with depolarization (9.38% ± 0.55% per mV, n = 41 in 26 cells, p < 10⁻³), whereas raw excitatory inputs are only modestly amplified (2.79% ± 0.61% per mV, n = 29 in 24 cells, p < 10⁻³). In TTX, the only modulation of PSP amplitude occurs through changes in the driving force. In this case, with the membrane non-linearity largely abolished, raw excitatory synaptic inputs do not change magnitude appreciably with depolarization while raw inhibitory inputs are amplified (-1.58% ± 0.98% per mV for excitation, n = 15 stellate threshold trials in 11 cells, p = 0.13; 5.39% ± 0.55% per mV for inhibition, n = 15 stellate threshold trials in 10 cells, p < 10⁻³). In raw control data, stellate cells in perithreshold membrane voltages showed significantly more modulation relative to TTX trials in both excitatory (p < 10⁻³, n = 29 stellate threshold trials in 24 cells, n = 15 TTX trials in 11 cells) and (p < 10⁻³, n = 41 stellate threshold trials in 26 cells, n = 15 TTX trials in 10 cells) inhibitory trials, reflecting the impedance-driven modulatory effect. Furthermore, PSP modulation was not significantly different from zero in TTX when the changing driving force was taken into account (0.77% ± 0.57% per mV; n = 15 excitatory trials in 11 cells; 15 inhibitory trials in 10 cells; p = 0.18), validating our correction procedure. In all, these results indicate that the ability for GABAergic synaptic inputs to hyperpolarize the membrane is likely to be substantially greater near the peak of an intrinsic MPO when compared to the trough, while the excitatory ability of AMPAergic synapses is only modestly enhanced by the same cyclic depolarization.

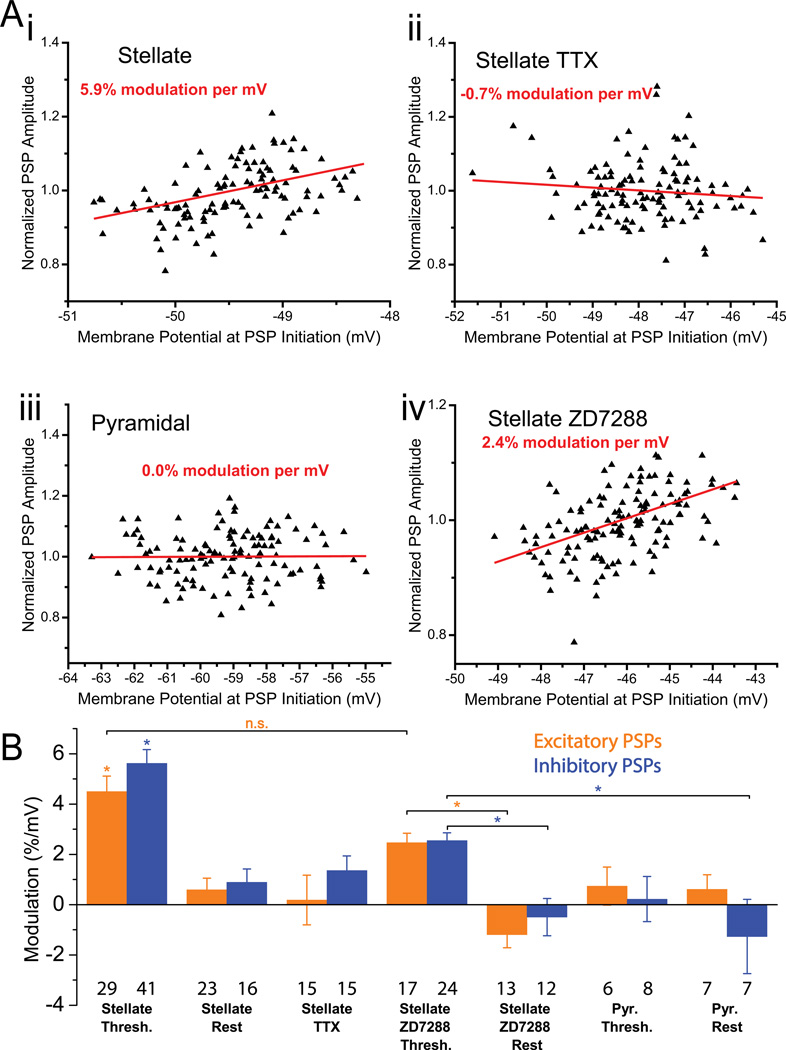
In Figure 4A, driving force corrected data are shown for both representative stellate and pyramidal neurons (top row), as well as in control conditions. A clear trend is apparent in the PSP amplitude-vs.-membrane-potential relationship, with PSP amplitudes increasing significantly as the neuron is depolarized. In the representative example of a stellate cell near threshold in Figure 4Ai, the corrected PSP amplitude appears to increase linearly with depolarization with a 5.90% increase in amplitude per mV of depolarization (r=0.315, p < 10⁻³). No such relationship was observed when these measurements were repeated in the presence of 0.5 µM TTX in the same cell in Fig 4Aii, which then exhibited a −0.76% decrease in amplitude per mV of depolarization (r = 0.105, p > 0.05). In a pyramidal neuron of the same cortical region (Fig. 4Aiii), a 0.04% increase in amplitude per mV of depolarization, r = 0.009, p > 0.05 was observed. These representative examples suggest that the modulation of PSP amplitude was indeed likely the result of the voltage-dependence of the stellate neuron impedance. To eliminate the effect of the hyperpolarization activated cation current, I_h (Harris and Constanti, 1995), the effect was also measured in the presence of 20 µM of ZD7288. In Figure 4Aiv, a representative sample is shown, exhibiting a 2.37% increase in amplitude per mV of depolarization (r=0.4682, p < 10⁻³), suggesting the effect is diminished but maintained.

Figure 4. Nonlinear integration of artificial synaptic inputs.

A Relationship between PSP amplitudes and membrane potential. There is a clear linear trend in stellate neurons near threshold under control conditions (i) but not in TTX (ii) or in pyramidal neurons (iii). For stellate neurons in ZD7288 (iv), the effect is reduced, but largely maintained. B Summary plots for the percent modulation of excitatory (orange) and inhibitory (blue) PSP amplitude per mV depolarization under the various conditions described. Stellates cells near threshold are significantly different (in both excitatory and inhibitory) from all other conditions (ANOVA with Tukey test for means, p < 10⁻²) except where otherwise noted. In ZD7288 trials, stellate cells near threshold were significantly different (ANOVA with Tukey test for means, p < 10⁻²) from stellates at rest, for both excitatory and inhibitory trials.

Across all recorded stellate cells (Fig. 4B), a significant increase in PSP amplitude was observed at perithreshold membrane potentials (5.15% ± 0.41% per mV; n = 29 excitatory trials in 24 cells, 41 inhibitory trials in 26 cells; p < 10⁻³). As expected, such non-linear integration of synaptic inputs was substantially reduced in these neurons at their resting potential (0.72% ± 0.34% per mV; n = 23 excitatory trials in 19 cells, 16 inhibitory trials in 16 cells; p < 10⁻²) and completely absent in the presence of TTX (0.77% ± 0.57% per mV; n = 15 excitatory trials in 11 cells, 15 inhibitory trials in 10 cells; p = 0.18). In nearby MEC layer II pyramidal neurons, artificial synaptic conductances were integrated linearly; the relationship between PSP amplitude and voltage was nearly flat—after compensating for changes in driving force—near threshold (0.44% ± 0.59% per mV; n = 6 excitatory trials in 6 cells, 8 inhibitory trials cells in 7 cells, p = 0.46) and at rest (-0.33% ± 0.80% per mV; 7 excitatory trials in 7 cells, 7 inhibitory trials in 8 cells; p = 0.69). The I_h current was blocked using ZD7288, and while the effect of membrane potential on PSP amplitude was reduced at threshold (2.51% ± 0.24% per mV; 17 excitatory trials in 11 cells, 24 inhibitory trials in 10 cells; p < 10⁻³), it was only fully eliminated at rest (-0.85% ± 0.44% per mV; 13 excitatory trials in 11 cells, 12 inhibitory trials in 10 cells; p = 0.07).

These relationships remain unchanged if excitatory and inhibitory trials are separated and similarly compared across all conditions. Near threshold, excitatory (inhibitory) PSPs increased in magnitude by 4.49% ± 0.62% per mV, n = 29 trials in 24 cells, p < 10⁻³ (5.62% ± 0.54%, n = 41 trials in 26 cells, p < 10⁻³). On average in stellate neurons, these values were significantly different from all other conditions (p < 10⁻² for excitatory trials, except compared to stellates in ZD7288 near threshold where p = 0.17; p < 10⁻³ for inhibitory trials). In turn, modulation values were near zero under the other conditions: stellates near rest 0.59% ± 0.46% per mV, n = 23 trials in 19 cells, p = 0.21 (inhibitory PSPs: 0.90% ± 0.53% per mV, 16 trials in 16 cells, p = 0.11), stellates in the presence of TTX 0.49% ± 0.99% per mV, n = 15 trials in 11 cells, p = 0.85 (inhibitory: 1.36% ± 0.57% per mV, 15 trials in 10 cells, p = 0.03), pyramidal cells near threshold 0.73% ± 0.76% per mV, n = 6 trials in 6 cells, p = 0.38 (inhibitory: 0.22% ± 0.90% per mV, 8 trials in 7 cells, p = 0.81), and pyramidal cells near rest 0.61% ± 0.58, 7 trials in 7 cells, p = 0.33 (inhibitory: −1.27 % ± 1.48% per mV, 7 trials in 8 cells, p = 0.42).

These findings bolster the argument that the observed PSP amplification is caused by the voltage dependence of the membrane impedance illustrated in Fig. 2 which is, in turn, mediated largely by the presence of a substantial persistent sodium conductance. Nevertheless, the impedance spectrum of stellate cells near threshold is in part attributable to I_h (Nolan et al., 2007), so to discriminate the effect of I_h on this modulation, similar trials were performed in the presence of 20 µM ZD7288. Stellate cells in ZD7288 showed subthreshold modulation of 2.47% ± 0.37% per mV, 17 trials in 11 cells, p < 10⁻³ (inhibitory: 2.54% ± 0.31% per mV, 24 trials in 10 cells, p < 10⁻³), whereas at rest the effect was eliminated with modulation of −1.19% ± 0.51, 13 trials in 11 cells, p < 10⁻² (inhibitory: −.49% ± 0.74% per mV, 12 trials in 10 cells, p = 0.52). ZD7288 subthreshold trials were significantly different from their corresponding rest trials (p < 10⁻³ in excitatory trials, p < 10⁻² in inhibitory trials).

Effects of membrane potential oscillation phase on synaptic integration

Thus far, the effect discussed has been between the corrected PSP amplitude and the membrane potential at which this PSP is elicited. To study the relationship of PSP amplitude to the oscillation phase of stellate cell intrinsic subthreshold oscillations, trials were detrended to account for slow drift in the voltage signal and PSPs were grouped according to their location within the oscillation bands. Using detrended data, the PSPs elicited during the 20% most depolarized membrane potentials were labeled peak phase PSPs, those elicited during the 20% most hyperpolarized were labeled trough phase PSPs, and the PSPs in the central 40% were classified as either rising or falling phase, depending on the voltage change prior to the PSP. The amplitude of PSPs in each group were averaged for each trial and compared using paired-samples t-tests. In excitatory (inhibitory) trials, peak phase PSPs were significantly larger in amplitude than their corresponding trough phase PSPs, with a calculated p < 10⁻², n = 29 trials in 24 cells (inhibitory: p < 10⁻³, n = 41 trials in 26 cells). In TTX, this peak phase vs. trough phase difference was not significant with a calculated p = 0.07, n = 15 trials in 11 cells (inhibitory: p = 0.08, 15 trials in 10 cells). Rising phase vs. falling phase paired comparisons in stellate excitatory (inhibitory) trials showed no significant difference with a calculated p = 0.23, n = 29 trials in 24 cells (inhibitory: p = 0.28, n = 41 trials in 26 cells); nor did the same comparisons for stellates in TTX with a calculated p = 0.72, 15 trials in 11 cells (inhibitory: p = 0.33, 15 trials in 10 cells). These findings suggest that PSP amplification is more directly a function of membrane voltage and is thus evident at the peak phase of the oscillation (versus the trough), and furthermore that the rising and falling phase do not have different effects on the amplification of synaptic inputs.

Discussion

In agreement with previous studies (Boehlen et al., 2013; Erchova et al., 2004; Nolan et al., 2007), we have demonstrated that the subthreshold impedance of stellate neurons in the MEC layer II is sensitive to voltage and that this dependence is brought about by the successive activation of increasing numbers of non-inactivating, “persistent” sodium channels in response to membrane depolarization. The effect of this nonlinearity is an increase in membrane impedance, particularly near the theta frequency band, as spike threshold is approached (Fig. 2). Using artificial post-synaptic conductance waveforms introduced during ongoing MPOs with dynamic clamp, we have shown that SCs exhibit voltage-dependent integration of synaptic inputs. Quantitatively, these results indicate that PSP amplitude may be modulated by up to 30–60% by the changing membrane impedance alone during an ongoing synaptically-driven MPO in vivo. Voltage-dependent synaptic integration is abolished by blocking Na⁺ channels and reduced by blocking HCN channels that underlie the hyperpolarization-activated cation current I_h. Our results complement those showing that SCs at different locations along the dorsal-ventral (DV) axis, and thus associated with different grid periods, process inputs differentially (Garden et al., 2008). Thus while we expect the mechanism described in this paper to not change along the DV axis, the effect is complementary to the increase in resistance along the DV axis described in Garden et al., 2008.

The nonlinear resonance of stellate cells is intriguing in the context of theta-frequency oscillations, which are commonly recorded in the MEC (Kramis et al., 1975; Mitchell and Ranck, 1980; Vanderwolf, 1969) and are accompanied by membrane-potential oscillations (MPOs) at theta frequencies near spike threshold (Domnisoru et al., 2013; Harvey et al., 2009; Quilichini et al., 2010; Schmidt-Hieber and Häusser, 2013). Both stellate cells and pyramidal cells phase lock to the theta rhythm and phase precess (Alonso and García-Austt, 1987; Frank et al., 2001; Hafting et al., 2008; Quilichini et al., 2010), consistent with their high impedances within the theta band. Our data suggest that, due to their impedance spectra having theta-centered resonance, stellate cells may show stronger frequency dependence in their phase locking. Furthermore, given that phase precession seems to be driven by periodic inputs that are faster than the average network activity (Schmidt-Hieber and Häusser, 2013), the cellular mechanisms of phase precession are likely to be identical to those underlying phase locking. This suggests that stellates will also show strong frequency preference in their phase precession.

While much of this study focused on the increase in impedance mediated by slowly inactivating Na⁺ channels, we also studied the effect of I_h in the membrane potential-dependent synaptic integration. I_h plays a prominent role in stellate cells electrophysiological dynamics (Dickson et al., 2000; Fernandez et al., 2013; Haas et al., 2007; Nolan et al., 2007; Richter et al., 2000), and its deactivation as the membrane potential is depolarized could contribute to the effect described in this paper. Experiments using ZD7288, an I_h blocker, maintained the effect relative to rest, but reduced the mean percent modulation per mV from approximately 5% to 2.5%. This suggests that the I_h deactivation approaching threshold could play a role in voltage-dependent synaptic integration, and that the increased low frequency impedance associated with eliminating I_h (Nolan et al., 2007) would reduce the impedance differential in the membrane voltage range studied here. It is also possible that ZD7288 introduces off target effects on sodium channels, and that the effect observed here is due to these off-target effect rather than through the block of I_h (Wu et al., 2012).

In addition to amplification by increasing subthreshold impedance, PSP amplitudes are also affected by changes in driving force as the membrane potential varies. For glutamatergic excitation, with a reversal potential of about 0 mV, a 1 mV depolarization of membrane potential will produce a roughly 2% decrease in synaptic current due to the change in driving force alone. Although estimates of the reversal potential of GABA_A channels vary considerably (Khirug et al., 2008; Vida et al., 2006; Woodruff et al., 2010), the effects of either shunting or hyperpolarizing GABA_A channels will be enhanced near threshold (e.g., by 4–5% if E_GABA = −75 mV). Effects of driving force combine approximately linearly with the effects of nonlinear impedance (Fig. 3D).

In this study, we have limited measurements and analysis to the dynamics of only the neuronal cell body. It is possible that the characteristics we describe here are substantially different at distal dendritic locations. However, a large number of inhibitory synapses are located on the cell body or at proximal dendritic sites of principal cells in the hippocampal formation (Freund and Buzsáki, 1996), indicating that the effects of nonlinear impedance are likely relevant for physiological inhibitory synaptic inputs in the intact brain. As excitatory inputs may arrive at more distal locations and because the density of sodium channels has been found to decrease with distance along dendritic processes in other cell types (Hu et al., 2010; Jarsky et al., 2005), it is possible that excitatory synaptic inputs are affected by the membrane nonlinearity to a lesser degree (Stuart and Sakmann, 1995).

The nonlinearity we describe here is likely present in any neuronal population possessing a substantial persistent sodium conductance below spike threshold, due to the simplicity of this mechanism. Neurons in the thalamus, neocortex, hippocampus, and cerebellum express such a conductance prominently (Crill, 1996), and for this reason one may presume that synaptic inputs are integrated in all of these cells in a manner that is nonlinear and depends significantly (5–10% / mV) on membrane voltage when engaged in oscillatory or other activity in which membrane potential traverses a large range of values.

The results we describe here should have substantial effects in vivo, on three time scales. On the time scale of crossings through one of the cells’ periodically spaced place fields, SCs exhibit sustained depolarizations lasting seconds (Domnisoru et al., 2013; Schmidt-Hieber and Häusser, 2013). Our results suggest that the effects of both excitation and (especially) inhibition are enhanced during these in-field periods, making the SCs easier to drive but also making it easier for inhibition to modulate this drive. On the time scale of the theta cycle (hundreds of ms), we would expect both the excitation arriving during the depolarizing phase, and any inhibitory inputs that help terminate the depolarizing phase, to be enhanced by nonlinear membrane impedance. Thus, the nonlinearity in the membrane may enhance the quality of phase locking to the network theta rhythm. Finally, on the time scale of short trains of action potentials (10 ms), membrane nonlinearity may serve as an additional form of negative feedback, amplifying the effects of inhibition. As the temporal lobe in general and the superficial entorhinal cortex in particular represent common foci for epileptic seizures (Bartolomei et al., 2005; Engel and Pedley, 2008; Spencer and Spencer, 1994), it is not unreasonable to expect that neurons in this area have developed numerous negative feedback mechanisms to regulate excitability.

Figure 5. Effect of membrane potential oscillation phase on synaptic integration.

A PSPs were grouped into four different categories: peak, trough, rising phase, and falling phase. Detrended data were divided into bands representing each category: the 20% most depolarized membrane potential were labeled “peak phase” trials, while the 20% most hyperpolarized band were labeled “trough phase” trials. From the middle band representing 40% of the membrane potential range, PSPs following an increase in membrane potential were labeled “rising phase” PSPs; those following a decrease in membrane potential were labeled “falling phase” PSPs. B A sample waveform average from one trial showing the PSP-triggered average of all peak phase PSPs and trough phase PSPs. An arrow denotes the beginning of the artificial PSP injection. Shaded region indicates standard error associated with the waveform average. Note the larger magnitude associated with peak phase PSPs relative to trough phase PSPs, as well as the intrinsic MPO preceding the PSP. C For each trial, the average PSP amplitude for peak (rising) phase PSPs are compared to the average PSP amplitude for trough (falling) phase PSPs (stellates near threshold, n = 29 in 24 cells for excitatory, n = 41 in 26 cells for inhibitory; stellates in TTX, n = 15 in 11 cells for excitatory, n = 15 in 10 cells for inhibitory). Peak phase PSP amplitudes were significantly larger (p < 10⁻³ for both inhibitory and excitatory, paired sample t-test) than their corresponding trough phase PSP amplitudes (i, ii). This effect was eliminated for PSPs in TTX, which showed no significant difference between matched peak vs. trough PSP amplitudes. Rising and falling phase PSPs showed now significant difference in any condition, for neither excitatory nor inhibitory trials.