Area MT Encodes Three-Dimensional Motion

Abstract

We use visual information to determine our dynamic relationship with other objects in a three-dimensional (3D) world. Despite decades of work on visual motion processing, it remains unclear how 3D directions—trajectories that include motion toward or away from the observer—are represented and processed in visual cortex. Area MT is heavily implicated in processing visual motion and depth, yet previous work has found little evidence for 3D direction sensitivity per se. Here we use a rich ensemble of binocular motion stimuli to reveal that most neurons in area MT of the anesthetized macaque encode 3D motion information. This tuning for 3D motion arises from multiple mechanisms, including different motion preferences in the two eyes and a nonlinear interaction of these signals when both eyes are stimulated. Using a novel method for functional binocular alignment, we were able to rule out contributions of static disparity tuning to the 3D motion tuning we observed. We propose that a primary function of MT is to encode 3D motion, critical for judging the movement of objects in dynamic real-world environments.

Introduction

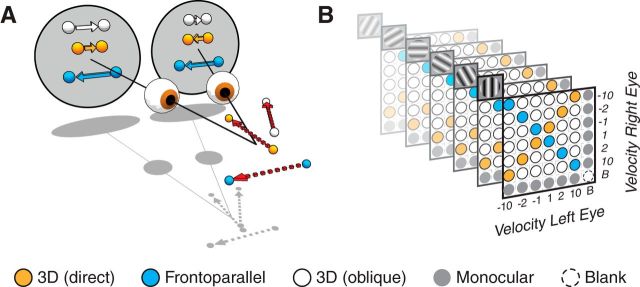
Objects moving through depth generate different motion signals in the two eyes. For instance, an object moving directly toward the bridge of the observer's nose will produce equal and opposite directions of motion in the two eyes—rightward motion in the left eye and leftward motion in the right eye (Fig. 1A, orange symbols). Oblique 3D trajectories will generate the same direction of motion, but different speeds, in the two eyes (Fig. 1A, white symbols). Only trajectories orthogonal to the line of sight generate similar velocities in the two eyes (frontoparallel motion; Fig. 1A, blue symbols). Recent psychophysical studies suggest that mechanisms based on the dynamic binocular information illustrated in Figure 1A play a central role in 3D motion perception (Cumming and Parker, 1994; Gray and Regan, 1996; Brooks and Stone, 2004; Fernandez and Farell, 2005; Harris et al., 2008; Shioiri et al., 2009; Czuba et al., 2010, 2011; Rokers et al., 2011; Sakano et al., 2012).

Figure 1.

3D motion and stimulus ensemble. A, Relationship between 3D motion trajectories and the retinal motion they induce. Motion straight toward a point between the observer's eyes provides equal and opposite motion signals to the two eyes (orange). Oblique trajectories can cause motion in the same direction but with different speeds in the two eyes (white). Frontoparallel motion (blue) provides similar motion signals to the two eyes. B, The stimulus ensemble used to probe 3D motion tuning in area MT. Matrix schematic of fully crossed monocular velocity pairings (x- and y-axes; ±1, 2, 10°/s, or [B]lank), presented at six grating orientations (depicted as repeated planes with corresponding grating icons). Conditions consisting of frontoparallel motion are indicated by blue; conditions consisting of equal and opposite motion in the two eyes, which would be induced by motion directly toward or away from the observer, are indicated in orange; conditions consistent with oblique 3D trajectories are shown in white; monocular stimulus conditions in gray.

Despite the obvious ecological relevance of 3D motion, it remains unclear how it is encoded in the visual system. In primates, motion processing occurs largely in cortex, beginning with primary visual cortex and including a host of higher cortical areas, particularly area MT (Maunsell and Newsome, 1987). MT neurons are sensitive to the direction of visual motion (Zeki, 1974; Maunsell and Van Essen, 1983a; Albright et al., 1984; Born and Bradley, 2005), and their activity has been related to motion perception (Salzman et al., 1990; Britten et al., 1996; Parker and Newsome, 1998). Many MT neurons are also sensitive to binocular disparity, and play a role in the perception of depth via stereopsis (Maunsell and Van Essen, 1983b; DeAngelis et al., 1998; Cumming and DeAngelis, 2001, Smolyanskaya et al., 2013).

Although MT has been linked closely to both visual motion processing and stereopsis, surprisingly little is known about its role in encoding 3D motion, the sort of motion frequently experienced in natural viewing. This is because virtually all studies investigating motion processing in MT have used frontoparallel or monocular motion stimuli. Several early studies provided anecdotal evidence for 3D motion tuning in MT (Zeki, 1974; Albright et al., 1984) but work by Maunsell and Van Essen (1983b) found none. Maunsell and Van Essen (1983b) also made the important point that 3D tuning needs to be clearly distinguished from interacting sensitivities to frontoparallel motion and static depth, an issue that plagued some early studies in cat (Cynader and Regan, 1978, 1982). Contrary to this ambiguous or negative evidence, recent human functional imaging work identified strong selective adaptation to 3D direction in the human MT/ MST complex (Rokers et al., 2009).

To determine whether MT neurons encode 3D motion, we presented a comprehensive set of motion stimuli, corresponding to a range of frontoparallel and 3D motion trajectories spanning known physiological and behavioral sensitivities (Beverley and Regan, 1975; Maunsell and Van Essen, 1983a; Czuba et al., 2010). Our stimulus ensemble allowed us not only to identify sensitivity to 3D motion, but also to determine direction tuning in 3D space and to understand how such tuning arises from the combination of inputs from the two eyes. We found widespread sensitivity to 3D motion, and identified multiple mechanisms for generating this tuning. These findings demonstrate that MT encodes the wide array of velocities that occur in dynamic 3D environments.

Materials and Methods

We performed extracellular recordings in two anesthetized, adult male macaque monkeys (Macaca fascicularis) using techniques previously described in detail (Smith and Kohn, 2008). In brief, anesthesia was induced with a ketamine-diazepam injection (10 and 1.5 mg/kg, respectively). Following intubation, anesthesia during preparatory surgery was maintained with 1.0–2.5% isoflurane in a 98% O₂, 2% CO₂ mixture. During recordings, anesthesia was maintained with sufentanil citrate (6–18 μg · kg⁻¹ · h⁻¹, adjusted as needed). Vecuronium bromide (0.15 mg · kg⁻¹ · h⁻¹) was used to minimize eye movements. Intravenous drugs were administered via saphenous catheters in a dextrose enriched (2.5%) Normosol-R solution used to maintain physiological ion balance. Vital signs (ECG, SpO₂, blood pressure, EEG, end-tidal CO₂, temperature, airway pressure, urinary output, and specific gravity) were continuously monitored to ensure anesthesia and physiological well being. Topical atropine was used to dilate the pupils and corneas were protected with gas-permeable contact lenses. A broad-spectrum antibiotic (Baytril, 2.5 mg/kg) and anti-inflammatory steroid (dexamethasome, 1 mg/kg) were administered daily. Optical refraction and supplementary lenses were used to focus the retinal image. All procedures were approved by the Institutional Animal Care and Use Committee of the Albert Einstein College of Medicine at Yeshiva University and were in compliance with the guidelines set forth in the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Recordings and visual stimulation.

MT recordings were conducted using a linear array of platinum-tungsten electrodes and tetrodes (Thomas Recording, spacing 305 μm), inserted 16 mm lateral from the midline and 6.5–7.5 mm posterior to the lunate sulcus at an angle of 20° from horizontal. Electrode locations were determined to be in MT by anatomical landmarks and by the directionally tuned neuronal responses with spatial receptive fields of expected size (Ungerleider and Desimone, 1986). Neural signals were amplified, bandpass filtered (0.5–8000 Hz), and digitized at 40 kHz (16-bit resolution). Digital signals were then high-pass filtered (4-pole Bessel filter, 300 Hz cutoff frequency) before automated spike detection (Plexon Omniplex). Waveforms that exceeded a user-defined threshold were stored to disk and manually sorted off-line into single units and cohesive multiunit groupings (Plexon Offline Sorter). We confirmed that our results were independent of sort quality, as defined by waveform signal-to-noise ratio (Kelly et al., 2007).

To achieve binocular alignment, we paired our MT recordings with primary visual cortex (V1) recordings, using a 10 × 10 microelectrode array (400 μm spacing, 1 mm length; Blackrock Microsystems) implanted ∼10 mm lateral to the midline and ∼4–6 mm posterior to the lunate. V1 receptive fields were ∼3° in eccentricity. Signals were amplified, bandpass filtered (0.3–7.5 kHz) and waveform snippets that exceeded a voltage threshold were digitized at 30 kHz.

Stimuli were presented using a custom mirror stereoscope and pair of linearized CRT displays (HP p1230, 40.6 × 30.5 cm viewable; 85 Hz progressive scan, 1024 × 768 pixel resolution each, mean luminance ∼40 cd/m²), positioned at a viewing distance of 54–80 cm, so that all V1 and MT receptive fields were fully within the viewable area. Displays were driven using a Mac Pro computer outfitted with a dual-monitor-spanning video splitter (Matrox DualHead2Go) to achieve frame-locked temporal synchrony between the two displays. Stimuli were generated using custom software (EXPO, http://corevision.cns.nyu.edu/expo).

MT spatial receptive fields were mapped by sequentially presenting small drifting gratings (∼3°, 1 cycle/deg, 8 Hz, 250 ms presentation) in a randomized position grid spanning both monitors (13 × 13 element grid per monitor). A high-resolution version of the receptive field mapping sequence was then performed, to allow precise alignment of the stimuli presented to the two eyes. For this mapping, we used parameters optimized for the V1 array, sampling locations ±2.5° from the estimated center of the aggregate V1 receptive field for each eye (0.5° grating diameter, 1 cycle/deg, 4 Hz, 250 ms presentation). The receptive field locations of binocularly driven channels with well defined spatial receptive fields (well fit by a 2D Gaussian function; see Fig. 8A, green symbols) were then used to compute a three-parameter matrix transformation (Nauhaus and Ringach, 2007) which aligned receptive field locations in the two eyes (see Fig. 8A, black symbols). We placed all subsequent stimuli in the center of the aggregate MT receptive field of one eye, and then used the matrix transform to translate and rotate the stimuli on the other eye's monitor. Our approach provides novel measurements of translation and interocular rotation, likely a combination of optical image rotation and cyclorotation, that play an important role in assuring accurate presentation of dichoptic stimuli. Binocular alignment was performed at the beginning of every electrode penetration or every 12 h, whichever came first. Transformation parameters were stable across measurements and animals (rotation ∼10°; translation depending on mirror position).

Figure 8.

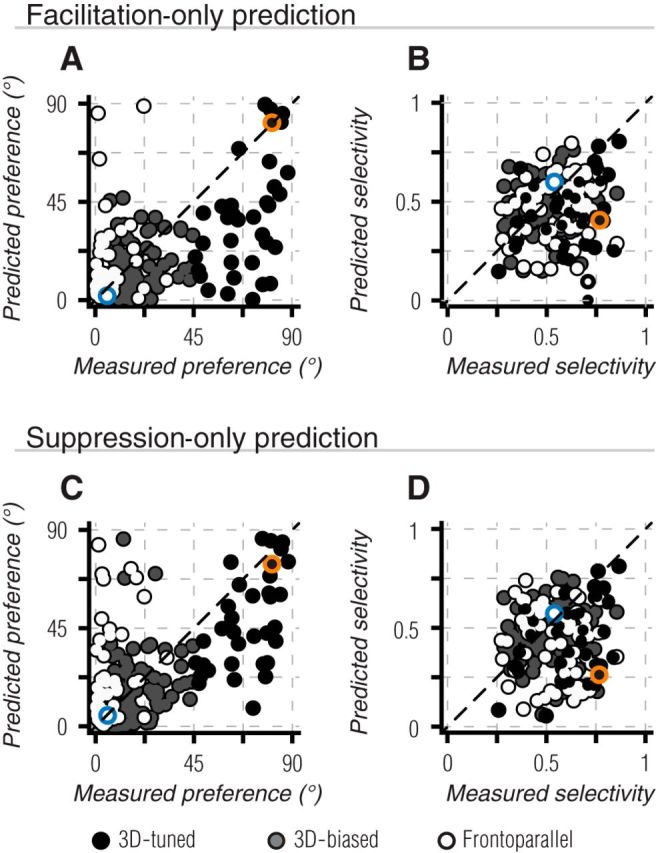
Nonlinear interactions in binocular motion preference and selectivity. A, B, Same as Figure 7 A,C, but based on predictions that only allowed decrements from measured responses. Thus, remaining deviations in predicted preference or selectivity arise from only facilitative binocular interactions. C, D, Same as A, B, but for predictions that only allowed response predictions greater than measured responses, thus deviations arise from only suppressive binocular interactions. All color conventions as in Figure 7. Neither modified prediction produced a significant improvement in tuning predictions (Table 1).

Binocular and monocular tuning for motion direction was measured using drifting full-contrast gratings (1 cycle/°, 16–20° diameter) presented in 12 uniformly spaced directions (0–330°, in 30° steps). Tuning was measured for three grating speeds (1, 2, and 10°/s) chosen to span retinal speeds that are consistent with ecologically plausible 3D motion (Czuba et al., 2010) and with those typically preferred by MT units for frontoparallel motion (Priebe et al., 2003). Binocular gratings were always presented with the same orientation in the two eyes, but speed and relative interocular direction (i.e., same or opposite sign) were varied within a fully crossed design matrix. Including blank trials, used to determine the spontaneous firing rate of each unit, the full stimulus matrix consisted of seven monocular speed/directions per eye (blank, −10, −2, −1, 1, 2, 10 °/s) and six distinct grating orientations (−90, −60, −30, 0, 30, 60°), resulting in 294 total conditions (Fig. 1B). Trials were presented consecutively (1 s duration; no interstimulus interval) in pseudorandom order, with 25 repetitions per condition.

The starting interocular difference in grating phase was randomized on every trial. The spatial frequency of 1 cycle/deg was chosen so that the largest of interocular phase disparities (180° out of phase: ±1° of binocular disparity) remained within the conventional range of binocular fusion, and allowed for an integer number of interocular phase cycles within each 1 s trial. Combined with the randomization of starting interocular phase, disparity content was effectively balanced within and across trials.

We made no attempt to explicitly separate the velocity-based or disparity-based binocular 3D motion cues. Our binocular grating stimuli gave rise to concurrent velocity- and disparity-based cues for motion toward or away from the observer.

Analysis of direction tuning.

The neuronal response for each trial was computed from the mean firing rate over an 850 ms time window, discarding the first 150 ms to account for onset latency and any unselective response transients at stimulus transitions. Bootstrapped mean and SEs were computed across the 25 repetitions of each motion condition using 1000 bootstrap repetitions. The spontaneous firing rate was computed from the last 200 ms of each blank trial presentation, and subtracted from each unit's mean firing rate.

Any units that did not exhibit a mean firing rate ≥10 Hz above the spontaneous rate in at least one motion condition (across all 288 binocular and monocular motion conditions; 27% of units), or did not maintain reasonable isolation throughout the ∼2 h grating stimulus sequence (4% of units) were discarded. We did not use any selection criteria based on tuning quality because some units were tuned for one form of motion (e.g., 3D) but not another (frontoparallel). We observed qualitatively similar motion tuning in MT, regardless of the precise selection criteria used.

Tuning was assessed by computing the vector sum of responses (Leventhal et al., 1995; O'Keefe and Movshon, 1998). For frontoparallel motion, the preferred direction was defined as follows:

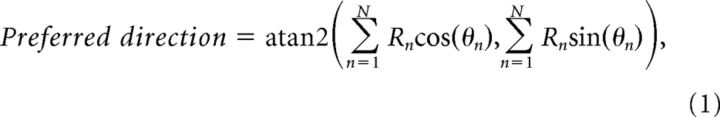where θ_n and R_n are the direction of motion and response strength for each of the n = 12 directions. Tuning selectivity was defined as follows:

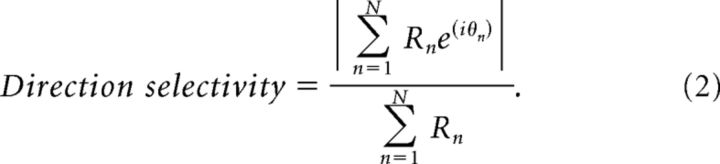For each unit, we computed bootstrapped mean and confidence intervals on direction preference and selectivity measurements by resampling at the individual trial level. That is, resampling with replacement from the original set of measured responses (25 trials per condition), then computing binocular preference and selectivity from the average of these responses. This process was repeated 1000 times to obtain bootstrap distributions of tuning measurements; the 95^th percent confidence intervals represent the 2.5^th to 97.5^th percentiles of this distribution.

For conditions with opposite motion in the two eyes (see Fig. 3B), similar computations were used, but with θ_n indicating the direction of motion in the left eye (with equal and opposite motion presented in the right eye). Tuning for both frontoparallel and opposite motion conditions was based on responses to the grating speed that evoked the strongest response across all binocular conditions.

Figure 3.

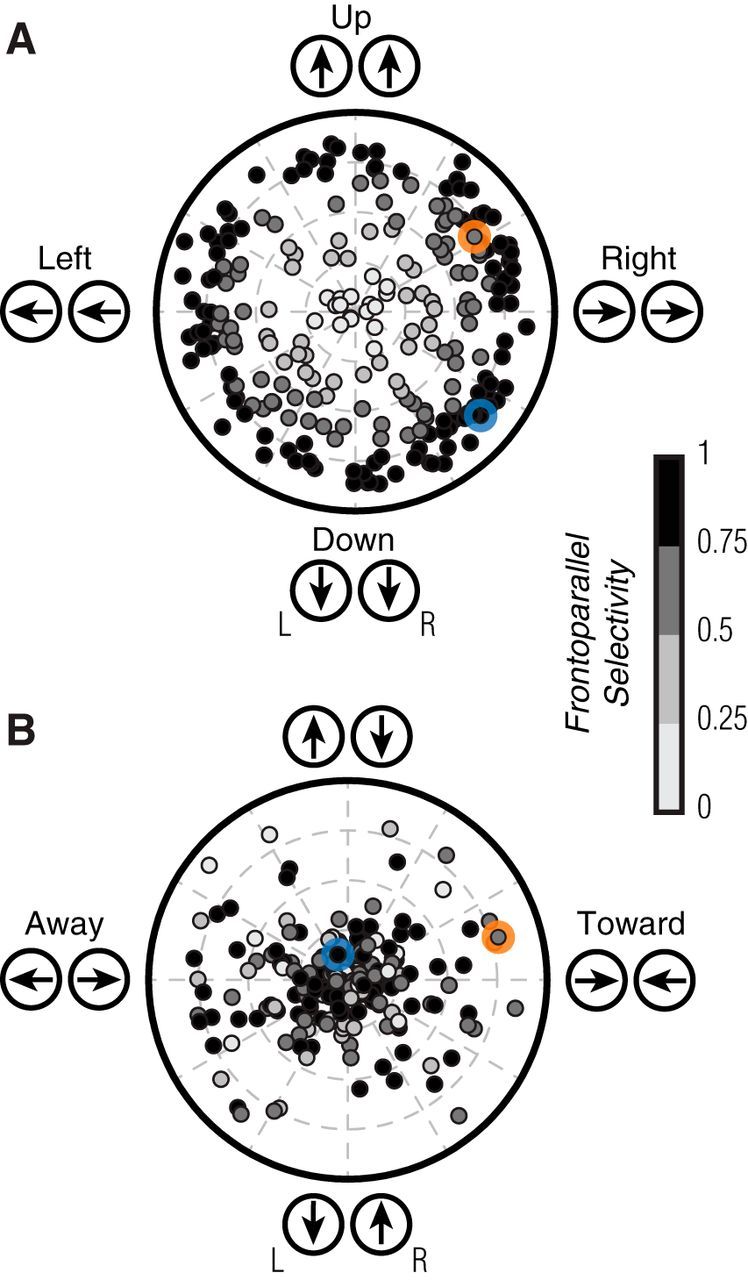
Direction tuning for binocular matched and opposite motion. A, Polar plot indicating the direction preference (angle) and selectivity (distance from origin) of each MT unit, measured with identical gratings presented to the two eyes (binocular frontoparallel motion). Most MT units were selective, with a broad range of preferences. The example units of Figures 2A–D and E–H are indicated by blue and orange markers, respectively. Shading of symbols indicates the selectivity for binocular frontoparallel motion, in both A and B. B, Polar plot for the tuning to gratings drifting in opposite directions in the two eyes. A substantial fraction of MT units were selective for opposite motion signals in the two eyes.

We measured tuning in a 3D motion space using a similar metric. We defined the direction of 3D motion, φ_n, for each binocular stimulus condition as follows:

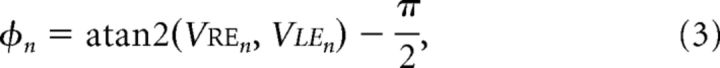where Vre_n and Vle_n are the stimulus velocities in the right and left eyes, respectively (Cynader and Regan, 1978). Although directions in binocular 3D motion space were computed in terms of the ratio of velocities presented to the two eyes, the resulting 3D directions are geometrically consistent with either disparity-based or velocity-based cues (Regan, 1993), both of which were present in the drifting binocular gratings we presented.

We then computed binocular preference and selectivity as in Equations 1 and 2, but substituting φ_n for θ_n. Tuning for each unit was based on responses to all binocular conditions from the grating orientation that evoked the maximal response (n = 36 stimulus conditions); that is, of the six matrices shown in Figure 1B, we used the one containing the maximal response. We presented each grating direction in our stimulus ensemble at three speeds. In determining 3D tuning, some 3D directions were thus sampled at multiple speeds. These were treated as separate measurements; that is, we added n vectors corresponding to this direction, each weighted by the response elicited by each of the n 3D speeds pointing in that direction. Although we did not sample uniformly from the space of 3D trajectories, our ensemble was symmetric about both the frontoparallel and 3D motion axes. Thus, it did not introduce any bias for motion in or out of the frontoparallel plane.

A cell was considered 3D-biased if it exhibited a significant differential response for toward versus away motion conditions based on a paired Wilcoxon signed rank test (n = 15 pairings). Mean responses were paired such that conditions with opposite toward/away motion components, but with matched frontoparallel components, were compared in a single statistical test for each cell (see Fig. 4A, inset, endpoints of orange lines).

Figure 4.

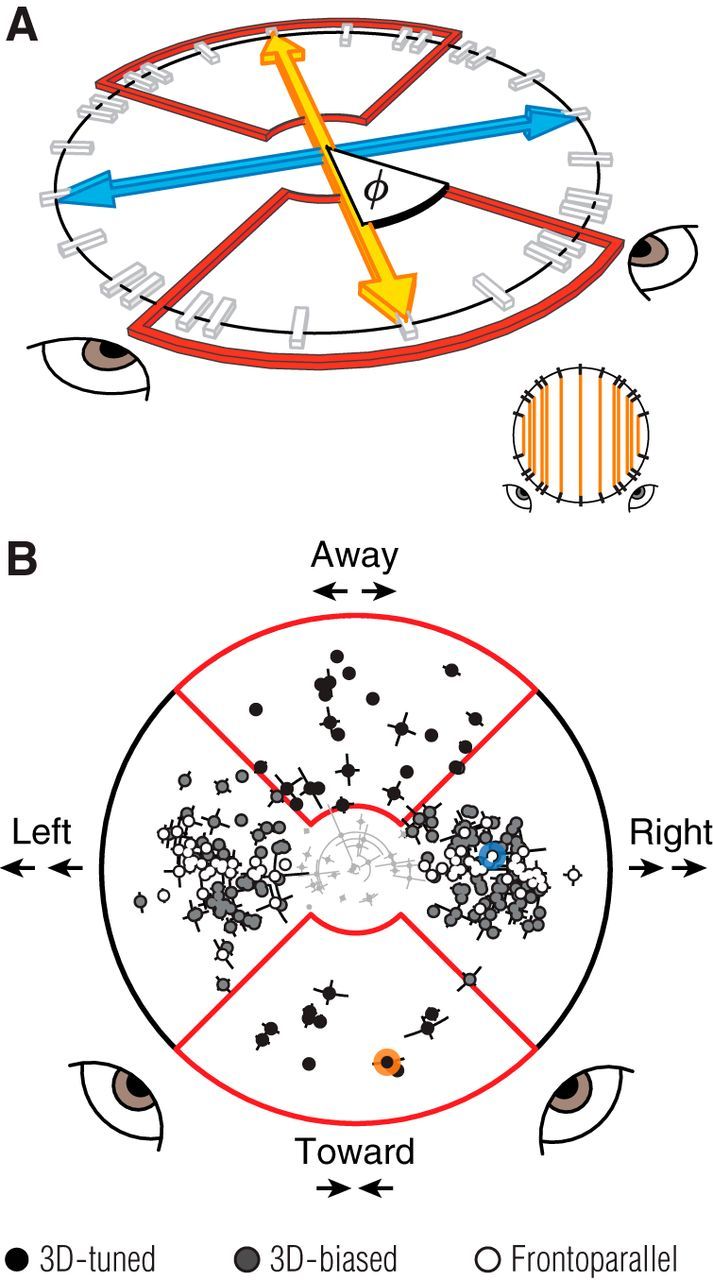
Binocular motion tuning. A, The 3D motion space sampled by our ensemble of binocular stimuli, in perspective view. The blue line indicates frontoparallel motion, corresponding to identical grating motion in the two eyes. The orange line indicates the 3D motion axis, directly toward or away from a point between the observer's eyes, corresponding to opposite grating motion in the two eyes. The tick marks on the circle in-depth indicate the sampled motion directions. The red outlined regions indicate the preference and selectivity boundary for 3D-tuned units. Orange lines in the inset (bottom right) show how motion conditions were paired to test for a bias in 3D motion responses. B, Binocular motion preference (angle) and selectivity (distance from origin) for each MT unit, in the space illustrated in A. The view has been rotated so that the 3D motion axis is vertical and the frontoparallel motion axis is horizontal. 3D-tuned units are indicated in black, 3D-biased units in gray, and frontoparallel units in white. Units that did not produce sufficient selectivity in this space (light gray, clustered near the origin; n=26) were excluded from further analyses. Error bars indicate 95% confidence intervals, based on bootstrap estimates. Red outlined regions indicate the preference and selectivity boundary for 3D-tuned units. The example units of Figures 2A–D and E–H are indicated by blue and orange markers, respectively. Most MT units preferred motion significantly off the frontoparallel axis.

Analyzing mechanisms of binocular motion tuning.

To determine the contribution of monocular response properties, we examined the relationship between 3D motion tuning and differences in monocular direction preferences and ocular dominance. To quantify ocular dominance, we used a monocularity index, defined as follows:

where R_max and L_max are the maximum responses in the left and right eye, respectively, across all the monocular stimulus conditions.

To conduct a more general test of how monocular responses contributed to binocular tuning, we evaluated how well the summed responses to monocular stimuli could predict responses to binocular stimuli, by calculating the proportion of variance accounted for as follows:

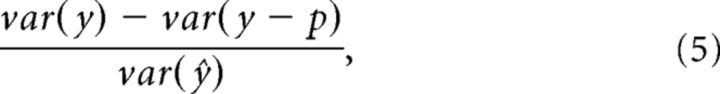where var indicates the variance of a quantity, y is a vector of mean responses to each of the binocular stimuli, p is the predicted response based on the summed monocular responses, and var(ŷ) is the predicted explainable variance of the noiseless response across conditions (Sahani and Linden, 2003). The quantity var(ŷ) was calculated as follows:

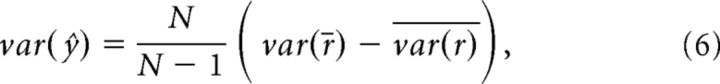where N is the number of repetitions (N = 25), var(r̄) is the variance across trial-averaged responses to the different stimulus conditions, and var(r) is the average, across trials, of the variance across conditions. This metric is an extension of a simple variance-accounted-for measure (or r²), in which the contribution of the neuron's inherent response variability is discounted. Note that in our case, the predicted response was based on simply summing responses to the constituent monocular gratings and did not involve any free parameters.

For each unit, predictions based on summed monocular responses were also used to compute binocular tuning predictions within the sampled 3D motion space (Eq. 3). Deviations between measured and predicted binocular tuning provided insight into how well monocular responses could account for not only responsivity (Eq. 6), but also binocular motion preference and selectivity (Eqs. 1 and 2, respectively).

Measuring and quantifying disparity tuning.

We measured disparity tuning using random dot stereograms presented in a range of frontoparallel motion directions (4 cardinal directions for one monkey, and all 12 grating directions for the other) and horizontal disparities (±1.6°, in 0.4° steps). Random-dot stereograms consisted of an equal number of dark and bright dots presented on a mid-gray background, with interleaved dot speeds of 2 and 10°/s. We measured disparity tuning with random dot stereograms because they allowed for a broader range of horizontal disparities than sinusoidal gratings (i.e., absolute, as opposed to relative disparity) and for presenting disparities for all motion directions (as opposed to gratings, for which horizontal disparity is undefined for vertical motion). Trials were presented consecutively (0.5 s duration; no interstimulus interval) in pseudorandom order, with 20 repetitions per condition.

We quantified the disparity tuning of each unit using a disparity discrimination index (DDI; Prince et al., 2002) as follows:

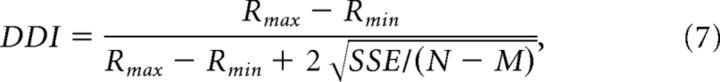where R_max and R_min are the mean responses to the most and least effective disparities, respectively; SSE is the sum squared error around each of the mean responses; N is the number of trials (N = 20); and M is the number of disparities tested (M = 9).

Results

We recorded 236 units in area MT of two anesthetized, paralyzed macaque monkeys. The spatial receptive fields of these units were 4–9° eccentric to fixation in the lower visual field.

MT tuning for frontoparallel and 3D motion signals

We measured MT spiking responses to drifting sinusoidal gratings, presented using a mirror stereoscope and dual monitor display. The stimulus ensemble (294 conditions) consisted of different combinations of gratings drifting in 12 directions at three different speeds (1, 2, or 10 °/s; Fig. 1B). On each trial, the grating direction and speed for one eye was paired with either a blank screen (monocular conditions) or a grating presented to the other eye (binocular conditions). For binocular conditions, gratings in the two eyes always had the same orientation, but they could drift either in the same or opposite direction, at the same or a different speed. Thus, our ensemble allowed us to measure monocular direction tuning, at three speeds, for each eye; binocular frontoparallel direction tuning, at three speeds, when the two eyes viewed identical stimuli; and a large number of binocular conditions with different motion in the two eyes, some of which are consistent with 3D motion trajectories, and some of which are essential for understanding how frontoparallel direction tuning relates to 3D motion tuning.

We characterized MT responses with respect to the relative velocities presented in each eye. With the wide range of vertical and horizontal motions in our design, this description allowed us to make straightforward comparisons between classical frontoparallel direction tuning and measurements that incorporated motion through depth. It is important to note that our stimuli, like natural objects, contained two binocular cues for 3D motion: interocular velocity differences and changing binocular disparities. Our experiments were designed to determine 3D direction tuning and to identify possible nonlinearities in binocular combination, and hence do not artificially dissociate velocity-based and disparity-based information. In the discussion, we briefly consider the possible contributions of velocity differences and changing disparities to the 3D motion tuning we observe.

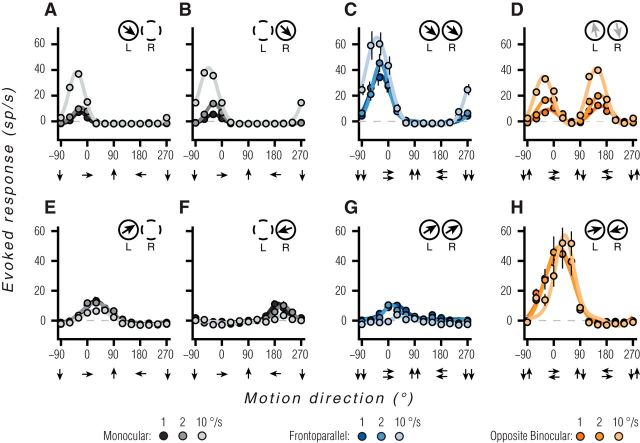
The responses of two example MT units to a subset of the stimulus conditions are shown in Figure 2. The first unit showed tuning typical of neurons previously reported in MT (Born and Bradley, 2005). Tuning was direction-selective, and similar for both monocular conditions (Fig. 2A,B; lighter line and marker color correspond to faster grating speeds) and for binocular frontoparallel motion (Fig. 2C). However, for stimuli consisting of opposite motion in the two eyes (Fig. 2D), this unit was not direction-selective. It responded when the preferred monocular motion direction was presented to either eye. This unit thus encodes frontoparallel motion, and would provide little information about motion toward or away from the observer.

Figure 2.

Example MT unit responses. A–D, An MT unit tuned for frontoparallel motion. A, Direction tuning for gratings presented to the left eye. Black, gray, and light gray lines correspond to speeds of 1, 2, and 10 °/s. Solid lines are the fits of a circular Gaussian function, used for display purposes only. Data points are the mean of 25 repetitions. Error bars represent 68% bootstrapped confidence intervals; equivalent to ±1 SEM (often smaller than data points). Inset, Top right shows the preferred direction based on the vector sum of responses for the left (L) and right (R) eye; outline dashed when monocular. B, Direction tuning for gratings presented to the right eye, following the conventions in A. C, Direction tuning for binocular presentation of identical gratings. Lighter shades of blue indicate faster speeds. D, Direction tuning for gratings drifting in opposite directions in the two eyes. Lighter shades of orange indicate faster speeds. Faint arrows in inset reflect the particularly weak selectivity in the preferred direction, corresponding to a bimodal tuning curve. E–H, Responses of an MT unit tuned for motion toward the observer. Direction tuning curves for monocular gratings (E, F), binocularly matched motion (G), and binocularly opposite motion (H).

In contrast, the unit shown in Figure 2E–H carried robust signals for 3D motion. This unit was direction-selective for monocular motion, but with opposite preferences in the two eyes: for the left eye, the unit preferred rightward motion (Fig. 2E); for the right eye, the unit preferred leftward motion (Fig. 2F). When identical stimuli were presented to the two eyes (Fig. 2G), tuning was similar to that measured in the left eye alone, with the monocular tuning of the right eye suppressed almost entirely. By conventional assays, this unit would be considered to be tuned for the direction of frontoparallel motion. However, the opposite direction preferences for the two eyes suggests that it might also encode binocular 3D motion information, and this was indeed the case. Presenting opposite directions of motion to the two eyes yielded a robust, tuned response, with a preference for stimulus conditions that correspond to motion toward the observer (Fig. 2H). Remarkably, the response to opposite binocular motion is approximately double that of the summed monocular responses, indicating a strong supralinear summation of monocular signals.

Tuning across the MT population

We summarized direction tuning across the population of recorded MT units (n = 236) with a number of metrics. First, we quantified tuning for binocular frontoparallel motion (i.e., the conditions considered in Fig. 2C,G), using a standard vector-sum metric (see Materials and Methods, Eq. 1, 2). The values of this metric are shown in Figure 3A, where the polar angle indicates the preferred direction and the distance from the origin indicates the selectivity: a value of 0 (i.e., at the origin) indicates equal responses to all stimuli, and a value of 1 indicates the cell responds to only a single direction of motion. The values for the example units of Figure 2A–D and E–H are highlighted by a blue or orange colored circle, respectively. The sampled population had a roughly uniform distribution of frontoparallel direction preferences and most units (77.1%) had selectivity values >0.5, consistent with previously reported values for MT (Marcar et al., 1995; O'Keefe and Movshon, 1998).

Tuning for binocularly opposite motion was quantified in a similar manner (Fig. 3B; see Materials and Methods, Eq. 1, 2). Selectivity for these stimuli was notably lower (median = 0.21), with most units (58%) having a value <0.25. This low selectivity usually involved orientation, tuned but nondirectional responses, as shown in Figure 2D (datum for this cell is indicated in Fig. 3B, blue circle). However, a significant subset of units showed strong selectivity for binocularly opposite motion: 19% had a selectivity value >0.5, and 8% >0.75. The preferences for these units were distributed across a range of directions, but there was a paucity of units preferring opposite vertical motions in the two eyes (Fig. 3B, directions at the top and bottom). Units with selectivity >0.5 had a mean orientation preference near horizontal (−11.0 ± 37.5°, n = 45), and the overall distribution of tuning for binocularly opposite motion deviated significantly from circular uniformity (modified Rayleigh test: p = 0.004; Moore, 1980). Thus, the tuning for binocularly opposite signals is biased for directions with ecological relevance: objects moving in depth can generate opposite horizontal motion signals, whereas opposite vertical motion signals are not generated by 3D trajectories (see Discussion).

The characterization of 3D motion tuning considered above relied on a small subset of the binocular stimulus conditions in our ensemble, those that are consistent with trajectories directly toward or away from the observer. However, oblique 3D trajectories produce more subtle differences between the motion signals in the two eyes (see Introduction). To determine the range of trajectories probed by our ensemble, we computed the 3D direction for each binocular stimulus based on the ratio of monocular velocities in the two eyes (Cynader and Regan, 1978; see Materials and Methods, Eq. 3). These directions are schematized, in perspective view, in Figure 4A. Points along the frontoparallel axis (blue arrow) correspond to conditions where the same direction and speed of motion was presented to both eyes. Points along the 3D motion axis (orange arrow), pointing toward and away from the observer correspond to equal and opposite motions in the two eyes. Conditions in between these cardinal axes (white ticks) correspond to trajectories with a mix of frontoparallel and 3D motion components.

We quantified binocular motion preference and selectivity for each MT unit (Fig. 4B), using the vector sum of its responses in this 3D space. MT units showed a broad range of direction preferences (polar angle) and selectivities (distance from the origin). We focused on those units with a selectivity value >0.25 (n = 210). Of these, we considered a unit to be “3D-tuned” if its preference was within 45° of the 3D motion axis (black points inside the red outlines in Fig. 4B), corresponding to motion trajectories approaching or receding from between the eyes. Seventeen percent of units preferred such motion. Of the remaining population, we considered a unit to be “3D-biased” if it exhibited significant differential 3D motion responses. This was defined as significantly and consistently stronger response to motion toward than away, or vice versa (p < 0.05, Wilcoxon paired signed rank test; Fig. 4A, inset, indicating how conditions were paired). An additional 53% of the recorded units fell into this category (Fig. 4B, gray points), meaning a total of 70% of MT neurons reliably encoded information about 3D direction. The remaining 30% of units were termed “frontoparallel” (white symbols).

It is important to note that the transformation from monocular velocity ratios (represented in Fig. 4) to real-world trajectories is dependent on both viewing distance and the distance between the eyes (∼3.5 cm for macaque). For instance, given a viewing distance of about an arm's length (macaque ≈ 30 cm), the range of trajectories that fall between the eyes (Fig. 4B, red box) span <3.5% of the visual field. Thus, the fact that 17% of MT units are 3D-tuned (for directions between the eyes) indicates an overrepresentation of signals toward or away from the animal. Similarly, many 3D trajectories will produce the monocular velocity ratios preferred by the majority of MT cells, the 3D-biased units, when viewing distances are large (Cynader and Regan, 1978).

In summary, a remarkable 70% of MT units encoded information about 3D motion, with an overrepresentation of sensitivity to motions directly toward and away from the head. Thus, although decades of work has emphasized that MT neurons are tuned for frontoparallel motion, most in fact encode 3D motion information.

Relationship between 3D motion tuning and monocular response properties

We next sought to determine the mechanisms responsible for generating 3D motion tuning in MT. Because our ensemble contained both monocular and binocular stimuli, we were able to probe how sensitivity to binocular combinations was related to responses to motion presented to either eye alone. Previous work has suggested that differences in monocular direction preferences (Zeki, 1974; Poggio and Talbot, 1981; Albright et al., 1984) and imbalanced responsivity in the two eyes (Poggio and Talbot, 1981; Sabatini and Solari, 2004) can contribute to 3D motion tuning. We first evaluated the relationship between these response properties and the 3D motion tuning we observed.

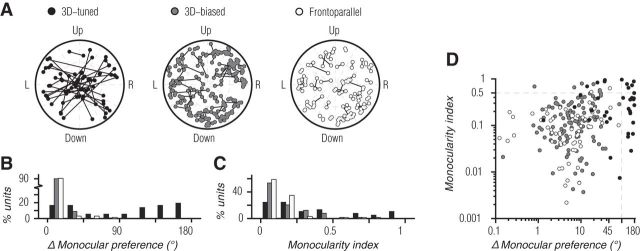
We found that 3D motion tuning often involved different preferences for motion direction in the two eyes, as is evident for the example unit in Figure 2E–H. Monocular motion tuning for each unit in the population is shown in Figure 5A, with a separate polar plot for each binocular tuning subset. Polar axes correspond to angular preference and selectivity (as shown for frontoparallel tuning in Fig. 3A) with a line segment connecting the left and right eye tuning for each unit. For 3D-tuned units (Fig. 5A, black points, left), there were many units with different monocular preferences, some of which were strongly tuned in both eyes (segments spanning the polar axes) and some of which were strongly monocular (one endpoint near the origin). 3D-tuned units with large differences in monocular preference had a tendency toward, but were not limited to, horizontal preferences (as in Fig. 3B); those with smaller differences did not correspond to simple reflections about the vertical meridian (e.g., 45° and 135°). In contrast, monocular tuning of 3D-biased (Fig. 5A, gray points, middle) and frontoparallel (Fig. 5A, white points, right) units was quite similar in the two eyes; all the connecting segments are relatively short (often occluded by the data points themselves).

Figure 5.

Relationship between 3D motion tuning and monocular response properties. A, Paired monocular preference and selectivity of each unit in the recorded population. From left to right: 3D-tuned, 3D-biased, and frontoparallel units. Polar axes correspond to angular preference and selectivity of monocular tuning, as in frontoparallel tuning shown in Figure 3A. Lines connect corresponding monocular preference of the left and right eye. B, Angular difference in monocular direction preferences for 3D-tuned (black bars), 3D-biased (gray bars), and frontoparallel units (white bars). Ordinate indicates the percentage of units within each subset of the population. C, Monocularity index of MT units, following the convention in B. D, Scatter plot of monocularity index as a function of the difference in monocular direction preference for each unit, colors following the convention in A.

Angular differences in monocular preference are summarized in Figure 5B (and the abscissa of Fig. 5D). The majority of MT units had similar preferences in the two eyes (86.6% with differences ≤45°). Of the units with more divergent preferences, most were 3D-tuned (Fig. 5B, black bars). The median difference in monocular preference for 3D-tuned, 3D-biased (Fig. 5B, gray bars), and frontoparallel (Fig. 5B, white bars) units was 107.8, 6.1, and 7.8°, respectively, a significant difference (p < 0.001; Kruskal–Wallis test). Importantly, differences in preference were not required for 3D motion tuning. One-third (33.3%) of 3D-tuned and nearly all (99%) 3D-biased units had a difference in preference of <45°. Thus, differences in monocular preference contribute to, but are not required for, generating 3D motion tuning.

To test the relevance of ocular dominance, we computed a monocularity index (see Materials and Methods, Eq. 4). Its value is zero when responses in the two eyes were exactly balanced and one when the unit responded only to input to one eye. Most MT units responded similarly to inputs from either eye, with a median monocularity index of 0.12 (Fig. 5C, ordinate of Fig. 5D), consistent with previous work (Zeki, 1974; Maunsell and Van Essen, 1983a,b). For 3D-tuned units, the median monocularity index was 0.24, compared with 0.11 and 0.09 for 3D-biased and frontoparallel units, respectively (p < 0.001; Kruskal–Wallis). Thus, 3D-tuned units had less balanced responses in the two eyes. However, even units with balanced monocular responses showed evidence of 3D motion tuning. 25% of 3D-tuned and 53.6% of 3D-biased units had monocularity indices <0.125. Imbalanced monocular responsivity therefore contributes to but is not required for generating 3D motion tuning.

To determine whether considering both of these two monocular response properties together could explain 3D motion tuning, we compared the monocularity index and difference in monocular preference for each cell (Fig. 5D). If 3D-tuned units could be explained entirely by these properties, all of these units should have either large differences in preference (abscissa) or large monocularity indices (ordinate). This was true for many but not all of these units, suggesting that additional mechanisms were responsible. Similarly, most 3D-biased units had neither large differences in preference nor a large monocular index.

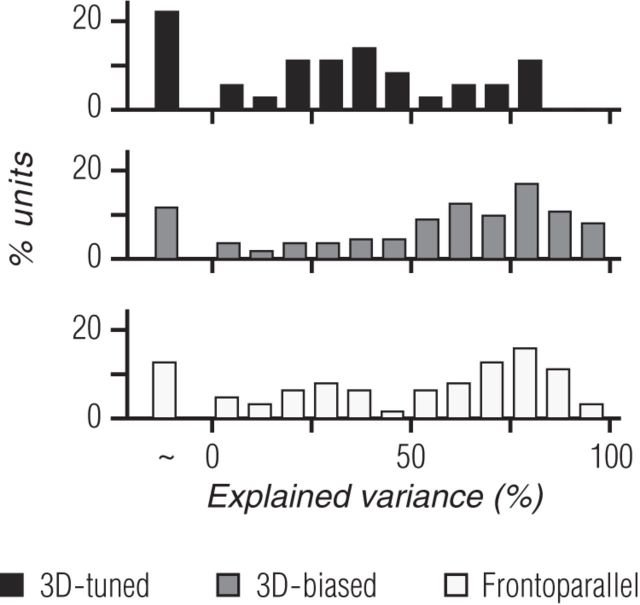
In addition to differences in monocular direction preferences and responsivity, there are numerous other monocular tuning characteristics that could give rise to 3D motion tuning. For instance, differences in speed preferences in the two eyes could result in a preference for oblique 3D motion trajectories. To more fully understand the monocular contribution to binocular motion responses, we compared each unit's measured binocular responses with predictions generated by summing its responses to the corresponding monocular gratings when presented alone. We found that this prediction could account for some, but not all, of the explainable variance in binocular motion responses (Fig. 6, Eq. 5, 6). Overall, monocular predictions accounted for a median of 64.3% of the explainable response variance across all recorded units. For 3D-biased (Fig. 6, middle row, gray bars) and frontoparallel (Fig. 6, bottom row, white bars) units, the median variance accounted for was 65.3 and 67.4%, whereas for 3D-tuned units (Fig. 6, top row, black bars) it was only 36.1%. Thus, monocular response properties are clearly relevant for understanding responses to binocular stimuli but they fail to fully explain them, particularly for 3D-tuned units.

Figure 6.

Distribution of explainable variance-accounted-for by the sum of monocular responses. Percentage of explained variance for 3D-tuned (black bars; top), 3D-biased (gray bars; middle), and frontoparallel units (white bars, bottom). The first bar in each histogram indicates cases in which the predictions failed, with the variance of the residual (measured−predicted) larger than that of the measured response.

Contribution of nonlinear binocular computations to binocular motion tuning

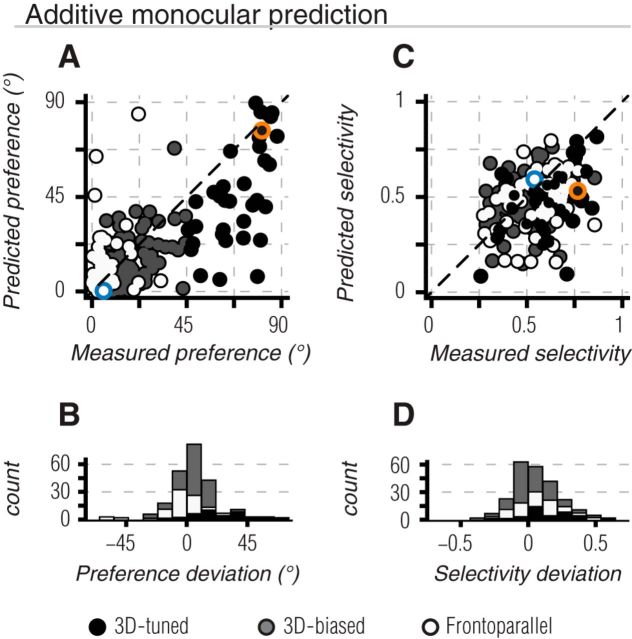
Given that responses to binocular stimuli were only partially explained by responses to the constituent monocular signals, this suggested that nonlinear (or technically, non-additive) combinations of monocular signals may contribute to binocular motion tuning. To test this, we first compared the predicted and measured binocular direction preference. The predicted preference was computed in an identical way to the measured preference (as in Fig. 4B), but the response in each binocular motion condition was derived from the summed responses of corresponding monocular motion conditions in the left and right eye. In Figure 7A, the “additive monocular” preference predictions are plotted as a function of the measured preference for each unit in the population. Preferences are quantified relative to the frontoparallel axis, such that values near zero indicate a preference for frontoparallel motion and those near 90 indicate a preference for motion along the 3D motion axis. Thus, any point below the line of unity corresponds to a measured preference that was closer to the 3D motion axis than predicted, whereas any point above the line of unity corresponds to a measured preference closer to the frontoparallel motion axis than predicted.

Figure 7.

Binocular tuning predictions based on summed monocular responses. A, Scatter plot of predicted binocular preference as a function of the measured binocular preference. Preferences are quantified relative to the frontoparallel axis shown in Figure 4, such that 0° indicates purely frontoparallel motion, and 90° indicates direct 3D motion. 3D-tuned, 3D-biased, and frontoparallel units are shown by black, gray, and white points, respectively. By definition, all 3D-tuned units lie to the right of x = 45°. Most of the units fall below the line of unity (black dashed line), reflecting an underestimate of the 3D component of binocular direction preference. B, Histogram of deviations between measured and predicted direction preference across the recorded population. Positive values indicate cases in which the measured preference was shifted toward the 3D motion axis (below unity in A). Negative values indicate shifts in preference toward the frontoparallel axis (above unity in A). C, D, Same as A, B but comparing measured and predicted selectivity. Both 3D-tuned and frontoparallel units exhibited stronger selectivity than predicted. Positive values in D indicate that the measured selectivity was greater than predicted; negative values indicate the opposite. Example units of Figures 2A–D and E–H are indicated in A, C by blue and orange markers, respectively.

We quantified the differences between measured and predicted binocular direction preferences (Fig. 7B), using positive values when the measured preference was shifted toward the 3D motion axis (below the line of unity), and using negative values when it was shifted toward the frontoparallel axis (above the line of unity). For most 3D-tuned units (92%), the measured preference was significantly closer to the 3D motion axis than predicted (Table 1; Fig. 7A,C, black points and bars; t test, p < 0.001). Most 3D-biased units (76%) also showed a preference closer to the 3D motion axis than predicted, but with a smaller mean angular deviation (gray points and bars; p < 0.001). Conversely, most frontoparallel units (65%) exhibited greater preference for frontoparallel directions than predicted (Fig. 7A,C, white points and bars; p = 0.002). We conducted a similar comparison between the predicted and measured selectivity for binocular motion (Fig. 7B,D). Selectivity was significantly stronger than predicted for 3D-tuned (t test, p < 0.001) and frontoparallel units (p = 0.008), but not for 3D-biased units (p = 0.18).

Table 1.

Deviations from predicted binocular motion preference and selectivity

	3D-tuned	3D-biased	Frontoparallel
Preference deviation
Additive monocular	23.3 ± 18.6°	4.6 ± 10.4°	−5.6 ± 14.0°
Facilitation only	31.0 ± 22.4°	4.8 ± 12.3°	−8.6 ± 17.3°
Suppression only	20.9 ± 17.9°	2.9 ± 15.0°	−13.2 ± 19.6°
Selectivity deviation
Additive monocular	0.136 ± 0.17	0.018 ± 0.14	0.057 ± 0.17
Facilitation only	0.170 ± 0.20	0.023 ± 0.15	0.069 ± 0.18
Suppression only	0.176 ± 0.20	0.041 ± 0.18	0.123 ± 0.24

Mean (±SD) of deviations between measured and predicted binocular motion preference and selectivity for the three binocular tuning subsets in the recorded population. Positive deviations in preference indicate a measured preference closer to the 3D motion axis than predicted. Negative deviations indicate a measured preference closer to the frontoparallel axis. Note that the deviations for facilitation-only and suppression-only need not sum to the additive monocular deviations.

Because binocular motion tuning deviated significantly from predictions based on summed monocular responses, we tested whether these deviations were due to nonlinear facilitation or suppression of responses. For example most 3D-tuned units preferred directions closer to the 3D motion axis than predicted (Fig. 7A, below unity); this could be due to unexpectedly strong responses to binocular motion in this direction, or to unexpectedly weak responses to frontoparallel motion. To determine the relative importance of binocular facilitation and suppression, we created modified predictions by rectifying additive monocular predictions in conditions where the difference between the measured and predicted binocular response was either positive (indicating facilitation) or negative (suppression). Thus, the importance of facilitation was evaluated by replacing the predicted response by the measured response whenever the difference indicated suppression. As a result, responses in this “facilitation-only” prediction were always equal to or smaller than the measured response. This removed any influence of response suppression but left cases of facilitation unaffected. For the “suppression-only” prediction, we replaced the predicted response with the measured response whenever the difference indicated facilitation. Importantly, for both predictions, rectification was applied to individual binocular conditions (i.e., each φ_n) before calculation of binocular tuning predictions (via Eqs. 1, 2).

If deviations in preference were due entirely to suppression or facilitation, one of these manipulations should have resulted in good agreement between the predicted and measured preference. This was not the case: neither facilitation-only nor suppression-only predictions provided a significant improvement over additive monocular predictions for direction preference (Fig. 8A,C; Table 1) or selectivity (Fig. 8B,D; Table 1) in any subset of binocularly tuned units (p > 0.05, K–S test). Thus, mechanisms that give rise to binocular motion tuning must involve a combination of facilitation for some binocular conditions and suppression for others.

We conclude that diverse mechanisms contribute to the generation of binocular motion tuning in MT. 3D tuning can be partially accounted for by monocular response properties, such as imbalanced responsivity and divergent direction preferences in the two eyes. However, our analysis revealed significant nonlinear binocular computations that enhance binocular motion preference and selectivity of both 3D and frontoparallel tuned units.

Ruling out a contribution of static disparity tuning

One well-studied binocular computation is selectivity for the static position-in-depth of a stimulus as defined by binocular disparity (Cumming and DeAngelis, 2001). Many MT neurons are tuned for static disparity (Maunsell and Van Essen, 1983b; Bradley et al., 1995; DeAngelis et al., 1998; DeAngelis and Uka, 2003). Previous work has shown that tuning for static disparity can give rise to ostensible tuning for 3D motion, if test stimuli produce an imbalanced distribution of binocular disparities across sampled 3D trajectories (Poggio and Talbot, 1981; Maunsell and Van Essen, 1983b). To avoid this confound, we randomized the relative phase of binocular grating pairs on every trial and presented each stimulus for at least one full cycle of relative interocular phases. Thus, any modulation due to static disparity tuning was unlikely to produce a directionally selective response across binocular motion conditions in our ensemble.

To test for any residual influence of static disparity on 3D motion tuning, we measured the disparity tuning of each neuron. Making accurate measurements of disparity tuning requires a precise estimate of gaze. To achieve this in anesthetized, paralyzed animals, we paired our MT recordings with concurrent multielectrode array recordings in primary visual cortex (V1). For each eye, we performed a high-resolution mapping of the spatial receptive fields of all sampled V1 units (Fig. 9A). We used responses from units with clearly defined spatial receptive fields in both eyes (Fig. 9A, green points) to determine the relative gaze (translation and rotation) of the two eyes. We then applied the requisite matrix transformation that would precisely align the placement of our stimuli on each eye's monitor (Fig. 9A, black points and lines).

Figure 9.

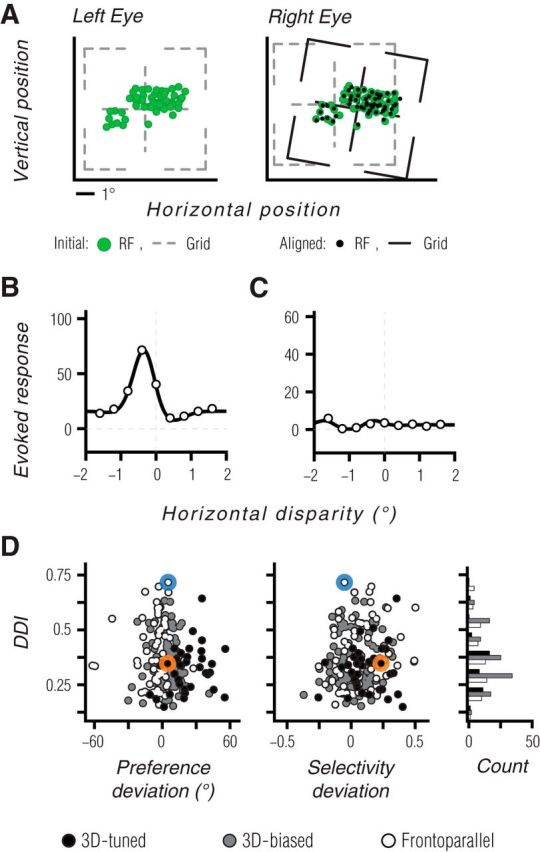
Tuning for static disparity does not explain 3D motion tuning. A, Our approach for achieving accurate measurements of disparity tuning in anesthetized, paralyzed animals. Panels show spatial receptive field centers (green points) in the left and right eyes, for a population of binocular V1 units recorded at the same time as an MT recording. Black points on the right eye panel indicate locations corresponding to the left eye receptive field centers, after applying the binocular alignment transformation. B, C, Disparity tuning curve for the example neuron of Figure 2A–D is shown in B, and for the neuron of Figure 2E–H in C. Measurements are based on coherent dot fields moving in the preferred frontoparallel direction, at a range of horizontal disparities. Solid lines show fits of a Gabor function (DeAngelis and Uka, 2003) used for display purposes only. D, A comparison of the DDI and the deviations between measured and predicted 3D motion preference and selectivity. Black, gray and white symbols indicate 3D-tuned, 3D-biased, and frontoparallel units, respectively. Blue and orange symbols indicate the data from the example units. A histogram of DDI values for each binocular tuning subset is shown in the far right. 3D-tuned units had slightly lower DDI values than other units. There was no consistent relationship between the DDI values and the deviations of the measured tuning properties from the monocular-based predictions.

With the stimulus position properly aligned, we measured disparity tuning in MT using moving dot stereograms presented at a range of binocular disparities (see Materials and Methods). The example MT unit tuned for frontoparallel motion (Fig. 2A–D) showed robust disparity tuning, with a preference for near disparities (Fig. 9B). On the other hand, the example 3D-tuned unit (Fig. 2E–H) showed no evidence of disparity tuning (Fig. 9C). Thus, disparity tuning is neither required nor sufficient for generating 3D motion tuning.

To evaluate the influence of disparity tuning across the sampled population, we computed a DDI (see Materials and Methods, Eq. 7) for each unit. DDI values near one indicate strong and consistent modulation of responsivity by static disparity. We compared the DDI values to the deviations between the predicted and measured binocular motion preferences and selectivities, shown previously in Figure 7. This provided two insights. First, there was no obvious relationship between DDI values and binocular preference or selectivity deviations (Fig. 9D). Second, there was no significant difference in the DDI values across the three subsets of binocularly tuned units (p = 0.11; Kruskall–Wallis). In fact, 3D-tuned units (Fig. 9, black points) had marginally weaker DDI values than frontoparallel units (Fig. 9, white points; median 0.34 vs 0.36; p = 0.06, Wilcoxon rank sum test). This is opposite to the trend expected if disparity tuning were driving 3D motion tuning. In addition, DDI values in 3D-tuned units often reflected modulation of weak responses to frontoparallel motion, because these units are not driven well by such stimuli. Thus, the failure of monocular predictions to account for responses to binocular 3D motion stimuli cannot be ascribed to neuronal tuning for static disparity.

We conclude that the tuning of MT neurons for 3D motion cannot be attributed to their tuning for static binocular disparity.

Discussion

Our results demonstrate clear and distinct 3D motion tuning in primate MT. Building on decades of work focused on MT tuning for frontoparallel motion and for static disparity, our recordings revealed that the majority of MT units encode 3D motion information. We found that 3D motion tuning was independent of other known selectivities in MT, and included an overrepresentation of trajectories directly approaching or receding from in between the eyes. This 3D tuning means that MT may play an important role in bridging the gap between simple retinal or frontoparallel motion computations and an ecologically relevant three-dimensional representation of the environment—features often reserved for more global motion computations seen in areas MSTd and 7a (Duffy and Wurtz, 1991; Siegel and Read, 1997).

Prior neurophysiological work in MT mentioned a small proportion of units that might exhibit 3D motion tuning by virtue of having opposite direction preferences in the two eyes (Zeki, 1974; Albright et al., 1984; for similar observations in V1 see Poggio and Talbot, 1981; for related work in the cat see Cynader and Regan, 1978, 1982; Toyama et al., 1985; Spileers et al., 1990). We also observed such units. They contributed primarily to the pool of 3D-tuned units, although one-third of 3D-tuned units had similar direction preferences in the two eyes and would have been missed in these previous studies. More importantly, by presenting a broad range of binocular motion stimuli, we found that more than half of MT units are 3D-biased, meaning that they responded significantly more to motion either toward or away, but with a preference that was between the frontoparallel and 3D motion axes. Thus, unlike previous studies, our results show that 3D motion sensitivity is preponderant in MT, rather than a rarity. Finally, our results investigated the mechanisms underlying 3D motion sensitivity. Previous reports of 3D motion sensitivity in MT measured either monocular or binocular responses, and thus could not identify the nonlinear summation of monocular signals that we found to play an important role in generating 3D motion tuning in MT.

Maunsell and Van Essen (1983b) also used binocular stimuli in MT, but found little evidence for 3D motion tuning. However, their study differs from ours in several key respects. Rather than exploring a broad battery of 3D directions, as in our design, their study focused on the relations between frontoparallel preference, static disparity tuning, and responses to a set of 3D motions constrained by the frontoparallel preference. They made the important point that earlier observations of 3D motion tuning in cat area 17 (Cynader and Regan, 1978, 1982) could have simply reflected an interaction of tuning for static disparity and for frontoparallel motion. This is because this earlier work used test stimuli that contained a biased sampling of binocular disparities across 3D motion trajectories. To avoid this confound in our study, we randomized the starting interocular phase of our stimuli and used test durations that allowed drifting grating stimuli to sweep through an integer number of interocular phase cycles on every trial (in fact, 80% of binocular conditions produced >3 interocular phase cycles/trial). Perceptually, this equates to a stimulus reaching the extreme of a stimulus volume (180° out of phase), “wrapping” to the opposite depth extreme, and then continuing motion in the same direction through depth. Thus, any contribution of static disparity preference (Maunsell and Van Essen, 1983b) would not likely contribute to a directional response, as toward and away conditions would produce an equal duty cycle of preferred and nonpreferred disparities. Furthermore, 3D-tuned units showed slightly weaker static disparity tuning than other types of units, and this tuning was based on weak responses to frontoparallel motion, ruling out any meaningful contribution of static disparity tuning to our results. Finally, we confirmed that 3D tuning was nearly identical whether based on the subset of trials for which the initial phase disparity was positive or negative (data not shown).

Maunsell and Van Essen (1983b) also proposed a neuron should only be defined as selective for 3D motion if its maximal response was not for frontoparallel motion at the preferred binocular disparity. Although differences in peak response levels are potentially critical in terms of signal-to-noise, it is now conventional to appreciate that neurons can be most informative about stimuli which modulate their activity strongly rather than drive them maximally (Dayan and Abbott, 2005). In addition, the realm of possible 3D motion stimuli is large, particularly if one considers more complete geometrical models that take into account the horizontal and vertical position of a stimulus in the visual field. Thus, comparisons of maximal response within constrained purely frontoparallel or purely toward or away stimulus classes may not be the optimal approach for understanding how 3D motion information is encoded under natural viewing conditions. Rather than searching for the optimal 3D and frontoparallel stimulus, we used a rich ensemble of stimuli to measure preference and selectivity in a 3D motion space.

At first glance, one might expect that putative 3D motion tuning should involve purely horizontal motion preference in the two eyes, because 3D trajectories primarily generate differences in horizontal motion signals upon the retinae. We found instead a range of preferences, but with a paucity of units preferring opposite vertical motion (Fig. 3B). Many MT units with preferences offset from purely horizontal still respond strongly to horizontal motion and, thus, could contribute to 3D motion perception. Indeed, perceptual work using drifting grating stimuli nearly identical to our binocularly opposite conditions has shown that stimuli with off-horizontal motion components generate 3D motion percepts (Rokers et al., 2011, their Fig. 1). A similar situation occurs in primary visual cortex, where horizontal disparity selectivity is evident in cells with a variety of orientation preferences (DeAngelis et al., 1991). Such cells are believed to contribute importantly to stereopsis (Ohzawa et al., 1996). We cannot exclude the possibility, however, that MT cells with selectivity for binocularly opposite vertical motion components underlie some other, presumably oculomotor, function.

We found that a range of mechanisms contribute to 3D motion tuning, including different monocular direction preferences and imbalanced responsivity. In addition, for most 3D-tuned and 3D-biased units, nonlinear summation of monocular signals strengthened selectivity and pushed tuning preferences toward the 3D motion axis. Nonlinear summation involved both response facilitation for some conditions, and suppression for others. Although these effects may serve some other functional purpose, it seems more parsimonious to suggest they arise from computations that enhance binocular tuning for 3D motion.

The specific mechanisms involved in the nonlinear combination of monocular signals will require further study. However it is unlikely that the suppressive component of nonlinear summation reflects simple sublinear summation of contrast signals (i.e., normalization; Carandini and Heeger, 2012). In V1, normalization within the receptive field is poorly tuned and typically monocular, even in binocular cells (Truchard et al., 2000). Such a signal would be unlikely to alter preference and selectivity. It remains possible that there is a more tuned normalization signal within MT (Heuer and Britten, 2002), where such nonlinearities have not been studied as extensively.

Another possibility is that motion opponency (Snowden et al., 1991; Qian and Andersen, 1994) or MT surround suppression (Raiguel et al., 1995) recruited by our large grating stimuli contributed to nonlinear summation of signals. Surround suppression has been implicated in MT tuning for 3D surface orientation and depth from motion (Xiao et al., 1995, 1997). However, previous studies which examined MT tuning for 3D surface orientation (Nguyenkim and DeAngelis, 2003) and the relative disparity of transparent motion planes (Krug and Parker, 2011) found that it was well described by linear combinations of the responses to components of the full stimuli; this was not the case for binocular motion tuning in our study. Therefore, nonlinearities we observed may be specific to stages of binocular integration involved in the encoding of 3D motion.

Our characterization of MT tuning for 3D motion relied on comparing velocities in the two eyes. The deviation between the predicted and observed tuning could, in principle, arise from an additional contribution of changing disparity signals provided by the binocular drifting grating stimuli we used. Perceptual work has shown clearly that human observers can use changing disparity cues to make judgments of 3D motion (Harris et al., 2008; Czuba et al., 2010). Although our approach was not designed to isolate the relative importance of these two cues in MT, recordings in awake primate MT from an accompanying paper by Sanada and DeAngelis (Sanada and DeAngelis, 2014) show that 3D motion tuning is due mostly to a comparison of monocular velocity signals with a weak contribution from changing disparity signals. It thus seems more likely that 3D motion tuning in MT involves an active mechanism that enhances tuning based on monocular velocity signals, beyond that provided by simple summation. Of course, this does not suggest that changing disparity signals do not contribute to 3D motion perception, as they might be represented more strongly in other cortical areas (Likova and Tyler, 2007; Rokers et al., 2009; Cardin and Smith, 2011), and may be more important under different experimental regimes or parameter ranges. More generally, we emphasize that additional work is required to determine the degree to which encoding of any of these 3D motion signals (in MT, or elsewhere) contribute to perceptual (or oculomotor) function.

Our discovery of a novel type of tuning in MT highlights the potential for continued and bidirectional interplay between psychophysics, fMRI, and neurophysiology. In the domain of motion perception, human fMRI has often lagged electrophysiology in measuring basic functional properties like tuning for frontoparallel motion (Huk et al., 2001). In this instance, human fMRI (in turn motivated by psychophysics) provided the initial evidence for 3D motion tuning in MT (Rokers et al., 2009), which our neurophysiological recordings have now confirmed and analyzed at the neuronal level. Our work shows that fMRI cannot only guide the locations of electrophysiological recordings in relatively unstudied areas (e.g., Tsao et al., 2006), but can also make mechanistic predictions that motivate the re-exploration of single-unit sensitivities even in seemingly well-understood brain areas like MT.