Abstract
The exact mechanisms whereby the cholinergic neurotransmitter system contributes to attentional processing remain poorly understood. Here, we applied computational modeling to psychophysical data (obtained from a spatial attention task) under a psychopharmacological challenge with the cholinesterase inhibitor galantamine (Reminyl). This allowed us to characterize the cholinergic modulation of selective attention formally, in terms of hierarchical Bayesian inference. In a placebo-controlled, within-subject, crossover design, 16 healthy human subjects performed a modified version of Posner's location-cueing task in which the proportion of validly and invalidly cued targets (percentage of cue validity, % CV) changed over time. Saccadic response speeds were used to estimate the parameters of a hierarchical Bayesian model to test whether cholinergic stimulation affected the trial-wise updating of probabilistic beliefs that underlie the allocation of attention or whether galantamine changed the mapping from those beliefs to subsequent eye movements. Behaviorally, galantamine led to a greater influence of probabilistic context (% CV) on response speed than placebo. Crucially, computational modeling suggested this effect was due to an increase in the rate of belief updating about cue validity (as opposed to the increased sensitivity of behavioral responses to those beliefs). We discuss these findings with respect to cholinergic effects on hierarchical cortical processing and in relation to the encoding of expected uncertainty or precision.
Keywords: acetylcholine, Bayesian inference, saccades, spatial attention
Introduction
Allocation of attentional resources rests on predictions about the likelihood of events. This is reflected in Posner's location-cueing paradigm, in which a cue indicates the most likely position of a target (Posner, 1980). Human and animal studies suggest that acetylcholine (ACh) regulates attentional processes by shaping interactions between (top-down) attentional biases and (bottom-up) sensory responses (McGaughy et al., 2002; Bentley et al., 2011). It has been proposed that procholinergic drugs shift the balance between stimulus-driven and expectation-guided processing, most likely by increasing thalamocortical input and favoring feedforward over feedback connections and lateral inputs (Hasselmo and McGaughy, 2004; Sarter et al., 2005). On theoretical grounds, it has been suggested that higher cholinergic levels report uncertainty of the cue-induced information and hence reduce expectation-guided biasing of attentional orienting (Yu and Dayan, 2005). This is consistent with more formal accounts of neuromodulation that regard changes in attentional gain as mediating changes in the expected precision of representations in cortical processing hierarchies (Feldman and Friston, 2010).
Here, we extend existing theoretical approaches by applying computational modeling to empirical data under a pharmacological manipulation with galantamine. We characterized the effects of predictions and uncertainty in a novel version of Posner's location-cueing paradigm using a hierarchical Bayesian model that provides a principled prescription of how expectancies are updated after new observations (Mathys et al., 2011; Vossel et al., 2014). This model can be regarded as a variant of predictive coding, in which updates are determined by prediction errors that are weighted by their salience or expected precision (inverse uncertainty). Crucially, this model contains parameters that allow for subject- and session-specific differences in updating: in our specific case, these parameters determine trial-by-trial changes in the belief that the target appears at the cued location (parameter ω) and changes in the superordinate hierarchical level describing beliefs about the volatility of these changes (parameter ϑ), respectively. A further parameter (ζ2) encodes the mapping from these beliefs to overt behavior.
By comparing model parameters between galantamine and placebo sessions, we tested how cholinergic stimulation affects the deployment of attention in relation to top-down predictions and confidence in those predictions. We hypothesized that, if ACh reports the expected precision of sensory prediction errors, we should observe faster Bayesian updating under galantamine because trial-wise updates are determined by precision-weighted prediction errors, under our hierarchical Bayesian model. More specifically, as detailed in Equation 1 below, the magnitude of the update is governed by the ratio between the precision of the prediction about the lower level and the precision of the belief at the level in question. Thus, the putative effect of ACh (increased uncertainty of top-down predictions or increased precision of bottom-up inputs) should increase the magnitude of trial-wise updates, and this should be reflected in higher values of the appropriate model parameters that control the rate of evidence accumulation. Our modeling approach also allows us to disambiguate between a cholinergic effect on belief updating (changes in ω) and a cholinergic effect on the sensitivity of responses to updated beliefs (changes in ζ2).
Materials and Methods
Subjects.
Seventeen healthy subjects gave written informed consent to participate in the study. One subject was excluded because of side effects in the galantamine session, which prevented completion of the task. Therefore, data from 16 subjects (8 males, 8 females; age range 19–30 years; mean age 23.4 years) were analyzed. All subjects were right-handed and had normal or corrected-to-normal vision. The study was approved by the NHS Research Ethics Committee (11/LO/1496). The following exclusion criteria applied: history of neurological or psychiatric disease, renal impairment, asthma, diabetes, intestinal diseases, cardiovascular disease, known allergies to the ingredients of the galantamine or placebo tablets, pregnancy or breast-feeding, intake of medication (other than contraceptives), and current participation in other pharmacological studies.
Drug administration and procedures.
Each subject attended an initial practice session, in which the task was explained and then performed. Subsequently, each subject was tested in two experimental sessions according to a within-subject crossover design. Testing in these two sessions took place at the same time of day, with test sessions separated by at least 4 d (mean ± SD, 7.2 ± 2.4 d). The elimination half-life of galantamine is 7–8 h (Huang and Fu, 2010). Drug administration was double-blinded such that subjects received either a tablet containing 8 mg galantamine (Reminyl) or a placebo (multivitamin) tablet that they ingested orally with water. The shape and color of the tablets were similar; and to further ensure blinding, subjects were prevented from looking at the tablets. Psychophysical testing started ∼60 min after drug administration, when galantamine levels should be highest (Huang and Fu, 2010).
Physiological and subjective measures.
Pulse rate and blood pressure were assessed before and ∼50 min after drug administration. Subjective drug effects were assessed 55 min after drug administration with visual analog scales for the three factors “alertness,” “contentedness,” and “calmness” (Bond and Lader, 1974). Moreover, the subjects completed a symptom checklist asking for known side effects of galantamine in which they rated feelings of nausea, headache, dizziness, drowsiness, feeling faint, sweating, feelings of general discomfort, and abnormal tiredness on a 7-point scale.
Changes in systolic/diastolic blood pressure and heart rate (differences between predrug and postdrug administration) as well as sum scores for “alertness,” “contentedness,” and “calmness” of the Bond and Lader (1974) scale were compared with separate within-subject ANOVAs with the factor drug (placebo, galantamine) using weight as a covariate. Wilcoxon's signed rank test was used to test for differences in physical side effects (ordinal rating scale). Because this nonparametric test did not allow us to consider the factor weight in the analysis, we additionally analyzed correlations between weight and the rating score difference between the drug and placebo session for each item using Spearman's rank correlation.
Stimuli and experimental paradigm.
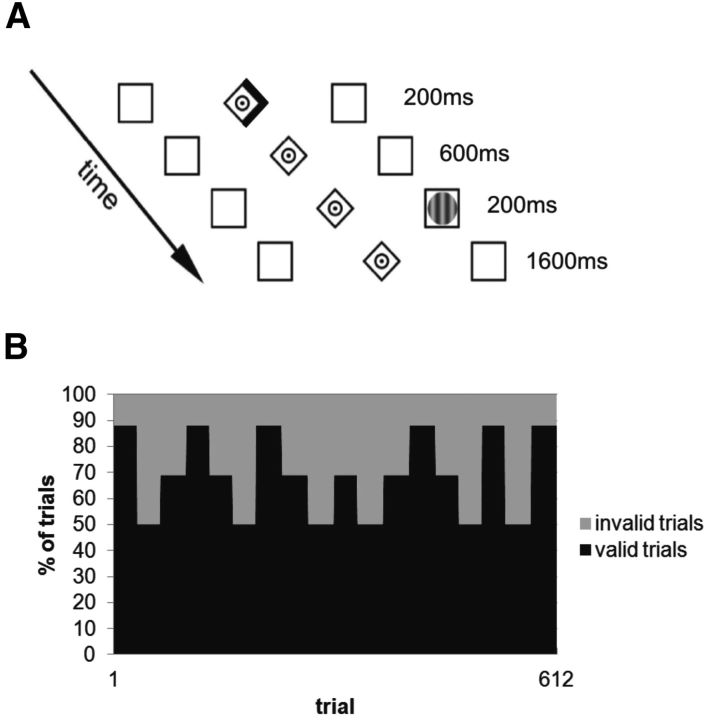
As in Vossel et al. (2014), we used a modified version of a location-cueing Posner task. Stimuli were presented with a viewing distance of 60 cm. On each trial, two peripherally located boxes were shown (1.9° wide and 8° eccentric in each visual field; Fig. 1) that could contain target stimuli. A central diamond (0.65° eccentric in each visual field) was placed between them, serving as a fixation point. Cues comprised a 200 ms increasing brightness of one side of the diamond, creating an arrowhead pointing to one of the peripheral boxes. After an 800 ms stimulus onset asynchrony, a target appeared for 200 ms in one of the boxes. The targets were circular sinusoidal gratings (1.3° visual angle).
Figure 1.
A, Illustration of the experimental task in which the location of a saccade target (circular grating) was precued by arrows. B, The predictive value of the cue (i.e., the proportions of valid and invalid trials) changed over the time of the experiment.
Subjects were instructed to maintain central fixation during the cue period and to make a saccade to the target stimulus as quickly as possible. The subjects were familiarized with the task in an initial practice session. Here, they performed 100 trials with constant 80% cue validity (% CV) and 121 trials with changes in % CV. The task in the two main experimental sessions comprised 612 trials with block-wise changes in % CV that were unknown to the subjects (Fig. 1). Each block with constant % CV contained an equal number of left and right targets, counterbalanced across valid and invalid trials. % CV changed after either 32 or 36 trials, switching unpredictably to levels of 88%, 69%, or 50%. Subjects were told in advance that there would be changes in % CV over the course of the experiment but were not informed about the levels of these probabilities or when they would change. Each subject was presented with the same sequence of trials in each session (compare Vossel et al., 2014). To jitter the intertrial interval and to allow for a direct comparison with a separate fMRI study (Vossel et al., unpublished observations), the trials were interspersed with 108 “null-trials,” where only the baseline display (the fixation point and peripheral boxes) was presented. The task lasted 35 min and comprised 4 short rest periods.
Eye movement data recording and analysis.
Eye movements were recorded from the right eye with an EyeLink 1000 desktop-mounted eye-tracker (SR Research) with a sampling rate of 1000 Hz. A 9-point eye-tracker calibration and validation was performed at the start of the experiment. The validation error was <1° of visual angle.
Eye movement data were analyzed with MATLAB (MathWorks) and ILAB (Gitelman, 2002). Blinks were filtered out and pupil coordinates within a time window of 20 ms around the blink were removed. After target onset, the first saccade was analyzed. Saccades were identified when the eye velocity exceeded 30°/s (Fischer et al., 1993; Stampe, 1993). After this threshold was reached, the beginning of the saccade was defined as the time when the velocity exceeded 15% of the trial-specific maximum velocity (Fischer et al., 1993). The saccade amplitude needed to subtend at least two-thirds of the distance between the fixation point and the actual target location. Saccadic reaction time was defined as the latency between target and saccade onset. Saccades in which the starting position was not within a region of 1° from the fixation point and saccades with a latency <90 ms were discarded from the analyses. Our analyses focused on inverse reaction times (i.e., response speed [RS]) because RSs are more normally distributed (Carpenter and Williams, 1995; Brodersen et al., 2008).
Classical inference.
To assess the effect of probabilistic context (true % CV) and drug, mean RSs for each subject and for each % CV condition were entered into a 2 (cue: valid, invalid) × 3 (% CV: 50%, 69%, 88%) × 2 (drug: galantamine, placebo) within-subjects ANOVA. The order of drug administration (placebo-drug, drug-placebo) was added as a between-subject factor, and each subject's weight was entered as a covariate because psychopharmacological drugs can have dose-dependent effects (Knecht et al., 2004; Newhouse et al., 2004; Chowdhury et al., 2012). In this analysis, evidence for an impact of probabilistic context would be reflected in a significant cue × % CV interaction, whereas a drug effect on the adaptation to the probabilistic context would be reflected by a significant cue × % CV × drug interaction. In addition to the analysis of mean RS in the six conditions, accuracy (% correct responses) in each condition was compared between drug and placebo session with an analogous 2 × 3 × 2 ANOVA model with session order as between-subject factor and weight as covariate. Condition-specific mean RSs under galantamine and placebo were also calculated separately for the two halves of the experiment and analyzed with a 2 (cue: valid, invalid) × 3 (% CV: 50%, 69%, 88%) × 2 (time: first half, second half) × 2 (drug: galantamine, placebo) within-subjects ANOVA (each % CV condition was presented 3 times in each half; compare Fig. 1). Results are reported at a significance level of p < 0.05 after Greenhouse–Geisser correction.
Bayesian modeling.
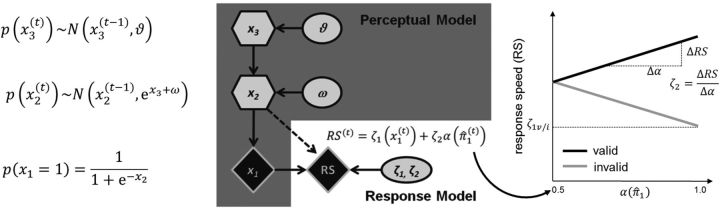
Hierarchical Bayesian models have proven very powerful for explaining the adaptation of behavior to probabilistic contexts in volatile environments (Behrens et al., 2007; den Ouden et al., 2010; Iglesias et al., 2013; Vossel et al., 2014). As in our previous study (Vossel et al., 2014), we used an adapted version of a generic hierarchical, approximately Bayes-optimal learning scheme proposed by Mathys et al. (2011) and used RS as the behavioral measure for estimating the model parameters. Throughout the manuscript, we refer to this Bayesian hierarchical model as the perceptual model because it provides a mapping from hidden states of the world (x) to sensory inputs (Daunizeau et al., 2010a, b; Vossel et al., 2014) (Fig. 2). The response model describes the mapping from the subject's beliefs, following inversion of the perceptual model (i.e., inference on the hidden states of the world based on sensory inputs), to observed responses (i.e., saccadic RS) (Fig. 2).
Figure 2.
Illustration of the perceptual and response models. The perceptual model comprises three hierarchical states (x1, x2, and x3). x2 and x3 evolve in time as hierarchically coupled Gaussian random walks (see equations on the left), and x2 determines the probability that the target appears at the cued location (x1 = 1). The session-specific parameters ω and ϑ affect the updating of the beliefs about the states x and are estimated from individual RS data on the basis of the attentional weight α(π̂1) that depends on the precision on the first level of the (inverted) perceptual model. Here, RS is supposed to vary linearly with α(π̂1) in valid trials and with 1 − α(π̂1) in invalid trials (right). Whereas ζ1ν and ζ1i determine the intercepts (i.e., the absolute level of RS) on valid and invalid trials, respectively, ζ2 governs the slope of the linear function and hence the strength of the association between RS and the attentional weight α(π̂1) as derived from the perceptual model. Ellipses represent constants; diamonds represent quantities that change with time (i.e., that carry a time index). Hexagons, like diamonds, represent quantities that change with time but additionally depend on their previous state in time in a Markovian fashion.
A detailed description of the perceptual and response models was provided by Mathys et al. (2011) and Vossel et al. (2014). The perceptual model comprises three states denoted by x that evolve at the second and third level as hierarchically coupled Gaussian random walks. In other words, the probability distribution of the values of x2 and x3 on a given trial (t) is centered on the value from the previous trial (t − 1) with a variance that is determined by the state of the next higher hierarchical level and/or subject-specific model parameters (Fig. 2, equations). The state x1 represents trial-wise events (sensory inputs), which in the present paradigm consisted of either a validly or invalidly cued target (with x1 = 1 for valid and x1 = 0 for invalid trials). The probability distribution of x1 = 1 corresponds to the subjects' estimate of % CV (i.e., the tendency that the target will appear at the cued location) and is governed by the supraordinate state of the model x2. x2 is a real number and the probability distribution of x1 given x2 is described by a logistic sigmoid (softmax) function, so that the states x1 = 0 and x1 = 1 are equally probable when x2 = 0. The variance of the update in x2 (i.e., how fast the belief about cue validity can change from trial to trial) is determined by two quantities: x3 (the next level of the hierarchy) and a parameter ω that can differ across subjects (or test sessions). In turn, the dispersion of the random walk (variance of the update) of x3 is determined by the subject/session-specific parameter ϑ. The session-specific parameters ω and ϑ were estimated from the individual RS data (see below). To map from sensory inputs to probabilistic representations or beliefs, the perceptual model needs to be inverted to obtain posterior densities for the three states x. In the following, the sufficient statistics of the subject's posterior belief will be denoted by μ (mean) and σ (variance) or π = (precision). We use the hat symbol (^) to denote predictions before the observation of x1 on a given trial.
As described by Mathys et al. (2011), variational model inversion under a mean field approximation yields simple analytical update equations, where belief updating rests on precision-weighted prediction errors. The update of the posterior mean μ at level i in the hierarchy on trial t has the following general form:
 |
This update equation bears structural similarity to reinforcement learning schemes, such as the Rescorla Wagner model (Rescorla and Wagner, 1972) in which prediction errors (δi−1(t)) are weighted by a learning rate. One crucial difference to these models is, however, that the learning rate in the present model is not fixed but varies with time as it adapts to the estimated volatility (i.e., the values at the higher levels of the model). This allows for quicker learning at times when the environment changes relative to more stable periods.
At the second level of the model, the precision weighting has a slightly different form because of the sigmoid transform that relates the second level to the first as follows:
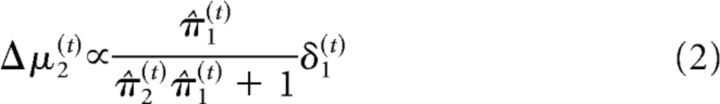 |
with
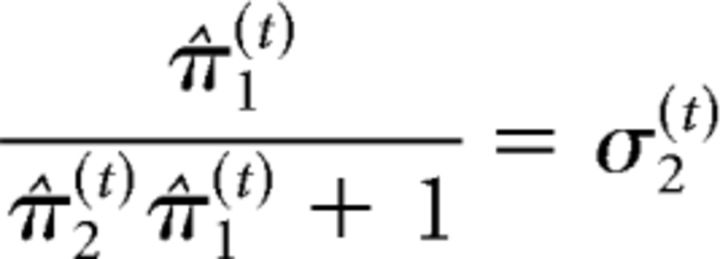 |
and
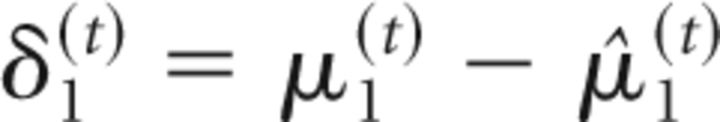 |
σ2(t) can be regarded as a time-varying learning rate. δ1(t) is the prediction error at the first level (i.e., the difference between observed outcome μ1(t) and prediction μ̂1(t) = s(μ2(t−1)). These update equations provide approximate Bayes optimal rules for the trial-by-trial updating of the beliefs that underlie the subject's estimate of the probability that the target will appear at the cued location on a particular trial (this is an individualized Bayes optimality, in reference to the session-specific values for the parameters ω and ϑ). At the third level of the model, the update equation can again be partitioned into a learning rate and prediction error term (δ2(t)) as follows:
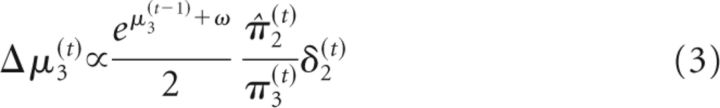 |
A response model was used to map from these posterior beliefs to observed responses (Fig. 2). In previous work (Vossel et al., 2014), we compared three alternative response models and observed in two independent datasets that the most plausible model was based upon the precision of the prediction on the first level of the perceptual model π̂1. In this model, π̂1 determines the attentional weight α(π̂1) (between 0 and 1) allocated to the cued location. The precision (inverse uncertainty or variance) of the prediction of a binary outcome (in our case at the first level, π̂1) has a minimal value of 4 when μ̂1 = 0.5 (both locations are equally likely) and approaches infinity as μ̂1 approaches 1. The most parsimonious way to ensure that α(π̂1) varies between 0 and 1 is to define α as the logistic sigmoid of π̂1, minus its minimum. Because the cue becomes a counterindication of outcome location when μ2 falls to <0 (or equivalently, when π̂1 drops to <0.5), a suitable definition of α for the whole range of π̂1 is as follows:
This ensures that attention to the cued location falls to 0 as μ̂1 approaches 0.
Trial-wise, RS can then be described as an affine function of α(π̂1):
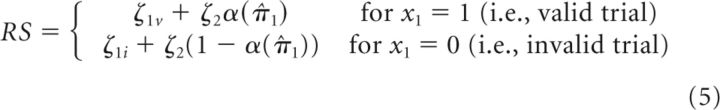 |
In this response model, the intercepts ζ1ν and ζ1i determine the baseline (i.e., no attention to outcome location) speed of responding in the two conditions. ζ2 quantifies the slope of the affine function (i.e., the strength of the increase in RS with increased attentional weight α(π̂1) (compare Fig. 2).
The perceptual model parameters ω and ϑ, as well as the response model parameters ζ1ν, ζ1i and ζ2 were estimated from the trial-wise RS measures using the BFGS optimization algorithm as implemented in the HGF toolbox (part of the open source TAPAS software suite: http://www.translationalneuromodeling.org/tapas/). This enabled us to evaluate the posterior densities of the model parameters under the Laplace assumption. A galantamine effect on the response model parameter ζ2 (i.e., the sensitivity to α(π̂1)) would reflect a nonspecific change in RSs with attentional gain. In contrast, altered Bayesian updating would be reflected in changes of the perceptual model parameters ω or ϑ. In other words, testing for drug (session) effects of these parameters allowed us to disambiguate between an effect on how RS depends upon beliefs and a drug effect on the accumulation or updating of beliefs per se.
These effects were tested using classical ANOVAs on the model parameters. First, a 2 (drug: placebo, galantamine) × 3 (model parameter: ω, ϑ, ζ2) within-subject ANOVA with session order as between-subject variable and weight as covariate was calculated. In addition, separate ANOVAs were calculated for the three different model parameters to elucidate the origin of the drug × model parameter interaction effect. Again, results are reported at a significance level of p < 0.05 after Greenhouse–Geisser correction.
Results
Classical inference
In total, 91.5 ± 2.08% (±SEM) and 88.7 ± 2.98% of trials were analyzed in placebo and galantamine sessions, respectively. Excluded trials were due to anticipated responses (placebo: 1.5 ± 0.5%; galantamine: 2.1 ± 0.7%), incorrect or missing saccades (placebo: 0.6 ± 0.2%; galantamine: 1.3 ± 0.4%), saccades not starting from the fixation zone (placebo: 3.3 ± 1.0%; galantamine: 3.7 ± 0.9%), or missing data points (e.g., due to blinks) (placebo: 3.1 ± 1.0%; galantamine: 4.2 ± 1.6%). The percentage of correct responses in the six different conditions in the drug and placebo session was analyzed with a 2 (cue: valid, invalid) × 3 (% CV: 50%, 69%, 88%) × 2 (drug: galantamine, placebo) within-subjects ANOVA with session order as between-subject factor and weight as covariate. This analysis did not reveal any significant effects.
With regard to mean RS in the different experimental conditions, the 2 (cue: valid, invalid) × 3 (% CV: 50%, 69%, 88%) × 2 (drug: galantamine, placebo) within-subjects ANOVA with session order as between-subject factor and weight as covariate revealed a significant drug × session order interaction (F(1,13) = 27.3, p < 0.001). This interaction resulted from a general speeding of responses in the second test session. Importantly, we observed a cue × % CV × drug interaction effect (F(1.62,21.12) = 5.1, p = 0.021), which was modulated by the weight of the subjects (F(1.63,21.23) = 4.9, p = 0.023).
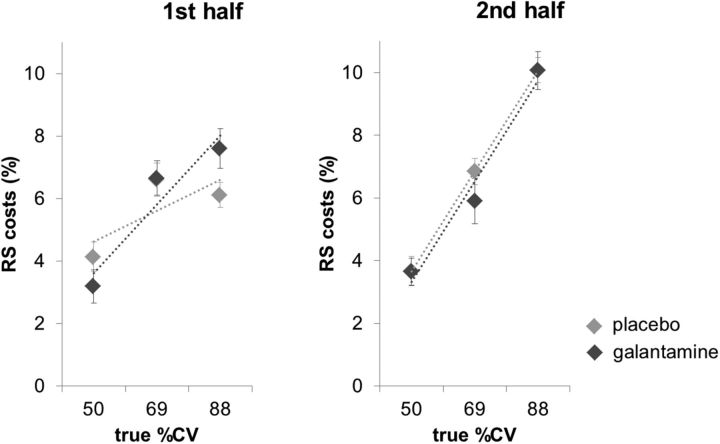
To test for effects of the time on task, we repeated the ANOVA with the additional factor time (first half, second half). This analysis showed a trend toward a cue × % CV × time × drug interaction effect (F(1.67,21.7) = 3.25, p = 0.066), which was modulated by weight (F(1.67,21.7) = 3.41, p = 0.059). Figure 3 illustrates this effect by plotting the relative RS differences between valid and invalid targets (i.e., RS costs; relative to the overall RS) as a function of true % CV and drug for the two halves of the experiment. It can be seen that the RS costs due to invalid cueing are affected by % CV, with this effect more pronounced under galantamine than under placebo (especially in the first half of the experiment). This interaction effect was not modulated by the order of drug administration.
Figure 3.
Illustration of the three-way interaction between cue, % CV, and drug for both halves of the experiment. For simplicity, relative RS differences between valid and invalid trials are shown. RS costs were related to the overall speed of responding and are expressed in percentage: (RS valid − RS invalid)/overall RS × 100. Error bars indicate SEM.
Together, the results from classical inference suggest a greater impact of the volatile probabilistic context (i.e., true % CV) on RS under galantamine. This pharmacological effect was modulated by the weight of the individual subjects, with stronger effects in lighter subjects, suggesting a dose-dependent effect. The order of drug administration did not affect the observed effects and only generally affected the overall speed of the response, which increased from the first to the second session.
It should be noted that trials were averaged across the unknown (experimentally manipulated) probability levels for the above ANOVAs. It is likely that the trials were heterogeneous in terms of subjective probability estimates, and our data suggest that these differ between the galantamine and placebo conditions. Below we test this hypothesis, asking whether the empirically observed differences in RS costs might reflect drug-induced alterations in the parameters of the Bayesian perceptual or the response model. A greater impact of true % CV under galantamine on RS could in principle arise from multiple factors. Cholinergic stimulation with galantamine could lead to a faster updating of beliefs after the observation of new data (i.e., to a higher learning rate). Alternatively, galantamine could increase the sensitivity of the overt behavioral response to the trial-wise beliefs without affecting updating or inference. In what follows, we tried to disambiguate these two hypotheses by modeling the empirically observed single-trial RSs in terms of hierarchical Bayesian updating.
Bayesian modeling
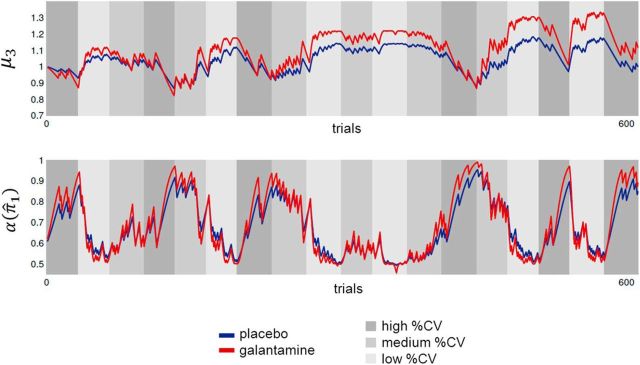
The ANOVA on the model parameters ω, ϑ, and ζ2 under placebo and galantamine, respectively (using weight as covariate and session order as between-subject factor), revealed a significant main effect of drug (F(1,13) = 7.0, p = 0.020) and a drug × weight interaction (F(1,13) = 6.64, p = 0.023). Importantly, however, we observed a significant drug × parameter interaction effect (F(1.04,13.5) = 6.6, p = 0.022) that was modulated by the weight of the subjects (F(1.04,13.5) = 6.2, p = 0.026). Separate post hoc ANOVAs for each model parameter revealed a significant increase of ω under galantamine (main effect of drug: F(1,13) = 6.9, p = 0.021) and a significant drug × weight interaction effect (F(1,13) = 6.5, p = 0.024), but no significant effect on ϑ (main effect of drug: p = 0.57; drug × weight interaction: p = 0.61) or ζ2 (main effect of drug: p = 0.19; drug × weight interaction: p = 0.20). To illustrate the effects of galantamine, we plotted the trajectories of the third and first level of the Bayesian model for a normalized weight of 68 kg (Fig. 4). At the third level of the model (representing the phasic volatility of cue validity changes; Fig. 4, top), the values of μ3 are increased under galantamine, relative to placebo. Our results, however, show that these changes are caused by faster updating at the second level (i.e., higher ω) and not by larger fluctuations at the third level (i.e., higher ϑ). With a higher value of parameter ω, the values of α(π̂1) change more quickly from trial to trial under galantamine, resulting in a faster adaptation to changes in probabilistic context (Fig. 4, bottom). This accelerated adaptation to the experimentally manipulated cue validity levels explains the greater dependency of RS costs on true cue validity levels under galantamine (compare Fig. 3).
Figure 4.
Illustration of the time course of the posterior expectations at the third level of the Bayesian model (μ3, top) and attentional gain allocated to the cued location α(π̂1) (bottom), based upon the group average values for ω and ϑ. Because of the dependency of the galantamine-induced increase of ω, we here exemplarily show the results for a normalized weight of 68 kg (placebo session: ω = −6.2, ϑ = 0.60; galantamine session: ω = −5.4, ϑ = 0.61). It can be seen that, under galantamine (red line, with a higher ω), the changes in α(π̂1) in the different true % CV conditions are more pronounced than under placebo (blue line). The same sequence of valid and invalid trials was presented each subject and in each experimental session because the parameters of the learning process depend on the exact sequence of trials used.
To illustrate the correspondence between the observed and predicted responses, we plotted observed and predicted RSs as a function of the precision-dependent attentional weight α(π̂1) (calculated on the basis of the group mean model parameters ω and ϑ in each session). Trials were binned according to values of α(π̂1) in 0.1 steps. In both sessions, observed RSs showed a good correspondence with the RSs predicted by our model (Fig. 5).
Figure 5.
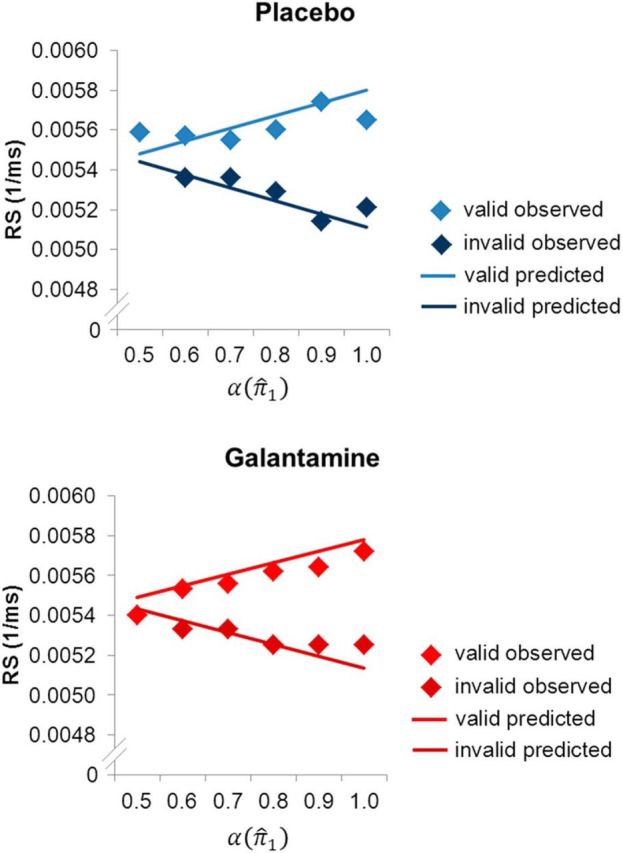
Illustration of observed and predicted RS in the placebo and galantamine session, respectively. Trials were grouped in 0.1 bins according to the attentional weights α(π̂1) as derived from the perceptual model with the group average model parameters. Mean observed RS was calculated for these binned trial categories (diamonds). Predicted RS in valid and invalid trials was calculated on the basis of the mean response model parameters (solid lines).
Physiological and subjective measures
Galantamine did not affect the changes in systolic or diastolic blood pressure from predrug to postdrug/placebo administration, and the covariate weight did not interact with this effect (all p values >0.14). The deceleration of the heart rate from predrug to postdrug/placebo administration was less pronounced under galantamine, and this effect was modulated by the weight of the subjects (main effect of drug: F(1,14) = 5.7, p = 0.032; drug × weight interaction effect: F(1,14) = 5.1, p = 0.041).
Ratings for “alertness,” “calmness,” and “contentedness” were not affected by galantamine, and no drug × weight interaction effects were observed (p > 0.15). Wilcoxon's signed rank tests for the different symptoms on the side effects rating scale revealed that feelings of nausea (Z = −2.37, p = 0.018), dizziness (Z = −2.49, p = 0.013), feeling faint (Z = −2.33, p = 0.02), and general discomfort (Z = −2.6, p = 0.009) were higher under galantamine than under placebo. However, the overall severity of the symptoms was low because most subjects rated the side effects as “very slight” or “slight.” Moreover, there were no significant correlations between the difference scores for the ratings of the drug and placebo session and the subjects' weight.
Discussion
By using a novel version of Posner's location-cueing task, with changes of the % CV over time, we observed that an enhancement of cortical cholinergic levels via galantamine led to a greater impact of probabilistic context on saccadic RS. The application of a Bayesian learning model for characterizing the trial-wise beliefs, about the % CV and its changes over time, and the precision of those beliefs, revealed this effect was best explained by faster updating under galantamine, as reflected in higher values of the model parameter ω. These psychopharmacological effects were dependent on the weight of the subjects (i.e., the effective dose of galantamine).
Our results suggest that galantamine affected the way in which beliefs were formed on the basis of trial history; specifically, the accumulation of sensory evidence in proportion to the expected precision of volatile contingencies. In other words, galantamine affected the computations underlying attentional deployment (rather than influencing the mapping from beliefs to responses, i.e., the response model parameter ζ2). Interestingly, we did not observe a drug-related speeding of responses specifically to invalidly cued targets, as has been shown in studies investigating the effects of nicotine in cueing paradigms with explicit knowledge of probabilistic context (Phillips et al., 2000; Thiel et al., 2005; Vossel et al., 2008). Our new finding suggests a more complex effect of enhanced cholinergic levels, so that the pharmacological effects of cholinergic agents in probabilistic cueing paradigms are critically influenced by the sequence in which the trials are presented. This interpretation of cholinergic action in the brain is also in accord with the assumption of previous theoretical notions posing that ACh controls the speed of the memory update (i.e., the learning rate) (Doya, 2002; Hirayama et al., 2004). Moreover, a separate line of research has suggested that ACh enhances synaptic plasticity, thereby facilitating the adaptation of neuronal systems to dynamic environments (Metherate and Weinberger, 1990; Kilgard and Merzenich, 1998; Thiel et al., 2001, 2002a, b).
It should be mentioned, however, that the action of ACh on attention may depend on the specific task used. For example, we cannot rule out that the effects of ACh may be different in paradigms with and without uncertainty about cue validity. This means the generality of our observed effects needs to be verified in further studies. The theory of visual attention (Bundesen, 1990) is an influential computational approach that quantifies putative components of attentional processing. It has been shown in whole and partial report paradigms (where subjects have to report targets with a specific feature, e.g., color; and ignore distractors) that nicotine improves perceptual thresholds but impairs subsequent perceptual speed as well as top-down attentional selectivity (i.e., the ability to distinguish between targets and distractors) (Vangkilde et al., 2011). However, to our knowledge, pharmacological effects on the updating of the theory of visual attention parameters as a result of learning have not yet been investigated. The theory of visual attention also quantifies attentional weights that determine the likelihood that a subject attends to the stimulus. It has been shown that the pertinence (priority) values, which affect these attentional weights, undergo changes if a former target stimulus turns into a distractor (Kyllingsbaek et al., 2001), and it would be interesting to relate the speed of this update to cholinergic neurotransmission.
Which mechanisms could lead to a faster updating of beliefs under galantamine? According to the update rules of our Bayesian model, faster trial-wise updating at the second level is determined by a ratio of precisions (compare Eqs. 1 and 2). In other words, either increased precision of the prediction about inputs from the lowest level (π̂1) or decreased precision of the belief at the second level (because this decreases the denominator π̂2π̂1 + 1 in Eq. 2) could cause faster updates of μ2 (and consequently α(π̂1)). It has recently been shown that galantamine boosts bottom-up sensory input in primary auditory cortex in a mismatch negativity paradigm (Moran et al., 2013). In particular, using simulated neuronal responses within the free energy minimization framework and empirical electroencephalographic data, this study suggests that galantamine enhances the gain of the superficial pyramidal cells in primary auditory cortex, thereby biasing perceptual inference toward bottom-up sensory inputs. Moreover, a recent neuronal network model addressing cholinergic effects on attentional modulation in visual cortex (Deco and Thiele, 2011) has claimed that nicotinic neurotransmission increases ascending thalamocortical input. This effect has also been investigated experimentally: in vitro recordings in rodent brain slices have shown that nicotine selectively enhances thalamocortical synapses (Gil et al., 1997). In vivo recordings in macaques revealed that nicotine enhances the gain of responses to visual stimuli in the thalamorecipient layer 4c of V1 (Disney et al., 2007).
A second mechanism causing faster updates of attentional expectancies is a reduced precision at the second level of the model (i.e., at higher levels of the cortical hierarchy). Psychopharmacological neuroimaging studies in humans have indeed reported activation decreases in areas such as the parietal cortex in response to nicotine (e.g., Thiel et al., 2005; Vossel et al., 2008), but this effect is predominantly seen during invalidly cued trials and interpreted as facilitated attentional shifting or enhanced processing efficiency. In contrast, studies using cholinesterase inhibitors have reported an enhancement of voluntary attentional modulation at the behavioral and neural level (Rokem et al., 2010; Bauer et al., 2012). Similarly, muscarinic blockade with scopolamine reduces spatial attentional top-down modulation of responses to visual stimuli in visual cortex (Herrero et al., 2008), and theoretical modeling has shown that inhibitory drive by muscarinic receptors may effectively render the system more sensitive to feedback influences (i.e., attentional modulation) (Deco and Thiele, 2011). The combination of psychopharmacological challenges with neuroimaging techniques with higher temporal resolution (such as EEG or MEG) will be required to elucidate the exact nature of cholinergic effects on the cue- and target-related responses to reveal top-down and bottom-up influences. Moreover, the use of the cholinesterase inhibitor galantamine in the present study precludes conclusions about the differential effects of nicotinic versus muscarinic cholinergic neurotransmission; further studies with selective agonists or antagonists are needed to disentangle these contributions.
Despite the nonselective affinity of galantamine, our results provide a new perspective on the effects of cholinergic neurotransmission on attentional processing by showing that cholinergic enhancement affects the computational mechanisms underlying the updating of perceptual beliefs according to Bayesian principles. Future studies should investigate at which level in the cortical hierarchy cholinergic stimulation exerts its primary effects and whether nicotinic and muscarinic cholinergic neurotransmission is differentially involved in these processes.
Footnotes
The work was supported by the Deutsche Forschungsgemeinschaft (SV, Vo1733/1-1), the Federal Ministry of Education and Research 01GQ1401 to S.V., the Wellcome Trust to K.J.F., the National Center of Competence in Research “Neural Plasticity and Repair” to C.M. and K.E.S., SystemsX.ch to K.E.S., and the René and Susanne Braginsky Foundation to K.E.S., R.J.D. was supported by Wellcome Trust Senior Investigator Award 098362/Z/12/Z. The Wellcome Trust Centre for Neuroimaging is supported by core funding from the Wellcome Trust 091593/Z/10/Z.
The authors declare no competing financial interests.
References
- Bauer M, Kluge C, Bach D, Bradbury D, Heinze HJ, Dolan RJ, Driver J. Cholinergic enhancement of visual attention and neural oscillations in the human brain. Curr Biol. 2012;22:397–402. doi: 10.1016/j.cub.2012.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens TE, Woolrich MW, Walton ME, Rushworth MF. Learning the value of information in an uncertain world. Nat Neurosci. 2007;10:1214–1221. doi: 10.1038/nn1954. [DOI] [PubMed] [Google Scholar]
- Bentley P, Driver J, Dolan RJ. Cholinergic modulation of cognition: insights from human pharmacological functional neuroimaging. Prog Neurobiol. 2011;94:360–388. doi: 10.1016/j.pneurobio.2011.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bond A, Lader M. The use of analogue scales in rating subjective feelings. Br J Clin Pharmacol. 1974;47:211–218. doi: 10.1111/j.2044-8341.1974.tb02285.x. [DOI] [Google Scholar]
- Brodersen KH, Penny WD, Harrison LM, Daunizeau J, Ruff CC, Duzel E, Friston KJ, Stephan KE. Integrated Bayesian models of learning and decision making for saccadic eye movements. Neural Netw. 2008;21:1247–1260. doi: 10.1016/j.neunet.2008.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bundesen C. A theory of visual attention. Psychol Rev. 1990;97:523–547. doi: 10.1037/0033-295X.97.4.523. [DOI] [PubMed] [Google Scholar]
- Carpenter RH, Williams ML. Neural computation of log likelihood in control of saccadic eye movements. Nature. 1995;377:59–62. doi: 10.1038/377059a0. [DOI] [PubMed] [Google Scholar]
- Chowdhury R, Guitart-Masip M, Bunzeck N, Dolan RJ, Düzel E. Dopamine modulates episodic memory persistence in old age. J Neurosci. 2012;32:14193–14204. doi: 10.1523/JNEUROSCI.1278-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daunizeau J, den Ouden HE, Pessiglione M, Kiebel SJ, Friston KJ, Stephan KE. Observing the observer: II. Deciding when to decide. PLoS One. 2010a;5:e15555. doi: 10.1371/journal.pone.0015555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daunizeau J, den Ouden HE, Pessiglione M, Kiebel SJ, Stephan KE, Friston KJ. Observing the observer: I. Meta-Bayesian models of learning and decision-making. PLoS One. 2010b;5:e15554. doi: 10.1371/journal.pone.0015554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco G, Thiele A. Cholinergic control of cortical network interactions enables feedback-mediated attentional modulation. Eur J Neurosci. 2011;34:146–157. doi: 10.1111/j.1460-9568.2011.07749.x. [DOI] [PubMed] [Google Scholar]
- den Ouden HE, Daunizeau J, Roiser J, Friston KJ, Stephan KE. Striatal prediction error modulates cortical coupling. J Neurosci. 2010;30:3210–3219. doi: 10.1523/JNEUROSCI.4458-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Disney AA, Aoki C, Hawken MJ. Gain modulation by nicotine in macaque V1. Neuron. 2007;56:701–713. doi: 10.1016/j.neuron.2007.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doya K. Metalearning and neuromodulation. Neural Netw. 2002;15:495–506. doi: 10.1016/S0893-6080(02)00044-8. [DOI] [PubMed] [Google Scholar]
- Feldman H, Friston KJ. Attention, uncertainty, and free-energy. Front Hum Neurosci. 2010;4:215. doi: 10.3389/fnhum.2010.00215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer B, Biscaldi M, Otto P. Saccadic eye movements of dyslexic adult subjects. Neuropsychologia. 1993;31:887–906. doi: 10.1016/0028-3932(93)90146-Q. [DOI] [PubMed] [Google Scholar]
- Gil Z, Connors BW, Amitai Y. Differential regulation of neocortical synapses by neuromodulators and activity. Neuron. 1997;19:679–686. doi: 10.1016/S0896-6273(00)80380-3. [DOI] [PubMed] [Google Scholar]
- Gitelman DR. ILAB: a program for postexperimental eye movement analysis. Behav Res Methods Instrum Comput. 2002;34:605–612. doi: 10.3758/BF03195488. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME, McGaughy J. High acetylcholine levels set circuit dynamics for attention and encoding and low acetylcholine levels set dynamics for consolidation. Prog Brain Res. 2004;145:207–231. doi: 10.1016/S0079-6123(03)45015-2. [DOI] [PubMed] [Google Scholar]
- Herrero JL, Roberts MJ, Delicato LS, Gieselmann MA, Dayan P, Thiele A. Acetylcholine contributes through muscarinic receptors to attentional modulation in V1. Nature. 2008;454:1110–1114. doi: 10.1038/nature07141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirayama J, Yoshimoto J, Ishii S. Bayesian representation learning in the cortex regulated by acetylcholine. Neural Netw. 2004;17:1391–1400. doi: 10.1016/j.neunet.2004.06.006. [DOI] [PubMed] [Google Scholar]
- Huang F, Fu Y. A review of clinical pharmacokinetics and pharmacodynamics of galantamine, a reversible acetylcholinesterase inhibitor for the treatment of Alzheimer's disease, in healthy subjects and patients. Curr Clin Pharmacol. 2010;5:115–124. doi: 10.2174/157488410791110805. [DOI] [PubMed] [Google Scholar]
- Iglesias S, Mathys C, Brodersen KH, Kasper L, Piccirelli M, den Ouden HE, Stephan KE. Hierarchical prediction errors in midbrain and basal forebrain during sensory learning. Neuron. 2013;80:519–530. doi: 10.1016/j.neuron.2013.09.009. [DOI] [PubMed] [Google Scholar]
- Kilgard MP, Merzenich MM. Cortical map reorganization enabled by nucleus basalis activity. Science. 1998;279:1714–1718. doi: 10.1126/science.279.5357.1714. [DOI] [PubMed] [Google Scholar]
- Knecht S, Breitenstein C, Bushuven S, Wailke S, Kamping S, Flöel A, Zwitserlood P, Ringelstein EB. Levodopa: faster and better word learning in normal humans. Ann Neurol. 2004;56:20–26. doi: 10.1002/ana.20125. [DOI] [PubMed] [Google Scholar]
- Kyllingsbaek S, Schneider WX, Bundesen C. Automatic attraction of attention to former targets in visual displays of letters. Percept Psychophys. 2001;63:85–98. doi: 10.3758/BF03200505. [DOI] [PubMed] [Google Scholar]
- Mathys C, Daunizeau J, Friston KJ, Stephan KE. A bayesian foundation for individual learning under uncertainty. Front Hum Neurosci. 2011;5:39. doi: 10.3389/fnhum.2011.00039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGaughy J, Dalley JW, Morrison CH, Everitt BJ, Robbins TW. Selective behavioral and neurochemical effects of cholinergic lesions produced by intrabasalis infusions of 192 IgG-saporin on attentional performance in a five-choice serial reaction time task. J Neurosci. 2002;22:1905–1913. doi: 10.1523/JNEUROSCI.22-05-01905.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metherate R, Weinberger NM. Cholinergic modulation of responses to single tones produces tone-specific receptive field alterations in cat auditory cortex. Synapse. 1990;6:133–145. doi: 10.1002/syn.890060204. [DOI] [PubMed] [Google Scholar]
- Moran RJ, Campo P, Symmonds M, Stephan KE, Dolan RJ, Friston KJ. Free energy, precision and learning: the role of cholinergic neuromodulation. J Neurosci. 2013;33:8227–8236. doi: 10.1523/JNEUROSCI.4255-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newhouse PA, Potter A, Singh A. Effects of nicotinic stimulation on cognitive performance. Curr Opin Pharmacol. 2004;4:36–46. doi: 10.1016/j.coph.2003.11.001. [DOI] [PubMed] [Google Scholar]
- Phillips JM, McAlonan K, Robb WG, Brown VJ. Cholinergic neurotransmission influences covert orienting of visuospatial attention in the rat. Psychopharmacology. 2000;150:112–116. doi: 10.1007/s002130000437. [DOI] [PubMed] [Google Scholar]
- Posner MI. Orienting of attention. Q J Exp Psychol. 1980;32:3–25. doi: 10.1080/00335558008248231. [DOI] [PubMed] [Google Scholar]
- Rescorla RA, Wagner AR. A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement. In: Black AH, Prokasy WF, editors. Classical conditioning, Vol II: Current research and theory. New York: Appleton-Century-Crofts; 1972. pp. 64–99. [Google Scholar]
- Rokem A, Landau AN, Garg D, Prinzmetal W, Silver MA. Cholinergic enhancement increases the effects of voluntary attention but does not affect involuntary attention. Neuropsychopharmacology. 2010;35:2538–2544. doi: 10.1038/npp.2010.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarter M, Hasselmo ME, Bruno JP, Givens B. Unraveling the attentional functions of cortical cholinergic inputs: interactions between signal-driven and cognitive modulation of signal detection. Brain Res Rev. 2005;48:98–111. doi: 10.1016/j.brainresrev.2004.08.006. [DOI] [PubMed] [Google Scholar]
- Stampe DM. Heuristic filtering and reliable calibration methods for video-based pupil-tracking systems. Behav Res Methods Instrum Comput. 1993;25:137–142. doi: 10.3758/BF03204486. [DOI] [Google Scholar]
- Thiel CM, Henson RN, Morris JS, Friston KJ, Dolan RJ. Pharmacological modulation of behavioral and neuronal correlates of repetition priming. J Neurosci. 2001;21:6846–6852. doi: 10.1523/JNEUROSCI.21-17-06846.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiel CM, Friston KJ, Dolan RJ. Cholinergic modulation of experience-dependent plasticity in human auditory cortex. Neuron. 2002a;35:567–574. doi: 10.1016/S0896-6273(02)00801-2. [DOI] [PubMed] [Google Scholar]
- Thiel CM, Henson RN, Dolan RJ. Scopolamine but not lorazepam modulates face repetition priming: a psychopharmacological fMRI study. Neuropsychopharmacology. 2002b;27:282–292. doi: 10.1016/S0893-133X(02)00316-0. [DOI] [PubMed] [Google Scholar]
- Thiel CM, Zilles K, Fink GR. Nicotine modulates reorienting of visuospatial attention and neural activity in human parietal cortex. Neuropsychopharmacology. 2005;30:810–820. doi: 10.1038/sj.npp.1300633. [DOI] [PubMed] [Google Scholar]
- Vangkilde S, Bundesen C, Coull JT. Prompt but inefficient: nicotine differentially modulates discrete components of attention. Psychopharmacology. 2011;218:667–680. doi: 10.1007/s00213-011-2361-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vossel S, Thiel CM, Fink GR. Behavioral and neural effects of nicotine on visuospatial attentional reorienting in non-smoking subjects. Neuropsychopharmacology. 2008;33:731–738. doi: 10.1038/sj.npp.1301469. [DOI] [PubMed] [Google Scholar]
- Vossel S, Mathys C, Daunizeau J, Bauer M, Driver J, Friston KJ, Stephan KE. Spatial attention, precision, and Bayesian inference: a study of saccadic response speed. Cereb Cortex. 2014;24:1436–1450. doi: 10.1093/cercor/bhs418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu AJ, Dayan P. Uncertainty, neuromodulation, and attention. Neuron. 2005;46:681–692. doi: 10.1016/j.neuron.2005.04.026. [DOI] [PubMed] [Google Scholar]