Nonlinear Structured Growth Mixture Models in Mplus and OpenMx

Abstract

Growth mixture models (GMMs; Muthén & Muthén, 2000; Muthén & Shedden, 1999) are a combination of latent curve models (LCMs) and finite mixture models to examine the existence of latent classes that follow distinct developmental patterns. GMMs are often fit with linear, latent basis, multiphase, or polynomial change models because of their common use, flexibility in modeling many types of change patterns, the availability of statistical programs to fit such models, and the ease of programming. In this paper, we present additional ways of modeling nonlinear change patterns with GMMs. Specifically, we show how LCMs that follow specific nonlinear functions can be extended to examine the presence of multiple latent classes using the Mplus and OpenMx computer programs. These models are fit to longitudinal reading data from the Early Childhood Longitudinal Study-Kindergarten Cohort to illustrate their use.

Among the first tasks in developmental studies are describing how individuals change (e.g., grow and/or decline) over time and how those changes differ from person to person (Baltes & Nesselroade, 1979; Wohlwill, 1973). In behavioral research, latent curve models (LCM) (and similar techniques) are often fit to examine within-person change and between person differences in change (see McArdle & Nesselroade, 2003; Willett & Sayer, 1994 for historical reviews). Many developmental processes exhibit nonlinear change patterns (Grimm, Ram, & Hamagami, in press) and researchers must turn to latent curve models that allow for nonlinearity in the change pattern. Nonlinearities in the within-person change processes can be modeled using a variety growth models (e.g., polynomial, exponential, sigmoid, multiphase, etc.) that take advantage of the latent curve modeling framework’s ability to accommodate nonlinear mathematical functions of time. A specific class of LCMs, referred to as Nonlinear Structured Latent Curve Models (NSLCM; Browne, 1993; Browne & du Toit, 1991), allow the within-person change process to follow inherently nonlinear mathematical functions and allow for between-person differences in key change components (see also Burchinal & Appelbaum, 1991, Grimm & Ram, 2009). Typological differences in development and change can be modeled using Growth Mixture Models (GMM; Muthén & Muthén, 2000; Muthén & Shedden, 1999). GMMs, a combination of LCMs and the finite mixture model, allow for probabilistic classification of individuals based on their longitudinal trajectories through a latent categorical variable. Combining these two extensions of LCMs, researchers have a range of available models for describing complex within-person change processes and between-person differences in various aspects of change. The combination of NSLCMs and GMMs approximate the nonlinear mixed-effects mixture model recently proposed (Harring, 2005; Kelley, 2005, 2008).

The purpose of this paper is to describe how NSLCMs and GMMs can be combined to study unobserved classes that follow nonlinear change functions using commonly available latent variable modeling software. After briefly reviewing basic elements of NSLCMs and GMMs, we describe how these models can be fit to longitudinal reading data from the Early Childhood Longitudinal Study using Mplus (Muthén & Muthén, 1998-2007) and OpenMx (Boker, et al., in press). The procedures are illustrated by example using an ongoing investigation of heterogeneity in the development of children’s reading ability from kindergarten through eighth grade.

Motivating Research Questions: Reading Development

Our example is derived from observed data as well as theoretical and empirical work on the development of reading during childhood. However, please note that the procedures illustrated can be applied to a variety of questions regarding behavioral development and change.

Qualitative differences in reading development

Previous research has documented the existence of multiple trajectories when tracking the development of children’s reading abilities through early childhood. For example, Pianta and colleagues (2008) found evidence of multiple classes in their examination of four assessments of reading obtained during elementary school as part of the NICHD Study of Early Child Care. Making use of GMMs they identified two types of children, a group of ‘fast readers’ whose developmental trajectories were characterized by early rapid growth followed by decelerated growth, and a group of ‘typical readers’ whose reading skills grew steadily over time. In a similar vein, Kaplan (2002) identified three types of reading trajectories that were characterized by differently shaped quadratic curves. The first was a ‘fast developing’ group with a mean trajectory similar in shape to Pianta et al’s ‘fast readers’. The second was a ‘normal developing group’ similar to the ‘typical readers’ and the third was a ‘slow developing’ group characterized by slow initial growth followed by accelerated growth. Finally, Muthén, Khoo, Francis, and Boscardin (2003) identified four classes of reading development from kindergarten through first grade. The first class showed no growth, two classes showed relatively stable growth over time but differed in their initial levels of performance, and the fourth class started with a high initial level performance and exhibited the greatest growth over the observation period. In sum, when examined for evidence of multiple latent classes, several studies have supported the need for multiple patterns of reading development across early childhood.

Nonlinear trajectories of reading development

Theories of reading development and learning, and many empirical data, are best characterized by nonlinear change patterns (e.g., Grimm & Ram, 2009; Kaplan, 2002; Pianta et al., 2008). Furthermore, theoretical notions regarding changes in reading skills that extend beyond first grade do not posit simple linear growth. Instead, there is a period of slow growth during kindergarten when most students are not exposed to academic endeavors. Then, as primary grades begin and students are exposed to a variety of new topics, the rate of growth increases. In later primary school, students refine their abilities, proficiency, and become quicker rather than being exposed to new material and therefore, growth slows. In line with these notions, research on the development of reading related activities, such as letter and word recognition, during the elementary school years has shown nonlinear change patterns best characterized by sigmoid (elongated s-shaped) curves capable of capturing the expected slow-fast-slow patterns of growth (Grimm & Ram, 2009).

Qualitative differences in nonlinear trajectories of development

Having established the elongated s-shaped nonlinearity in reading skill development across childhood, a natural next question is: Are there multiple classes or sub-populations of individuals who develop in qualitatively different ways? The objective is to evaluate whether and how many distinct types of nonlinear developmental trajectories are exhibited by children as they develop their reading skills from kindergarten through 8^th grade.

Example Data: ECLS-K Reading Achievement

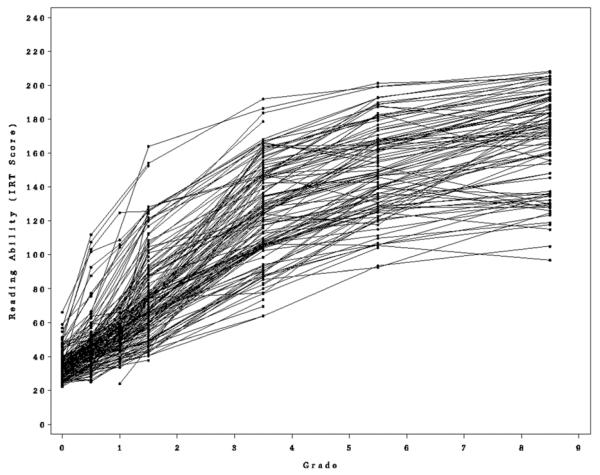
The Early Childhood Longitudinal Study – Kindergarten (ECLS-K) cohort is a longitudinal study of more than 21,000 children who entered kindergarten in 1998 and were followed through 8^th grade. Reading achievement was assessed on seven occasions: fall and spring of kindergarten and 1^st grade, and the spring of 3^rd, 5^th, and 8^th grades. Reading assessments in the ECLS-K were adaptive and scaled with an item response model. Observed scores represent a continuous scale and carry the same meaning throughout the study. Figure 1 is a longitudinal plot of reading achievement scores for a 1% random sample of participants. The longitudinal trajectories are obviously nonlinear with respect to grade (time). Previous analyses (Grimm & Ram, in press) of these data have found the Gompertz curve to be an adequate representation of the within-change process and between-person differences therein. However, the longitudinal trajectories may be better represented by a growth mixture model with latent classes differing in their average rate of approach to the asymptote, timing of change, and total amount of change (asymptotic level).

Figure 1.

Longitudinal plot of observed reading trajectories for a 1% random sample from the Early Childhood Longitudinal Study – Kindergarten cohort.

Background on Analytic Models

In this section we briefly review the mathematical underpinnings of NSLCMs and GMMs, as relevant for our illustrative application. Given our concentration here on programming and implementation using Mplus and OpenMX software we purposefully remain brief and refer readers to additional sources where more detailed accounts of each model, the combined model, and other strategies for application (see Browne, 1993; Browne & du Toit, 1991; Grimm, Ram, & Hamagami, in press; Harring, 2005; Harring, Cudeck, & du Toit, 2006; Kelly, 2005, 2009; Ram & Grimm, 2009).

Nonlinear Structural Latent Curve Models

As mentioned, longitudinal reading data have previously been subjected to a collection of nonlinear growth curves (Grimm & Ram, in press). It was determined that a Gompertz model with variation in the rate of approach to the asymptote, timing of accelerated changes, and total amount of change to the upper asymptote adequately represented individual change patterns. The Gompertz growth curve can be written as

$$y_{\mathit{nt}}=i+a_n\cdot \exp \left(-\exp \left(-r_n\left(t-d_n\right)\right)\right)$$ (1)

where i is the universal lower asymptote, a_n is the individual total amount of change from the lower to upper asymptotes, r_n represents the individual rate of approach to the asymptote, and d_n is the timing of accelerated changes for individual n and is referred to as the timing parameter. The rate of change based on the Gompertz model varies with time; however, the changes are most rapid when t = d_n and at this time the instantaneous rate of change is $\frac{(a_n\cdot r_n)}{e}$ per unit of t. With respect to our illustrative data, a_n represents the total amount of expected change in reading ability and, because the lower asymptote does not vary over participants, the upper potential for reading ability for each individual, r_n controls how quickly learning takes place for each individual once it begins, and d_n represents the time when each individual’s learning rate reaches its maximum.

The model of Eq. 1 is a Nonlinear Random Coefficient Model (or fully nonlinear mixed-model) because there are latent random coefficients (a_n, d_n, & r_n) that enter the model nonlinearly. This can be shown by taking the partial derivative of Eq. 1 with respect to each latent random coefficient. When doing this, the partial derivatives are shown to depend on one or more latent random coefficient. Thus, this model cannot be directly estimated as a structural equation model, but can be approximated through linearization following the work of Browne and du Toit (1991). In brief, the model of Eq. 1 can be re-expressed with i, a_n, d_n, and r_n as latent variables with factor loadings equivalent to the partial derivatives of the target function with respect to each latent variable. The factor loadings of latent variables are complex nonlinear functions; however, they only vary with time making the model estimable using general structural equation modeling software.

Following the steps laid out by Browne & duToit (1991) the target function of the Gompertz curve, written using the means of latent variables i, a, d, and r is

$${\mu }_t={\mu }_i+{\mu }_a\cdot \exp \left(-\exp \left(-{\mu }_r\left(t-{\mu }_d\right)\right)\right).$$ (2)

Taking the partial derivative of Eq. 2 with respect to each mean, the Gompertz curve at the individual level can be re-expressed as

$$y_{\mathit{nt}}=x_i\cdot \frac{\partial {\mu }_t}{\partial {\mu }_i}+x_{\mathit{an}}\cdot \frac{\partial {\mu }_t}{\partial {\mu }_a}+x_{\mathit{rn}}\cdot \frac{\partial {\mu }_t}{\partial {\mu }_r}+x_{\mathit{dn}}\cdot \frac{\partial {\mu }_t}{\partial {\mu }_d}+e_{\mathit{nt}},$$ (3)

where y_nt are repeated measures, x_i is the universal lower asymptote, $\frac{\partial {\mu }_t}{\partial {\mu }_i}$ is the partial derivative of the target function with respect to μ_i, x_an is the individual amount of change from lower to upper asymptote, $\frac{\partial {\mu }_t}{\partial {\mu }_a}$ is the partial derivative of the target function with respect to μ_a, x_rn is individual rate of approach to the asymptote, $\frac{\partial {\mu }_t}{\partial {\mu }_r}$ is the partial derivative of the target function with respect to μ_r, x_dn is an individual timing coefficient, and $\frac{\partial {\mu }_t}{\partial {\mu }_d}$ is the partial derivative of the target function with respect to μ_d. Now, the partial derivatives of Eq. 3 with respect to the latent variables (latent random coefficients; x_an, x_rn, & x_dn) only depend on parameters (fixed-effects) and not on any latent variable. The model is now linear (or additive) with respect to latent variables and can be estimated as a structural equation model. The model can now be viewed as a restricted common factor model (see Meredith & Tisak, 1990) with the factor loadings set equal to the partial derivatives. This type of model is often referred to as a Nonlinear Structured Latent Curve Model because the latent variables (latent random coefficients) enter the model linearly, but the parameters (fixed effects) enter the model nonlinearly. Specifically, the general LCM is written as

$${\mathbf{y}}_i=\Lambda {\eta }_i+{\epsilon }_i,$$ (4)

where y_i is a p × 1 vector of repeated measures for individual i, Λ is a p × q matrix of factor loadings, η_i is a q × 1 vector of latent factor scores (i.e., intercept or lower asymptote, rate of change, etc.), and ε_i is a p × 1 vector of residual scores. In the Gompertz curve of Eq. 3 $\Lambda =\left(\begin{array}{cccc}\hfill \frac{\partial {\mu }_t}{\partial {\mu }_i}\hfill & \hfill \frac{\partial {\mu }_t}{\partial {\mu }_a}\hfill & \hfill \frac{\partial {\mu }_t}{\partial {\mu }_r}\hfill & \hfill \frac{\partial {\mu }_t}{\partial {\mu }_d}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \frac{\partial {\mu }_t}{\partial {\mu }_i}\hfill & \hfill \frac{\partial {\mu }_t}{\partial {\mu }_a}\hfill & \hfill \frac{\partial {\mu }_t}{\partial {\mu }_r}\hfill & \hfill \frac{\partial {\mu }_t}{\partial {\mu }_d}\hfill \end{array}\right)$, where the columns define the factors, x_i, x_an, x_rn , and x_dn, respectively. Individual latent factor scores are written as deviations from the sample mean as

$${\eta }_i=\alpha +{\zeta }_i,$$ (5)

where α is a q × 1 vector of latent variable means and ζ_i is a q × 1 vector of individual mean deviations. Combining Eq. 4 and 5 gives the full latent growth model,

$${\mathbf{y}}_i=\Lambda \alpha +\Lambda {\zeta }_i+{\epsilon }_i.$$ (6)

The population mean vector (μ) and expected covariance matrix (Σ) of the model are

$$\begin{array}{c}\hfill \mu =\Lambda \alpha \hfill \\ \hfill \Sigma =\Lambda \Psi {\Lambda }^{\prime }+\Theta \hfill \end{array}$$ (7)

where Ψ is a q × q latent variable covariance matrix and Θ is a p × p diagonal residual covariance matrix. It is important to note that the latent variable means for x_rn and x_dn are fixed at 0, but the means of r_n and d_n are estimated parameters in the equations for the partial derivatives in Λ and thus, estimated with the model. See Browne and du Toit (1991) for complete details.

Growth Mixture Models

The objective of growth mixture modeling is to further examine heterogeneity in change that may be manifested as multiple unobserved groups following distinct developmental patterns (McLachlan & Peel, 2000, Muthén & Muthén, 2000, 2002; Muthén & Shedden, 1999). Growth mixture modeling extends the growth model by incorporating a categorical latent variable bringing an additional dimension of between-person differences. In GMMs, population heterogeneity is described in two ways – between class heterogeneity and within-class heterogeneity. Extending the expectations for the latent growth curve in Eq. 7 to accommodate k = 1 to K latent classes, the expectations of the growth mixture model can be written as

$$\begin{array}{c}\hfill \mu =\sum _{k=1}^K{\pi }_k\left({\Lambda }_k{\alpha }_k\right)\hfill \\ \hfill \Sigma =\sum _{k=1}^K{\pi }_k\left({\Lambda }_k{\Psi }_k{\Lambda }_k^{\prime }+{\Theta }_k\right),\hfill \end{array}$$ (8)

where π_k is the proportion of participants in class k (average probability of class membership in class k). Class proportions range between zero and one (0 ≤ π_k ≤1) with the constraint that their sum equals one (${\sum }_{k=1}^K{\pi }_k=1$). The matrices of Eq. 8 contain the same parameters as in Eq. 7; however each matrix is potentially class specific (subscripted by k), which allows for the additional aspect of heterogeneity in development. However, in practice, certain matrices are often specified to be class non-invariant, such as the latent variable covariance, residual covariance, and factor loading matrices, which places the focus of class differences on the means of the latent variables. In this project, we fit three series of growth mixture models differing in the class invariant matrices. In a similar vein as Ram & Grimm (2009), the first set of models allowed α, Λ, and the matrix housing the additional estimated parameters to be class non-invariant, the second set additionally allowed Ψ to be class non-invariant, and the third set additionally allowed Θ to be class non-invariant.

Programming NSLCMs and GMMs

In this section, descriptions of how NSLCMs and the extension to GMMs can be applied to the example data using Mplus and OpenMx are presented. Mplus (Muthén & Muthén, 1998-2007) is a general latent variable modeling program that can conduct a variety of statistical analyses including structural equation modeling (SEM) and mixture modeling. OpenMx (Boker, et al., in press) is a free and open source latent variable modeling program for use within R (R Core Development Team, 2009) that can handle SEM and mixture modeling. These programs were chosen because they are two of the only programs able to fit SEMs in combination with mixture models that allow for nonlinear constraints. Complete programming scripts for all models fit in each program and the electronic appendices referred to in the subsequent programming descriptions are available at http://psychology.ucdavis.edu/labs/Grimm/personal/downloads.html. Important elements of each script are described so that users may adapt them for their own applications. Within each section, basic familiarity with the Mplus or OpenMX software and programming environment is assumed.

Mplus

NSLCM

Although growth curves can be specified in multiple ways using Mplus, we use the standard SEM approach to facilitate linking and parallelism across programs. For ease of reading, Mplus scripts are presented in Courier New font to distinguish program specific commands from text. In the scripts we use CAPITAL letters for Mplus commands and lower case letters for objects specific to the dataset and model. Throughout this description we refer to code for fitting this model that is available in Electronic Appendix A.

Three key elements of the model, the (Means, Covariances, & Factor Loading Pattern) are specified using the MODEL and MODEL CONSTRAINT statements, with the rest of the script following the usual set-up needed for reading data into the program and requesting particular types of estimation and output.

In the first part of the MODEL statement, four latent variables (i, a, d, & r) are specified representing the four latent variables of the Gompertz curve of Eq. 3 and their factor loadings. As outlined above, the factor loadings are the partial derivatives of the target function taken with respect to each mean. Factor loadings for i are fixed at 1, using @ to denote a fixed parameter, because the partial derivative of the target function (Eq. 2) with respect to μ_i is 1. Factor loadings for a, d, and r are specified with labels contained within parentheses, which will be used later in the MODEL CONSTRAINT command to force the factor loadings to equal the appropriate partial derivative.

Second, means and intercepts are specified by placing names of latent and observed variables within square brackets. The intercepts of the observed scores are fixed at 0 as per usual practice in LCMs whereas the means of latent variables i and a are given labels for use with the MODEL CONSTRAINT command. The mean of i is given a starting value of −4 using * to denote a starting value and labeled (mu_i). Similarly, the mean of a is given a starting value and label (mu_a). In accordance with the specification given above the means of r and d are fixed at zero.

Third, variances and covariances of the latent and manifest variables are specified. In Mplus, variances are specified by listing variable names and covariances are specified using the WITH command. In our example residual variances of observed variables are specified without an invariance constraint in order to accommodate potential floor and ceiling effects in the longitudinal reading data. Next, variances and covariances of latent variables are specified, along with starting values.

Finally, the MODEL CONSTRAINT command is used to finish specifying the pattern of change by setting the factor loadings equal to the partial derivatives of the target function. First, two additional parameters are created and starting values provided using the NEW command. These parameters were named mu_r and mu_d to remain consistent with the naming of the means of latent variables. Next, a series of equations are specified for each of the factor loadings of the latent variables making use of the labels defined previously. The labels of the factor loadings are on the left-hand side of the constraints (i.e., equations) and the associated partial derivative of the target function is given on the right-hand side of the equation. Constraints for each set of factor loadings only differ with respect to the timing of the measurement occasions. Specific to our example, the time metric used in these models was grade in school at assessment with 0 representing fall of kindergarten and a one unit change in t indicating one year change in grade (assessments took place either in the fall or spring of the school year). Grade in school at assessment was chosen as the time metric because reading related skills has been shown to be more influenced by schooling (instructional time) as opposed to age (Morrison, Smith, & Dow-Ehrensberger, 1995). However, assessment age could be used as the time metric in a similar manner¹. Partial derivatives are specified using the labels of parameters defined in the NEW command (mu_r & mu_d) and provided for the means of the latent variables (in this case only mu_a is used as mu_i falls out when taking the partial derivatives). Together these four portions of script specify the elements needed for fitting the NSLCM.

Extension of NSLCMs to GMMs

The complete Mplus script described here, a 2-class Gompertz growth mixture model with α, Λ, and the matrix housing the additional estimated parameters allowed to vary of classes, is available in Electronic Appendix B. Here, we highlight the additions to the NSLCM script to include latent classes.

First, for every GMM, the number of classes must be specified a priori. Often, as done here, several models are fit varying the number of classes and then compared. The name of the latent class variable and how many categories it contains are specified in the VARIABLE: section as CLASSES = c(2), where c is the name of the latent class variable and 2 is the number of latent classes. Additionally, the type of analysis is changed to MIXTURE in the ANALYSIS command (ANALYSIS: TYPE = MIXTURE).

Second, statements must be added to the MODEL: section in order to specify the particular elements that do and do not differ among the latent classes – similar to multiple group modeling where group-specific model statements are necessary to specify which parameters are invariant and which are allowed to vary across groups. In the GMM, an %OVERALL% model is specified, which is the Gompertz curve specified previously with a few minor changes in the labels. Specifically, labels are only provided for estimated parameters that are invariant over classes in the %OVERALL% statement. Therefore, the labels for the factor loadings and means of latent variables have been removed because they are allowed to differ across classes. In contrast, labels are included for all variance and covariance parameters as they are forced to be invariant across classes. The %OVERALL% statement is followed by class specific model statements, %C#1% for class 1 and %C#2% for class2, where only the particular elements of the Gompertz curve allowed to vary between latent classes are specified. In these sections, factor loadings for the latent variables and latent variable means are re-defined with labels reflecting the class number - labels have a 1 or a 2 at the end.

Finally, changes are made in the MODEL CONSTRAINT: command because these constraints are now class-specific. As done previously, additional parameters are specified using the NEW command - mu_d1 and mu_r1 for class 1 and mu_d2 and mu_r2 for class 2. Similarly, factor loading constraints are specified separately for each class. In particular, the factor loadings for first class are set equal to the partial derivatives of Eq. 2 using mu_d1, mu_r1, and mu_a1 and the factor loadings for the second class are set equal to the partial derivatives of Eq. 2 using mu_d2, mu_r2, and mu_a2. The mean of the lower asymptote is contained in the class specific model statements; however, the label is the same across classes forcing the mean of the lower asymptote to be invariant over classes. With these changes, an Mplus script for a NSLCM is extended to include latent classes.

OpenMx

NSLCM

As per the presentation of programming scripts, OpenMx commands are written in Courier New font. Throughout this description we refer to code for fitting this model that is available in Electronic Appendix C. To facilitate reading of the code, we have kept a separation of the OpenMx and R namespaces. Matrices, algebras, and models in OpenMx are ‘named entities’, and are stored as R ‘objects’. While it is possible to store an OpenMx matrix named ‘a’ in an R object called ‘a’, we avoid using the same names for OpenMx entities and R objects to avoid confusion of the two namespaces.

The first section of the script loads the OpenMx library into R, reads the ECLS-K data, provides variable names, and assigns them to the dataset. Next, major components of the model are specified. First, several matrices are specified to describe on the factor analytic part of the growth curve. Matrices are created using the mxMatrix() function, and customized using the arguments of that function. The first R object, factorMeans, is a matrix containing the means of the four latent variables (i, a, d, & r). The means of the first two latent variables are freely estimated (free = ‘TRUE’) and the second two are fixed (free = ‘FALSE’). Starting values and labels are given using values and labels, respectively. If a starting value is given and the parameter is not freely estimated, such as the means of latent variables d and r, then the parameter is fixed at the starting value. The last aspect of factorMeans is the name of the OpenMx matrix, which is mu. The next R object, factorCov, is the matrix of latent variable covariances, where starting values and labels are applied to the variances and covariances of latent variables i, a, d, and r. The factor variance of i as well as its covariances with the remaining latent variables are set to zero by stating free = ‘FALSE’ and specifying a starting value of 0. The remaining parameters of the latent variable covariance matrix are freely estimated (free = ‘TRUE’) and the OpenMx matrix name is phi. Next, the R object, manCov, is the matrix of residual variances and covariances among manifest variables. Variances of manifest variables are freely estimated and labels are applied by combining e with the measurement occasion number. Thus, e1 is the label for the residual variance of the first measurement occasion (fall of kindergarten). The name of this OpenMx matrix is resid.

The only model matrix yet to be defined is the factor loading matrix. Before defining the factor loading matrix, a series of matrices are specified to define the model constraints for the factor loadings of the Gompertz curve of Eq. 3. The first of these is the R object unit, which is a column matrix of 1s. The OpenMx matrix name is one and will define the factor loadings for the lower asymptote latent variable, i. Next, the R object time is specified, which is a column matrix with values corresponding to the spacing between measurement occasions based on grade of assessment in 1-year increments. The OpenMx matrix name is t. Matrices for the parameters contained within the factor loadings of Eq. 3 are then specified in aParameter, dParameter, and rParameter, which are R objects. Each is a column matrix with entries with the same label and, thus, represent a single parameter. The entries for the matrix aParameter are given the same label as the mean of the latent variable a. The matrix dParameter and rParameter are place holders for the d and r parameters of the Gompertz curve and function the same way as the new command in Mplus. These R objects are given OpenMx matrix names alpha, rho, and delta.

The factor loading matrix is specified one column at a time and the columns are then combined into a single matrix. The four columns of the factor loading matrix have R object names l1, l2, l3, and l4 with OpenMx matrix names lambda1, lambda2, lambda3, and lambda4. The first column, l1, is set equal to the R object Unit, the matrix previously defined containing a column of 1s. The second through fourth columns are defined using the mxAlgebra() function to set each column to the partial derivatives of the target function using matrices previously defined. It’s important to note that the OpenMx matrix names are used in these model constraints as opposed to the R object names. After defining each column of the factor loading matrix, the columns are combined to define the factor loading matrix. The factor loading matrix, R object name loadings, is defined using mxAlgebra and the cbind command available through R to combine columns lambda1-lambda4 into a single matrix with OpenMx matrix name lambda. All matrices needed to define the Gompertz growth curve are now complete.

The final part of the script defines the model’s expectations. The mean and covariance expectations of Eq. 7 and specified in R objects meanAlg and covAlg and given OpenMx names mean and cov, respectively. The full model, R object named model, is defined using mxModel() by specifying all of R objects previously defined followed by mxFIMLObjective() to call the Full Information Maximum Likelihood Objective function with expectations defined in the OpenMx names cov and mean. The model is then run using mxRun() calling R object model, and results are put into an R object named results. The summary of results displays fit statistics and parameter estimates.

Extension of NSLCMs to GMMs

The complete OpenMx script for a 2-class Gompertz growth mixture model α, Λ, and the matrix housing the additional estimated parameters allowed to vary of classes is located in Electronic Appendix D. In OpenMx, the 2-class growth mixture model is specified as a 2-group growth model with unknown group membership. A third model, called the parent or super model, contains both of the group-specific models and an objective function that combines the two models. Matrices with parameters allowed to vary over classes are specified to be class specific, such that a matrix or algebra in the single-class model is replaced by separate matrices or algebras for each class suffixed with either a 1 or 2 depending on the class. For example, the script contains two R objects (factorMeans1 & factorMeans2) for the means of latent variables as the mean of the upper asymptote is allowed to vary over classes. Similarly, R objects that contain the r and d parameters are class specific – rParameter1, rParameter2, dParameter1, and dParameter2. Additionally, the R object containing the a parameter used in the model constraints for the factor loadings are class specific – aParameter1 and aParameter2. Finally, columns that make up the factor loading matrix are class specific and utilize OpenMx matrices from the respective class. These columns are combined and make up the factor loading matrix and contained in R objects loadings1 and loadings2 (OpenMx objects lambda1 and lambda2). In this specification, model matrices can contain both parameters that are class specific and class invariant. These matrices are specified for each class, and common labels are used for class invariant parameters.

The next part of the script contains the model’s expectations where the mean and covariance expectations from Eq. 8 are specified. As in Eq. 8, expectations are written for each class - meanAlg1 and covAlg1 for class 1 and meanAlg2 and covAlg2 for class 2. Model expectations are given OpenMx names mean1, cov1, mean2, and cov2. Next, two R objects, representing model statements for each class, are specified using mxModel(). The model statements include all of the R objects defined followed by mxFIMLObjective to call the Full Information Maximum Likelihood Objective function with expectations defined in OpenMx names cov1 and mean1 for class 1 and cov2 and mean2 for class 2.

For a multiple group or mixture model, a parent model is specified, which combines the models from each group or latent class. Several additional R objects are required in the parent model to fit the mixture model. First, R object classP is specified as a 2×1 column matrix containing two proportions labeled, pclass1 and pclass2, representing the estimated proportion of individuals contained within each latent class. This matrix is given OpenMx name classProbs. Second, a series of matrices and algebras are specified to constrain the sum of class probabilities to equal 1, First, R object classS is specified using mxAlgebra as the sum of OpenMx matrix classProbs. This matrix is given OpenMx name classSum. Next, R object constant is specified as a 1×1 identity matrix and given OpenMx matrix name con. Next, R object classC, the constraint on the class probabilities is specified using mxConstraint() where classSum is set equal to con, and this constraint is given OpenMx name classCon.

Finally, algObj, the fit function for the mixture model, is specified as −2 times the sum of the log of two objective functions, one for each latent class, each multiplied by the proportion of individuals assigned to each latent class, and given the OpenMx name mixtureObj. The fit function, mixtureObj, is placed in R object obj using mxAlgebraObjective(). The final part of the script is the mxModel statement for the mixture model. The mxModel command includes all of the R objects defined for the parent model and is placed in R object mixedModel. The model is run using mxRun and output is requested using summary.

Analysis Plan

As mentioned earlier, a series of NSLCMs were previously fit to the longitudinal reading data and a Gompertz model with no variation in the lower asymptote was determined to be the best fitting model of those examined (Grimm & Ram, in press). The series of NLSCM were fit to determine the functional form that best represented individual changes in reading achievement and between-child differences therein and obtain baseline fit statistics for comparison purposes with the growth mixture models. Fit statistics and parameter estimates for the Gompertz growth curve are contained in the first column of Table 1 and 2, respectively.

Table 1.

Fit Statistics for Gompertz Growth Model and Gompertz Growth Mixture Models.

	M1: Growth Model	M2A: 2-Class GMM	M3A: 3-Class GMM1,2,3	M2B: 2-Class GMM	M3B: 3- Class GMM1,2,3	M2C: 2-Class GMM1,3	M3C: 3-Class GMM1,3
Fit Statistics
χ 2	8,185	--	--	--	--	--	--
Parameters	17	21	25	27	37	34	51
RMSEA	.147	--	--	--	--	--	--
CFI	.896	--	--	--	--	--	--
TLI	.879	--	--	--	--	--	--
−2LL	737,782	725,384	723,997	723,381	724,848	719,680	715,412
AIC	737,816	725,814	724,047	723,435	724,922	719,748	715,514
BIC	737,951	725,981	724,246	723,645	725,216	720,019	715,919
ABIC	737,897	725,914	724,167	723,564	725,098	719,910	715,757
Bootstrap LRT p-value	--	<.001	<.001	<.001	<.001	<.001	<.001
Entropy	--	.912	.687	.904	.608	.749	.671

Note: ‘--’ indicates fit statistic not available, χ² = maximum likelihood chi-square value, Parameters = Number of estimated parameters, RMSEA = Root Mean Square Error of Approximation, CFI = Comparative Fit Index, TLI = Tucker-Lewis Index, −2LL = −2 log-likelihood, AIC = Akaike Information Criteria, BIC = Bayesian Information Criteria, ABIC = Sample size Adjusted BIC, ¹latent variable covariance matrix was not positive definite, ²best log-likelihood was not replicated (from Mplus with multiple sets of starting values), ³Bootstrap LRT p-value may not be trustworthy.

Table 2.

Parameter Estimates and Fit Statistics for Gompertz Growth Model and Gompertz Growth Mixture Models.

	M1: Gompertz NSLCM	M2B: 2-Class Gompertz GMM
Sample Size	20,871	19,594	1,277
Means
i	21.080*	20.336*	20.336*
a	144.857*	144.468*	155.472*
r a	.564*	.548*	.916*
d a	1.522*	1.614*	0.409*
Variances
a	546.764*	542.193*	201.202*
r	.007*	.002*	.158*
d	.238*	.113*	.141*
Latent Variable Covariances
a & r	.899*	1.064*	−2.658*
a & d	−5.421*	−4.097*	.414
r & d	−.014*	−.011*	−.035*
Residual Variances
Reading Fall K	20.812*	15.174*
Reading Spring K	25.136*	18.423*
Reading Fall 1st	94.496*	92.181*
Reading Spring 1st	146.729*	148.118*
Reading Spring 3rd	130.397*	150.784*
Reading Spring 5th	85.498*	79.602*
Reading Spring 8th	251.851*	271.518*

^*Note: indicates a significant parameter at p < .01,

^aindicates value not contained with α matrix, but estimated through the factor loadings.

The three series of Gompertz mixture models were fit varying the number of classes. The number of classes was increased until the Bayesian Information Criteria (BIC) did not improve or convergence/estimation issues were encountered. Models were compared using information criteria (AIC, BIC, & ABIC), entropy, a measure of confidence in class assignments, and the Bootstrap Likelihood Ratio Test (LRT), which compares the fit of the estimated growth mixture model to the fit of a growth mixture model with one less class. P-values for the Bootstrap LRT are estimated and values less than .05 indicate the estimated growth mixture model fits better than the model with one less class. Additionally, the theoretical underpinnings of the latent classes as well as estimated parameters of the growth mixture model were taken into account because these are necessary aspects of model comparison and selection (see Nylund, Asparouhov, & Muthén, 2007; Ram & Grimm, 2009 for additional details regarding model choice in growth mixture modeling).

Results

Fit statistics for the three series of Gompertz growth mixture models are contained in Table 1. Models M2A and M3A are the 2- and 3-class models from the first series (α, Λ, and the matrix housing the additional estimated parameters were class non-invariant), models M2B and M3B are the 2- and 3-class models from the second series (additionally allowed Ψ to be class non-invariant), and models M2C and M3C are the 2- and 3-class models from the third series (additionally allowed Θ to be class non-invariant).

Overall, the information criteria (AIC, BIC, & ABIC) favored some form of growth mixture model over the growth model; however, due to the large sample size information criteria are likely to favor more complex models. Further studying iteration history, convergence, estimated parameters, entropy, and the bootstrap LRT indicated that two of the models, M2A and M2B, were justifiable with no convergence or estimation issues, smooth iteration histories, high entropy, small p-values for the bootstrap LRT, and estimated parameters describing class trajectories mapping onto previous work. These models were both 2-class models describing similar trajectories, but differed with respect to whether the latent variable covariance matrix was constrained to be invariant over classes. Model M2B, with no invariance constraint, fit slightly better with respect to the information criteria and the estimated latent variable covariance parameters were sizably different in the two classes. Therefore, Model M2B was chosen as the best representation of the longitudinal reading trajectories of the models considered.

Parameter estimates the Gompertz growth model and model M2B are contained in Table 2. Latent classes from this 2-class model distinguished between children who followed a normative trajectory (normative) and children who followed an accelerated trajectory (early readers). The normative class contained the majority of children (94%) and had an average amount of change to the upper asymptote of 144.468, an average rate of approach equal to .548, and an average timing of the accelerated changes of 1.614. Thus, children in this class of readers showed, on average, their fastest rate of learning towards the spring of first grade and were changing at an instantaneous rate of 29.12 points per grade. There was large variability in the total amount of reading change (${\sigma }_a^2$ = 542.193), a small, but significant amount of variability in the rate of approach to the asymptote (${\sigma }_r^2$ =.002), and significant variability in the timing of the accelerated changes (${\sigma }_d^2$ =.113). Furthermore, children in this class who changed more tended to approach the asymptote more quickly (σ_a,r =1.064), children who changed more tended to change earlier (σ_a,d =−4.097), and children who approached their asymptote more quickly tended to change earlier (σ_r,d =−.011).

Children in the early reader class tended to have a quicker rate of approach to the asymptote, greater amounts of change, and tended to change earlier. The average amount of change to the upper asymptote for this class was 155.472, the average rate of approach to the asymptote was .916 with an average timing of accelerated changes of .409. Children in this class showed, on average, their fastest rate of learning towards the spring of kindergarten and were changing at an instantaneous rate of 52.39 points per grade. There was a relatively small amount of variability in the expected total amount of reading change (${\sigma }_a^2$ = 201.202), comparatively large amount of variability in the rate of approach to the asymptote (${\sigma }_r^2$ =.158), and significant variability in the timing of the accelerated changes (${\sigma }_d^2$ =.141). Children in this class who changed more tended to approach the asymptote more slowly (σ_a,r =−2.658) and children who approached their asymptote more quickly tended to change earlier (σ_r,d =−.035). In this class, the total amount of change was unrelated to the timing of changes (σ_a,d =.414). A plot of the predicted mean trajectories for the two classes is contained in Figure 2. The mean curve for class 1 and 2 show the nonlinear change pattern of the Gompertz curve; however, class 2 shows the rapid increases characteristic of the Gompertz curve earlier, changes occur more rapidly, and there is more change overall than the first class.

Figure 2.

Mean predicted trajectories for each latent class based on the 2-class Gompertz growth mixture model with mean and latent variable differences between classes.

Discussion

In this paper, recent advances in longitudinal mixture modeling were discussed – the combination of nonlinear structured growth curve models with the finite mixture model. These models enable researchers to further study the ways in which individuals change and how their trajectories differ. The combination of nonlinear mixed-effects models and the finite mixture models has been previously described, but these models have not been fit with commonly available software. The approach taken here is based on a linearization of the nonlinear mixed-effects model, which serves as an approximation, and the mixture model is then built upon this approximation. This method is not optimal, but has the same goal of describing unobserved heterogeneity in nonlinear trajectories.

Between-Person Differences in Change

Developmentalists are interested in describing how individuals change over time and how individuals differ in change. A first important component of interindividual differences is the variability in growth parameters. Latent growth curves allow for a specific type of variation in growth parameters, namely, variation that is normally distributed. The growth mixture model allows for additional aspects of between-person variability in change – in essence relaxing the constraint that the between-person variability is normally distributed. However, the growth mixture model is not without its controversies. Researchers often take the growth mixture model (or other latent class models) as evidence the sample was drawn from multiple populations. However, the finite mixture model is simply attempting to account for non-normality in the observed data that may be caused by multiple populations, but may be caused by factors unrelated to multiple populations (see Bauer & Curran, 2003 & commentaries). Thus, determining when latent classes are meaningful can be difficult. Researchers should consider all of the statistical information provided along with the theoretical notions guiding the developmental process and previous research.

A second important component of individual differences is whether individuals have fundamentally different change patterns, not just differences in the magnitude of the same change pattern. This component of individual differences can be studied with multiple group growth curves, if the grouping variable is known, and growth mixture models, if the grouping variable is unknown. The illustrative example focused on latent class differences in the magnitude of parameters from the Gompertz model, but every child was expected to follow the change pattern of the Gompertz curve. However, this did not have to be the case as the within-person change pattern can vary over classes. Thus, one class may show Gompertz growth and the second may show logistic growth. Even though these patterns of change are similar, they differ in their developmental asymmetry.

Reading Development

The results regarding within-person change and between-person differences in change suggest the longitudinal trajectories in the ECLS-K are best described by a mixture of two distributions with differences in the amount of change, rate of change, and timing of change. The first class described the normative development pattern with accelerated changes occurring in the spring of first grade. The second class described a group of early readers who tended to show more overall growth, a faster rate of growth, and earlier growth when compared with the class of readers following the normative pattern of change.

These classes map well onto work conducted by Pianta et al. (2008) with data from the National Institute of Child Health and Human Development’s Study of Early Childcare and Youth Development where a small class of early readers were separated from a class of children following the normative developmental pattern. However, the work by Kaplan (2002) and Muthén et al. (2003) also identified a class of slow readers that was not identified here. These differences were likely due to the shorter period of observation and choice of within-class growth curve. The model fit here allowed for within-class variability in the amount of change, rate of change, and timing of accelerated change whereas Muthén et al. (2003) fit linear and Kaplan (2002) fit quadratic change models. However, Kaplan noted that the slow reading class was more difficult to distinguish from the typical reading group than the early reading class.

Thus, the class of early readers has been replicated across multiple data sets and likely represents an important class of readers with a distinct trajectory from the typical developing class. The slow reading class, on the other hand, has not been replicated in this study indicating children who show slow reading development may not have a growth trajectory distinct from the typically change pattern. More research is needed to determine the conditions under which a class of slow readers can be identified, what early childhood characteristics or skills are most strongly related to class membership, and what early childhood characteristics or skills are most strongly related to the variation shown in the typically developing class because this class represents the majority of children (~94%) and much variation in the amount of reading growth, rate of growth, and timing of growth.

Mplus and OpenMx

Mplus and OpenMx are two latent variable modeling programs with the ability of fitting such models as these programs allow for nonlinear constraints and mixture distributions. Mplus has several benefits for fitting these models as its mixture capabilities have been rigorously studied (e.g., Muthén, 2003; Nylund, Asparouhov, & Muthén, 2007), multiple sets of starting values are generated to avoid local optima, and several additional indices of model fit are reported (e.g., entropy & Bootstrap Likelihood Ratio Test). Mplus also summarizes individual class probabilities, can output individual class probabilities, and the latent classes can be predicted and used as predictors of outcome variables.

Despite, its youth, OpenMx also has several benefits for model fitting. OpenMx is open source, and thus, free both to use and to append and tailor to individual needs. The package is documented with a traditional manual, discussion forums, wikis, and example scripts. OpenMx works as a package within R, a powerful statistics software environment, and thus benefits from all of the resources of R, including a flexible programming language, graphics, and the ability to function across computing platforms (Windows, Mac, Linux, etc). Additionally, OpenMx allows for parallelization, enabling the program to run multiple models simultaneously across multiple processors and multiple computers. This feature is beneficial for mixture modeling as models with different sets of starting values can be fit quickly. Finally, identical parameter estimates were obtained from OpenMx and Mplus for the chosen models.

Concluding Remarks

In conclusion, nonlinear structured growth mixture models provide several possibilities for describing within-person change and between-person differences in such change. This combination of models allows for the possibility of several interesting combinations of latent classes - latent classes may simply differ in the means of the latent variables (similar to what was shown for changes in reading ability), or latent classes may have fundamentally different patterns of change. By explicitly allowing for multiple distinct change patterns, nonlinear structured growth mixture models allow researchers to study the various ways people and groups may differ in their development, which should bring us closer to understanding individual differences in time-related change.