Net uptake of atmospheric CO₂ by coastal submerged aquatic vegetation

Abstract

‘Blue Carbon’, which is carbon captured by marine living organisms, has recently been highlighted as a new option for climate change mitigation initiatives. In particular, coastal ecosystems have been recognized as significant carbon stocks because of their high burial rates and long-term sequestration of carbon. However, the direct contribution of Blue Carbon to the uptake of atmospheric CO₂ through air-sea gas exchange remains unclear. We performed in situ measurements of carbon flows, including air-sea CO₂ fluxes, dissolved inorganic carbon changes, net ecosystem production, and carbon burial rates in the boreal (Furen), temperate (Kurihama), and subtropical (Fukido) seagrass meadows of Japan from 2010 to 2013. In particular, the air-sea CO₂ flux was measured using three methods: the bulk formula method, the floating chamber method, and the eddy covariance method. Our empirical results show that submerged autotrophic vegetation in shallow coastal waters can be functionally a sink for atmospheric CO_2. This finding is contrary to the conventional perception that most near-shore ecosystems are sources of atmospheric CO₂. The key factor determining whether or not coastal ecosystems directly decrease the concentration of atmospheric CO₂ may be net ecosystem production. This study thus identifies a new ecosystem function of coastal vegetated systems; they are direct sinks of atmospheric CO₂.

Introduction

Identifying the locations and mechanisms responsible for changing global atmospheric CO₂ is still a critical challenge for predicting future interactions between the carbon cycle and climate. The ocean has recently been identified as an important stock of ‘Blue Carbon’, which is carbon captured by marine living organisms (Nellemann et al., 2009). The Blue Carbon that accumulates in sediments can be separated from the global atmosphere for millennia, whereas the carbon sequestered in terrestrial ecosystems is separated for only several dozen years (Mateo et al., 1997; McLeod et al., 2011). Some studies have estimated that the rate of carbon accumulation is higher in coastal sediments (238 Tg C yr⁻¹) than that in open ocean sediments (6 Tg C yr⁻¹) (Nellemann et al., 2009). However, unlike sequestration in terrestrial ecosystems, coastal carbon burial does not lead directly to an uptake of atmospheric CO₂. This is because (i) the water column separates the atmosphere from benthic systems (thus, for example, air-sea CO₂ gas exchange is affected by carbon input from incoming waters, buffer effect, and the residence time of the water column), and (ii) buried sedimentary carbon is composed of allochthonous sources in addition to autochthonous sources (Gazeau et al., 2005; Borges et al., 2006; Fourqurean et al., 2012).

Rigorous evidence for the uptake of atmospheric CO₂ and its quantification are required if the assessment of Blue Carbon is to be a valid measure of climate change. However, the extent of ‘on-site’ uptake of atmospheric CO₂ by coastal ecosystems through direct air-sea CO₂ gas exchange remains unclear. The current perception is that the direct relationship between Blue Carbon and atmospheric CO₂ uptake varies among geographical regions. Open oceans and continental shelves have functioned as net sinks of atmospheric CO₂ on geological timescales (Tsunogai et al., 1999; Takahashi et al., 2009). This role is evidenced by the fact that high nutrient concentrations and the increases in atmospheric CO₂ since the industrial revolution have led to high rates of primary production on continental shelves (Tsunogai et al., 1999; Chen & Borges., 2009; Takahashi et al., 2009). The dominant air-sea CO₂ gas exchange is, therefore, an influx into the seawater that balances the fugacity of CO₂ (fCO₂) and dissolved inorganic carbon (DIC) against the excess of primary production over respiration. In contrast, estuarine waters are net sources of CO₂ to the overlying atmosphere because of the predominance of CO₂ efflux from the surface seawater, a consequence mainly of the input of DIC and organic carbon from land and the excess of mineralization and respiration over primary production (Raymond & Cole, 2001; Borges et al., 2004, 2005; Jiang et al., 2008; Laruelle et al., 2010; Cai, 2011; Chen et al., 2013; Regnier et al., 2013). Shallow near-shore waters have also been shown to be sources of CO₂ to the atmosphere; this finding was based on the measurements of air-sea CO₂ gas exchange adjacent to mangroves and salt marshes (Borges et al., 2005; Bouillon et al., 2007). However, little is yet known about the air-sea CO₂ gas exchange and its determinants in shallow coastal waters with submerged aquatic vegetation (SAV) such as seagrass and seaweed systems (Smith, 1981; Frankignoulle, 1988; Gazeau et al., 2005), where the vegetation directly takes up DIC in the water column. This lack of knowledge reflects the difficulties of comprehensive measurements of the inherently complex and dynamic carbon flows and stocks in aquatic systems (Frankignoulle, 1988; Kayanne et al., 1995; Borges et al., 2005; Barrón et al., 2006; Tokoro et al., 2008; Koné et al., 2009). For instance, the relationship between biogeochemical processes (primary production, respiration, calcification, and mineral dissolution) and air-sea CO₂ exchange in aquatic systems is non-linear and strongly affected by various chemical and physical factors such as the buffer effect of the carbonate system (Weiss, 1974), residence time (Gazeau et al., 2005), and turbulence at the water surface (Wanninkhof, 1992).

In this study, we investigated carbon flows, including air-sea CO₂ fluxes, changes of DIC, net ecosystem production, and carbon burial rates in boreal, temperate, and subtropical seagrass meadows over different temporal and spatial scales. We then quantified the ecosystem function of direct CO₂ uptake from the atmosphere by shallow coastal waters with SAV.

Materials and methods

Study sites

In situ measurements were conducted at boreal (Furen lagoon), temperate (Kurihama Bay), and subtropical (Fukido estuary) sites (Fig.1). Because seagrass meadows at these sites are located adjacent to river mouths, the effect of carbon inputs from land and community metabolism could be both observed and measured. In addition, the broad range of latitudes encompassed by this study made it possible to comprehensively analyse the effects of water temperature and light, which regulate almost all of the carbon flows, including those associated with community metabolism and the carbonate system.

Figure 1.

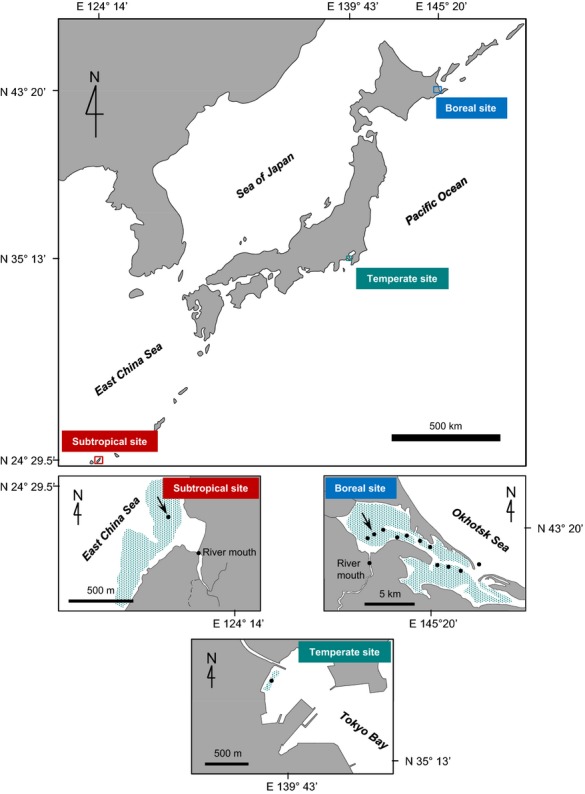
Location of study sites. The distribution of seagrass at each site is indicated by shading. The locations of water sampling sites are indicated by closed circles. Arrows indicate where air-sea CO₂ fluxes were measured by the eddy covariance method. At the boreal site, we also performed a 48-h time series of discrete water sampling at the location indicated by the arrow.

Furen lagoon, Hokkaido, Japan (43°19′46.5˝N, 145°15′27.8˝E), is a semi-enclosed body of water with an area of 57.4 km². Most of the lagoon is shallow (about 1 m deep), and much of the bottom (about 70%) is covered with seagrass meadows (dominant species: Zostera marina). The aboveground seagrass biomass ranges from 16 to 318 g dry weight (dw) m⁻², according to a 2011 annual field survey. The chlorophyll a concentration, measured with an in situ fluorometer (Compact CLW; JFE Advantech, Nishinomiya, Japan), ranges from 2 to 7 μg l⁻¹, according to August and November 2010 field surveys. The lagoon is brackish (salinity: 6–31) and is much affected by input from rivers, which flows through farmland where livestock is raised and fodder crops are grown. The nutrient levels range from 0.6 to 121 μmol N l⁻¹ (DIN) and from 0.3 to 2.6 μmol P l⁻¹ (DIP) (Montani et al., 2011).

Kurihama Bay, Tokyo, Japan (35°13′ 21.6˝N, 139°42′ 51.4˝E), is located at the mouth of Tokyo Bay. Seagrass meadows are found along the coastline at a water depth of about 3–4 m. According to a March 2010 field survey, the aboveground seagrass biomass is 38–98 g dw m⁻² (dominant species: Z. marina), and chlorophyll a concentrations are 1–4 μg l⁻¹. The inflowing Hirasaku River, which runs through urban areas, affects water quality (e.g. lowers salinity) during low tide (salinity: 29–33). The nutrient levels are 8–29 μg N l⁻¹ (DIN) and 0.4–1 μg l⁻¹ (DIP) according to field surveys from December 2012 to June 2013.

The Fukido estuary, Okinawa, Japan (24°29′ 22.1˝N, 124°13′40.5˝E), is located at the mouth of the Fukido River, which flows out from a mangrove forest. The estuary is more open to the sea than the other two sites. In a July 2011 field survey, the aboveground seagrass biomass was 32–88 g dw m⁻² (dominant species: Cymodocea serrulata, Thalassia Hemprichii, and Enhalus acoroides), and phytoplankton chlorophyll a concentrations were 0.1–2 μg l⁻¹. The salinity ranges from 29 to 33. The nutrient levels range from 0.5 to 2 μmol N l⁻¹ (DIN) and from 0.01 to 0.03 μmol P l⁻¹ (DIP) (Watanabe, 2004).

Air-sea CO₂ flux

We determined the air-sea CO₂ flux by three methods: the bulk formula method, the floating chamber method, and the eddy covariance method. We used three methods because each method has strengths and limitations with respect to technical difficulty, the spatial and temporal scale of interest, data accuracy and uncertainty, and costs.

Bulk formula method

The bulk formula method determines air-sea CO₂ fluxes (F) by using the difference of fugacity between the air and the surface of the water in addition to the gas transfer velocity (k) determined from empirical relationships with the wind speed above the surface of the water (Wanninkhof, 1992; McGillis et al., 2001). The equation for the method is as follows:

1

where the CO₂ solubility in water (S) is a function of water temperature and salinity (Weiss, 1974). The fugacity of CO₂ in water (fCO_2water) and that in air (fCO_2air) were measured with a CO₂ fugacity analyser through an equilibrator system (CO2-09, Kimoto electric) (Saito et al., 1995) or estimated using chemical equilibrium relationships and the total alkalinity (TA) and DIC of the water samples (Zeebe & Wolf-Gladrow, 2001). Water temperature and salinity were measured with a conductivity/temperature sensor (Compact-CT; JFE Advantech). The gas transfer velocity (k) is generally assumed to be determined by the physical condition of the water surface and has been empirically estimated by using the wind speed above the water surface. In this study, we used the following empirical equation to estimate k (Wanninkhof, 1992):

2

where U₁₀ is the wind speed at a height of 10 m above the water surface. We determined U₁₀ by assuming that there was a logarithmic relationship between wind speed, height above the water and the roughness of water surface (10⁻⁴ cm) (Kondo, 2000). We measured the wind speed at the height of a sonic anemometer (CSAT-3; Campbell Scientific, North Logan, UT, USA), which was deployed 2.5–4.5 m above the surface of the water. The Schmidt number (Sc) was determined from the water temperature and salinity near the water surface (Jähne et al., 1987).

The measurements were carried out on a research vessel. At the boreal site, continuous measurements were performed every hour for 2 days in August and November 2010. In addition, discrete measurements were performed from June to November 2011 (when the lagoon surface was not frozen) along a survey line from the river mouth to the mouth of the lagoon, which connects to the open ocean. The incoming water was also sampled in the river and in the open ocean. At the temperate site, the measurements were performed for 2 days and for 1 day during daylight hours in March 2010 and April 2013 respectively. At the subtropical site, the measurements were performed for 2 days during daylight hours in August 2011.

The bulk formula method has the advantage of relative ease from a technical standpoint, and it is the method most frequently and widely used. However, in most previous studies, the empirical relationship between the parameter k and wind speed has been determined from measurements made elsewhere, such as at open ocean or lake sites. Direct determination of k is recommended in coastal areas, where wind and current stresses on the water surface are likely to be different from the analogous stresses on open surfaces (Raymond & Cole, 2001; Borges et al., 2004; Tokoro et al., 2007, 2008).

Floating chamber method

In the floating chamber method, air-sea CO₂ fluxes are determined from the change in CO₂ concentration inside a chamber floating on the water surface (Frankignoulle, 1988; Borges et al., 2004; Vachon et al., 2010). The floating chamber used here was a rectangular polyvinyl chloride box (50 cm × 50 cm × 22 cm high, and weighing 17 kg) with polystyrene foam floats. The fCO₂ analyser mentioned above was connected to the chamber by a Teflon tube for measurement of fCO₂ inside the chamber. Details of this method are described elsewhere (Tokoro et al., 2007, 2008). The validity of the method has been quantitatively confirmed by a comparison of turbulence near the water surface inside and outside of the floating chamber (Tokoro et al., 2008; Vachon et al., 2010). The measurements were carried out on a research vessel in parallel with the bulk formula method measurements. Thus, the measurement duration and site were the same as for the bulk formula method, except for an annual discrete measurement at the boreal site in 2011 (the bulk formula method only).

The advantage of this method is that it provides a direct measurement of the flux. The disadvantage of the method is that under highly turbulent conditions the measurements are problematic because bubbles enter the chamber, or the chamber rolls over. In addition, the temporal and spatial ranges of the measurements are narrower than the corresponding ranges of the eddy covariance method.

Eddy covariance method

This method determines the air-sea CO₂ flux by using the vertical motion of the atmosphere and atmospheric CO₂ concentrations measured at a high frequency (10–20 Hz) to capture the micro-metrological behaviour of atmospheric eddy diffusion, which transports CO₂ vertically.

The calculation of the air-sea CO₂ flux (F) was implemented every 30 min by using the following equation:

3

where the coefficients F₁ and F₂ are correction terms based on the transfer functions that correct the frequency attenuation of the air-sea CO₂ flux caused by the response time of the sensor, path-length averaging, sensor separation, signal processing, and flux-averaging time (Massman, 2000). The first term on the right-hand side of Eqn 3 is the product of F₁ and the uncorrected air-sea CO₂ flux calculated as the covariance of the CO₂ density ρ_c and vertical wind speed w (the bar and the prime mark indicate the mean and the deviation from the mean respectively). The second and third terms are the Webb-Pearman-Leuning correction of latent heat and sensible heat respectively (Webb et al., 1980). The other symbols in Eqn 3 are as follows: ρ_d, dry air density; ρ_v, water vapour density; T_a, air temperature; and μ, ratio of molar weight of dry air to water vapour. The wind speed was corrected by using a double rotation to make the average vertical wind speed zero during the 30-min time interval (Lee et al., 2004). All the data were measured at 20 Hz and detrended using an exponential moving average (McMillen, 1988). The smoothing coefficient (= 1.7 × 10⁻³) was determined by using a cospectrum to maximize inclusion of low-frequency flux contributions and to minimize exclusion of time-variant fluctuations (not real turbulent fluctuation) (Lee et al., 2004).

The eddy covariance system was installed on a platform at both the boreal and subtropical sites. We used an open-path CO₂ analyser (LI-7500A; LI-COR, Lincoln, NE, USA) and a 3-D sonic anemometer (CSAT-3, Campbell Scientific). The devices were deployed at a height of 2.5–5.5 m from the surface of the water, depending on the tide. The measurements at the boreal site were performed from July to August and during November 2010. The measurements at the subtropical site were performed from July to August 2011.

The advantage of the eddy covariance method is that it enables direct flux estimates to be made continuously and automatically over broad spatial and temporal ranges. The footprint (measurement area), which depends on several factors, including measurement height, wind speed, atmospheric stability, and the roughness of measurement site (10⁻⁴ cm) (Schuepp et al., 1990), ranges from several hundred square metres to several square kilometres on the windward side of the measurement site. Therefore, the method has been widely used to estimate terrestrial atmospheric CO₂ fluxes (Lee et al., 2004). The method has also been used to estimate air-sea CO₂ fluxes in the ocean and coastal seas (McGillis et al., 2001; Vesala et al., 2006; Kondo & Tsukamoto, 2007; Zemmelink et al., 2009; Huotari et al., 2011; Polsenaere et al., 2012) and to estimate sediment-water O₂ fluxes (Berg et al., 2003; Kuwae et al., 2006). However, several studies have reported that results from the eddy covariance method are inconsistent with results from other methods, such as the bulk formula method (Kondo & Tsukamoto, 2007; Zemmelink et al., 2009). In addition, this method requires sufficient spatial uniformity within the study area. Data management with respect to several atmospheric conditions that affect the footprint of the measurement area (Schuepp et al., 1990), such as the wind direction and atmospheric stability, is therefore required for quality control. Moreover, this method is costly, not easy to deploy, and requires heavy data processing compared to the other methods.

Water sampling and data collection

Water samples for DIC measurement were collected in 250-ml Schott Duran bottles, which were poisoned with saturated mercuric chloride (200 μl per bottle) to prevent DIC changes due to biological activities (Dickson et al., 2007). DIC and TA were determined using a continuous-flow analyser (MDO-02, Kimoto electric, Osaka, Japan) (Kimoto et al., 2002; Watanabe et al., 2004) and a batch-sample analyser (ATT-05, Kimoto electric). The precision of the continuous-flow analyser and the batch-sample analyser were ± 2 and ± 4μmol kg⁻¹-water for DIC and ± 3 and ± 3 μmol kg⁻¹-water for TA respectively. The samples were collected during the time when the bulk formula measurements were made. However, the DIC and TA data at the subtropical site were not used because the relationships between salinity, DIC, and TA were inconsistent.

Net ecosystem production (NEP)

Net ecosystem production was estimated based on water depth and the temporal variation of ‘ΔDIC’, which is the difference between the observed DIC change and the value estimated from the mixing ratio of water and the DIC change due to calcification. The equations are as follows;

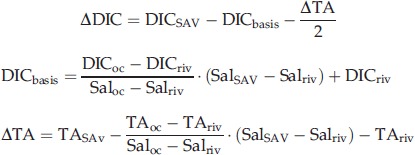4

where DIC_SAV, TA_SAV, and Sal_SAV are the DIC, TA and salinity, respectively, measured within a SAV system. DIC_basis is the DIC estimated from the mixing ratio of river water and open ocean water. ΔTA is the TA change due to biogeochemical processes such as calcification and mineral dissolution. The parameters with the subscripts ‘oc’ (open ocean) and ‘riv’ (river) are those measured outside the boundary of the SAV system. Because DIC and TA are not affected by changes in pressure and water temperature, the coastal (brackish) water DIC and TA are completely determined from the mixing ratio of freshwater (from rivers) and seawater (from the open ocean) in the absence of ecosystem production, respiration/decomposition, and calcification. If these processes are taking place, the magnitude of the effects can be quantified from the difference between the measured DIC or TA and the DIC or TA estimated from the mixing ratio. In the case of the calcification process, the DIC change is expected to be half the TA change estimated from Eqn 4 (Zeebe & Wolf-Gladrow, 2001).

NEP was then calculated from ΔDIC as follows:

5

where n is the number of water samples that were collected every hour during the 48-h measurement period. The parameters Dw (n) and t(n) are the water depth and the time of collection of sample n respectively. Eqn 5 is based on the fact that the residence time of the water mass of the collected water samples was more than 1 h. The residence time was confirmed by in situ current measurements with several 2-D current velocimeters (Compact-EM, JFE Advantech).

To estimate how much light intensity affects NEP, the NEP data were fit to a photosynthesis–irradiance curve (Jassby & Platt, 1976):

6

where P_max is the estimated maximum photosynthetic rate, R is the estimated respiration rate, α is the initial slope of the photosynthesis–irradiance curve, and I is the photosynthetic photon flux density (PPFD) in water. P_max, R, and α were determined by least squares to give the best agreement between the calculated and measured NEP. PPFD was measured using a PPFD meter (MDS-MkV/L, JFE Advantech) located on the same platform with the eddy covariance instruments. ΔDIC was not determined at the subtropical site because of the short residence time of the water mass.

Carbon burial rate

Sediment cores (1 m) were collected from three locations at the boreal site with a PVC corer. To determine the bulk density, gamma ray attenuation was measured with a Multisensor Core Logger (MSCL-S; GeoTek Ltd., Northamptonshire, UK). Core samples consisted of 1-cm slices taken throughout the length of the core for geochemical and additional geophysical analyses. Each sample slice was analysed to determine water content, total organic carbon (TOC) content, and radiocarbon date (¹⁴C). Samples were prepared by drying the sediment (60 °C for 24 h) and measuring the net water loss (i.e. water content). The sediment was then acid washed to remove inorganic carbon. The TOC content was measured using an elemental analyser (Flash EA 1112, Thermo Electron, Bremen, Germany). The ¹⁴C dating was performed by accelerator mass spectrometry (AMS). Ages are reported in calibrated years before ‘present’ (BP), 1950 being the base year. ‘Present’ carbon burial rates were calculated from the TOC content of the top 1 cm of sediment; deeper sediment was affected by early diagenetic alteration. Burial rates were estimated from a linear average ¹⁴C age and the cumulative amount of TOC calculated from bulk density, water content, and surface TOC content.

Statistical analysis

Factors affecting the air-sea CO₂ flux were statistically analysed using structured equation modelling (SEM). An a priori selection of candidate explanatory variables and model structure (direct and indirect relationships between the variables) were based on the principle of parsimony and scientific plausibility (Wang & Cai, 2004; de la Paz et al., 2007; Gupta et al., 2009; Hunt et al., 2011). We used the software package R (3.0.0) and the SEM library.

Results

Air-sea CO₂ flux

Our results showed that the air-sea CO₂ fluxes were variable and depended on the measurement timescale and season of the year. Monthly air-sea CO₂ fluxes at both the boreal site (Furen lagoon) and the subtropical site (Fukido estuary) measured by the eddy covariance system were negative (i.e. from the atmosphere into the water) in the summer (Furen: −1.46 ± 0.38 μmol-C m⁻² s⁻¹; Fukido: −1.00 ± 0.11 μmol-C m⁻² s⁻¹; mean ± 95% confidence interval, the same hereafter; Fig.2a and c). We also found the air-sea CO₂ fluxes to be negative when measured by alternative methods on diurnal timescales at the boreal site (bulk formula: −0.12 ± 0.09 μmol-C m⁻² s⁻¹; floating chamber: −0.07± 0.03 μmol-C m⁻² s⁻¹; Fig.3a) but not at the subtropical site (bulk formula: 0.12 ± 0.06 μmol-C m⁻² s⁻¹; floating chamber: 0.12 ± 0.05 μmol-C m⁻² s⁻¹; Fig.3c). In winter, the CO₂ gas exchange flux was also negative at the temperate site (Kurihama Bay) (bulk formula: −2.90 × 10⁻² ± 1.55 × 10⁻²), but the boreal site was a source of atmospheric CO₂ (eddy covariance: 0.42 ± 0.15 μmol-C m⁻² s⁻¹; bulk formula: 0.01 ± 0.01μmol-C m⁻² s⁻¹; floating chamber: 0.06 ± 0.10 μmol-C m⁻² s⁻¹,) (Fig.2b and Fig.3b). The estimated annual air-sea CO₂ flux at the boreal site was also negative (bulk formula: −1.76 × 10⁻² ± 1.50 × 10² μmol-C m⁻²s⁻¹; Fig.4), even though the winter flux was positive on a diurnal basis.

Figure 2.

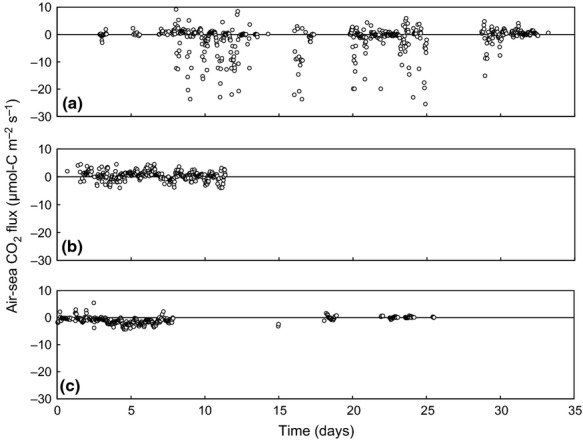
The air-sea CO₂ flux measured by the eddy covariance method at the boreal site (Furen lagoon) in the summer (a) and winter (b) of 2010, and at the subtropical site (Fukido estuary) in the summer of 2011 (c).

Figure 3.

Diurnal air-sea CO₂ fluxes measured by the bulk formula method and the floating chamber method. (a): Boreal site (Furen lagoon) in summer (bulk formula: −0.12 ± 0.09 μmol-C m⁻² s⁻¹; floating chamber: −0.07 ± 0.03 μmol-C m⁻² s⁻¹, mean ± 95% confidence interval), (b): Boreal site (Furen lagoon) in winter (bulk formula: 0.01 ± 0.01 μmol-C m⁻² s⁻¹; floating chamber: 0.06 ± 0.10 μmol-C m⁻² s⁻¹; mean ± 95% confidence interval), (c): Subtropical site (Fukido estuary) in summer (bulk formula: 0.12 ± 0.06 μmol-C m⁻² s⁻¹; floating chamber: 0.12 ± 0.05 μmol-C m⁻² s⁻¹, mean ± 95% confidence interval). Shading indicates the periods of darkness.

Figure 4.

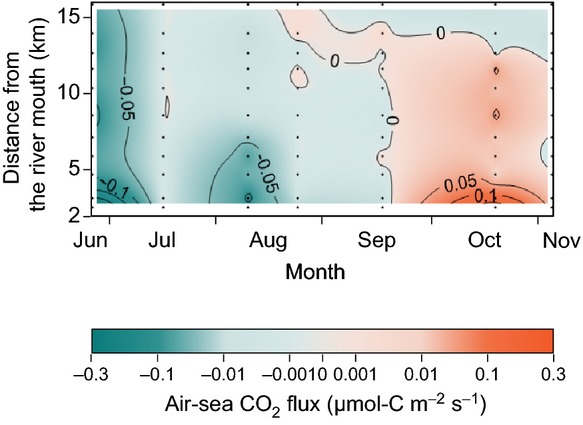
Annual air-sea CO₂ flux at the boreal site determined by the bulk formula method. Units: μmol-C m⁻² s⁻¹. Negative fluxes (influx of CO₂ into seawater) are indicated by blue, and positive fluxes by red. The annual average of the air-sea CO₂ flux at the boreal site was negative (−1.76 × 10⁻² ±1.50 × 10⁻² μmol-C m⁻² s⁻¹), the indication being that the boreal site was a net sink of atmospheric CO₂. The growing season for seagrasses is from May to August, and the decay season is from September to November at the site (unpublished data). The seawater was frozen from December to April at the site.

Factors affecting air-sea CO₂ fluxes

There was a significant positive correlation between the air–water CO₂ flux and the measured ΔDIC (P < 0.0001) (Fig.5). SEM showed that the variability of our air-sea CO₂ flux results at the boreal and temperate sites (i.e. the extent to which and whether the system was a sink or source of overlying atmospheric CO₂) was determined by geophysical and geographical factors such as wind speed, temperature, salinity, and TA, as well as indirectly by ΔDIC (the extent of biogeochemical processes such as ecosystem production and respiration; positive: heterotrophy; negative: autotrophy) (Fig.6).

Figure 5.

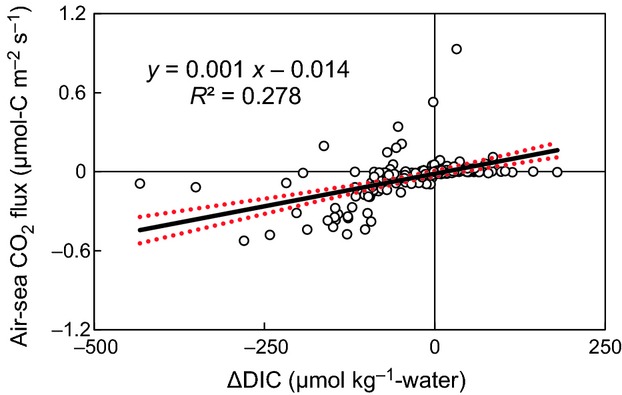
Air-sea CO₂ flux vs ΔDIC (n = 170) at the boreal and temperate sites. ΔDIC is the difference between the observed DIC change and the value estimated from the mixing ratio and the DIC change due to calcification. The value of ΔDIC thus indicates the extent of biogeochemical processes such as ecosystem production and respiration (positive: heterotrophy; negative: autotrophy). The air-sea CO₂ fluxes, including both the monthly and diurnal fluxes, were measured by using the bulk formula method. The 95% confidence limits to the regression line are indicated by the red dashed curves.

Figure 6.

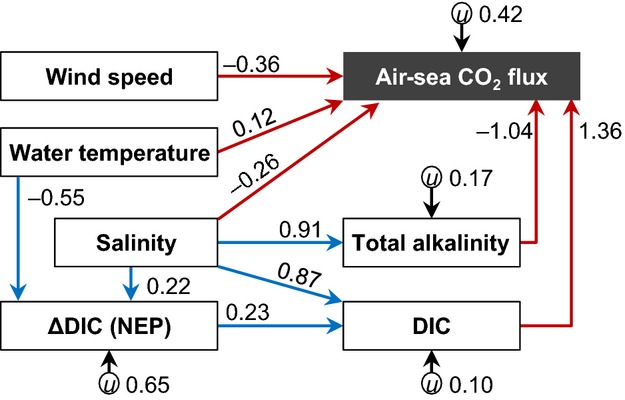
Result of the SEM analysis (n = 170) showing direct factors (red arrows) and indirect factors (blue arrows) affecting the air-sea CO₂ flux at the boreal and temperate sites. The value of a coefficient indicates the relative influence of the path. All the path coefficients are statistically significant (P < 0.05). The parameter u represents unknown factors.

Net ecosystem production (NEP)

The fitting of the photosynthesis–irradiance curve to measured NEP was statistically significant (P < 0.0001) at the boreal site in summer; the estimated summer maximal NEP and respiration were 27.2 mmol-C m⁻² h⁻¹ (7.56 μmol-C m⁻² s⁻¹) and 21.3 mmol-C m⁻² h⁻¹ (5.92 μmol-C m⁻² s⁻¹) respectively (Fig.7a and 8a). In turn, in winter, the fitting of the photosynthesis–irradiance curve to measured NEP was not statistically significant (P > 0.05) at the boreal site (Fig.7b and 8b). At the boreal site in summer, the estimated compensation light intensities (NEP = 0) was 41.1 μmol-photons m⁻² s⁻¹, and the initial slopes of the photosynthesis–irradiance curves was 0.154 ([mmol-C m⁻² h⁻¹]/[μmol-photons m⁻² s⁻¹]).

Figure 7.

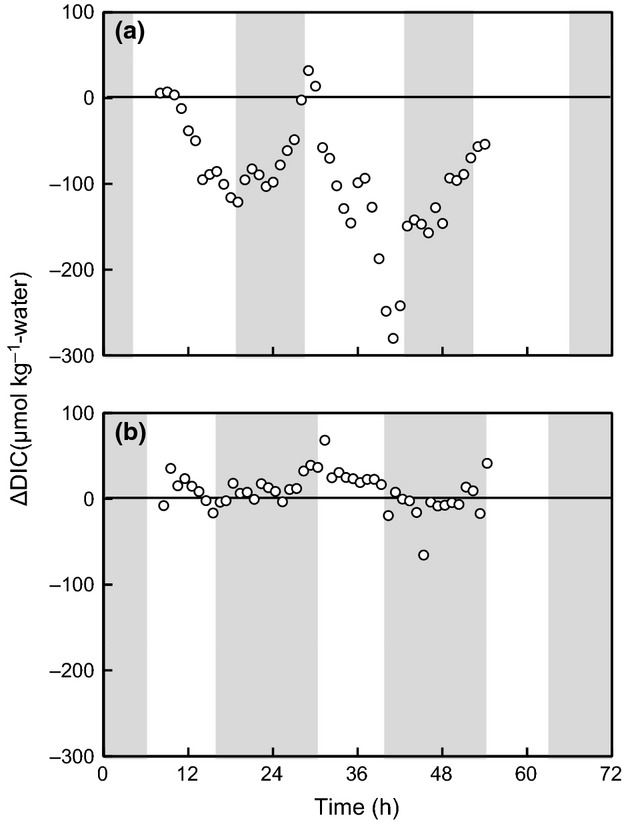
Diurnal ΔDIC changes at the boreal site in summer (a) and winter (b). Shading indicates the periods of darkness.

Figure 8.

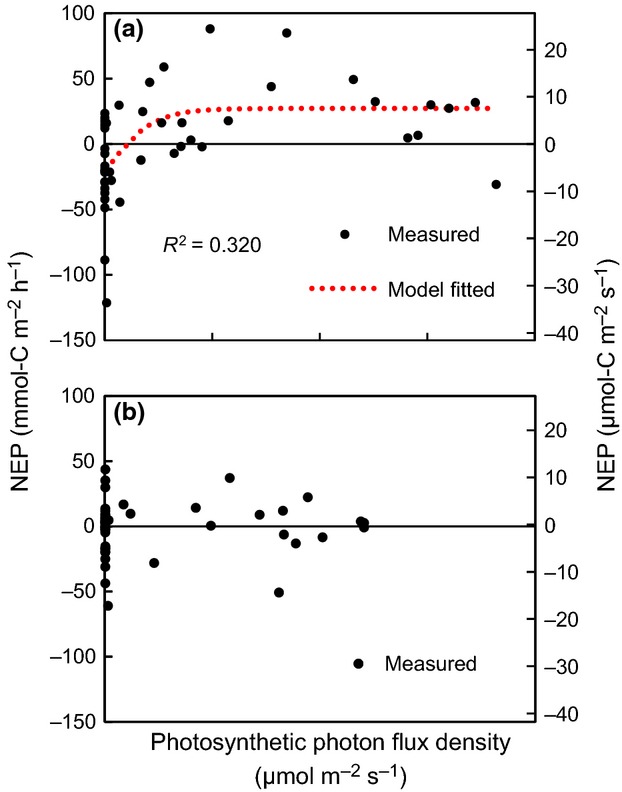
Net ecosystem production (NEP) at the boreal site in summer (a) and winter (b). The fitting of the photosynthesis–irradiance curve (red lines) to measured NEP was statistically significant (P < 0.0001) in summer but not in winter (P > 0.05).

Carbon burial rate

The sedimentation rate calculated from the linear average ¹⁴C age of the entire cores was 3.7 ± 1.8 mm yr⁻¹ (n = 3). The mass accumulation rate was estimated to be 238 ± 107 g m⁻² yr⁻¹ (n = 3). The TOC content of the top 1 cm of sediment was 2.8 ± 1.4% (n = 9). The carbon burial rate estimated from the sedimentation rate and the TOC content was then estimated to be 458 ± 156 mmol-C m⁻² yr⁻¹ (0.348 ± 0.119 μmol-C m⁻² s⁻¹) (n = 9).

Discussion

This study revealed that SAV systems, which hitherto have been regarded as a source of atmospheric CO₂, can function as a CO₂ sink by directly absorbing and sequestering atmospheric CO₂ (Fig.9). The direct sink of atmospheric CO₂ in shallow coastal water with SAV is regulated by the ecosystem metabolism, carbon input from land, and associated mineralization and respiration.

Figure 9.

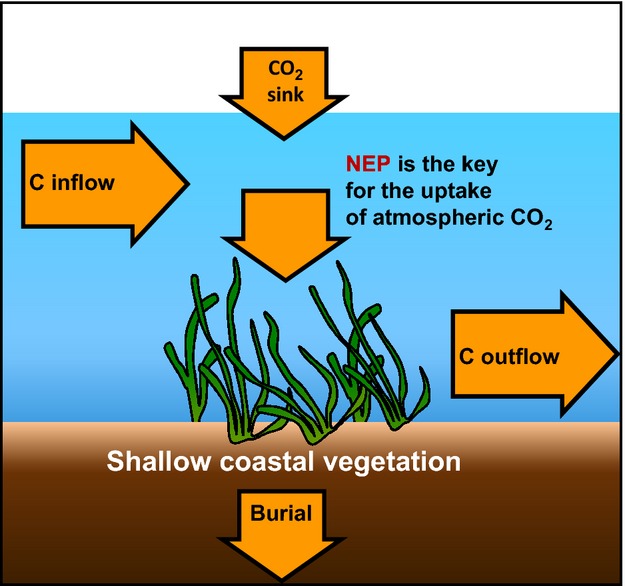
Summary of this study. The system of submerged aquatic vegetation (SAV) in shallow coastal waters was functionally a sink of overlying atmospheric CO₂. The key factor determining whether coastal ecosystems directly take up atmospheric CO₂ may be net ecosystem production.

We believe that the design of our measurements can provide a conservative estimate of a negative flux, i.e. the system functioned as a sink of atmospheric CO₂, although we acknowledge that estimation of an annual flux based on discrete measurements is associated with considerable uncertainty (Fig.4). The conservative nature of the estimate is based on our finding that seawater fCO₂ values were higher (lower influx of atmospheric CO₂ into the seawater) from early morning to noon, when the samples were taken, than during the afternoon (Fig.10a). These diurnal changes are explained by the net autotrophy of the biological community from sunrise to sunset, the result being a continuous uptake of DIC and fCO₂. Thus, our estimation of the net annual influx of atmospheric CO₂ at the boreal site, based on data collected from early morning to noon (including cloudy days), is basically conservative, given the fact that the flux is zero or slightly negative during the freezing season (Nomura et al., 2010).

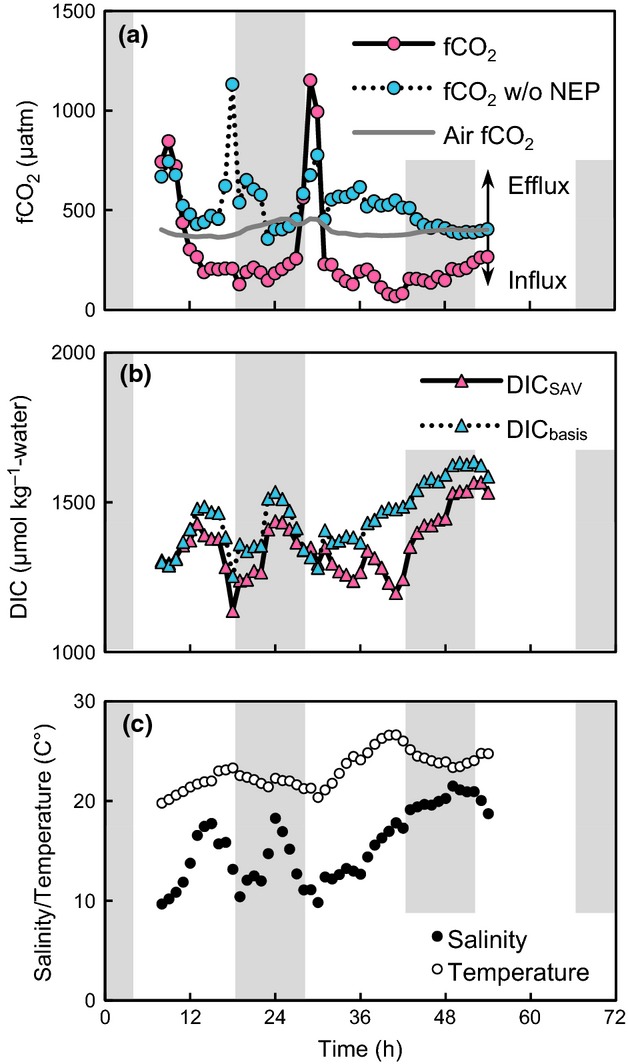
Representative data for the diurnal cycle of observed fCO₂ in the water and estimated fCO₂ in the water on the assumption that the NEP was zero (fCO₂ without NEP) at the boreal site in the summer of 2010 (a). Parameters related to fCO₂ in the water, such as DIC (DIC_SAV and DIC_basis in Eqn 4) (b), water temperature, and salinity (c) are also presented. Shading indicates the period of darkness. The peaks of fCO₂ in the water at about 10 and 30 h were caused by an intermittently high fCO₂ water inflow from the river, as indicated by the low salinity and moderate DIC at the time.

The difference in the air-sea CO₂ flux results between the three methods might stem from differences in the spatial scales of the measurements and differences in the exact positions of the measurement between the methods, in addition to differences associated with the advantages and limitations of each method (see Materials and methods). For example, the measurement area of the floating chamber method (<1 m²) was much smaller than that of the eddy covariance method (several hundred m² to several km²). This difference in area can highlight the possible spatial dependence of the real fluxes. Moreover, the footprint of the eddy covariance measurement is, in reality, located on the windward side of the instrument because of the nature of the measurement, the result being that the position representative of the measured flux might be offset from the other methods. We feel that quantitative analysis of the differences in flux values between methods, a phenomenon that has also been shown elsewhere (e.g. Zemmelink et al., 2009), should be a focus of future studies.

The importance of NEP as a sink for atmospheric CO₂ is supported by the significant correlation between the air-sea CO₂ flux and ΔDIC (Fig.5). SEM also showed that the variability in the air-sea CO₂ flux results was determined by geophysical and geographical factors as well as by ΔDIC (Fig.6). One of the major factors determining NEP is light intensity, which is implicitly included as an ‘unknown factor’ in the model. The diurnal changes of ΔDIC showed clear patterns that were related to light intensity (Figs7 and 8) as has also been indicated elsewhere (Gazeau et al., 2005).

Because the relative influence of DIC on ΔDIC was not high compared to the influence of other factors (Fig.6), it appears that NEP is less important than other factors in determining whether a body of water is a sink or source of CO₂ to the overlying atmosphere. However, NEP did contribute very much to the influx of atmospheric CO₂ by changing the balance of the two most important factors, TA and DIC, in the overall air-sea CO₂ flux. Below we use a theoretical analysis to deduce the impact of NEP on the air-sea CO₂ flux. Because DIC_basis and TA_basis (see Eqn 4) were estimated from the mixing of only river water and open ocean water, the fCO₂ values calculated on the basis of chemical equilibrium with DIC_basis and TA_basis ignore NEP. This fCO₂ without NEP (524 ± 10 μatm) at the boreal site in summer was higher than atmospheric fCO₂ (397 ± 3 μatm) during most of the measurement period (Fig.10). The implication of this result is that the site would be a net source of atmospheric CO₂ without NEP. Note that the net sink of atmospheric CO₂ at our sites is not due to incoming river water because in all three of the systems studied, the fCO₂ of the incoming river water (Furen: 3214 ± 2776 ppm; Kurihama: 642 ppm; Fukido: 910 ± 216 ppm) was higher than the fCO₂ at the measurement sites.

The balance of carbon input, NEP, buffer effect, and the residence time of water masses should be a driver of fCO₂ change in SAV systems and, consequently should determine whether the SAVs are a net sink or source of atmospheric CO₂ (Gazeau et al., 2005). However, the capacity of SAVs to take up atmospheric CO₂ may be underestimated in this study compared with the average capacity of seagrass meadows globally (Duarte et al., 2013). Even if one assumes that the annual average NEP at the boreal site equals the average of the estimated NEP in summer and winter (13 mmol-C m⁻² day⁻¹; Fig.8a, b), the annual NEP is smaller than the global average (Duarte et al., 2013) (Table1). Considering the previously discussed importance of NEP to the air-sea CO₂ flux, the global average atmospheric CO₂ influx may be higher than the average of our sites, given that the fact that the global average NEP is larger than the NEP of our sites. However, some sites have been reported to be atmospheric CO₂ sources, even under autotrophic conditions (e.g. Gazeau et al., 2005), a consequence of the high carbon input and the short residence time of the water masses.

Table 1.

Comparison of various rates related to carbon flow in different shallow vegetated ecosystems (mean ± standard error: mmol-C m⁻² day⁻¹)

	GPP	R	NEP	GPP/R	Carbon burial	Air–water CO2 flux
Global Mangroves	476*	426*	50*	1.12	32*	51§
Global Salt marshes	820*	459*	361*	1.79	34*	59§
Global Seagrasses	225 ± 11†	188 ± 10†,¶	27 ± 6†	1.20	0.6–45.2‡	ND
Boreal site (this study)	560 (summer)	509 (summer)	−21–52**	0.60–1.10	0.80–2.43	(−10–0.8: BF)
					(−6–5: FC)
					(−126–36: EC)††
Temperate site (this study)	ND	ND	ND	ND	ND	(−3: BF)††
Subtropical site (this study)	230–570‡‡	181–570‡‡	−123–49‡‡	0.73–1.27‡‡	ND	(10: BF)
					(10: FC)
					(−86: EC)††

GPP, gross primary production; R, net ecosystem respiration; NEP, net ecosystem production; ND, not determined. GPP in this study was calculated as NEP + R, assuming that R was the same during the day and night (Duarte et al., 2010).

^*From Duarte et al. (2005).

^†Converted from oxygen-based units (Duarte et al., 2010) to carbon-based units, assuming that both photosynthetic quotients and respiratory quotients are equal to 1.

^‡From Duarte et al. (2013).

^§From Borges et al. (2005).

^¶As net community respiration, i.e. excluding abiotic processes (Duarte et al., 2010).

^**Diurnally averaged value of estimated NEP.

^††Averaged value of the bulk formula method (BF), the floating chamber method (FC), and the eddy covariance method (EC).

^‡‡From Watanabe (2004).

Interannual measurement and numerical simulation of carbon flows in SAVs are required, given the inherently complex and dynamic environment of SAV systems (Champenois & Borges, 2012). For example, continuous measurements of incoming water carbonate systems and current velocities are needed to reduce uncertainty in the relationship between coastal carbon flows and SAVs.

We propose that the air-sea CO₂ flux is an important carbon sequestration process that should be taken into consideration. To date, carbon burial rates have been considered to be the most important flow for the stock of carbon because some atmospheric carbon can be sequestered in sediments for millennia (Mateo et al., 1997; McLeod et al., 2011; Fourqurean et al., 2012). However, the air-sea CO₂ flux is determined by the net carbon balance of the other fluxes: input, export, NEP, and burial (Fig.9). This implies that even if a certain SAV system is autotrophic (NEP >0) and evidences a high carbon burial rate, the system can function as a net source of atmospheric CO₂ if the carbon input rate is high. Our findings indicate that coastal conservation and restoration can be a means of mitigating climate change. Furthermore, our results should add a new ecosystem service to coastal ecosystems as a direct atmospheric CO₂ sink.