Detecting Local Residue Environment Similarity for Recognizing Near-Native Structure Models

Abstract

We developed a new representation of local amino acid environments in protein structures called the Side-chain Depth Environment (SDE). An SDE defines a local structural environment of a residue considering the coordinates and the depth of amino acids that locate in the vicinity of the side-chain centroid of the residue. SDEs are general enough that similar SDEs are found in protein structures with globally different folds. Using SDEs, we developed a procedure called PRESCO (Protein Residue Environment SCOre) for selecting native or near-native models from a pool of computational models. The procedure searches similar residue environments observed in a query model against a set of representative native protein structures to quantify how native-like SDEs in the model are. When benchmarked on commonly used computational model datasets, our PRESCO compared favorably with the other existing scoring functions in selecting native and near-native models.

Introduction

Structural similarities and commonalities at various levels have been found in protein tertiary structures. At a global structural level, there are abundant folds that arise from proteins with different evolutionary histories (superfolds)¹. At a smaller structural level, commonly occurring secondary structure arrangements have been found², which are often called super-secondary structures³. Moreover, common fragment conformations were found in structures from proteins with different folds^4-6. At the stereochemical structure level, interaction patterns of residues⁷ and bond angles in main-chains⁸ and side-chains⁹ have been extensively studied. Observed structural patterns are not only important for understanding physical nature of the protein structures but are also practically useful as a source of information for validating protein crystal structures¹⁰ as well as computationally predicted protein structure models.

In protein structure prediction, commonly occurring structure units (e.g. fragments) can be used as building blocks of protein structure models^11,12. Alternatively, observed structural patterns can be represented as scoring functions (e.g. knowledge-based statistical potentials) that guide modeling procedures^11,13-15 and are also used for selecting the native structure or near-native structure models (often called decoys) from a pool of alternative models^16,17. For example, pairwise residue contact potentials, which are derived from the statistics of physically contacting amino acid residues observed in representative protein structures, are one of the most frequently used scores for structure prediction^7,18,19. In addition to atom/residue contact potentials, various types of knowledge-based scores have been developed, which capture residues' or atoms' propensities of angles^20,21, accessible surface area²², and number of contacts²³, to name a few. Tasks of knowledge-based scores are, in principle, twofold: one is to build and select “protein-like” models, i.e. models that have geometrical features that agree with those in known structures. Another purpose is to construct sequence-specific structures by capturing local and global sequence-structure corresponding patterns (the extreme is homology modeling). It is ideal if a scoring function performs well for these two purposes simultaneously, but it is not an easy task. There are instances that the lowest energy states led by physics-based potentials are not close to the native structures of proteins²⁴.

In order to generate protein-like models that are also native structures, a scoring function must capture sequence-specific structural patterns while remaining sufficiently general to apply to multiple proteins. This can be achieved by describing structures at a level somewhere between the residue level and the whole protein level. Such structure representation should consider residues in their structural environment, which includes interactions with local and distant residues.

The concept of residue environment has been studied both computationally and experimentally over a decade. Manavalan and Ponnuswamy observed that surrounding residues for a certain residue have a biased distribution that reflects cooperativity of the residue pairs^25,26. Karlin et al. investigated the atom density, which was defined as the count of atoms within a certain distance from each residue, and found that the densities differ depending on the residue at the center²⁷. It was shown that the secondary structure prediction accuracy for residues with a high residue-wise contact order is worse than average, suggesting that distant contacts affect secondary structure formation²⁸. Experiments have also demonstrated that the environment affects the secondary structure of the same amino acid sequences^29,30. Following these observations, several groups developed scoring functions that describe residue environments or multi-residue interactions for protein structure predictions and structure-based function predictions. Along this line, knowledge-based contact potentials that consider interactions between three or four residues were developed^31-33. DeGrado and his colleagues developed an atom “microenvironment” potential, which consider the number of different types of atoms within a certain radius of a center atom³⁴. The Levitt group developed a hydrophobicity score that considers hydrophobic residue interactions within a sphere of 10 ų⁵. Simons et al. defined a residue environment as the number of residues within a 10 Å sphere and used it as a part of definitions of the scoring function for their ab initio protein structure prediction method³⁶. Mooney et al. used a residue environment representation that captures atoms within concentric spheres around a Cβ atom of a residue to recognize functional sites of proteins³⁷.

In this work, we developed a new representation of local amino acid environments in protein structures called the Side-chain Depth Environment (SDE). The SDE considers three important structural features of a residue environment: the side-chain centroids of a chain fragment centered on the target residue, the number of surrounding residues within a sphere around the target residue, and the depth of these surrounding residues. The residue depth quantifies location of a residue relative to the protein surface³⁸. We chose the residue depth as one of the structural features because it was shown to be an effective scoring term in a fold recognition method²². First, we show that SDEs capture the characteristic environment of each amino acid. Subsequently, we show that SDEs are general enough that similar SDEs are found in protein structures with globally different folds. Because similar SDEs are found in native protein structures of different folds, they can be applied for detecting near-native models from a pool of decoys. Given a structure model to be evaluated, the more residues of the model in SDEs similar to those in known native structures, the more likely the model is close to the native structure.

Using the SDEs, we developed a scoring procedure for selecting native or near-native models from a pool of decoys (decoy selection) named PRESCO (Protein Residue Environment SCOre). The protocol searches similar SDEs and a main-chain environment named the Main-chain Residue Environment (MRE) observed in a query model against a set of representative native protein structures. We benchmarked the ability of native and near-native model selection by PRESCO on decoy datasets that are commonly used for examining scoring functions for protein models. We show that our procedure compared favorably with the other existing scoring functions by significant margins.

Materials and Methods

Database of reference protein structures

We used a non-redundant protein dataset for investigating local structure similarity of proteins. The dataset was also used as a reference database for assessing protein structure models (decoys) using the residue environment scores. 4803 non-redundant protein structures with a resolution better than 2.0 Å and a pair-wise sequence identity of less than 30% between each other were downloaded from the PISCES server (Oct. 17, 2008 version)³⁹. This set was further reduced to 2536 proteins by removing chains with missing residues or missing backbone atoms.

Decoy sets for native/near-native structure recognition tests

To test how well the new residue environment scores perform in discriminating native or near-native models from other models with poorer quality, we used four decoy sets, the Decoy ‘R’ Us set⁴⁰, the Moulder decoy set⁴¹, the I-TASSER decoy set⁴², and the Rosetta decoy set⁴³. In addition, we also tested the residue environmental scores on the Fiser's CASP model set⁴⁴. Each set consists of subsets with a native protein structure associated with decoy structures. The Decoy ‘R’ Us set include eight sets, 4state_reduced, Fisa, Fisa_casp3, Lmds, Lattice_ssfit, hg_structal, ig_structal, ig_structal_hires that consists of 144 subsets in total, each of which contains the native structure of a protein and on average 271.19 decoys of the protein. The Moulder set has 20 subsets, each of which contains 319.3 decoys on average. The I-TASSER set consists of 56 subsets, which contain on average 438.2 decoys. The Rosetta sets has 58 subsets with 100 decoys. The Fiser set consists of 143 proteins used as prediction targets in the CASP5 to CASP8 and their prediction models. On average there are 18.3 models per target.

Removal of homologous proteins from the representative structure database

When the environment score was computed for a structure model, all database proteins that have more than 25 % sequence identity with the target protein are excluded from the database. Clustal Omega⁴⁵ was used for computing the sequence identity.

Local structural environment of residues, SDE

Characteristic physicochemical properties of each amino acid should reflect the structural environments of amino acids in native protein structures. To describe the environment of a residue, we wanted to consider the main-chain conformation around the residue of interest, the number of surrounding residues and their relative positions, and the depth of the surrounding residues from the protein surface. These features altogether capture multi-body interactions of residues in a comprehensive manner.

The residue depth is defined as the distance between a given residue and the nearest water molecule located close to the solvent-accessible surface³⁸. We used the side-chain to represent a residue position because the residue specificity originates from side-chains and the side-chain packing is a dominant factor of protein folding^15,46.

For a given residue in a protein structure, residues with a similar structural environment, SDE, in different proteins were identified by the following procedure:

1. Side-chain centroids of the target residue and structures in a reference database are computed. The side-chain centroid of a residue is the average positions of all heavy atoms in the side-chain. Atoms in the backbone are not included.

2. To ensure that residues locate in similar main-chain conformations, side-chains along local fragments are compared. Nine consecutive side-chain centroids along the protein backbone (four residues before and after the query residue) were compared with structures in the database and the 500 most similar fragments having the lowest root mean square deviation (RMSD) with the query fragments are kept for the subsequent steps. The rotation matrix and the translation vector used for aligning the two fragments are stored.

3. Next, neighboring residues within a sphere of an 8.0 Å radius centering on the side-chain centroid of the query residue are compared with those for the 500 fragments stored in Step 2. Fragments are discarded if the numbers of neighboring side-chain centroids in the two spheres are different. 8.0 Å was chosen because an early work showed a residue's cooperativity is effective up to 8.0 Ų⁶.

4. For each of the remaining fragments, one-to-one correspondence of neighboring side-chain centroids in the sphere to those in the query residue is computed. This is done by superimposing the neighboring centroids using the stored rotation matrix in Step 2 and pairing side-chain centroids of the two spheres by their distances.

5. Finally, the root mean square distance of the residue depth (residue-depth RMSD) of corresponding neighboring side-chain centroids is computed.

Thus, similarity in residue environment indicates that the residues share similar main-chain conformation and the same number of neighboring residues that are located at similar depth in the protein structures (Figure 1).

Figure 1.

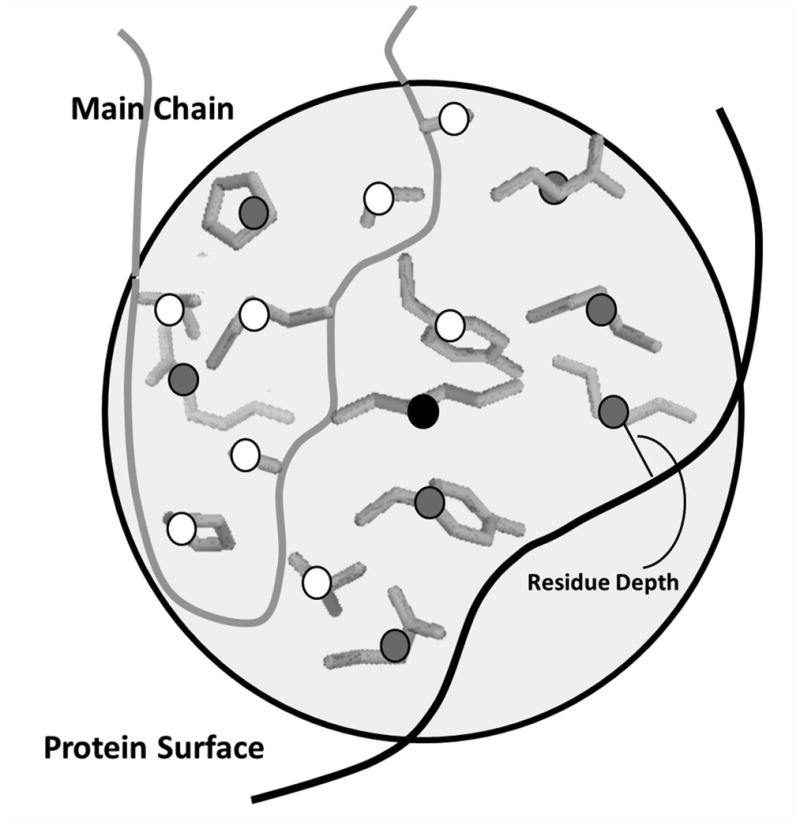
Side-chain depth environment (SDE). The SDE of an amino acid (black circle) is defined as the depth of the side-chain centroids within a sphere of 6.0 or 8.0 Å (gray and white circles) from the center amino acids. To find similar SDEs from a database, the RMSD of nine side-chains (white circles) including the center one, the number of side-chain centroids in the sphere, and the residue depth of the side-chains are considered.

Results

Characterization of SDEs in representative native protein structures

To begin with, we examined SDEs of amino acid residues in representative native protein structures. Figure 2 shows the distribution of the number of side-chain centroids within the sphere of 8.0 Å for each amino acid residues. Consistent with previous works⁴⁷, the number of neighboring residues clearly reflects hydrophobicity of amino acids. Isoleucine and valine, the two most hydrophobic amino acids according to the Kyte-Doolittle hydrophobicity scale⁴⁸, show the highest median, followed by leucine, phenylalanine, and alanine, which are also highly hydrophobic amino acids (Figure 2A). In contrast, hydrophilic amino acids have the least number of neighboring residues; these include arginine, lysine, asparagine, aspartic acid, glutamine, and glutamic acid. The average number of neighboring residues of each amino acid has a significant Pearson's correlation coefficient of 0.793 to the Kyte-Doolittle hydrophobicity scale.

Figure 2.

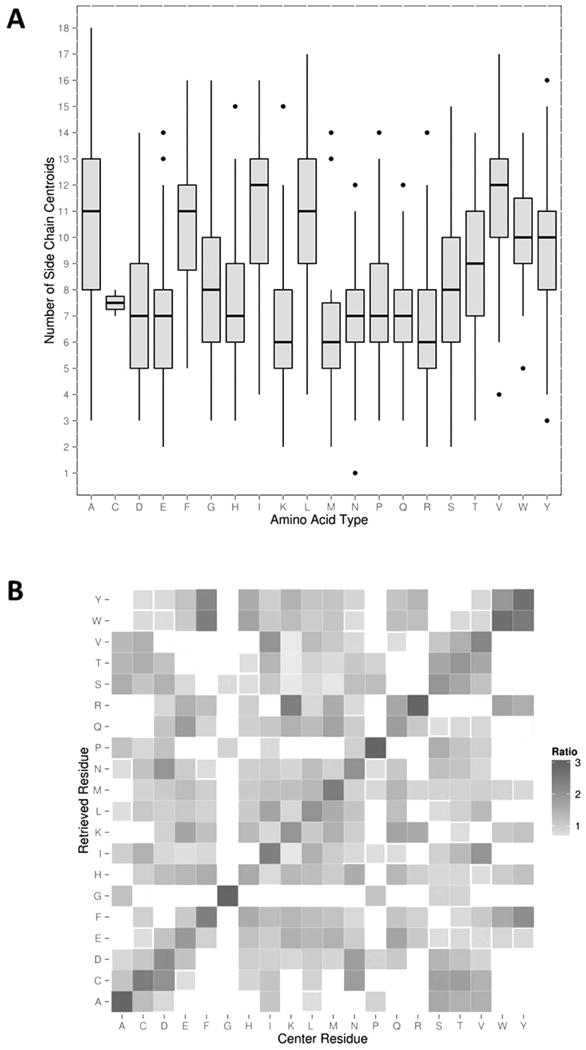
Characteristics of SDEs. (A) The distribution of the number of side-chain centroids in the sphere of an 8.0 Å radius for each residue type shown in a box-and-whisker plot. The bar inside the box shows the median and the two ends of the box show the first and third quartiles. Outliers (shown as dots) are defined as more than 1.5 times the interquartile range (the third quartile minus the first quartile) outside the first or third quartiles. (B) Residues with similar SDEs identified by database searches for each residue type. For the SDE of each residue in each protein in the reference database, the top 40 most similar SDEs in terms of the residue depth RMSD were retrieved. Then fraction of 20 different residues retrieved for each residue type was computed and normalized by the overall fraction of the residue in the reference database. The color scale shows the enrichment, the darker the higher ratio of the residue relative to the background fraction.

In Figure 2B, we examined residues that have similar SDEs for each residue type. The color scale indicates enrichment of the amino acid type among residues with similar SDEs. Concretely, the enrichment is computed as the fraction of each amino acid among the top 40 most similar residues divided by the background fraction of the amino acid. In all the amino acids except for glutamine, the identical amino acids (shown in the diagonal positions in the heat map) have the largest enrichment. In the case of glutamine, glutamic acid came to the top with a ratio of 1.88 and the glutamine itself was the close second with 1.83. Amino acids that are different but have similar physicochemical properties to the query amino acid tend to have an enrichment ratio over 1.0. Such examples include arginine, which had lysine with the second largest enrichment (2.44) and isoleucine, which had valine with the second largest enrichment. The highest enrichment, 6.88, was observed for glycine with itself. Proline also showed a high enrichment of 5.01 with itself. To summarize, Figure 2A shows that the number of side-chains within a sphere of 8.0 Å radius, which is used as a filtering step for finding similar SDEs, mainly contains the hydrophobicity information of residues whereas the residue depth (Figure 2B) further encodes residue-specific environment features. These results suggested that the SDE can be used for designing a scoring function for quantifying native-likeness of computational protein structure models.

Similar SDEs are found in proteins with globally very different structures (Figure 3). Figure 3A shows the distribution of the residue depth RMSD of surrounding side-chain centroids of SDEs in comparison with the global RMSD of protein structures where the two SDEs were taken from. For a SDE, the depth RMSD and the global RMSD of protein structures for the top 5 most similar SDEs were plotted. Global RMSDs were computed by Bioshell⁴⁹. It is shown that the proteins with similar SDEs have very different global structure (on average around 13 Å) and the depth RSMD and the global RMSD have virtually no correlation. The same conclusion was drawn when we compared the conventional RMSD of side-chain centroids in SDEs against the global RMSD of the protein structures (Figure 3B). Thus, not only the depth RMSD but also the constellation of side-chains in SDEs does not have correlation to the global RMSD of the protein structures.

Figure 3.

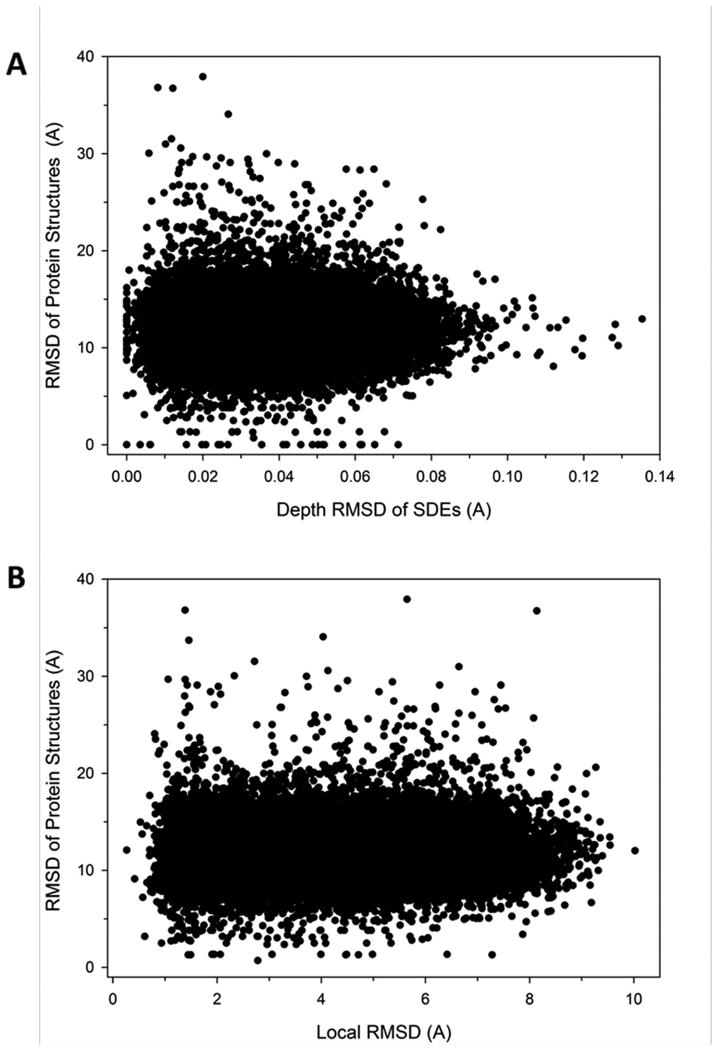
Global structural similarity of proteins that have similar side-chain environments. (A) Global coordinate RMSD of protein structures whose residue has similar SDEs. For each residue in the reference protein database, five most similar residues to the query residue in terms of SDEs were selected. Their depth RMSD of the side-chains in a sphere of 8.0 Å and the global RMSD of the whole protein structures were computed. Global RMSD was computed with BioShell, which computes RMSD of gapped structure alignment between two proteins. (B) For the same residue pairs shown in the plot A, the conventional RMSD of the neighboring side-chain centroids were compared with the global RMSD of the proteins.

In Figure 4 we show examples of similar SDEs found in proteins with different folds. In all cases the pairs have a small depth RMSD, ranging from 0.022 to 0.037 Å. In the first example (Figure 4A), SDEs taken from helices of two different fold class (left: 1iib, an αβ class protein; right: 1ykh, α class) are shown. They have seven side-chains in the SDEs and their depth RMSD is 0.022 Å. In the second example (Figure 4B), similar SDEs are taken from globally different folds. Six residues are included in the SDEs, which are located at an end of a helix. The next SDE pair (Figure 4C) includes 13 residues that are distant in sequences. The SDE in 1e6i consists of residues in three α-helices while the one from 1bqcA have residues from two α-helices and one β-strand. In the last pair (Figure 4D), two SDEs are taken from different secondary structure combinations: on the left, side-chains are taken from β-sheets and two α helices in 1ew4, while the SDE on the right (2bj0A) consist of residues from two β-sheets.

Figure 4.

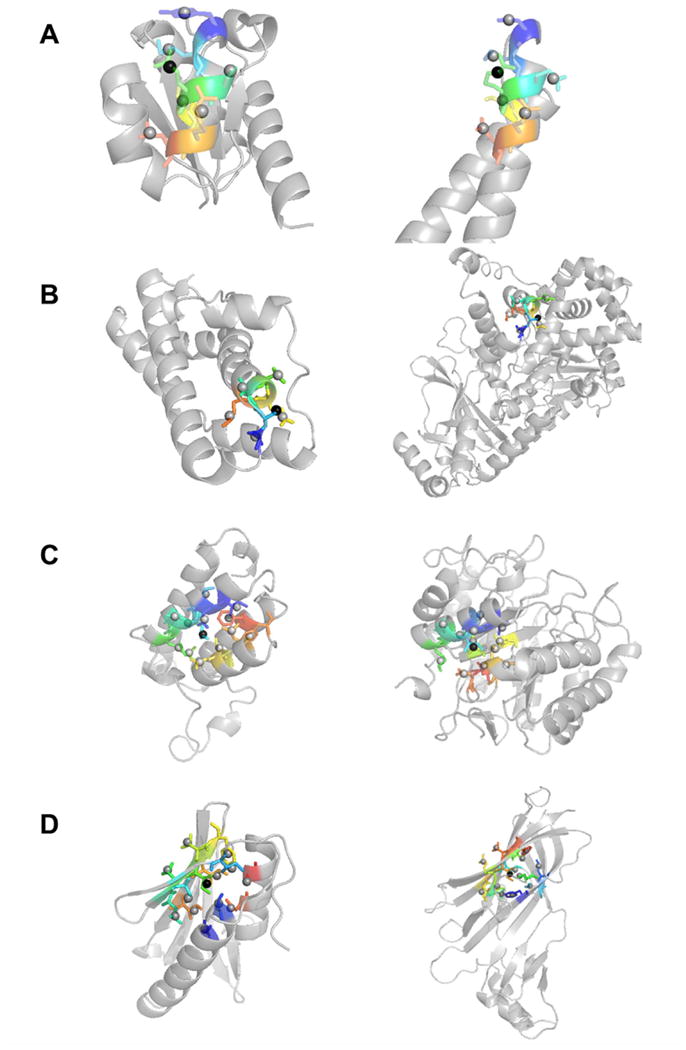
Examples of similar SDEs. Residues included in SDEs are shown in color. (A) SDE of residue 64 (Glu) of IIBcellobiose (PDB code: 1iib) (left) and residue 146 (Arg) of RNA polymerase II mediator complex protein MED7 (1ykh, chain A) (right). The center side-chain is shown in black spheres. 8.0 Å was used for the sphere to define SDEs. Both SDEs contain seven side-chain centroid points of neighboring residues (shown in the stick representation). The residues are 60, 61, 63, 64, 65, 67, and 68 for 1iib and 32, 33, 35, 36, 37, 39, and 40 from 1ykhA. The depth RMSD (dRMSD) of the two SDEs is 0.022 Å. (B) Residue 40 (Ser) in fertilization protein (1lis) and residue 312 (Ser) of Anthrax lethal factor (1yqyA). Six residues are included: residue 39, 40, 41, 42, 43, 44 for 1lis and 311, 312, 313, 314, 315, 316 from 1yqyA dRMSD: 0.023 Å. (C) SDEs of residue 12 (Leu) in bromodomain of GCN5 (PDB: 1e6i) and residue 71 (Ile) of β-mannose (1bqcA). 13 residues are in the SDEs, 8, 9, 11, 12, 13, 15, 16, 46, 49, 50, 53, 58, and 64 for 1e6i and 67, 68, 70, 71, 72, 74, 75, 81, 83, 113, 114, 117, and 121 for 1bqcA The depth RMSD is 0.037 Å. (D) Residue 41 (Ile) of map kinase 14 (1ew4) and residue 196 (Ile) of tetracycline repressor (2bj0A). 13 residues are included. 1ew4: 39, 40, 41, 42, 43, 17, 21, 30, 32, 49, 51, 91, 95; and 2bj0A 194, 195, 196, 197, 198, 31, 33, 50, 137, 139, 161, 175, 177. dRMSD: 0.035 Å.

Procedure of selecting native/near-native models

In this section, we describe the procedure to evaluate decoys and to select ones from a pool of decoys that are likely to be the native or close to the native structures. Briefly, in the scoring procedure named PRESCO (Protein Residue Environment SCOre) a count will be accumulated for a query model if residues in the model have similar environments to those of similar amino acid type in representative native structures. In addition to the SDE, we introduce another environment score, the Main-chain Residue Environment (MRE), which considers main-chain fragment conformation around the target residue. In the decoy selection procedure, similarity of both SDEs and MREs of target residues to representative proteins are considered. Before providing the steps of computing PRESCO, we explain the MRE.

The MRE compares the main-chain conformation of the fragment of five residues centered on the target residue against fragments in the database of representative proteins. The similarity of two fragments is quantified by the RMSD of four main-chain heavy atom positions (N, Cα, C, and O) and the Cβ position of all the residues in a fragment. This representation was shown to perform better than a Cα representation of fragments in identifying amino acid patterns that fold into the fragment conformation⁵⁰. For glycine, a pseudo Cβ atom position is computed using the TINKER package⁵¹.

Figure 5 gives the overall PRESCO procedure. For each of the residues in a query model, MRE and two SDEs of different radii, 8.0 Å and 6.0 Å, are computed. They are then compared with those for residues in a structure database, as represented in the three branches in the flowchart. The left most branch explains steps to compute a score that comes from comparison of MREs of the target model to those in the representative protein structure database. As described in the Method section, the database consists of 2536 non-redundant native protein structures. For a MRE computed for a residue in the query model, the 25 closest (i.e. lowest RMSD) MREs in the database are retrieved and sorted by their RMSD. This process is done for all the fragments in the model (L-4 fragments, where L is the length of the model). Because fragments are taken by a sliding window that moves by one residue at a time, a residue in the middle of the protein will be covered by 25 × 5 = 125 fragments, while residues close to the terminus of the chain have fewer fragments. The MRE-based score given to an amino acid position in a model is the weighted average of the amino acid similarity score between the amino acid in the query fragment and each of retrieved fragments. Amino acid similarity score is defined by an amino acid similarity matrix chosen for MRE. A weight is assigned to each retrieved fragment, which reflects similarity of the fragment to the query fragment. The weights and an amino acid similarity matrix used were determined by a small benchmark study described in the next section. Taken together, a MRE-based score of a query model is computed as

Figure 5.

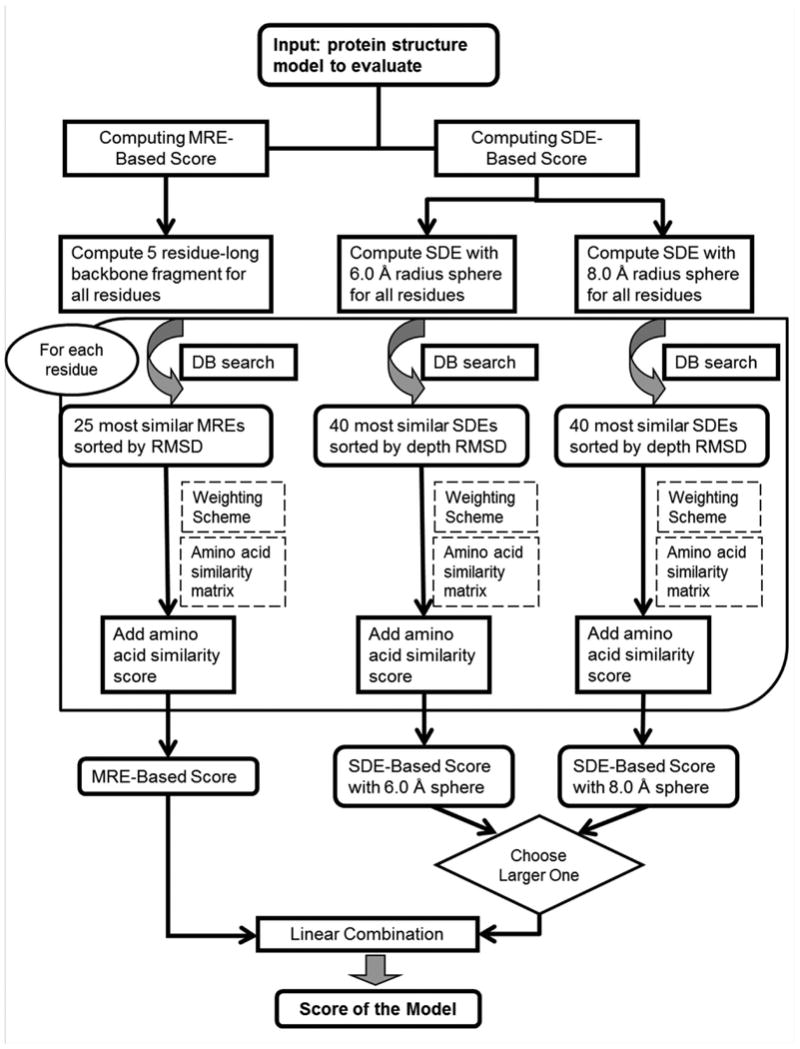
Schematic diagram of the PRESCO scoring system for evaluating decoys. For each residue in a decoy to be evaluated, two residue environments, MRE and SDE, are constructed and compared against residues in the database of representative proteins. Two sphere sizes, 8.0 Å and 6.0 Å, are used for SDE. Similar MRE/SDEs found in the database are sorted according to their similarity to that of the target residue. A score for a target residue is a weighted sum of the amino acid similarity score, and the score of the decoy is the sum of the score given to each residue. See text for more details.

$$\text{MRE\_based\_Score}=\sum _{\mathrm{i}=1}^{\mathrm{L}}\sum _{j=1}^K{w}_j{M}_{a_i-a_j(i)},$$ (Eq. 1)

where L is the length of the model, K is the number of fragments that cover the residue i. K=125 if the position i is between 5 to L-4, while K reduces to 25*i if i < 5 (N-terminus) and 25*(L-i+1) if i > L-4 (C-terminus). w_j is the weight given to the j-th fragment and M_ai-aj(i) is the amino acid similarity score taken from the matrix M for the amino acid at the position i in the query model and the amino acid in the fragment j that is aligned with amino acid i of the query.

The second and the third branches represent computation of scores by comparing SDEs in the query models to the representative structure database. For each residue in the query model, two SDEs are constructed with radii of 6.0 Å and 8.0 Å. It was found that the score with the 8.0 Å radius gave more correct native structure selections than 6.0 Å but 6.0 Å worked better for a certain smaller fraction of the cases (data not shown). Then, following the procedure to find similar SDEs as described above, for each residue the 40 most similar (i.e. smallest depth RMSD) SDEs to the query SDE are selected. Then, similar to the branch for MRE, a score is computed for the query residue, which is the weighted sum of the amino acid similarity values between the query residue and residues retrieved in the database search. The score for a query model is the sum of the residue-based score:

$$\text{SDE\_based\_Score}=\sum _{\mathrm{i}=1}^{\mathrm{L}}\sum _{j=1}^N{w}_j{S}_{a_i-a_j},$$ (Eq. 2)

where N=40, the number of SDEs retrieved from the database and S_ai-aj is the amino acid similarity score taken from a matrix S for residue i in the query and residue j retrieved from the database. The SDE-based scores for a query model is computed with the 6.0 Å (the middle branch in Figure 5) and the 8.0 Å (the right branch) radii separately, which are subsequently compared and a larger one is chosen. Finally, the MRE- and the SDE-based scores will be linearly combined to yield the final score of the query model. The weighting scheme for the linear combination is discussed in the next section. The two scores based on MRE and SDE complement each other. The MRE assesses how native the structure is in terms of local main-chain fragment similarity, while the SDE evaluates the structure from the view point of side-chain packing.

Weighting schemes and amino acid similarity matrices

The combinations of weights and amino acid similarity matrices used in the PRESCO model evaluation procedure (Figure 5) were determined based on the native structure selection test performed on 30 decoy target sets, which were randomly chosen from the Rosetta decoy set⁴³. A decoy target set in the Rosetta set consists of one native structure and 100 decoy structures with varied RMSDs to the native structure of a protein. Using different weighting schemes and amino acid similarity matrices in Eqns. 1 and 2, we examined how many times the native structure was selected with the highest score among the 30 decoy sets.

Three weighting schemes were tested:

1. RMSD-based weights: the weight w_i to a retrieved i-th MRE or SDE is computed based on the RMSD value of the main-chain fragment to the query environment for MRE and side-chain centroids in the sphere for SDE. It is inversely proportional to the power α of the RMSD.

   $${\mathrm{w}}_{\mathrm{i}}=1/{(\text{RMSD})}^{\alpha }$$ (Eq. 3)

   Thus, retrieved MRE/SDE with a small RMSD has a larger weight. 11 values, 0.005, 0.01, 0.05, 0.1, 0.2, 0.5, 0.7, 0.8, 0.9, 1.0, and 2.0, were tested for α.

2. Rank-based weights: MREs/SDEs retrieved from the database are ranked by their RMSD (MREs) or the depth RMSD (SDEs) to the query. Then, each MRE/SDE is weighted according to its rank:

   $${\mathrm{w}}_{\mathrm{i}}=\stackrel{1}{}/\underset{\left\{\lfloor n_i/\beta \rfloor +1\right\},}{}$$ (Eq. 4)

   where n_i is the rank of the MRE/SDE. For MRE, n_i will range between 1 to 25 while it ranges between 1 to 40 for SDE. ⌊·⌋ is the floor function which takes the largest integer that does not exceed the inside value, and β is a parameter. Four values, 1, 2, 5, 10, and 15 were tested for β.

3. Exponential weights: The weight decays as the rank of MRE/SDE decreases:

   $${\mathrm{w}}_{\mathrm{i}}=exp(-\gamma \ast (n_i-1)/(N-1)),$$ (Eq. 5)

   where γ is the parameter to be optimized, n_i is the rank of MRE/SDE, N is the total number of retrieved environments for a query, i.e. 25 for MRE and 40 for SDE. Six values between 0.5 and 2.5 were tested for γ: 0.5, 0.7, 0.8, 0.9, 1, 1.5, and 2.5.

Seven amino acid similarity matrices were tested. These matrices are labeled as BLOSUM30⁵², QU_C1 (QU_C930101)⁵³, QU_C2 (QU_C930102)⁵³, QUIB (QUIB020101)⁵⁴, KOLA (KOLA920101)⁵⁵, CCPC⁵⁶, and CC80⁵⁶. Shown in parentheses are the ID in the AAIndex database⁵⁷ if the matrix is indexed. Except for BLOSUM30, which is a standard matrix for sequence alignment, the other six matrices were chosen because they performed well in computing aligning distantly related protein sequences⁵⁶. These matrices capture amino acids' preference of structural contexts in protein tertiary structures. QU_C1 and QU_C2 capture amino acid residue contact propensities. KOLA is based on the similarity of the dihedral angles of amino acids. QUIB was numerically optimized to minimize the average RMSD of aligned proteins in benchmark databases. CCPC is based on the correlation coefficients of an amino acid residue contact potential, while CC80 is a linear combination of CCPC and KOLA.

Selecting weight and matrix combinations on the 30 decoy sets

First, we benchmarked the combinations of the weights and matrices on the 30 Rosetta decoy sets in terms of their native structure recognition ability. Figure 6A and 6B show the results of using the MRE and the SDE, respectively. BLOSUM30 showed higher success rates for the MRE than for the SDE with many weight combinations. CCPC is another matrix that performed better for the MRE than the SDE particularly with the exponential weights (Eq. 5). On the other hand, QU_C1, QU_C2, and KOLA performed better for the SDE than the MRE. Among the weights tested, RMSD-based weights (a) of 0.5 or larger consistently performed poorly while large exponential weights (γ) of 1.0 or larger gave a high native recognition rate for several matrices for both MRE and SDE. The highest number of successful native recognition was 17, which was achieved by CCPC when applied to the MRE as well as QU_C2 and QUIB applied to the SDE.

Figure 6.

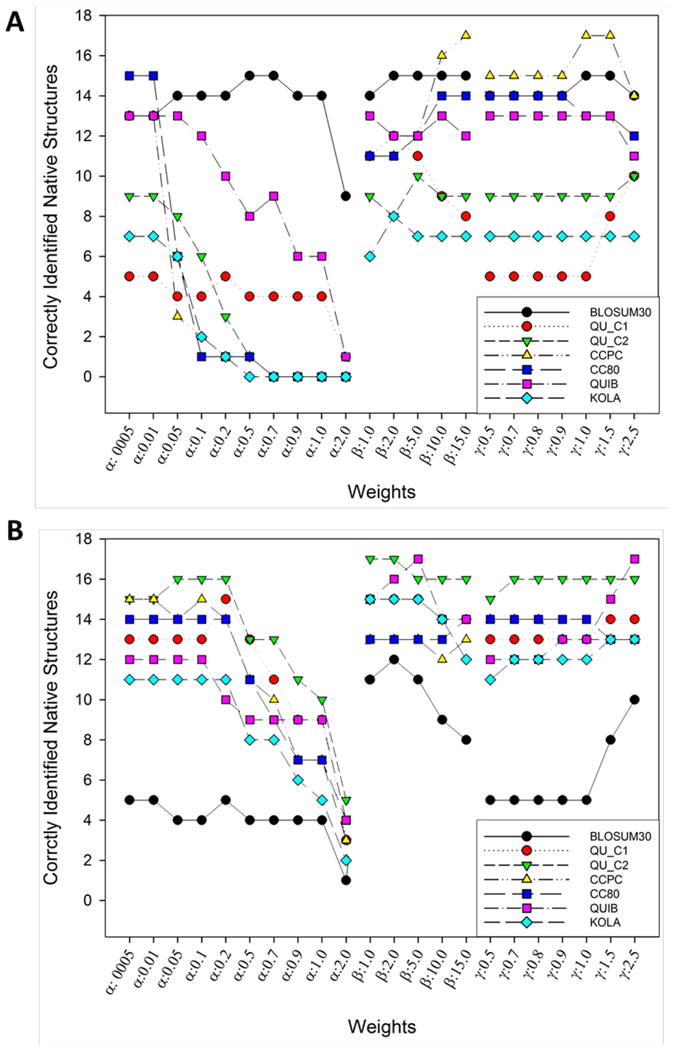
The number of successfully identified native structures in 30 Rosetta decoy sets. Seven matrices were tested in combinations with 22 weights for native structure recognition. α is a parameter for the RMSD-based weight (Eq. 3); β is a parameter for the rank-based weight (Eq. 4); and y is a parameter for the exponential weight (Eq. 5).

From these results, we have chosen all the weight and matrix combinations that gives over 15 native recognitions from both MRE (Fig. 6A) and SDE (Fig. 6B), and further tested linear combinations of the MRE and the SDE in the native recognition:

$$\mathit{\text{Combined\_Score}}={\mathit{\text{MRE}}}_i+w\ast {\mathit{\text{SDE}}}_j,$$ (Eq. 6)

where MRE_i and SDE_j are one of the selected weight-matrix combinations from MRE and SDE. w is a weight value that ranged from 0.05 to 10.0 with an interval of 0.05.

Among the linear combinations tested, combinations of BLOSUM30 (exponential weight, γ = 1.5) for the MRE and QU_C2 (γ = 1.0) for the SDE with weight values between 1.15 to 1.45 or 1.7 to 2.05 gave the largest number of native recognition of 24. We found that all the Combined Scores that recognized native structures 22 or more consisted of a limited variety of matrices. BLOSUM30 (ranked-based weight with β = 10 or exponential weight with γ = 1.5), CC80 (RMSD-based weight with α=0.01), and QUIB (exponential weight with γ = 1.5) were selected for the MREs, while the following eight were selected for the SDEs: CC80 (RMSD-based weight with α=0.01), CCPC (RMSD-based weight with α=0.01), QU_C1 (ranked-based weight with β = 10), QU_C2 (RMSD-based weight with α=0.01; ranked-based weight with β = 1.0 or 2.0; and exponential weight with γ = 1.0 or 1.5). Therefore, we only used these matrix and weight combinations for MREs and SDEs in the subsequent analyses.

Native structure recognition test

Using the selected MREs and SDEs, we tested the native recognition ability of the scores on a larger dataset. The dataset consists of five previously published decoy sets (see Materials and Methods). This is a standard dataset for testing potentials and scoring functions, which has been used by several recent papers^33,42,58,59. We tested our scores in two ways. First, we concentrated on the ability to select native structures from decoys as done in a previous work⁴². Then we examined RMSD and TM-score⁶⁰ of selected decoys when native structures are not included in the dataset, as this is more close to realistic scenarios in protein structure prediction. As described in Materials and Methods, for each query protein, all similar protein structures were removed from the database if they have more than 25% sequence identity to the query. The performance of the native/decoy selection by our scores was compared with seven other knowledge-based statistical potentials, DFIRE⁶¹, dDFIRE⁶², DOPE⁶³, RW, RWplus⁴², OPUS-PSP⁵⁸, and GOAP⁵⁹. For our residue environment scores, the best performing MRE and SDE in terms of the total number of native structure recognition, CC80 and QUIB, respectively, as well as the three best linear combinations of MRE and SDE are shown. The results are summarized in Table I.

Table I. Performance of native structure recognition.

Decoy Sets	DFIRE a)	dDFIRE	DOPE	RW	RWplus	OPUS-PSP	GOAP	MRE (CC80) b)	SDE (QUIB) c)	Combinations of MRE & SDE d)			# Target s e)
										BLSM30 +QU_C2	BLSM30 +QU_C2	CC80+ QU_C1
4state_reduced	6 (-3.48)f)	7 (-4.15)	7 (-3.66)	6 (-3.45)	6 (-3.51)	7 (-4.49)	7(-4.38)	7 (13.60)	7 (3.68)	7 (8.88)	7 (9.07)	7 (8.50)	7
Fisa	3 (-4.87)	3 (-3.80)	3 (-3.91)	3 (-4.87)	3 (-4.79)	3 (-4.24)	3 (-3.97)	2 (1.16)	2 (4.13)	2 (3.46)	2 (3.44)	3 (3.51)	4
Fisa_casp3	4 (-4.80)	4 (-4.83)	3 (-5.06)	4 (-5.22)	4 (-5.17)	5 (-6.33)	5 (-5.27)	2 (3.67)	1 (3.10)	3 (4.41)	3 (4.45)	4 (4.03)	5
Lmds	7 (-0.88)	6 (-2.44)	7 (-1.34)	7 (-1.20)	7 (-1.03)	8 (-5.63)	7 (-4.07)	10 (8.20)	6 (4.25)	10 (8.86)	10 (9.04)	10 (7.70)	10
Lattice_ssfit	8 (-9.44)	8 (-10.12)	8 (-7.43)	8 (-8.15)	8 (-8.85)	8 (-6.75)	8 (-8.38)	8 (7.38)	8 (7.77)	8 (8.66)	8 (8.69)	8 (7.09)	8
hg_structal	12 (-1.97)	16 (-1.33)	----g)	----	12 (-1.74)	18 (1.87)	22 (-2.73)	28 (5.14)	11 (1.27)	27 (3.82)	27 (3.89)	27 (4.13)	29
ig_structal	0 (0.92)	26 (-1.02)	----	----	0 (1.11)	20 (0.69)	47 (-1.62)	61 (7.69)	6 (0.28)	61 (6.93)	61 (6.97)	61 (7.11)	61
ig_structal_hires	0 (0.17)	16 (-2.05)	----	----	0 (0.32)	14 (-0.77)	18 (-2.35)	20 (4.35)	6 (0.09)	20 (4.17)	20 (4.18)	20 (4.21)	20
Moulder	19 (-2.97)	18 (-2.74)	19 (-3.09)	19 (-2.79)	19 (-2.84)	19 (-4.84)	19 (-3.58)	20 (13.58)	16 (2.87)	20 (6.73)	20 (6.90)	20 (7.20)	20
ROSETTA	20 (-1.82)	12 (-0.83)	21 (-1.61)	20 (-1.62)	20 (-1.47)	39 (-3.00)	45 (-3.70)	25 (1.90)	31 (2.20)	41 (2.91)	41 (2.91)	39 (2.74)	58
I-TASSER	49 (-4.02)	48 (-5.03)	30 (-2.18)	53 (-4.42)	56 (-5.77)	55 (-7.43)	45 (-5.36)	56 (9.61)	47 (3.43)	56 (7.30)	56 (7.38)	56 (7.20)	56
#Total	128	164	98/168	120/168	135	196	226	239	141	255	255	255	278
(Z-score)	(-1.94)	(-2.52)	(-2.47)	(-3.23)	(-2.13)	(-2.86)	(-3.57)	(6.78)	(2.14)	(5.70)	(5.76)	(5.65)

The largest values for each dataset are shown in bold.

^a)Values for DFIRE to GOAP were taken either from the paper by Zhou & Skolnick (2011) or by Zhang & Zhang (2010).

^b)Results of MRE using CC80 (RMSD-based weight, α = 0.01), which showed the largest number of successful native recognition at #Total among preselected four MREs, is shown.

^c)SDE using QUIB (exponential weight, γ=2.5), which performed best among eight selected SDEs.

^d)Three combined_scores shown are BLOSUM30 (γ=1.5)+2.05*QU_C2(γ=1.0), BLOSUM30 (P=10)+2.9*QU_C2(γ=1.5), and CC80 (α=0.01)+0.85*QU_C1(β=5.0).

^e)The number of subsets in each decoy set is shown. A subset consists of the native structure of a protein and decoy structures.

^f)The number in a parenthesis is the average Z-score of the native structure among decoy structures. Values of DFIRE to GOAP are negative because the potentials are negative values for favorable atom interactions while MRE and SDE have positive scores for native structures.

^g)Values for DOPE and RW are left empty for hg_structal, ig_structal, and ig_stractal_hire because the paper by Zhang & Zhang (2010) which showed the results for DOPE and RW did not have results for those.

The performance of our residue environment-based scores, particularly the combinations of MRE & SDE, was better than the other potentials in terms of the total number of correctly recognized native structures. Among the 278 decoy targets in total, the Combined Scores successfully recognized native structure for 255 cases. The MRE (CC80) performed better than the SDE and the three Combined Scores gave further improvement, which is consistent with what we observed for the 30 Rosetta decoy set. Noticeable improvement relative to the other scores was made in the native selection for the datasets of Lmds, Moulder, I-TASSER, ig_structal, and ig_structal_hires. For these five sets, our residue-environment scores recognized native structures perfectly; all 10 natives in the Lmds, 20 natives in the Moulder, 56 natives in I-TASSER, 61 natives in ig_structal and 20 natives in ig_structal_hires decoy sets. MRE also successfully identified 28 natives in hg_structal decoy set. Two of our Combined Scores performed also well for the ROSETTA set, recognizing 41 out of 58, second to GOAP.

The performance by MRE on the hg_structal, ig_structal and ig_structal_hires sets (109 native recognitions) are noticeable, which is more than 25% increase from that of the previous best performing potential, GOAP (87 native recognitions). These three decoy sets are products of high accurate homology modeling⁴⁰. The average RMSD of the decoy models to its native are 2.38 Å (ig_structal), 2.55 Å (ig_structal_hires), and 4.10 Å (hg_structal). In Table I, it was observed that the accurate native recognition mainly come from MRE. By a close investigation, interestingly, MRE's performance was found to be nearly independent of the choice of substitution matrix and weighting schemes. (CCPC(β =10): 107, blosum30(γ =1.5): 110, CC80(α =0.01): 109, QU_C1(β =2.0): 109, QU_C2(γ =1.5): 109, QUIB(γ =0.9): 110 natives were successfully recognized by MRE).

It is also worthwhile to note that our residue-environment scores recognized native structures with high Z-scores compared to the others. For the Lmds set, the second Combind Score showed the highest Z-score of 9.04, while the MRE score achieved 13.58 for the Moulder set. The MRE score also showed significantly high Z-score of 13.60 for the 4state_reduced set and 9.61 for the I-TASSER set. The Z-scores by MRE for the 4_state_reduced set is three times higher than OPUS-PSP, which recognized the same number of natives. In the case of the I-TASSER set, the Z-score of 9.61 by MRE is almost twice higher than RWplus that recognized the same number of natives (56). This noticeable Z-score difference is equally observed in the hg_structal, ig_structal, and ig_structal_hires decoy sets. Our MRE results showed the highest Z-scores, 5.14 (hg_structal), 7.69 (ig_structal) and 4.35 (ig_structal_hires), which is on average more than two times better results than those of the second best one, GOAP. The three combinations of MRE and SDE also presented similar results.

Average global RMSD and TM-score of decoys

Next, we calculated the quality of top scored decoy structures (excluding the native structures) by our residue environment scores (Table II). The Rosetta decoy set, which was the most difficult in the native structure recognition in Table I, as well as the I-TASSER set were used. For the Rosetta set, the SDE with QUIB showed the smallest RMSD for all Top-1, Top-5, and Top-10. It also showed the best (largest) TM-score for Top-1 and Top-5, and the second best TM-score (0.553) for Top-10. The combined score of CC80 and QU_C1 (rightmost column) performed second best to the SDE in terms of RMSD for all Top-1, Top-5, and Top-10. The MRE with CC80, which performed better than the SDE for the native structure recognition (Table I) did not perform well for the decoy selection.

Table II. Average RMSD and TM-score of decoys.

Decoy Sets		DFIREa)	DOPE	RW	RWplus	MRE (CC80)b)	SDE (QUIB)	Combinations of
								MRE & SDE
								BLSM30 +QU_C2	BLSM30 +QU_C2	CC80+Q U_C1
ROSETTA Decoys	Top-1	7.36	7.43	7.62	7.48	7.90	6.63	7.06	7.04	6.82
		(0.469)	(0.466)	(0.460)	(0.464)	(0.452)	(0.489)	(0.488)	(0.489)	(0.492)
	Top-5	6.08	6.10	6.04	6.01	6.18	5.63	5.97	5.99	5.76
		(0.533)	(0.536)	(0.537)	(0.525)	(0.517)	(0.541)	(0.531)	(0.531)	(0.534)
	Top-10	5.79	5.85	5.78	5.76	5.61	5.42	5.71	5.63	5.53
		(0.559)	(0.555)	(0.560)	(0.560)	(0.545)	(0.553)	(0.548)	(0.551)	(0.553)
I-TASSER Decoys	Top-1	5.61	5.31	5.22	5.19	6.04	5.26	5.25	5.28	5.18
		(0.558)	(0.560)	(0.569)	(0.575)	(0.539)	(0.570)	(0.559)	(0.558)	(0.574)
	Top-5	4.45	4.21	4.30	4.29	4.62	4.26	4.30	4.31	4.36
		(0.612)	(0.613)	(0.616)	(0.608)	(0.593)	(0.622)	(0.608)	(0.610)	(0.605)
	Top-10	3.95	3.89	3.89	3.89	4.24	3.98	4.10	4.12	4.12
		(0.632)	(0.631)	(0.633)	(0.625)	(0.609)	(0.635)	(0.622)	(0.619)	(0.620)

Native structures were excluded from the datasets. The best RMSD (Å) and the TM-score (in parentheses) within Top 1, 5, 10 decoys selected by each scoring function are shown.

^a)Data for DFIRE to RWPlus are taken from the paper by Zhang & Zhang (2010).

^b)the same configurations at Table I were used for MRE, SDE, and the combinations.

For the I-TASSER decoy set, the combined score with CC80 and QU_C1 showed the smallest RMSD for Top-1 rank. In the case of Top-5 and Top-10, DOPE⁶³ was the best in the RMSD, and the SDE was a close second. SDE also was the best in terms of TM-score for Top-5 and Top-10. Overall, we can conclude that the SDE performed the best for selecting low RMSD and large TM-score decoys.

Correlation coefficient of energy scores with TM-score of models

This test was done to examine near-native model selection performance of the scoring functions. Therefore, native structures were not included in the decoy set. Pearson's correlation coefficient (CC) of the scores with TM-scores of models as well as the average TM-score of the top-scoring models of each decoy sets were reported in Table III.

Table III. Average Pearson's correlation coefficient of energy score with TM-score and average TM-score of selected models.

Decoy Sets	DFIREa)	RWplus	dDFIRE	OPUS-PSP	GOAP	MRE (CC80) b)	SDE (QUIB)	Combinations of MRE & SDE			# Targets
								BLSM30+	BLSM30+	CC80+QU
								QU_C2	QU_C2	_C1
4state_reduced	-0.635 0.659	-0.606 0.667	-0.693 0.732	-0.589 0.755	-0.694 0.818	0.065 0.353	0.660 0.745	0.423 0.700	0.420 0.700	0.365 0.645	7
Fisa	-0.446 0.449	-0.462 0.434	-0.461 0.454	-0.282 0.405	-0.347 0.475	0.310 0.419	0.410 0.447	0.433 0.478	0.436 0.478	0.401 0.411	4
Fisa_casp3	-0.243 0.288	-0.240 0.277	-0.149 0.309	-0.095 0.270	-0.221 0.300	0.179 0.295	0.325 0.303	0.310 0.324	0.306 0.324	0.312 0.336	5
Lmds	-0.118 0.333	-0.147 0.346	-0.248 0.364	-0.091 0.339	-0.146 0.339	0.014 0.350	0.148 0.334	0.055 0.350	0.056 0.361	0.061 0.353	10
Lattice_ssfit	-0.094 0.247	-0.097 0.251	-0.070 0.266	-0.051 0.248	-0.058 0.248	0.007 0.242	0.118 0.274	0.080 0.240	0.078 0.254	0.069 0.263	8
hg_structal	-0.817 0.890	-0.806 0.891	-0.796 0.891	-0.752 0.891	-0.825 0.889	0.265 0.802	0.801 0.889	0.758 0.881	0.756 0.882	0.699 0.879	29
ig_structal	-0.785 0.945	-0.782 0.948	-0.766 0.948	-0.779 0.953	-0.865 0.946	0.245 0.923	0.832 0.939	0.738 0.935	0.744 0.934	0.715 0.937	61
ig_structal_hires	-0.876 0.947	-0.879 0.950	-0.844 0.946	-0.832 0.946	-0.885 0.944	0.343 0.933	0.897 0.939	0.823 0.945	0.827 0.943	0.799 0.941	20
Moulder	-0.859 0.734	-0.840 0.745	-0.881 0.748	-0.802 0.738	-0.886 0.771	0.198 0.409	0.900 0.774	0.811 0.721	0.809 0.725	0.743 0.707	20
ROSETTA	-0.441 0.507	-0.444 0.505	-0.393 0.480	-0.343 0.506	-0.476 0.511	0.163 0.484	0.307 0.525	0.281 0.522	0.277 0.523	0.317 0.527	58
I-TASSER	-0.519 0.571	-0.488 0.577	-0.525 0.578	-0.284 0.547	-0.477 0.567	0.102 0.541	0.503 0.570	0.395 0.559	0.393 0.558	0.387 0.574	56
All average	-0.613 0.689	-0.605 0.692	-0.601 0.691	-0.521 0.688	-0.632 0.697	0.185 0.632	0.598 0.697	0.523 0.688	0.523 0.689	0.510 0.690	278

Native structures are excluded from all sets. Bold character entries are the best results in the respective decoy set. The first number in each cell is the Pearson correlation coefficient; the second number is the TM-score of lowest energy (highest score in our case) selected model.

^a)The values for DFIRE, RWplus, dDFIRE, OPUS-PSP, and GOAP were taken from the paper by Zhou & Skolnick (2011).

^b)The same configurations at Table I were used for MRE, SDE, and the combinations.

The best results in CC among our scores came from SDE results, 0.598. SDE using the QUIB matrix showed the largest CC among all scores in the fisa_casp3, Lattice_ssfit, ig_structal_hires, and Mourlder sets. However, GOAP and the other three potentials showed slightly larger average CC values. In terms of the average TM-score of the top-scoring model, SDE showed the largest value of 0.697, which is a tie with GOAP. This result indicates that SDE is good at selecting near-native decoys on average, which was consistent for SDE with the results in Table II and Table III. Combinations of MRE and SDE gave similar results with the SDE.

Examples of correlations of the residue environment score and the RMSD of decoys are shown in Figure 7. In these three decoy sets, native structures were recognized with significantly higher MRE, SDE, and Combined Scores compared to the decoys. The MRE score (left panels) had weak correlation to RMSD of decoys; however, the score gap between native structures and decoy structures was larger than the SDE. The SDE had larger correlation to RMSD than the MRE, and the combined scores had comparable correlation coefficients to the SDE.

Figure 7.

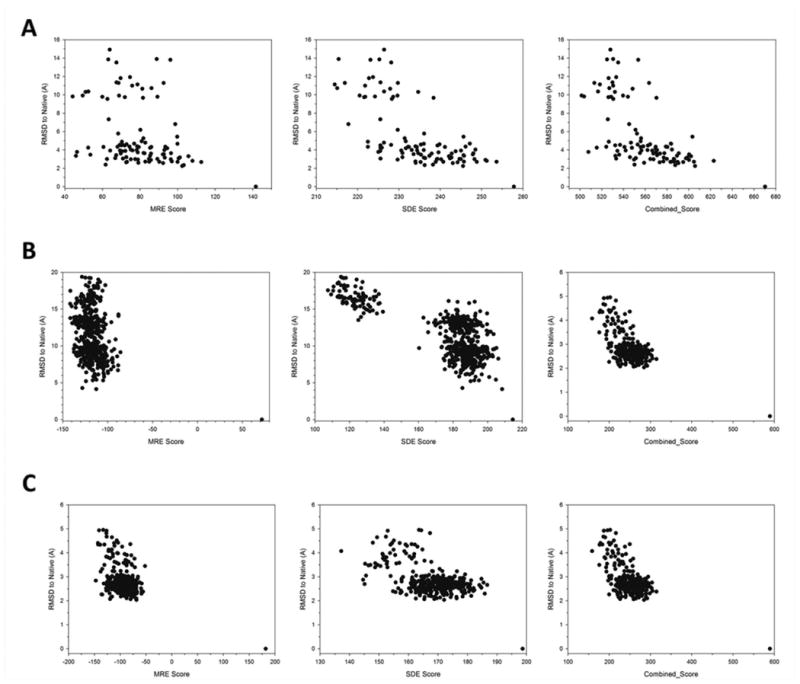
Examples of correlation between the environment scores and RMSD. RMSD of decoys are plotted relative to the residue environment scores for decoy sets of three proteins. Left, MRE (CC80 with γ=1.5); middle, SDE (QU_C2 with γ=2.0); Combined Score with MRE (CC80 with γ=1.5) and SDE (QU_C2 with γ=2.0) with a weight value of 2.05 were used. (A) 2chf from the Rosetta decoy set; Correlation coefficients (CC) are -0.31, -0.67, and -0.62, respectively from left to right. (B) 1gnuA from the I-TASSER decoy set. CC are -0.31, -0.74, and -0.77, respectively. (C) 1csp from the I-TASSER decoy set. CC are -0.50, -0.55, and -0.63, respectively.

Performance on the Rykunov & Fiser's CASP model sets

We further tested the residue environment scores on prediction models submitted to the Critical Assessment of Techniques for Protein Structure Prediction (CASP) 5 to 8, which were compiled by Rykunov & Fiser⁴⁴ (Table IV). We show results of the same MRE and SDE and three combined scores shown in Table I and II. In addition, results of two extra combined scores that exhibited good performance are shown. The first one is a combination of MRE with BLOSUM30 and SDE with QU_C1 and the second one is a linear combination of two SDEs with CC80 and BLOSUM30. We wanted to try a combination of two SDEs because the SDE score performed well in model recognition in the absence of native structures (Table II, Table III, Figure 7).

Table IV. Performance on the Rykunov and Fiser CASP5-8 decoy set.

Scoring Function		Models only		Native included
		Average Rank a)	Ranked 1b)	Average Rankc)	ranked 1d)
MRE (CC80) e)		6.77	29	1.32	131
SDE (QUIB)		2.89	56	1.98	97
Combinations of MRE & SDE	BLSM30+QU_C2	5.59	39	1.60	121
	BLSM30+QU_C2	5.62	38	1.78	118
	CC80+QU_C1	5.07	37	1.92	113
	BLSM30+QU_C1	6.79	31	1.18	139
	CC80(SDE)+BLSM30(SDE)	2.82	66	1.99	89
Random		9.72	13.9	10.1	8.3

Values of the best performance are highlighted in bold.

^a)The average rank of lowest energy (highest scored; in the case of our residue environment scores) decoy by GDT_TS score in the absence of native structure.

^b)The number of sets when the best model was ranked as first in the absence of native structure.

^c)The average rank of the lowest energy (highest scored; in the case of our residue environment scores) decoy by GDT_TS when native structures are present.

^d)The number of sets when the best model was ranked as first when native structures are present.

^e)MRE using CC80 (RMSD-based weight, α = 0.01) and the SDE using QUIB (exponential weight, γ=2.5). In addition, results of five combined scores are shown. The first three are the same combinations of a MRE and a SDE as shown in Tables 1 and 2: BLOSUM30 (γ=1.5)+2.05*QU_C2(γ=1.0), BLOSUM30 (β=10)+2.9*QU_C2(γ=1.5), and CC80 (α=0.01)+0.85*QU_C1(β=5.0). The last two are new combined scores: Blosum30 (β =10.0)+1.15*QU_C1(β =5.0), and the last one combines two scores from SDEs, CC80(α =0.01)+6.7*Blosum30 (β =2.0).

When the native structures are included (the right half of the table), the combination of BLOSUM30 and QU_C1 showed the smallest average rank (1.18) and the largest number of successful recognition of native structures (139). MRE performed better than SDE. When native structures were excluded (the left half of the table), different scoring functions showed up as top performing. The two SDE score combinations, CC80 and BLOSUM30, had the best average rank of 2.82 followed by SDE alone. Thus, SDE consistently performed well in the model recognition in the absence of native structures as observed in Table II, Table III, and Table IV.

Examples of different performance of PRESCO and pairwise potentials

Here we show examples from the native selection test (Table I) that illustrate the characteristic PRESCO's performance in comparison with the existing statistical potentials. In Table V, we show native selection results of four decoy sets, for which PRESCO showed significantly better performance than the other potentials. For the Lmds decoy sets of 1bba and 1fc2, both MRE and SDE selected the native at the top rank among 501 decoys in the dataset while the native was ranked almost at the bottom by the other four potentials. Indeed, 1bba and 1fc2 are small proteins and known as difficult decoy sets as several existing potentials^58,61,64-66 failed to recognize the native structures among the decoys. The two decoys sets, 1fbi and 3hfm, in the Ig_structal set present the same story: MRE recognized the native at the top and SDE identified the native at the 4^th and 14^th for 1fbi and 3hfm, respectively, while the other potentials ranked the native almost at the bottom of the rank.

Table V. Illustrative performance of PRESCO.

Decoy Set	PDB ID	DFIRE	RWplus	OPUS-PSP	GOAP	MRE	SDE
Lmds	1fc2	500/501 a)	501/501	409/501	489/501	1/501	1/501
	1bba	501/501	501/501	501/501	501/501	1/501	1/501
Ig_structal	1fbi	61/61	59/61	57/61	46/61	1/61	4/61
	3hfm	59/61	59/61	57/61	55/61	1/61	14/61

^a)The rank of the native structures (left) among the total number of decoys (right) is shown.

In Figure 8, we closely investigated the difference between SDE and two potentials, GOAP and DFIRE, which are well-known and widely used potentials. For the 1fc2 decoy sets, GOAP selected a decoy with an RMSD of 4.42 Å (1fc2.60276.pdb) with the lowest (i.e. best) energy, -5445.20 (-126.6 per residue), while the native structure has a GOAP energy of -4072.89 (-94.7 per residue). Figure 8A shows the breakdown of the energy difference of individual residues in the decoy and the native by SDE, MRE, GOAP, and DFIRE. Residues with the negative energy difference (y-axis) have a lower (thus preferred) energy for the native over the decoy. It is shown that GOAP has only 13 residues among 43 residues that have a lower energy in the native than in the decoy, while SDE preferred the native over the decoy for 25 residues. We further focused our attention to Residue 12, isoleucine (ILE12) because the evaluation of this residue's conformation by SDE and GOAP were very different: SDE strongly preferred the native structure for this residue over the decoy with the residue-wise energy of -618.3 (native) and 155.3 (decoy), while GOAP gave a preferable, negative residue-wise energy (-197.2) for the decoy. The side-chain centroid position of ILE12 in the decoy is 7.37 Å away from its correct position when the decoy is superimposed with the native, and consequently, ILE12 is in a very different environment in the decoy in comparison with the native: It is exposed outside in the decoy (Fig. 8B, residues in red) while it is buried in the core in the native (Figure 8C). Although an exposed hydrophobic residue is in general not preferred, ILE12 in the decoy has negative energies by GOAP (Figure 8D) partly because of interactions with neighboring hydrophobic residues, PHE26, LEU30, and LEU41, all of which deviated from their correct positions by 3.41, 1.55, and 3.82 Å, respectively (Figure 8E). On the other hand, SDE correctly considered the native, buried environment is more preferable than the exposed environment in the decoy for ILE12. In Table VI, top 5 most similar residue environments for ILE12 in the native and the decoy structure that were identified by SDE are summarized. In the case of ILE12 in the native, all the five identified environments are centered on hydrophobic amino acids, isoleucine or leucine, which locate at packing interfaces of helices and loops in protein structures that are globally different from 1fc2. In contrast, similar environments of ILE12 in the decoy are all exposed, including those which are centered on glutamic acid residues. Thus, SDE clearly distinguished very different environments of ILE12 in the native and in the decoy structures.

Figure 8.

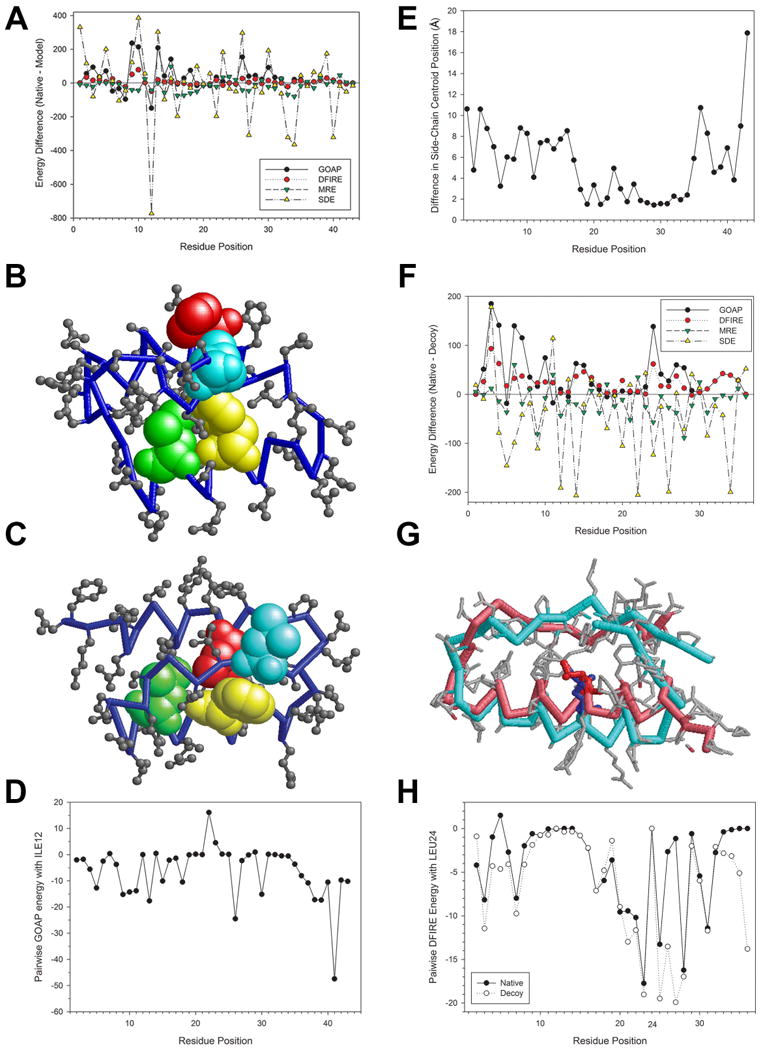
Examples of residue-wise energies by SDE and other potentials. Two decoy sets included in the Lmds set, 1fc2 and 1bba, were used. As shown in Table V, SDE and MRE successfully identified the native structure among 501 decoys for these two decoy sets. A to E are comparison between the SDE and GOAP energies at individual residues in the native structure of 1fc2 and the lowest GOAP energy decoy, 1fc2.60276.pdb. F to H are comparison between the SDE and DFIRE energies at each residue in the native of 1bba and the lowest DFIRE energy decoy, 1bba.1697.pdb. (A) Energy difference at each residue between the native 1fc2 and the decoy 1fc2.60276.pdb by GOAP, DFIRE, MRE, and SDE. The y-axis shows the residue-wise energy difference between the native and the decoy. A negative value indicates that the residue has a lower energy in the native than the decoy. SDE and MRE scores are negated so that they have the same sign as the other two potentials. (B) The structure of the decoy 1fc2.60276.pdb. ILE12 is shown in red, and three residues that have preferable GOAP energy between 1LE12, namely, PHE26, LEU30, and LEU41 are shown in yellow, green, and cyan, respectively. (C) The native structure of 1fc2. ILE12, PHE26, LEU30, and LEU41 are shown in the same colors as in the panel B. (D) The pairwise GOAP energies between ILE12 and the other residues in the decoy 1fc2.60276.pdb. (E) The Euclidean distance of side-chain centroids of each residue in the native and the decoy after the two structures are superimposed by the LGA program. A high distance (y-axis) indicates that the residue position in the decoy is far off from its correct position. (F) Energy difference at each residue between the native 1bba and the decoy 1bba.1697.pdb by GOAP, DFIRE, MRE, and SDE. (G) Superimposition of the native structure (pink) of 1bba and the decoy 1bba.1697.pdb (cyan). LEU24 are shown in the stick representation in red and blue in the native and the decoy, respectively. (H) Pairwise DFIRE energies between LEU24 and each residue in the native (filled circles) and in the decoy 1bba.1697.pdb (open circles).

Table VI. Top 5 most similar environments identified by SDE.

Target Residue	Rank	Native
		PDB ID	Res. Pos.a)	AA Type b)
ILE12 in 1fc2 (native)	1	2ahmA c)	44	ILE
	2	2bgiA	173	LEU
	3	1iznA	21	ILE
	4	1p3dA	317	LEU
	5	1m15A	181	LEU
ILE12 in a decoy 1fc2.60276.pdb d) (lowest energy by GOAP)	1	2b81A	142	ALA
	2	1uddA	93	GLU
	3	2c31A	22	MET
	4	1ykhA	133	LEU
	5	1m5wA	146	GLU
LEU24 in 1bba (native)	1	1ub9A	91	LEU
	2	1ppjC	160	LEU
	3	1fxkC	121	ILE
	4	1bh9A	61	VAL
	5	1n5uA	183	ASP
LEU24 in a decoy 1bba.1697.pdb e) (lowest energy by DFIRE)	1	1x8yA	370	ASP
	2	1bh9A	62	ILE
	3	2a61A	128	ILE
	4	1txlA	210	GLU
	5	1vf7A	81	GLN

Top five most similar residue environments of the target residues in the native and in the lowest energy decoy (defined by GOAP/DFIRE) were selected by SDE.

^a)Residue position.

^b)Amino acid type.

^c)According to SDE, ILE44 of 2ahmA has the most similar residue environment with the target residue, ILE12 in the native structure of 1fc2.

^d)1fc2.60276.pdb was selected by GOAP as the lowest energy decoy among the decoy set. Because ILE12 has a different residue environment in the decoy from that in the native, the five most similar environments are different from those for ILE12 in the native.

^e)1bba.1697.pdb was selected by DFIRE as the lowest energy decoy among the decoy set.

In the panels F-H in Figure 8, performance of SDE is compared with DFIRE. A decoy with an RMSD of 6.07 Å (1bba.1697.pdb) is selected as the lowest energy by DFIRE. Figure 8F shows that DFIRE (red) considered that the majority of the residues (33 out of 36 residues) have a lower energy in the decoy than in the native. In contrast, SDE energy is lower in the native, often substantially lower, than in the decoy for many residues (21 out of 36 residues). For 1bba, we further investigate energies for LEU24, because SDE and MRE evaluated energy of this residue very differently from DFIRE and GOAP (Figure 8F): DFIRE and GOAP strongly preferred the decoy over the native while SDE and MRE considered the native is more preferable structure for this residue. From the structure imposition of the native and the decoy (Figure 8G), difference of environment of LEU24 in the native and decoy is not very obvious, although two helices in the native are packed slightly tighter than those in decoys. A close examination of the pairwise DFIRE energy between LEU24 and each residue (Figure 8H) shows that the energy profile for the native and the decoy are almost the same with some difference observed for residue 25 to 27, which have lower energy in the decoy than in the native. On the other hand, SDE preferred the native for LEU24 to the decoy, which is also evident in the top five most similar environments for LEU24 detected by SDE (Table 5). The four most similar environments to LEU24 in the native are those from hydrophobic amino acids that locate inside of proteins, while similar environments for LEU24 in the decoy included exposed residues.

The purpose of showing the examples is to illustrate the performance of PRESCO in comparison with pairwise potentials. Of course PRESCO's performance was not always better than the two potentials in the entire benchmark test; nevertheless the examples show the advantage that the residue environment-based score can achieve.

Discussion

We have developed two residue environment sores, the Main-chain Residue Environment (MRE) and the Side-chain Depth Environment (SDE). The Protein Residue Environment Score (PRESCO), which uses MRE and SDE, compared favorably against existing knowledge-based statistical potentials in recognizing native and close-to-native decoys. Notably, MRE and SDE have complementary strength: MRE performs well in identifying native structures (Table I, Table V) while the SDE score has better correlation to the RMSD of decoys and thus works better in recognizing near-native decoys when native structure is not included (Table II, Table III, Table IV).

As scoring decoys is a central problem in protein structure prediction, various potentials have been developed for the native structure/near-native decoy selection. In contrast to most of the knowledge-based statistical potentials that capture preference of pairwise interactions between atom or atom groups including the potentials compared with PRESCO in the current work, PRESCO was designed to capture multi-body interactions of residue side-chains. It was shown that such residue environments captured by PRESCO exist in proteins of different folds. PRESCO does not need the reference state, which is often problematic in designing statistical potentials. Through this work we have shown that considering residue environments for capturing multi-body interactions may be a promising alternative direction to the conventional two-body statistical potentials for protein structure prediction and modeling. Similar ideas of residue environment scores will be also effectively applied for validating crystal structures of proteins and for protein design.