Abstract
Mathematical modeling can be a valuable tool for studying infectious disease outbreak dynamics and simulating the effects of possible interventions. Here, we describe approaches to modeling cholera outbreaks and how models have been applied to explore intervention strategies, particularly in Haiti. Mathematical models can play an important role in formulating and evaluating complex cholera outbreak response options. Major challenges to cholera modeling are insufficient data for calibrating models and the need to tailor models for different outbreak scenarios.
11.1 Introduction
Even though early studies of cholera have become exemplars of modern epidemiology (e.g., Snow (1855); Koch (1886, 1893)), predicting and managing cholera outbreaks is still a major challenge in the developing world. Improvements in sanitation and the use of oral rehydration therapy have greatly reduced the burden of disease, but we lack a predictive framework for anticipating outbreaks and planning for interventions. Mathematical modeling is one approach to synthesizing our knowledge of cholera into a quantitative framework. Mathematical models have been used to study the dynamics of disease outbreaks and predict the effectiveness of potential intervention strategies (Garnett et al, 2011; Hutubessy et al, 2011).
Recommendations for the response to cholera outbreaks have evolved over the past decade. Earlier guidelines emphasized case management and discouraged the use of vaccines until post-emergency (Connolly, 2005). Later, pre-emptive vaccination was proposed for use during complex emergencies (Chaignat and Monti, 2007), and mass vaccination was being considered for containing outbreaks (Global Task Force on Cholera Control, 2010). However, vaccination is usually not a practical option because of the small global supply of cholera vaccine. Recent massive and prolonged outbreaks of cholera in Haiti and several countries in Africa renewed interest in creating a global cholera vaccine stockpile, which would increase availability of the vaccine for emergency use as well as for seasonal epidemics (Waldor et al, 2010; World Health Organization, 2010, 2012; Holmgren, 2012; International Vaccine Institute, 2012; Martin et al, 2012). But even if more vaccine were available, there is a lack of guidance for its use. Mathematical modeling can help fill this gap.
As the options for cholera outbreak responses become more complex, there is a greater need for quantitative frameworks such as mathematical modeling to both evaluate and help formulate them (Clemens, 2011). In particular, the ongoing multiyear epidemic in Haiti has challenged us to plan for more comprehensive, integrated, and long-term strategies for cholera outbreaks that would involve improved identification and treatment of cases, increased access to clean water, and vaccine (Ivers et al, 2010; Farmer et al, 2011). Because cholera vaccine has rarely been used during an outbreak, modeling may be needed to extrapolate what little has been observed. Because there are many competing needs for scarce resources during complex emergencies, modeling may be required to help weigh the costs and benefits of different options (Miller Neilan et al, 2010). In this chapter, we describe how mathematical models have been applied to study cholera.
11.2 Mathematical Models of Cholera Transmission
Here, we describe basic mathematical models of cholera transmission, then we discuss approaches to making more detailed cholera outbreaks models, including the addition of contaminated water supplies, spatial effects, within-household transmission, and interventions.
11.2.1 Modeling Cholera Transmission Within a Well-Mixed Population
Basic mathematical model of infectious disease transmission describe the transitions of individuals among susceptible, infectious, and recovered states. In a susceptible-infected-recovered (SIR) model, susceptible individuals become infected at a rate proportional to the number of infected individuals, infected individuals recover at a constant rate, and recovered individuals are immune to infection (Kermack and McKendrick, 1927). To account for the incubation period of a disease, one may introduce a transient “exposed” state for infected individuals before they become infectious (e.g., an SEIR model). This basic model generates a single epidemic peak, but variants that include the waning of immunity or the introduction of new susceptibles can produce cyclical dynamics (Hethcote, 2000).
This basic modeling framework can be adapted to specific infectious agents by tuning infectiousness and recovery rate parameters to match the known natural history parameters or outbreak dynamics of a pathogen. A mathematical model of cholera could include an incubation period of a few hours to a few days and an infectious period of one or two weeks (Longini et al, 2007; Chao et al, 2011). To include multi-season dynamics, waning immunity can be added to the model (e.g., an SIRS model) (Koelle and Pascual, 2004; Koelle et al, 2005; Rinaldo et al, 2012). One may also add symptomatic and asymptomatic infections, which could play different roles in disease transmission and surveillance (Longini et al, 2007; King et al, 2008; Nelson et al, 2009; Andrews and Basu, 2011).
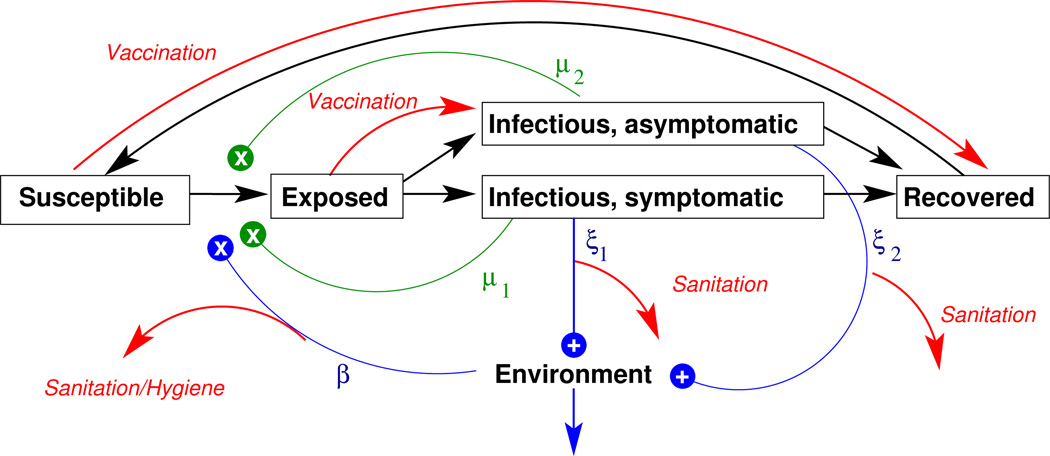
Many cholera models assume that individuals become infected by consumption of V. cholerae from the environment and therefore include an explicit environmental compartment (Codeço, 2001; Tien and Earn, 2010). A susceptible individual’s risk of infection, λ, at time t can be expressed as λ(t) = μI(t) + βB(t), where μ is the rate of exposure between individuals, I(t) is the number of infectious individuals at time t, β is the rate of exposure to the environment, and B(t) is the level of contamination of the environment. Note that the first term is proportional to the number of infectious individuals, and we refer to this as the ciclo corto (“short cycle”) transmission pathway. This route is also known as “person-to-person” transmission and accounts for infections occurring during the short time window of an infected close contact’s infectious period. The second term is proportional to the level of contamination in the environment and is also known as ciclo largo (“long cycle”) transmission, which could be caused by exposure to sewage or contaminated water not necessarily traceable to an infected contact. A cholera model can include either or both of these terms. Inserting the environment into the chain of cholera transmission can create a lag in the generation time and allows for cholera transmission to occur in the absence of infected individuals, which can help the disease persist in a population. Fig. 11.1 diagrams a modeling framework that includes both ciclo corto and ciclo largo transmission.
Fig. 11.1.
Basic cholera model diagram. Individuals can be Susceptible to cholera, Exposed, Infectious (either symptomatically or asymptomatically), or Recovered (and immune to infection). Black arrows indicate transitions between these states. Infectious individuals shed cholera into the environment (indicated by the “+”s). Susceptible individuals become infected by exposure to Vibrio cholerae from the Environment (the ciclo largo route indicated by blue “x”) at the rate of β or “directly” from Infectious individuals at the rate of μ (the ciclo corto route indicated by green “x”s). After an incubation period, individuals transition from the Exposed to the Infectious state. Infectious individuals shed vibrios into the environment at rate ξ. Symptomatic and asymptomatic may have different levels of infectiousness, indicated by the subscripts following ξ and μ. Red arrows indicate possible effects of interventions labeled in italics, including vaccination, sanitation, and improved hygiene.
Different models based on alternative sets of assumptions may be able to fit observations equally well. For example, simple SIR models of cholera can produce outbreak dynamics nearly indistinguishable from those that include ciclo largo transmission. However, a particular intervention may target one of these routes of transmission more than the other. Therefore, to accurately predict the effectiveness of interventions, one should include the major routes of exposure.
With high quality surveillance data, models might be used to determine the relative contribution of ciclo corto and ciclo largo transmission. In regions with seasonal cholera epidemics, outbreaks may be triggered by V. cholerae in the aquatic reservoir while secondary transmission (ciclo corto) drives dramatic local outbreaks (Franco et al, 1997; Ruiz-Moreno et al, 2010). King et al (2008) used over fifty years of cholera mortality data from Bengal to test alternative models of disease transmission and found support for a large role for ciclo largo transmission in certain districts. Mukandavire et al (2011) used weekly surveillance data to estimate the relative contributions of ciclo corto and ciclo largo transmission of a major outbreak in Zimbabwe that started in 2008. They concluded that the relative contributions of these two routes of transmission were different by province, which may be due to differences in the modes of transmission. Studies such as these reveal spatial heterogeneities in cholera transmission.
11.2.2 Spatial Modeling, Pathogen Movement
For disease outbreaks in small, tightly-connected communities, models of single well-mixed populations may be the most appropriate and parsimonious approach. However, if an outbreak encompasses a large population or if the geographic region includes heterogeneities relevant to disease transmission, such as population density, socioeconomic differences, or geographic features that could block or enhance transmission, then models may need to include multiple interacting populations.
There are several options for geographically subdividing a population for modeling purposes. An obvious choice would be to match the spatial resolution of available surveillance data, so that each reporting area is a single subpopulation within a “metapopulation” or “patch” model (Tuite et al, 2011; Andrews and Basu, 2011). However, surveillance data may be coarse, and disease outbreaks may occur on a much finer scale. One could instead use finer political boundaries (e.g., districts or other administrative boundaries (Bertuzzo et al, 2011)), geographical/geological features (e.g., watersheds (Rinaldo et al, 2012)), or a fine regular grid (Longini et al, 2007; Chao et al, 2011). Using smaller geographic units may better capture spatial heterogeneity relevant to cholera transmission, but can complicate the model with excessive parameters and lead to a loss of generality of modeling results.
Perhaps the spatial resolution of the model should not be determined by convenient political boundaries, but instead by the “natural scale” of cholera outbreaks. Cholera outbreaks are known to be fast and produce sharply peaked epidemic curves, but when case reporting is aggregated by large geographic regions, such as at the country-level, sharp epidemic spikes and outbreak dynamics in general can be masked. Trying to fit a single epidemic curve that is actually the aggregate of multiple spatially separated outbreaks will result in misleading results (Grad et al, 2012). Unfortunately, the scale of an outbreak probably depends on local environmental and sociological factors. Spatial analyses and sequencing of cholera isolates may help identify distinct outbreaks in endemic settings (Stine et al, 2008), which could help modelers dis-aggregate concurrent but distinct outbreaks.
Metapopulation models include mechanisms governing the flow of the infectious agent among the populations. Many models assume that pathogens are transported primarily by infectious people. In such models, susceptible people in one community can be infected by infectious people in neighboring communities. This is usually implemented by setting the force of infection in a community to be a function of both the number of infectious individuals residing in the community and the number of infectious individuals in neighboring communities. Thus, an infectious person contributes to infections in co-located susceptibles and in neighboring populations, often with a force of infection inversely proportional to distance (Bertuzzo et al, 2011; Tuite et al, 2011; Mari et al, 2012). In addition to using geographic distance, one can assume that individuals living along major transportation routes are more mobile and can spread disease farther than those who are more isolated (Chao et al, 2011). In agent-based, or individual-based, models in which each person is individually represented, infectious individuals can move from location to location, infecting individuals as they travel (Longini et al, 2007; Chao et al, 2011). Eventually, studies that track cell phones and other mobile devices might tell us how people actually move during an outbreak (Chunara et al, 2012; Bengtsson et al, 2011; Khan et al, 2012).
Alternatively, models can assume that the pathogen moves via the environment. The environmental reservoirs of adjacent populations can be linked, which would cause V. cholerae shed by one population to diffuse to neighboring populations (Bertuzzo et al, 2010, 2011; Mari et al, 2012), or hydrology can be modeled so that communities can infect populations that are downstream (Chao et al, 2011; Rinaldo et al, 2012). Including realistic hydrology may be important when rivers play a major role in cholera transmission. Some cholera models include the transport of the pathogen through both people and the environment (Chao et al, 2011; Rinaldo et al, 2012).
11.2.3 Transmission Within Households and Hyperinfectivity
High secondary attack rates have been observed within households of cases (Mosley et al, 1965; McCormack et al, 1968; Mosley et al, 1968; Harris et al, 2008;Weil et al, 2009; Kendall et al, 2010). Although a common sources of exposure could account for many of these heavily infected households, studies of the time intervals between cases or that genotype infecting strains have found patterns of transmission consistent with ciclo corto transmission (Snow, 1855; Tamayo et al, 1965; Kendall et al, 2010). A tell-tale sign of ciclo corto transmission would be the rapid appearance of secondary cases consistent with the incubation period of cholera.
A large inoculum of V. cholerae is required to infect an individual (Cash et al, 1974; Levine et al, 1979; Suntharasamai et al, 1992), which makes ciclo corto transmission appear to be physiologically challenging. There are several possible mechanisms for transmission within a household. For example, a household’s food or water supply could be contaminated by an infected individual (St Louis et al, 1990; Albert et al, 1997; Rabbani and Greenough, 1999; Roberts et al, 2001; Palit et al, 2012). Another possibility is that V. cholerae “hyperinfectious” state facilitates ciclo corto transmission. V. cholerae can be orders of magnitude more infectious within the first several hours after excretion from its host (Merrell et al, 2002). This hyperinfectious state of the pathogen would have a much lower infectious dose, which could allow for rapid transmission among close contacts.
Hartley et al (2006) modeled the effects of hyperinfectivity by including two environmental reservoirs; infectious individuals contribute to a highly infectious environmental reservoir, which transitions to a second, less infectious reservoir. Including the hyperinfectious reservoir allowed the model to replicate the “explosive” dynamics of outbreaks (Hartley et al, 2006; Morris, 2011). However, rapid cholera outbreaks can also be modeled using simple SIR models without explicitly including hyperinfectivity (Pascual et al, 2006). It may be impossible to resolve the role of hyperinfectivity in actual outbreaks using models alone – careful epidemiological studies are required. Conversely, it is not obvious which modeling framework should be used, and it may depend on the particular scenario and possible interventions being considered.
Regardless of the actual mechanism invoked, models can include cholera transmission within house-holds in order to capture the elevated attack rates within households with index cases (Chao et al, 2011). Including within-household transmission may be necessary to model certain household-level interventions, such as targeting certain individuals for vaccination in order to protect their families (Ali et al, 2008).
11.2.4 Modeling Interventions
Models can be used to estimate the effectiveness of intervention strategies. Interventions in the cholera modeling literature have included vaccination and improvements in sanitation and hygiene.
The effect of vaccines can be modeled in several ways, depending on assumptions about the vaccine’s mode of protection (Halloran et al, 1999). Most cholera models assume that vaccination has the same protective effect as natural infection, so vaccinated susceptibles are simply treated as resistant individuals (Miller Neilan et al, 2010; Bertuzzo et al, 2011; Tuite et al, 2011; Andrews and Basu, 2011; Azman et al, 2012), as shown in Fig. 11.1. However, vaccination may have immunological consequences different from natural infection (Leung et al, 2012; Arifuzzaman et al, 2012). In one challenge study, vaccine appears to protect against symptomatic illness but not necessarily against infection (Black et al, 1987). If one assumes that asymptomatically infected individuals are infectious, then those protected by vaccine could still transmit disease. The model described in Chao et al (2011) assumes that vaccinees are not protected against infection but have a lower probability of becoming symptomatic upon infection, as shown in Fig. 11.1.
Unvaccinated individuals may be indirectly protected when a sufficient number of their contacts are vaccinated (Fox et al, 1971). Models can be used to compute the critical vaccination fraction, or the fraction of the population that needs to be vaccinated to essentially stop local transmission (Hill and Longini, 2003). If the basic reproductive number, R0 is known, then the critical vaccination fraction is approximately (1/VE)(1 − 1/R0), where VE is the vaccine efficacy against infection. More detailed transmission models can be used to make more refined estimates for the critical vaccination fraction and other measures of indirect protection. In a large cholera vaccine trial, herd immunity was observed (Ali et al, 2005), and a modeling study used these results to explore the effectiveness of different levels of vaccine coverage (Longini et al, 2007). The Longini et al (2007) study estimated that the critical vaccination fraction of the study population was about 70%.
Improvements in sanitation and hygiene are essential non-pharmaceutical measures for cholera outbreak control. Interventions that reduce the consumption of contaminated water, such as the provision of clean water or the promotion of chlorination, can be modeled as a reduction in the exposure to cholera from the environment (Miller Neilan et al, 2010; Tuite et al, 2011; Chao et al, 2011; Mari et al, 2012). Interventions that better manage the waste of infected individuals, such as the cleaning or building of latrines, could be modeled as a reduction in the contribution of infected individuals to the environmental reservoir (Chao et al, 2011; Mari et al, 2012). Both of these approaches to modeling improved sanitation and hygiene are depicted in Fig. 11.1.
11.3 Modeling the 2010 Cholera Outbreak in Haiti
In October 2010, cases of cholera began appearing in central Haiti, the start of a massive and prolonged epidemic that spread across the country and sickened over half a million people within a year (Walton and Ivers, 2011; Cravioto et al, 2011). The conditions in Haiti seemed perfect for cholera transmission, with unrepaired damage from a major earthquake earlier in the year and Hurricane Tomas striking soon after the first cases of cholera were identified. Public health workers were trained to treat cases, and temporary cholera treatment centres were quickly established. Haiti’s Ministère de la Santé Publique et de la Population (MSPP) launched a media campaign to promote better sanitation and hygiene (Centers for Disease Control and Prevention (CDC), 2010).
Several modeling efforts began soon after the first cases were reported (Bertuzzo et al, 2011; Tuite et al, 2011; Andrews and Basu, 2011; Chao et al, 2011; Abrams et al, 2012). All of these studies attempted to reproduce the dynamics of the epidemic for a single season at the department level, the spatial resolution of reported case and hospitalisation counts publicly released by MSPP. Two modeling groups divided the departments into much smaller regions to implement more realistic cholera transmission dynamics (Bertuzzo et al, 2011; Chao et al, 2011). All of these modeling studies focused on the size and duration of the first, and largest, wave of the epidemic, but the first were published in March of 2011, months after the peak actually occurred.
What emerged from the modeling community was a set of models and a small body of literature on modeling cholera during an outbreak. Common themes were the spatial coarseness of the surveillance data, the limited impact a small supply of vaccine would have on a nationwide outbreak, and the need for better surveillance. Most of the modeling groups used the case and hospitalisation estimates from the MSPP, but one of the studies attempted to estimate and correct for the different reporting rates by department (Andrews and Basu, 2011).
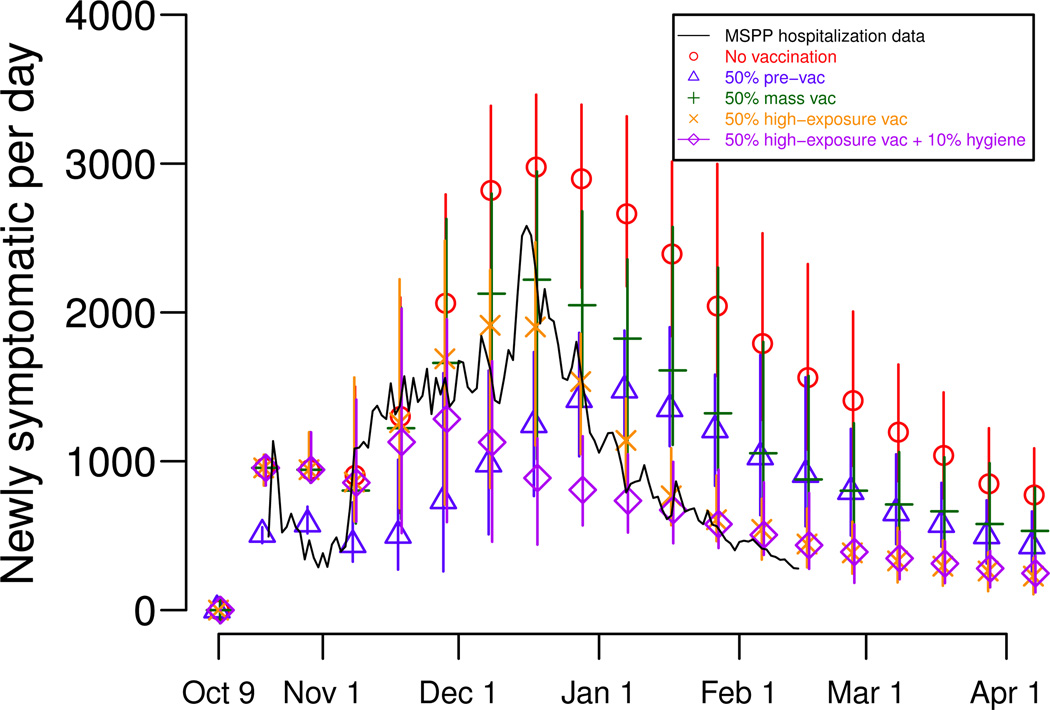
Chao et al (2011) modeled scenarios in which there was much more vaccine than was actually available at the time. The study suggested that achieving high levels of coverage in regions with high exposure to cholera, particularly along rivers, could have had a major impact on the course of the epidemic. However, the study found that mass vaccination alone would have been insufficient to stop the spread of cholera – improving sanitation and hygiene to reduce the public’s exposure to the pathogen was also necessary to greatly reduce cholera transmission in Haiti (Fig. 11.2). The results highlight the need to target vaccination campaigns and other interventions efficiently when resources are scarce.
Fig. 11.2.
Simulated effects of interventions during the first wave of the 2010 cholera epidemic in Haiti. The stochastic model described in Chao et al (2011) was run 50 times per scenario, and the points plot the median attack rates for the stochastic simulations and the lines represent the range of the minimum and maximum attack rates. Several intervention scenarios were modeled: no intervention (in red), vaccination well before the epidemic (pre-vaccination, in blue), vaccination after the first cholera cases were confirmed (mass vaccination, in green), vaccination targeted to communities near rivers after the first cholera cases were confirmed (high-exposure vaccination, in yellow), and prioritizing vaccination and educational campaigns to improve hygiene and sanitation to communities near rivers after the first cholera cases were confirmed (in purple). Note that pre-vaccination delays the epidemic peak, while reactive strategies tend to reduce but not delay the peak.
11.4 Discussion and Conclusions
We have described a variety of approaches to modeling cholera outbreaks. The same modeling frameworks can be used to describe both epidemic and endemic cholera, but the modeler must make the appropriate choices of initial conditions, parameterization, and possibly model structure. For cholera outbreaks in non-endemic regions, there may be little prior immunity, a high attack rate, similar attack rates among age groups, and high symptomatic fractions (Sack, 2003; Sack et al, 2004). The issues more important in endemic regions, such as drivers of seasonality and environmental predictors of outbreaks, may be of little concern and can be omitted from models when one is interested solely in outbreaks in non-endemic settings. Therefore, when formulating a model, one should consider the population of interest (e.g., size, heterogeneity, prior exposure history), available interventions (e.g., vaccination, sanitation improvements), available surveillance data (e.g., spatial scale, age distributions, reporting rates), and time scale (e.g., days, months, or years).
Models with different assumptions may fit the dynamics of a particular outbreak equally well. In some cases, model selection might not be an important issue. But when one wants to perturb the dynamics of cholera transmission by simulating in- terventions, different models could produce dramatically different projections of the effectiveness of interventions. Complex models will also encounter problems of identifiability, making it impossible to find a unique “best” set of parameters. More detailed epidemiological studies of cholera transmission are needed in order to better parameterize transmission models. Sensitivity analyses of cholera models may help us prioritize such studies by identifying the most important gaps in our understanding of the disease (Grad et al, 2012).
In general, infectious disease modelers find it difficult to find epidemic data of sufficient quality for model-fitting. Public health departments generally release surveillance data aggregated over large spatial scales. More detailed outbreak data is usually obtainable only through direct collaborations with the outbreak investigators, which is rare in the modeling world. Therefore, there are few modeling studies of real outbreaks and many studies of the properties of the models themselves. The dearth of data and well-parameterized models may lead to the overgeneralization of modeling results. There is a clear need for more modeling studies of actual outbreaks, which would require either more direct collaborations between modelers and surveillance groups or more receptiveness to sharing outbreak data with modelers and other analysts.
Modeling studies can be a valuable source of information for public health officials evaluating potential interventions for cholera outbreaks (Garnett et al, 2011; Hutubessy et al, 2011). Most published studies that evaluate the cost-effectiveness of cholera vaccination do not include a dynamic model of disease transmission (Sack, 2003; Jeuland et al, 2009; Cook et al, 2009; Kim et al, 2011; Reyburn et al, 2011). Dynamic transmission models such as those described here capture indirect protection, which increases the estimated effectiveness of mass vaccination and other interventions (Brisson and Edmunds, 2003). Based on earlier studies, many concluded that reactive vaccination would not be helpful during outbreaks (Sommer and Mosley, 1973; Naficy et al, 1998). However, large and prolonged outbreaks could be mitigated using reactive vaccination, particularly if interventions target key populations (Chao et al, 2011; Azman et al, 2012). Models could and should be used to weigh the costs and benefits of different interventions for a range of scenarios, from seasonal endemic cholera outbreaks to epidemics exacerbated by natural disasters (Legros et al, 1999; Calain et al, 2004; Jeuland et al, 2009; Chaignat and Monti, 2007; Global Task Force on Cholera Control, 2010).
Contributor Information
Dennis L. Chao, Center for Statistics and Quantitative Infectious Diseases, Vaccine and Infectious Disease Division, Fred Hutchinson Cancer Research Center, Seattle, WA 98109, USA, dchao@fhcrc.org
Ira M. Longini, Jr., Department of Biostatistics, Colleges of Public Health and Health Professions, and Medicine, and Emerging Pathogens Institute, University of Florida, Gainesville, FL 32611, USA
J. Glenn Morris, Jr., Emerging Pathogens Institute, University of Florida, Gainesville, FL 32610, USA
References
- Abrams JY, Copeland JR, Tauxe RV, Date KA, Belay ED, Mody RK, Mintz ED. Real-time modelling used for outbreak management during a cholera epidemic, Haiti, 2010–2011. Epidemiol Infect. 2012:1–10. doi: 10.1017/S0950268812001793. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert MJ, Neira M, Motarjemi Y. The role of food in the epidemiology of cholera. World Health Stat Q. 1997;50(1–2):111–118. [PubMed] [Google Scholar]
- Ali M, Emch M, von Seidlein L, Yunus M, Sack DA, Rao M, Holmgren J, Clemens JD. Herd immunity conferred by killed oral cholera vaccines in Bangladesh: a reanalysis. Lancet. 2005;366(9479):44–49. doi: 10.1016/S0140-6736(05)66550-6. [DOI] [PubMed] [Google Scholar]
- Ali M, Emch M, Yunus M, Sack D, Lopez AL, Holmgren J, Clemens J. Vaccine protection of Bangladeshi infants and young children against cholera: implications for vaccine deployment and person-to-person transmission. Pediatr Infect Dis J. 2008;27(1):33–37. doi: 10.1097/INF.0b013e318149dffd. [DOI] [PubMed] [Google Scholar]
- Andrews JR, Basu S. Transmission dynamics and control of cholera in Haiti: an epidemic model. Lancet. 2011;377(9773):1248–1255. doi: 10.1016/S0140-6736(11)60273-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arifuzzaman M, Rashu R, Leung DT, Hosen MI, Bhuiyan TR, Bhuiyan MS, Rahman MA, Khanam F, Saha A, Charles RC, Larocque RC, Weil AA, Clements JD, Holmes RK, Calderwood SB, Harris JB, Ryan ET, Qadri F. Antigen-specific memory T cell responses after vaccination with an oral killed cholera vaccine in Bangladeshi children and comparison to responses in patients with naturally acquired cholera. Clin Vaccine Immunol. 2012;19(8):1304–1311. doi: 10.1128/CVI.00196-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azman AS, Luquero FJ, Rodrigues A, Palma PP, Grais RF, Banga CN, Grenfell BT, Lessler J. Urban cholera transmission hotspots and their implications for reactive vaccination: Evidence from Bissau City, Guinea Bissau. PLoS Negl Trop Dis. 2012;6(11):e1901. doi: 10.1371/journal.pntd.0001901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengtsson L, Lu X, Thorson A, Garfield R, von Schreeb J. Improved response to disasters and outbreaks by tracking population movements with mobile phone network data: A post-earthquake geospatial study in Haiti. PLoS Med. 2011;8(8):e1001,083. doi: 10.1371/journal.pmed.1001083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertuzzo E, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A. On spatially explicit models of cholera epidemics. J R Soc Interface. 2010;7(43):321–333. doi: 10.1098/rsif.2009.0204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertuzzo E, Mari L, Righetto L, Gatto M, Casagrandi R, Blokesch M, Rodriguez-Iturbe I, Rinaldo A. Prediction of the spatial evolution and effects of control measures for the unfolding Haiti cholera outbreak. Geophys Res Lett. 2011;38:L06–L403. [Google Scholar]
- Black RE, Levine MM, Clements ML, Young CR, Svennerholm AM, Holmgren J. Protective efficacy in humans of killed whole-vibrio oral cholera vaccine with and without the B subunit of cholera toxin. Infect Immun. 1987;55(5):1116–1120. doi: 10.1128/iai.55.5.1116-1120.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brisson M, Edmunds WJ. Economic evaluation of vaccination programs: The impact of herd-immunity. Med Decis Making. 2003;23(1):76–82. doi: 10.1177/0272989X02239651. [DOI] [PubMed] [Google Scholar]
- Calain P, Chaine JP, Johnson E, Hawley ML, O’Leary MJ, Oshitani H, Chaignat CL. Can oral cholera vaccination play a role in controlling a cholera outbreak? Vaccine. 2004;22(19):2444–2451. doi: 10.1016/j.vaccine.2003.11.070. [DOI] [PubMed] [Google Scholar]
- Cash RA, Music SI, Libonati JP, Snyder MJ, Wenzel RP, Hornick RB. Response of man to infection with Vibrio cholerae. I. clinical, serologic, and bacteriologic responses to a known inoculum. J Infect Dis. 1974;129(1):45–52. doi: 10.1093/infdis/129.1.45. [DOI] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention (CDC) Update: cholera outbreak—Haiti, 2010. MMWR Morb Mortal Wkly Rep. 2010;59(45):1473–1479. [PubMed] [Google Scholar]
- Chaignat CL, Monti V. Use of oral cholera vaccine in complex emergencies: what next? Summary report of an expert meeting and recommendations of WHO. J Health Popul Nutr. 2007;25(2):244–261. [PMC free article] [PubMed] [Google Scholar]
- Chao DL, Halloran ME, Longini IM., Jr Vaccination strategies for epidemic cholera in Haiti with implications for the developing world. Proc Natl Acad Sci U S A. 2011;108(17):7081–7085. doi: 10.1073/pnas.1102149108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chunara R, Andrews JR, Brownstein JS. Social and news media enable estimation of epidemiological patterns early in the 2010 Haitian cholera outbreak. Am J Trop Med Hyg. 2012;86(1):39–45. doi: 10.4269/ajtmh.2012.11-0597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clemens JD. Vaccines in the time of cholera. Proc Natl Acad Sci U S A. 2011;108(21):8529–8530. doi: 10.1073/pnas.1105807108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Codeço CT. Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect Dis. 2001;1:1. doi: 10.1186/1471-2334-1-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connolly MA, editor. Geneva: World Health Organization; 2005. Communicable disease control in emergencies: A field manual. [Google Scholar]
- Cook J, Jeuland M, Maskery B, Lauria D, Sur D, Clemens J, Whittington D. Using private demand studies to calculate socially optimal vaccine subsidies in developing countries. J Policy Anal Manage. 2009;28(1):6–28. doi: 10.1002/pam.20401. [DOI] [PubMed] [Google Scholar]
- Cravioto A, Lanta CF, Lantagne DS, Nair GB. New York: United Nations; 2011. Final Report of the Independent Panel of Experts on the Cholera Outbreak in Haiti. [Google Scholar]
- Farmer P, Almazor CP, Bahnsen ET, Barry D, Bazile J, Bloom BR, Bose N, Brewer T, Calderwood SB, Clemens JD, Cravioto A, Eustache E, Jérôme G, Gupta N, Harris JB, Hiatt HH, Holstein C, Hotez PJ, Ivers LC, Kerry VB, Koenig SP, LaRocque RC, Léandre F, Lambert W, Lyon E, Mekalanos JJ, Mukherjee JS, Oswald C, Pape JW, Gretchko Prosper A, Rabinovich R, Raymonville M, Réjouit JR, Ronan LJ, Rosenberg ML, Ryan ET, Sachs JD, Sack DA, Surena C, Suri AA, Ternier R, Waldor MK, Walton D, Weigel JL. Meeting cholera’s challenge to Haiti and the world: A joint statement on cholera prevention and care. PLoS Negl Trop Dis. 2011;5(5):e1145. doi: 10.1371/journal.pntd.0001145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox JP, Elveback L, Scott W, Gatewood L, Ackerman E. Herd immunity: basic concept and relevance to public health immunization practices. Am J Epidemiol. 1971;94(3):179–189. doi: 10.1093/oxfordjournals.aje.a121310. [DOI] [PubMed] [Google Scholar]
- Franco AA, Fix AD, Prada A, Paredes E, Palomino JC, Wright AC, Johnson JA, McCarter R, Guerra H, Morris JG., Jr Cholera in Lima, Peru, correlates with prior isolation of Vibrio cholerae from the environment. Am J Epidemiol. 1997;146(12):1067–1075. doi: 10.1093/oxfordjournals.aje.a009235. [DOI] [PubMed] [Google Scholar]
- Garnett GP, Cousens S, Hallett TB, Steketee R, Walker N. Mathematical models in the evaluation of health programmes. Lancet. 2011;378(9790):515–525. doi: 10.1016/S0140-6736(10)61505-X. [DOI] [PubMed] [Google Scholar]
- Global Task Force on Cholera Control. Geneva: World Health Organization; 2010. Oral cholera vaccines in mass immunization campaigns: Guidance for planning and use. http://whqlibdoc.who.int/publications/2010/9789241500432_eng.pdf. [Google Scholar]
- Grad YH, Miller JC, Lipsitch M. Cholera modeling: challenges to quantitative analysis and predicting the impact of interventions. Epidemiology. 2012;23(4):523–530. doi: 10.1097/EDE.0b013e3182572581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halloran ME, Longini IM, Jr, Struchiner CJ. Design and interpretation of vaccine field studies. Epidemiol Rev. 1999;21(1):73–88. doi: 10.1093/oxfordjournals.epirev.a017990. [DOI] [PubMed] [Google Scholar]
- Harris JB, LaRocque RC, Chowdhury F, Khan AI, Logvinenko T, Faruque ASG, Ryan ET, Qadri F, Calderwood SB. Susceptibility to Vibrio cholerae infection in a cohort of household contacts of patients with cholera in Bangladesh. PLoS Negl Trop Dis. 2008;2(4):e221. doi: 10.1371/journal.pntd.0000221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartley DM, Morris JG, Jr, Smith DL. Hyperinfectivity: a critical element in the ability of V. cholerae to cause epidemics. PLoS Med. 2006;3(1):e7. doi: 10.1371/journal.pmed.0030007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hethcote HW. The mathematics of infectious diseases. SIAM Review. 2000;42(4):599–653. [Google Scholar]
- Hill AN, Longini IM., Jr The critical vaccination fraction for heterogeneous epidemic models. Mathematical Biosciences. 2003;181:85–106. doi: 10.1016/s0025-5564(02)00129-3. [DOI] [PubMed] [Google Scholar]
- Holmgren J. A case for control of cholera in Africa by vaccination. Lancet Infect Dis. 2012;12(11):818–819. doi: 10.1016/S1473-3099(12)70204-9. [DOI] [PubMed] [Google Scholar]
- Hutubessy R, Henao AM, Namgyal P, Moorthy V, Hombach J. Results from evaluations of models and cost-effectiveness tools to support introduction decisions for new vaccines need critical appraisal. BMC Med. 2011;9:55. doi: 10.1186/1741-7015-9-55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Vaccine Institute. An investment case for the accelerated introduction of oral cholera vaccines. Seoul: International Vaccine Institute; 2012. URL www.ivi.int/publication/IVI_Global_cholera_case.pdf. [Google Scholar]
- Ivers LC, Farmer P, Almazor CP, Léandre F. Five complementary interventions to slow cholera: Haiti. Lancet. 2010;376(9758):2048–2051. doi: 10.1016/S0140-6736(10)62243-X. [DOI] [PubMed] [Google Scholar]
- Jeuland M, Cook J, Poulos C, Clemens J, Whittington D. Cost-effectiveness of new-generation oral cholera vaccines: a multisite analysis. Value Health. 2009;12(6):899–908. doi: 10.1111/j.1524-4733.2009.00562.x. [DOI] [PubMed] [Google Scholar]
- Kendall EA, Chowdhury F, Begum Y, Khan AI, Li S, Thierer JH, Bailey J, Kreisel K, Tacket CO, LaRocque RC, Harris JB, Ryan ET, Qadri F, Calderwood SB, Stine OC. Relatedness of Vibrio cholerae O1/O139 isolates from patients and their household contacts, determined by multilocus variable-number tandem-repeat analysis. J Bacteriol. 2010;192(17):4367–4376. doi: 10.1128/JB.00698-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London Series A. 1927;115:700–721. [Google Scholar]
- Khan K, McNabb SJ, Memish ZA, Eckhardt R, Hu W, Kossowsky D, Sears J, Arino J, Johansson A, Barbeschi M, McCloskey B, Henry B, Cetron M, Brownstein JS. Infectious disease surveillance and modelling across geographic frontiers and scientific specialties. Lancet Infect Dis. 2012;12(3):222–230. doi: 10.1016/S1473-3099(11)70313-9. [DOI] [PubMed] [Google Scholar]
- Kim SY, Choi Y, Mason PR, Rusakaniko S, Goldie SJ. Potential impact of reactive vaccination in controlling cholera outbreaks: An exploratory analysis using a Zimbabwean experience. S Afr Med J. 2011;101(9):659–664. [PubMed] [Google Scholar]
- King AA, Ionides EL, Pascual M, Bouma MJ. Inapparent infections and cholera dynamics. Nature. 2008;454(7206):877–880. doi: 10.1038/nature07084. [DOI] [PubMed] [Google Scholar]
- Koch R. Further researches on cholera. Br Med J. 1886;1(1306):62–66. doi: 10.1136/bmj.1.1306.62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch R. Ueber den augenblicklichen Stand der bakteriologischen Cholera-diagnose. Medical Microbiology and Immunology. 1893;14:319–338. [Google Scholar]
- Koelle K, Pascual M. Disentangling extrinsic from intrinsic factors in disease dynamics: a nonlinear time series approach with an application to cholera. Am Nat. 2004;163(6):901–913. doi: 10.1086/420798. [DOI] [PubMed] [Google Scholar]
- Koelle K, Rodó X, Pascual M, Yunus M, Mostafa G. Refractory periods and climate forcing in cholera dynamics. Nature. 2005;436(7051):696–700. doi: 10.1038/nature03820. [DOI] [PubMed] [Google Scholar]
- Legros D, Paquet C, Perea W, Marty I, Mugisha NK, Royer H, Neira M, Ivanoff B. Mass vaccination with a two-dose oral cholera vaccine in a refugee camp. Bull World Health Organ. 1999;77(10):837–842. [PMC free article] [PubMed] [Google Scholar]
- Leung DT, Rahman MA, Mohasin M, Patel SM, Aktar A, Khanam F, Uddin T, Riyadh MA, Saha A, Alam MM, Chowdhury F, Khan AI, Charles R, Larocque R, Harris JB, Calderwood SB, Qadri F, Ryan ET. Memory B cell and other immune responses in children receiving two doses of an oral killed cholera vaccine compared to responses following natural cholera infection in Bangladesh. Clin Vaccine Immunol. 2012;19(5):690–698. doi: 10.1128/CVI.05615-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levine MM, Nalin DR, Rennels MB, Hornick RB, Sotman S, Van Blerk G, Hughes TP, O’Donnell S, Barua D. Genetic susceptibility to cholera. Ann Hum Biol. 1979;6(4):369–374. doi: 10.1080/03014467900003751. [DOI] [PubMed] [Google Scholar]
- Longini IM, Jr, Nizam A, Ali M, Yunus M, Shenvi N, Clemens JD. Controlling endemic cholera with oral vaccines. PLoS Med. 2007;4(11):e336. doi: 10.1371/journal.pmed.0040336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mari L, Bertuzzo E, Righetto L, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A. Modelling cholera epidemics: the role of waterways, human mobility and sanitation. J R Soc Interface. 2012;9(67):376–388. doi: 10.1098/rsif.2011.0304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin S, Costa A, Perea W. Stockpiling oral cholera vaccine. Bull World Health Organ. 2012;90(10):714. doi: 10.2471/BLT.12.112433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormack WM, Chowdhury AM, Jahangir N, Ahmed AB, Mosley WH. Tetracycline prophylaxis in families of cholera patients. Bull World Health Organ. 1968;38(5):787–792. [PMC free article] [PubMed] [Google Scholar]
- Merrell DS, Butler SM, Qadri F, Dolganov NA, Alam A, Cohen MB, Calderwood SB, Schoolnik GK, Camilli A. Host-induced epidemic spread of the cholera bacterium. Nature. 2002;417(6889):642–645. doi: 10.1038/nature00778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller Neilan RL, Schaefer E, Gaff H, Fister KR, Lenhart S. Modeling optimal intervention strategies for cholera. Bull Math Biol. 2010;72(8):2004–2018. doi: 10.1007/s11538-010-9521-8. [DOI] [PubMed] [Google Scholar]
- Morris JG., Jr Cholera-modern pandemic disease of ancient lineage. Emerg Infect Dis. 2011;17(11):2099–2104. doi: 10.3201/eid1711.111109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosley WH, Alvero MG, Joseph PR, Tamayo JF, Gomez CZ, Montague T, Dizon JJ, Henderson DA. Studies of cholera El Tor in the Philippines. 4. Transmission of infection among neighbourhood and community contacts of cholera patients. Bull World Health Organ. 1965;33(5):651–660. [PMC free article] [PubMed] [Google Scholar]
- Mosley WH, Ahmad S, Benenson AS, Ahmed A. The relationship of vibriocidal antibody titre to susceptibility to cholera in family contacts of cholera patients. Bull World Health Organ. 1968;38(5):777–785. [PMC free article] [PubMed] [Google Scholar]
- Mukandavire Z, Liao S, Wang J, Gaff H, Smith DL, Morris JG., Jr Estimating the reproductive numbers for the 2008–2009 cholera outbreaks in Zimbabwe. Proc Natl Acad Sci U S A. 2011;108(21):8767–8772. doi: 10.1073/pnas.1019712108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naficy A, Rao MR, Paquet C, Antona D, Sorkin A, Clemens JD. Treatment and vaccination strategies to control cholera in sub-Saharan refugee settings: a cost-effectiveness analysis. JAMA. 1998;279(7):521–525. doi: 10.1001/jama.279.7.521. [DOI] [PubMed] [Google Scholar]
- Nelson EJ, Harris JB, Morris JG, Jr, Calderwood SB, Camilli A. Cholera transmission: the host, pathogen and bacteriophage dynamic. Nat Rev Microbiol. 2009;7(10):693–702. doi: 10.1038/nrmicro2204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palit A, Batabyal P, Kanungo S, Sur D. In-house contamination of potable water in urban slum of Kolkata, India: a possible transmission route of diarrhea. Water Sci Technol. 2012;66(2):299–303. doi: 10.2166/wst.2012.177. [DOI] [PubMed] [Google Scholar]
- Pascual M, Koelle K, Dobson AP. Hyperinfectivity in cholera: a new mechanism for an old epidemiological model. PLoS Med. 2006;3(6):e280. doi: 10.1371/journal.pmed.0030280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabbani GH, Greenough WB., 3rd Food as a vehicle of transmission of cholera. J Diarrhoeal Dis Res. 1999;17(1):1–9. [PubMed] [Google Scholar]
- Reyburn R, Deen JL, Grais RF, Bhattacharya SK, Sur D, Lopez AL, Jiddawi MS, Clemens JD, von Seidlein L. The case for reactive mass oral cholera vaccinations. PLoS Negl Trop Dis. 2011;5(1):e952. doi: 10.1371/journal.pntd.0000952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rinaldo A, Bertuzzo E, Mari L, Righetto L, Blokesch M, Gatto M, Casagrandi R, Murray M, Vesenbeckh SM, Rodriguez-Iturbe I. Reassessment of the 2010–2011 Haiti cholera outbreak and rainfall-driven multiseason projections. Proc Natl Acad Sci U S A. 2012;109(17):6602–6607. doi: 10.1073/pnas.1203333109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts L, Chartier Y, Chartier O, Malenga G, Toole M, Rodka H. Keeping clean water clean in a Malawi refugee camp: a randomized intervention trial. Bull World Health Organ. 2001;79(4):280–287. [PMC free article] [PubMed] [Google Scholar]
- Ruiz-Moreno D, Pascual M, Emch M, Yunus M. Spatial clustering in the spatio-temporal dynamics of endemic cholera. BMC Infect Dis. 2010;10:51. doi: 10.1186/1471-2334-10-51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sack DA. When should cholera vaccine be used in cholera-endemic areas? J Health Popul Nutr. 2003;21(4):299–303. [PubMed] [Google Scholar]
- Sack DA, Sack RB, Nair GB, Siddique AK. Cholera. Lancet. 2004;363(9404):223–233. doi: 10.1016/s0140-6736(03)15328-7. [DOI] [PubMed] [Google Scholar]
- Snow J. On the mode of communication of cholera. London: John Churchill; 1855. [Google Scholar]
- Sommer A, Mosley WH. Ineffectiveness of cholera vaccination as an epidemic control measure. Lancet. 1973;1(7814):1232–1235. doi: 10.1016/s0140-6736(73)90540-0. [DOI] [PubMed] [Google Scholar]
- St Louis ME, Porter JD, Helal A, Drame K, Hargrett-Bean N, Wells JG, Tauxe RV. Epidemic cholera in West Africa: the role of food handling and high-risk foods. Am J Epidemiol. 1990;131(4):719–728. doi: 10.1093/oxfordjournals.aje.a115556. [DOI] [PubMed] [Google Scholar]
- Stine OC, Alam M, Tang L, Nair GB, Siddique AK, Faruque SM, Huq A, Colwell R, Sack RB, Morris JG., Jr Seasonal cholera from multiple small outbreaks, rural Bangladesh. Emerg Infect Dis. 2008;14(5):831–833. doi: 10.3201/eid1405.071116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suntharasamai P, Migasena S, Vongsthongsri U, Supanaranond W, Pitisuttitham P, Supeeranan L, Chantra A, Naksrisook S. Clinical and bacteriological studies of El Tor cholera after ingestion of known inocula in Thai volunteers. Vaccine. 1992;10(8):502–505. doi: 10.1016/0264-410x(92)90347-m. [DOI] [PubMed] [Google Scholar]
- Tamayo JF, Mosley WH, Alvero MG, Joseph PR, Gomez CZ, Montague T, Dizon JJ, Henderson DA. Studies of cholera El Tor in the Philippines. 3. Transmission of infection among household contacts of cholera patients. Bull World Health Organ. 1965;33(5):645–649. [PMC free article] [PubMed] [Google Scholar]
- Tien JH, Earn DJD. Multiple transmission pathways and disease dynamics in a waterborne pathogen model. Bull Math Biol. 2010;72(6):1506–1533. doi: 10.1007/s11538-010-9507-6. [DOI] [PubMed] [Google Scholar]
- Tuite AR, Tien J, Eisenberg M, Earn DJD, Ma J, Fisman DN. Cholera epidemic in Haiti, 2010: using a transmission model to explain spatial spread of disease and identify optimal control interventions. Ann Intern Med. 2011;154(9):593–601. doi: 10.7326/0003-4819-154-9-201105030-00334. [DOI] [PubMed] [Google Scholar]
- Waldor MK, Hotez PJ, Clemens JD. A national cholera vaccine stockpile–a new humanitarian and diplomatic resource. N Engl J Med. 2010;363(24):2279–2282. doi: 10.1056/NEJMp1012300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walton DA, Ivers LC. Responding to cholera in post-earthquake Haiti. N Engl J Med. 2011;364(1):3–5. doi: 10.1056/NEJMp1012997. [DOI] [PubMed] [Google Scholar]
- Weil AA, Khan AI, Chowdhury F, Larocque RC, Faruque ASG, Ryan ET, Calderwood SB, Qadri F, Harris JB. Clinical outcomes in household contacts of patients with cholera in Bangladesh. Clin Infect Dis. 2009;49(10):1473–1479. doi: 10.1086/644779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization. Cholera vaccines: WHO position paper. Wkly Epidemiol Rec. 2010;85(13):117–128. [PubMed] [Google Scholar]
- World Health Organization. Geneva: World Health Organization; 2012. Meeting report of the WHO Technical Working Group on creation of an oral cholera vaccine stockpile. [Google Scholar]