Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Nov 20.
Published in final edited form as: J Theor Comput Chem. 2014;13(3):1440007. doi: 10.1142/S0219633614400070

On the electrostatic properties of homodimeric proteins

Brandon Campbell 1, Marharyta Petukh 1, Emil Alexov 1, Chuan Li 1,✉
PMCID: PMC4238107  NIHMSID: NIHMS590109  PMID: 25419028

Abstract

A large fraction of proteins function as homodimers, but it is not always clear why the dimerization is important for functionality since frequently each monomer possesses a distinctive active site. Recent work (PLoS Computational Biology, 9(2), e1002924) indicates that homodimerization may be important for forming an electrostatic funnel in the spermine synthase homodimer which guides changed substrates toward the active centers. This prompted us to investigate the electrostatic properties of a large set of homodimeric proteins and resulted in an observation that in a vast majority of the cases the dimerization indeed results in specific electrostatic features, although not necessarily in an electrostatic funnel. It is demonstrated that the electrostatic dipole moment of the dimer is predominantly perpendicular to the axis connecting the centers of the mass of the monomers. In addition, the surface points with highest potential are located in the proximity of the interfacial plane of the homodimeric complexes. These findings indicate that frequently homodimerization provides specific electrostatic features needed for the function of proteins.

Keywords: electrostatics, Poisson-Boltzmann equation, homodimers, electrostatic field, electrostatic funneling

Introduction

The role of electrostatics in the cell is evident by the fact that biological macromolecules are made of atoms carrying partial charges and frequently the net charge of the macromolecules is different from zero [1]. There are hundreds of thousands of different macromolecules and substrates in living cells and each receptor must recognize its specific binding partners among a plethora of other molecules in order to carry out the needed functions for life [2,3,4,5]. Not only must proteins identify their partners among many others, but frequently the identification and binding must be done quickly and over relatively large distances [6,7,8,9,10]. The best candidate among the molecular forces for providing such a long-range guiding mechanism is the electrostatic force [11,12,13,14].

Homodimeric proteins represent a large fraction of biologically active units in the cell [15,16,17,18,19]. Since homodimeric proteins are made of two identical chains carrying the same net charge, it is expected that in most cases the electrostatic forces will oppose binding [20]. However, homodimerization is frequently found to be necessary for the function of many proteins [21,22,23,24]. In some cases, the homodimerization results in a formation of a functionally important homodimeric interface [25,26]. In many other cases, homodimers are formed from two monomers with distinctive active sites being far away from the dimer interfaces [27,28]. For these cases, there should be some advantageous effect, different from forming a functionally important homodimeric interface and being important so as to pay the price of overcoming unfavorable electrostatic repulsion between identical chains forming the homodimer. For some cases the homodimerization is necessary for the regulation [28,29,30]. For others, as in the case of the human spermine synthase protein, the dimerization works as a switch [27,31] and creates an electrostatic funnel which steers the delivery of the reactants to the active sites of the complex [32]. With this work, we explore the possibility that such an effect, the electrostatic steering effect, may be common among homodimeric proteins, to deliver the substrates to the active site(s) or to enhance the molecular recognition.

In order to address the abovementioned effects on homodimer complexes a database of such complexes has been created and analyzed. To create the database we extracted a selection of 204 homodimeric proteins using the PDBsum database (http://www.ebi.ac.uk/pdbsum/) [33,34]. Using these proteins and grouping them into subclasses according to their function, we show that the dimerization creates specific electrostatic features which can guide the molecular recognition or substrate binding.

Methods

Database Creation

To create the database of homodimers, the word “homodimer” was searched using the PDBsum database which searches the header records of PDB files located in the Protein Data Bank (http://www.pdb.org). The search resulted in a list of 445 different PDB files which were then manually inspected to determine if the resulting files are indeed homodimers. Files with incomplete information were removed from this list resulting in a total of 204 PDB files (Table 1S in supplementary material). Out of these protein homodimers, some files also included other biological molecules (i.e. DNA bound to homodimeric transcription factors), and these non-protein molecules were removed from the structural files. The homodimers were visually inspected with regard to their binding mode and it was observed that some of them form symmetrical dimers (mirrored monomers), while others showed no symmetry of the binding mode.

Furthermore, the homodimers were grouped into four groups. The first selection was based on the Enzyme Commission Number (EC) and resulted in six subgroups: oxidoreductases (EC1), transferases (EC2), hydrolases (EC3), lyases (EC4), isomerases (EC5), and ligases (EC6). However, EC subgroups 4–6 had only a few structural representatives and were deleted from the database. Thus, after the first selection, three groups were formed: EC1, EC2 and EC3. The second selection was based on proteins identified as transcription factors and DNA binding proteins called the DNA subgroup, resulting in the last fourth group. The remaining entries that did not fit into these subgroups were separated and included in analysis when discussing the database as a whole. The contents of the database and each group and their relative percentages of the overall database are provided in Table 1.

Electrostatic and geometric calculations using DelPhi

For calculations each structural file in the database was fixed for missing atoms and residues using Profix from the JACKAL package (http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software:Jackal) and protonated using MCCE [35,36]. In addition, each PDB file was split by chain designator and three files were generated: two files containing the atomic coordinates of each monomer and another file that contains the entire homodimeric structure. DelPhi [37,38,39] was run on each of these three files, and from the output the location of the geometric center for each monomer and the locations of the centers of positive and negative charges for the homodimer were determined. These runs were conducted using Clemson University’s High Performance Computing cluster, Palmetto (http://citi.clemson.edu/palmetto/). The following parameters were used for the DelPhi runs: percent of protein filling the cube – 70%; scale – 1.0 grids/Å; amber force field; a dielectric constant of 4 for the protein and 80 for the solvent; the water probe radius 1.4 Å.

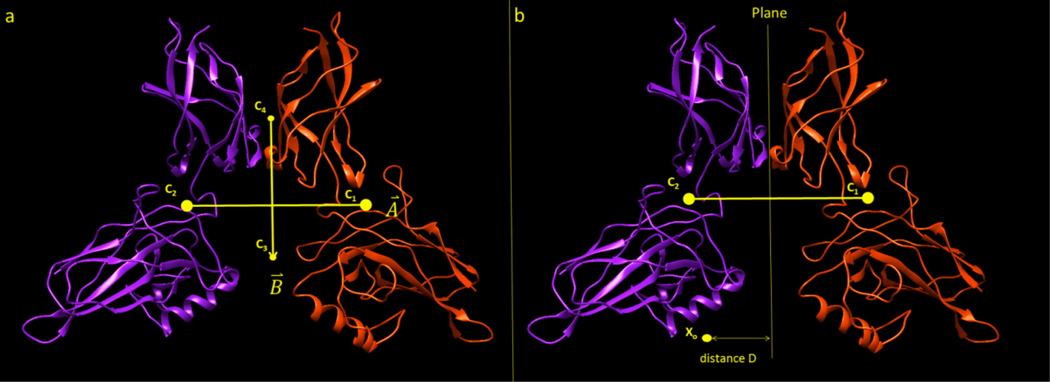
  1. Calculating the angle between the center of masses of monomers and the total electrostatic dipole moment of the homodimer: Using the point locations of the geometric centers of each monomer, C1(x1, y1, z1) and C2(x2, y2, z2) respectively, a geometric center vector A⃗ was generated from C1 to C2 (Figure 1a). Using the locations of the centers of positive and negative charges for the entire homodimeric complex, C3(x3, y3, z3) and C4(x4, y4, z4), a electric dipole moment vector B⃗ was generated from C3 to C4. In this approach the center of the vector coincides with the middle point between C3 and C4, and no offset was introduced even for cases for which the net charge is different from zero (the distribution of the net charge is provided in supplementary material Fig. 2S). To make vector B⃗ an electric dipole moment vector, it was multiplied by the absolute value of the smaller position or negative charge of the dimer (although the charge cancels in eq. (1)). The angle between these two vectors was then calculated via the formula
    θ=arccos(A→·B→|A→||B→|), (1)
    where θ is the angle between the geometric center vector A⃗ and the dipole moment vector B⃗. It should be mentioned that the magnitude of both vectors, A⃗ and B⃗, are significantly different from zero, ranging from 2 Å to 76 Å for vector A⃗, and from 2 eÅ to 1400 eÅ for vector B⃗. This assures that the denominator in the eq. (1) is significantly different from zero.
  2. Calculating the distance between the interfacial dimeric plane and the surface points with largest magnitude of the electrostatic potential: The interface between the two monomers of the homodimeric complex was modeled with the plane ax + by + cz + d = 0, consisting of the points with equal distance to C1 and C2 (Figure 1b). The distance from arbitrary point X0(x0, y0, z0) to the plane can be then calculated by
    D=ax0+by0+cz0+da2+b2+c2. (2)

Figure 1.

Figure 1

Open in a new tab

Illustration of the geometrical quantities used in the analysis. a.) Vectors A⃗ and B⃗ are created between the points C1, and C2 (the points of geometrical center of mass for each protein within the homodimer), and C3 and C4 (the centers of negative and positive charges, respectively). b.) The geometrical centers are used to generate a plane perpendicular to the line connecting C1, C2 and intersecting it at the middle. The distance D is the length between any point Xo and the length of the perpendicular line from Xo to the plane.

Determining the positions of largest positive and negative potentials

To indicate and rank the positions X0(x0, y0, z0) of largest positive and negative potentials around the proteins we utilized the BION webserver (http://compbio.clemson.edu/bion_server/) [40]. The algorithm implemented in BION relies on a Delphi generated potential map in conjunction with an in-house clustering algorithm [41]. The predictions are based on the magnitude of the electrostatic potential at selected surface-bound grid points and biophysical properties of ions such as radius and charge. Two types of ions were used as probes: Ca++ for determining the positions with largest negative potential and an artificial Ca−− for finding the positions with largest positive potential. The representative grid points are sorted in descending order (by absolute value) of the potential and the position of a given point within this list is termed Rank. For the current project we used a maximum of 10 top ranked points.

Visualization

The potential map was obtained in a CUBE format file from DelPhi [39]. The CUBE output file represents the electrostatic potential at each grid point within the grid. This output was then visualized with VMD software [42] in order to plot the electrostatic potential and electrostatic field lines. The electrostatic field lines are shown as lines where the red color represents negative potential and the blue represents positive potential. For further visualizations of the proteins the program CHIMERA was also used [43].

Results and discussion

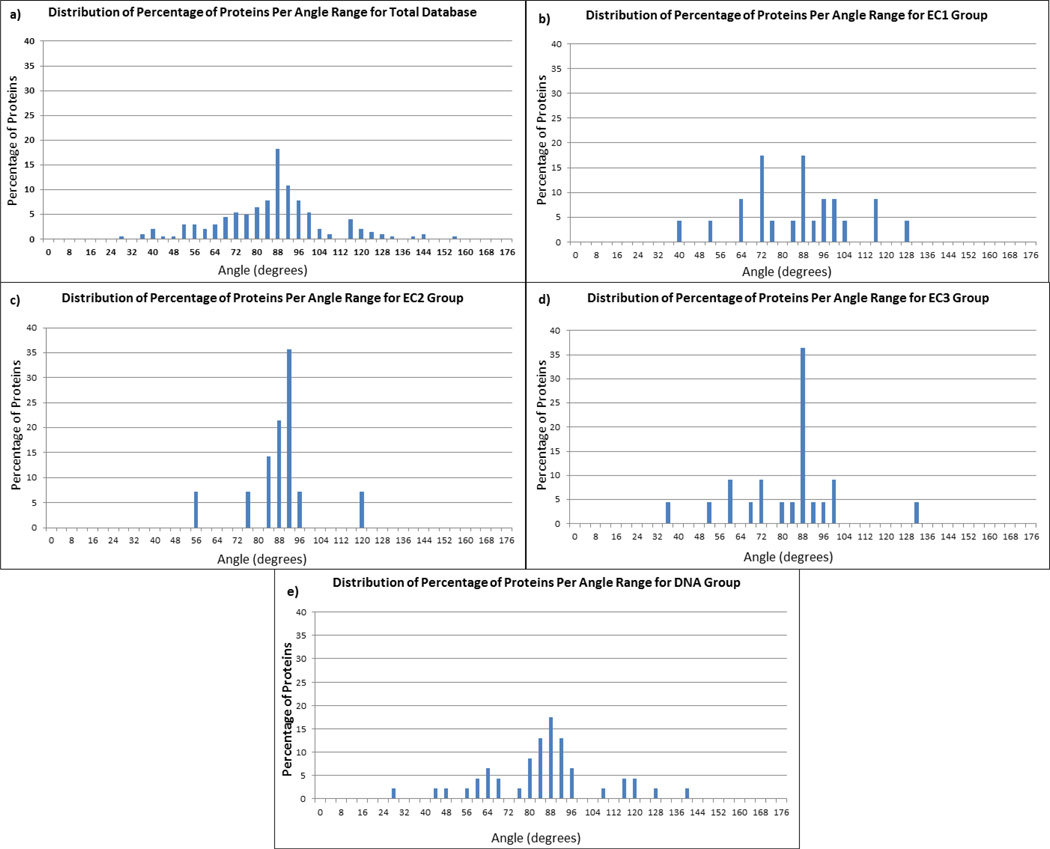
We begin our analysis with the investigation of the entire dataset focusing on the distribution of the angle between the global electrostatic dipole moment of each homodimer (vector B⃗) and the vector A⃗ connecting the centers of mass of each monomer. Figure 2a shows the angle distribution for the total dataset of 204 homodimers. It can be seen that the vast majority of the angles are very close to 90 degrees indicating that vector A⃗ and the dipole moment vector B⃗ are perpendicular. The graph resembles a normal distribution with a mean angle value of 87.6 degrees and 74% of the proteins lie within one standard deviation of the mean. Such a strong signal indicates that homodimerization indeed provides a specific electrostatic environment. Since the electrostatic dipole moment is perpendicular to the vector A⃗ connecting the centers of mass of each monomer, the global electrostatic potential lines will be focused around the vicinity of the dimer interface. Thus, for homodimers binding other charged biological macromolecules or substrates, the electrostatic potential will be providing guidance.

Figure 2.

Figure 2

Open in a new tab

Distribution of the angle between the geometric center vector and electric dipole moment vector. The percentage is taken with respect to the number of cases in each group as follows: a) all proteins in the entire database, b) proteins in the EC1 group, c) proteins in the EC2 group, d) proteins in the EC3 group, and e) proteins in the DNA group.

Continuing the analysis with the subgroups EC1, EC2, EC3 and DNA (Figure 2b–e respectively) it can be seen that the data follows the same trend. While the representative cases for these subgroups are not numerous enough to suggest a normal distribution, still one appreciates that the majority of the cases are also very close to 90 degrees. Particularly, for EC1 subgroup a large amount of cases have angle ranges between 82 and 98 degrees and nearly all the cases for EC2 are represented in this same range. The EC3 subgroup has the most scattered data but does have the largest amount of cases between 86 and 90 degrees. The DNA group shows the best results out of all the subgroups. Over half of the cases for this group are within the range of 82 and 98 degrees. It is no surprise that the DNA group shows the most convincing results in terms of enhanced electrostatics since transcription factors and DNA binding proteins bind to the highly charged DNA molecule. Therefore, a dipole moment perpendicular to the geometrical center of the complex will guide the homodimer in its approach to the DNA and will facilitate the complex formation.

The motivation to study the distribution of the points with maximal (absolute positive or negative) potential stems from the relation between the electrostatic potential and the corresponding electrostatic field, the latter being a gradient of the potential. Since the presence of an electrostatic “funnel” cannot be easily quantified, an alternative way is to model the distribution of the highest potential, which in turn can serve as an indicator of where the opposite charged substrate may be delivered. Thus, if these points of maximal potential are located at or close to the dimeric interface, this will indicate that dimerization enhances the electrostatic properties of the dimer.

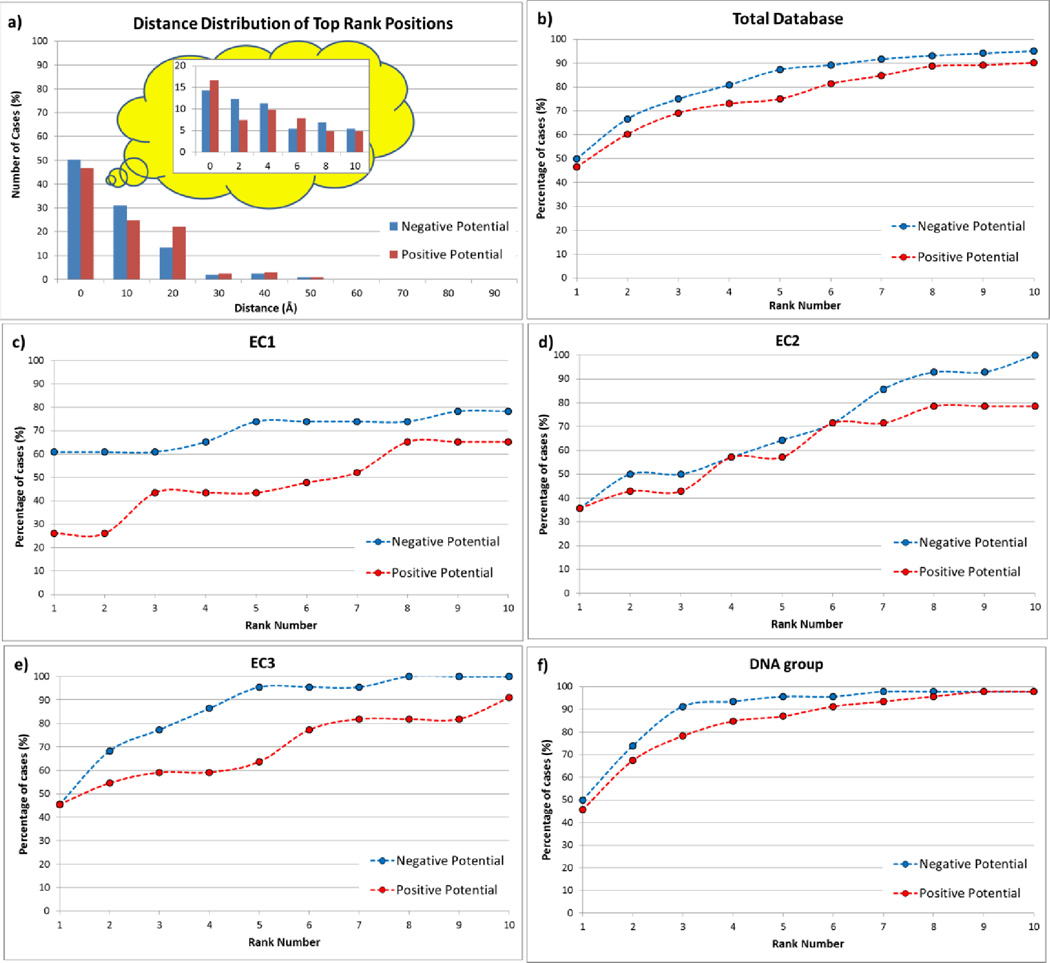
To analyze the distribution of positive and negative potentials around the homodimers we generated enrichment curves for each group of proteins in the database. The question which is intended to be addressed is if the points with largest negative and positive potentials are located on or close to the plane of the dimeric interface. The results are shown in Figure 3b–f. The y-axis represents the accumulative number of cases (true cases) being identified as located on or close to the interfacial plane. A point is considered to be true if it is located at a distance smaller than 10 Å away from the interface. The x-axis of the figure represents the accumulative Ranks. In order to explain the construction of the graphs the following example is provided: If 10% of the first Rank points are within 10 Å from the interface, the graph point will be x=1, y=10%. Only one success is counted per protein, i.e. if the first Rank point for protein “X” is a true point, the other nine predictions are ignored. This is done to assure that the enrichment curve does not exceed 100%. Proceeding to the second Rank points, we apply the same protocol, and if we identify 15% second Rank pints as true points, the next point on the graph will be x=2, y=25% (Note: Proteins for which first Rank point were identified as true are removed, and the “y” value is cumulative).

Figure 3.

Figure 3

Open in a new tab

a.) Distance distribution of the top rank positions from the interfacial plane calculated from BION server for all proteins in the entire database. b.) Enrichment curve of the top ten rank positions for all proteins in entire database. c.) Enrichment curve of the top ten rank positions for all proteins in the EC1 group. d.) Enrichment curve of the top ten rank positions for all proteins in the EC2 group. e.) Enrichment curve of the top ten rank positions for all proteins in the EC3 group. f.) Enrichment curve of the top ten rank positions for all proteins in the DNA group.

The results shown in Figure 3a–b are for the entire dataset. It can be seen that in 50% of the cases the highest negative potential point is on or close to the interfacial plane and 45% of the case the same is observed for the point with largest positive potential (Figure 3a). This indicates that homodimerization indeed creates an electrostatic environment for which the potential is the strongest around the interfacial plane. Furthermore, the enrichment curves presented in Figure 3b demonstrate that if one takes into account all ten predictions for each homodimer, there almost always will be a prediction on or close to the interfacial plane (the enrichment curves reaching 100%).

Based on the functionality of the homodimer enzymes one may expect that oxidoreductases (EC1) and hydrolase (EC3) should have a strong electrostatic potential at the active site. Moreover, DNA is known to be a highly charged macromolecule and the proteins binding to it (DNA group) must be driven by electrostatics and should have electrostatic field promoting the binding. On the other hand, the functionality of transferases (EC2), the enzymes that are involved in transferring chemical groups from one protein to another or within the same protein, may not necessarily be driven by electrostatics, since the chemical groups being involved may not be charged. It should also be taken into account that for DNA group homodimers the distribution of the points with strongest positive potential is most important, not the points with negative potential. The same is valid for all other homodimers, if there is information about the polarity of the interacting partner or substrate. At the same time, it should be clarified that in many cases, the highest potential points of different polarity are located at the opposite sides on the homodimer, as for example DNA binding homodimers. Thus, the positive potential point enhances the binding while the negative potential point at the opposite side of the homodimer provides the correct orientation by keeping the opposite side away from the DNA.

Having in mind these considerations below we proceed with the analysis of subgroups. One can see that for EC1 subgroup the first ranked negative potential position is more than 60 % of the cases (Figure 2c). The percentage is a little lower for EC3 and DNA subgroups (45% and 50% respectively), but still remarkably high (Figure 3e and f respectively). On the other hand, as it is expected, for transferases (EC2) the electrostatics is not involved much in enzyme functionality, and the top ranked negative potential position is only 35% of cases (Figure 2d). Fewer differences are seen for the enrichment curves for the highest positive potential points. As it was suggested above, the DNA subgroup shows almost no difference for negatively and positively charged potential points, while the EC1 and EC3 subgroups demonstrate the largest difference. Perhaps this is due to the specific binding partners and substrates being recognized by the homodimers in our dataset, but unfortunately we do not have such information.

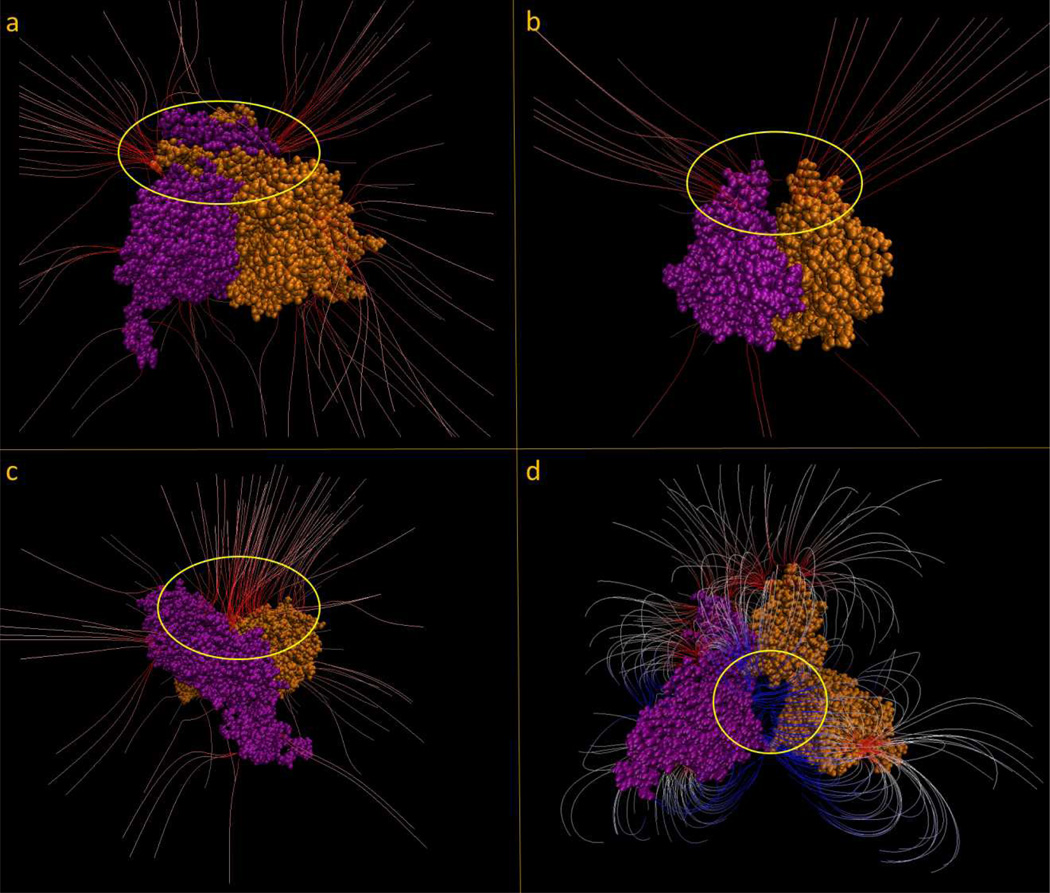
In order to demonstrate the electrostatic features suggested by the above analysis, we present a case from each subgroup where the electrostatic field lines are generated from the corresponding potential map. For each of the figures, the space of interest is circled in yellow. As a representative for the EC1 subgroup, the protein 3MAP [42] with an angle value of 86.9 degrees between the geometrical center vector and dipole moment vector is shown in Figure 4a. A large density of negatively charged electrostatic field lines funneling into the homodimer interface from either side can be seen. While there are many other field lines distributed around the protein, the largest density of field lines (represented by the intensity of the red color) are located in this region. The protein 4GTU [43] with an angle value of 77.8 degrees is shown in Figure 4b as a representative for EC2 subgroup. It can be seen that the electrostatic field lines form kind of funnel into an interfacial cleft formed by homodimerization. The next subgroup, the EC3 subgroup, is represented by the protein 1EK1 [44] with an angle value of 88.4 degrees (Figure 4c). Similar to the example from the EC1 group we see field lines distributed around the protein, but the highest density and highest charged field lines are funneling into the interface of the two monomers. From the DNA group, Figure 4d shows the protein 2RAM [45] with an angle value of 92.3 degrees. The two monomers of this protein form a pocket (circled in yellow) in which DNA binds to. We see a large density of positively charged (blue) field lines all funneling into this pocket. This positively charged funnel pulls the negatively charged DNA into the pocket for the function of the protein to take place. Note that these examples are not exclusive and for many of the homodimers in the dataset, the “funneling” effect cannot be easily demonstrated. The main obstacle of providing a more quantitative measure of the existence of “funneling” stems from the ambiguity of generating electrostatic field distribution for cases having relatively weak fields. The outcome depends on the VMD parameters used to convert the electrostatic potential distribution into the electrostatic field distribution. Because of that our analysis mostly emphasizes on the measurable quantities such as the dipole moment orientation and the distribution of the points with maximal potential, rather than the subjective claims of “funnel” existence. These cases are provided for illustration only.

Figure 4.

Figure 4

Open in a new tab

a.) Shows the protein 3MAP and the interfacial area circled in yellow. Drawing method: FieldLines; GradientMag: 3.48; Min Length: 25.95; Max Length: 38.42; Coloring Scale Data range: −1.50 to 1.50. b.) Shows the protein 4GTU and the interfacial area circled in yellow. Drawing method: FieldLines; GradientMag: 2.08; Min Length: 32.19; Max Length: 47.78; Coloring Scale Data range: −2.00 to 2.00; c.) Shows the protein 1EK1 and the interfacial area circled in yellow. Drawing method: FieldLines; GradientMag: 4.10; Min Length: 38.42; Max Length: 66.49; Coloring Scale Data range: −3.00 to 3.00; d.) Shows the protein 2RAM and the DNA binding cleft circled in yellow. Drawing method: FieldLines; GradientMag: 1.61; Min Length: 16.59; Max Length: 47.78; Coloring Scale Data range: −1.00 to 1.00.

Conclusion

It was demonstrated that homodimerization frequently results in electrostatic potential and field being strongest on or nearby the dimeric interface and dimeric plane, which is referred to as “electrostatic enhancement”. However, the calculated effects depend on the functionality of the corresponding homodimers and presumably on the physico-chemical properties of the interacting partners, including substrates. The “electrostatic enhancement” is strongly present for EC3 and DNA subgroups, and less manifested for EC2 subgroup, but still involving more than 50% of examined cases. Similar observations were made in terms of the dipole moment of the homodimers, although the effect is not so pronounced. Again, the EC3 and DNA subgroups manifest the largest fraction of cases with dipole moments perpendicular to the axis of geometrical centers of the monomers. However, EC2 also shows significant preference toward the same trend, but the number of cases is relatively small, so it is difficult to draw a definite conclusion. The distribution of the angle of the dipole moment is much broader for EC1 group, which is along the findings observed for the strongest potential discussed above. Combining all these observations together, and having in mind that electrostatics is pH- and salt-dependent and that “electrostatic enhancement” is homodimerization dependent, one can speculate that the “electrostatic enhancement” can serve as an important regulator of an homodimer’s activity.

Supplementary Material

suppl. matherial and table

Acknowledgement

We thank Barry Honig for the continuous support. The work was supported by a grant from NIH, NIGMS, grant number R01GM093937.

References

  • 1.Alberts B. Molecular biology of the cell: Garland Science. 2000 [Google Scholar]
  • 2.Schreiber G, Keating AE. Protein binding specificity versus promiscuity. Current opinion in structural biology. 2011;21:50–61. doi: 10.1016/j.sbi.2010.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Stoevesandt O, Taussig MJ. Affinity proteomics: the role of specific binding reagents in human proteome analysis. Expert review of proteomics. 2012;9:401–414. doi: 10.1586/epr.12.34. [DOI] [PubMed] [Google Scholar]
  • 4.Rohs R, Jin X, West SM, Joshi R, Honig B, et al. Origins of specificity in protein-DNA recognition. Annual review of biochemistry. 2010;79:233. doi: 10.1146/annurev-biochem-060408-091030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Przytycka TM, Singh M, Slonim DK. Toward the dynamic interactome: it's about time. Briefings in bioinformatics. 2010;11:15–29. doi: 10.1093/bib/bbp057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Elcock AH, Gabdoulline RR, Wade RC, McCammon JA. Computer simulation of protein-protein association kinetics: acetylcholinesterase-fasciculin. Journal of molecular biology. 1999;291:149–162. doi: 10.1006/jmbi.1999.2919. [DOI] [PubMed] [Google Scholar]
  • 7.Wlodek ST, Shen T, McCammon JA. Electrostatic steering of substrate to acetylcholinesterase: analysis of field fluctuations. Biopolymers. 2000;53:265–271. doi: 10.1002/(SICI)1097-0282(200003)53:3<265::AID-BIP6>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
  • 8.Schreiber G, Shaul Y, Gottschalk KE. Electrostatic design of protein–protein association rates. Protein Design: Springer. 2006:235–249. doi: 10.1385/1-59745-116-9:235. [DOI] [PubMed] [Google Scholar]
  • 9.Alsallaq R, Zhou HX. Electrostatic rate enhancement and transient complex of protein–protein association. Proteins: Structure, Function, and Bioinformatics. 2008;71:320–335. doi: 10.1002/prot.21679. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Pang X, Zhou KH, Qin S, Zhou H-X. Prediction and Dissection of Widely-Varying Association Rate Constants of Actin-Binding Proteins. PLoS computational biology. 2012;8:e1002696. doi: 10.1371/journal.pcbi.1002696. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Zhang Z, Witham S, Alexov E. On the role of electrostatics in protein–protein interactions. Physical biology. 2011;8:035001. doi: 10.1088/1478-3975/8/3/035001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Kukic P, Nielsen JE. Electrostatics in proteins and protein-ligand complexes. Future medicinal chemistry. 2010;2:647–666. doi: 10.4155/fmc.10.6. [DOI] [PubMed] [Google Scholar]
  • 13.Sinha N, Smith-Gill SJ. Electrostatics in protein binding and function. Current Protein and Peptide Science. 2002;3:601–614. doi: 10.2174/1389203023380431. [DOI] [PubMed] [Google Scholar]
  • 14.Sheinerman FB, Norel R, Honig B. Electrostatic aspects of protein–protein interactions. Current opinion in structural biology. 2000;10:153–159. doi: 10.1016/s0959-440x(00)00065-8. [DOI] [PubMed] [Google Scholar]
  • 15.Jones S, Thornton JM. Principles of protein-protein interactions. Proceedings of the National Academy of Sciences. 1996;93:13–20. doi: 10.1073/pnas.93.1.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Bulenger S, Marullo S, Bouvier M. Emerging role of homo-and heterodimerization in G-protein-coupled receptor biosynthesis and maturation. Trends in pharmacological sciences. 2005;26:131–137. doi: 10.1016/j.tips.2005.01.004. [DOI] [PubMed] [Google Scholar]
  • 17.Deloulme JC, Gentil BJ, Baudier J. Monitoring of S100 homodimerization and heterodimeric interactions by the yeast two-hybrid system. Microscopy research and technique. 2003;60:560–568. doi: 10.1002/jemt.10298. [DOI] [PubMed] [Google Scholar]
  • 18.Van Brocklyn JR, Behbahani B, Lee NH. Homodimerization and heterodimerization of S1P/EDG sphingosine-1-phosphate receptors. Biochimica et Biophysica Acta (BBA)-Molecular and Cell Biology of Lipids. 2002;1582:89–93. doi: 10.1016/s1388-1981(02)00141-5. [DOI] [PubMed] [Google Scholar]
  • 19.Matthews JM, Sunde M. Dimers, oligomers, everywhere. Protein Dimerization and Oligomerization in Biology: Springer. 2012:1–18. doi: 10.1007/978-1-4614-3229-6_1. [DOI] [PubMed] [Google Scholar]
  • 20.Talley K, Ng C, Shoppell M, Kundrotas P, Alexov E. On the electrostatic component of protein-protein binding free energy. BMC Biophysics. 2008;1:2. doi: 10.1186/1757-5036-1-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Angers S, Salahpour A, Bouvier M. Dimerization: an emerging concept for G protein-coupled receptor ontogeny and function. Annual review of pharmacology and toxicology. 2002;42:409–435. doi: 10.1146/annurev.pharmtox.42.091701.082314. [DOI] [PubMed] [Google Scholar]
  • 22.Béland M, Motard J, Barbarin A, Roucou X. PrPC homodimerization stimulates the production of PrPC cleaved fragments PrPN1 and PrPC1. The Journal of Neuroscience. 2012;32:13255–13263. doi: 10.1523/JNEUROSCI.2236-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Petrova IM, Lahaye LL, Martiáñez T, de Jong AW, Malessy MJ, et al. Homodimerization of the Wnt Receptor DERAILED Recruits the Src Family Kinase SRC64B. Molecular and cellular biology. 2013;33:4116–4127. doi: 10.1128/MCB.00169-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Ishitani S, Inaba K, Matsumoto K, Ishitani T. Homodimerization of Nemo-like kinase is essential for activation and nuclear localization. Molecular biology of the cell. 2011;22:266–277. doi: 10.1091/mbc.E10-07-0605. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Cheng J, Goldstein R, Stec B, Gershenson A, Roberts MF. Competition between Anion Binding and Dimerization Modulates Staphylococcus aureus Phosphatidylinositol-specific Phospholipase C Enzymatic Activity. Journal of Biological Chemistry. 2012;287:40317–40327. doi: 10.1074/jbc.M112.395277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Bae JY, Park HH. Crystal structure of NALP3 protein pyrin domain (PYD) and its implications in inflammasome assembly. Journal of Biological Chemistry. 2011;286:39528–39536. doi: 10.1074/jbc.M111.278812. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Pegg AE, Michael AJ. Spermine synthase. Cellular and molecular life sciences. 2010;67:113–121. doi: 10.1007/s00018-009-0165-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Tsuchiya D, Shimizu N, Tomita M. Cooperativity of two active sites in bacterial homodimeric aconitases. Biochemical and biophysical research communications. 2009;379:485–488. doi: 10.1016/j.bbrc.2008.12.096. [DOI] [PubMed] [Google Scholar]
  • 29.Béland M, Roucou X. Homodimerization as a molecular switch between low and high efficiency PrPC cell surface delivery and neuroprotective activity. Prion. 2013;7:0–1. doi: 10.4161/pri.23583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Li D, Sinha KK, Hay MA, Rinaldi CR, Saunthararajah Y, et al. RUNX1-RUNX1 homodimerization modulates RUNX1 activity and function. Journal of Biological Chemistry. 2007;282:13542–13551. doi: 10.1074/jbc.M700074200. [DOI] [PubMed] [Google Scholar]
  • 31.Wu H, Min J, Zeng H, McCloskey DE, Ikeguchi Y, et al. Crystal Structure of Human Spermine Synthase IMPLICATIONS OF SUBSTRATE BINDING AND CATALYTIC MECHANISM. Journal of Biological Chemistry. 2008;283:16135–16146. doi: 10.1074/jbc.M710323200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Zhang Z, Zheng Y, Petukh M, Pegg A, Ikeguchi Y, et al. Enhancing Human Spermine Synthase Activity by Engineered Mutations. PLoS computational biology. 2013;9:e1002924. doi: 10.1371/journal.pcbi.1002924. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.de Beer TA, Berka K, Thornton JM, Laskowski RA. PDBsum additions. Nucleic acids research: gkt940. 2013 doi: 10.1093/nar/gkt940. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Laskowski RA, Hutchinson EG, Michie AD, Wallace AC, Jones ML, et al. PDBsum: a Web-based database of summaries and analyses of all PDB structures. Trends in biochemical sciences. 1997;22:488–490. doi: 10.1016/s0968-0004(97)01140-7. [DOI] [PubMed] [Google Scholar]
  • 35.Georgescu RE, Alexov EG, Gunner MR. Combining Conformational Flexibility and Continuum Electrostatics for Calculating pKas in Proteins. Biophysical Journal. 2002;83:1731–1748. doi: 10.1016/S0006-3495(02)73940-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Alexov E, Gunner M. Incorporating protein conformational flexibility into the calculation of pH-dependent protein properties. Biophysical Journal. 1997;72:2075–2093. doi: 10.1016/S0006-3495(97)78851-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Smith N, Witham S, Sarkar S, Zhang J, Li L, et al. DelPhi web server v2: incorporating atomic-style geometrical figures into the computational protocol. Bioinformatics. 2012;28:1655–1657. doi: 10.1093/bioinformatics/bts200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Sarkar S, Witham S, Zhang J, Zhenirovskyy M, Rocchia W, et al. DelPhi web server: a comprehensive online suite for electostatic calculations of biological macromolecules and their complexes. Commun Comput Phys. 2012 doi: 10.4208/cicp.300611.201011s. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Li L, Li C, Sarkar S, Zhang J, Witham S, et al. DelPhi: a comprehensive suite for DelPhi software and associated resources. BMC Biophysics. 2012;5:9. doi: 10.1186/2046-1682-5-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Petukh M, Kimmet T, Alexov E. BION web server: predicting non-specifically bound surface ions. Bioinformatics. 2013;29:805–806. doi: 10.1093/bioinformatics/btt032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Petukh M, Li C, Alexov E. Predicting Non-Specifically Bound Ions: Application to Bion Webserver and Beryllium Disease. Biophysical Journal. 2013;104:506. [Google Scholar]
  • 42.Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. Journal of molecular graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  • 43.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, et al. UCSF Chimera—a visualization system for exploratory research and analysis. Journal of computational chemistry. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

suppl. matherial and table
NIHMS590109-supplement-suppl__matherial_and_table.docx (43.3KB, docx)

RESOURCES