Using Extreme Phenotype Sampling to Identify the Rare Causal Variants of Quantitative Traits in Association Studies

Abstract

Variants identified in recent genome-wide association studies based on the common-disease common-variant hypothesis are far from fully explaining the hereditability of complex traits. Rare variants may, in part, explain some of the missing hereditability. Here, we explored the advantage of the extreme phenotype sampling in rare-variant analysis and refined this design framework for future large-scale association studies on quantitative traits. We first proposed a power calculation approach for a likelihood-based analysis method. We then used this approach to demonstrate the potential advantages of extreme phenotype sampling for rare variants. Next, we discussed how this design can influence future sequencing-based association studies from a cost-efficiency (with the phenotyping cost included) perspective. Moreover, we discussed the potential of a two-stage design with the extreme sample as the first stage and the remaining nonextreme subjects as the second stage. We demonstrated that this two-stage design is a cost-efficient alternative to the one-stage cross-sectional design or traditional two-stage design. We then discussed the analysis strategies for this extreme two-stage design and proposed a corresponding design optimization procedure. To address many practical concerns, for example measurement error or phenotypic heterogeneity at the very extremes, we examined an approach in which individuals with very extreme phenotypes are discarded. We demonstrated that even with a substantial proportion of these extreme individuals discarded, an extreme-based sampling can still be more efficient. Finally, we expanded the current analysis and design framework to accommodate the CMC approach where multiple rare-variants in the same gene region are analyzed jointly.

INTRODUCTION

Genome-wide association studies (GWAS) have been successfully performed in hundreds of human traits. These studies are based on the common-disease common-variant hypothesis [Reich and Lander, 2001] and have resulted in thousands of susceptibility loci identified and replicated across all traits [Hindorff et al., 2010]. However, these common variants are far from fully explaining the total hereditability of those traits [McCarthy et al., 2008; Ioannidis et al., 2009; Maher, 2008]. Rare variants may, in part, account for the missing hereditability. Human exome sequencing has shown that nonsynonymous SNPs impacting protein function tend to be rare [Ng et al., 2008], with these rare functional variants often having a larger estimated effect in comparison with common variants [Frazer et al., 2009]. In addition, previous sequencing studies focused on specific candidate genes have demonstrated an effect of rare variants on complex traits [Ramser et al., 2008; Nejentsev et al., 2009; Ji et al., 2008].

To systematically identify the rare causal variants in the genome, there are several challenges that need to be addressed. Due to the low minor allele frequency (MAF), rare causal variants are more likely to be in weak linkage disequilibrium (LD) with nearby markers, making it infeasible to tag those variants. This will limit the success of cost reduction strategies by restricting the number of measured variants. Thus, it is preferable to measure all variants via whole-genome or at least whole-exome sequencing using sequencing techniques with high coverage. Furthermore, although collectively the rare variants may contribute considerably, the impact of a single variant may be small. Consequently, large sample sizes will be needed to detect specific rare causal variants with traditional designs. The current monetary cost associated with next-generation sequencing in large sample sizes limits the feasibility of traditional study designs and motivates the need for alternative solutions.

Here, we explored the potential of extreme-phenotype sampling (EPS), an idea with a long history in linkage analysis and LD mapping, in association studies aiming at rare causal variants of quantitative traits [Gu et al., 1997; Liang et al., 2000; Risch and Zhang, 1995; Wallace et al., 2006; Chen et al., 2005; Slatkin, 1999]. Based on a previously proposed analysis framework [Huang and Lin, 2007], we developed a corresponding power calculation method for EPS. We further investigated the usefulness of this design in future sequencing-based association studies from a cost-efficiency perspective with both genotyping and phenotyping costs taken into account. To address the practical limitations of the one-stage EPS when the source population is limited, we explored a two-stage design with the extreme sample sequenced in the first stage and the remaining nonextreme subjects utilized in the second stage. Analysis strategies for this extreme two-stage design were discussed and the corresponding optimization approaches were proposed. To address additional difficulties, such as potential phenotypic heterogeneity and measurement errors in the very extreme, we further explored the potential of an “almost-extreme” sample—an approach in which the very most extreme individuals are discarded in order to obtain a more robust inference. Finally, to demonstrate application of these ideas to analysis approaches aimed at testing multiple rare variants jointly in a region, we expanded the framework to accommodate the popular CMC approach [Li and Leal, 2008].

MATERIALS AND METHODS

EPS AND THE ANALYSIS FRAMEWORK

Assume that there is a genetic factor G associated with a quantitative trait ϒ:

$${\Upsilon }_g={\mathrm{\mu }}_g+\mathrm{\epsilon },$$

$${\mathrm{\mu }}_g={\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}g,$$

$$\mathrm{\epsilon }~N(0,{\mathrm{\delta }}^2).$$

We assume that ϒ follows a normal distribution with mean µ_g and variance δ² when G = g. β₀ is the mean of ϒ when G is absent, and β₁ represents the additive effect of G.

The extreme sample is defined by sampling individuals from the tails of ϒ, i.e., ϒ < C₂ or ϒ > C₁, C₁ > µ_y > C₂. Here we assume that C₁ and C₂ define the Kth and 1−Kth quantile in each extreme end of ϒ with the same number of individuals sampled from the two ends, although the following methods can be easily generalized to scenarios with asymmetric cutoffs.

According to Huang et al. [24], we can model the distribution of ϒ conditional on G and the sampling framework. This is a variation of the truncated normal distribution [Johnson and Kotz, 1970] if we believe that ϒ follows a normal distribution conditional on G, with the density function:

$$f(\Upsilon =y|G=g,\Upsilon >C_1\text{or}\Upsilon <C_2)=\frac{\mathbb{N}({\mathrm{\mu }}_g,{\mathrm{\delta }}^2)}{1-\mathrm{\Phi }\left(\frac{C_1-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right)+\mathrm{\Phi }\left(\frac{C_2-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right)}.$$ (2)

Here ℕ(µ_g, δ²) is the normal density function with mean µ_g and variance δ² and φ is the cumulative normal function. Its likelihood can be easily maximized numerically and the hypothesis of no association between ϒ and G can be tested using a likelihood ratio test.

POWER CALCULATION FOR EPS

To comprehensively illustrate the performance of EPS for rare variants, we developed a power calculation approach for the analysis framework proposed by Huang and Lin [2007] based on the likelihood theory. Under the null hypothesis, the likelihood ratio test statistics approximately follow a χ² distribution.

Under the alternative hypothesis, the likelihood ratio statistics approximately follow a noncentral χ² distribution, L ~ χ²(λ, η) where the noncentrality parameter (NCP) η can be calculated as η = N γ, with γ as the expected log likelihood contribution for a single subject. The power of likelihood ratio test is then:

$$\Gamma =1-\mathrm{\Psi }(\mathrm{\Lambda },\mathrm{\lambda },\mathrm{\eta }).$$ (3)

Details of the calculation of γ as well as the consistency of this power calculation approach with empirical power are shown in Appendix A.

INFLUENCE OF MAF

Across different minor allele frequencies (MAFs), we compared the advantage of EPS with two other designs to detect a single causal variant in the genome: (1) the cross-sectional design in which subjects are randomly sampled with a corresponding linear regression analysis to assess the association between ϒ and G; and (2) a “case-control” design with a corresponding likelihood ratio test for the genotype frequency difference in cases and controls. For the “case-control” design, the threshold employed to dichotomize the quantitative trait is assumed to be the upper 10% percentile of the quantitative trait ϒ (although conclusions are similar for thresholds of 20, 10, 5, or 1%). Equal numbers of cases and controls were randomly sampled, and allele frequencies in the cases were compared with controls. Assuming one million independent variants in the genome, we used a genome-wide significance threshold of 0.05/1 M = 5.0 × 10 ⁻⁸.

To illustrate the performance of the various approaches across a range of MAF, we compared the NCPs of each design for a given sample size when the causal effect of the variant is fixed. We calculated the ratio of the NCPs, using the cross-sectional design as a reference.

The calculation of the NCP follows standard procedures for the cross-sectional and case-control designs [Gauderman and Morrison, 2006]. Note that here we assume a large source population in which to sample from for EPS.

COST-EFFECTIVENESS OF EPS

Let N_Γ denote the sample size needed to achieve a given power Γ with the upper and lower Kth percentile of the distribution of ϒ sequenced in EPS. If S₁ and S₂ are the sequencing and phenotyping costs for a single individual, the cost of EPS is:

$$S=S_1{N}_{\mathrm{\Gamma }}+\frac{S_2{N}_{\mathrm{\Gamma }}}{2K}.$$

Let N_Γ, represent the number of subjects to be sequenced to achieve the same power in the cross-sectional design. Thus, the cost of the cross-sectional design is:

$$S\prime =(S_1+S_2)N_{\mathrm{\Gamma }\prime }.$$

We used the cost ratio of the cross-sectional design vs. EPS to represent the relative cost-effectiveness of EPS. With a given sequencing/phenotyping cost ratio r = S₁/S₂, this total cost ratio is:

$$\frac{S\prime }{S}=\frac{(S_1+S_2)N_{\mathrm{\Gamma }\prime }}{S_1{N}_{\mathrm{\Gamma }}+\frac{S_2{N}_{\mathrm{\Gamma }}}{2K}}=\frac{2K(1+r)\gamma }{(2K+r)\gamma \prime }.$$

Here γ and γ′ is the expected log likelihood contribution for a single subject in EPS and cross-sectional design, respectively. S′/S is a function of K and can be maximized numerically with simple optimization approach such as a golden section search [Kiefer, 1953].

For different sequencing/phenotyping cost ratios, r, we calculated S′/S and the corresponding optimized Ks.

TWO-STAGE EXTREME SAMPLING DESIGN

Suppose a random sample of n individuals is available for genotyping and in the first stage of the extreme two-stage design, whole-genome sequencing of M markers is performed on individuals in the upper and lower K percentile of ϒ. That is, the total number of individuals sequenced in the first stage is a proportion of the total number of n individuals (π_sample = 2 K). Let π_marker be the proportion of markers selected for genotyping in the remaining n(1 − π_sample) individuals with nonextreme phenotypes. Here for simplification we require that for the markers to be followed up in the second stage, the P-values should be less than π_marker in the first stage.

There are two possible strategies for the joint analysis of the two-stage data in the extreme two-stage design. The first strategy is similar in spirit to the joint analysis in the traditional two-stage design [Skol et al., 2006], in which the test statistics in the two stages are combined to produce a joint test statistic. We call this strategy as the statistics-combining strategy. The second strategy directly combines the data on the markers genotyped in both stages and is named as the data-combining strategy. Here we focus only on the data-combining strategy. For completeness, details of the statistics-combining strategy and comparison of the two strategies are shown in Appendix B.

In the data-combining strategy, we combine the data for the Mπ_marker SNPs in the two stages and the joint test statistics (T_joint) are easily generated based on the joint data. For the Mπ_marker SNPs genotyped in the second stage, the joint statistics are actually equivalent to the test statistics in the cross-sectional design in which all the individuals are sequenced simultaneously. Then a significance threshold considering all the M markers is applied to the Mπ_marker test statistics in the second stage. This is equivalent to performing a costly cross-sectional design, but only reporting the results of the Mπ_marker SNPs. Under the null hypothesis this approach is conservative, since with Λ₁ and Λ_genome being the critical values for the first stage and genome-wide significance level and T₁ and T_joint being the corresponding test statistics, it is always true that

$$\text{Pr}(T_{\text{joint}}<{\mathrm{\Lambda }}_{\text{Genome}},T_1>{\Lambda }_1)\le \text{Pr}(T_{\text{joint}}>{\mathrm{\Lambda }}_{\text{Genome}}).$$

Despite its conservative nature, under the alternative hypothesis there is a modest gain in power when comparing the data-combining strategy to the statistics-combining strategy (see Appendix B).

We compared the extreme two-stage design (based on the data-combining strategy) with the traditional two-stage design with cross-sectional random sample in both stages, and a one-stage cross-sectional design in which whole-genome sequencing is performed on all the available subjects.

OPTIMIZATION OF THE EXTREME TWO-STAGE DESIGN

Suppose that in a two-stage design with the extreme sample as the first stage, the total genotyping cost available is Δ. Assume that per SNP genotyping cost is τ₁ for the first-stage whole genome sequencing and τ₂ for the second-stage customized genotyping. Then for a given proportion (π_sample) of individuals allocated in the first stage, the proportion of markers (π_marker) passed to the second stage genotyping can be calculated as:

$${\mathrm{\pi }}_{\text{marker}}=\frac{\mathrm{\Delta }-N{\tau }_1{\mathrm{\pi }}_{\text{sample}}M}{N(1-{\mathrm{\pi }}_{\text{sample}}){\tau }_{2}M}.$$

Here M is the number of SNPs in the first stage. If we assume Δ = ψNτ₁ M and τ₂/τ₁ = ρ, then for any 0<ψ≤l, we have:

$${\mathrm{\pi }}_{\text{marker}}=\frac{\mathrm{\psi }-{\mathrm{\pi }}_{\text{sample}}}{(1-{\mathrm{\pi }}_{\text{sample}})\mathrm{\rho }}.$$

For the data-combining strategy, the power of the two-stage design can be written as:

$$\text{Pr}(T_{\text{joint}}>{\mathrm{\Lambda }}_{\text{Genome}},T_1>{\mathrm{\Lambda }}_1|\mathrm{\theta })=\text{Pr}(T_{\text{joint}}>{\mathrm{\Lambda }}_{\text{Genome}}|\mathrm{\theta })\text{Pr}(T_1>{\mathrm{\Lambda }}_1|\mathrm{\theta }),$$

since with given parameter θ, T_joint is not affected by the selection of Λ₁. Thereby with fixed total sample size, optimizing the two-stage design (with this analysis strategy) is equivalent to optimizing Pr(T₁ >Λ₁), which is actually the power of one-stage EPS with a K value of π_sample/2 and alpha level of π_marker There is no closed form solution that can maximize Pr(T₁ > Λ₁). However, we can calculate it for any 0<π_sample ≤ ψ, and the π_sample (and the corresponding π_marker) can be easily optimized to get a maximized Pr(T₁ > Λ₁) with simple optimization techniques.

The statistics-combining strategy can be optimized in a similar way, although the optimized π_sample (and the corresponding π_marker) is different for the two analysis strategies. Comparison of the optimization results of the two strategies can be found in Appendix C.

EXTENSION OF THE ANALYSIS AND POWER CALCULATION FRAMEWORK

Almost-extreme sampling

The very extremes of the phenotypes, although in theory highly informative, can be vulnerable to potential measurement errors and phenotype heterogeneity. In practice, the investigators might want to discard the very extremes and use the almost-extreme sample for more robust hypothesis inference. This leads to a slightly different likelihood with a modified truncation function:

$$f(\Upsilon =y|G=g,{\mathrm{\mu }}_g>C_2>\Upsilon >C_4\text{or}{C}_3>\Upsilon >C_1>{\mathrm{\mu }}_g)=\frac{\mathbb{N}({\mathrm{\mu }}_g,{\mathrm{\delta }}^2)}{\mathrm{\Phi }\left(\frac{C_2-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right)-\mathrm{\Phi }\left(\frac{C_4-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right)+\mathrm{\Phi }\left(\frac{C_3-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right)-\mathrm{\Phi }\left(\frac{C_1-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right)}.$$

Here C₁ and C₂ define the extreme phenotype to sample from, and C₃ and C₄ define the extreme tails of the phenotypic distribution in which individuals are discarded. The power calculation and design optimization procedures discussed previously can be easily extended to the almost-extreme sample.

From single-SNP to multiple-SNP based analysis

In the previous sections, we focus on single-SNP based analysis in EPS. Nevertheless, several multiple-SNP- or gene-region-based rare-variant analysis strategies have been proposed as powerful alternatives to single-marker-based strategies [Li and Leal, 2008; Madsen and Browning, 2009; Zawistowski et al., 2010; Asimit and Zeggini, 2010; Bansal et al., 2010]. In particular, the CMC approach proposed by Li and Leal [2008] is conceptually straightforward and more efficient than a single-marker-based analysis. Based on the CMC strategy, we extend the likelihood-based extreme sample analysis framework to incorporate multiple variants in the same gene region. Thus, supposing that in a gene region M rare-variants G₁, G₂ … G_M with MAFs p₁, p₂ … p_M are associated with ϒ with effects β₁, β₂,… β_M, a new variable can be defined by collapsing those rare variants:

$$G_{\text{CMC}}=\{\begin{array}{cc}1\hfill & \text{if}\sum _{m=1:M}{G}_m>0,\hfill \\ 0\hfill & \text{Otherwise}.\hfill \end{array}$$

The likelihood of the CMC-based extreme-value analysis can be approximately calculated as:

$$L(\Upsilon =y|G_{\text{CMC}},\Upsilon >C_1\text{or}\Upsilon <C_2)=\frac{\mathbb{N}({\mathrm{\mu }}_{\text{CMC}},{\mathrm{\delta }}^2)}{1-\mathrm{\Phi }\left(\frac{C_1-{\mathrm{\mu }}_{\text{CMC}}}{\mathrm{\delta }}\right)+\mathrm{\Phi }\left(\frac{C_2-{\mathrm{\mu }}_{\text{CMC}}}{\mathrm{\delta }}\right)},$$

$${\mathrm{\mu }}_{\text{CMC}}={\mathrm{\beta }}_0+{\mathrm{\beta }}_{\text{CMC}}{G}_{\text{CMC}}.$$

Here β_CMC represents the marginal association of G_CMC with the outcome, which is determined by the MAFs of the M markers, the corresponding LD structure as well as the effects of each marker. Similar to single-variant-based analysis, this likelihood can be easily maximized. Furthermore, power calculation and design optimization procedures used for the single-variant analysis can be easily extended to CMC with flexibility in specification of the MAFs and effects of the M markers.

As an example, we calculated the power of the CMC-based analysis for three sampling scenarios of 800 individuals: the extreme, random, and case-control sample. For simplification, we assume that there are 100 SNPs with MAF < 0.01 in the gene-region, with 10 or 20 of these SNPs causal. The causal SNPs were assumed to contribute equally to the phenotype variance with a total variance contribution of 0.02.

RESULTS

EPS IN RARE VARIANTS

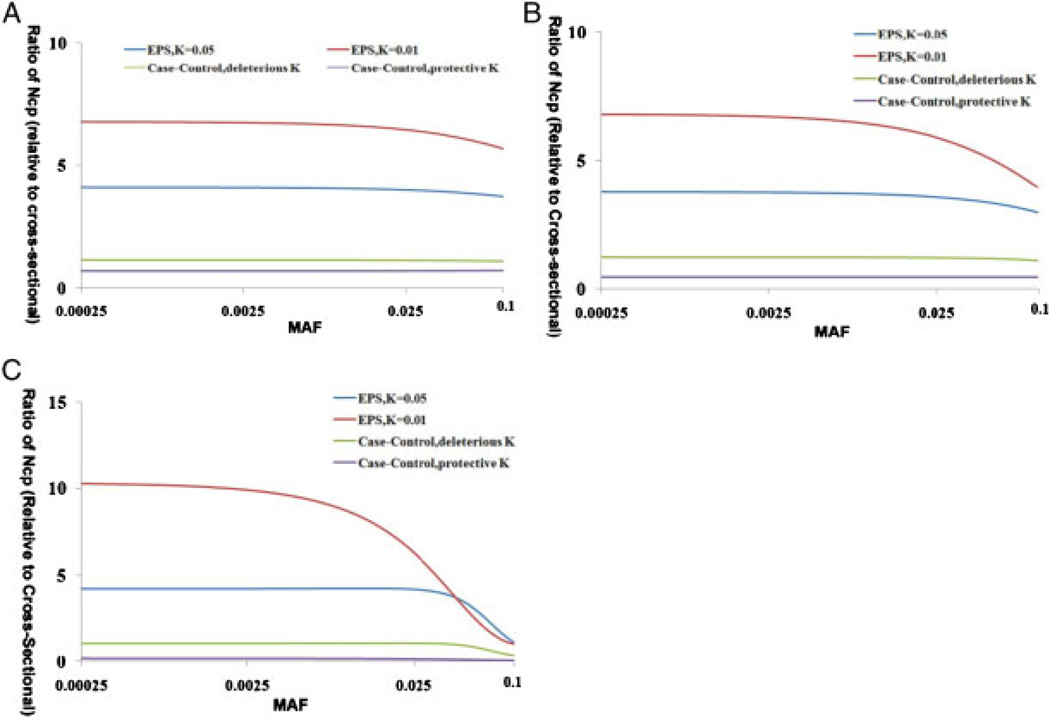
The NCP ratio in the EPS or case-control design relative to the cross-sectional design with the same sample size is shown in Figure 1. The NCP ratio of EPS is always greater than 1 and is always larger than that of the case-control design. Moreover, this advantage in NCP ratio is enhanced for rare variants. For example, when the effect size is fixed at 0.5, the NCP ratio for EPS (K = 0.01) relative to the cross-sectional design changes from 3.95 to 6.06 when the MAF changes from 0.1 to 0.02. More extreme K values and larger effect sizes lead to increased gains for the EPS approach. There is a slight increase in the NCP ratio for the case-control design as the MAF decreases.

Fig. 1.

Influence of the MAF on the performance of different designs. (A) Performance of EPS across different MAFs when β₁ equals 0.25. (B) Performance of EPS across different MAFs when β₁ equals 0.5. (C) Performance of EPS across different MAFs when β₁ equals 1. MAF, minor allele frequency; EPS, extreme-phenotype sampling.

COST-EFFICIENCY OF EPS

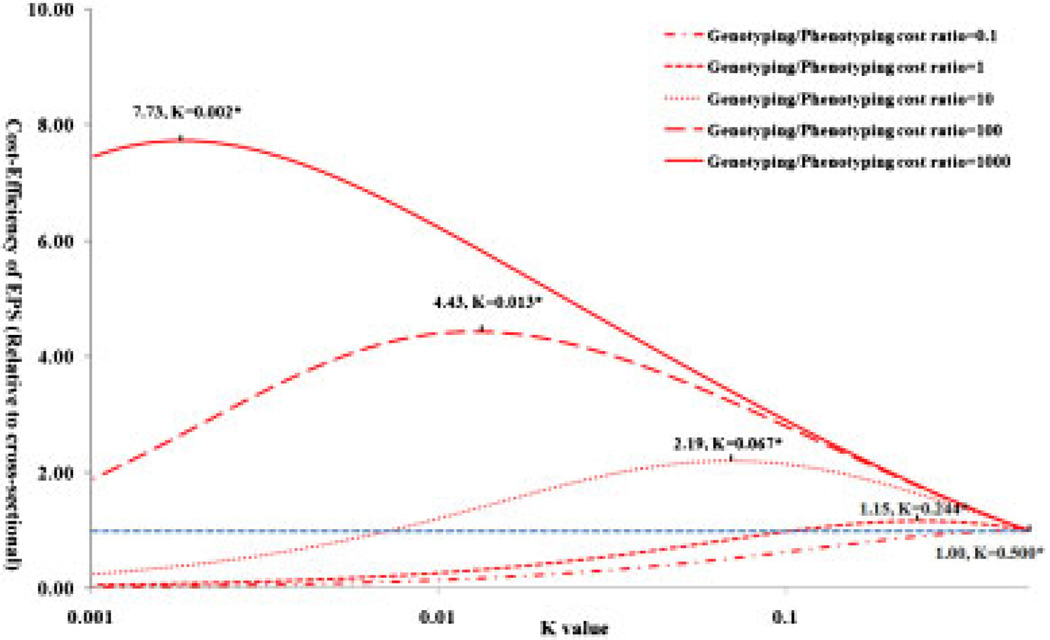
The relative cost-efficiency of EPS with different K values when the genotyping/phenotyping cost ratio varies is demonstrated in Figure 2. Here, the cost-efficiency is measured by the ratio of the total cost to achieve 80% power (including both phenotyping and genotyping cost) with the EPS to that with the cross-sectional design. EPS is less cost-efficient than a cross-sectional design when phenotyping is more expensive than genotyping. When the genotyping/phenotyping cost ratio is low (≤10), the gain in cost-efficiency is marginal and EPS can be less cost-efficient especially for a poorly chosen K. However, when the genotyping/phenotyping cost ratio is high (>10) EPS is more cost-efficient even with a suboptimal K. With an optimized K, this advantage in cost-efficiency is further improved. For example, when the genotyping/phenotyping cost ratio is 100, EPS can be 4.43 times more cost-efficient than the cross-sectional design for an optimal K of 0.013.

Fig. 2.

Cost-efficiency of EPS with different genotyping/phenotyping cost ratios. EPS, extreme-phenotype sampling.

PERFORMANCE OF THE EXTREME TWO-STAGE DESIGN

In more realistic scenarios, the size of the source population available for sampling is limited. In this scenario, the power of the proposed extreme two-stage design and traditional two-stage design is compared in Table I. With similar proportions of samples allocated in stage 1 (π_sample) and similar proportions of markers selected to follow up in stage 2 (π_marker), an extreme sampling procedure in the first stage can greatly increase the power of the two-stage design. Furthermore, to achieve nearly the same power as the more costly one-stage design, much less genotyping is required in the first stage of the extreme two-stage design. For example, when a variant with MAF of 0.005 contributes 0.25% variance (with a β of 0.5), a sample of 18,177 individuals is required to be sequenced to achieve a power of 90% for the cross-sectional design with a genome-wide significance level of 5.0 × 10⁻⁸. Similar power can be achieved by sequencing only 20% of the subjects in the extreme two-stage design (corresponding to a K of 0.10) when π_marker = 0.001 for the second stage. In contrast with the same π_marker and π_sample, the power of the traditional two-stage design is only 20%.

TABLE I.

Power of extreme two-stage and traditional two-stage designs with different proportion of subjects (π_Sample) allocated in the stage1^a

	β = 0.71b		β = 0.50c		β = 0.35d
πSample	Extreme two-stage	Traditional two-stage	Extreme two-stage	Traditional two-stage	Extreme two-stage	Traditional two-stage
0.05	0.52	0.03	0.50	0.03	0.48	0.03
0.1	0.78	0.11	0.77	0.11	0.74	0.11
0.2	0.89	0.36	0.88	0.36	0.88	0.36
0.4	0.90	0.76	0.90	0.76	0.90	0.76
0.6	0.90	0.88	0.90	0.88	0.90	0.88

^aThe proportion of markers selected to follow up in stage 2 (π_marker) is set to be 0.001. The MAF of the causal SNP is set to be 0.005. Genome-wide significance level is set to be 5.0 × 10⁻⁸. In the extreme two-stage design, we assume individuals from π_sample/2 proportion on both tails of the phenotype are located in the first stage; in the traditional two-stage design, π_sample proportion of individuals is randomly located in the first stage.

^bCorresponding to a variance contribution of 0.5%, total sample size is set to be 9,100 to ensure a maximum power of 0.90.

^cCorresponding to a variance contribution of 0.25%, total sample size is set to be 18,177 to ensure a maximum power of 0.90.

^dCorresponding to a variance contribution of 0.125%, total sample size is set to be 36,331 to ensure a maximum power of 0.90.

OPTIMIZATION OF THE EXTREME TWO-STAGE DESIGN

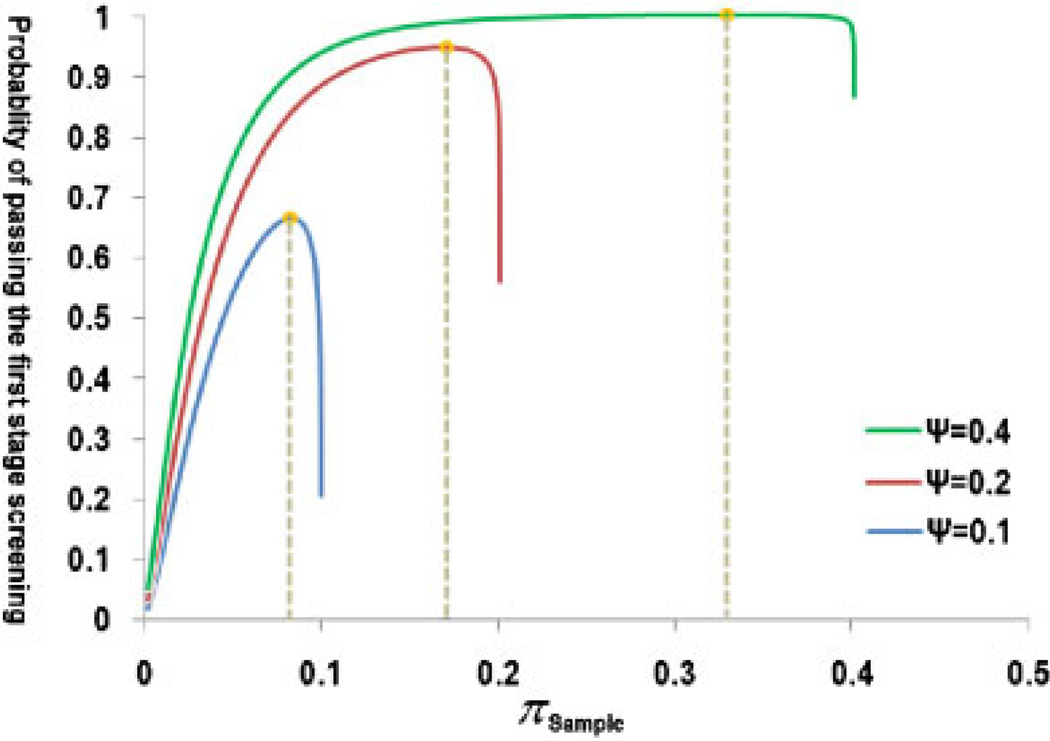
Figure 3 presents examples of optimizing the extreme two-stage design under various genotyping budgets (ψ) when the per SNP genotyping cost ratio (ρ) in the two stages equals 0.1. The optimized π_sample and the maximum power of the extreme two-stage design are further shown in Table II. With an optimized extreme two-stage design, a genotyping budget (ψ) about 20% of that in a one-stage design can yield a power (88%) close to the maximum (90%).

Fig. 3.

An example of the optimization of the extreme two-stage design.

TABLE II.

Optimized π_sample and power of the extreme two-stage design based on the data-combining strategy^a

ψ	Optimized πsample	Optimized power
0.1	0.081	0.73
0.2	0.163	0.88
0.3	0.244	0.90
0.4	0.321	0.90
0.5	0.396	0.90

^aTotal sample size in the two-stage design is 9,140 individuals; the genome-wide α level is set to be 5.0 × 10⁻⁸. A causal SNP with a MAF of 0.005 is assumed to contribute to 0.5% of the phenotypic variance (corresponding to a β of 0.71). ψ is the proportion of individuals that can be sequenced if all the costs are allocated in the first stage. Per SNP genotyping cost in the two stages are set to be 1:10.

EFFICIENCY OF THE ALMOST-EXTREME SAMPLE

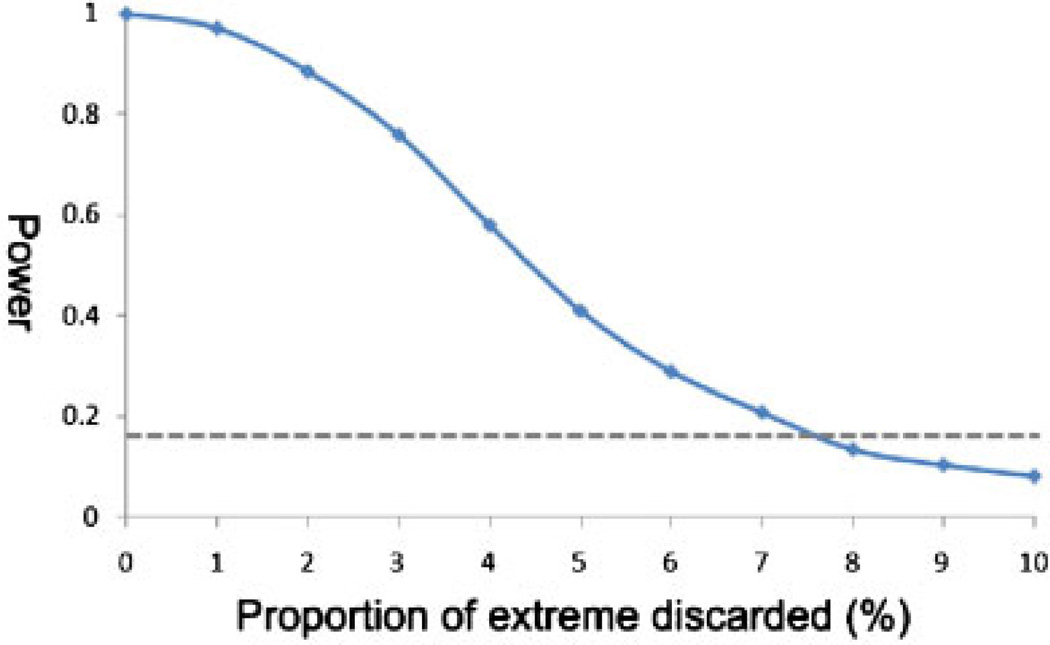
Efficiency of the almost-extreme sample compared with a random sample is demonstrated in Figure 4. As expected, although the almost-extreme sample is less powerful than the extreme sample (with no individuals in the very extremes discarded), the sampling approach can be more powerful than a cross-sectional sample even with a substantial proportion of the very extremes discarded. For example, after discarding the top 5% of individuals with extreme phenotypes in both tails, the power of an almost-extreme sample from the 5–10% and 90–95% quantile can be more than twice that of a random sample of similar size.

Fig. 4.

Performance of the almost-extreme sampling.

CMC APPROACH FOR THE EXTREME SAMPLE

Table III compares the power of the CMC-based analysis strategies in an extreme, a cross-sectional and a case-control sample. Consistent with the single-variant based results, the CMC strategy shows increased power with the extreme sample. For example, with 20 causal SNPs each contributing 0.1% of the phenotypic variance, an extreme sample of 800 individuals from the 5% quantile of the upper and lower tails can achieve more than 80% of power using the CMC strategy. In comparison, with a random and case-control sample of the same size, the power is 30 and 16% respectively.

TABLE III.

Power of different designs for CMC-based analysis strategy

		Power
# of causal variants	Variance contribution per SNP (%)	Random sample	Case-control sample	Extreme sample
10	0.2	0.190	0.118	0.655
20	0.1	0.298	0.156	0.816

We assume there are 100 SNPs with MAF<0.01 in the gene-region, 10 or 20 of which are causal. The causal SNPs are assumed to contribute equally to the phenotypic variance with a total variance contribution of 0.02. Sample sizes for different designs are all set to 800 individuals.

DISCUSSION

The idea of sampling the extremes was initially proposed in linkage analysis as a way to increase efficiency [Gu et al., 1997; Liang et al., 2000; Risch and Zhang, 1995]. In LD mapping for common variants, this idea has also been introduced and demonstrated [Wallace et al., 2006; Chen et al., 2005; Slatkin, 1999]. However although intuitively attractive, application of this design has been limited. Even with increased awareness of this design for future large-scale association studies aimed at rare variants [Li and Conti, 2009; Cirulli and Goldstein, 2010], the potential gain by sampling the extremes and more importantly, technical details of this design have not been well established. Aiming at providing insights and tools for planning future large-scale association studies, we explored the advantage of EPS for rare variants. By accounting for both genotyping and phenotyping costs, we demonstrated the potential cost advantages of this design. Additionally, since a straightforward implementation of sampling the extremes requires a large source population, we proposed a two-stage design with the extreme sample as the first stage and the nonextreme sample as the second stage. We show that even with a limited source population, this two-stage design can achieve similar power as the one-stage design with much less cost.

Based on the power calculation approach proposed, we compared the performance of EPS with two traditional designs, the cross-sectional design based on the random sampling and a “case-control” design in which cases and controls are defined by a clinical diagnosis criterion dichotomizing an underlying observable quantitative trait. The rationale for including the case-control design in this comparison is that, often in clinical practice, diseases such as hypertension and obesity are defined by setting a threshold for quantitative traits [Chobanian et al., 2003; Expert Committee on the Diagnosis and Classification of Diabetes Mellitus, 2003]. Despite the potential gain by using a quantitative trait, many case-control studies of this nature have been performed [Niu et al., 2010; Yamada et al., 2006; Lin et al., 2010; Schleinitz et al., 2010]. Performance of different designs is evaluated as NCP ratio, using the cross-sectional design as a reference. The NCP ratio can be viewed as an inverse of the ratio of sample size to be sequenced to achieve the same power. For example, with an MAF of 0.05 and effect size of 0.5, we observed an NCP ratio of 3.91 when comparing EPS (K = 0.01) to cross-sectional design, which indicates that 3.91 times fewer subjects are needed in the EPS to achieve the same power as the cross-sectional design.

We observed that the NCP ratio of EPS is always greater than 1 and much larger than the case-control designs. This indicates the advantage of the EPS relative to the traditional designs, with a substantially smaller sample size required to achieve the same power. This advantage of EPS is consistent with results in previous investigations demonstrating the efficiency of EPS [Wallace et al., 2006; Chen et al., 2005; Slatkin, 1999, Huang and Lin, 2007].

More interestingly, we observed a consistent increase in the NCP ratio when the MAF decreases. Similar trends can be observed when comparing the NCP of EPS to that of the case-control design (details not shown). Thus, the advantage of EPS over traditional designs increases as the MAF decreases. Moreover, this enhancement of performance increases with larger causal effect. When considering that rare causal variants may have stronger effects than more common variants [Ng et al., 2008; Frazer et al., 2009], the potential advantage of EPS designs could be substantial. This, combined with the fact that EPS is also more efficient with common variants, makes EPS a viable alternative to traditional designs for future sequencing-based association studies in which both common and rare variants are targeted.

Although the sample size sequenced in EPS can be much less than that in traditional designs, a much larger source population must be pre-phenotyped to generate this extreme sample. Thus, it is imperative to account for the phenotyping costs when designing an EPS-based study. Our results demonstrate that EPS can be less cost-efficient than the cross-sectional design when the genotyping/phenotyping cost ratio is low. This potentially explains the limited application of such approaches for linkage analysis and LD mapping, in which a limited number of markers are genotyped with a low genotyping/ phenotyping cost ratio. However, in future whole genome-sequencing-based association studies, the genotyping/ phenotyping cost ratio are expected to continue to be high, especially for studies in which the phenotype information has already been collected, as is common in large biobanks such as GenBank [Benson et al., 2008] and the UK BioBank [Oilier et al., 2005].

In contrast to these large biobanks, it is more likely that the population available for sampling is relatively small. For example, in the University of Southern California Children’s Health Study [Salam et al., 2004], only 10,000 individuals are available for potential genotyping or sequencing. If we only incorporate the individuals with extreme phenotypes for an optimized cutoff or K-value that is most cost-efficient for an assumed infinite source population, we may, in practice, have much less power due to the limited sample sizes. As an alternative, an extreme sample with a more conservative K can serve as the first stage for a two-stage design. A similar idea has been discussed in previous investigations [Song et al., 2009; Zhou et al., 2011]. In this design, the top hits in the first stage can be further evaluated in the second stage, in which the remaining nonextreme samples can be genotyped with customized SNP-chips. By limiting the number of individuals in the costly first stage and incorporating EPS, we show that this approach can be more cost-efficient than the comparable two-stage designs without sampling conditioned on the phenotype. This novel two-stage approach makes it more feasible to incorporate an extreme two-stage design for future sequencing-based association studies with limited source populations. However, investigators need to be aware that some SNPs identified through sequencing may fail with followup via customized genotyping. This might limit the application of many two-stage designs in practice, as well as the extreme sampling two-stage design.

Our investigation of EPS is based on the analysis framework proposed by Huang et al in 2007 [24]. By taking the sampling framework into account, this likelihood-based method yields unbiased estimates for the genetic effects and is highly flexible. Huang and Lin [2007] demonstrated that this approach is also more powerful than other methods, such as the combined-test based approaches proposed by Chen et al. [2005] and Slatkin [1999], a Hotellin’g T² test proposed by Wallace et al [2006] as well as the naive case-control analysis which ignores the trait value and compares the allele frequencies in upper and lower extreme sample.

In a recent investigation evaluating the extreme sample in association analysis aiming at rare variants, Xing and Xing [2009] claimed that the extreme sample is more efficient in detecting common rather than rare variants and is efficient only when the level of declaring significance is not stringent. However, this study was based on a Fisher’s combined P-values from two analyses: a logistic regression treating the upper extreme as cases and the lower extreme as controls, and a linear regression on the association between the quantitative trait and the genotype, ignoring the truncated distribution. The contradictory conclusion drawn by this study may be due, in part, to the less efficient analysis framework [Huang and Lin, 2007] in which issues of data sparseness and the level of conservativeness of the test is largely unknown. In our simulation, comparing the performance of the likelihood-based analysis and approach presented by Xing and Xing [2009] (Supplemental Table I), we demonstrated that although the power of Xing and Xing approach is comparable to that of the likelihood-based approach under a significance threshold of 0.05, its performance deteriorates sharply with more stringent significance levels. This observed deterioration explains why Xing and Xing concluded that the extreme sample is more efficient only when the significance level is not stringent. Here, we demonstrate that using the likelihood-based approach, extreme-value sampling remains efficient even with more stringent significant levels.

In this investigation, we mostly focused on single-marker-based association tests in EPS. However, the likelihood-based analysis framework can be easily expanded to incorporate multiple markers, haplotypes, or even risk index analyses for rare variants. Furthermore, several approaches have recently been proposed for grouped or pooled analysis of rare variants in a gene region [Li and Leal, 2008; Madsen and Browning, 2009; Zawistowski et al., 2010; Asimit and Zeggini, 2010; Bansal et al., 2010]. Those ideas can also be applied to EPS-based samples. As an example of how extreme sampling may perform with these subsequent analyses techniques, we adapted the likelihood analysis framework for the CMC approach, a relative straightforward but powerful rare-variant analysis strategy. We demonstrated that with the higher information content in the extreme sample, the performance of CMC-based analysis strategy can be substantially improved in comparison with traditional designs. The power calculation and design optimization procedures we developed for single-variant based analysis are easily extended for the CMC strategy.

While clear advantages exist in applying EPS for a quantitative trait, the realization of such advantages depends greatly on the underlying diseases mechanism. In practice, it may be more likely that the very extremes of a phenotype distribution (K< 0.001, for example) may consist of unknown genetic heterogeneity due to genes with large effects (i.e. Mendelian disorders). In such cases, the corresponding variants will be enriched in the extreme sample. While this may help to understand the genetic heterogeneity of the phenotype, the power to detect rare variants with more moderate or weak genetic effects may be reduced. Thus depending on the purpose of the study, investigators should be cautious when choosing very extreme K-values, even if in certain scenarios the very extreme K-values may be more cost-effective for either the one-stage or two-stage extreme-value design. As a more robust alternative in practice, investigators can use the almost-extreme sampling instead of the very extremes. For such sampling schemes, we demonstrated that even after discarding a significant proportion of the individuals with very extreme phenotypes, the almost-extreme sampling can still be more efficient than the traditional designs when using a corresponding likelihood-based analysis framework.

Likewise, the potential gains in efficiency of EPS with a quantitative trait relative to a case-control analysis may rely on the appropriateness of using a quantitative trait to represent a truly dichotomous diseases state. Clearly, when disease status is defined by a convenient dichotomization of an underlying continuous variable, the resulting case-control design is less efficient for detecting rare risk variants. In addition, its power to detect protective variants, rare or common, is even more limited. This kind of disease diagnosis criterion is common in clinical practice and investigators should be aware of the potential inefficiency of the case-control design. However, the alternative scenario in which case status captures a more complex underlying mechanism, such as cancer or cardiovascular disease, may also be true. Here, the use of EPS may be limited and the investigators need to evaluate the appropriateness of using underlying quantitative traits as a proxy for these disease mechanisms. However, despite these potential caveats, we have demonstrated and provided the framework for evaluating the potential advantage for EPS in both single-stage and two-stage approaches, thus increase the feasibility of this approach in practice. Software for evaluating various study designs scenarios is available from the authors.

APPENDIX A. POWER CALCULATIONS FOR THE EPS

In the power calculation approach we proposed, γ is the expected log likelihood contribution for a single subject and is calculated as follows:

$$\mathrm{\gamma }=2\{E(l_{\text{Alt}})-E(l_{\text{Null}})\},$$

$$E(l_{\text{Alt}})=\sum _g{P}_g\left\{{\int }_{-\infty }^{C_1}\right[-\text{log}\mathrm{\delta }-\frac{{(y-{\mathrm{\mu }}_g)}^2}{2{\mathrm{\delta }}^2}-\text{log}(\mathrm{\Omega })]\mathrm{d}y+{\int }_{-\infty }^{C_2}[-\text{log}\mathrm{\delta }-\frac{{(y-{\mathrm{\mu }}_g)}^2}{2{\mathrm{\delta }}^2}-\text{log}(\mathrm{\Omega })]\mathrm{d}y\},$$

$$E(l_{\text{Null}})=\sum _g{P}_g\left\{{\int }_{-\infty }^{C_1}\right[-\text{log}\mathrm{\delta }-\frac{{(y-{\alpha }_0)}^2}{2{\mathrm{\delta }}_0^2}-\text{log}({\mathrm{\Omega }}_0)]\mathrm{d}y+{\int }_{-\infty }^{C_2}[-\text{log}\mathrm{\delta }-\frac{{(y-{\alpha }_0)}^2}{2{\mathrm{\delta }}_0^2}-\text{log}({\mathrm{\Omega }}_0)\left]\mathrm{d}y\right\}$$

$$\mathrm{\Omega }=1-\mathrm{\Phi }\left(\frac{C_2-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right)+\mathrm{\Phi }\left(\frac{C_1-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right),$$

$${\mathrm{\Omega }}_0=1-\mathrm{\Phi }\left(\frac{C_2-{\alpha }_0}{{\mathrm{\delta }}_0}\right)+\mathrm{\Phi }\left(\frac{C_1-{\alpha }_0}{{\mathrm{\delta }}_0}\right).$$

Here α₀ and δ₀ are values that maximize the likelihood under the alternative hypothesis and P_g is the expected genotype frequencies in the extreme sample.

The proposed power calculation method is evaluated by comparing it with the empirical power based on 1,000 replications. As expected, highly consistent results are observed across different effect sizes and MAFs, as is shown in Supplemental Figure 1.

APPENDIX B. DETAILS OF THE STATISTICS-COMBINING STRATEGY FOR THE EXTREME TWO-STAGE DESIGN

For the first stage extreme-sample, as an alternative to the likelihood ratio test, an approximately equivalent Wald’s test can be performed:

$$z_1=\frac{{\widehat{\mathrm{\beta }}}_1}{{\widehat{\sigma }}_2}$$

In the n (1–π_sample) individuals with nonextreme phenotypes genotyped in the second stage, the distribution of ϒ conditional on G and sampling follows truncated normal distribution:

$$f(\Upsilon =y|G=g,C_2<\Upsilon <C_1)=\frac{\mathbb{N}({\mathrm{\mu }}_g,\mathrm{\delta })}{\mathrm{\Phi }\left(\frac{C_1-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right)-\mathrm{\Phi }\left(\frac{C_2-{\mathrm{\mu }}_g}{\mathrm{\delta }}\right)}.$$ (A2)

Similar to the first-stage extreme sample, its likelihood can be maximized and a Wald test statistics can be constructed:

$$z_2=\frac{{\widehat{\mathrm{\beta }}}_1}{{\widehat{\sigma }}_2}$$

Under the null hypothesis, both z₁ and z₂ approximately follow the standard normal distribution. Thus, a joint statistic can be constructed as:

$$z_{\text{joint}}=z_1\sqrt{w}+z_2\sqrt{1-w}.$$

Here, we set w to be:

$$w=\frac{I_1}{I_1+I_2}.$$

Here I₁ and I₂ are the observed Fisher’s information for β₁ and β₂ in the two samples.

Under the null hypothesis with given z₁ = t, z_joint follows a normal distribution with mean $\sqrt{\mathit{\text{wt}}}$ and variance 1. Then similarly to the traditional joint analysis for the two-stage GWAS, the probability of detecting the association with given w can be calculated as:

$$\text{Pr}(|z_{\text{joint}}|>T_{\text{joint}},|z_1|>T_1)=\int \text{Pr}(|z_{\text{joint}}|>T_{\text{joint}},|z_1|>T_1,z_1=t)\mathrm{d}t,={\int }_{t=T_1}^{+\infty }\text{Pr}(|z_{\text{joint}}|>T_{\text{joint}},z_1=t)\mathrm{d}t+{\int }_{t=-\infty }^{-T_1}\text{Pr}(|z_{\text{joint}}|>T_{\text{joint}},z_1=t)\mathrm{d}t,={\int }_{t=T_1}^{+\infty }[1-\mathrm{\Phi }(T_{\text{joint}}-\sqrt{w}t)+\mathrm{\Phi }(-T_{\text{joint}}-\sqrt{w}t)]\mathbb{N}(t)\mathrm{d}t,+{\int }_{t=-\infty }^{-T_1}[1-\mathrm{\Phi }(T_{\text{joint}}-\sqrt{w}t)+\mathrm{\Phi }(-T_{\text{joint}}-\sqrt{w}t)]\mathbb{N}(t)\mathrm{d}t.$$

Here T₁ is the corresponding threshold for z₁ to be selected for second stage, and T_joint is the critical value for z_joint, which can be calculated by allowing z₁ and z_joint follows their null distribution.

Supplemental Figure 2 compares the performance of the two analysis strategies for the extreme two-stage design. The power of the data-combining and the statistics-combining strategies are both calculated based on 1,000 simulation replicates, although the power of the statistics-combining strategy can also be calculated numerically. Slight loss in power is observed in the statistics-combining strategy. For example, when π_sample is 0.2 and π_marker is 1.0 × 10⁻³, the statistics-combining strategy has a power of 0.845, while the power of the data-combining strategy is 0.898. The gain in power in the data-combining strategy is probably due to the difference of allele frequencies between the extreme and nonextreme sample.

APPENDIX C. DIFFERENT OPTIMIZATION RESULTS OF THE STATISTICS-COMBINING STRATEGY AND DATA-COMBINING STRATEGIES

In Supplemental Figure 3, we compared the optimized π_sample of the two analysis strategies when the per SNP genotyping cost ratio and total genotyping cost in the two stages are fixed. Clearly, the optimized π_sample is larger for the statistics-combining strategy.