Skip to main content
PMC home page
Brain Connectivity logoLink to Brain Connectivity
. 2014 Nov 1;4(9):702–708. doi: 10.1089/brain.2014.0295

Decreased Effective Connectivity from Cortices to the Right Parahippocampal Gyrus in Alzheimer's Disease Subjects

Guangyu Chen 1, B Douglas Ward 1, Gang Chen 1, Shi-Jiang Li 1,✉
PMCID: PMC4238239  PMID: 25132215

Abstract

The purpose of this study was to detect effective connectivity (EC) changes in the default mode network and hippocampus network in 20 patients with Alzheimer's disease (AD) and 20 cognitively normal (CN) subjects, using multivariate Granger causality. The authors used the maximum coefficients in the multivariate autoregression model to quantitatively measure the different EC strength levels between the CN and AD groups. It was demonstrated that the EC strength difference can classify AD from CN subjects. Further, the right parahippocampal gyrus (PHP_R) showed imbalanced bidirectional EC connections. The PHP_R received weaker input connections from the neocortices, but its output connections were significantly increased in AD. These findings may provide neural physiological mechanisms for interpreting AD subjects' memory deficits during the encoding processes.

Key words: : Alzheimer's disease, classification, functional connectivity, functional MRI, Granger causality, parahippocampal gyrus

Introduction

Alzheimer's disease (ad) is a progressive, age-related neurodegenerative disease that is the most frequent form of age-related dementia. AD destroys brain cells, causing memory, cognitive, and behavioral problems. This is often severe, affecting work, lifelong hobbies, and social life. Resting-state functional magnetic resonance imaging (R-fMRI) has been used extensively to diagnose AD (Chen et al., 2011; Greicius et al., 2004; Li et al., 2002) and assess treatment (Goveas et al., 2011; Li et al., 2012; Sole-Padulles et al., 2013). These studies were based on the cross-correlation coefficient between the spontaneous blood oxygen level-dependent (BOLD) signals in the brain. However, the functional connectivity calculations, which are based on a synchronous relationship, provided no directional information, known as effective connectivity (EC) or causal connection, among brain regions.

Recent developments demonstrated that the EC between two signals can be detected with two popular methods: Granger causality (GC) (Granger, 1969) and dynamic causal modeling (DCM) analyses (David et al., 2006). Both methods have shown distinct and complementary functions in relation to the detection of causality (Friston et al., 2013). They differ in that the DCM method is highly dependent on the predefined or hypothesis models, whereas the GC technique does not need predefined model. On the other hand, the specification and interrogation of the DCM model allow us to better determine the hidden causality (Boly et al., 2012), which is specified by the model assumption. The present study focused on the GC-based analysis method.

GC has been employed to successfully map the EC from the frontal areas to the parietal areas in the brains of subjects during a visuomotor mapping task (Goebel et al., 2003). In the R-fMRI studies, the test proved to be a feasible method to study the EC network architecture at voxel (Wu et al., 2013) or regional (Deshpande et al., 2011; Liao et al., 2010; Uddin et al., 2009) levels. It also improved disease classification (Deshpande et al., 2010). Several studies investigated brain EC, using GC on subjects with AD (Liu et al., 2012; Miao et al., 2011) and amnestic mild cognitive impairment (Adamcio et al., 2010; Liang et al., 2014), which is often considered to be prodromal AD. However, these studies had several limitations. For example, the degree of nodes in the EC network was quantitatively compared between AD and cognitively normal (CN) subjects, but the EC strength was not directly measured (Liu et al., 2012). In another study, the independent component analysis was employed to investigate the EC between different brain networks, but the causality between different brain regions was not available (Miao et al., 2011). In using the multivariate GC method, it was reported that scattered EC strength changes occurred in subjects with amnestic mild cognitive impairment (Adamcio et al., 2010), compared with CN subjects. The result did not correct the multiple comparison error. The brain regions showed EC changes that did not relate to the functional areas of memory, such as the parahippocampal gyrus and hippocampus.

In this study, the authors employed the GC to understand the neural mechanisms of AD memory deficits. It was shown that, in early AD, the episodic memory deficit, in particular, occurred with the memory-encoding deficit (White and Ruske, 2002) rather than during memory retrieving (Greene et al., 1996).They hypothesized that the EC network pattern related to the memory-encoding process would be significantly impaired, and those related to memory-retrieving processes would also be affected. They employed the multivariate GC to quantify the EC strength among brain regions in the classic default mode network (DMN) (Greicius et al., 2003) and the hippocampus network (HN) (Allen et al., 2007). They utilized the support vector machine (SVM) to determine EC patterns and further classify the CN and AD, using the Leave-One-Out (LOO) algorithms to validate the power of the classification method.

Materials and Methods

MRI data acquisition and subjects

This Institutional Review Board-approved study was conducted in compliance with the HIPAA regulations. Each participant provided written informed consent. A total of 40 human participants, including 20 CN subjects (11 males, 9 females, age 74.6±6.6 years, mini-mental state examination (MMSE) scores: 29±1.3) and 20 mild AD subjects (14 males, 6 females, age 77.57±6.57 years, MMSE scores: 24.75±2.6), were recruited for this study. Due to limited brain coverage, one AD subject and three CN subjects were excluded from the further data analysis. Specific MRI imaging protocols were previously described (Chen et al., 2011). In brief, MRI measurements were carried out using a 3T GE Signa whole-body scanner with a standard transmit–receive head coil. High-resolution SPGR three-dimensional images were acquired in the axial direction for anatomical reference (echo time [TE]=4 msec, repetition time [RT]=10 msec, inversion time=450 msec, flip angle=12°, 144 slices, slice thickness=1 mm and matrix size=256×192). For the R-fMRI measurement, 36 sagittal slices were obtained in 6 min with a single-shot gradient echo–echo planar imaging (EPI) pulse sequence with TE of 25 msec, TR of 2 sec, flip angle of 90°, slice thickness of 4 mm, matrix size of 64×64, and field of view of 24 cm. The subjects were instructed to close their eyes during the scan.

Data analysis

Image preprocessing: The fMRI data analysis was carried out using the AFNI software (http://afni.nimh.nih.gov/afni) and MATLAB programs (The MathWorks, Inc., Natick, MA). In brief, motion correction was performed by volume registration on the R-fMRI data (3dvolreg); detrending was carried out to remove Legendre polynomials (3dDetrend). Averaged signals from white matter and cerebrospinal fluid and the six-motion vectors were removed from each voxel time series as nuisance repressors. In addition, global signals were regressed out from the whole brain. Finally, a band-pass filter was applied to keep only low-frequency fluctuations within 0.015 and 0.1 Hz frequency range.

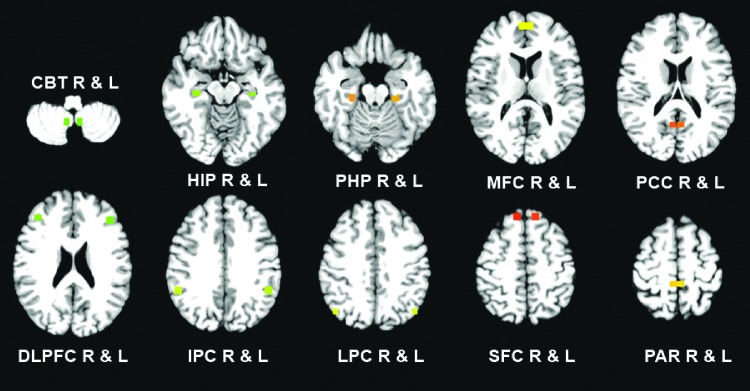
The authors employed the multivariate GC method (Blinowska et al., 2004) and selected 20 brain regions from the HN (Allen et al., 2007) and DMN (Greicius et al., 2004), as shown in Figure 1. The 20 regions of interest for the GC analysis include the bilateral cerebellar tonsil (CBT_L and CBT_R), hippocampus (HIP_L and HIP_R), parahippocampal gyrus (PHP_L and PHP_R), medical frontal cortex (MFC_L and MFC_R), posterior cingulated cortex (PCC_L and PCC_R), dorsolateral prefrontal cortex (DLPFC_L and DLPFC_R), inferior parietal cortex (IPC_L and IPC_R), lateral parietal cortex (LPC_L and LPC_R), superior frontal cortex (SFC_L and SFC_R), paracentral gyrus (PAR_L and PAR_R). R, right; L, left.

FIG. 1.

FIG. 1.

Open in a new tab

Twenty regions of interest (ROI) for Granger causality analysis: the bilateral cerebellar tonsil (CBT), hippocampus (HIP), parahippocampal gyrus (PHP), medical frontal cortex (MFC), posterior cingulated cortex (PCC), dorsolateral prefrontal cortex (DLPFC), inferior parietal cortex (IPC), lateral parietal cortex (LPC), superior frontal cortex (SFC), paracentral gyrus (PAR). R, right; L, left.

Their coordinates are listed in the Supplementary Table S1 (Supplementary Data are available online at www.liebertpub.com/brain). Each region was represented with a cube of 27 adjacent voxels around the center coordinates. The average time series over the 27 voxels for each region was extracted and there were 20 regionwise time series.

Analysis of GC

As described above, the 20 regionwise time series may be expressed as follows in Equation 1.

graphic file with name eq1.gif

where m represented the number of brain regions. The multivariate auto regression (MVAR) model (Eq. 2) was employed to measure the values of all possible EC strengths from all other regions to region j.

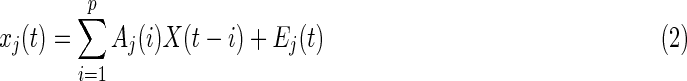graphic file with name eq2.gif

where Inline graphic are the regression coefficients. The parameter p is the model order or the lag parameter. Aj(i) is the regression coefficient matrix, E is the residual error matrix. X is the time series matrix of different regions. To determine the optimal lag parameter p, Akaike Information Criterion (AIC) (Akaike, 1974) was used to minimize the chosen criterion (AIC) and was calculated as follows (Eq. 3):

graphic file with name eq3.gif

where n is the number of time points. In their study, they found that the optimal time lag p is 2, which was consistent with a previous study (Harrison et al., 2003).

To find the EC between regions j and k, partial regression (Eq. 4) for each regionwise time series was calculated:

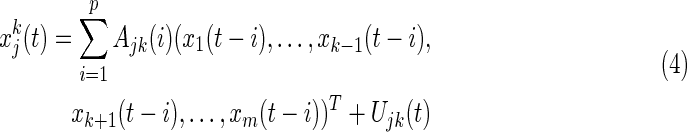graphic file with name eq4.gif

where the lag parameter p is 2, as determined above, 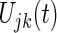Inline graphic is the module residual.

The F-test (Eq. 5) was calculated as follows:

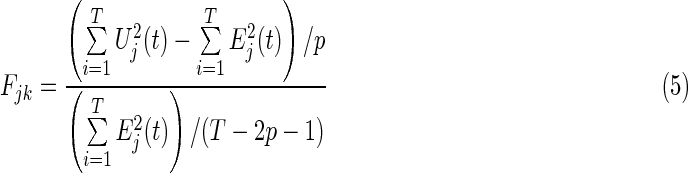graphic file with name eq5.gif

If the result of the F-test of residuals of full (Eq. 2) and partial (Eq. 4) regressions is significant, the EC of k causes j is significant. Previous studies employed the F-test of residuals to determine the significance of EC, however, the EC strength was not provided (Goebel et al., 2003). In the present study, the authors used the maximum value of the regression coefficient matrix A in Equations (2) and (4) to represent the EC strength. Let Amax be the EC strength matrix. The entry (Amax(ij)) represents the EC strength from region i to region j. The Amax(ij) is calculated by:

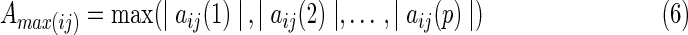graphic file with name eq6.gif

Group-level analysis

For each individual subject, there is one EC matrix (Amax); the matrix size is 20 by 20. To find a difference pattern in Amax between the CN group and the AD group, for each EC (region i to region j) edge, the Wilcoxon Rank Sum test was used to compare the mean between the CN and AD groups.

The Wilcoxon Rank Sum test results revealed a set of edges whose EC strengths were significantly different between the AD and CN groups without correcting multiple comparison errors. To correct this error and establish a threshold, Monte Carlo simulation was performed, using 1000 random permutations between AD and CN subjects. They determined that a brain region has significant EC connections (p<0.05), if it had at least three edges with individual significant EC strengths. In other words, they deemed a brain region insignificant, if it had less than three significant EC connections.

Classification methodology

The above EC pattern may discriminate between AD and CN subjects. The difference in EC strengths between CN and AD groups may be separated into two different patterns. One set of edges, the Increased Network, showed higher EC strength in AD subjects, as opposed to CN subjects. The other set of edges, the Decreased Network, showed significantly lower EC strength in AD subjects than in the CN subjects. That is

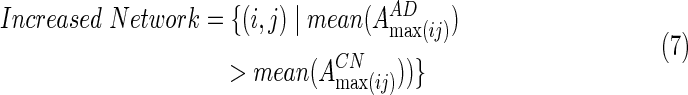graphic file with name eq7.gif
graphic file with name eq8.gif

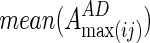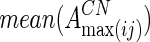where Inline graphic and Inline graphic are averaged values of EC strength between regions i and j in AD and CN groups, respectively. For the increased network, they calculated the increased network index (INI) for each subject s, as follows:

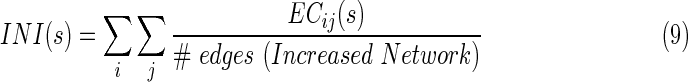graphic file with name eq9.gif

where 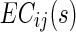Inline graphic is the EC strength between region i and j for subject s, #edges refers to the total number of EC of the increased network. Similarly, they calculated the decreased network index (DNI) for subject s, as below:

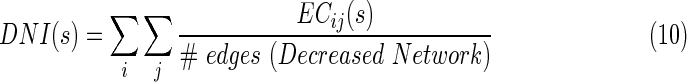graphic file with name eq10.gif

where 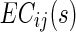Inline graphic is the EC strength for subject s in the decreased network.

For classification, the two index (INI and DNI) values were obtained for each individual subject. Then, an SVM automatic classification algorithm was employed to separate CN subjects from AD subjects (Mourao-Miranda et al., 2005).

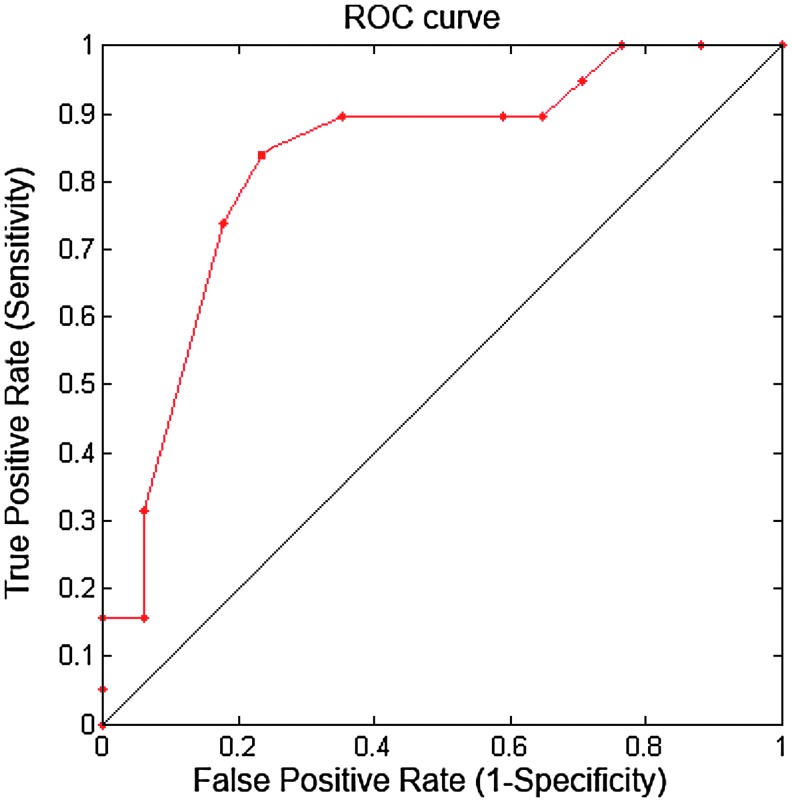
Because the same subjects were used for training and classification, this could result in an overly optimistic estimate of the error rate. When data sets have a limited size, as in the present situation, the LOO Method is often used to cross-validate the classifier (Richard and Johnson, 1982; Sergios Theodoridis, 2006). That is, the classification criteria are determined, using all subjects except the one subject to be evaluated. This entire process is repeated for each subject, one at a time, providing an unbiased estimate of the classification error rate. The most important variable is the classification threshold (CT) value. Specifically, they performed 36 LOO processes. With each LOO procedure, they performed a classification with 181 different CT values. Then, the misclassification probabilities were estimated by the following equations (Cont=CN) and generate all values in the ROC curve as plotted in Figure 3.

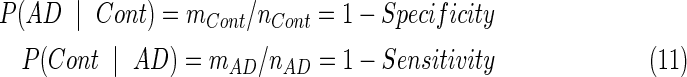graphic file with name eq11.gif

FIG. 3.

FIG. 3.

Open in a new tab

The receiver operating characteristic (ROC) curve of the classification between CN and AD groups, which is cross-validated with the Leave-One-Out method. The area under the ROC curve is 0.83.

The LOO method pseudocodes, which were applied specifically to their EC-based classification method, are listed in the Supplementary Table S2.

Results

Group analysis of EC strength

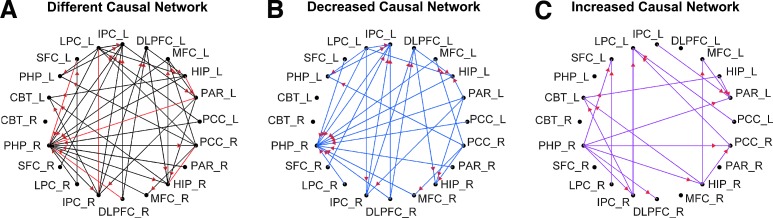
Wilcoxon Rank Sum test was performed for each EC between CN and AD. Figure 2A demonstrates the difference in the directional EC network wherein the ECs have significantly different strengths between AD and CN. The red edges are bidirectional and the non-red edges are unidirectional. This difference network was further separated into a set of decreased EC strength connections (Fig. 2B) and a set of increased EC strength connections (Fig. 2C) in the AD group compared with the CN group. Specifically, the EC strengths from 10 neocortex regions (SFC_L, LPC_L, IPC_L, MFC_L, PAR_L, PCC_L, PAR_R, MFC_R, DLPFC_R, and LPC_R) connecting to the PHP_R were significantly decreased, whereas the EC strength from PHP_R connected to the neocortex regions of SFC_L, PAR_L, PCC_R, DLPFC_R, and IPC_R was significantly increased.

FIG. 2.

FIG. 2.

Open in a new tab

Difference in effective connectivity (EC) patterns between Alzheimer's disease (AD) and cognitively normal (CN) group. (A) The different EC connection patterns between AD and CN groups. Red edges show bidirectional EC; blue edge show unidirectional EC. The different EC patterns were separated into two different patterns, according to their EC strengths. (B) The decreased EC strength in which the AD group has significantly weaker strength of each edge than the CN group. (C) The increased EC strength in which the AD group has significantly higher strength of each edge than the CN group. Red arrows indicate the EC direction. The arrow direction indicates the causal relationship between the nodes from one to the other.

The weights of INI and DNI in SVM classification

The weights for INI and DNI in the SVM classification are 1.34 and 1, respectively (Supplementary Fig. S1). The increased EC network has 34% more weight on classifying AD than the decreased EC network. That means the INI index has more relative importance when classifying the AD index, as opposed to that of the DNI. The model of the SVM classification is C=0.2+1.34×INI−DNI. C is the model value for each subject. If C<0, then the subject is classed as CN. If C>0, the subject is classified as AD.

The power of the EC-based classification

The classification error rate was estimated using the LOO method. At this point, a Type I Error indicates a false positive in that a CN subject was falsely classified as an AD subject. Conversely, a Type II Error, or false negative means that an AD subject was falsely classified as a CN Subject. The probability of a Type I or II error was estimated by the proportion of misclassifications within each group. The results from the SVM classification with INI and DNI indices and the LOO error correction were plotted in the receiver operating characteristic (ROC) curve, as shown in Figure 3. The ROC curves show the tradeoff between sensitivity and specificity. The ROC area under the curve is 0.83.

Brain atrophy

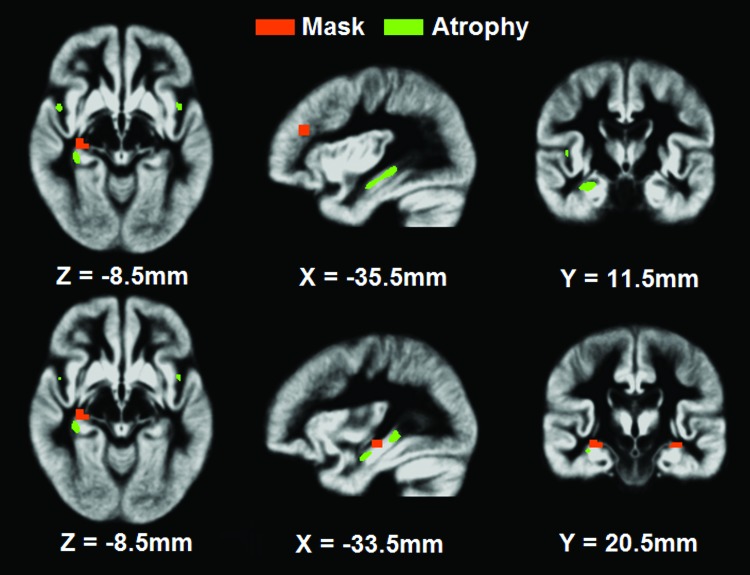
Previous neuroimaging studies demonstrated that brain atrophy exists in AD (Buckner et al., 2005; Greicius et al., 2004). Because brain atrophy could confound the EC measurement, it was important to check if the atrophy was present in the selected brain regions (the cubes of 27 voxels). The authors conducted voxel-based morphometry analysis (Mechelli et al., 2005), using the SPM software. Figure 4 shows that brain atrophy existed; however, it did not overlap with selected regions.

FIG. 4.

FIG. 4.

Open in a new tab

Possible brain atrophy in the selected 20 ROIs for Granger causality analysis. The selected 20 ROIs (red) were not overlapping with the atrophic areas (green) in the AD group.

Discussion

Their results corroborate earlier findings and also extend them in four important ways. First, this study adopted the multivariate GC method to test and compare the ECs among 20 brain regions in DMN and HN between AD and CN groups. They further employed the method to quantitatively measure the EC strength by using the maximum MVAR model coefficients. This approach made it possible to compare the different levels of EC strength between CN and AD groups and provide a new biomarker to classify CN and AD subjects by measuring INI and DNI indices.

Second, previous studies demonstrated asymmetric atrophy in AD (Derflinger et al., 2011). Moreover, the right side PHP deficit correlated best with memory and mental status decline (Keilp et al., 1996; Schmidt-Wilcke et al., 2009). Their results are consistent with these previous findings. They found that the AD asymmetric alterations showing the largest changed area was located in PHP_R, however, there were minor changes in PHP_L. The authors further showed that EC strengths have directional connection information. In fact, these strengths, which were connected to the PHP_R region from 10 neocortical regions, were significantly decreased. These directional EC connection patterns may better characterize the disease progression.

Third, the PHP is an essential link between the neocortex and hippocampus (de Curtis and Pare, 2004; van Strien et al., 2009). Indeed, this important region is involved in many complex functions, such as memory, sensory representation, spatial orientation, and object recognition (Hayes et al., 2007; Murray and Richmond, 2001). The PHP regions they selected included the entorhinal and perirhinal cortices (coordinates in Talairach space [x, y, z] for the right PHP is [25, −26, −14] and for the left is [−25, −26, −14]). Anatomically, the entorhinal cortex is the source of perforant pathway, which projects to all hippocampal formation fields. The perirhinal cortex receives sensory information from all sensory regions of the neocortex. Therefore, the PHP regions that they selected represented the anatomical gate for the hippocampus to receive and send information to the neocortex. The observed decreased EC input from the neocortical regions to PHP in this study may suggest that the gate function of the PHP may be disrupted in the AD group. It is conceivable that this disrupted gateway may result in memory encoding deficit symptoms in patients with AD.

Fourth, the most challenging and complicated question is why the PHP_R showed imbalanced bidirectional EC connections. That is, how does one explain why the PHP_R received weaker input connections from the neocortical regions, yet its output connections to these regions were significantly increased with the presence of AD. Their hypothesis is that the weaker input connections from the neocortices may be related to their disrupted feedback system in the neocortices (Lavenex and Amaral, 2000) and the stronger output connections from the PHP to the neocortex may be associated with the detrimental feed-forward systems in the PHP.

It has been suggested that layers II/III/V/VI in two brain regions have most of the feedback synaptic connections, whereas layer IV has major feed-forward synaptic connections (Markov et al., 2013). Previous studies showed that AD has major neurofibrillary tangle accumulation in layer III/V of temporal, parietal, and frontal association cortices (Arnold et al., 1991; Pearson et al., 1985). Patients with AD lose large pyramidal neurons in layers III and V (Brun and Englund, 2002). It is conceivable that the presence of neurofibrillary tangle and the loss of pyramidal neurons in layers III/V may have had an impact on the feedback synaptic connections. These mechanisms may have served as a means of interpreting the observed decrease in EC strength from the neocortices to the PHP.

In discussion of observed EC strength increase from the PHP to the neocortices, it is important to note that the acetylcholine level in normal subjects is enhanced during memory encoding (Hasselmo and McGaughy, 2004). The high acetylcholine level partially suppresses excitatory feed-forward connections, which project from the PHP area to associate neocortex (Hasselmo, 1999, 2006). On the contrary, due to the cholinergic degeneration evident in patients with AD (Francis et al., 1999), the inhibitory function of the acetylcholine could be weakened, resulting in increased EC strengths from the PHP to the neocortices.

Limitations

Although they provided inferences to interpret why the PHP_R showed imbalanced bidirectional EC connections in the AD subject group, a few questions still remain. For example, due to the limitation of the spatial resolution (i.e., 3.75 mm) in the EPI images, they could not distinguish the signals at the laminar level of the cortices. They could not separate feedback connections from feed-forward connections, as proposed recently in a bow-tie model (Markov et al., 2013). In the future, they will develop an ultra-high resolution functional MRI technique that can achieve 0.4 mm or less of in-plane resolution to test their hypothesis.

In addition to the limited spatial resolution, the current study also is limited by the temporal resolution of the TR of 2 sec. To find the EC, the GC test requires specifying the lag time points in their algorithm (Eq. 2). They employed the commonly used AIC method (Goebel et al., 2003; Roebroeck et al., 2005; Uddin et al., 2009) and found the lag time is 4 sec. However, the spontaneous BOLD signal is an indirect measure of neural activity. Although there is no literature to confirm the true causal relationships within such long time interval of 4 sec in R-fMRI data, the ECs of fMRI BOLD signals showed the robustness to a wide variety of changes in hemodynamic response properties (Seth et al., 2013). It is expected that the recent advanced fast imaging technique (Zahneisen et al., 2012) could reduce TR to 100 msec to alleviate the limitation in the spatial resolution.

The small sample size of this study could limit the study's power. This will result in an overestimate of the classification. Although a relatively unbiased LOO method was applied to error estimation, it was imperfect. In the future, they will study more subjects to examine the EC between AD and CN and use another independent group to validate the classification method.

Supplementary Material

Supplemental data
Supp_Table1.pdf (21.7KB, pdf)
Supplemental data
Supp_Table2.pdf (18.5KB, pdf)
Supplemental data
Supp_Fig1.pdf (59.2KB, pdf)

Author Disclosure Statement

No competing financial interests exist.

References

  1. Adamcio B, Sperling S, Hagemeyer N, Walkinshaw G, Ehrenreich H. 2010. Hypoxia inducible factor stabilization leads to lasting improvement of hippocampal memory in healthy mice. Behav Brain Res 208:80–84 [DOI] [PubMed] [Google Scholar]
  2. Akaike H. 1974. A new look at the statistical model identification. IEEE Trans Automat Control 19:8 [Google Scholar]
  3. Allen G, Barnard H, McColl R, Hester AL, Fields JA, Weiner MF, Ringe WK, Lipton AM, Brooker M, McDonald E, Rubin CD, Cullum CM. 2007. Reduced hippocampal functional connectivity in Alzheimer disease. Arch Neurol 64:1482–1487 [DOI] [PubMed] [Google Scholar]
  4. Arnold SE, Hyman BT, Flory J, Damasio AR, Van Hoesen GW. 1991. The topographical and neuroanatomical distribution of neurofibrillary tangles and neuritic plaques in the cerebral cortex of patients with Alzheimer's disease. Cereb Cortex 1:103–116 [DOI] [PubMed] [Google Scholar]
  5. Blinowska KJ, Kus R, Kaminski M. 2004. Granger causality and information flow in multivariate processes. Phys Rev E Stat Nonlin Soft Matter Phys 70:050902. [DOI] [PubMed] [Google Scholar]
  6. Boly M, Moran R, Murphy M, Boveroux P, Bruno MA, Noirhomme Q, Ledoux D, Bonhomme V, Brichant JF, Tononi G, Laureys S, Friston K. 2012. Connectivity changes underlying spectral EEG changes during propofol-induced loss of consciousness. J Neurosci 32:7082–7090 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brun A, Englund E. 2002. Regional pattern of degeneration in Alzheimer's disease: neuronal loss and histopathological grading. Histopathology 41:40–55 [PubMed] [Google Scholar]
  8. Buckner RL, Snyder AZ, Shannon BJ, LaRossa G, Sachs R, Fotenos AF, Sheline YI, Klunk WE, Mathis CA, Morris JC, Mintun MA. 2005. Molecular, structural, and functional characterization of Alzheimer's disease: evidence for a relationship between default activity, amyloid, and memory. J Neurosci 25:7709–7717 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chen G, Ward BD, Xie C, Li W, Wu Z, Jones JL, Franczak M, Antuono P, Li SJ. 2011. Classification of Alzheimer disease, mild cognitive impairment, and normal cognitive status with large-scale network analysis based on resting-state functional MR imaging. Radiology 259:213–221 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. David O, Kiebel SJ, Harrison LM, Mattout J, Kilner JM, Friston KJ. 2006. Dynamic causal modeling of evoked responses in EEG and MEG. Neuroimage 30:1255–1272 [DOI] [PubMed] [Google Scholar]
  11. de Curtis M, Pare D. 2004. The rhinal cortices: a wall of inhibition between the neocortex and the hippocampus. Prog Neurobiol 74:101–110 [DOI] [PubMed] [Google Scholar]
  12. Derflinger S, Sorg C, Gaser C, Myers N, Arsic M, Kurz A, Zimmer C, Wohlschlager A, Muhlau M. 2011. Grey-matter atrophy in Alzheimer's disease is asymmetric but not lateralized. J Alzheimers Dis 25:347–357 [DOI] [PubMed] [Google Scholar]
  13. Deshpande G, Li Z, Santhanam P, Coles CD, Lynch ME, Hamann S, Hu X. 2010. Recursive cluster elimination based support vector machine for disease state prediction using resting state functional and effective brain connectivity. PLoS One 5:e14277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Deshpande G, Santhanam P, Hu X. 2011. Instantaneous and causal connectivity in resting state brain networks derived from functional MRI data. Neuroimage 54:1043–1052 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Francis PT, Palmer AM, Snape M, Wilcock GK. 1999. The cholinergic hypothesis of Alzheimer's disease: a review of progress. J Neurol Neurosurg Psychiatry 66:137–147 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Friston K, Moran R, Seth AK. 2013. Analysing connectivity with Granger causality and dynamic causal modelling. Curr Opin Neurobiol 23:172–178 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Goebel R, Roebroeck A, Kim DS, Formisano E. 2003. Investigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magn Reson Imaging 21:1251–1261 [DOI] [PubMed] [Google Scholar]
  18. Goveas JS, Xie C, Ward BD, Wu Z, Li W, Franczak M, Jones JL, Antuono PG, Li SJ. 2011. Recovery of hippocampal network connectivity correlates with cognitive improvement in mild Alzheimer's disease patients treated with donepezil assessed by resting-state fMRI. J Magn Reson Imaging 34:764–773 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Granger CWJ. 1969. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37:5 [Google Scholar]
  20. Greene JD, Baddeley AD, Hodges JR. 1996. Analysis of the episodic memory deficit in early Alzheimer's disease: evidence from the doors and people test. Neuropsychologia 34:537–551 [DOI] [PubMed] [Google Scholar]
  21. Greicius MD, Krasnow B, Reiss AL, Menon V. 2003. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci U S A 100:253–258 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Greicius MD, Srivastava G, Reiss AL, Menon V. 2004. Default-mode network activity distinguishes Alzheimer's disease from healthy aging: evidence from functional MRI. Proc Natl Acad Sci U S A 101:4637–4642 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Harrison L, Penny WD, Friston K. 2003. Multivariate autoregressive modeling of fMRI time series. Neuroimage 19:1477–1491 [DOI] [PubMed] [Google Scholar]
  24. Hasselmo ME. 1999. Neuromodulation: acetylcholine and memory consolidation. Trends Cogn Sci 3:351–359 [DOI] [PubMed] [Google Scholar]
  25. Hasselmo ME. 2006. The role of acetylcholine in learning and memory. Curr Opin Neurobiol 16:710–715 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hasselmo ME, McGaughy J. 2004. High acetylcholine levels set circuit dynamics for attention and encoding and low acetylcholine levels set dynamics for consolidation. Prog Brain Res 145:207–231 [DOI] [PubMed] [Google Scholar]
  27. Hayes SM, Nadel L, Ryan L. 2007. The effect of scene context on episodic object recognition: parahippocampal cortex mediates memory encoding and retrieval success. Hippocampus 17:873–889 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Keilp JG, Alexander GE, Stern Y, Prohovnik I. 1996. Inferior parietal perfusion, lateralization, and neuropsychological dysfunction in Alzheimer's disease. Brain Cogn 32:365–383 [DOI] [PubMed] [Google Scholar]
  29. Lavenex P, Amaral DG. 2000. Hippocampal-neocortical interaction: a hierarchy of associativity. Hippocampus 10:420–430 [DOI] [PubMed] [Google Scholar]
  30. Li SJ, Li Z, Wu G, Zhang MJ, Franczak M, Antuono PG. 2002. Alzheimer disease: evaluation of a functional MR imaging index as a marker. Radiology 225:253–259 [DOI] [PubMed] [Google Scholar]
  31. Li W, Antuono PG, Xie C, Chen G, Jones JL, Ward BD, Franczak MB, Goveas JS, Li SJ. 2012Changes in regional cerebral blood flow and functional connectivity in the cholinergic pathway associated with cognitive performance in subjects with mild Alzheimer's disease after 12-week donepezil treatment. Neuroimage 60:1083–1091 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Liang P, Li Z, Deshpande G, Wang Z, Hu X, Li K. 2014. Altered causal connectivity of resting state brain networks in amnesic MCI. PLoS One 9:e88476. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Liao W, Mantini D, Zhang Z, Pan Z, Ding J, Gong Q, Yang Y, Chen H. 2010. Evaluating the effective connectivity of resting state networks using conditional Granger causality. Biol Cybern 102:57–69 [DOI] [PubMed] [Google Scholar]
  34. Liu Z, Zhang Y, Bai L, Yan H, Dai R, Zhong C, Wang H, Wei W, Xue T, Feng Y, You Y, Tian J. 2012. Investigation of the effective connectivity of resting state networks in Alzheimer's disease: a functional MRI study combining independent components analysis and multivariate Granger causality analysis. NMR Biomed 25:1311–1320 [DOI] [PubMed] [Google Scholar]
  35. Markov NT, Ercsey-Ravasz M, Van Essen DC, Knoblauch K, Toroczkai Z, Kennedy H. 2013. Cortical high-density counterstream architectures. Science 342:1238406. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mechelli A, Price CJ, Friston KJ, Ashburner J. 2005. Voxel-based morphometry of the human brain: methods and applications. Curr Med Imaging Rev 1:105–113 [Google Scholar]
  37. Miao X, Wu X, Li R, Chen K, Yao L. 2011. Altered connectivity pattern of hubs in default-mode network with Alzheimer's disease: an Granger causality modeling approach. PLoS One 6:e25546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mourao-Miranda J, Bokde AL, Born C, Hampel H, Stetter M. 2005. Classifying brain states and determining the discriminating activation patterns: support vector machine on functional MRI data. Neuroimage 28:980–995 [DOI] [PubMed] [Google Scholar]
  39. Murray EA, Richmond BJ. 2001. Role of perirhinal cortex in object perception, memory, and associations. Curr Opin Neurobiol 11:188–193 [DOI] [PubMed] [Google Scholar]
  40. Pearson RC, Esiri MM, Hiorns RW, Wilcock GK, Powell TP. 1985. Anatomical correlates of the distribution of the pathological changes in the neocortex in Alzheimer disease. Proc Natl Acad Sci U S A 82:4531–4534 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Richard A, Johnson DWW. 1982. Applied Multivariate Statistical Analysis. Upper Saddle River, NJ: Prentice-Hall [Google Scholar]
  42. Roebroeck A, Formisano E, Goebel R. 2005. Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage 25:230–242 [DOI] [PubMed] [Google Scholar]
  43. Schmidt-Wilcke T, Poljansky S, Hierlmeier S, Hausner J, Ibach B. 2009. Memory performance correlates with gray matter density in the ento-/perirhinal cortex and posterior hippocampus in patients with mild cognitive impairment and healthy controls—a voxel based morphometry study. Neuroimage 47:1914–1920 [DOI] [PubMed] [Google Scholar]
  44. Sergios Theodoridis KK. 2006. Pattern Recognition. Waltham, MA: Academic Press [Google Scholar]
  45. Seth AK, Chorley P, Barnett LC. 2013. Granger causality analysis of fMRI BOLD signals is invariant to hemodynamic convolution but not downsampling. Neuroimage 65:540–555 [DOI] [PubMed] [Google Scholar]
  46. Sole-Padulles C, Bartres-Faz D, Llado A, Bosch B, Pena-Gomez C, Castellvi M, Rami L, Bargallo N, Sanchez-Valle R, Molinuevo JL. 2013. Donepezil treatment stabilizes functional connectivity during resting state and brain activity during memory encoding in Alzheimer's disease. J Clin Psychopharmacol 33:199–205 [DOI] [PubMed] [Google Scholar]
  47. Uddin LQ, Kelly AM, Biswal BB, Castellanos FX, Milham MP. 2009. Functional connectivity of default mode network components: correlation, anticorrelation, and causality. Hum Brain Mapp 30:625–637 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. van Strien NM, Cappaert NL, Witter MP. 2009. The anatomy of memory: an interactive overview of the parahippocampal-hippocampal network. Nat Rev Neurosci 10:272–282 [DOI] [PubMed] [Google Scholar]
  49. White KG, Ruske AC. 2002. Memory deficits in Alzheimer's disease: the encoding hypothesis and cholinergic function. Psychon Bull Rev 9:426–437 [DOI] [PubMed] [Google Scholar]
  50. Wu GR, Stramaglia S, Chen H, Liao W, Marinazzo D. 2013. Mapping the voxel-wise effective connectome in resting state FMRI. PLoS One 8:e73670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Zahneisen B, Hugger T, Lee KJ, LeVan P, Reisert M, Lee HL, Asslander J, Zaitsev M, Hennig J. 2012. Single shot concentric shells trajectories for ultra fast fMRI. Magn Reson Med 68:484–494 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental data
Supp_Table1.pdf (21.7KB, pdf)
Supplemental data
Supp_Table2.pdf (18.5KB, pdf)
Supplemental data
Supp_Fig1.pdf (59.2KB, pdf)

Articles from Brain Connectivity are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES