Skip to main content
PMC home page
Brain Connectivity logoLink to Brain Connectivity
. 2014 Nov 1;4(9):718–726. doi: 10.1089/brain.2014.0305

Investigating the Capability to Resolve Complex White Matter Structures with High b-Value Diffusion Magnetic Resonance Imaging on the MGH-USC Connectom Scanner

Qiuyun Fan 1,,*,✉, Aapo Nummenmaa 1,,*, Thomas Witzel 1, Roberta Zanzonico 1, Boris Keil 1, Stephen Cauley 1, Jonathan R Polimeni 1, Dylan Tisdall 1, Koene RA Van Dijk 1,,2, Randy L Buckner 1,,2, Van J Wedeen 1, Bruce R Rosen 1, Lawrence L Wald 1
PMCID: PMC4238244  PMID: 25287963

Abstract

One of the major goals of the NIH Blueprint Human Connectome Project was to map and quantify the white matter connections in the brain using diffusion tractography. Given the prevalence of complex white matter structures, the capability of resolving local white matter geometries with multiple crossings in the diffusion magnetic resonance imaging (dMRI) data is critical. Increasing b-value has been suggested for delineation of the finer details of the orientation distribution function (ODF). Although increased gradient strength and duration increase sensitivity to highly restricted intra-axonal water, gradient strength limitations require longer echo times (TE) to accommodate the increased diffusion encoding times needed to achieve a higher b-value, exponentially lowering the signal-to-noise ratio of the acquisition. To mitigate this effect, the MGH-USC Connectom scanner was built with 300 mT/m gradients, which can significantly reduce the TE of high b-value diffusion imaging. Here we report comparisons performed across b-values based on q-ball ODF metrics to investigate whether high b-value diffusion imaging on the Connectom scanner can improve resolving complex white matter structures. The q-ball ODF features became sharper as the b-value increased, with increased power fraction in higher order spherical harmonic series of the ODF and increased peak heights relative to the overall size of the ODF. Crossing structures were detected in an increasingly larger fraction of white matter voxels and the spatial distribution of two-way and three-way crossing structures was largely consistent with known anatomy. Results indicate that dMRI with high diffusion encoding on the Connectom system is a promising tool to better characterize, and ultimately understand, the underlying structural organization and motifs in the human brain.

Key words: : diffusion MRI, HARDI, high b-value, Human Connectome Project, multi-shell acquisition, structural connectivity

Introduction

Diffusion magnetic resonance imaging (dMRI) is a noninvasive method for measuring tissue microstructure that works by probing the MR signal attenuation due to the diffusion of water molecules (Stejskal and Tanner, 1965). Early diffusion images demonstrated the anisotropy of water diffusion in white matter, with increased diffusion along the principal axonal direction (Chien et al., 1990). Subsequently, diffusion tensor imaging was proposed by Basser and colleagues (1994) to more fully characterize the anisotropy of Brownian motion of water molecules in tissues and has been widely used to measure white matter structural properties in neuroimaging studies.

However, due to the underlying assumption of Gaussian diffusion, tensor-based methods cannot resolve intravoxel fiber crossings. To reveal the non-Gaussian diffusion profile stemming from crossing fibers, more complete angular sampling of the diffusion signal is necessary to resolve multiple crossing fibers. Furthermore, as the b-value is increased, the remaining signal becomes increasingly reflective of water diffusion in highly restrictive water compartments. Thus, it is commonly recognized that the improved diffusion contrast from higher b-values provides improved contrast in the angular domain (Alexander and Barker, 2005; Cho et al., 2008; Clark and Le Bihan, 2000; Descoteaux et al., 2009; Jensen et al., 2005; Jones et al., 2013; Tournier et al., 2004, 2008; Tuch, 2004; Yoshiura et al., 2001; Zhan and Yang, 2006). For example, Tournier modeled the voxel as multiple populations of stacked cylinders and showed that, as the b-value increases, the angular plots of the diffusion profile become narrower (Tournier, 2011). However, the question remains as to when the lower signal-to-noise ratio (SNR) of the higher b-value acquisition negates the benefit of this increased angular contrast.

To answer this question White and Dale (2009) modeled the fiber orientation estimate uncertainty as a function of b-value and spherical harmonic expansion order (L) using a tensor fiber model and concluded that a b-value of about 6200 sec/mm2 was needed for L=8 for their modeled SNR. More recently, Tournier et al. (2013) found that the L>0 content of the spherical harmonic series of diffusion weighted (DW) signal increases as b-value increases. Using their experimental conditions, it was suggested that the highest attainable angular contrast could be achieved with a b-value of 3000 sec/mm2. Since the tradeoff is between contrast and noise level, the optimum b-value was expected to increase if SNR could be improved by other means.

In this report, we experimentally study the effect of increasing b-value on the angular contrast and resultant detection of multiple fiber crossings, extending our preliminary analysis (Nummenmaa et al., 2014). We use a set of real spherical harmonics (Descoteaux et al., 2007) for the reconstruction of q-ball (Tuch, 2004) diffusion orientation distribution function (ODF) from high angular resolution diffusion imaging (HARDI) data collected on a scanner capable of obtaining very high gradient strengths up to 300 mT/m. This unique scanner was constructed by Siemens for the MGH-USC Human Connectome Project (HCP) consortium (McNab et al., 2013; Setsompop et al., 2013) and was based on their 3T Magnetom Skyra platform. With this scanner, very high b-values can be obtained at short echo times (TE), allowing us to assess the benefit of higher diffusion contrast with minimal loss of sensitivity from T2 decay. We quantify the number of resolved ODF peaks representing different fiber populations in each voxel while varying the b-value and angular sampling resolution. We also study the shape and quantify the angular frequency content of the ODF as a function of b-value. Finally, we perform tractography on some of the datasets to illustrate the potential implications of higher b-value acquisitions for mapping structural brain connectivity.

Materials and Methods

Data acquisition

The MRI data were acquired from three healthy adults on the 3T Siemens MGH-USC Connectom scanner. The participants gave written informed consent, and the experiments were carried out with approval from the institutional review board. The higher strengths of the Connectom gradients lead to proportionately larger eddy currents, and a more precise calibration of the eddy current pre-emphasis and B0 compensation was performed by taking into account the second-order terms of eddy currents, so that eddy-current-induced distortions in the images would be low enough to be corrected with standard post-processing methods. A custom-made, 64-channel, phased array coil was used for signal reception (Keil et al., 2013). The diffusion acquisition was performed using a monopolar Stejskal-Tanner pulsed gradient spin echo, echo planar imaging (EPI) sequence. A fast low-angle-excitation echo train (Bhat et al., 2014; Polimeni et al., 2013) scan line correction technique allowed for acquisition of a stable autocalibration signal. Parallel imaging using generalized autocalibrating partially parallel acquisition (GRAPPA) method was combined with blipped-controlled aliasing in parallel imaging simultaneous multi-slice (SMS) EPI (Feinberg et al., 2010; Feinberg and Setsompop, 2013; Moeller et al., 2010; Setsompop et al., 2012a,b) to accelerate image acquisition.

Each dataset also included a high-resolution T1-weighted anatomical scan acquired with the magnetization-prepared rapid gradient echo (MPRAGE) sequence along with diffusion scans at multiple b-values. Two subjects were scanned with diffusion protocol No. 1 consisting of four different b-values of 1000 sec/mm2 (64 directions), 3000 sec/mm2 (64 directions), 5000 sec/mm2 (128 directions), and 10,000 sec/mm2 (256 directions). Different b-values were achieved by varying the diffusion gradient amplitudes. The gradient pulse duration (δ) and diffusion time (Δ) were fixed at 12.9 and 21.8 msec, respectively. Other scanning parameters included TE/repetition time (TR)=57/8800 msec, field of view (FOV)=21×21 cm2, 96 slices, 1.5 mm isotropic voxels, partial Fourier=6/8, GRAPPA iPAT factor=3, SMS=1, band width (BW)=1984 Hz/pixel, and echo spacing of 0.63 msec. The total acquisition time for each subject was ∼89 min.

To compare different b-value acquisitions with identical angular resolution, one subject was scanned with diffusion protocol No. 2 consisting of three different b-values: 3000 sec/mm2 (256 directions), 5000 sec/mm2 (256 directions), and 10,000 sec/mm2 (256 directions), and the 10k (i.e., b=10,000 sec/mm2) shell was averaged for two repetitions. Other imaging parameters included δ/Δ=11.4/27.2 msec, TE/TR=59/4500 msec, FOV=21×21 cm2, 98 slices, 1.5 mm isotropic voxels, partial Fourier=7/8, GRAPPA iPAT factor=3, SMS=2, shift factor=3, BW=1984 Hz/pixel, and echo spacing of 0.63 msec. The total acquisition time was ∼89 min. For both protocols, a non-DW image (b=0 image) was acquired every 14 images. As in diffusion protocol No. 1, different b-values were achieved by varying the diffusion gradient amplitudes.

Data preprocessing

Diffusion data preprocessing consisted of two steps: gradient nonlinearity distortion correction and motion/eddy current distortion correction. The gradient nonlinearity distortions were corrected using in-house developed MATLAB tools, which computed the nonlinear transformation from the distorted image to the undistorted image given the spatial map of gradient nonlinearity for the particular gradient coil used for imaging (Glasser et al., 2013; Jovicich et al., 2006). Image data were resampled using spline interpolation.

The b=0 images interspersed throughout the diffusion scans were used to estimate head motions with respect to the initial time point (first b=0 image), where the rigid transformations were calculated with the boundary-based registration tool in the FreeSurfer package version 5.3.0 (Greve and Fischl, 2009) using the MPRAGE anatomical data as a reference. For each b=0 image, this transformation was then applied to itself and the following 13 DW image volumes to correct for head movements. Eddy current distortions (as well as residual motion) were corrected using the “EDDY” tool in FSL version 5.0 (Andersson et al., 2012). The diffusion data were concatenated across different shells and corrected jointly for eddy current distortion. The gradient direction table was adjusted to account for rigid transformations resulting from motion and eddy current corrections.

q-Ball ODF comparison across b-values

Characterizing the shape of the ODF

The q-ball ODFs were reconstructed for each shell with maximum spherical harmonic order of eight and Laplace-Beltrami regularization weight parameter of 0.006 (Descoteaux et al., 2007), and the ODFs were normalized by subtracting the ODF minimum. First, in order to compare the shape of the ODF across different b-values, the ODFs of different b-values were overlaid for qualitative visual evaluation. Second, as a quantitative figure of merit, the ODF peak height, or quantitative anisotropy, was used to measure fiber-crossing properties (Yeh et al., 2010). In this study, up to three dominant peaks were considered, as illustrated in Figure 1. Particularly, in regions with known multiple crossing fibers, larger second and third peaks were desirable features for the purpose of resolving these crossing structures.

FIG. 1.

FIG. 1.

Open in a new tab

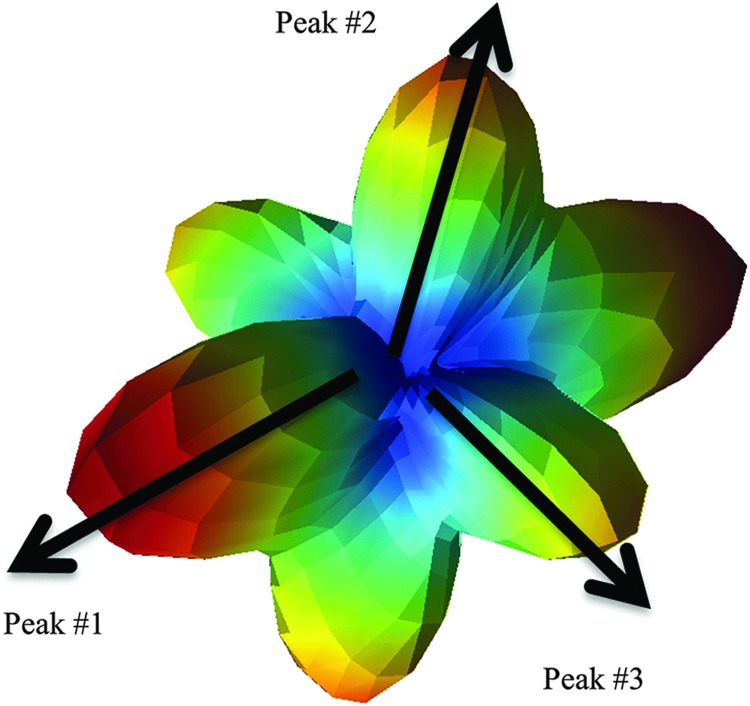
Illustration of the figure of merit based on peak height of the crossing-fiber orientation distribution function (ODF).

Power spectrum of the harmonic series of the ODF

Higher spherical harmonic orders correspond to higher angular frequencies in the harmonic series expansion, and thus can characterize the sharper features of the shape of ODF. To quantify the sharpness of the ODF reconstructions as a function of increasing b-value, the relative power contribution of order L in the spherical harmonic series of the ODF (EL) was computed according to (Hess et al., 2006).

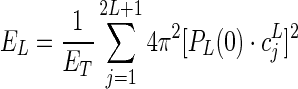graphic file with name eq1.gif

In the aforementioned equation, ET is the total power of up to eighth-order spherical harmonic representation of all L≥2, such that 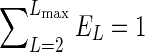Inline graphic; PL(x) is the Legendre polynomial of order L; and 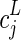Inline graphic is the jth spherical harmonic coefficient of the ODF of order L. The power fractions were calculated on a voxel-wise basis with the same Laplace-Beltrami regularization parameter (λ=0.006) used in the ODF shape comparisons. Finally, the power fractions were averaged across all white matter voxels. Since the zero-order spherical harmonic component does not contribute to ODF anisotropy, it was not included in the analysis.

Estimating number of fibers in white matter voxels

To assess the ability to resolve crossing fibers, the number of voxels with single or multiple fibers in the white matter was counted and compared across b-values.

A white matter mask was obtained from the automated Freesurfer segmentation of the MPRAGE image. The transformation used to coregister the b=0 image and MPRAGE image was used to align the white matter mask with the diffusion data. To avoid partial volume effects from cerebrospinal fluid (CSF), the white matter mask was further thresholded based on the mean diffusivity (MD) of the voxels within the mask (Jeurissen et al., 2013). Briefly, the voxels with MD higher than [median (MD)+1.5×IQR (MD)] were removed, where IQR is the interquartile range over the white matter mask.

ODF peak orientations were found by searching 642 evenly distributed spherical sample points for local maxima. Subsequently, a series of thresholding criteria for the peaks was applied locally in each voxel, including (1) the amplitudes of the second and the third peaks needed to be ≥5% of the first peak to become a candidate and (2) a candidate peak was excluded if its orientation yielded a crossing angle smaller than 35° from any peak(s) with higher amplitude. Since ODF peaks with lower amplitudes have a higher chance of resulting from noise, setting thresholds on the amplitude of the peak was commonly adopted to remove spurious peaks (Cohen-Adad et al., 2011; Jeurissen et al., 2013). The angular threshold between candidate peaks was imposed because the angular resolution of the eighth-order spherical harmonic, calculated as the full width at half maximum of the main lobe, is ∼35° (Hess et al., 2006).

Additionally, a global threshold on the ODF peaks was derived as follows. The standard deviation of the DW signal across different gradient directions in CSF within the lateral ventricles was used to estimate the temporal noise fluctuations in the DW images, assuming isotropic diffusion in CSF. The level of noise fluctuation at each b-value was separately estimated using the mean temporal fluctuation in the mask of the lateral ventricles. The calculated standard deviation was then used to generate 50,000 instances of Gaussian-distributed random noise, which were used to generate synthetic ODFs. The maximum amplitude of fluctuation in each synthetic ODF was then determined. The distribution of these maximum amplitudes provided an estimate of the distribution of maximum peak amplitudes due to noise (hereafter referred to as noise peaks). The mean and standard deviation of the noise peaks were then calculated to provide global threshold values that could be applied to all the voxel-wise-calculated ODFs.

To explore the impact of the global thresholds on the ODF-based metrics, a range of threshold values were tested. Specifically, the threshold was calculated as N (N=0, 0.5, 1,…, 10) times the standard deviation above the mean of the noise peaks. N=2 was selected to report the spatial distribution of white matter voxels containing one, two, and three fibers.

Tractography

In addition to the crossing-fiber ODF metrics, we performed tractography using DSI studio (http://dsi-studio.labsolver.org/) to assess the potential impact of improved local ODF estimates on the reconstructed tracts. We performed whole-brain deterministic fiber tracking, selected the fibers that passed through the corpus callosum, and compared the resulting fiber tracts by visual inspection.

Results

The shape of the ODF across b-values

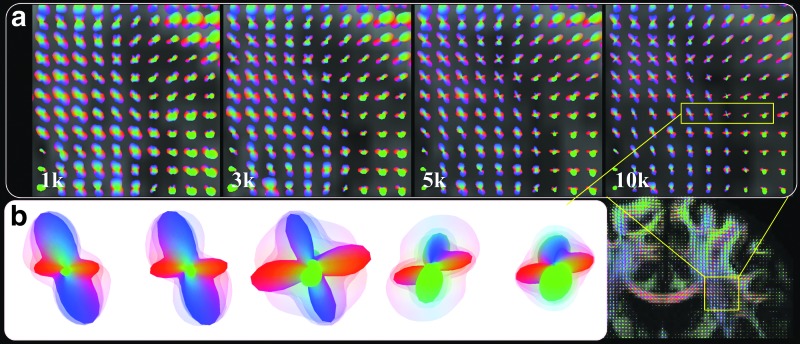
The q-ball ODFs of different b-values from one subject scanned with protocol No. 1 are shown in Figure 2. In a region of interest near the centrum semiovale, the sharpness of the ODF is clearly found to increase as b-value increases (Fig. 2a). To facilitate visual comparison, the ODFs of different b-values are overlaid together to demonstrate any differences (Fig. 2b). The ODFs of the 10k shell are shown in opaque color, while the other shells are denoted in transparent color, with the 1k shell being the outmost layer, and the 3k and 5k shells being consecutive layers inward, respectively.

FIG. 2.

FIG. 2.

Open in a new tab

The q-ball ODF comparisons across b-values. (a) A region of interest (10×10 voxels) in the centrum semiovale is shown as a function of the increasing b-value. (b) The ODFs of four different b-values overlaid together for five consecutive voxels. The ODF of the 10k shell is shown in opaque color, while the transparent color (from outside to inward) denotes the ODFs of the 1k, 3k, and 5k shells, respectively. The ODFs were scaled to have the same maximum amplitude to facilitate the visual comparison.

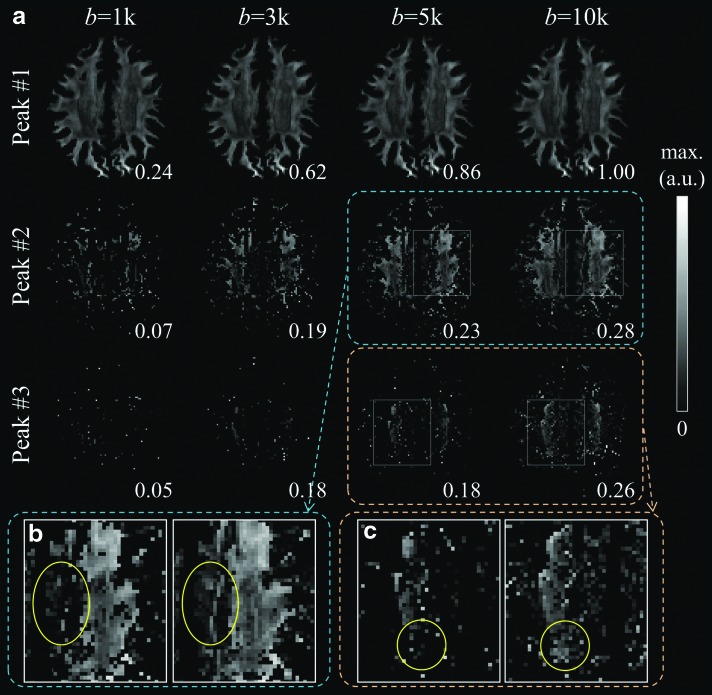
The ODF-peak-height metrics were calculated for each of the three dominant peaks and compared across b-values. In this analysis, the average of the largest ODF inside the white matter of each shell was globally scaled to one to prevent noise amplification, and then the ODF was normalized locally by subtracting the minimum. As shown in Figure 3a, when the gray scales were adjusted to reflect the full dynamic range of ODF-peak-heights for each b-value, the spatial maps of the heights of the most dominant ODF peaks (peak No. 1) were largely identical across different b-values. This indicates that the white matter structures represented by the most dominant ODF peak could be resolved identically across different b-values. For the peak No. 2, the 5k and 10k shells were able to resolve more crossing structures than the 1k and 3k shells, and the 10k shell showed somewhat improved continuity in the spatial maps than the 5k shell (Fig. 3b). Peak No. 3 was largely absent in the lower b-value data (i.e., 1k and 3k), while the 10k shell showed superior performance than the 5k shell in resolving crossing structures that were anatomically plausible (Fig. 3c). For each of the three peaks, the peak heights (relative to the overall size of the ODF) increased as b-value increased, mainly due to the decrease in the isotropic “baseline” in the ODF. Taken together, the results showed both qualitatively and quantitatively that the higher b-value acquisitions were able to capture finer details of the ODFs better, leading to improved delineation of more complex three-way fiber crossings.

FIG. 3.

FIG. 3.

Open in a new tab

Comparison of the ODF peak heights. (a) The peak heights of the three dominant ODF peaks for different b-values. (b, c) A closer look at the 5k and 10k shells shows regions circled where crossing structures resolved with the 10k shell were missing in the 5k shell data. The gray scale was adjusted separately for each image to show the full dynamic range. For each of the individual images, the maximum image intensity relative to the maximum of peak No. 1 of the 10k shell was labeled on the figure.

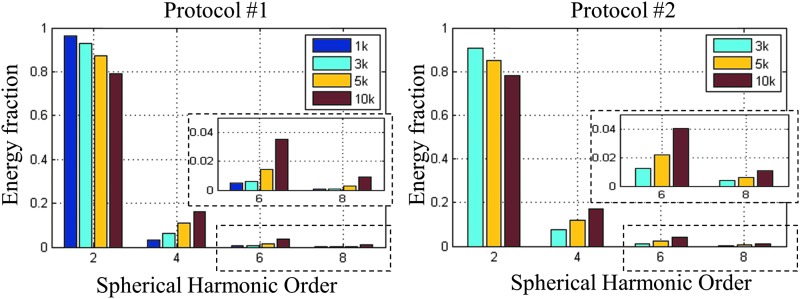
The power spectrum in the harmonic series of the ODF

The relative power contributions of different angular frequencies to the ODF reconstruction are shown in Figure 4. The results demonstrate that the ODFs reconstructed from higher b-value data showed a larger fraction of energy in the higher harmonic orders. This was consistent with the qualitative ODF sharpening observed with increasing b-value. To investigate the potential influence of unmatched angular resolution in the different shells in protocol No. 1, the same figure of merit was calculated with the data acquired with protocol No. 2. The results show that while all the shells have identical 256 diffusion weighting directions (matched to the 10k shell of protocol No. 1), the same effect of increasing power fraction in the higher-order harmonics with increasing b-value was still observed. We can therefore conclude that the higher b-value data contained a higher degree of spatial detail in the ODFs.

FIG. 4.

FIG. 4.

Open in a new tab

The power contribution to ODF anisotropy for b-values ranging from 1k to 10k sec/mm2. The left and right panels show the results for diffusion protocols No. 1 and No. 2, respectively.

Estimating number of fibers in white matter voxels

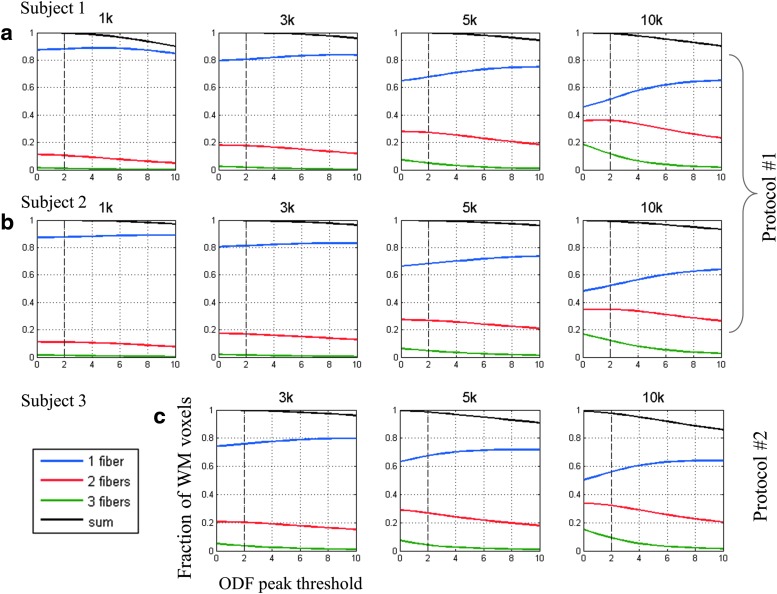
The relationship between threshold values and the fraction of the white matter voxels containing one, two, or three fibers was explored first (Fig. 5). As the threshold increased, the smallest ODF peaks (peak No. 3) lower than the threshold were removed, and thus the fraction of white matter voxels containing three-way crossings monotonically decreased. For voxels containing a single fiber (blue curve) and two-way crossings (red curve), two mechanisms simultaneously contributed to the observed changes. In the single-fiber case, (1) as the threshold increased, the voxels in which the peak No. 2 and peak No. 3 were removed became single-fiber voxels, thereby contributing to a positive change (i.e., the fraction of single-fiber voxels increased) and (2) when the threshold exceeded the largest peak in a particular voxel, this voxel was considered as containing no fiber at all, and this will consequently contribute to a negative change. The fraction of the sum of voxels containing at least one fiber (black curve) is a reflection of the degree of stringency of the threshold; that is, when the curve decreased from unity, it indicated that the threshold started to become overly stringent, assuming at least one fiber compartment exists in these white matter voxels. Figure 5 shows that with increasing b-values, a higher fraction of white matter voxels was identified as containing multiple fibers. This trend was not attributable to higher angular resolution in the shells with higher b-value, since similar results were found in the dataset acquired with protocol No. 2.

FIG. 5.

FIG. 5.

Open in a new tab

Fractions of white matter voxels with single and multiple fibers for different values of threshold. The ODF peak threshold was labeled as N (N ranges from 0 to 10) times standard deviation above the mean of the noise peaks. Data from subjects 1 and 2 (a, b) were acquired with the same imaging protocol No. 1, where number of diffusion directions in the 1k, 3k, 5k, and 10k shells was 64, 64, 128, and 256, respectively; data from subject 3 (c) were acquired with protocol No. 2, with 256 diffusion directions in all three shells.

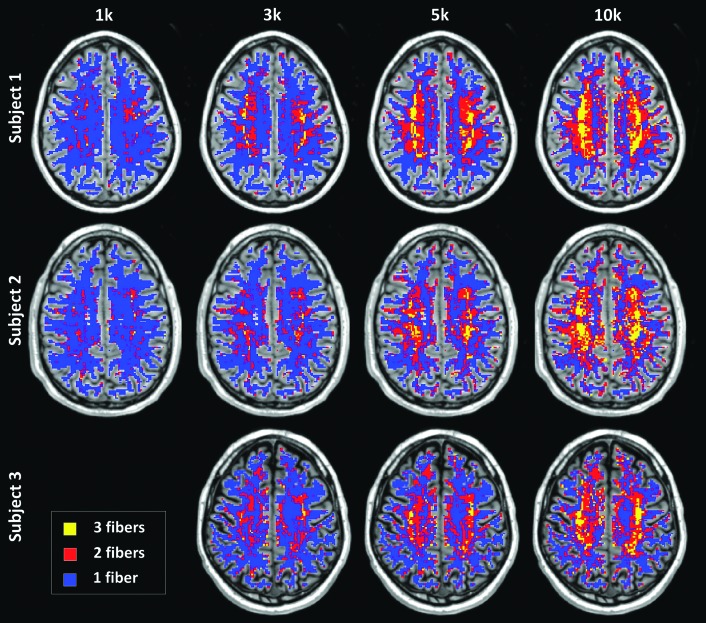
The spatial distribution of the number of fibers is shown in Figure 6, where the ODF peak threshold was selected to be two times the standard deviation above the mean of the noise peaks. A higher percentage of white matter voxels was identified as containing crossing fibers (Fig. 6) as b-value increased. These maps of distribution are largely consistent with known anatomy. For instance, the centrum semiovale region, which is expected to contain voxels with three-way crossings of the cortico-spinal tract, superior longitudinal fasciculus, and the inter-hemispheric association fibers, was better delineated by the higher b-value acquisitions.

FIG. 6.

FIG. 6.

Open in a new tab

The number of fibers in each white matter voxel for different b-values (columns) and subjects (rows). Color coding: yellow, three or more fibers; red, two fibers; and blue, one fiber.

Impacts on the fiber tractography

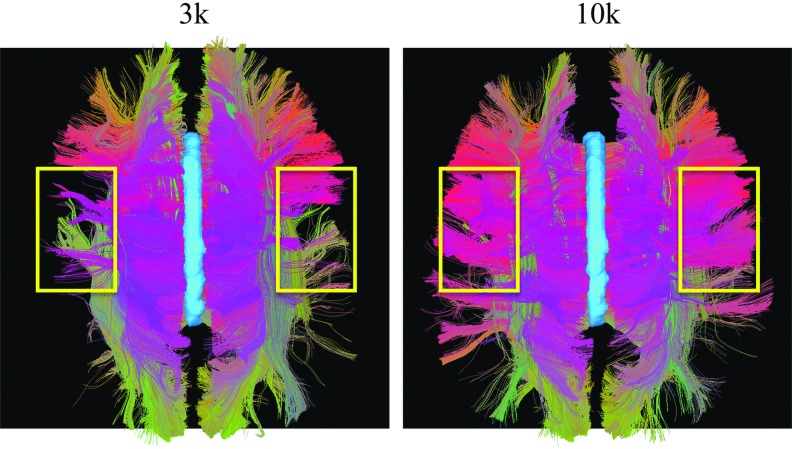
As an outcome measure of the improved local ODF estimates due to higher b-value, the fiber tracts obtained from the 3k and 10k shells of the dataset acquired with protocol No. 2 are shown from the top view in Figure 7. By visual inspection, a greater number and more evenly distributed array of trans-callosal tracts were better captured by the 10k shell data than those at lower b-values. As known crosshemispheric connectivity predicts trans-callosal fibers tracking broadly to homologous cortex, the apparent loss of these fibers at lower b-values was indicative of greater difficulty in resolving tracts through this region. This may well arise because these tracts need pass through the region of three-way crossings in the centrum semiovale, and thus are highly sensitive to ODF quality in these regions.

FIG. 7.

FIG. 7.

Open in a new tab

Fiber tractography comparison between the 3k and 10k shells. The fiber tracts passing through the corpus callosum (in light blue) were selected from the whole-brain tractography. In the region circled in yellow, the trans-callosal tracts were better captured by the 10k shell data, presumably due to the improved three-way-crossing ODF estimates in the centrum semiovale.

Discussion

The aim of this study was to investigate the potential of high b-value diffusion data in resolving complex white matter structures, such as two-way and three-way fiber crossings. In comparisons across b-values, we observed increased sharpness in the q-ball ODF reconstruction as b-value increased. This was quantitatively reflected in a larger energy fraction of higher-order terms in the spherical harmonic series of the ODF as the b-value increased, as well as an increased fraction of white matter with two-way or three-way fiber crossing structures resolved.

The q-ball approximation of the diffusion ODF was calculated by the means of the Funk-Radon transformation (FRT) of the diffusion signal (Tuch et al., 2003). The value of the ODF along certain direction was obtained by summing the diffusion signals along a circle perpendicular to that direction. Thus, a heuristic interpretation of the ODF-sharpening effect comes from angular specificity to fiber orientations in the DW signal. Specifically, with increasing diffusion weighting, the DW signal decays faster as the diffusion weighting direction deviates from the directions perpendicular to fiber orientations (Tournier et al., 2013). As a result, the much-reduced amplitude in DW signals that are not perpendicular to the fiber orientations contributes to the dampening of the lowest values between ODF peaks, giving rise to a sharper shape and less overlap between ODF peaks.

Since each of the spherical shells with different b-values had identical δ/Δ and varied only in gradient amplitude, we can also consider each of these shells as representing a spherical section of the Cartesian q-space (Callaghan, 1993). The ODF sharpening in the present case can therefore be alternatively explained in a more mathematical way using the q-space formalism (Callaghan, 1993; Wedeen et al., 2005). In brief, the “Bessel beam” kernel that the q-ball reconstruction implicitly incorporates when using the FRT to reconstruct the ODFs becomes narrower with increasing q-values, resulting in better angular resolution at the cost of reduced SNR [for further details see (Tuch, 2004; Tuch et al., 2003)].

In counting the number of fibers, the thresholds applied to the peak heights of the q-ball ODF may play a critical role in determining the fraction of white matter voxels containing one, two, or three fibers. For this reason, we provided the results of the metrics with a range of threshold values, aiming to illustrate this variation. The fraction of white matter voxels detected as containing crossing structures decreased as the value used for thresholding increased, but comparing between shells, higher b-value shells showed a superior performance of resolving more fiber crossings (i.e., two-way and three-way crossings), when the threshold value was fixed.

Given the tradeoff between diffusion contrast and SNR, the benefit of increasing diffusion weighting will gradually diminish due to decreasing image SNR. Thereby, the empirically optimal b-value varies with the specific experimental settings that may affect image SNR, such as the voxel size, the TE needed to achieve the gradient diffusion encoding and EPI readout parameters, the receiver coils, and the noise enhancement from acceleration factors. The optimal b-value to resolve complex white matter structures also depends on intrinsic tissue properties. For example, some regions in the brain may involve shallower crossing angles or a smaller volume fraction in one fiber component than others, and thus require enhanced angular separation of crossing structures with higher b-value. Thus, the problem of designing an optimal diffusion acquisition protocol is complex, both because the intrinsic properties of the fiber geometry vary considerably across the brain, and perhaps more fundamentally because this structure, in its details, is still unknown and indeed controversial (Catani et al., 2012; Wedeen et al., 2012a,b). It is also worth mentioning that, when higher diffusion encoding is applied, more directions need to be sampled in order to make use of the richer angular information in the DW signal. The optimal b-value has been studied previously by different groups; for example, 6200 sec/mm2 was proposed for minimized variance in FOD estimator (White and Dale, 2009), and 3000 sec/mm2 for highest achievable angular resolution in the DW signal in single-fiber voxels (Tournier et al., 2013). It is not surprising that the suggested optimal b-value will vary with the specific experimental scenarios. Our Connectom scanner benefited from the shorter TEmin and improved sensitivity of the 64-channel head coil. At high spatial resolution (1.5 mm isotropic), we observed increasing benefits in resolving complex white matter structures when the b-value increased from 1k to 10k sec/mm2.

To summarize, we performed comparisons with in vivo human diffusion data of up to b=10k sec/mm2 collected on the HCP MGH-USC Connectom scanner. We observed sharper q-ball ODF as the b-value increases. As a result, the crossing structures were detected in an increasingly larger fraction of white matter voxels and the map of two-way and three-way crossing structures grew with increasing b-value to cover much of the white matter. The results show that high b-value dMRI is beneficial for improving the angular resolution of HARDI methods and thus the capability of resolving complex white matter structures.

Conclusion

The results indicate that dMRI with high diffusion encoding on the Connectom system is a promising tool to better characterize, and ultimately understand, the underlying structural organization and motifs in the human brain.

Acknowledgments

The work is supported by the funding from the National Institutes of Health, NIH Blueprint Initiative for Neuroscience Research grant U01MH093765, NIH NIBIB grant K99EB015445, and the Instrumentation grants 1S10RR023401, 1S10RR019307, and 1S10RR023043.

Author Disclosure Statement

Dr. L.L.W. reports nonfinancial support from Siemens Healthcare. The remaining authors have no conflicts of interest to declare.

References

  1. Alexander DC, Barker GJ. 2005. Optimal imaging parameters for fiber-orientation estimation in diffusion MRI. Neuroimage 27:357–367 [DOI] [PubMed] [Google Scholar]
  2. Andersson JL, Xu J, Yacoub E, Auerbach E, Moeller S, Ugurbil K. A Comprehensive Gaussian Process Framework for Correcting Distortions and Movements in Diffusion Images. In Proceedings of the International Society for Magnetic Resonance in Medicine, Melbourne, Australia, 2012, p. 2426 [Google Scholar]
  3. Basser PJ, Mattiello J, LeBihan D. 1994. MR diffusion tensor spectroscopy and imaging. Biophys J 66:259–267 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bhat H, Polimeni JR, Cauley SF, Setsompop K, Wald LL, Heberlein K. Motion Insensitive ACS Acquisition Method for In-Plane and Simultaneous Multi-Slice Accelerated EPI. In Proceedings of the International Society for Magnetic Resonance in Medicine, Milan, Italy, 2014, p. 644 [Google Scholar]
  5. Callaghan PT. 1993. Principles of Nuclear Magnetic Resonance Microscopy. (Corrected ed.). Oxford: Clarendon Press [Google Scholar]
  6. Catani M, Bodi I, Dell'Acqua F. 2012. Comment on “The geometric structure of the brain fiber pathways”. Science 337:1605. [DOI] [PubMed] [Google Scholar]
  7. Chien D, Buxton RB, Kwong KK, Brady TJ, Rosen BR. 1990. MR diffusion imaging of the human brain. J Comput Assist Tomogr 14:514–520 [DOI] [PubMed] [Google Scholar]
  8. Cho KH, Yeh CH, Tournier JD, Chao YP, Chen JH, Lin CP. 2008. Evaluation of the accuracy and angular resolution of q-ball imaging. Neuroimage 42:262–271 [DOI] [PubMed] [Google Scholar]
  9. Clark CA, Le Bihan D. 2000. Water diffusion compartmentation and anisotropy at high b values in the human brain. Magn Reson Med 44:852–859 [DOI] [PubMed] [Google Scholar]
  10. Cohen-Adad J, Descoteaux M, Wald LL. 2011. Quality assessment of high angular resolution diffusion imaging data using bootstrap on Q-ball reconstruction. J Magn Reson Imaging 33:1194–1208 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Descoteaux M, Angelino E, Fitzgibbons S, Deriche R. 2007. Regularized, fast, and robust analytical Q-ball imaging. Magn Reson Med 58:497–510 [DOI] [PubMed] [Google Scholar]
  12. Descoteaux M, Deriche R, Knösche TR, Anwander A. 2009. Deterministic and probabilistic tractography based on complex fibre orientation distributions. IEEE Trans Med Imaging 28:269–286 [DOI] [PubMed] [Google Scholar]
  13. Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Gunther M, Glasser MF, Miller KL, Ugurbil K, Yacoub E. 2010. Multiplexed echo planar imaging for sub-second whole brain FMRI and fast diffusion imaging. PLoS One 5:e15710. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Feinberg DA, Setsompop K. 2013. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. J Magn Reson 229:90–100 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M, Consortium, WU-Minn HCP. 2013. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80:105–124 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Greve DN, Fischl B. 2009. Accurate and robust brain image alignment using boundary-based registration. Neuroimage 48:63–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hess CP, Mukherjee P, Han ET, Xu D, Vigneron DB. 2006. Q-ball reconstruction of multimodal fiber orientations using the spherical harmonic basis. Magn Reson Med 56:104–117 [DOI] [PubMed] [Google Scholar]
  18. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. 2005. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 53:1432–1440 [DOI] [PubMed] [Google Scholar]
  19. Jeurissen B, Leemans A, Tournier JD, Jones DK, Sijbers J. 2013. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum Brain Mapp 34:2747–2766 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Jones DK, Knösche TR, Turner R. 2013. White matter integrity, fiber count, and other fallacies: the do's and don'ts of diffusion MRI. Neuroimage 73:239–254 [DOI] [PubMed] [Google Scholar]
  21. Jovicich J, Czanner S, Greve D, Haley E, van der Kouwe A, Gollub R, Kennedy D, Schmitt F, Brown G, Macfall J, Fischl B, Dale A. 2006. Reliability in multi-site structural MRI studies: effects of gradient non-linearity correction on phantom and human data. Neuroimage 30:436–443 [DOI] [PubMed] [Google Scholar]
  22. Keil B, Blau JN, Biber S, Hoecht P, Tountcheva V, Setsompop K, Triantafyllou C, Wald LL. 2013. A 64-channel 3T array coil for accelerated brain MRI. Magn Reson Med 70:248–258 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. McNab JA, Edlow BL, Witzel T, Huang SY, Bhat H, Heberlein K, Feiweier T, Liu K, Keil B, Cohen-Adad J, Tisdall MD, Folkerth RD, Kinney HC, Wald LL. 2013. The Human Connectome Project and beyond: initial applications of 300 mT/m gradients. Neuroimage 80:234–245 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Uğurbil K. 2010. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med 63:1144–1153 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Nummenmaa A, Witzel T, Renvall V, Rosen B, Wedeen V, Wald L. Resolving Multiple Fiber Crossings with High b-Value and High Angular Resolution q-Ball Imaging. In Proceedings of the International Society for Magnetic Resonance in Medicine, Milan, Italy, 2014, p. 0978 [Google Scholar]
  26. Polimeni JR, Bhat H, Benner T, Feiweier T, Inati SJ, Witzel T, Heberlein K, Wald LL. Sequential-Segment Multi-Shot Auto-Calibration for GRAPPA EPI: Maximizing Temporal SNR and Reducing Motion Sensitivity. In Proceedings of the International Society for Magnetic Resonance in Medicine, Salt Lake City, Utah, USA, 2013, p. 2646 [Google Scholar]
  27. Setsompop K, Cohen-Adad J, Gagoski BA, Raij T, Yendiki A, Keil B, Wedeen VJ, Wald LL. 2012a. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage 63:569–580 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. 2012b. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 67:1210–1224 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SF, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen BR, Wedeen V, Wald LL. 2013. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage 80:220–233 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Stejskal EO, Tanner JE. 1965. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys 42:5 [Google Scholar]
  31. Tournier J-D. 2011. The biophysics of crossing fibers. In: Jones DK. (ed.) Diffusion MRI: Theory, Methods, and Application. New York: Oxford University Press; pp. xvi, p. 767 [Google Scholar]
  32. Tournier JD, Calamante F, Connelly A. 2013. Determination of the appropriate b value and number of gradient directions for high-angular-resolution diffusion-weighted imaging. NMR Biomed 26:1775–1786 [DOI] [PubMed] [Google Scholar]
  33. Tournier JD, Calamante F, Gadian DG, Connelly A. 2004. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage 23:1176–1185 [DOI] [PubMed] [Google Scholar]
  34. Tournier JD, Yeh CH, Calamante F, Cho KH, Connelly A, Lin CP. 2008. Resolving crossing fibres using constrained spherical deconvolution: validation using diffusion-weighted imaging phantom data. Neuroimage 42:617–625 [DOI] [PubMed] [Google Scholar]
  35. Tuch DS. 2004. Q-ball imaging. Magn Reson Med 52:1358–1372 [DOI] [PubMed] [Google Scholar]
  36. Tuch DS, Reese TG, Wiegell MR, Wedeen VJ. 2003. Diffusion MRI of complex neural architecture. Neuron 40:885–895 [DOI] [PubMed] [Google Scholar]
  37. Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weisskoff RM. 2005. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med 54:1377–1386 [DOI] [PubMed] [Google Scholar]
  38. Wedeen VJ, Rosene DL, Wang R, Dai G, Mortazavi F, Hagmann P, Kaas JH, Tseng WY. 2012a. Response to comment on “the geometric structure of the brain fiber pathways”. Science 337:1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Wedeen VJ, Rosene DL, Wang R, Dai G, Mortazavi F, Hagmann P, Kaas JH, Tseng WY. 2012b. The geometric structure of the brain fiber pathways. Science 335:1628–1634 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. White NS, Dale AM. 2009. Optimal diffusion MRI acquisition for fiber orientation density estimation: an analytic approach. Hum Brain Mapp 30:3696–3703 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Yeh FC, Wedeen VJ, Tseng WY. 2010. Generalized q-sampling imaging. IEEE Trans Med Imaging 29:1626–1635 [DOI] [PubMed] [Google Scholar]
  42. Yoshiura T, Wu O, Zaheer A, Reese TG, Sorensen AG. 2001. Highly diffusion-sensitized MRI of brain: dissociation of gray and white matter. Magn Reson Med 45:734–740 [DOI] [PubMed] [Google Scholar]
  43. Zhan W, Yang Y. 2006. How accurately can the diffusion profiles indicate multiple fiber orientations? A study on general fiber crossings in diffusion MRI. J Magn Reson 183:193–202 [DOI] [PubMed] [Google Scholar]

Articles from Brain Connectivity are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES