Quantification of the Statistical Effects of Spatiotemporal Processing of Nontask fMRI Data

Abstract

Nontask functional magnetic resonance imaging (fMRI) has become one of the most popular noninvasive areas of brain mapping research for neuroscientists. In nontask fMRI, various sources of “noise” corrupt the measured blood oxygenation level-dependent signal. Many studies have aimed to attenuate the noise in reconstructed voxel measurements through spatial and temporal processing operations. While these solutions make the data more “appealing,” many commonly used processing operations induce artificial correlations in the acquired data. As such, it becomes increasingly more difficult to derive the true underlying covariance structure once the data have been processed. As the goal of nontask fMRI studies is to determine, utilize, and analyze the true covariance structure of acquired data, such processing can lead to inaccurate and misleading conclusions drawn from the data if they are unaccounted for in the final connectivity analysis. In this article, we develop a framework that represents the spatiotemporal processing and reconstruction operations as linear operators, providing a means of precisely quantifying the correlations induced or modified by such processing rather than by performing lengthy Monte Carlo simulations. A framework of this kind allows one to appropriately model the statistical properties of the processed data, optimize the data processing pipeline, characterize excessive processing, and draw more accurate functional connectivity conclusions.

Introduction

Spatiotemporal processing is a common practice in both task and nontask functional magnetic resonance imaging (fMRI) studies as a way to “improve” the resulting images. Although such processing makes the image data more “appealing” by alleviating it of “noise,” it could unknowingly lead to misguided conclusions as it alters the signal (mean) and noise (variance and correlation) properties of data. In recent studies, it has been shown that spatial processing operations, such as spatial filtering in both the spatial frequency space (k-space) and image space domains (Nencka et al., 2009), induce artificial correlations. Moreover, parallel MRI (pMRI) models, such as SENSitivity Encoding (SENSE) (Pruessmann et al., 1999) and Generalized Autocalibrating Partially Parallel Acquisition (GRAPPA) (Griswold et al., 2005), have been shown to induce artificial correlations between previously aliased voxels in the reconstructed images (Bruce et al., 2011, 2012; Bruce and Rowe 2013, 2014; Karaman et al., 2013). Task and nontask fMRI studies typically employ both spatial and temporal filtering, together with additional signal regression operations (Glover et al., 2000; Hahn and Rowe, 2012). While these spatial and temporal processing operations could induce artificial correlations in the acquired data, traditional task and nontask fMRI models assume independence between voxels, and therefore they do not account for the spatial correlation between voxels or temporal correlation within each voxel's time series. As these correlations are of no biological origin, they can result in increased Type I/Type II errors in both task and nontask fMRI. Even though the structure of the induced correlations can be estimated through time-consuming simulations, there is an apparent need for the development of tools that can precisely quantify the implications of spatial and temporal processing operations and means of accounting for these implications in the final analysis. If the effects that such operations have on the statistical properties of the acquired data are unaccounted for, neuroscientists could draw inferences from the processed data that are inconsistent with those of the original data.

Many studies have considered means of evaluating preprocessing by either using time-consuming Monte Carlo (MC) simulations (Barry et al., 2011; Della-Maggiore et al., 2002; Strother, 2006) or empirically optimizing the processing procedures (LaConte et al., 2003; Shaw et al., 2003). Such work aims to determine the best results through the evaluation of the effect of preprocessing on the computed time series statistics, while the true statistical properties of the data are not typically included into given task and nontask fMRI models. Bowman (2005) presented a spatiotemporal model that partitions voxels into functionally related networks and captures correlations between voxels through a simultaneous a spatial autoregression. Other promising work has shown that accounting for background spatial correlation inherent in neuroimaging data, which is caused by non-neurophysiologic associations and image processing, can improve functional connectivity measurements. (Patel et al., 2006). A study by Deshpande and colleagues (2009) introduced the measure of integrated local correlation for assessing local coherence and corrected the inherent correlation in fMRI data due to the image acquisition and reconstruction processes. Derado and colleagues (2010) proposed a two-stage model that accounts for both spatial and temporal correlations in fMRI data. However, these approaches either do not account for temporal correlations or do not provide a theoretical estimation of spatiotemporal correlations of the voxel measurements to be accounted for in the task and nontask fMRI models.

Many studies have aimed to rid the data of “noise’ through both spatial and temporal processing. However, little attention is ever paid to the degree to which processing operations change the true statistical properties of the acquired data. Previous studies conducted by our group have incrementally developed the necessary tools to evaluate and incorporate the statistical impact of spatial and temporal processing operators into the final analysis of task and nontask fMRI data. A real-valued isomorphism of the complex-valued inverse Fourier transformation (IFT) matrix operator was described by Rowe and colleagues (2007) to relate the signal and noise characteristics of k-space measurements and reconstructed voxel measurements. Representing Fourier reconstruction as a single matrix operator formed the basis for another study by Nencka and colleagues (2009) in which A Mathematical Model for Understanding the STatistical effects of k-space preprocessing (AMMUST-k), was developed to represent various spatial processing operations performed on the acquired spatial frequencies in terms of real-valued linear isomorphisms. The AMMUST-k framework was further expanded to incorporate parallel MR reconstruction models, SENSE and GRAPPA, by representing each model as a series of real-valued matrix operators (Bruce et al., 2011, 2012; Bruce and Rowe, 2013). Representing the reconstruction and spatial processing in this way makes it possible to precisely compute the covariance (and ultimately correlation) induced by such operations into the image space data.

In this article, we develop “A Mathematical Model for Understanding the STatistical effects of time series preprocessing” (AMMUST-t), by further advancing the AMMUST-k framework to include temporal processing of the data together with spatial processing and pMRI reconstruction operations. With a framework of this kind, one can precisely quantify the degree to which the mean and covariance between both voxels and time points are modified by each processing operation individually or by all processes collectively, without the need for lengthy simulations that can only approximate these changes. Such a framework can be used by neuroscientists to assess their processing pipelines by characterizing excessive processing, and ultimately aid in producing more accurate functional connectivity statistics. In this article, we first develop time series operators for common processing operations such as image registration (Jenkinson et al., 2002), dynamic magnetic field correction (Hahn et al., 2009), slice timing correction (Huettel et al., 2004), and temporal filtering (Huettel et al., 2004), and illustrate the effects of these operators with a low dimensional example. We then demonstrate the effects of commonly used operations such as spatial smoothing, temporal filtering, and a SENSE image reconstruction with higher dimension theoretical data and on experimental phantom and nontask human subject data.

Materials and Methods

AMMUST-t framework

The real-valued IFT matrix operator

was developed by Rowe and colleagues (2007) to quantify the precise linear combination of k-space measurements that form each voxel value in the reconstructed image. The operators, Ω_R and Ω_I, are formed using the Kronecker product, ⊗, by

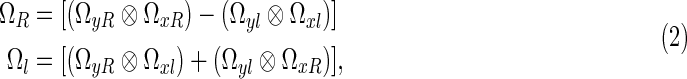where the Fourier matrices, Ω_x and Ω_y Fourier reconstruct the columns and rows of the acquired k-space, respectively. The jk^th element of the n×n Fourier matrix Ω_x can be written as 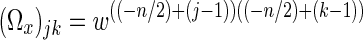, where j and k are the indices from 1 to n and w=(1/n)exp(i2π/n). The matrix Ω_y similarly follows with n replaced by m. To apply the IFT operator, Ω, in Eq. (1), the complex-valued spatial frequency matrix is reformatted into a real-valued vector that is formed by stacking the rows of the real components of on top of the rows of the imaginary components. For an m×n image of p=mn voxels, the frequency space measurements can therefore be represented by a 2p×1 column vector, s=(s_R′,s_I′)′, where s_R=(s_R1,…,s_Rp)′ and s_I=(s_I1,…,s_Ip)′ are p×1 real-valued column vectors that consist of the real and imaginary observations of p voxels, respectively. Applying the Ω operator to the real-valued frequency vector,

produces a vector, y, with all real reconstructed voxel values stacked by row on top of all imaginary reconstructed voxel values. The formalism in Eq. (3) can be generalized to

where the operator O signifies an arbitrary series of linear processing operations (Nencka et al., 2009) and/or parallel reconstruction operators (Bruce et al., 2011, 2012) expressed in matrix form.

In the AMMUST-t framework, we extend the framework in Eq. (4) to combine temporal processing operations with the previously developed spatial processing and reconstruction operations. In such a framework, the vector of the observed k-space observation can be represented as a concatenation of N k-space signal vectors, with each of these vectors representing one 2p×1 time point image vector. The time series frequency measurements can therefore be represented by a 2pN×1 column vector, s_T=(s_1R′,s_1I′,…,s_NR′,s_NI′)′ where s_tR and s_tI are the real and imaginary frequency space column vectors at time point t. The reconstructed and processed time series, y_T, can then be obtained from the acquired signal vector, s_T, by

The operator matrix, O_T, is formed through the multiplication of a k-space processing operator, K, a reconstruction operator, R, an image space processing operator, I, and finally a temporal processing operator, T, as

Time series operators

As most of the existing spatial and temporal processes are linear in nature, or their application to the data can often be represented in a linear way, many commonly used processing operations can be integrated into the O_T operator of the AMMUST-t framework. In this section, we demonstrate the construction of matrix operators for a collection of common processing operations that might be considered in this framework. These operators include the generalization of individual time point k-space, image space, and reconstruction operators, the performance of temporally dynamic B-field corrections, the shifting and rotating of images for registration, temporal filtering, and slice timing correction.

Generalized k-space, Image space, and SENSE reconstruction operators

In the AMMUST-k framework, k-space and image space processing operations, O_K and O_I, are temporally unvarying, and equivalently applied to each image in a time series. These operations include the incorporation of intra-acquisition decay and static magnetic field (B-field), the performance of zero filling, apodization, smoothing, and partial Fourier reconstruction. In AMMUST-t, applying such operators to the newly parametrized time series data requires an operator of higher dimensionality. If the same image processing steps are performed on all time points of an acquired k-space time series, the time series k-space and image space processing operators, K and I, can be formed with a Kronecker product between the previously described image processing operator and an identity matrix with dimension matching the number of time series points as K=I_N⊗O_K and I=I_N⊗O_I, respectively. The resulting operators are therefore block diagonal where each block corresponds to an instance of the processing operators. As previously described, a generalization of the SENSE reconstruction operator, Ω_SE, can be performed in a similar fashion to the k-space and image space processing operations by R=I_N⊗Ω_SE.

Dynamic B-field correction

In Echo Planar Imaging (EPI), magnetic field inhomogeneities can result in severe artifacts such as image warping and signal loss. Since the characteristics of B-field inhomogeneity are affected by respiration and motion, in a time-dependent manner, dynamic B-field correction may need to be performed before the analysis of task and nontask fMRI data. Such correction can be included into AMMUST-t framework by altering the IFT operator in Eq. (1). The magnetic field inhomogeneity to be corrected can be estimated through relative field measurements (Hahn et al., 2009) or intra-acquisition measurements (Roopchansingh et al., 2003). With the estimated offset, ΔB, for each k-space vector, the IFT operator can then be multiplied by exp(−iγΔB(x, y)t(k_x,k_y)), where t(k_x,k_y) represents the time at which the k-space point corresponding to the row of the Fourier encoding matrix was acquired. As such, the individual blocks along the diagonal of the time series reconstruction operator, R, can be adjusted to correct the B-field inhomogeneity effects at the corresponding time point.

Image registration

Head motion can be a severe problem for the statistical analysis of the fMRI data since the time course of one single voxel would represent a signal derived from different parts of the brain when the subject moves. Image registration is used for motion correction in fMRI and performed by shifting each image according to independently determined motion parameters. In-plane motion correction can be performed by integrating the registration into the time-series reconstruction operator, R, as in the case of dynamic B-field correction. As both image space translation and in-plane rotation can be considered as shifts on x and y axes, multiplying the k-space data with an appropriate phase before the Fourier reconstruction yields a correctional shift in image space after reconstruction as a result of the Fourier shift theorem.

For an image space translation of (δ_x, δ_y) and in-plane rotation of ψ, the required image space shift for a voxel at (x, y) in image space is Δx=δ_x+x(cosψ−1)−ysinψ, and Δy=δ_y+y(cosψ−1)−xsinψ. Therefore, for a single image with the aforementioned motion parameters, the row of the IFT operator that represents the image space point (x, y) must have each element multiplied by the exponential term, exp(−i2π(Δ_xk_x/p_x+Δ_yy_x/p_y)), where k_x and k_y are integers representing the k-space indices of the column of the IFT operator, and p_x and p_y are the number of k-space points in the x and y directions, respectively. The complex-valued IFT operators for each time point can be formed by modifying the real valued isomorphism in Eq. (1) and then appropriately positioned along the diagonal of the time series reconstruction operator, R. The motion parameters of image space translation, (δ_x, δ_y), and in-plane rotation, ψ, can be determined through available software (Cox, 1996; Jenkinson et al., 2002), or through external means, such as a tracking device that measures head motion (Tremblay et al., 2005). A three-dimensional registration operator can be also constructed by utilizing three-dimensional Fourier transforms.

Temporal filtering

The process of temporal filtering can be performed through an application of Fourier shift theorem. The temporal filtering process is mathematically identical to the line shifting process used to correct Nyquist ghosts in EPI. First, the vector of reconstructed images can be reordered to a vector of reconstructed voxel time series through a permutation matrix, P_T. Then, each time series can be Fourier transformed into the temporal frequency domain by a block diagonal matrix, Ω_T, where each block is a real-valued isomorphism of a one-dimensional time series Fourier transform matrix. Each transformed time series can then be multiplied by a diagonal matrix, Φ, with diagonal elements comprised of frequency space weighting for temporal. The temporally filtered image time series vector then can be obtained through the IFT and inverse permutation, T=P_T⁻¹Ω_T⁻¹Φ Ω_TP_T.

Slice timing correction

In fMRI, the MR scanner acquires different slices of the brain sequentially throughout the repetition time (TR) period, resulting in a temporal offset between slices. As knowledge of the exact acquisition timing is essential for fMRI, differential slice acquisition times should be accounted for, especially for acquisitions with long TRs. Slice timing correction is performed in image space after k-space processing, reconstruction, and registration to align all slices with the same reference time point. The slice timing process can be performed similar to the process of temporal filtering. After transforming the vector of reconstructed images into a temporal frequency vector, multiplication with a matrix that consists of sines and cosines to create the additional phase shift for the time series is performed. The vectors of temporal frequencies can then be inverse Fourier transformed to obtain temporally shifted time series, and then the inverse of the original permutation matrix is performed to obtain temporally shifted images. It has been shown that the shifting of k-space lines does not induce correlations in the acquired data if the acquired k-space data is assumed to be uncorrelated (Nencka et al., 2009).

Nontask fMRI

In nontask fMRI, the null hypothesis assumes no correlation between voxels, and thus any statistically significant correlation observed in the data denotes a functional connection between voxels. With the amount of processing performed in nontask fMRI studies through operations such as spatial filtering, temporal filtering, nuisance signal regression, and global signal regression, the statistical properties of the processed voxels are far removed from those of the acquired data. When time series processing operations, O_T, are applied to a data vector in Eq. (5), s_T=s₀+η, which is comprised of a mean vector of complex-valued spatial frequencies, in a real-valued form, s₀, added to a noise vector, η, with a mean of zero and a covariance of Γ, then the time series image vector, y_T=O_Ts_T, has a mean and covariance of

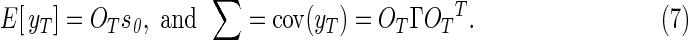As the vector of images, y_T, is comprised of a stack of N image space vectors, each length 2p×1, the spatiotemporal covariance matrix, Σ, in Eq. (7) is of dimension 2pN×2pN.

In prior studies to analyze the effects of processing, the covariance induced by a processing step was estimated using lengthy Markov Chain MC simulations (Barry et al., 2011; Della-Maggiore et al., 2002; Strother, 2006). As in many statistical technique applied in practice, the choice of sample size plays an important role in the accuracy of the covariance structure analysis. It has been cautiously suggested that the sample size should always be more than 10 times the number of free model parameters (Hu et al., 1992; Jaccard and Wan, 1996). The estimation of the spatiotemporal covariance structure with the use of MC simulations therefore would simulate a time series with at least 10pN data vectors from which the covariance in Eq. (7) would be estimated. The MC simulation approach, which determines only an approximation of the true induced covariance structure, would require increasingly large numbers of simulated data arrays when the dimensions of the frequency space measurements increase. However, the linear framework in Eq. (7), which involves the generation of sparse and/or block diagonal matrices, provides a precise quantification of the exact induced covariance structure directly without the need to generate a single data vector.

The 2p×2p blocks along the diagonal of Σ in Eq. (7) contain the spatial covariance matrices for the individual images, and are partitioned into quadrants that contain the real by real, real by imaginary, and imaginary by imaginary covariances. The spatiotemporal correlation matrix is obtained from the covariance matrix by

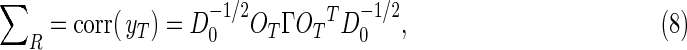where D₀ is a diagonal matrix of the variances drawn from the diagonal of the covariance matrix. To deduce the covariance induced solely by the operation O_T, one merely assumes an inherent identity covariance in the data, Γ=I.

It is a common practice in nontask fMRI to use the 2p×2p spatial covariance matrix, Σ_ρ, which is estimated from time series observations. It is shown in the Appendix that the average of the diagonal blocks of the large spatiotemporal covariance matrix, Σ, is the expected value of the spatial covariance matrix, Σ_ρ. For functional connectivity analysis, the spatial covariance matrix, Σ_ρ, is converted into a spatial correlation matrix, Σ_Rρ.

Another practice in nontask fMRI is to analyze the temporal covariance matrix, Σ_v, which represents a single voxel's time series covariance matrix. Although the large covariance matrix Σ contains the components necessary to compute Σ_v, Σ must be permuted by a matrix, P, which reorders the reconstructed data from a vector of N vectors of p observations stacked above each other to the reconstructed time series vector of p vectors of N observations stacked above each other. The reordered covariance matrix is thus

where each block Σ_ij is a 2N×2N temporal covariance matrix between spatial elements i and j. The diagonal blocks of Σ_T are the temporal covariance matrices for the p individual voxels, Σ_v. The v^th voxel covariance matrix is of the form

Results

Theoretical illustration

To illustrate the linearization of the aforementioned time series processing operations, and to quantify the correlations induced by such operations, a time series of 490 images was generated with a single 96×96 slice of true noiseless brain phantom with a maximum magnitude of 10. Although the methodology to represent slice timing correction and image registration as real-valued matrix operators is introduced in the previous section, the correlations induced by these processing would vary in each acquisition since their operators are dependent on the shift parameters. As such, within this illustration, the operations that we choose to illustrate the methodology are spatial smoothing, SENSE reconstruction, and temporal filtering, which have data-independent parameter settings and are commonly used in many nontask fMRI studies. For an effective illustration of the statistical impacts of the SENSE reconstruction in time series images, the k-space data was subsampled by an acceleration factor of A=3 with N_C=4 coils in the light of the findings of the previous studies, which examine the artificial correlations induced by the pMRI techniques at an individual time point (Bruce et al., 2011, 2012; Bruce and Rowe 2013, 2014). After reconstruction, spatial filtering was performed with a Gaussian smoothing kernel with an image space full width at half maximum (fwhm) of three pixels. A temporal filtering operator was generated to band-pass filter the voxel time series to observe frequencies below 0.08 Hz and above 0.009 Hz as it is a common practice in nontask fMRI studies to eliminate blood oxygenation level-dependent (BOLD) signal changes correlated with physiological effects such as respiration (Biswal et al., 1995).

To closely illustrate the time series processing operators, a 6×6 region of interest (ROI) was selected within the brain phantom in the first 8 time points of the generated data. As the data was subsampled by A=3 with N_C=4 coils, the SENSE reconstruction operator is of dimension 576×768, and the spatial smoothing and temporal operators are of dimension 576×576. Figure 1a–c show the time series operators for SENSE reconstruction, spatial smoothing, and temporal filtering that were used to compute the operator-induced spatiotemporal correlation matrices, assuming an underlying k-space identity covariance structure, Γ=I.

FIG. 1.

Time series operators for an acquisition of N=8 repetitions of a 6×6 region of interest. (a) SENSitivity Encoding (SENSE) reconstruction operator, R=I_N⊗Ω_SE from N_C=4 coils with an acceleration factor of A=3. (b) Smoothing operator, I, with fwhm=3. (c) Temporal filtering operator, T=P_T⁻¹Ω_T⁻¹ΦΩ_TP_T.

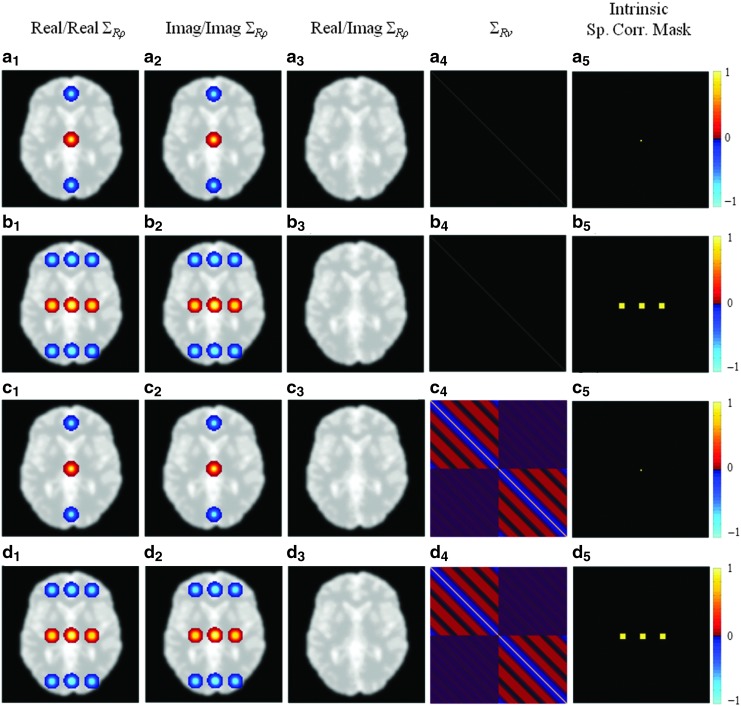
Illustrated in Figure 2a–c are the theoretical correlation matrices that are induced by the SENSE reconstruction, spatial smoothing, and temporal filtering, respectively. The first, second, and third columns of Figure 2 illustrate the correlation matrices calculated from the large covariance matrix, Σ, spatial covariance matrix, Σ_ρ, and temporal covariance matrix, Σ_v, about the center voxel, respectively. Figure 2d shows the overall correlation matrices when SENSE reconstruction, spatial smoothing, and temporal filtering are considered together. Figure 2a₂ and b₂ show that the SENSE reconstruction induces spatial correlations between voxels that are previously aliased with each other, while smoothing induces correlations in the neighborhood of the voxels, as expected. Temporal filtering does not alter spatial correlations, as shown in Figure 2c₂, as the process is purely temporal. Temporal correlations are only altered by temporal filtering, as seen in Figure 2a₃, b₃, and c₃. The correlation maps in the case that the processes are considered together may appear to be dominated by individual processes, as seen in Figure 2d₁–d₃. However, the correlation map is not a simple superimposition of the individual processes, which highlights the advantage of the proposed AMMUST-t framework that provides an exact quantification of the final correlation structure.

FIG. 2.

Theoretical spatiotemporal correlation matrices that are induced by the consideration of (a₁–a₃) SENSE reconstruction from N_C=4 coils with an acceleration factor of A=3, (b₁–b₃) spatial smoothing, (c₁–c₃) temporal filtering, (d₁–d₃) SENSE reconstruction, spatial smoothing, and temporal filtering. First column: large correlation matrix, Σ_R. Second column: spatial correlation matrix, Σ_Rρ. Third column: center voxel's temporal correlation matrix, Σ_Rv.

To observe the effects of the processing operations on the spatiotemporal correlation structure of the data, we computed both theoretical and MC-simulated spatial and temporal correlations between the real components (real/real), between the imaginary components (imaginary/imaginary), and between the real and imaginary (real/imaginary) components of the reconstructed voxel values. For MC simulation, a single 96×96 slice was generated for a time series of 490 images by y_t=r_t+ɛ_t, where r_t is a 2N_C×mn matrix whose first N_C rows are the real noiseless images and the second N_C rows are the imaginary noiseless images. The noise matrix ɛ_t=z_t is a 2N_C×mn random matrix drawn from the standard normal distribution when the initial identity voxel covariance is assumed. If the initial voxel covariance is assumed to be nonidentity, ɛ_t was generated by ɛ_t=z_tQ_Γ where Q_Γ is the second unitary matrix in the singular value decomposition of the nonidentity voxel covariance structure Γ=P_ΓΣ_ΓQ_Γ^T. The theoretical operator-induced correlations were computed by Eq. (8), whereas MC-simulated correlations were estimated from 100 simulations.

Correlations in the theoretical and MC-simulated illustrations are analyzed for the spatially smoothed SENSE reconstructed images with and without the application of band-pass filtering under the assumption of identity or nonidentity intrinsic k-space covariance structure. In the case of the nonidentity spatial covariance, the intrinsic k-space covariance structure was designed in such a way that three ROIs are assumed to be inherently correlated with each other with a magnitude of 0.9. These regions are selected in the areas that are similar to the motor cortices and supplementary motor area, as presented in Figure 3b₅ and d₅. Our MC simulation results have shown that the spatial and temporal correlation maps, with and without an inherent correlation, are visually the same as the theoretical operator-induced correlations after applying a threshold of±0.15, and thus only operator induced correlations are shown in Figure 3. The center voxel has been picked as the seed voxel to present the theoretical operator-induced spatial and temporal correlations although a similar correlation structure can be observed around any voxel.

FIG. 3.

Presented on a magnitude brain phantom underlay are theoretical operator induced real/real, imaginary/imaginary, real/imaginary spatial correlations, and temporal correlations of the center voxel under the assumption of SENSE reconstruction and smoothing with (a₁–a₄) identity intrinsic k-space covariance, (b₁–b₄) nonidentity intrinsic k-space covariance, (c₁–c₄) band-pass filtering with identity intrinsic k-space covariance, (d₁–d₄) band-pass filtering with nonidentity intrinsic k-space covariance. The intrinsic spatial correlation masks for the considered cases are illustrated in (a₅–d₅).

The first three vertical panels of Figure 3 denote the theoretical operator induced real/real, imaginary/imaginary, and real/imaginary spatial correlations for the various cases. Figure 3a and c show the correlation results for the smoothed SENSE reconstructed data with and without band-pass filtering under the assumption of an identity inherent spatial correlation, respectively. It is apparent, in Figure 3a and c that the induced spatial correlations appear in cluster of the voxels instead of individual voxels, as a result of the smoothing operation. It is of note that the center voxel shows negative real/real and imaginary/imaginary correlations with a cluster of voxels in the center of the upper and lower folds due to the choice of A=3. The increased spatial correlation between the center voxel with its neighbors can also be observed in real/real and imaginary/imaginary correlations. It can be seen in Figure 3a₃ and c₃ that there is no correlation induced between the center voxel's real and imaginary measurements. As expected, temporal filtering does not alter the spatial correlation structure since Figure 3a₁–a₃ are identical to Figure 3c₁–3c₃.

Figure 3b and d show the correlation results for the smoothed SENSE reconstructed data with and without band-pass filtering under the assumption of a nonidentity inherent spatial correlation, respectively. As in Figure 3a₃ and c₃, there is no correlation induced between the center voxel's real and imaginary measurements either with or without band-pass filtering. One can see in Figure 3b₁, 3b₂, 3d₁ and 3d₂ that the real/real and imaginary/imaginary spatial correlations between the voxels that are in the originally correlated ROIs are spread to adjacent voxels by the smoothing operator. Additionally, there is a negative real/real and a negative imaginary/imaginary correlation between the three clusters of correlated voxels and the respective regions from the top and bottom folds. This structure underlines that the inherent true correlation can be observed both in its original location and in the regions that were previously aliased with this original region. This artificially amplified and induced correlation structure could be misinterpreted as a network of functional connectivity in the brain if no steps were taken to identify processing-induced correlations.

The fourth panel of Figure 3 denotes the operator-induced temporal correlations for the various cases. Figure 3a₄ and b₄ show the temporal correlation matrix of the center voxel when only SENSE reconstruction and smoothing are considered under the assumption of identity and nonidentity initial spatial correlation, respectively. As expected, the temporal correlation structure is not altered by SENSE reconstruction or smoothing as it is shown to be identity for the center voxel. It can be observed in Figure 3c₄ and d₄ that the temporal correlation structure within the real and imaginary components of the data is altered by temporal filtering with and without presence of initial spatial correlation. Such altered correlations arise from the convolution of the temporal filtering kernel with the voxel time series.

While the AMMUST-t linear framework could provide a tool for neuroscientists to precisely quantify the correlations induced by spatial and temporal processing, it requires the multiplication of a series of linear matrix operators of very large dimensionality. As such, we have developed computationally efficient algorithms by employing parallel computing, matrix partitioning, and sparse matrix multiplication techniques. The linear operators introduced in this framework have been implemented in Matlab (The Mathworks, Natick, MA).

Experimental illustration

To analyze the statistical implications of time series processing, two sets of data were acquired for a series of 510 TRs from an array of eight receiver coils in a 3.0T General Electric Signa LX MR imager. Due to the computational load, the data set was reduced to only N_C=4 evenly spaced coils by using every other coil, starting with the coil in the anterior. The first set of data imaged a spherical agar phantom, while the second set was of a nontask human subject. Both data sets were comprised of seven 2.5 mm thick axial slices that are 96×96 in dimension for a 24.0 cm FOV, with the phase encoding direction oriented as anterior to posterior. The data set had a TR of 1 s, an echo time (TE) of 45.4 ms, an effective echo spacing of 0.816 ms, a flip angle of 45°, and an acquisition bandwidth of 125 kHz. As the data were acquired with time varying TE in the first 20 TRs, the remaining 490 images from N_C=4 equally spaced coils were used in the SENSE reconstruction. Data were acquired with an EPI pulse sequence and reconstructed using locally developed software. Subsampling was simulated for A=3 by deleting lines of k-space in each of the acquired data sets. To estimate the error in the center frequency and group delay offsets between odd and even k-space lines, three navigator echoes of the center line of k-space were acquired (Nencka et al., 2008).

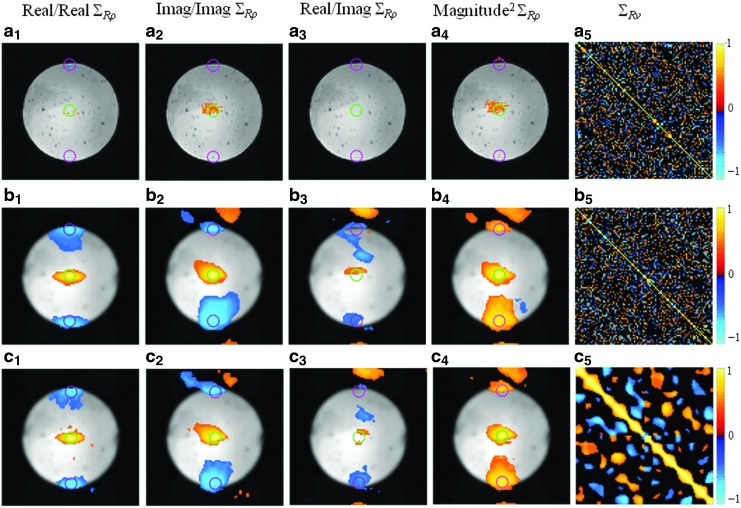
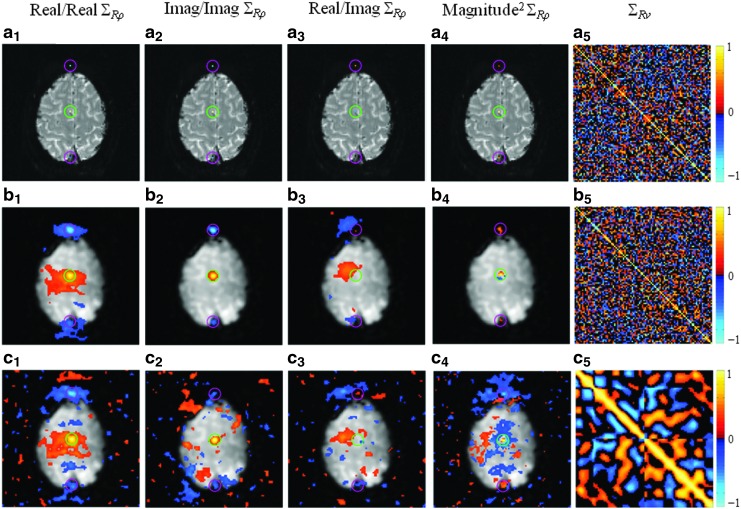
We present experimentally computed spatial and temporal correlations about the seed voxel for three different cases. The correlation maps that are presented in Figures 4a and 5a are computed from SENSE reconstructed images without spatial smoothing or temporal filtering. The SENSE reconstructed images that were used to compute the correlations presented in Figures 4b and 5b have been spatially filtered by a Gaussian smoothing kernel operator, whereas the ones that were used to compute the correlations given in Figures 4c and 5c have been both spatially filtered and band-pass filtered with cutoff frequencies at 0.009 and 0.08 Hz (Biswal et al., 1995). Presented spatial correlations between the real/real, imaginary/imaginary, and real/imaginary and the spatial correlations for magnitude-squared data were estimated over the time series. The magnitude-squared correlation structure is observed here because it is asymptotically equivalent to the correlations of magnitude data and linear in nature when magnitude correlations are not. To estimate the temporal correlation maps, both the spherical agar phantom and nontask human subject time series data were divided into 10 sequential 49 time point experiments after removing the first 20 time points. The resulting data was then used to calculate the sample temporal correlation matrix of the center voxel for the various cases.

FIG. 4.

Presented on a magnitude spherical agar phantom underlay are estimated real/real, imaginary/imaginary, real/imaginary, magnitude-squared spatial correlations, and temporal correlations of the center voxel throughout the time series of 490 images with (a₁–a₅) SENSE reconstruction; (b₁–b₅) SENSE reconstruction and smoothing; (c₁–c₅) SENSE reconstruction, smoothing, and band-pass filtering. Correlations are presented with a threshold of ±0.35.

FIG. 5.

Estimated real/real, imaginary/imaginary, real/imaginary, magnitude-squared spatial correlations, and temporal correlations about the center voxel throughout the time series of 490 nontask human subject images with (a₁–a₅) SENSE reconstruction; (b₁–b₅) SENSE reconstruction and smoothing; (c₁–c₅) SENSE reconstruction, smoothing, and band-pass filtering. Correlations are presented with a threshold of ±0.25.

Phantom data

The spherical phantom data was considered for an experimental analysis to bridge the gap between the theoretical illustration and the application to human subject data, as the phantom is not prone to physiological effects and subject movement. The center voxel was selected as the seed voxel to experimentally analyze the induced correlation structure by spatiotemporal processing to be consistent with the presented theoretical induced correlation analysis.

Presented in Figure 4a₁–a₄, b₁–b₄, and c₁–c₄ are the real/real, imaginary/imaginary, real/imaginary, and magnitude-squared spatial correlations between the center voxel and all the other voxels that were computed from SENSE reconstructed data with and without the application of spatial smoothing and low-pass temporal filtering. The correlations presented in Figure 4 were threshold at±0.35 (p∼0.05) (Greicius et al., 2003). As the center voxel was selected as the seed voxel, two fold regions are expected to exhibit correlations with the center voxel due to the choice of A=3. Two pink circles are placed around the corresponding previously aliased voxels, upper and lower folds, in Figure 4 where the seed voxel is indicated by a small green circle. It can be observed in Figure 4a₁, a₂, and a₄ that there is a negative real/real, a negative imaginary/imaginary, and a positive magnitude-squared correlation between the voxels in the lower and upper folds and the seed voxel. The correlations in the circles appear to be at individual voxels although additional imaginary and magnitude-squared spatial correlations can be observed around the center voxel as well. This may be due to B-field inhomogeneities that have not been completely corrected.

The correlations between the previously aliased voxels and the seed voxel are spread to clusters of voxels with the application of smoothing, as presented in Figure 4b₁, b₂, b₄, c₁, c₂, and c₄. While the correlation structure in the folds and in the center exhibits an oval shape due to the overlap in the reduced FOV image and Nyquist ghosting that has not been completely removed, it can be seen that the neighborhoods of the seed voxel and the upper and lower folds still exhibit the strongest correlation. It is important to note that while there is no real/imaginary correlation between the center voxel and the other voxels as seen in Figure 4a₃, real/imaginary correlations can be observed in the center, upper, and lower folds with the application of smoothing. By comparing Figure 4b₁–b₄ with Figure 4c₁–c₄, it can be seen that temporal filtering slightly alters the spatial correlation structure.

The temporal correlation matrix of the center voxel after SENSE reconstruction without smoothing is given in Figure 4a₅. Presented in 4b₅ and c₅ are the temporal correlation matrices for the center voxel computed from SENSE reconstructed and spatially smoothed time series data with and without band-pass filtering. It is apparent when comparing Figure 4b₅ and c₅ that band-pass filtering induces local temporal correlations as the main diagonal is widened and the correlations before filtering are smoothed. As expected, spatial smoothing does not alter the temporal correlation structure. It is of note that, while such a correlation structure in the processed time series data can be expected, a precise theoretical quantification, as proposed in this article, would allow one to account for processing-induced correlations in the final analysis of their data.

Human subject data

As with the theoretically generated brain phantom data and experimental spherical phantom data, the center voxel was selected as the seed voxel for the correlation analysis in the human subject data. Figure 5a₁–a₄ show the real/real, imaginary/imaginary, real/imaginary, and magnitude-squared spatial correlations for the seed voxel that were computed from SENSE reconstructed time series. Presented in Figure 5b₁–b₄, and c₁–c₄ are the spatial correlations about the seed voxel computed from SENSE reconstructed and spatially smoothed data with and without the application of temporal band-pass filtering. Similarly, with the spherical phantom data results, two small pink circles are placed around the previously aliased voxels in Figure 5 while the seed voxel is indicated by a small green circle.

The experimental spatial correlations, which exceed a threshold of±0.25, show a negative real/real and imaginary/imaginary correlation and a positive magnitude-squared correlation between the seed voxel and the upper and lower folds, as shown in Figure 5a₁, a₂ and a₄. While there are no correlated voxels in real/imaginary theoretical correlation structure in Figure 3a₃, and the experimental spatial correlations computed from spherical phantom in Figure 4a₃, there appears to be a nonzero real/imaginary correlation structure in Figure 5a₃. It can be seen in Figure 5b₁–b₄ and 5c₁–c₄ that spatial smoothing further spreads the SENSE-induced correlations in the folds and induces positive correlation in the neighborhood of the seed voxel. While it is primarily the amplified SENSE-induced spatial correlations, real/real spatial correlation maps given in Figure 5b₁ and c₁ exhibit an oval shape of clusters in the fold regions and seed voxel region. This may be due to the noise amplification in the un-aliased images. Similarly, with the experimental real/imaginary correlation results of the spherical phantom data, both positive and negative real/imaginary correlations can be observed throughout the images in Figure 5b₃ and c₃. This may be a result of Nyquist ghosting that has not been completely removed and that the brain occupies a small portion of the full FOV, which results in aliasing between the center voxel and the voxels in space. By comparing Figure 5b₁–b₄ with Figure 5c₁–c₄, it is interesting to note that the spatial correlation structure is significantly scattered throughout the image after band-pass filtering.

Illustrated in Figure 5a₅, b₅, and c₅ are the temporal correlation maps about the center voxel computed from the SENSE reconstructed data without spatial smoothing or temporal filtering, with only spatial smoothing, and with both spatial smoothing and temporal filtering, respectively. Similarly, with the theoretical-induced correlation results and experimental agar phantom results, the temporal filtering process alters the time series correlation structure by widening the main diagonal, which implies local temporal correlations. It is of note here that the theoretical operator-induced correlations in Figure 3 were calculated under the assumption of independence between time points. As such, it is evident that the temporal correlation structure in Figure 5c₅ is the smoothed version of the existing temporal correlations in the data in Figure 5b₅ rather than exhibiting only a widened main diagonal as in Figure 3d₄.

The experimental spatial and temporal correlation results of both the agar phantom and human subject align with the theoretical illustration in Figure 3, and illustrate that SENSE reconstruction and smoothing induce spatial correlations that could result in false positive and negatives in a functional connectivity analysis and misinterpreted if they are not precisely quantified or accounted for. Furthermore, the temporal correlations induced by temporal operators, such as low-pass and high-pass filtering, and artificially induced spatial correlations could result in false positive and negatives in fMRI activation statistics as they would make the assumption of independency between voxels invalid. As it becomes increasingly more difficult to derive the true correlation structure with the use of lengthy MC simulations or the parametric covariance functions once the data has been processed, the accuracy of the final analysis of the processed data can be significantly improved with the use of the proposed theoretical linear framework.

Discussion and Conclusion

In this work, we develop a mathematical framework that allows one to analytically observe the effects of commonly used spatial and temporal preprocessing on observed voxel measurements in nontask fMRI. This framework represents the processing pipeline as a linear isomorphic matrix operator by breaking up each process into a sequence of steps that can be carried out through a collection of matrix operators. With the entire processes represented in this way, the exact correlation structure induced by each operation both spatially between voxels and temporally within each voxel's time series can be precisely quantified. We also present the techniques for linearizing common processing operations such as dynamic B-field correction, image registration, temporal filtering, slice timing correction, and generalizing individual k-space and image space processing in addition to image reconstruction.

Although the statistical impacts of spatial smoothing, SENSE pMRI reconstruction, and temporal filtering on the processed data has been presented in detail, additional processing operations can be represented as linear operators and adopted into the AMMUST-t framework. For instance, regressing out the average signal from different regions of the brain such as white matter and cerebrospinal fluid (CSF) or from whole-brain with the use of global signal regression techniques have been commonly used in nontask fMRI studies. White matter and CSF signal regression is used to remove the non-neural fluctuations such as subject motion and physiological effects while the global signal regression is used to remove the spontaneous BOLD fluctuations common to the whole brain. As the mean white matter, CSF or whole brain time series are used as temporal covariates and removed from the data through linear regression in these processing steps; they can also be represented by linear operators, and included into the Ammust-t framework.

While most existing processes are linear in nature, there are select image registration (Klein et al., 2009; Poldrack et al., 2011), spatial normalization (Ashburner and Friston, 1999), spatial smoothing (Smith and Brady, 1997), and high-pass filtering (Marchini and Riley, 2000) operations that can be nonlinear. Although such operations typically use nonlinear calculations to determine various parameters, their application to data is (in most instances) linear. As such, linear representations for nonlinear processes that are widely used in biomedical image processing software can also be included into the AMMUST-t framework.

Data acquired for nontask fMRI studies have a true inherent, but unknown, spatiotemporal covariance structure. As the goal of these studies is to determine, utilize, and analyze this structure, it becomes increasingly more difficult to derive the true covariance once the data has been processed. This article provides the researchers a means of retaining knowledge of the processing steps performed on the acquired data and guidance to be aware of the presence of these correlations between spatial regions and time points they may be investigating. As such, the implementation of the AMMUST-t framework provides neuroscientists with a means of determining whether or not their selection of reconstruction and processing operations is excessive by observing the artificial correlations that they have induced into their data.

To provide a benchmark analysis of the operator-induced correlation structure, we utilize the AMMUST-t framework to compute spatial covariance matrix and an individual voxel's temporal covariance matrix, both commonly used nontask fMRI analysis studies, from an analytically derived spatiotemporal covariance matrix. As the proposed method can easily be applied to data sets in which the implications of processing have been noted, it provides a novel informative tool for preventing possible false positive rates that can result from processing and reconstruction operators. The application of the framework could enable neuroscientists to reap the benefits of spatial and temporal processing while simultaneously determining an acceptable data processing pipeline and identifying the true statistical interpretation of their data.

Appendix

Consider the large, processed covariance matrix, Σ. The (i,j)^th element may be calculated as

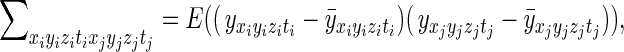where (x_i,y_i,z_i,t_i) are the spatial and temporal indices for the i^th element of the reconstructed and processed vector y, (x_j,y_j,z_j,t_j) are the spatial and temporal indices for the vector's j^th element, and 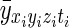is the mean measurement of voxel (x_i,y_i,z_i) at time point t in repeated acquisitions. An expansion of the product yields

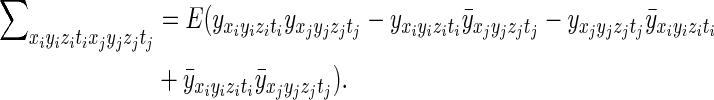Similarly, the spatial covariance matrix, Σ_ρ, may be considered on an element by element basis

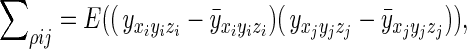where is the temporal mean of the voxel (x_i,y_i,z_i) over the course of a time series. In a time series with n points, Σ_ρ may be calculated as

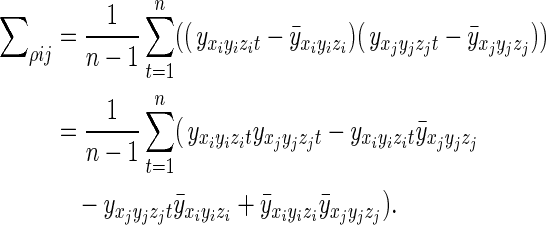With Σ_ρ in mind, consider the average of the diagonal blocks of the large, processed covariance matrix, Σ. Specifically, let

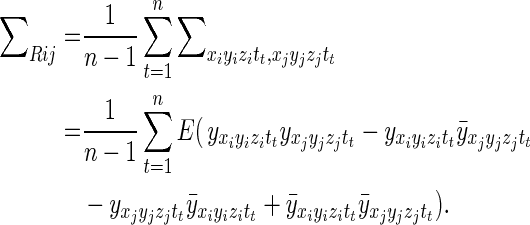Assuming that the voxel mean does not change over time, as should be the case in a resting state study of a stationary subject, 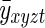is equal to 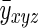. In light of this, it is apparent that the average of the diagonal blocks of the large processed covariance matrix, Σ, is the expected value of the spatial covariance matrix, Σ_ρ

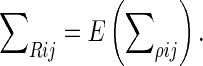Thus, the spatial covariance matrix may be computed as the average of the diagonal blocks of the large, processed covariance matrix.

Acknowledgments

This work was supported by NIH NS087450. The digital phantom that is used to present theoretical illustration results in this article was provided by Volkan Emre Akpinar from the Department of Neurosurgery at Medical College of Wisconsin in Milwaukee, WI.

Author Disclosure Statement

No competing financial interests exist.