Determination of Multivalent Protein–Ligand Binding Kinetics by Second-Harmonic Correlation Spectroscopy

Abstract

Binding kinetics of the multivalent proteins peanut agglutinin (PnA) and cholera toxin B subunit (CTB) to a GM₁-doped 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) lipid bilayer were investigated by both second-harmonic correlation spectroscopy (SHCS) and a traditional equilibrium binding isotherm. Adsorption and desorption rates, as well as binding affinity and binding free energy, for three bulk protein concentrations were determined by SHCS. For PnA binding to GM₁, the measured adsorption rate decreased with increasing bulk PnA concentration from (3.7 ± 0.3) × 10⁶ M^–1·s^–1 at 0.43 μM PnA to (1.1 ± 0.1) × 10⁵ M^–1·s^–1 at 12 μM PnA. CTB–GM₁ exhibited a similar trend, decreasing from (1.0 ± 0.1) × 10⁹ M^–1·s^–1 at 0.5 nM CTB to (3.5 ± 0.2) × 10⁶ M^–1·s^–1 at 240 nM CTB. The measured desorption rates in both studies did not exhibit any dependence on initial protein concentration. As such, 0.43 μM PnA and 0.5 nM CTB had the strongest measured binding affinities, (3.7 ± 0.8) × 10⁹ M^–1 and (2.8 ± 0.5) × 10¹³ M^–1, respectively. Analysis of the binding isotherm data suggests there is electrostatic repulsion between protein molecules when PnA binds GM₁, while CTB–GM₁ demonstrates positive ligand–ligand cooperativity. This study provides additional insight into the complex interactions between multivalent proteins and their ligands and showcases SHCS for examining these complex yet technologically important protein–ligand complexes used in biosensors, immunoassays, and other biomedical diagnostics.

Multivalent protein binding interactions have attracted much attention in biomolecule detection, biological separations, biosensors, and immunological assays.¹⁻⁶ Multivalent protein–ligand interactions have shown stronger binding, reduced nonspecific interactions, and increased aggregation on surfaces relative to monovalent interactions.^4,5,7,8 Multivalent protein–carbohydrate interactions in particular have a significant biological role in cell trafficking and recognition,⁹ pathogen attachment and uptake,^1,10 and tumor cell differentiation based on glycolipid/glycoprotein expression.^11,12 Although the diverse cellular and analytically beneficial binding properties have led to much research on multivalent protein–ligand interactions, there is still much that is not understood about their complex binding properties, especially at surfaces.⁴

Most multivalent protein–carbohydrate interactions continue to be analyzed with simple binding models that operate under the assumption that binding is reversible and each binding event occurs independently without ligand–ligand or protein–protein interactions.^4,13 Many studies have shown the interactions between multivalent proteins and carbohydrates are indeed cooperative in nature^7,8 with strong ligand–ligand and/or protein–protein interactions that affect the apparent binding affinity. Only a few studies have examined the binding affinities as a function of ligand density,⁷ and even fewer studies have investigated the dependence of binding affinity on protein concentration.¹⁴ These previous studies suggest that multivalent protein–carbohydrate interactions are far more intricate than simple binding models alone can predict. The ability to more efficiently and precisely measure the binding kinetics of these multivalent protein–carbohydrate interactions will provide further understanding of the binding properties of these complex interactions. Such information would allow for more effective design of biosensors and drugs that utilize multivalent protein–ligand interactions. Two proteins that can be used as archetypes to examine the influences of protein concentration, cooperative behavior, and electrostatics on the complex binding properties of multivalent protein–ligand interactions are cholera toxin (CT) and peanut agglutinin (PnA). CT and PnA are both commonly used in biosensors and medical diagnostics due to their highly specific interaction with the most abundant ganglioside in cell membranes, monosialotetrahexosylganglioside (GM₁), making further investigation of the binding properties of these multivalent interactions particularly biologically valuable.

Cholera toxin, a pathogen secreted from the bacterium Vibrio cholerae, is an AB₅ cytotoxin composed of a central A subunit surrounded by five identical B subunits that form a pentameric ring.⁷ It is the cholera toxin B subunit (CTB) that is responsible for binding to the cell surface via the pentasaccharide moiety of the ganglioside GM₁.¹⁵ Following attachment of the B subunits to the cell membrane, the toxic A subunit enters the cell and causes an elevated level of cyclic AMP in the small intestines that leads to fluid loss.²² A myriad of techniques, including fluorescence,^2,3,7 surface plasmon resonance (SPR),^16,17 enzyme-linked immunosorbent assay (ELISA),¹ and differential scanning calorimetry,⁸ have been implemented to examine the specific binding kinetics of the CTB–GM₁ interaction. Although most of the studies have shown CTB exhibits almost no nonspecific interactions with membranes without GM₁, the reported specific binding affinities range from 10⁶ M^–1 to 10¹¹ M^–1.^2,3,7,16,17 Some of this disparity may be attributed to experimental differences such as ligand density, incubation time, and mass-transport limitations. Several studies have found the Hill–Waud model, a cooperative binding model that accounts for cooperative behavior between ligand molecules, to more accurately describe the CTB–GM₁ interactions as compared to the more common Langmuir model.^2,7 However, many studies that examine the CTB–GM₁ interaction at low nanomolar concentrations in order to determine the cooperative behavior require extremely long incubation periods to obtain an accurate steady-state response. As such, inconsistent and lower binding affinities are often measured because the data obtained were limited by mass transport.¹⁸ A method that can measure CTB binding to GM₁ for several CTB bulk concentrations after steady-state equilibrium has been reached would eliminate mass-transport effects and provide the binding kinetics as a function of bulk CTB concentration.

Similar to CTB, the multivalent carbohydrate binding lectin PnA has been extensively used in bioanalytical assays; however, its binding properties to various carbohydrate moieties are usually only qualitatively examined and have been less frequently quantified. Peanut (Arachis hypogaea) agglutinin is a tetrameric lectin that binds specifically to terminal d-galactosyl groups.^6,19 This carbohydrate-free protein is known for its anti-T activity and is routinely used in serology to monitor polyagglutinability.^6,20,21 Its high specificity for galactosyl groups, with a decrease in affinity from Galβ1,3GalNAc to GalNH₂ to Gal, has made PnA a useful aid in characterizing the specific glycoprotein/glycolipid expression on the cell surface of malignant cancer cells.^6,12 The widespread use of PnA as a biochemical tool for carbohydrate separation has made it the subject of much research.^4,13,19 Techniques such as carbon NMR,^19,22 ELISA,^5,23 fluorescence,²⁰ and ultraviolet difference spectroscopy²⁴ have been used to determine the binding properties of PnA to various carbohydrate groups, gangliosides, and glycolipids. However, very few of these studies have moved beyond the traditional Langmuir binding model used to determine thermodynamic binding affinity for monovalent interactions, and to our knowledge there is no study of the dependence of the binding kinetics on bulk PnA concentration. While previous studies have shown the highly specific nature of the PnA–GM₁ interaction, investigating the binding kinetics of PnA to GM₁ as a function of PnA concentration would provide additional valuable information on the intricate binding properties of this multivalent protein binding complex.

In this study the multivalent interactions of CTB and PnA to GM₁ doped into a planar supported lipid bilayer (PSLB) are investigated by second-harmonic correlation spectroscopy (SHCS). PSLBs were chosen as the binding platform as they mimic the native cell surface where GM₁ is present, reduce nonspecific binding, and allow precise control over GM₁ density.²⁵ The SHCS technique used for these studies offers the advantage of determining the binding kinetics at individual protein concentrations using minimal analyte and, most importantly, under steady-state equilibrium to reduce mass-transport effects. SHCS has previously been used to determine the diffusion of large dye molecules and amphiphilic head groups of long hydrocarbon chains.²⁶⁻²⁸ More recently, SHCS was used to accurately determine the binding kinetics of the small molecule (s)-(+)-1,1′-bi-2-naphthol (SBN) intercalating into a PSLB.²⁹ The current study is the first to extend the SHCS technique to detection and investigation of protein binding at a surface. Use of SHCS to measure the binding kinetics separately for several bulk protein concentrations, as well as to examine the cooperative and electrostatic contributions of these multivalent protein–ligand interactions, provides additional insight for their use in biosensors, medical diagnostics, and drug development.

Experimental Section

Materials, preparation of PSLBs, and details of SHG experiments are described in Supporting Information.

Second-Harmonic Correlation Spectroscopy

SHCS has been described in detail in an earlier publication.²⁹ Briefly, in SHCS the fluctuations in the second harmonic (SH) signal are measured as a function of time and autocorrelated to determine dynamic molecular events occurring at the surface. Although the mean SH intensity is proportional to the square of the surface density of molecules (N), through heterodyne mixing of the mean SH intensity and the intensity from individual fluctuations, the heterodyned intensity will be linearly related to N. The fluctuations observed in the measured SH signal are a result of any dynamic processes of the molecules within the observation volume that cause changes in the SH intensity on the time scale of the time step taken between data points, τ.^30,31 For the reversible binding of molecules at a surface, these dynamic processes can include diffusion in and out of the observation volume and absorption and desorption of the molecules to the surface.³⁰⁻³² The surface specificity of SHCS eliminates the contributions from diffusion of molecules in solution, such that the only contributing factors to the correlated fluctuations in the SH signal are from the surface binding kinetics.²⁹

The normalized time-dependent autocorrelation function, G(τ), for a typical reversible binding interaction, where any surface diffusion through the observation area is much slower than the binding kinetics, will have the form of a first-order exponential decay, given by³¹

1

where N_C is a normalization constant related to the surface density of adsorbed protein molecules, [P] is the bulk solution protein concentration, and k_on and k_off are the adsorption and desorption rates, respectively. By use of eq 1, both adsorption and desorption rates can be retrieved from the autocorrelation of the SH signal of a single protein concentration, allowing the binding properties to be easily determined as a function of bulk protein concentration. The equilibrium binding constant, K_a, which describes the complete reaction, can then be determined for each protein concentration:

2

Autocorrelating the SH signal and analyzing the correlated surface binding events by use of eqs 1 and 2 allows adsorption and desorption rates, as well as energetics of association at a single bulk protein concentration, to be determined.

Another advantage of SHCS as compared to linear fluorescence correlation spectroscopy (FCS) is that the coherent nature of SHG allows the SH intensity from individual fluctuations to be amplified by the mean SH intensity through heterodyning. Since the fluctuations oscillate around the mean SH intensity, the mean SH intensity in essence acts like a local oscillator, enhancing the SH intensity of an individual fluctuation. The overall heterodyned output intensity can be written as

3

where N_μ and N_fluct represent the mean number of molecules and the number of molecules giving rise to an individual fluctuation, respectively. ⟨β_ijk⟩ represents the average ensemble molecular hyperpolarizability of the molecules at the surface, where the indices denote the input (i, j) and output (k) fields, which can be described by any of the three Cartesian coordinates (x, y, z). The heterodyning effect will be described in more detail in an upcoming paper; however, similar heterodyne mixing has been used and detailed for dynamic light scattering (DLS) and X-ray photon correlation spectroscopy (XPCS).³³⁻³⁵ Two important properties of heterodyning are apparent in the above expression; first, the cross-term of eq 3 exhibits a linear relationship between the overall heterodyned SH intensity and N_fluct, and second, N_fluct is enhanced by N_μ. This leads to decreased noise in the correlation data as the mean SH intensity increases. As a result, the number of molecules giving rise to an individual fluctuation, N_fluct, can be very small compared to the mean number of molecules in SHCS while still being detectable.³³⁻³⁵

SHCS data were collected for proteins associating with GM₁ doped into a 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) bilayer at three separate bulk protein concentrations after steady-state equilibrium had been reached. Data were collected for every pulse of the laser, so that the time interval between data points was dictated by the 20 Hz (50 ms) repetition rate of the laser. The fast Fourier transform multiplied by its complex conjugate was determined for 20 data sets, each consisting of 5000 data points (1.4 h total collection time). After averaging, an inverse Fourier transform was performed to obtain the correlation data.

Results and Discussion

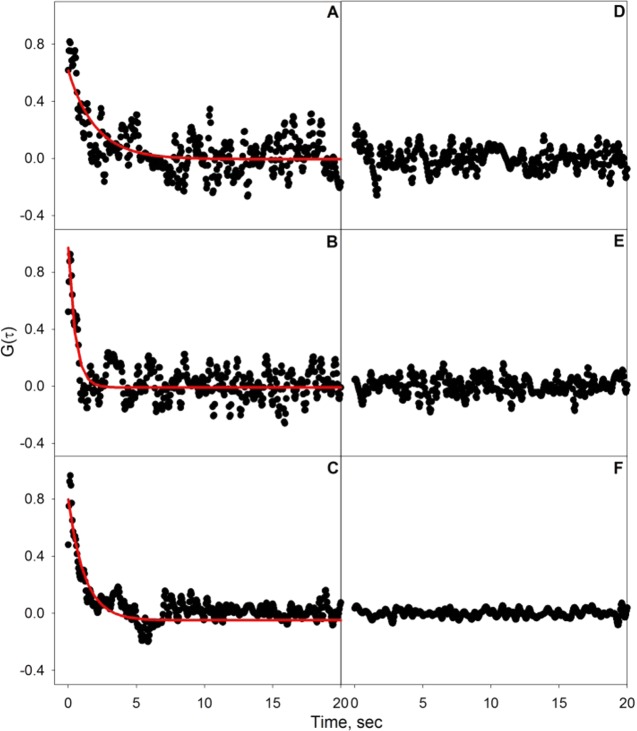
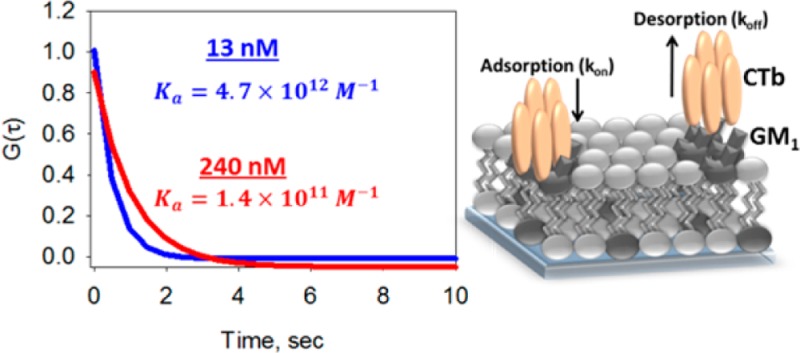
Affinities for CTB and PnA binding to GM₁ were examined as a function of bulk protein concentration by SHCS. After an appropriate incubation time for a steady-state response to be reached, the SH signal was collected for every pulse of a 20 Hz laser as a function of time for three bulk concentrations of CTB (0.5, 13, and 240 nM) binding to a 1 mol % GM₁-doped DOPC lipid bilayer (data shown in Supporting Information). The SH signal was cross-correlated with itself to extract the correlated molecular binding kinetics. As most of the fluctuations seen in the SH signal are uncorrelated noise, these high-frequency contributions (filtered at 15 times the Nyquist limit) and the first point of the autocorrelation were removed.³⁶ The resulting normalized correlation data, G(τ), from the average of 20 data sets for each of the three CTB concentrations binding to a 1 mol % GM₁-doped DOPC lipid bilayer are shown in Figure 1A–C. SHCS data were also collected for nonspecific binding of CTB, where each of the three CTB concentrations was exposed to a DOPC bilayer that did not contain GM₁. The normalized correlation data of 20 averaged data sets are shown for each of the three CTB concentrations binding to a pure DOPC bilayer in Figure 1D–F. To allow comparison between the noise of the specific and nonspecific correlation data, the time-zero point of the autocorrelation of the nonspecific binding of CTB was normalized to time-zero of the correlation data of the specific binding of CTB to a 1 mol % GM₁-doped DOPC bilayer for each CTB concentration. It is important to note that, before normalization, the magnitude of the noise of the nonspecific binding correlation data remained the same for all three nonspecific correlation data, as the mean SH intensity was the same with no apparent increase in signal as protein is added. It is apparent from the nonspecific autocorrelation data that there is no appreciable nonspecific binding as there is no correlation seen, meaning the correlated events giving rise to G(τ) in Figure 1A–C all arise from the specific binding interactions between CTB and 1 mol % GM₁. The lack of correlated events in Figure 1D–F, when GM₁ is not present in the bilayer, also emphasizes that correlated proportional noise from the laser and/or vibrations from the optics are not contributing to the observed correlations seen in Figure 1A–C, as these contributions would be seen in the nonspecific correlation data if they were present.^37,38 Additionally, in our previous study in which the intercalation of SBN into a DOPC membrane was examined by SHCS, correlation data displayed a much larger reaction rate, approximately 6 times greater, than seen here for CTB. If the origins of the correlation data measured here were due to correlated fluctuations in the laser source or detector, the same rate should have been measured for both studies, which is clearly not the case.²⁹ In the same study, correlation data of a pure DOPC bilayer without addition of any SBN was also investigated and displayed no correlated events, further demonstrating the absence of correlated proportional noise or correlated noise from the bilayer.²⁹

Figure 1.

Autocorrelation data for CTB binding to a 1 mol % GM₁-doped DOPC bilayer at CTB concentrations of (A) 0.5, (B) 13, and (C) 240 nM, with fits to eq 1 indicated by the red lines. Also shown are autocorrelations of CTB exposed to a pure DOPC bilayer at (D) 0.5, (E) 13, and (F) 240 nM. Nonspecific CTB autocorrelations have been normalized to the corresponding specific binding data as mentioned in the text.

SHCS has previously been used to measure the translational and/or rotational diffusion of dye molecules and hydrocarbon chain-substituted amphiphiles on surfaces.²⁶⁻²⁸ In order to rule out the possibility of rotational and translational motion on the observed dynamics presented in Figure 1, the time scale of such events was considered for the experimental conditions used in this study. For example, a FCS study of the rotational diffusion of antimicrobial peptides found that the correlation function time constant was nanoseconds.³⁹ This is much faster than the 50 ms time interval used in this study, meaning the correlation data collected here are insensitive to these fast dynamics. In another FCS study, the translational diffusion of CTB bound to GM₁-doped lipids was investigated and a correlation function time constant of 6 ms was reported for a spot size of 50 nm.⁴⁰ Using fluorescence recovery after photobleaching (FRAP), Kelly et al.⁴⁰ determined the diffusion coefficient of CTB in a lipid bilayer to be 0.12 ± 0.03 μm²/s. If Brownian diffusion is assumed, CTB would be expected to take a time t to diffuse a mean squared distance r according to t = r²/4D. For the spot size used in this study, ∼1 mm², it would take CTB approximately 2.5 × 10⁶ s to diffuse through the illumination area. Consequently, this much slower rate compared to the binding kinetics observed in Figure 1 would not contribute to the correlation data presented here.

Correlation data for the specific binding of CTB to 1 mol % GM₁ doped into a DOPC bilayer were fit to eq 1 with parameters k_on, k_off, and N_c. The results of nonlinear least-squares regression of the data in Figure 1A–C to eq 1 are shown in Table 1. The measured adsorption rate decreased with increasing protein concentration, from (1.0 ± 0.1) × 10⁹ M^–1·s^–1 when only 0.5 nM CTB is present to (1.5 ± 0.01) × 10⁸ M^–1·s^–1 for 13 nM CTB to (3.5 ± 0.2) × 10⁶ M^–1·s^–1 for 240 nM CTB. The decrease in adsorption rate with increasing CTB concentration seen in the SHCS data might be explained in terms of electrostatics by using the electrostatic potential map of CTB shown in Supporting Information. The binding plane surface of CTB has a positive potential and would be greatly attracted to the negatively charged terminal sialic acid of GM₁, leading to the rather fast adsorption rate seen here for low concentrations of CTB. However, as more CTB is bound to the surface, the neutral top plane of bound CTB would be exposed to incoming CTB molecules and essentially screen the negatively charged sialic acids at the membrane surface. As more CTB binds, the attraction between the negative sialic acid and the binding plane of CTB would lessen, leading to a slower rate of adsorption as the concentration of CTB increased.

Table 1. Measured Adsorption and Desorption Rates and Equilibrium Binding Affinity for Cholera Toxin Subunit B, Determined by SHCS.

[CTB] (nM)	kon (×108 M–1·s–1)	koff (×10–5 s–1)	Ka (×1012 M–1)
0.5	10 ± 1	3.6 ± 0.5	28 ± 5
13	1.50 ± 0.01	3.2 ± 0.4	4.7 ± 0.7
240	0.035 ± 0.002	2.5 ± 0.2	0.14 ± 0.01

The results seen for the 240 nM CTB–GM₁ interaction are similar to the k_on value reported in an SPR study by Kuziemko et al.¹⁶ (1.27 × 10⁶ M^–1·s^–1), where the binding of 120–240 nM CTB to a 5 mol % GM₁-doped lipid bilayer was investigated, suggesting that SHCS can accurately predict the adsorption rate for the CTB–GM₁ complex. It is important to note that the authors in the SPR study took extreme precautions to make sure mass transport did not limit or affect the binding kinetics and as such collected their CTB–GM₁ binding data under steady-state conditions.¹⁶ Not only were the SHCS data collected after steady-state equilibrium had been reached (up to 16 h at 0.5 nM CTB) but also the SHCS analysis of the kinetics is inherently minimally affected by mass transport as the diffusion of the protein molecules to the surface occurs at a much longer time scale (10^–8 cm²·s^–1)⁴¹ compared to the binding kinetics. As has been done in FCS, the difference in time scale can be used to separate out the contributions from binding kinetics and diffusion.⁴²⁻⁴⁴ The SHCS data and the data collected by Kuziemko et al.¹⁶ produce similar adsorption rates, as both were collected under steady-state conditions where mass transport did not affect the measured binding kinetics.

The desorption rates obtained from the fit to eq 1 were (3.6 ± 0.5) × 10^–5 s^–1 for 0.5 nM CTB, (3.2 ± 0.4) × 10^–5 s^–1 for 13 nM CTB, and (2.5 ± 0.2) × 10^–5 s^–1 for 240 nM CTB. The desorption rates were all in good agreement with each other and did not significantly change with CTB concentration. To further verify the SHCS results, a desorption experiment at all three CTB concentrations was performed by flowing excess phosphate-buffered saline (PBS) through the flow cell and monitoring the SH intensity over time (data shown in Supporting Information). The desorption rate of CTB from GM₁ remains relatively constant with increasing CTB concentration, from (3.07 ± 0.02) × 10^–5 s^–1 at 0.5 nM CTB to (3 ± 1) × 10^–5 s^–1 at 13 nM to (3.6 ± 0.8) × 10^–5 s^–1 at 240 nM. Additionally, all desorption rates are close to those predicted by SHCS. The good agreement of SHCS desorption rates with those obtained through a separate desorption experiment confirm the ability of SHCS to predict accurate binding kinetics for surface protein–ligand interactions. To further verify the predicted k_on values obtained by SHCS and to decouple the closely related fitting parameters of eq 1, the k_off values obtained from independent desorption experiments were fixed in eq 1 and the nonlinear regression was run with only two parameters, k_on and N_c. The results produced the same values (within error) for k_on and N_c as those shown in Table 1 that were determined for the three-parameter fit, albeit with smaller error. Thus, although it is not wholly necessary to determine the desorption rate separately to obtain accurate binding kinetics by SHCS, it does lower the error and is a simple way to confirm the SHCS predicted binding kinetics.

The equilibrium binding affinity was calculated from adsorption and desorption rates determined from the SHCS data in Figure 1 by use of eq 2, and the results are shown in Table 1. K_a decreased with increasing CTB concentration, from (2.8 ± 0.5) × 10¹³ M^–1 at 0.5 nM CTB to (4.7 ± 0.7) × 10¹² M^–1 at 13 nM CTB to (1.4 ± 0.1) × 10¹¹ M^–1 at 240 nM CTB. The K_a determined here for 240 nM CTB binding to GM₁ is in good agreement with the SPR study by Kuziemko et al.¹⁶ for the CTB–GM₁ interaction under steady-state equilibrium for the CTB concentration range 120–240 nM, 2.6 × 10¹¹ M^–1 (K_d = 4.61 × 10^–12 M). Additionally, similar concentration-dependent protein–ligand binding kinetics have been reported in the literature. For example, at low wheat germ agglutinin (WGA) protein concentrations (20 pM–10 μM), WGA experienced a much higher affinity for its ligand than at higher WGA concentrations (5–200 μM).^4,45 This is consistent with the trends seen here obtained via SHCS, where the lowest CTB concentration has the highest binding affinity for GM₁. The good agreement with literature steady-state binding kinetic values and previously reported binding affinity trends demonstrates that SHCS can be used to accurately measure multivalent protein–ligand interactions at the surface with negligible mass-transport affects.

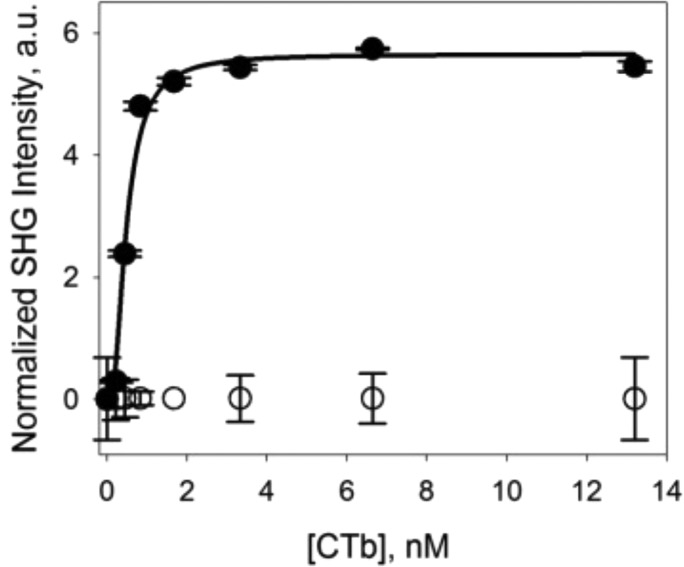
To further examine the binding properties of the CTB–GM₁ complex, a steady-state equilibrium isotherm was collected for CTB bulk concentrations ranging from 0.22 to 13 nM (Figure 2). At each concentration, the protein was allowed to reach equilibrium before the next concentration was equilibrated with the surface. The data collection took a total of 49 h to complete as the lower concentrations took between 10 and 14 h to reach steady-state equilibrium. Nonspecific binding of CTB to a pure DOPC bilayer was also examined and plotted in Figure 2 (○). It is apparent from the data in Figure 2 that there is negligible nonspecific binding observed over the entire CTB concentration range examined, which is consistent with the data determined by SHCS.

Figure 2.

SH intensity versus bulk CTB concentration binding to 1 mol % GM₁ doped into a DOPC bilayer recorded at steady-state equilibrium (●) and to a pure DOPC bilayer (○). The solid line represents the fit to the Hill–Waud binding model. Error bars represent the standard deviation from two independent experiments.

In a study by Shi et al.⁷ where the binding of CTB to 1 mol % GM₁ doped into a lipid bilayer was examined by fluorescence, it was found that the CTB–GM₁ interaction fit best to the Hill–Waud cooperative model. As such, the data in Figure 2 (●) were fit to both the Langmuir model (eq 4) and the Hill–Waud model (eq 5). As we have shown in previous work,⁴⁶ the simplified Langmuir isotherm model in terms of SH intensity used to fit the data can be expressed as follows:

4

where I_SHG^max is the SH intensity at binding site saturation, K_a is the equilibrium binding affinity, and [P] is the protein concentration. The Hill–Waud model in terms of SH intensity can be expressed as follows (detailed derivation in Supporting Information):

5

where n is the Hill coefficient describing the affinity of the protein for its ligand when another ligand is already bound. When n > 1, there is an increase in the affinity of the protein for its ligand once another ligand is bound (positive cooperativity), and when n < 1, there is a decrease in the affinity of the protein for its ligand once another ligand is bound (negative cooperativity).⁷ The data in Figure 2 were found to statistically fit best to the Hill–Waud model by use of an f-test. The resulting K_a was (3.2 ± 0.3) × 10⁹ M^–1 with a Hill coefficient of 2.0 ± 0.5. These results indicate that there is a positive cooperative interaction between ligand molecules and that once one ligand is bound by CTB, there is an increased affinity for CTB to bind to the neighboring ligand molecules. Although both the K_a and n values determined here are statistically the same as those reported by Shi et al.,⁷K_a = (3.2 ± 0.7) × 10⁹ M ^–1 [K_d = (0.31 ± 0.05) × 10^–9 M] and n = 1.9, the K_a is much lower than that obtained by SHCS. This discrepancy between isotherm data and SHCS data is most likely due to the influence of mass transport on the binding kinetics obtained from the isotherm data of CTB binding to GM₁. Although CTB was allowed to incubate with the surface for an extended period of time (up to 14 h) and the bulk protein solution was replaced every 5–10 min, true steady-state equilibrium was likely not obtained, especially at the lowest CTB concentrations, where small changes in signal were harder to distinguish. It is true that continuous flow would reduce mass-transport effects even more; however, given the incubation time required at the lower CTB concentrations and the amount of analyte needed, such an experiment would be unreasonable in terms of the time required to perform the analysis and the cost of materials. Furthermore, a similar mass-transport investigation has already been performed by Kuziemko et al.¹⁶ at higher CTB concentrations and has shown that the binding kinetics are drastically affected by flow rate. In the work presented by Kuziemko et al., which reported the same binding kinetics as SHCS for 240 nM CTB, multiple flow rates were investigated and an optimal flow rate was chosen such that the binding kinetics of CTB to GM₁ showed no limitation by mass transport. The good agreement between the steady-state equilibrium results obtained by Kuziemko et al.¹⁶ and those obtained by SHCS suggests that the SHCS data are void of mass-transport effects and provide more precise results for the binding of CTB to GM₁ as compared to the isotherm study, which is likely mass-transport-limited. Additionally, as mentioned earlier, SHCS has the ability to determine the binding kinetics without contributions from diffusion even when data collection is not done under true steady-state equilibrium conditions, as these two events occur at different time scales and will appear as two separate decays in the correlation data.^42,44

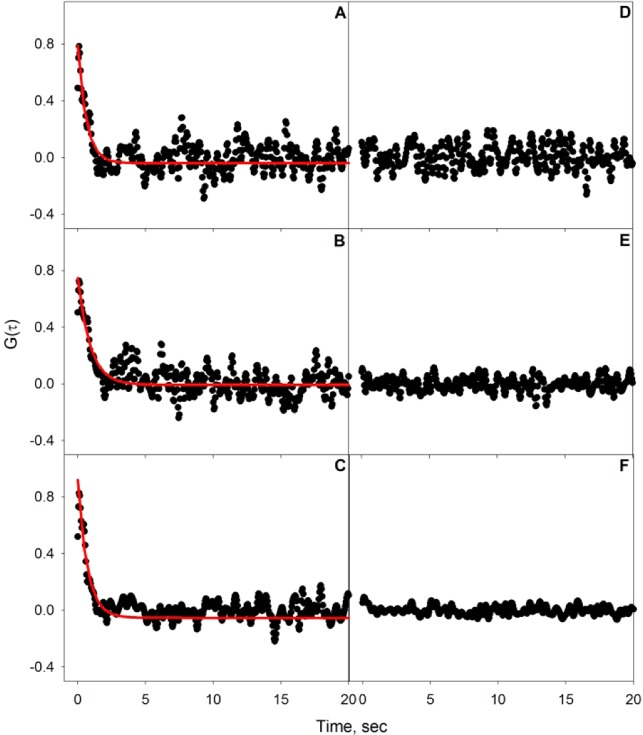
In addition to the CTB–GM₁ binding study, SHCS was also used to investigate the binding kinetics of the multivalent binding protein PnA to 5 mol % GM₁ doped into a DOPC lipid bilayer. The SHCS data collected for PnA concentrations of 0.43, 3, and 12 μM binding to a 5 mol % GM₁-doped DOPC bilayer are shown in Supporting Information. The normalized correlation data obtained from the average of 20 data sets are shown for each of the three PnA concentrations in Figure 3A–C. As before, the first point of the correlation data and high-frequency contributions (filtered at 15 times the Nyquist limit) have been removed, as they contain contributions from the photon shot noise of the detection system. Autocorrelation was also performed on the average of 20 data sets for PnA concentrations 0.43, 3, and 12 μM binding to a pure DOPC bilayer without the ligand GM₁. The normalized correlation data for nonspecific binding of PnA to DOPC are shown in Figure 3D–F. The time-zero point of the nonspecific correlation curves were normalized to the corresponding specific correlation data at time zero to allow comparison of the relative magnitudes of specific and nonspecific correlation data. Here again we note that, before normalization, the noise of all three nonspecific autocorrelations was relatively the same and oscillated about the same mean SH intensity. There is no correlation seen in Figure 3D–F, suggesting that there is negligible nonspecific binding of PnA to a pure DOPC bilayer for all PnA concentrations studied. As such, the correlated events seen in the data shown in Figure 3A–C are attributed solely to the specific binding of PnA to 5 mol % GM₁.

Figure 3.

Autocorrelation data for PnA binding to 5 mol % GM₁-doped DOPC bilayer at PnA concentrations of (A) 0.43, (B) 3, and (C) 12 μM, with fits to eq 1 indicated by the red lines. Also shown are the autocorrelations of PnA exposed to a pure DOPC bilayer at concentrations of (D) 0.43, (E) 3, and (F) 12 μM. The nonspecific PnA autocorrelations have been normalized to the corresponding specific binding data as mentioned in the text.

As with CTB, the normalized autocorrelation data for specific binding of PnA to 5 mol % GM₁ doped into a DOPC bilayer for the three bulk PnA concentrations were fit to eq 1 with the parameters k_on, k_off and N_C, and the results from the nonlinear least-squares regression are shown in Table 2. The measured adsorption rates decreased as the bulk PnA concentration decreased, from (3.7 ± 0.3) × 10⁶ M^–1·s^–1 at 0.43 μM PnA to (3.9 ± 0.3) × 10⁵ M^–1·s^–1 at 3 μM PnA to (1.1 ± 0.1) × 10⁵ M^–1·s^–1 at 12 μM PnA. The desorption rates did not change (within experimental error) with increasing PnA concentration, from (1.0 ± 0.2) × 10^–3 s^–1 at 0.43 μM PnA to (2.2 ± 0.2) × 10^–3 s^–1 at 3 μM PnA to (2.7 ± 0.2) × 10^–3 s^–1 at 12 μM PnA. The concentration-dependent binding kinetics seen for PnA–GM₁ are similar to those observed for CTB–GM₁, discussed earlier, and can similarly be explained in terms of high-affinity binders at low concentrations and electrostatics. PnA (pI ∼ 6)⁴⁷ has a slight negative charge at neutral pH and GM₁ contains a negatively charged terminal sialic acid, which could repel the PnA molecules from the surface. The electrostatic repulsion between negatively charged PnA molecules and negatively charged immobilized GM₁ could cause a reduction in the adsoprtion rate of additional protein molecules binding to the surface as the PnA surface density increases with increasing bulk concentration.

Table 2. Measured Adsorption and Desorption Rates and Equilibrium Binding Affinity for Peanut Agglutinin, Determined by SHCS.

[PnA] (μM)	kon (×105 M–1·s–1)	koff (×10–3 s–1)	Ka (×108 M–1)
0.43	37 ± 3	1.0 ± 0.2	37 ± 8
3.0	3.9 ± 0.3	2.2 ± 0.2	1.7 ± 0.2
12.2	1.1 ± 0.1	2.7 ± 0.2	0.41 ± 0.05

In addition to the adsorption and desorption rates, equilibrium binding affinity, K_a, was calculated for each PnA concentration by use of eq 2, and the results are shown in Table 2. The highest K_a, (3.7 ± 0.8) × 10⁹ M^–1, was observed for the 0.43 μM PnA–GM1 interaction, followed by (1.7 ± 0.2) × 10⁸ M^–1 for 3 μM PnA and (4.1 ± 0.5) × 10⁷ M^–1 for 12 μM PnA. This decrease in K_a with increasing PnA concentration suggests that electrostatic repulsion between negatively charged PnA molecules and negatively charged immobilized GM₁ may reduce the binding affinity at higher PnA concentrations.

The K_a values obtained by SHCS are much higher than those typically reported for PnA binding to GM₁.^6,13 In a study that monitored the binding of PnA to a 4.8 mol % GM₁-doped lipid bilayer on the surface of a gold electrode by quartz crystal microbalance (QCM), the K_a (8.3 × 10⁵ M^–1) was found to be 3–4 orders of magnitude smaller than that found by SHCS.¹³ However, in the QCM study the K_a was determined by a typical binding isotherm with bulk PnA concentration ranging from ∼0.25 to 6 μM.¹³ For a more direct comparison, a similar binding isotherm was collected here for PnA binding to a 5 mol % GM₁-doped DOPC lipid bilayer by SHG spectroscopy. The SH signal was monitored over time and increased as the bulk PnA concentration increased from 0.22 to 12.2 μM, shown in Figure 4 (▲). To keep the experimental parameters the same as those in the QCM study, multiple injections were not made and each protein concentration was allowed to incubate with the surface for only ∼30 min. Due to the slightly negative charge of PnA at pH 7.4 (pI ∼ 6),⁴⁷ the data in Figure 4 were fit to the Frumkin model, which accounts for any electrostatic interactions between charged protein molecules, and the typical Langmuir model (eq 4). An f-test was performed to determine which model statistically fit best to the data with a confidence level of 95%. The Frumkin model has been previously expressed in terms of SH intensity and can be written as⁴⁸

6

The above equation is similar to the Langmuir model with the additional electrostatic term g. The g coefficient describes electrostatic interactions between charged protein molecules on the surface, where g < 0 indicates a repulsive electrostatic interaction between protein molecules and g > 0 indicates an attractive electrostatic protein–protein interaction.⁴⁸

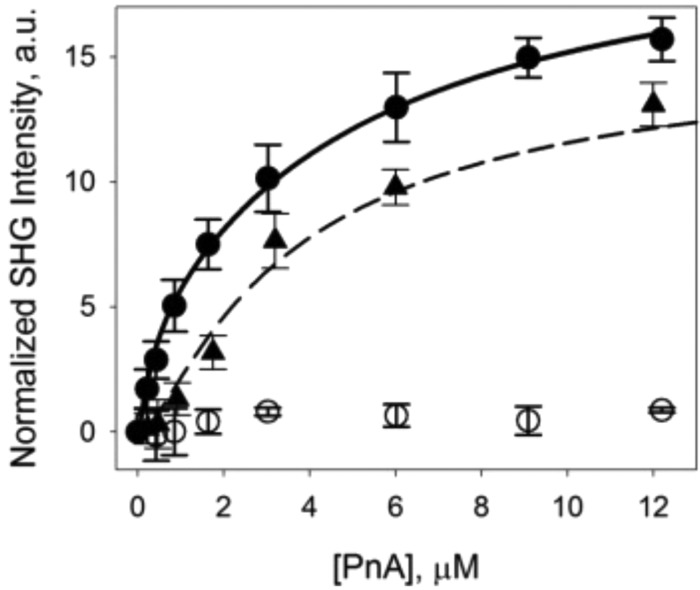
Figure 4.

SH intensity versus bulk PnA concentration binding to 5 mol % GM₁ doped into a DOPC bilayer recorded at steady-state equilibrium (●), at non-steady-state equilibrium (▲), and to a pure DOPC bilayer (○). Lines represent the fits to the Frumkin binding model (solid) and Langmuir model (dashed). Error bars represent the standard deviation from three independent experiments.

The single-solution isotherm in Figure 4 (▲) was found to statistically fit best to the Langmuir model (eq 4). The K_a determined from the nonlinear least-squares fit to eq 4 for PnA binding to a 5 mol % GM₁-doped DOPC bilayer was found to be (5.4 ± 0.7) × 10⁵ M^–1. This K_a value is similar to that reported by Janshoff et al.¹³ for the QCM study (K_a = 8.4 × 10⁵ M^–1) but still 2–3 orders of magnitude lower than that measured by SHCS.

Since the previous isotherm is most likely mass-transport-limited, a quasi-continuous flow isotherm was also collected for PnA binding to a 5 mol % GM₁-doped DOPC bilayer. To account for depletion of the bulk protein concentration as PnA molecules bound to the surface, multiple injections were made every 5–10 min at each PnA concentration in the range 0.22–12.2 μM until steady-state equilibrium had presumably been reached, as no visible increase in signal was seen from an additional injection of the same PnA bulk concentration (data shown in Figure 4, ●). The discrepancy between the isotherm collected with a single solution of PnA and that collected with a quasi-continuous flow is particularly apparent at lower PnA concentrations (Figure 4). This suggests that the single-solution isotherm data were indeed not collected under steady-state conditions and therefore gave an underestimated K_a value. The data in Figure 4 (●) were fit to both eq 4 (Langmuir model) and eq 6 (Frumkin model) and were found to statistically fit best to the Frumkin model. The determined K_a from the nonlinear least-squares fit to eq 6 was (3.0 ± 0.2) × 10⁶ M^–1 with a g value of −536 ± 50 J/mol. This K_a is ∼6 times greater than that seen for the isotherm not conducted under steady-state conditions as well as that reported by Janshoff et al.¹³ Although this K_a is still ∼1 order of magnitude lower than that obtained for the highest PnA concentration (12 μM) by SHCS, the difference in the K_a values obtained from the quasi-continuous flow isotherm and the single-injection isotherm illustrates the tremendous importance of allowing low protein concentrations sufficient incubation time with the surface in order to reach steady-state equilibrium, which in the case of PnA took up to 2 h at the low 0.22 and 0.43 μM concentrations. Further studies of PnA–GM₁ adsorption were conducted under a continuous flow at a rate of 3 mL/s (data shown in Supporting Information) and showed a faster adsorption rate compared to the single-injection quasi-continuous flow isotherm shown in Figure 4 (●), suggesting the binding affinity from the isotherm is still mass-transport-limited. It is important to remember that the SHCS data are void of any mass-transport effects, as the diffusion of molecules occurs at a much longer time scale than the binding kinetics observed in this study. As such, the predicted K_a from the quasi-continuous flow isotherm is lower than that determined by SHCS due to mass-transport effects.

Despite the mass-transport limitations on the binding isotherms, one characteristic apparent from the quasi-continuous flow isotherm that was not seen in the single-injection isotherm is that there is repulsion between the PnA molecules, resulting in a better fit to the Frumkin model and a negative g value. The large negative g value suggests that there is a large electrostatic repulsion between charged protein molecules at the surface, which could hinder binding and slow the adsorption rate as the surface density of PnA increases. Although this electrostatic repulsion between charged PnA molecules is reasonable when the negative pI ∼ 6 of PnA is considered,⁴⁷ the electrostatic potential map was also calculated to further quantify the charge distribution of surface residues of PnA and is shown in Supporting Information. Essentially, the entire solution-exposed surface of PnA has a negative potential, which explains the rather high electrostatic repulsive constant measured by use of the Frumkin model. Additionally, the highly negative PnA surface would be repelled by the negative sialic acid terminus on GM₁, which could explain the decreasing adsorption rate with increasing PnA concentration as measured by SHCS.

The importance of incubation time and mass-transport-limited kinetics was also demonstrated in a lectin iodination study by Emerson and Juliano,⁴ where PnA binding to N-acetylgalactose receptors on Chinese hamster ovarian (CHO) cells for the PnA concentration range 10–60 μM was examined. In this study PnA was allowed to incubate with the surface for twice the amount of time as the QCM study (at least 1 h) and a much higher PnA concentration was used. A higher K_a of (4.5 ± 1) × 10⁶ M^–1 was measured as compared to the QCM study. Although the reported K_a is similar to that obtained from our quasi-continuous flow isotherm, it is important to note that the iodination study was conducted with a much higher PnA concentration range and this could contribute to the discrepancy in the measured binding affinity. In the same iodination study by Emerson and Juliano,⁴ the interaction of wheat germ agglutinin (WGA) with CHO cell receptors for bulk WGA concentration range 5–200 μM was investigated and found to have a binding affinity of 1.6 × 10⁶ M^–1; however, a similar iodination study by Stanley and Carver⁴⁵ reported a K_a ∼2 orders of magnitude greater for the WGA concentration range 20 pM–10 μM. These two iodination studies suggest that the binding affinities of lectins are highly dependent on protein concentration, which is also consistent with the data from the SHCS studies presented here. To compare the results of Emerson and Juliano⁴ obtained under steady-state equilibrium, SHCS was performed on 60 μM PnA (the highest concentration used by Emerson and Juliano) binding to a 5 mol % GM₁-doped DOPC bilayer.

The SHCS data for 60 μM PnA binding to 5 mol % GM₁ were filtered at 15 times the Nyquist limit to reduce the proportional noise and were fit to eq 1 with the parameters k_on, k_off, and N_C (data shown in Figure 5). The resulting adsorption and desorption rate determined from the fit were (3.1 ± 0.3) × 10⁴ M^–1·s^–1 and (3.7 ± 0.5) × 10^–3 s^–1, respectively, giving a K_a of (8.4 ± 1.4) × 10⁶ M^–1. The K_a obtained from the SHCS analysis of 60 μM PnA is similar to that obtained by Emerson and Juliano.⁴ Since Emerson and Juliano allowed PnA to incubate with the surface longer and at a much higher concentration as compared to the QCM study, it is likely that the results have minimal mass-transport effects, and this is most likely why the binding constant of the iodination study is consistent with that obtained by SHCS for 60 μM PnA.

Figure 5.

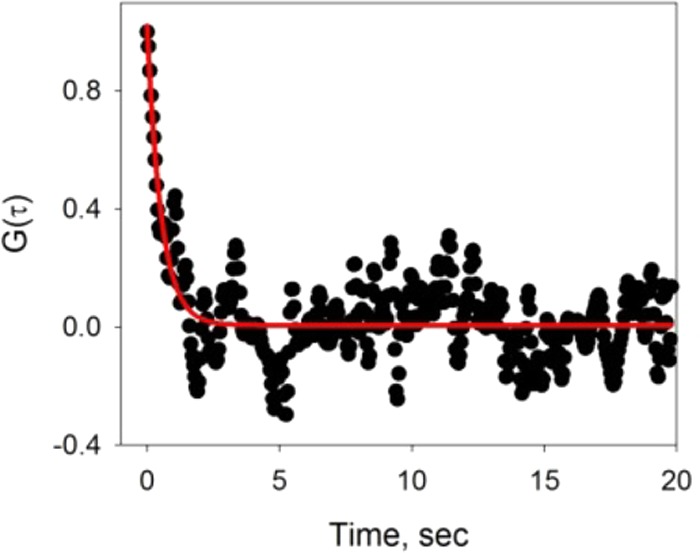
Autocorrelation data for 60 μM PnA binding to a 5 mol % GM₁-doped DOPC bilayer, with fit to eq 1 indicated by the red line.

The results from this study emphasize the tremendous importance of conducting kinetic measurements under steady-state equilibrium conditions. The agreement between data for 60 μM PnA binding to GM₁ measured by SHCS and data from the iodination study conducted under conditions minimizing mass-transport effects suggests that SHCS measures binding kinetics that are not mass-transport-limited. The importance of eliminating mass transport was also seen from comparison of the binding kinetics for CTB binding to GM₁ measured by SHCS and an SPR study where the flow rate was such that data were collected under steady-state conditions. The incubation time was also shown to significantly affect mass transport and measured binding affinity, as seen from the PnA–GM₁ isotherms conducted with different incubation times and flow rates. An inherent advantage of SHCS over the typical binding isotherms used to quantify protein–ligand interactions is that the nature of SHCS analysis allows the binding kinetics to be determined with negligible mass-transport effects as diffusion occurs at a much different time scale, meaning the reported SHCS binding kinetic values are inherently void of mass-transport effects. Therefore, the adsorption rate determined by SHCS is not artificially lowered by nonequilibrium conditions and is ultimately more likely to provide an accurate adsorption rate for multivalent protein–ligand interactions at a surface.

Summary

In the studies presented here, binding kinetics of multivalent protein–ligand interactions between PnA–GM₁ and CTB–GM₁ were investigated by both SHCS and a traditional equilibrium binding isotherm. Adsorption and desorption rates and overall binding affinity for three separate protein concentrations were determined by SHCS, while the cooperative binding behavior and electrostatics of multivalent protein–ligand interactions were investigated by binding isotherms. The results demonstrate the complexity of multivalent protein–ligand interactions and suggest the binding kinetics are dependent on bulk protein concentration. Due to the extremely high sensitivity of SHG, sigmoidal behavior at low PnA concentrations was detectable, suggesting there is electrostatic repulsion between the charged PnA protein molecules. Both the PnA–GM₁ and CTB–GM₁ studies demonstrate the importance of eliminating the influence of mass transport on binding kinetics. More importantly, this study illustrates that, by combining SHCS with conventional isotherm studies, additional information on the complex interactions between multivalent proteins and ligands can be obtained. While a binding isotherm can provide useful information on electrostatics and cooperative binding behavior of the multivalent protein–ligand interaction, it overlooks the concentration dependence of the binding kinetics. On the other hand, use of SHCS to examine the binding kinetics of multivalent protein–ligand interactions at a surface provides extremely valuable information on the binding kinetics as a function of protein concentration. Furthermore, SHCS requires much less time and analyte to determine the binding kinetics for a single concentration as compared to isotherm studies. The results of this study provide further understanding of the binding kinetics of two important multivalent protein–ligand interactions, which can provide greater insight into what parameters should be considered (protein concentration, mass transport, and cooperative interactions) when such multivalent protein–ligand complexes are used in biosensors, immunoassays, and other biomedical diagnostics.

Supporting Information Available

Additional text describing materials, experimental preparation, Hill–Waud derivation, and flow rate adsorption study of PnA to GM₁; 10 figures showing fluorescence microscopic images, extinction coefficient spectra of CTB and PnA, raw data for CTB binding (Figure 1) and PnA binding (Figure 3), electrostatic potential maps of CTB and PnA, and plots of SH intensity vs time for desorption of CTB, adsorption and desorption of PnA, and continuous-flow adsorption of PnA. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States