SWIFT—Scalable Clustering for Automated Identification of Rare Cell Populations in Large, High-Dimensional Flow Cytometry Datasets, Part 2: Biological Evaluation

Abstract

A multistage clustering and data processing method, SWIFT (detailed in a companion manuscript), has been developed to detect rare subpopulations in large, high-dimensional flow cytometry datasets. An iterative sampling procedure initially fits the data to multidimensional Gaussian distributions, then splitting and merging stages use a criterion of unimodality to optimize the detection of rare subpopulations, to converge on a consistent cluster number, and to describe non-Gaussian distributions. Probabilistic assignment of cells to clusters, visualization, and manipulation of clusters by their cluster medians, facilitate application of expert knowledge using standard flow cytometry programs. The dual problems of rigorously comparing similar complex samples, and enumerating absent or very rare cell subpopulations in negative controls, were solved by assigning cells in multiple samples to a cluster template derived from a single or combined sample. Comparison of antigen-stimulated and control human peripheral blood cell samples demonstrated that SWIFT could identify biologically significant subpopulations, such as rare cytokine-producing influenza-specific T cells. A sensitivity of better than one part per million was attained in very large samples. Results were highly consistent on biological replicates, yet the analysis was sensitive enough to show that multiple samples from the same subject were more similar than samples from different subjects. A companion manuscript (Part 1) details the algorithmic development of SWIFT. © 2014 The Authors. Published by Wiley Periodicals Inc.

Introduction

Flow cytometry (FC) is a powerful technology for rapid multivariate analysis of individual cells. It has become indispensable for basic and clinical studies in many areas, including immunology, cancer, and stem cell biology. A challenge for data analysis is created by current cytometers that analyze >20 properties on more than 10⁶ cells/sample ^1,2. Conventional manual, sequential bivariate gating cannot simultaneously analyze many dimensions, and is time-consuming, subjective, and irreproducible ³. Several flow cytometry clustering algorithms have been developed to address these issues ^4–21. Clustering of flow cytometry data is complicated by the very high dynamic ranges and variable distributions (shapes) of subpopulations. Model-based methods may conform better with the expected overlap in biological cell subpopulations, but do not normally scale well to very large datasets, and have a high computational load.

A particular challenge in flow cytometry is to identify rare subpopulations in large, complex samples, for example T cells secreting cytokines in response to antigen stimulation ^3,22,23; stem cells in peripheral blood ²⁴; or residual cancer cells after therapy ²⁵. In highly diverse populations, many clusters may need to be resolved to discern the rare subpopulations. The true diversity of cell populations analyzed by flow cytometry, for example human peripheral blood mononuclear cells (PBMC), can be very large—even if 16 antibodies against different antigens are used to define subpopulations, the addition of further antibodies identifies further subdivisions. Recent advances in mass spectrometry-based flow cytometry allow the measurement of more than 30 properties ²⁶ and provide very high resolution of complex populations. Therefore, the normal goal of flow cytometry analysis methods is not to define homogeneous subpopulations, but to provide a practical separation of subpopulations, at the level of resolution defined by the antibody panel.

To deal with the large dynamic range and asymmetry of flow cytometry subpopulations, we have developed Scalable Weighted Iterative Flow-clustering Technique (SWIFT), a three-stage approach based on a scalable and efficient Gaussian mixture model-based clustering method, followed by splitting and merging steps to adjust the number of clusters, identify rare subpopulations, and conform to non-Gaussian distributions. Both splitting and merging use unimodality as the guiding principle for cluster separation, as this is an intuitively reasonable criterion that approximates common practice in manual gating. The algorithmic development of SWIFT is described in detail in the accompanying article ²⁷, where its performance is also evaluated using simple synthetic and semisynthetic datasets for which ground truth is known. This article focuses on the application of SWIFT in analyses typical in immune response evaluation. SWIFT objectively identifies rare, biologically meaningful subpopulations in large, high-dimensional samples (e.g., clusters as rare as one part per million cells). This method also allows objective estimation of cluster number, and stringent comparison between similar samples by co-clustering.

In addition to the primary clustering analysis of large, high-dimensional sample data, the resulting large quantity of processed data necessitates efficient methods for further analysis of the cluster data. To take advantage of the richness of data available in the SWIFT results, we have also developed SWIFT-dependent auxiliary methods for visualization and other postclustering analyses to facilitate rigorous comparisons between samples, as well as exploration of datasets for discovery research.

Methods

Subjects

Blood was collected from healthy human subjects, ages 19–49 years. No subjects reported influenza-like illnesses (ILI). All procedures and the consent form were approved by the Research Subjects Review Board at the University of Rochester Medical Center, Rochester, New York.

Sample Processing

PBMC were isolated from sodium heparinized peripheral blood by Ficoll-Hypaque™ gradient centrifugation, washed and cryopreserved in 90% FBS and 10% DMSO (Sigma-Aldrich, St. Louis, MO). Cells were frozen to −80 °C using an isopropanol-filled, controlled-rate freezing device. After 24–48 h at −80 °C, the vials were transferred into liquid nitrogen for long-term storage.

Peptide Antigens

Individual peptides consisting of 15–17 amino acid residues, offset by 5 amino acids, were designed for sequences present in different combinations of H1N1 strains of influenza A. In particular, pool 1 contained peptides present in influenza A/New Caledonia/20/99 but not A/California/04/2009 or A/Brisbane/59/2007 × A/Puerto Rico/8/1934, i.e. these peptides were expected to stimulate long-term, multiply-boosted T cell responses (for more details of the peptide pools, see Ref.28. These peptides, and a pool of CD4 T cell-restricted epitopes from tetanus toxoid ^29–31, were synthesized by Mimotopes. Peptide pools were used at final concentrations of 0.1 µg/mL/peptide (influenza) and 3 µg/mL/peptide (tetanus).

Ex vivo Stimulation

PBMC were rapidly thawed in RPMI 1640 (Cellgro, Manassas, VA), supplemented with penicillin (50 IU/mL)-streptomycin (50 µg/mL) (GIBCO, Carlsbad, CA), 10 µg/mL DNase (Sigma-Aldrich, St. Louis, MO) and 8% FBS (assay medium). Cells were centrifuged and resuspended in RPMI 1640, supplemented with penicillin (50 IU/mL)-streptomycin (50 µg/mL), and 8% FBS and rested overnight in a 37 °C 5% CO₂ incubator. On the day of the assay, cell viability was tested by trypan blue exclusion dye, and 1–2 × 10⁶ cells/well in assay medium were plated into a 96-well V-bottom plate (BD, Franklin Lakes, NJ). A 200 µL PBMC suspension was stimulated with 0.3% DMSO (no antigen control), groups of influenza peptides, tetanus peptides, or staphylococcal enterotoxin-B (1 µg/mL, SEB, Sigma-Aldrich, St. Louis, MO) for a total of 10 h. Ten µg/mL brefeldin A (BD, Franklin Lakes, NJ) and 2 µM monensin (Sigma-Aldrich, St. Louis, MO) were added for the last 8 h of culture.

Intracellular Cytokine Staining (ICS)

PBMC were labeled with surface antibodies then fixed and permeabilized for ICS using a micromethod ³². The 15-color flow cytometry antibody panel is shown in Supporting Information Table 1. Cell data were acquired using an LSR II cytometer (BD Immunocytometry Systems). Manual data analysis was performed using FlowJo™ software (Treestar, San Carlos, CA).

Results and Discussion

SWIFT Algorithm Design for Detection of Rare Subpopulations

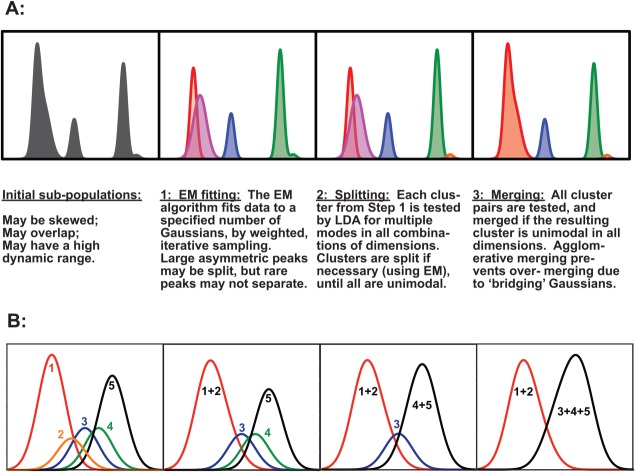
Several common flow cytometry data characteristics were considered in the design of a program that could detect very rare subpopulations. (a) Flow cytometry often produces data with high numbers of dimensions (e.g., 20) from large numbers of cells (e.g., millions) per sample. (b) Flow cytometry data have a high dynamic range, e.g., biologically significant subpopulations can be present at the level of 25 cells in several million. (c) Some subpopulations are asymmetric in one or more dimensions. (d) Subpopulations can overlap. The overall SWIFT strategy is summarized in Figure 1A and described in detail in the companion paper ²⁷. A brief summary of the steps in SWIFT follows.

Figure 1.

The SWIFT strategy for primary clustering, splitting, and merging. (A) Demonstration of the three steps in SWIFT to cluster the data using the EM algorithm; split multimodal clusters; and merge overlapping clusters. One dimension is shown for clarity—SWIFT actually operates in all dimensions simultaneously. (B) Merging proceeds sequentially, testing all possible overlapping pairs by the KL divergence and merging the most similar pair only if the merged result is unimodal. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Scalable mixture model fitting

We have chosen to use model-based clustering, to better approximate the potentially overlapping clusters found in flow cytometry data. First, data are preprocessed by censoring off-scale values (typically <1% in a good-quality sample), compensating, and applying an inverse hyperbolic sine transformation to stabilize Gaussian features across the entire data range. SWIFT then selects a small, uniform, random sample of the total dataset, and identifies initial clusters by the Expectation-Maximization (EM) algorithm for Gaussian mixture modeling (GMM). Large clusters are well-represented by the initial sampling, but rare subpopulations will not be detected as distinct clusters. SWIFT next fixes the parameters of the most populous Gaussian components and draws a new sample according to a weighted distribution that decreases the representation of the populous clusters and increases the weight of smaller clusters in the new sample. These steps are repeated until all cells have been evaluated. The iterative approach selectively improves the chances of sampling from rare subpopulations. Finally, the Incremental EM (IEM) algorithm is applied to the entire dataset to correct any deviations potentially introduced by the sequential iterative process. The computational complexity for SWIFT’s weighted iterative sampling scales less than linearly in the number of data points. Hence, this step is scalable for large datasets, and enhances the detection of rare subpopulations.

Multimodality splitting

Further enhancement of the identification of rare subpopulations is provided by a splitting step. In the first step, the EM algorithm fits multiple Gaussians to large, non-Gaussian clusters before assigning Gaussian components to smaller clusters. Because of the high dynamic range of subpopulation sizes, complexity of high dimensional datasets, non-Gaussian subpopulations, and potential underestimation of the initial cluster number, the data fitted to some Gaussian clusters can remain multimodal in one or more dimensions. SWIFT tests all clusters resulting from step 1 for unimodality in all data dimensions and along the principal component axes. Multimodal clusters are further split using the EM algorithm until all clusters are unimodal. Oversampling sparse background clusters before splitting enhances the detection of very small subpopulations. As the overlap of subpopulations can represent a continuum of cases, a cutoff criterion is required to decide when to split the initial clusters. The multimodality criterion for splitting is arbitrary, but this is an intuitively reasonable criterion that approximates common manual gating practice, and in practice this criterion successfully isolates biologically significant subpopulations (below).

Agglomerative merging

Because the initial assumption of simple Gaussian subpopulations is in general not valid with flow cytometric data, some modification of the simple GMM is required. More complicated parametric models [FLAME, flowClust ^7,19] allow greater flexibility in data fitting but add very significant computational cost. Because sums of Gaussians can approximate a wide class of distributions, our approach instead is to merge overlapping clusters using, once again, the criterion of unimodality. The differences between all possible pairs of clusters with any overlap are measured by the Kullback–Leibler (K–L) divergence, and the most similar pair is merged if the resulting cluster would be unimodal along: (a) the linear-discriminant-analysis (LDA) dimension along which the pair is most separated, (b) all data dimensions and (c) the principal component axes. K–L divergences are recalculated for the new cluster, and the merging step is repeated until no more merges are possible without compromising unimodality. Sequential merging provides robust merging and prevents “bridging” clusters from causing over-merging and generating bimodal clusters (Fig. 1B). This step allows SWIFT to represent the skewed non-Gaussian distributions commonly found in flow cytometry data ^{7,17,21,33–35}, and corrects for any over-estimation of cluster numbers in the first two steps. Finally, all events (including those initially censored) are assigned to the clusters in the final template based on probability of membership, both fractionally (to accurately estimate subpopulation sizes) and stochastically (to generate suitable data for examining the clusters in flow cytometry analysis programs).

Performance Characteristics of SWIFT: Convergence of Cluster Numbers

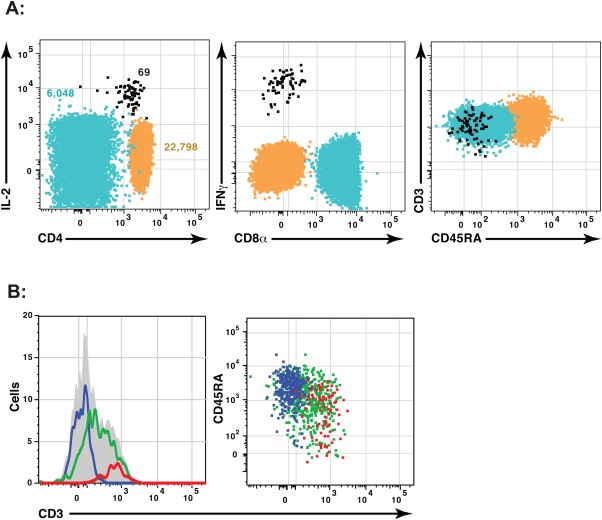
SWIFT successfully identifies clusters over a wide dynamic range. Figure 2A shows three clusters (selected from 1,172 clusters) in a sample of human PBMC stimulated with influenza antigens and stained with a 15-color panel. The small cluster (69 cells) comprises influenza-specific T cells expressing interferon gamma (IFNγ), whereas the large cluster (22,798 cells) represents a relatively homogenous subpopulation of naïve CD4 T cells. Figure 2B demonstrates merging, with an example of three clusters resulting from the first two steps of SWIFT. These clusters have substantial overlap, and were merged in step 3 to form a single merged cluster (gray area) that is skewed but not multimodal.

Figure 2.

SWIFT detects Gaussian and skewed clusters over a large dynamic range. A combined sample of 3 million human PBMC stimulated with tetanus and influenza peptides was analyzed by SWIFT, using two scatter and 15 fluorescence dimensions. (A) Three merged clusters (out of 872) were chosen to illustrate the wide variation in cluster size. (B) An example of merging shows three split clusters (left, colored lines; right, colored dots) that were combined by SWIFT into a single merged cluster (solid gray). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In addition to the identification of rare subpopulations and asymmetric subpopulations, the splitting and merging steps in SWIFT have the further benefit of converging on a stable cluster number. The EM algorithm requires an initial estimate of K, the cluster number, which is used for the first clustering step. However, if this number is too low, the splitting stage will generate a large increase in cluster number in the second step, and if the initial estimate of K is too high, the final merging step will perform a large number of merging operations. The effect of these two steps is to converge on a relatively stable final number of clusters, varying by only 1.3-fold even when the input initial estimate of K was varied over a 100-fold range (Fig. 3A). The Bayesian information criterion (BIC) was also tested in SWIFT as a criterion for determining K, but was slower and less robust than the modality-based splitting and merging steps in SWIFT (data not shown). SWIFT exhibits strong self-normalizing behavior to converge on a stable number of clusters. Although the final number of clusters is higher than determined by other flow cytometry analysis programs, the level of resolution described by SWIFT is consistent with the known biological diversity of the cell populations (see below).

Figure 3.

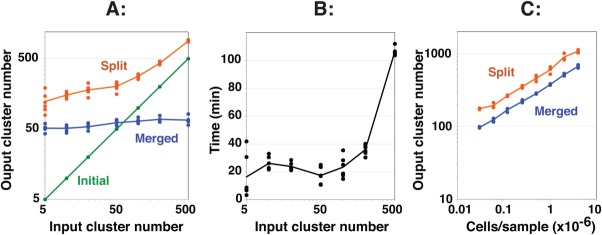
Performance characteristics of SWIFT including robust convergence on a final cluster number. A single sample of influenza-stimulated human PBMC was analyzed by ICS and flow cytometry, and then a random subset of 100,000 cells was clustered in SWIFT using seven fluorescence and two scatter dimensions. (A) Different values of the input cluster number were used in the first step (six replicates per point). The numbers of clusters found after the first (Initial, green), second (Split, orange), and third (Merged, blue) steps are shown. (B) Run times for the analyses in A are shown. Analysis was performed on a 2.4 GHz Mac Pro with 8 cores. (C) Samples containing different cell numbers, randomly sampled from a concatenate of influenza-stimulated human PBMC samples, were analyzed in triplicate in SWIFT using 100 input clusters. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

SWIFT run times (Fig. 3B) reached a minimum at about 50 input clusters for the sample (100,000 cells) shown in Figure 3A. At very low input cluster numbers the first step is rapid, but this is outweighed by the extensive splitting that occurs in the second step. At higher input cluster numbers the duration of the initial EM clustering step increases.

As expected, the number of detected clusters increases with the total cell number (Fig. 3C) and also with the number of dimensions used for clustering (data not shown). Detecting rare subpopulations requires enough data for the rare subpopulations to appear as distinct clusters, above the threshold of clustering (about 20 cells for 20-dimensional data in SWIFT). Thus, the sensitivity of discovering very small clusters can be increased by combining samples, or reduced by taking stochastic subsets of samples. The resolution of the analysis can also be modified by considering either merged or unmerged clusters.

The source code for SWIFT can be downloaded from http://www.ece.rochester.edu/projects/siplab/Software/SWIFT.html. The installation of the SWIFT program, and the cluster analysis of a typical sample, are described in Tutorial 1 (see Supporting Information).

Postprocessing and Visualization of Cluster Data

SWIFT clustering results are complex and require further analysis—depending on settings, 100–1,000 clusters are detected in 19-dimensional analysis (15 colors plus four scatter) of large (>1 million) human PBMC samples. We have developed several auxiliary tools to assist the further analysis of SWIFT cluster data. To facilitate the application of expert knowledge, SWIFT assigns cells to clusters and the SWIFT output includes a FCS file that incorporates cluster information to allow visualization and gating of clusters in standard flow cytometry analysis programs.

Soft clustering and stochastic assignment

SWIFT initially produces soft clustering results, in which each cell (event) has a membership probability between 0 and 1 in each cluster. This is useful for numerical output, but difficult to represent graphically for data exploration by experts. After clustering, SWIFT therefore stochastically assigns events to each cluster, in proportion to membership probabilities. This results in overlapping clusters that provide more realistic population shapes than hard boundaries, and more correctly describes the ambiguity inherent in overlapping populations. However, in this method, as in manual gating, the “true” cluster membership of a cell in the overlap regions cannot be defined.

Visualizing output from SWIFT–cluster gating

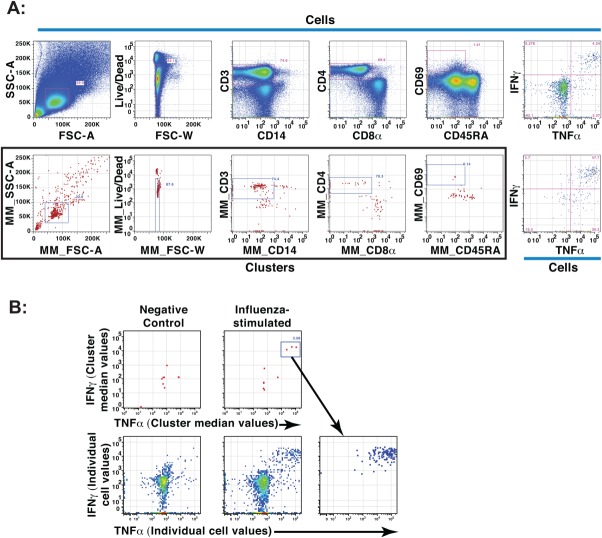
After assignment to a cluster, each cell is assigned, in addition to its original private values, the median values of its cluster in each dimension. These values are written as extra parameters in the output .FCS file. Cells can then be plotted at their cluster median values using standard flow cytometry analysis programs (e.g., FlowJo™), with each cluster appearing as a single point. Thus intact clusters can be gated conventionally as if they were single events (Fig. 4A). At any stage, the diversity of cells in gated clusters can then be revealed by plotting the private channel values. As both split and merged cluster medians are provided in SWIFT output, increased resolution can be obtained by examining the split clusters. Cluster median display and gating provides a convenient way to explore the SWIFT clusters and their constituent cells, with the advantage of applying expert knowledge for interpretation AFTER the primary analysis, to retain as much objectivity as possible. Visualization of clustering data is demonstrated in Tutorial 2 (see Supporting Information).

Figure 4.

Cluster gating to identify activated CD4 T cell clusters. Aliquots of human PBMC from a healthy donor were incubated with or without influenza antigens and analyzed by ICS and flow cytometry. (A) After analysis of an influenza-stimulated sample by SWIFT, the events were visualized in FlowJo™ according to individual event values (top) or common cluster median values (red dots, bottom, boxed). Live, activated CD4 T cells were identified by sequential gating, using similar gates for both events and clusters. The final panels (right) show individual cells identified by event gating (top) or cluster gating (bottom). MM denotes “merged medians.” (B) Stimulated and unstimulated samples were analyzed individually by SWIFT; activated memory CD4 T cells were identified by cluster gating as in A, and then displayed according to the cluster median (top) or individual (bottom) fluorescence values for IFNγ and TNFα. The three IFNγ⁺ TNFα⁺ clusters, present only in the stimulated sample, are displayed as events in the right panel. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Biological Evaluation of SWIFT’s Ability to Detect Biologically Important Rare Populations

A critical question for all clustering methods is whether the resulting clusters correspond to biologically relevant populations. This is particularly important with SWIFT, which resolves large numbers of clusters in complex samples. We have used detection of rare but expected populations, combinations of artificial mixtures, and sample comparisons to provide external criteria for evaluating SWIFT performance.

SWIFT identifies rare cytokine-secreting T cell populations

As a stringent test of the ability of SWIFT to identify rare, but biologically significant populations, we stimulated human PBMC with influenza peptide antigens to induce rare (<0.01%) cytokine-secreting populations absent in negative controls ^22,36. Influenza-stimulated and control PBMC samples from normal donors were clustered in SWIFT, and analyzed by cluster gating. After gating on activated CD4 T cell clusters (CD3⁺, CD8⁻, CD4⁺, CD14⁻, CD69⁺) as in Figure 4A, small clusters were detected in influenza peptide-stimulated samples but not in control samples (Fig. 4B). Examination of the individual clusters showed that these contained the cytokine-secreting cells that were the target of the experiment. Each cluster contained cells expressing IL-2, TNFα, IFNγ, and/or CCL4.

SWIFT shows excellent accuracy using an experimental dataset with ground truth

To generate a real-world experimental dataset with ground truth, we analyzed separate mouse and human cell samples with complementary fluorescence labels, then merged the data electronically and clustered using SWIFT, without using the mouse/human labels. SWIFT identified 35 and 21 clusters that contained >90% mouse or human cells, respectively. No clusters fell into an intermediate category [see companion paper, ²⁷]. For comparison we also used FLOCK ¹², which also resolved mostly human or mouse clusters, but had more overlap, possibly due to the smaller number of clusters detected.

Comparing Cluster Output from SWIFT

Cluster matching is a difficult problem

Most flow cytometry experiments are performed for the purpose of comparing populations between different samples. Because of overlap of populations and ambiguity of clustering, matching of clusters is difficult between complex samples. Clustering has been described as an ill-posed problem ³⁷ and different algorithms can provide different solutions ^38–44. Because of the high dimensionality and inherent ambiguity in flow cytometry data, a clustering algorithm can be trapped in different local optima and provide multiple valid solutions ^45,46. The problem of matching clusters across different datasets ^47,48 is especially challenging with the high cluster numbers and range of sizes that SWIFT detects in large, high-dimensional datasets. Thus comparing two independently clustered samples is difficult.

Zero or near-zero populations can not be clustered directly

There is an additional and very important problem if a population is detectable in one sample but is absent or has very low membership in a second sample—this population cannot be enumerated by direct clustering in the second sample if the number of cells is too low to cluster. A specific example of this is seen in Figure 4B, in which the number of cytokine-secreting cells in the negative controls is nonzero, but too low to identify as a separate cluster. Correct comparison of the positive and negative samples requires enumeration of the small number of cells in this region in the negative control.

Co-clustering sidesteps the cluster matching problem and allows rigorous comparison, even between samples with missing populations

Fortunately, the cluster matching problem can be avoided by co-clustering samples ⁴⁹, i.e., by clustering a concatenate consisting of either the entire .fcs data files for all samples, or of a random subset of events from each sample (to keep the total number of events within a reasonable range). This allows a consensus clustering result to emerge, which often reflects the underlying populations better than any single sample. Joint clustering constrains all samples to the same consensus clusters, allowing rigorous comparison between samples by avoiding the problem of alternate clustering solutions. Samples to be co-clustered should be relatively similar, and staining and analysis procedures must be as uniform as possible, although normalization ⁵⁰ may allow more variable samples to be co-clustered in the future. If rare subpopulations of interest are present only in a few samples, care must be taken to ensure that these populations are not masked by background events from an excess of samples without these subpopulations. Differences between samples are revealed by comparing, for each cluster from each sample, both the numbers of events and the multidimensional medians. This approach is particularly powerful for enumerating cells in biologically interesting cell populations (e.g., antigen-stimulated T cells) that are almost absent in negative control samples.

To demonstrate the strength of the co-clustering approach, two flow cytometry data files from influenza-stimulated and unstimulated samples were merged, co-clustered by SWIFT (resulting in 911 clusters), and further analyzed by manual cluster median gating. Four clusters of activated CD4 T memory cells (CD3⁺, CD4⁺, CD8^–, CD14^–, CD45RA^–, CD69⁺) were identified, producing combinations of the four cytokines (IL-2, IFNγ, TNFα, and CCL4) characteristic of influenza responses (Fig. 5A). The majority of the cells in each of these four clusters was derived from the stimulated sample, not the negative control. Cluster 4 contained most of the CCL4+ cells, and cluster 3 comprised cells with low IL-2 expression. Although clusters 1 and 2 expressed similar levels of the four cytokines shown, these clusters were distinguished by slightly different background values in the CD45RA, IL-17, and CD8 dimensions.

Figure 5.

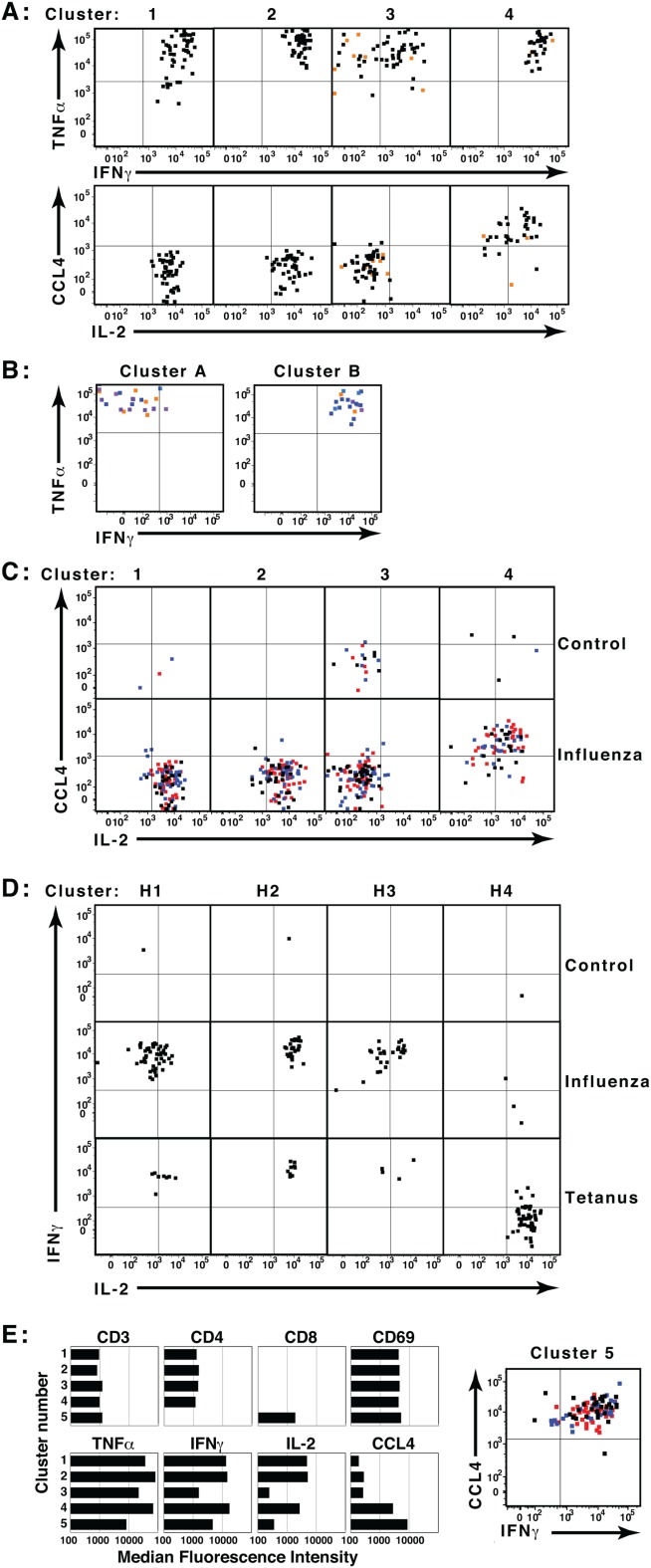
Co-clustering and template assignment to rigorously compare samples. Aliquots of human PBMC were incubated in triplicate in the presence or absence of influenza or tetanus toxin peptides, then analyzed by ICS and flow cytometry. (A) Files from one unstimulated and one influenza-stimulated sample were concatenated and analyzed in SWIFT. Activated memory CD4 T cell clusters were identified by cluster gating, and the expression of four cytokines by cells in each cluster is shown. Black and red dots represent cells from the stimulated and unstimulated samples, respectively. (B) Eighteen files from triplicate samples incubated with no antigen, tetanus peptides, or four pools of influenza peptides were merged electronically into a single concatenate. Low doses of antigens were deliberately chosen so that the cytokine-producing populations in the merged sample would be very rare. The combined sample of 27.2 million cells was then analyzed in SWIFT, resulting in 1,814 split and 1,524 merged clusters. Cytokine-producing memory CD4 T cell split clusters were identified by cluster gating, and the cells in two small clusters (24 and 19 cells) are shown. Both clusters included cells from tetanus (orange) and influenza (blue) but not unstimulated samples. (C) Triplicate control and influenza-stimulated samples were assigned to the template derived in A. Triplicates are indicated by black, red, and blue dots. (D) All cells in control, influenza, and tetanus samples were assigned to a SWIFT template from concatenated tetanus- and influenza-stimulated samples. Four activated CD4 T cell merged clusters were identified by cluster gating (H1, H2, H3, and H4). (E) Clusters in the two-file concatenate (from panel A) were selected according to low staining by the live/dead marker (<1,000). Median fluorescence values are shown for all five clusters in which the ratio of influenza-stimulated to control samples was >6. These included the four CD4 T cell clusters identified in A, and one CD8 T cell cluster. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Sensitivity and resolution of SWIFT

To determine the sensitivity of SWIFT for detecting small populations in very large samples, a sample was produced by electronically merging 18 .FCS files from an experiment comparing the responses to different influenza peptide pools. Low-responding and negative control samples were deliberately included in this concatenate, to ensure that small populations would be present. This sample of 27.2 million events was then clustered by SWIFT, resulting in the identification of 1,814 split clusters. Several of these were cytokine-producing activated memory CD4 T cells, and two smaller clusters are shown in Figure 5B. Both clusters comprised cells expressing TNFα and IL-2, whereas IFNγ was expressed by the cells in Cluster B but not Cluster A. These cells were derived from influenza- or tetanus-stimulated samples, but not from unstimulated samples. The detection of cytokine-producing populations as small as 19 and 24 cells, from a sample of 27.2 million events, demonstrates that SWIFT has a sensitivity of better than one part per million. This compares very favorably with other methods, for example a recently-described automated clustering technique for flow cytometry data found rare subpopulations at a level of 0.01% ⁵¹.

SWIFT analyzes flow cytometry data at high resolution, generating larger numbers of clusters than many other methods. In a moderate-sized sample (100,000 cells, seven colors) SWIFT finds ∼60 clusters (Fig. 3A), similar to numbers obtained by other methods. In larger PBMC samples with more dimensions (one million cells, 15 colors), SWIFT resolves ∼500 clusters. We believe that this high level of resolution is appropriate for several reasons. First, SWIFT is designed to detect rare cells, and a high level of resolution is necessary to reveal these subpopulations. Second, SWIFT generates ∼1,500 clusters from a CyTOF® ⁵² sample with 33 antibody dimensions (data not shown). This is a relatively small increase as compared to the potentially enormous increase that could result from adding 18 more dimensions if SWIFT were spuriously splitting subpopulations. Third, even at a resolution of ∼500 clusters, the rare cytokine-producing clusters are not present in large numbers (e.g., 6) and the distinguishing features of each cluster (e.g., the combination of cytokines expressed) can normally be identified by examination in visualization software such as FlowJo™ (Fig. 5A). Thus SWIFT appears to resolve genuinely different subpopulations, albeit at very high resolution.

Assigning cells to a cluster template extends traditional batch analyses

In the previous section, co-clustering of large concatenates allowed comparisons between several samples, but large experiments, particularly clinical studies, often generate thousands of samples that include hundreds of millions of cells. To extend SWIFT’s comparisons to these larger datasets, we have established a templating procedure that allows batch processing of large numbers of samples using an auxiliary program, “SWIFT assign”. One of the output files of SWIFT is a cluster template that includes the location, dispersion, and proportion of all clusters, and events in additional samples are then assigned to the clusters in this template. This template/assign strategy is flexible, as templates can be produced from single samples to establish a master template; combinations of samples to produce a consensus template; or stochastic subsets of cells to optimize run times and the sensitivity of detection of small clusters. In all cases, the sample(s) chosen to generate the template must include all subpopulations to be analyzed. Templating allows the identification of cluster memberships down to zero in individual samples, which is essential for comparing stimulated and control samples. It also allows the clustering run to be performed at an optimal cell number (e.g., 1–5 million cells). Both co-clustering and template assignment identify small differences between similar samples, and solve the problem of enumerating an absent or very small population, e.g., 0–5 cells in a negative control. Note the initial template clusters are unimodal due to the criteria in the splitting and merging steps in SWIFT, but occasionally the cells assigned to a cluster from another sample may yield a multimodal population. The generation of SWIFT cluster templates and their use in sample comparisons are demonstrated in Tutorial 3 (see Supporting Information).

Assignment of cells in additional samples to a cluster template is fast, e.g., about 1 min for a sample with 1 million cells on a desktop computer. Thus, even if SWIFT clustering of the consensus sample requires significant time, e.g. 2 h (see Supporting Information for sample run times), analysis of hundreds of samples can be completed rapidly.

The template produced in Figure 5A was applied to three replicate samples each of unstimulated and influenza-stimulated cells. Substantial numbers of stimulated cells were assigned to the four cytokine-producing cell clusters (Fig. 5C), whereas none of the three control samples contributed substantially to any of the clusters except cluster 3. Triplicate cultures showed excellent consistency.

SWIFT distinguishes subtleties between small cytokine-secreting populations

A cluster template was produced from merged influenza and tetanus antigen-stimulated samples, and additional samples were assigned to this template (Fig. 5D). In contrast to influenza responses, tetanus toxoid-specific responses are biased towards T cells producing IL-2 and TNFα rather than IFNγ ³⁶. Among four activated T cell clusters identified by SWIFT, the influenza-stimulated sample contributed more strongly to the three IFNγ⁺, IL-2⁺ clusters, whereas the tetanus sample contributed more to the IFNγ^–, IL-2⁺ cluster. Very few cells from the control sample were assigned to any of the four clusters. Thus in these experiments and others, SWIFT identified rare, biologically significant cell populations that are consistent with current biological interpretations.

Identification of clusters by SWIFT with minimal operator input

To test whether SWIFT could objectively identify antigen-specific T cell populations with very few assumptions, the SWIFT-derived clusters (Fig. 5A) of merged triplicate influenza-stimulated and control samples were classified by only two rules: live cell clusters were identified by low expression of the live/dead marker, and the live clusters were ranked according to the ratio of cells in each cluster derived from stimulated versus unstimulated samples. The five top-ranked clusters comprised the same four activated CD4 memory T cells identified by cluster gating (Fig. 5A), plus one activated CD8 T cell cluster (Fig. 5E).

Robustness and Reproducibility

As model-based clustering of complex flow cytometry populations can have multiple valid solutions, repeated clustering of the same sample in SWIFT does not result in identical cluster locations, and individual cells can be assigned to different clusters. Because typical flow cytometry datasets contain extensive overlap between populations, neither manual nor automated methods can assign cells unambiguously in the overlap regions, therefore either stochastic assignment or membership probabilities have to be used. Consequently, the locations and sizes of the clusters are more consistent than the assignments of the individual cells to a cluster.

Testing SWIFT robustness

SWIFT robustness was evaluated by generating a cluster template from one sample, then assigning cells to this template from three experimental replicate samples from the same subject, or from different subjects analyzed under the same conditions on the same day. The numbers of cells assigned to each cluster from the replicate samples were tightly correlated, whereas samples from different subjects were more variable (Fig. 6A). After assigning cells from different samples to the cluster template, the medians of the resulting clusters were recalculated and compared with the medians of the original template, i.e., testing the “goodness of fit” between template and sample. Experimental replicate samples agreed well, whereas some samples from different individuals were more diverse (Fig. 6B).

Figure 6.

Reproducibility of SWIFT clustering. PBMC samples from seven subjects were analyzed by ICS and flow cytometry. (A,B) Three replicate aliquots (X1, X2, and X3) from one subject, as well as samples from three additional subjects (P1, Y1, and O1), were assigned to a SWIFT cluster template produced from a sample from subject (X) Correlations of cells/cluster (Panel A), or the median fluorescence values for CD45RA (Panel B) are shown. (C, D) PBMC from eight independent blood samples (drawn over a period of 208 days) from three subjects (61, 62, 68) were stimulated with two pools of influenza peptides, SEB, or no antigen, and analyzed by ICS and flow cytometry. (C) A cluster template was produced from one influenza peptide pool-stimulated sample of subject 61, and all other samples assigned to this template. The heat map represents the R ² correlation values between all pairs of samples stimulated with the same influenza peptide pool, comparing the numbers of cells assigned to each cluster (left) or the median fluorescence intensity of the CD45RA staining in each cluster in each sample (right). (D) Two independent operators manually identified the activated memory CD4 T cells expressing TNFα and IFNγ in samples from subjects 61 and 62. One SWIFT template was produced from each subject, from concatenates of four antigen-stimulated samples. All samples were assigned to both templates, and the clusters containing activated memory CD4 T cells expressing TNFα or IFNγ identified. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

To distinguish between variability contributed by different subjects versus that due to different blood samples, we compared eight different blood samples taken over a period of 208 days from three subjects. All samples were cryopreserved, then analyzed on the same day. Figure 6C shows that the cluster results were generally more consistent between blood samples from the same subject, and more different when compared between subjects. As in Figures 6A and 6B, the cluster sizes were more variable than the median fluorescence values of each cluster (note different scale for heat maps). Thus cluster properties are consistent between replicate samples, yet SWIFT sensitively detects differences between non-identical samples, e.g., from different normal subjects.

Reproducibility between SWIFT and manual gating

Although in the long term our goal is to exceed the capacity of manual gating for detection and reliable quantitation of rare populations, an important interim goal is to show that SWIFT reliably recapitulates the overall results of manual gating. Human PBMC stimulated with different antigens were analyzed by manual gating by two experts (using the same gating protocol), and in parallel by two clusterings by SWIFT followed by cluster identification as above. Populations of activated CD4 T cells producing IFNγ and TNFα were enumerated by both methods, and the results compared. Manual gating and SWIFT clustering agreed well over a wide range (Fig. 6D), from negative controls, to antigen stimulations, to SEB polyclonal stimulations. SWIFT typically found slightly higher numbers of positive cells, possibly due to the more liberal cluster boundaries that could be achieved using simultaneous gating in all dimensions.

Note that the template/assign procedure is well-suited to datasets that are similar, particularly different stimulations from the same person. It can also handle variations between subjects and experimental days, provided that care is taken to keep the staining procedure and cytometer setup parameters as constant as possible using strict protocols ⁵³. Samples with more variation would require the application of normalization techniques [e.g. ⁵⁰] before the templating procedure could be used.

SWIFT is Optimized for Rare Populations

Algorithmic analysis of flow data is now possible using several alternative strategies. Several of these techniques now rival manual analysis methods, as evaluated by the ability to reproduce manual gating, and possibly more importantly, to objectively classify flow cytometry samples according to external clinical criteria ⁵⁴. Different algorithms perform better at different challenges, as expected due to their different strategies. SWIFT and its adjunct programs have been optimized to detect very rare populations, and the templating strategy allows stringent comparisons between large numbers of samples. The particular ability of SWIFT to detect rare populations in large datasets was demonstrated by comparing with three other programs, FLAME, flowMerge, and flowMeans ^7,20,21, using graded sample sizes, and testing for the identification of rare cytokine-producing populations (see Supporting Information for details). To achieve fine resolution and high sensitivity, SWIFT uses multiple steps to optimize the identification of clusters in complex high-dimensional samples across a very wide dynamic range. This program can not only replace manual gating with a more rapid, objective method, but can also discover changes not seen in manual gating, for two reasons: SWIFT can evaluate all subpopulations in complex samples; and simultaneous multidimensional clustering can detect more subtle changes than sequential bivariate manual gating.

Supporting Information

Additional Supporting Information may be found in the online version of this article.