Technology-enhanced Interactive Teaching of Marginal, Joint and Conditional Probabilities: The Special Case of Bivariate Normal Distribution

Summary

Data analysis requires subtle probability reasoning to answer questions like What is the chance of event A occurring, given that event B was observed? This generic question arises in discussions of many intriguing scientific questions such as What is the probability that an adolescent weighs between 120 and 140 pounds given that they are of average height? and What is the probability of (monetary) inflation exceeding 4% and housing price index below 110? To address such problems, learning some applied, theoretical or cross-disciplinary probability concepts is necessary. Teaching such courses can be improved by utilizing modern information technology resources. Students’ understanding of multivariate distributions, conditional probabilities, correlation and causation can be significantly strengthened by employing interactive web-based science educational resources. Independent of the type of a probability course (e.g. majors, minors or service probability course, rigorous measure-theoretic, applied or statistics course) student motivation, learning experiences and knowledge retention may be enhanced by blending modern technological tools within the classical conceptual pedagogical models.

We have designed, implemented and disseminated a portable open-source web-application for teaching multivariate distributions, marginal, joint and conditional probabilities using the special case of bivariate Normal distribution. A real adolescent height and weight dataset is used to demonstrate the classroom utilization of the new web-application to address problems of parameter estimation, univariate and multivariate inference.

INTRODUCTION

Diverse arrays of interesting scientific questions that frequently arise in everyday life may require probability reasoning to obtain exact or approximate answers. Examples of such inquiries include Given that an adolescent is of average height, what is the probability the adolescent weighs between 120 and 140 pounds?, What is the probability of (monetary) inflation exceeding 4% and housing price index below 110? and What is the probability that the second card drawn (without replacement) from a standard 52-card deck is a diamond given that the first drawn card was a king? These questions provide specific examples of conditional, joint and marginal distributions in multivariate (bivariate, in this case) settings, respectively. Generally, there are two strategies for solving such problems – analytical (using theory and first-principles) or experimental (using simulations, approximations or estimations). Solutions to such challenges may be specific or generic, numeric or qualitative, algorithmic or computational.

In multidisciplinary probability courses, utilizing modern information technology (IT) resources (Algozzine et al. 2011; Huang et al. 2011) may impact the instructors’ teaching strategies and enhance students’ learning and classroom experiences. Understanding joint, marginal and conditional probabilities for modeling and comprehension of the world around us requires both rigorous training and at the same time effective pedagogical approaches for teaching visual, active or didactic learners (Dietz and Stevenson 2011; Jahnavi and Patra 2012). The basic ideas of multivariate distributions, conditional probabilities and correlation may lead to misconceptions or fallacies in some students’ understanding that can be avoided by employing interactive web-based science education resources (Dinov and Christou 2011; Hwang et al. 2011). Building on the available Statistics Online Computational Resource (SOCR) infrastructure (Dinov 2006; Christou and Dinov 2011), we demonstrate one example of an IT-enhanced interactive instructional resource for teaching multivariate distributions, marginal, joint and conditional probabilities using the special case of the bivariate Normal distribution.

BIVARIATE PROBABILITIES

Suppose we are observing a natural process that generates two (or more) observations X and Y. For example, earthquakes’ location, magnitude and depth (Ayalew et al. 2011); vital signs of humans (body temperature, arterial pressure and respiration) (Henneman et al. 2012); stellar mass, radius and luminosity (Newton et al. 2011); phenotypic (age, race and morbidity) and genotypic characteristics (single nucleotide polymorphisms) in childhood-onset schizophrenia (Stephens et al. 2012), and so on. Such random observations of continuous or discrete processes may be thought of as instance measurements. The bivariate Normal distribution has some interesting properties (Lancaster 1957; Fraser and Streit 1980; Patel and Read 1996). The density function of bivariate Normal distribution is defined in terms of a two-dimensional mean–vector, specifying the center location of the distribution in the two-dimensional plane, and a 2 × 2 variance–covariance matrix, which characterizes the amount of dispersion along the main X and Y directions, as well as the correlation between X and Y. For the bivariate Normal distribution, the two marginal distributions are also (univariate) normal with means and variances according to the corresponding components of the bivariate distribution parameters (mean–vector and the variance–covariance matrix). Finally, the conditional probability distributions are also normal with explicit closed form expressions for their mean and dispersion parameters in terms of the corresponding bivariate density. The Appendix section includes the conceptual definitions and theoretical formulations necessary to apply and compute marginal, conditional and joint probability calculations, as well as the explicit expressions for the marginal and conditional probabilities.

Webapp

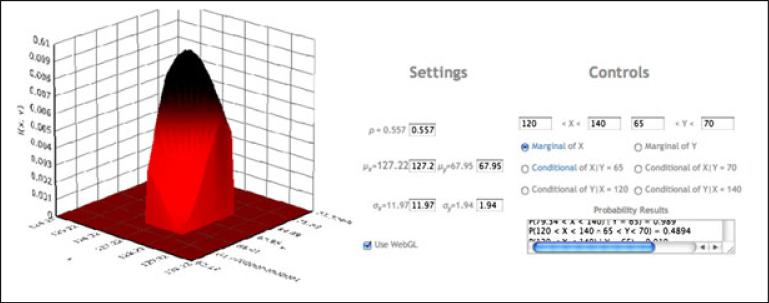
To improve students’ learning experiences and augment the instructors’ strategies of teaching probability theory and multivariate distributions, we designed, implemented and openly disseminated an interactive web-application (webapp) that demonstrates these concepts using bivariate Normal distribution (Castillo and Galambos 1989). The SOCR (Dinov and Christou 2009) bivariate Normal distribution webapp (http://socr.ucla.edu/htmls/HTML5/BivariateNormal/) requires a modern web-browser with HTML and JavaScript support. It includes a three-dimensional view of the bivariate distribution (based on WebGL) and includes a paired activity (see below). Instructors and learners may use the settings panel to initialize the webapp. The control panel allows selection of the appropriate bivariate limits for the X and Y variables and specification of the desired joint, marginal or conditional probability function. In addition to the interactive three-dimensional graph for the joint probability, the webapp provides a complementary one-dimensional Normal distribution graph for computing user-specified marginal or conditional distributions. Entering any non-numerical characters in the settings or control panels resets the parameter to infinity (∞).

The webapp allows three-dimensional rotation of the bivariate Normal distribution by clicking and dragging the mouse on the graph. For browsers without WebGL support, the three-dimensional graph shows a wireframe distribution instead of the standard triangulated surface. The webapp shows all probability results a text area. The webapp, Figure 1, is HTML5-standard compliant and should work on all modern browsers (including mobile devices) without ny special installations or configurations.

Fig. 1.

The Statistics Online Computational Resource (SOCR) bivariate Normal distribution web-application (webapp) user interface. The webapp is initiated using the settings parameters on the top-left. The control panel allows specification of the type and range of the probability density calculation. The graphs on the bottom illustrate the visual representations of the probabilities as areas under the curves/surfaces.

LEARNING ACTIVITY

We designed a complementary hands-on learning activity (http://wiki.stat.ucla.edu/socr/index.php/SOCR_BivariateNormal_JS_Activity) that aims the following:

• Provide a visualization tool for better understanding of multivariate distributions (e.g. bivariate Normal distribution).

• Clarify the definitions and interplay between marginal, conditional and joint probability distributions.

• Demonstrate how to calculate the marginal, conditional and joint probabilities for Bivariate Normal.

• Show how correlation influences the distribution of two normally distributed variables. Demonstrate that when X and Y have joint bivariate Normal distribution with zero correlation, then X and Y must be independent.

• Build a framework for generalizing the univariate Normal distribution to higher dimensions.

In our experience, teaching probability theory and multivariate distributions, students have responded overwhelmingly positively to the experience of interactively computing marginal, conditional and joint bivariate (Normal) probabilities, formulating research hypotheses, quickly validating them using the webapp and answering concrete scientific questions using the univariate and bivariate Normal distribution calculators. Indeed, instructors embedding the bivariate Normal distribution webapp and activity in their curricula need to demonstrate in class the tight integration of the course-specific conceptual materials, the applications they are addressing, and the graphing and computing resources provided in the webapp.

APPLICATION: HUMAN HEIGHTS AND WEIGHTS

One example demonstrating the classroom utilization of the new bivariate Normal distribution webapp addresses the first specific scientific question we presented in the Introduction: Given that an adolescent is of average height, what is the probability the adolescent weighs between 120 and 140 pounds? To answer this question, we first start with some real data about adolescents’ Heights (measured in inches, in) and Weights (measured in pounds, lb) (http://wiki.stat.ucla.edu/socr/index.php/SOCR_Adolescents_HeightsWeights) (Leung et al. 1996; So et al. 2008). All the calculations and interpretations below explicitly assume that the data are representative of the population of adolescents, which is the focus of the driving motivation questions. If this assumption is invalid, the statistical inference may be misguided. When there is a discrepancy between the population we are trying to make inference about and the data available for quantitative analysis, one needs to redesign the experiment starting with the initial data collection to ensure the data represent a random sample from the target population.

Parameter estimation

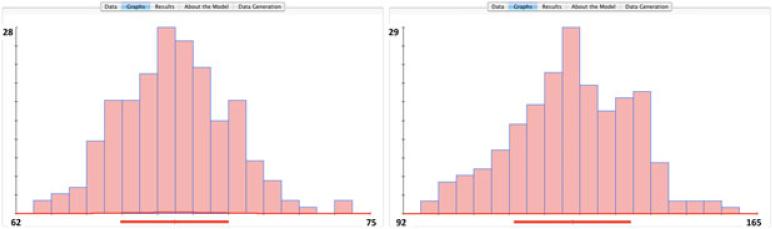
We can start by copy-pasting the data (initial 200 observations, or even the entire 25,000 row dataset) in the SOCR Modeler (http://socr.ucla.edu/htmls/SOCR_Modeler.html). Then, we can estimate the mean and standard deviation of the Height and Weight variables, as well as investigate the distributions of the two variables. By looking at these distributions, we can conclude that Height and Weight roughly follow a Normal distribution, Figure 2. Quantile–Quantile probability plots (Al-Aziz et al. 2010; Dinov and Christou 2011) and Kolmogorov–Smirnoff test (Che et al. 2009) can be employed to obtain additional qualitative and quantitative support for normality of the weight and height measurements in this large sample. The SOCR Modeler generates estimates of the mean height (67.95 in), height standard deviation (1.94 in), mean weight (127.22 lb) and the standard deviation of weight (11.96 lb), Figure 3. The results also indicate the strength of the statistical evidence to reject a null hypothesis that the sample distribution may be modeled by Normal distribution (with the estimated mean and standard deviation).

Fig. 2.

Distributions of adolescents’ height (inches), left, and weight (pounds), right.

Fig. 3.

Estimation of the mean and standard deviation for adolescents’ height (left) and weight (right), and the corresponding Kolmogorov–Smirnoff test quantitatively indicating the good fit between the data and the corresponding Normal distribution models.

To estimate the correlation between height and weight, we use the SOCR linear regression applet (http://www.socr.ucla.edu/htmls/ana/Simple Regression_Analysis.html). Mapping height as dependent and weight as independent variables, and clicking ‘Calculate’ computes a linear model including the correlation between height and weight $(\widehat{\rho }=0.557)$, Figure 4.

Fig. 4.

Using Statistics Online Computational Resource (SOCR) linear regression applet to compute the correlation ρ = Corr(C2 = height, C3 = weight).

So far, we have X = height, Y = weight variables with the following distributions: $X\sim N({\widehat{\mu }}_X=67.95,{\widehat{\sigma }}_X^2={1.94}^2)$, $Y\sim N({\widehat{\mu }}_Y=127.22,{\widehat{\sigma }}_Y^2={11.96}^2)$ and $\widehat{\rho }=\mathrm{Corr}(X,Y)=0.557$. Now, plugging these five estimated quantities (the hat notation ‘^’ indicates data-driven parameter estimates) into the SOCR Bivariate Normal webapp (http://socr.ucla.edu/ htmls/HTML5/BivariateNormal/) allows us to explore the marginal, joint and conditional probabilities.

Marginal probabilities

When looking at marginal distributions, we disregard the variable(s) we do not care about. For the bivariate normal case, the marginal distribution of a single variable is the (univariate) distribution of the variable itself.

Disregarding weight, what is the probability that a randomly selected adolescent will be between 65 and 70 inches tall? Look at the marginal distribution of height. The probability that the height of (a randomly selected) adolescent will be between 65 and 70 in is P(65 ≤ X ≤ 70) = 0.799, Figure 5.

Fig. 5.

Supports for the marginal distributions of X = height, left, and Y = weight, right.

The histogram for weight spanned an interval of 92–165 lb, Figure 2, and the marginal (model) distribution of weight is supported on the interval [79, 175] pounds. This interval is larger because the (sample) histogram of weight is not perfectly symmetric. The Normal distribution model does a good job of capturing the overall shape of weight (see above). The histogram of height spans an interval from 62 to 75 in, Figure 2, and the support of the (model) marginal distribution of height in the webapp is [60, 75] inches. Indirectly, this agreement is largely because the distribution of human heights is known to be symmetric, bell-shaped and unimodal (Gudbjartsson et al. 2008; Weedon et al. 2008) and can be approximated well by a Normal distribution. Specifying desired X and Y limits in the Controls panel allows for the calculations of concrete marginal probabilities.

Joint probability

What is the probability of a randomly selected adolescent being between 65 and 70 inches tall and weighing between 120 and 140 pounds? To answer this question, change the Bivariate Normal limits to 120 < X < 140 and 65 < Y < 70. Figure 6 shows the graphical illustration of this joint probability and the corresponding quantitative results.

Fig. 6.

Joint probability calculations: P(65 < X < 70∩ 120 < Y < 140) = 0.4894.

Conditional probability

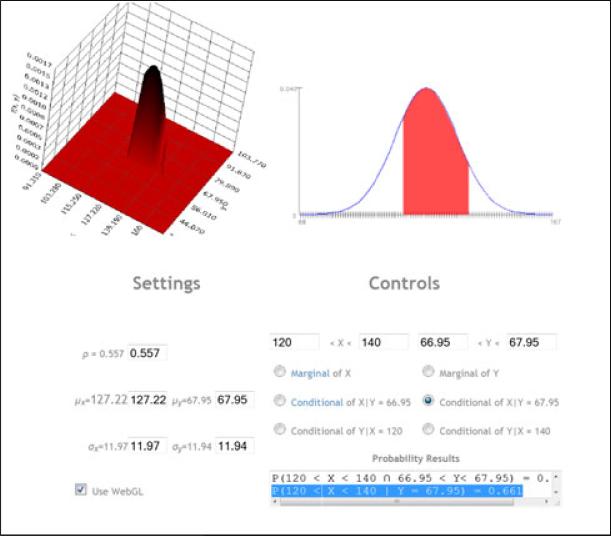
The answer to one of the original questions, P(120 ≤ Y ≤ 140|X = 67.95), Given that an adolescent is of average height, what is the probability the adolescent weighs between 120 and 140 pounds?, requires the conditional distribution of weight given a known height. First, we need to change the Bivariate Limits so height only includes the specified average height: 67.95. Then we can compute the conditional probability that an adolescent weighs between 120 and 140 lb, given they are of average height, P(120 ≤ Y ≤ 140|X = 67.95) = 0.661, Figure 7. Note that the last conditional distribution is univariate (in Y). Thus, to generate the three-dimensional plot on the top-left of Figure 7, we extended the conditional range of X to 66.95 < X < 67.95.

Fig. 7.

Conditional probability calculations: P(120 ≤ Y ≤ 140|X = 67.95) = 0.661.

DISCUSSION

Curricular integration of technology, observational and research-derived data, and interactive simulations has potential to improve K-16 science education and enhance the learning experiences of students at different levels (Jordan and Haines 2006; Franklin et al. 2007; Holbrook and Rannikmae 2007; Shelley et al. 2009). The availability of interesting motivational datasets, access to appropriate web-based tools for data manipulations and limited technical instructional skills are among the factors inhibiting the adoption of technology and integration of real datasets in the modern science education curricula (Dinov and Christou 2011).

This article presents a modern IT-blended interactive teaching approach for multivariate distributions, marginal, joint and conditional probabilities. We developed a pair of a learning activity and a dynamic webapp for the special case of bivariate Normal distribution, which demonstrate applied and theoretical multivariate concepts. Instructors may augment the applications presented here by using other continuous or discrete multivariate data (e.g. http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data). For instance, one can discuss the need for variable transformations, data distribution parametric assumptions and joint or conditional probabilities in the case of exploring monetary inflation and housing prices (using a 50-year SOCR Inflation vs. Housing Price Index dataset, http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_ MonetaryBaseStocksInterest1959_2009). Open-source and community-based development, validation and support for computational resources, instructional materials and interactive learning activities are critical for training the next generation of skilled, productive and imaginative citizens.

APPENDIX

In this appendix, we include some of the more theoretical considerations for defining, computing and applying marginal, conditional and bivariate normal probability calculations. Random observations of continuous (e.g. time, longitude and latitude for a vehicle or a plane) or discrete processes (e.g. number of customers arriving at a store within a fixed timeframe, weight in kilograms and height in centimeters, as whole numbers, for a human subject, outcomes of a real or virtual bivariate die and coin of experiment) are commonly represented as stochastic measurements or variables. In a typical bivariate situation, the answer to an a priori scientific question may require computing the joint probability density function for the process, f_X,Y(x,y). Let A ⊆ Ω_X and B ⊆ Ω_Y represent (non-trivial) subsets (e.g. intervals) of the ranges of the variables X and Y, Ω_X and Ω_Y, respectively. Assuming the joint density is known, the general form of the conditional probability of X given Y, i.e. X|Y, (for continuous variables) is given by

$$P(X\in A\mid Y\in B)=\frac{{\int }_{y\in B}{\int }_{x\in A}{f}_{X,Y}(x,y)dxdy}{{\int }_{y\in B}{\int }_{x\in {\Omega }_X}{f}_{X,Y}(x,y)dxdy}$$

The expression in the discrete variable case is similar with summation replacing the integration operators. In the special case where B = {y₀}, representing a single value, the conditional probability satisfies this equation $P(X\in A\mid Y=y_o){\int }_{x\in {\Omega }_x}{f}_{X,Y}(x,y_o)dx={\int }_{x\in A}{f}_{X,Y}(x,y_o)dx$. Clearly, if the set (range) A is trivial, then the conditional probability is zero. A note of caution here is that if A is non-trivial and Y is a continuous variable, a problem arises when we attempt to define the conditional probability, P(X|Y), as the probability P(Y = y_o) = 0, and both sides of the previous equation are trivial; this is the Borel– Kolmogorov paradox illustrating the ambiguity of defining conditional probability (Rao 1988). However, this problem may be circumvented by employing measure-theoretic definition of conditional expectation (Shafer and Vovk 2006; Billingsley 2012). Note that the joint density function could be defined more generally on any well-defined region in two-dimensional, not necessarily a Cartesian product of the marginal ranges, as we defined it earlier. The complexity of specifying the boundary (and the inside) of the support/domain of the bivariate density (using general Lebesgue integrals (Kiefer and Schwartz 1965; Stein 1981)) abstracts the notation and obfuscates the direct correspondence between the theoretical formulation and the computational application of the probability distribution and inference.

These are generic descriptions of the bivariate joint and conditional probabilities. Now, suppose that X has specifically Normal distribution, the conditional mean of X given Y = y_o, E(X|Y = y_o), is linear in Y, and the conditional variance of X given Y = y_o, Var(X|Y = y_o), is constant. Under these three predicaments, the conditional probability distribution of X given Y = y_o, f_X|Y=yo(X, Y) = fX|Y_o(X, Y), is given by $f_{X\mid y_o}\sim N({\mu }_{X\mid y_o}={\mu }_X+\rho \frac{{\sigma }_X}{{\sigma }_Y}(y_o-{\mu }_Y);{\sigma }_{X\mid y_o}^2={\sigma }_X^2(1-{\rho }^2))$, (Gut 2009; Franke et al. 2011) where $X\sim N({\mu }_X;{\sigma }_X^2)$ ; the expectation and variance of Y are E(Y) = μ_Y and $\mathrm{Var}\left(Y\right)=\mathsf{E}\left(Y^2\right)-{\mu }_Y^2={\sigma }_Y^2$; and the bivariate correlation $\rho =\mathrm{Corr}(X,Y)=\frac{\mathsf{E}\left((X-{\mu }_X)(Y-{\mu }_Y\right)}{{\sigma }_X{\sigma }_Y}$. Note that Y is not necessarily required itself to be normally distributed. However, if Y is also normally distributed, $Y\sim N({\mu }_Y;{\sigma }_Y^2)$; we can explicitly compute the conditional and joint probabilities using the (marginal) density of Y, $f_Y\left(y\right)=\frac{1}{{\sigma }_Y\sqrt{2}\pi }{e}^{-\frac{{(y-{\mu }_Y)}^2}{2{\sigma }_Y^2}}$. If we denote the conditional distribution of X given Y = y_o by

$$\begin{array}{cc}\hfill g_{X\mid Y}(x\mid y_0)& =\frac{1}{{\sigma }_{X\mid Y}\sqrt{2\pi }}{e}^{-\frac{{(x-{\mu }_{X\mid Y})}^2}{2{\sigma }_{X\mid Y}^2}}\hfill \\ \hfill & =\frac{1}{{\sigma }_X\sqrt{1-{\rho }^2}\sqrt{2\pi }}{e}^{-\frac{{(x-{\mu }_X-\rho \frac{{\sigma }_X}{{\sigma }_Y}(y_o-{\nu }_Y))}^2}{2{\sigma }_X^2(1-{\rho }^2)}}\hfill \end{array}$$

Then, the joint probability density function of X and Y is Bivariate Normal and has the following closed form expression:

$$f_{X,Y}(x,y)=g_{X\mid Y}(x\mid y)f_Y\left(y\right)=\frac{1}{2\pi {\sigma }_X{\sigma }_Y\sqrt{1-{\rho }^2}}{e}^{-q(x,y)}$$

where

$$q(x,y)=\frac{1}{2}\left(\frac{1}{1-{\rho }^2}\right)\left({\left(\frac{x-{\mu }_X}{{\sigma }_X}\right)}^2-2\rho \left(\frac{x-{\mu }_X}{{\sigma }_X}\right)\left(\frac{y-{\mu }_Y}{{\sigma }_Y}\right)+{\left(\frac{y-{\mu }_Y}{{\sigma }_Y}\right)}^2\right)$$

The case of multivariate (three-dimensional or higher) joint, marginal and conditional probability distributions may be worked out similarly; however, the complexity added by using more than two variables may impact the a priori assumptions and make the calculations more intricate.