LSRN: A PARALLEL ITERATIVE SOLVER FOR STRONGLY OVER- OR UNDERDETERMINED SYSTEMS

Abstract

We describe a parallel iterative least squares solver named LSRN that is based on random normal projection. LSRN computes the min-length solution to min_x∈ℝⁿ ‖Ax − b‖₂, where A ∈ ℝ^{m × n} with m ≫ n or m ≪ n, and where A may be rank-deficient. Tikhonov regularization may also be included. Since A is involved only in matrix-matrix and matrix-vector multiplications, it can be a dense or sparse matrix or a linear operator, and LSRN automatically speeds up when A is sparse or a fast linear operator. The preconditioning phase consists of a random normal projection, which is embarrassingly parallel, and a singular value decomposition of size ⌈γ min(m, n)⌉ × min(m, n), where γ is moderately larger than 1, e.g., γ = 2. We prove that the preconditioned system is well-conditioned, with a strong concentration result on the extreme singular values, and hence that the number of iterations is fully predictable when we apply LSQR or the Chebyshev semi-iterative method. As we demonstrate, the Chebyshev method is particularly efficient for solving large problems on clusters with high communication cost. Numerical results show that on a shared-memory machine, LSRN is very competitive with LAPACK’s DGELSD and a fast randomized least squares solver called Blendenpik on large dense problems, and it outperforms the least squares solver from SuiteSparseQR on sparse problems without sparsity patterns that can be exploited to reduce fill-in. Further experiments show that LSRN scales well on an Amazon Elastic Compute Cloud cluster.

1. Introduction

Randomized algorithms have become indispensable in many areas of computer science, with applications ranging from complexity theory to combinatorial optimization, cryptography, and machine learning. Randomization has also been used in numerical linear algebra (for instance, the initial vector in the power iteration is chosen at random so that almost surely it has a nonzero component along the direction of the dominant eigenvector), yet most well-developed matrix algorithms, e.g., matrix factorizations and linear solvers, are deterministic. In recent years, however, motivated by large data problems, very nontrivial randomized algorithms for very large matrix problems have drawn considerable attention from researchers, originally in theoretical computer science and subsequently in numerical linear algebra and scientific computing. By randomized algorithms, we refer, in particular, to random sampling and random projection algorithms [8, 23, 9, 22, 2]. For a comprehensive overview of these developments, see the review of Mahoney [18], and for an excellent overview of numerical aspects of coupling randomization with classical low-rank matrix factorization methods, see the review of Halko, Martinsson, and Tropp [14].

We are interested in high-precision solving of linear least squares (LS) problems that are strongly over- or underdetermined and possibly rank-deficient. In particular, given a matrix A ∈ ℝ^{m × n} and a vector b ∈ ℝ^m, where m ≫ n or m ≪ n and we do not assume that A has full rank, we wish to develop randomized algorithms to accurately solve the problem

$${\text{minimize}}_{x\in {ℝ}^n}{\Vert Ax-b\Vert }_2.$$ (1.1)

If we let r = rank(A) ≤ min(m, n), then recall that if r < n (the LS problem is underdetermined or rank-deficient), then (1.1) has an infinite number of minimizers. In that case, the set of all minimizers is convex and hence has a unique element having minimum length. On the other hand, if r = n so that the problem has full rank, there exists only one minimizer to (1.1), and hence it must have the minimum length. In either case, we denote this unique min-length solution to (1.1) by x*, and we are interested in computing x* in this work. That is,

$$x^{*}=\text{arg min}{\Vert x\Vert }_2\text{subject to}x\in \text{arg}\underset{z}{\text{min}}{\Vert Az-b\Vert }_2.$$ (1.2)

LS problems of this form have a long history, traced back to Gauss, and they arise in numerous applications. The demand for faster LS solvers will continue to grow in light of new data applications and as problem scales become larger and larger.

In this paper, we describe an LS solver called LSRN for these strongly over- or underdetermined, and possibly rank-deficient, systems. LSRN uses random normal projections to compute a preconditioner matrix such that the preconditioned system is provably extremely well-conditioned. Importantly for large-scale applications, the preconditioning process is embarrassingly parallel, and it automatically speeds up with sparse matrices and fast linear operators. LSQR [21] or the Chebyshev semi-iterative (CS) method [12] can be used at the iterative step to compute the min-length solution within just a few iterations. We show that the latter method is preferred on clusters with high communication cost.

Because of its provably good conditioning properties, LSRN has a fully predictable run-time performance, just like direct solvers, and it scales well in parallel environments. On large dense systems, LSRN is competitive with LAPACK’s DGELSD for strongly overdetermined problems, and it is much faster for strongly underdetermined problems, although solvers using fast random projections, like Blendenpik [2], are still slightly faster in both cases. On sparse systems without sparsity patterns that can be exploited to reduce fill-in (such as matrices with random structure), LSRN runs significantly faster than competing solvers, for both the strongly over- or underdetermined cases.

In section 2 we describe existing deterministic LS solvers and recent randomized algorithms for the LS problem. In section 3 we show how to do preconditioning correctly for rank-deficient LS problems, and in section 4 we introduce LSRN and discuss its properties. Section 5 describes how LSRN can handle Tikhonov regularization for both over- and underdetermined systems, and in section 6 we provide a detailed empirical evaluation illustrating the behavior of LSRN.

2. Least squares solvers

In this section we discuss related approaches, including deterministic direct and iterative methods as well as recently developed randomized methods, for computing solutions to LS problems, and we discuss how our results fit into this broader context.

2.1. Deterministic methods

It is well known that x* in (1.2) can be computed using the singular value decomposition (SVD) of A. Let A = UΣV^T be the compact SVD, where U ∈ ℝ^{m × r}, Σ ∈ ℝ^{r × r}, and V ∈ ℝ^{n × r}, i.e., only singular vectors corresponding to the nonzero singular values are calculated. We have x* = V Σ⁻¹U^Tb. The matrix V Σ⁻¹U^T is the Moore–Penrose pseudoinverse of A, denoted by A^†, which is defined and unique for any matrix. Hence we can simply write x* = A^†b. The SVD approach is accurate and robust to rank-deficiency.

Another way to solve (1.2) is using a complete orthogonal factorization of A. If we can find orthonormal matrices Q ∈ ℝ^{m × r} and Z ∈ ℝ^{n × r}, and a matrix T ∈ ℝ^{r × r}, such that A = QTZ^T, then the min-length solution is given by x* = ZT⁻¹Q^Tb. We can treat SVD as a special case of complete orthogonal factorization. In practice, complete orthogonal factorization is usually computed via rank-revealing QR factorizations, making T a triangular matrix. The QR approach is less expensive than SVD, but it is slightly less robust at determining the rank of A.

A third way to solve (1.2) is by computing the min-length solution to the normal equation A^TAx = A^Tb, namely

$$x^{*}={(A^{T}A)}^{†}{A}^{T}b=A^T{(A{A}^T)}^{†}b.$$ (2.1)

It is easy to verify the correctness of (2.1) by replacing A by its compact SVD UΣV^T. If r = min(m, n), a Cholesky factorization of either A^TA (if m ≥ n) or AA^T (if m ≤ n) solves (2.1) nicely. If r < min(m, n), we need the eigensystem of A^TA or AA^T to compute x*. The normal equation approach is the least expensive of the three direct approaches, but it is also the least accurate, especially on ill-conditioned problems. See Chapter 5 of Golub and Van Loan [11] for a detailed analysis.

Instead of these direct methods, we can use iterative methods to solve (1.1). If all the iterates {x^(k)} are in range(A^T) and if {x^(k)} converges to a minimizer, it must be the minimizer having minimum length, i.e., the solution to (1.2). This is the case when we use a Krylov subspace method starting with a zero vector. For example, the conjugate gradient (CG) method on the normal equation leads to the min-length solution (see Paige and Saunders [20]). In practice, CGLS [16] or LSQR [21] are preferable because they are equivalent to applying CG to the normal equation in exact arithmetic but they are numerically more stable. Other Krylov subspace methods such as the CS method [12] and LSMR [10] can solve (1.1) as well.

Importantly, however, it is in general hard to predict the number of iterations for CG-like methods. The convergence rate is affected by the condition number of A^TA. A classical result [17, p. 187] states that

$$\frac{{\Vert x^{(k)}-x^{*}\Vert }_{A^{T}A}}{{\Vert x^{(0)}-x^{*}\Vert }_{A^{T}A}}\le 2{\left(\frac{\sqrt{\kappa (A^{T}A)}-1}{\sqrt{\kappa (A^{T}A)}+1}\right)}^k,$$ (2.2)

where ‖z‖_A^TA = z^TA^TAz = ‖Az‖² for any z ∈ ℝⁿ, and where κ(A^TA) is the condition number of A^TA under the 2-norm. Estimating κ(A^TA) is generally as hard as solving the LS problem itself, and in practice the bound does not hold in any case unless reorthogonalization is used. Thus, the computational cost of CG-like methods remains unpredictable in general, except when A^TA is very well-conditioned and the condition number can be well estimated.

2.2. Randomized methods

In 2007, Drineas et al. [9] introduced two randomized algorithms for the LS problem, each of which computes an approximate solution x̂ in 𝒪(mn log(n/ε) + n³/ε) time such that ‖Ax̂ − b‖₂ ≤ (1 + ε)‖Ax* − b‖₂ given ε > 0. Both of these algorithms apply a randomized Hadamard transform to the columns of A thereby generating a problem of smaller size, one using uniformly random sampling and the other using a sparse random projection. They proved that, in both cases, the solution to the smaller problem leads to relative-error approximations of the original problem. The algorithms are suitable when low accuracy is acceptable, but the ε dependence quickly becomes the bottleneck otherwise. Using those algorithms as preconditioners was also mentioned in [9]. This work laid the ground for later algorithms and implementations.

Later, in 2008, Rokhlin and Tygert [22] described a related randomized algorithm for overdetermined systems. They used a randomized transform named SRFT that consists of m random Givens rotations, a random diagonal scaling, a discrete Fourier transform, and a random sampling of rows. They considered using their method as a preconditioning method for CG-like methods. They proved that if the sample size is greater than 4n², the condition number of the preconditioned system is bounded above by a constant, with high probability. This leads to a total running time of 𝒪((log n + log(1/ε))mn + n⁴). However, sampling this many rows in practice would adversely affect the running time of their solver. They illustrated examples for which sampling 4n rows sufficed, which reduces the running time to 𝒪((log n + log(1/ε))mn + n³), but they did not provide a rigorous proof.

Then, in 2010, Avron, Maymounkov, and Toledo [2] implemented a high-precision LS solver, called Blendenpik, and compared it to LAPACK’s DGELS and to LSQR without preconditioning. Blendenpik uses a Walsh–Hadamard transform, a discrete cosine transform, or a discrete Hartley transform for blending the rows/columns, followed by a random sampling, to generate a problem of smaller size. The R factor from the QR factorization of the smaller matrix is used as the preconditioner for LSQR. Based on their analysis, the condition number of the preconditioned system depends on the coherence or statistical leverage scores of A, i.e., the maximal row norm of U, where U is an orthonormal basis of range(A). We note that a solver for underdetermined problems is also included in the Blendenpik package.

In 2011, Coakley, Rokhlin, and Tygert [3] described an algorithm that is also based on random normal projections. It computes the orthogonal projection of any vector b onto the null space of A or onto the row space of A via a preconditioned normal equation. The algorithm solves the overdetermined LS problem as an intermediate step. They show that the normal equation is well-conditioned and hence the solution is reliable. Unfortunately, no implementation was provided. For an overdetermined problem of size m × n, the algorithm requires applying A or A^T 3n + 6 times, while LSRN needs approximately 2n + 200 matrix-vector multiplications under the default setting. Asymptotically, LSRN will become faster as n increases beyond several hundred. See section 4.4 for further complexity analysis of LSRN. Moreover, if this algorithm is applied to (though not originally designed for) approximately rank-deficient problems, it becomes less reliable than LSRN in determining the effective rank. See sections 4.3 and 6.4 for theoretical analysis and empirical evaluation, respectively.

2.3. Relationship with our contributions

All the approaches mentioned in section 2.2 assume that A has full rank, and for those based on iterative solvers, none provides a small constant upper bound on the condition number of the preconditioned system with 𝒪(n) sample size that is independent of the coherence. For LSRN, Theorem 3.2 ensures that the min-length solution is preserved, independent of the rank, and Theorems 4.4 and 4.5 provide bounds on the condition number and number of iterations, independent of the spectrum and the coherence of A. In addition to handling rank-deficiency well, LSRN can even take advantage of it, resulting in a smaller condition number and fewer iterations.

Some prior work on the LS problem has explored “fast” randomized transforms that run in roughly 𝒪(mn log m) time on a dense matrix A, while the random normal projection we use in LSRN takes 𝒪(mn²) time. Although this could be an issue for some applications, the use of random normal projections comes with several advantages. First, if A is a sparse matrix or a linear operator, which is common in large-scale applications, then the FFT-based fast transforms are no longer “fast.” Second, the random normal projection is easy to implement using threads or MPI, and it scales well in parallel environments. Third, the strong symmetry of the standard normal distribution helps give the strong high probability bounds on the condition number in terms of sample size. These bounds depend on nothing but s/r, where s is the sample size. For example, if s = 4r, Theorem 4.4 ensures that, with high probability, the condition number of the preconditioned system is less than 3.

This last property about the condition number of the preconditioned system makes the number of iterations and thus the running time of LSRN fully predictable, as for a direct method. It also enables use of the CS method, which needs only one level-1 and two level-2 BLAS operations per iteration, and is particularly suitable for clusters with high communication cost because it does not have vector inner products that require synchronization between nodes. Although the CS method has the same theoretical upper bound on the convergence rate as CG-like methods, it requires accurate bounds on the singular values in order to work efficiently. Such bounds are generally hard to come by, limiting the popularity of the CS method in practice, but they are provided for the preconditioned system by our Theorem 4.4, and we do achieve high efficiency in our experiments.

3. Preconditioning for linear least squares

In light of (2.2), much effort has been made to transform a linear system into an equivalent system with reduced condition number. This preconditioning, for a square linear system Bx = d of full rank, usually takes one of the following forms:

$$\begin{array}{cc}\hfill \text{left preconditioning}& M^{T}Bx=M^{T}d,\hfill \\ \hfill \text{right preconditioning}& BNy=d,x=Ny,\hfill \\ \hfill \text{left and right preconditioning}& M^{T}BNy=M^{T}d,x=Ny.\hfill \end{array}$$

Clearly, the preconditioned system is consistent with the original system, i.e., has the same x* as the unique solution, if the preconditioners M and N are nonsingular.

For the general LS problem (1.2), more care should be taken so that the preconditioned system will have the same min-length solution as the original. For example, if we apply left preconditioning to the LS problem min_x ‖Ax − b‖₂, the preconditioned system becomes min_x ‖M^TAx − M^Tb‖₂, and its min-length solution is given by

$$x_{\text{left}}^{*}={(M^{T}A)}^{†}{M}^{T}b.$$

Similarly, the min-length solution to the right preconditioned system is given by

$$x_{\text{right}}^{*}=N{(AN)}^{†}b.$$

The following lemma states the necessary and sufficient conditions for A^† = N(AN)^† or A^† = (M^TA)^†M^T to hold. Note that these conditions holding certainly implies that $x_{\text{right}}^{*}=x^{*}$ and $x_{\text{left}}^{*}=x^{*}$, respectively.

Lemma 3.1. Given A ∈ ℝ^{m × n}, N ∈ ℝ^{n × p}, and M ∈ ℝ^{m × q}, we have

1. A^† = N(AN)^† if and only if range(NN^TA^T) = range(A^T).

2. A^† = (M^TA)^† M^T if and only if range(MM^TA) = range(A).

Proof. Let r = rank(A) and UΣV^T be A’s compact SVD as in section 2.1, with A^† = V Σ⁻¹U^T. Before continuing our proof, we reference the following facts about the pseudoinverse:

1. B^† = B^T(BB^T)^† for any matrix B.

2. For any matrices B and C such that BC is defined, (BC)^† = C^†B^† if (i) B^TB = I or (ii) CC^T = I or (iii) B has full column rank and C has full row rank.

Let us now prove the “if” part of the first statement. If range(NN^TA^T) = range(A^T) = range(V), we can find a matrix Z with full row rank such that NN^TA^T = V Z. Then,

$$N{(AN)}^{†}=N{(AN)}^T{(AN{(AN)}^T)}^{†}=N{N}^T{A}^T{(AN{N}^T{A}^T)}^{†}=VZ{(U\mathrm{\Sigma }{V}^{T}VZ)}^{†}=VZ{(U\mathrm{\Sigma }Z)}^{†}=VZ{Z}^{†}{\mathrm{\Sigma }}^{-1}{U}^T=V{\mathrm{\Sigma }}^{-1}{U}^T=A^{†}.$$

Conversely, if N(AN)^† = A^†, we know that range(N(AN)^†) = range(A^†) = range(V) and hence range(V) ⊆ range(N). Then we can decompose N as ${(V{V}_c)}_{(\begin{array}{c}\hfill Z\hfill \\ \hfill Zc\hfill \end{array})}=VZ+V_c{Z}_c$, where V_c is orthonormal, V^TV_c = 0, and $(\begin{array}{c}\hfill Z\hfill \\ \hfill Zc\hfill \end{array})$ has full row rank. Then,

$$0=N{(AN)}^{†}-A^{†}=(VZ+V_c{Z}_c){(U\mathrm{\Sigma }{V}^T(VZ+V_c{Z}_c))}^{†}-V{\mathrm{\Sigma }}^{-1}{U}^T=(VZ+V_c{Z}_c){(U\mathrm{\Sigma }Z)}^{†}-V{\mathrm{\Sigma }}^{-1}{U}^T=(VZ+V_c{Z}_c)Z^{†}{\mathrm{\Sigma }}^{-1}{U}^T-V{\mathrm{\Sigma }}^{-1}{U}^T=V_c{Z}_c{Z}^{†}{\mathrm{\Sigma }}^{-1}{U}^T.$$

Multiplying by $V_c^T$ on the left and UΣ on the right, we get Z_cZ^† = 0, which is equivalent to Z_cZ^T = 0. Therefore,

$$\text{range}(N{N}^T{A}^T)=\text{range}((VZ+V_c{Z}_c){(VZ+V_c{Z}_c)}^{T}V\mathrm{\Sigma }{U}^T)=\text{range}((VZ{Z}^T{V}^T+V_c{Z}_c{Z}_c^T{V}_c^T)V\mathrm{\Sigma }{U}^T)=\text{range}(VZ{Z}^T\mathrm{\Sigma }{U}^T)=\text{range}(V)=\text{range}(A^T),$$

where we used the facts that Z has full row rank and hence ZZ^T is nonsingular, Σ is nonsingular, and U has full column rank.

To prove the second statement, let us take B = A^T. By the first statement, we know B^† = M(BM)^† if and only if range(MM^TB^T) = range(B^T), which is equivalent to saying A^† = (M^TA)^†M^T if and only if range(MM^TA) = range(A).

Although Lemma 3.1 gives the necessary and sufficient condition, it does not serve as a practical guide for preconditioning LS problems. In this work, we are more interested in a sufficient condition that can help us build preconditioners. To that end, we provide the following theorem.

Theorem 3.2. Given A ∈ ℝ^{m × n}, b ∈ ℝ^m, N ∈ ℝ^{n × p}, and M ∈ ℝ^{m × q}, let x* be the min-length solution to the LS problem min_x ‖Ax − b‖₂, $x_{\mathit{\text{right}}}^{*}=N{y}^{*}$, where y* is the min-length solution to min_y ‖ANy − b‖₂, and let $x_{\mathit{\text{left}}}^{*}$ be the min-length solution to min_x ‖M^TAx − M^Tb‖₂. Then,

• $x_{\mathit{\text{right}}}^{*}=x^{*}$ if range(N) = range(A^T),

• $x_{\mathit{\text{left}}}^{*}=x^{*}$ if range(M) = range(A).

Proof. Let r = rank(A), and let UΣV^T be A’s compact SVD. If range(N) = range(A^T) = range(V), we can write N as V Z, where Z has full row rank. Therefore,

$$\text{range}(N{N}^T{A}^T)=\text{range}(VZ{Z}^T{V}^{T}V\mathrm{\Sigma }{U}^T)=\text{range}(VZ{Z}^T\mathrm{\Sigma }{U}^T)=\text{range}(V)=\text{range}(A^T).$$

By Lemma 3.1, A^† = N(AN)^† and hence $x_{\text{left}}^{*}=x^{*}$. The second statement can be proved by similar arguments.

4. Algorithm LSRN

In this section we present LSRN, an iterative solver for solving strongly over- or underdetermined systems based on “random normal projection.” To construct a preconditioner we apply a transformation matrix whose entries are independent random variables drawn from the standard normal distribution. We prove that the preconditioned system is almost surely consistent with the original system, i.e., both have the same min-length solution. At least as importantly, we prove that the spectrum of the preconditioned system is independent of the spectrum of the original system, and we provide a strong concentration result on the extreme singular values of the preconditioned system. This concentration result enables us to predict the number of iterations for CG-like methods, and it also enables the use of the CS method, which requires an accurate bound on the singular values to work efficiently. We also present an error analysis for approximately rank-deficient problems.

4.1. The algorithm

Algorithm 1 shows the detailed procedure of LSRN to compute the min-length solution to a strongly overdetermined problem, and Algorithm 2 shows the detailed procedure for a strongly underdetermined problem. We refer to these two algorithms together as LSRN. Note that they only use the input matrix A for matrix-vector and matrix-matrix multiplications, and thus A can be a dense matrix, a sparse matrix, or a linear operator. In the remainder of this section we focus on analysis of the overdetermined case. We emphasize that analysis of the underdetermined case is quite analogous.

Algorithm 1.

LSRN (computes x̂ ≈ A^†b when m ≫ n).

Choose an oversampling factor γ > 1 and set s = ⌈γn⌉. Generate G = randn(s, m), i.e., an s-by-m random matrix whose entries are independent random variables following the standard normal distribution. Compute à = GA. Compute Ã’s compact SVD ŨΣ̃ṼT, where r = rank(Ã), Ũ ∈ ℝs × r, Σ̃ ∈ ℝr × r, Ṽ ∈ ℝn × r, and only Σ̃ and Ṽ are needed. Let N = ṼΣ̃−1. Compute the min-length solution to miny ‖ANy − b‖2 using an iterative method. Denote the solution by ŷ. Return x̂ = Nŷ.

Algorithm 2.

LSRN (computes x̂ ≈ A^†b when m ≪ n).

Choose an oversampling γ > 1 and set s = ⌈γm⌉. Generate G = randn(n, s), i.e., an n-by-s random matrix whose entries are independent random variables following the standard normal distribution. Compute à = AG. Compute Ã’s compact SVD ŨΣ̃ṼT, where r = rank(Ã), Ũ ∈ ℝn × r, Σ̃ ∈ ℝr × r, Ṽ ∈ ℝs × r, and only Ũ and Σ̃ are needed. Let M = ŨΣ̃−1. Compute the min-length solution to minx ‖MTAx − MTb‖2 using an iterative method, denoted by x̂. Return x̂.

4.2. Theoretical properties

The use of random normal projection offers LSRN some nice theoretical properties. We start with consistency.

Theorem 4.1. In Algorithm 1, we have x̂ = A^†b almost surely.

Proof. Let r = rank(A) and UΣV^T be A’s compact SVD. We have

$$\text{range}(N)=\text{range}(Ṽ{\mathrm{\Sigma ̃}}^{-1})=\text{range}(Ṽ)=\text{range}({Ã}^T)=\text{range}(A^T{G}^T)=\text{range}(V\mathrm{\Sigma }{(GU)}^T).$$

Define G₁ = GU ∈ ℝ^{s × r}. Since G’s entries are independent random variables following the standard normal distribution and U is orthonormal, G₁’s entries are also independent random variables following the standard normal distribution. Then given s ≥ γn > n ≥ r, we know G₁ has full column rank r with probability 1. Therefore,

$$\text{range}(N)=\text{range}(V\mathrm{\Sigma }{G}_1^T)=\text{range}(V)=\text{range}(A^T),$$

and hence by Theorem 3.2 we have x̂ = A^†b almost surely.

A more interesting property of LSRN is that the spectrum (the set of singular values) of the preconditioned system is solely associated with a random matrix of size s × r, independent of the spectrum of the original system.

Lemma 4.2. In Algorithm 1, the spectrum of AN is the same as the spectrum of $G_1^{†}={(GU)}^{†}$, independent of A’s spectrum.

Proof. Continue to use the notation from the proof of Theorem 4.1. Let $G_1=U_1{\mathrm{\Sigma }}_1{V}_1^T$ be G₁’s compact SVD, where U₁ ∈ ℝ^{s × r}, Σ₁ ∈ ℝ^{r × r}, and V₁ ∈ ℝ^{r × r}. Since range(Ũ) = range(GA) = range(GU) = range(U₁) and both Ũ and U₁ are orthonormal matrices, there exists an orthonormal matrix Q₁ ∈ ℝ^{r × r} such that U₁ = ŨQ₁. As a result,

$$Ũ\mathrm{\Sigma ̃}{Ṽ}^T=Ã=GU\mathrm{\Sigma }{V}^T=U_1{\mathrm{\Sigma }}_1{V}_1^T\mathrm{\Sigma }{V}^T=ŨQ_1{\mathrm{\Sigma }}_1{V}_1^T\mathrm{\Sigma }{V}^T.$$

Multiplying by Ũ^T on the left-hand side of each, we get $\mathrm{\Sigma ̃}{Ṽ}^T=Q_1{\mathrm{\Sigma }}_1{V}_1^T\mathrm{\Sigma }{V}^T$. Taking the pseudoinverse gives $N=Ṽ{\mathrm{\Sigma ̃}}^{-1}=V{\mathrm{\Sigma }}^{-1}{V}_{1}V{\mathrm{\Sigma }}_1^{-1}{Q}_1^T$. Thus,

$$AN=U\mathrm{\Sigma }{V}^{T}V{\mathrm{\Sigma }}^{-1}{V}_1{\mathrm{\Sigma }}_1^{-1}{Q}_1^T=U{V}_1{\mathrm{\Sigma }}_1^{-1}{Q}_1^T,$$

which gives AN’s SVD. Therefore, AN’s singular values are $\text{diag}({\mathrm{\Sigma }}_1^{-1})$, the same as $G_1^{†}’s$ spectrum, but independent of A’s.

We know that G₁ = GU is a random matrix whose entries are independent random variables following the standard normal distribution. The spectrum of G₁ is a well-studied problem in random matrix theory, and in particular the properties of extreme singular values have been studied. Thus, the following lemma is important for us. We use 𝒫(·) to refer to the probability that a given event occurs.

Lemma 4.3 (see Davidson and Szarek [4]). Consider an s × r random matrix G₁ with s > r, whose entries are independent random variables following the standard normal distribution. Let the singular values be σ₁ ≥ ⋯ ≥ σ_r. Then for any t > 0,

$$\text{max}\{𝒫({\sigma }_1\ge \sqrt{s}+\sqrt{r}+t),𝒫({\sigma }_r\le \sqrt{s}-\sqrt{r}-t)\}<e^{-t^2/2}.$$ (4.1)

With the aid of Lemma 4.3, it is straightforward to obtain the concentration result of σ₁(AN), σ_r(AN), and κ(AN) as follows.

Theorem 4.4. In Algorithm 1, for any $\alpha \in (0,1-\sqrt{r/s})$, we have

$$\text{max}\left\{𝒫\right({\sigma }_1(AN)\ge \frac{1}{(1-\alpha )\sqrt{s}-\sqrt{r}}),𝒫({\sigma }_r(AN)\le \frac{1}{(1+\alpha )\sqrt{s}+\sqrt{r}}\left)\right\}<e^{-{\alpha }^{2}s/2}$$ (4.2)

and

$$𝒫(\kappa (AN)=\frac{{\sigma }_1(AN)}{{\sigma }_r(AN)}\le \frac{1+\alpha +\sqrt{r/s}}{1-\alpha -\sqrt{r/s}})\ge 1-2e^{-{\alpha }^{2}S/2}.$$ (4.3)

Proof. Set $t=\alpha \sqrt{s}$ in Lemma 4.3.

In order to estimate the number of iterations for CG-like methods, we can now combine (2.2) and (4.3).

Theorem 4.5. In exact arithmetic, given a tolerance ε > 0, a CG-like method applied to the preconditioned system min_y ‖ANy − b‖₂ with y⁽⁰⁾ = 0 converges within $(\text{log}\epsilon -\text{log}2)/\text{log}(\alpha +\sqrt{r/s})$ iterations in the sense that

$${\Vert {ŷ}_{CG}-y^{*}\Vert }_{{(AN)}^T(AN)}\le \epsilon {\Vert y^{*}\Vert }_{{(AN)}^T(AN)}$$ (4.4)

holds with probability at least 1 − 2e^−α2s/2 for any $\alpha \in (0,1-\sqrt{r/s})$, where ŷ_CG is the approximate solution returned by the CG-like solver and y* = (AN)^†b. Let x̂_CG = Nŷ_CG be the approximate solution to the original problem. Since x* = Ny*, (4.4) is equivalent to

$${\Vert {\mathrm{x̂}}_{CG}-x^{*}\Vert }_{A^{T}A}\le \epsilon {\Vert x^{*}\Vert }_{A^{T}A},$$ (4.5)

or in terms of residuals,

$${\Vert {\mathrm{r̂}}_{CG}-r^{*}\Vert }_2\le \epsilon {\Vert b-r^{*}\Vert }_2,$$ (4.6)

where r̂_CG = b − Ax̂_CG and r* = b − Ax*. Notice that A^T r* = 0. Equation (4.6) implies

$${\Vert A^T{\mathrm{r̂}}_{CG}\Vert }_2={\Vert A^T{\mathrm{r̂}}_{CG}-A^T{r}^{*}\Vert }_2\le \epsilon {\Vert A\Vert }_2{\Vert b-r^{*}\Vert }_2.$$

If n is large and thus s is large, we can set α very small but still make 1 − 2e^−α2s/2 very close to 1. Moreover, the bounds in (4.3) and (2.2) are not tight. These facts allow us to ignore α in a practical setting when we solve a large-scale problem. For example, to reach precision ε = 10⁻¹⁴, it is safe in practice to set the maximum number of iterations to $(\text{log}\epsilon -\text{log}2)/\text{log}\sqrt{r/s}\approx 66/\text{log}(s/r)$ for a numerically stable CG-like method, e.g., LSQR. We verify this claim in section 6.2.

In addition to allowing us to bound the number of iterations for CG-like methods, the result given by (4.2) also allows us to use the CS method. This method needs only one level-1 and two level-2 BLAS operations per iteration, and, importantly, because it does not have vector inner products that require synchronization between nodes, this method is suitable for clusters with high communication cost. It does need an explicit bound on the singular values, but once that bound is tight, the CS method has the same theoretical upper bound on the convergence rate as other CG-like methods. Unfortunately, in many cases, it is hard to obtain such an accurate bound, which prevents the CS method from becoming popular in practice. In our case, however, (4.2) provides a probabilistic bound with very high confidence. Hence, we can employ the CS method without difficulty. For example, let n = r = 1000 and choose s = 2000 and $\alpha =\sqrt{-2\text{log}(0.01)/s}\approx 0.0679$. By (4.2), we have σ₁(AN) < 0.0994 and σ_r(AN) > 0.0126 with probability at least 0.99. Moreover, because (4.2) is not tight, we may be able to use tighter bounds in practice to get a better convergence rate, while still maintaining a failure rate of 0.01. For completeness, Algorithm 3 describes the CS method we implemented for solving LS problems. For discussion of its variations, see Gutknecht and Rollin [13].

Algorithm 3.

Chebyshev semi-iterative (CS) method (computes x ≈ A^†b).

Given A ∈ ℝm × n, b ∈ ℝm, and a tolerance ε > 0, choose 0 < σL ≤ σU such that all nonzero singular values of A are in [σL, σU] and let $d=({\sigma }_U^2+{\sigma }_L^2)/2$ and $c=({\sigma }_U^2-{\sigma }_L^2)/2$ . Let x = 0, υ = 0, and r = b. for $k=0,1,\dots ,\lceil (\text{log}\epsilon -\text{log}2)/\text{log}\frac{{\sigma }_U-{\sigma }_L}{{\sigma }_U+{\sigma }_L}\rceil$ do $\beta \leftarrow \{\begin{array}{cc}0\hfill & \text{if}k=0,\hfill \\ \frac{1}{2}{(c/d)}^2\hfill & \text{if}k=1,\hfill \\ {(\alpha c/2)}^2\hfill & \text{otherwise},\hfill \end{array}\alpha \leftarrow \{\begin{array}{cc}1/d\hfill & \text{if}k=0,\hfill \\ d-c^2/(2d)\hfill & \text{if}k=1,\hfill \\ 1/(d-\alpha c^2/4)\hfill & \text{otherwise}.\hfill \end{array}$ υ ← βυ + ATr. x ← x + αυ. r ← r − αAυ. end for

4.3. Approximate rank-deficiency

Our theory above assumes exact arithmetic. For rank-deficient problems stored with limited precision, it is common for A to be approximately but not exactly rank-deficient, i.e., to have small but not exactly zero singular values. A common practice for handling approximate rank-deficiency is to set a threshold and treat as zero any singular values smaller than the threshold. (This is called truncated SVD.) In LAPACK, the threshold is the largest singular value of A multiplied by a user-supplied constant, called RCOND. Let A ∈ ℝ^{m × n} with m ≫ n be an approximately rank-k matrix that can be written as A_k + E, where k < n and A_k is the best rank-k approximation to A. For simplicity, we assume that a constant c > 0 is known such that σ₁ ≥ σ_k ≫ cσ₁ ≫ σ_{k + 1} = ‖E‖₂. If we take the truncated SVD approach, c can be used to determine the effective rank of A, and the solution becomes $x^{*}=A_k^{†}b$. In LSRN, we can perform a truncated SVD on à = GA, where the constant c is used to determine the effective rank of Ã, denoted by k̃. The rest of the algorithm remains the same. In this section, we present a sufficient condition for k̃ = k and analyze the approximation error of x̂, the solution from LSRN. For simplicity, we assume exact arithmetic and exact solving of the preconditioned system in our analysis. Recall that in LSRN we have

$$Ã=GA=G{A}_k+GE,$$

where G ∈ ℝ^{s × m} is a random normal projection. If γ = s/n is sufficiently large, e.g., 2.0, and n is not too small, Lemma 4.3 implies that there exist 0 < q₁ < q₂ such that, with high probability, G has full rank and

$$q_1{\Vert Gw\Vert }_2\le {\Vert w\Vert }_2\le q_2{\Vert Gw\Vert }_2,\forall w\in \text{range}(A).$$ (4.7)

Theorem 4.6. If (4.7) holds, σ_{k + 1} < cσ₁q₁/q₂, and σ_k > cσ₁ (1 + q₂/q₁), we have k̃ = k, so that LSRN determines the effective rank of A correctly, and

$${\Vert \mathrm{x̂}-x^{*}\Vert }_2\le \frac{6{\Vert b\Vert }_2}{({\sigma }_k{q}_1/q_2)({\sigma }_k{q}_1/q_2-{\sigma }_{k+1})}·{\sigma }_{k+1}.$$

Proof. Equation (4.7) implies

$${\sigma }_1(Ã)=\underset{{\Vert x\Vert }_2\le 1}{\text{max}}{\Vert Ãx\Vert }_2\le \underset{{\Vert x\Vert }_2\le 1}{\text{max}}{\Vert Ax\Vert }_2/q_1\le {\sigma }_1/q_1,$$ (4.8)

$${\sigma }_1(Ã)=\underset{{\Vert x\Vert }_2\le 1}{\text{max}}{\Vert Ãx\Vert }_2\ge \underset{{\Vert x\Vert }_2\le 1}{\text{max}}{\Vert Ax\Vert }_2/q_2\le {\sigma }_1/q_2,$$ (4.9)

and hence σ₁/q₂ ≤ σ₁(Ã) ≤ σ₁/q₁. Similarly, we have ‖GE‖₂ = σ₁(GE) ≤ σ_{k + 1}/q₁. Let Ã_k be Ã’s best rank-k approximation and let ${Ũ}_k{\mathrm{\Sigma ̃}}_k{Ṽ}_k^T$ be its SVD. We have

$${\sigma }_{k+1}(Ã)={\Vert {Ã}_k-Ã\Vert }_2\le {\Vert G{A}_k-Ã\Vert }_2={\Vert GE\Vert }_2\le {\sigma }_{k+1}/q_1.$$ (4.10)

Note that range(A_k) ⊂ range(A). We have

$${\sigma }_k(G{A}_k)=\underset{\upsilon \in \text{range}({(G{A}_k)}^T),{\Vert \upsilon \Vert }_2=1}{\text{min}}{\Vert G{A}_k\upsilon \Vert }_2\ge \underset{\upsilon \in \text{range}(A_k^T),{\Vert \upsilon \Vert }_2=1}{\text{min}}{\Vert A_k\upsilon \Vert }_2/q_2={\sigma }_k/q_2,$$

where $\text{range}({(G{A}_k)}^T)=\text{range}(A_k^T)$ because G has full rank. Therefore,

$${\sigma }_k(Ã)={\sigma }_k({Ã}_k)\ge {\sigma }_k(G{A}_k)-{\Vert {Ã}_k-G{A}_k\Vert }_2\ge {\sigma }_k/q_2-{\sigma }_{k+1}/q_1.$$ (4.11)

Using the assumptions σ_{k + 1} < cσ₁ q₁/q₂ and σ_k > cσ₁ (1 + q₂/q₁) and the bounds (4.8)–(4.11), we get

$$c{\sigma }_1(Ã)\ge c{\sigma }_1/q_2>{\sigma }_{k+1}/q_1\ge {\sigma }_{k+1}(Ã)$$

and

$${\sigma }_k(Ã)\ge {\sigma }_k/q_2-{\sigma }_{k+1}/q_1>{\sigma }_k/q_2-c{\sigma }_1/q_2\ge c{\sigma }_1/q_1\ge c{\sigma }_1(Ã).$$

Thus if we use c to determine the effective rank of Ã, the result would be k, the same as the effective rank of A.

Following the LSRN algorithm, the preconditioner matrix is $N={Ṽ}_k{\mathrm{\Sigma ̃}}_k^{-1}$. Note that AN has full rank because k = rank(N) ≥ rank(AN) ≥ rank(GAN) = rank(Ũ_k) = k. Therefore, LSRN’s solution can be written as

$$\mathrm{x̂}=N{(AN)}^{†}b={(AN{N}^{†})}^{†}b={(A{Ṽ}_k{Ṽ}_k^T)}^{†}b.$$

For the matrix $A{Ṽ}_k{Ṽ}_k^T$, we have the following bound on its kth singular value:

$${\sigma }_k(A{Ṽ}_k{Ṽ}_k^T)=\underset{\upsilon \in \text{range}({Ṽ}_k),{\Vert \upsilon \Vert }_2=1}{\text{min}}{\Vert A{Ṽ}_k{Ṽ}_k^T\upsilon \Vert }_2\ge q_1\underset{\upsilon \in \text{range}({Ã}_k^T),{\Vert \upsilon \Vert }_2=1}{\text{min}}{\Vert GA{Ṽ}_k{Ṽ}_k^T\upsilon \Vert }_2\ge q_1\underset{\upsilon \in \text{range}({Ã}_k^T),{\Vert \upsilon \Vert }_2=1}{\text{min}}{\Vert {Ã}_k\upsilon \Vert }_2={\sigma }_k{q}_1/q_2-{\sigma }_{k+1}.$$

The distance between A_k and $A{Ṽ}_k{Ṽ}_k^T$ is also bounded:

$${\Vert A_k-A{Ṽ}_k{{Ṽ}_k}^T\Vert }_2\le q_2{\Vert G{A}_k-Ã{Ṽ}_k{{Ṽ}_k}^T\Vert }_2\le q_2({\Vert G{A}_k-Ã\Vert }_2+{\Vert Ã-Ã{Ṽ}_k{Ṽ}_k^T\Vert }_2)\le 2q_2{\Vert G{A}_k-Ã\Vert }_2\le 2q_2{\Vert GE\Vert }_2\le 2{\sigma }_{k+1}{q}_2/q_1.$$

For perturbation of a pseudoinverse, Wedin [25] shows that if rank(A) = rank(B), then

$${\Vert B^{†}-A^{†}\Vert }_2\le 3{\Vert A^{†}\Vert }_2{\Vert B^{†}\Vert }_2{\Vert A-B\Vert }_2.$$

Applying this result, we get

$${\Vert x^{*}-\mathrm{x̂}\Vert }_2\le {\Vert A_k^{†}-{(A{Ṽ}_k{Ṽ}_k^T)}^{†}\Vert }_2{\Vert b\Vert }_2\le 3{\Vert A_k^{†}\Vert }_2{\Vert {(A{Ṽ}_k{Ṽ}_k^T)}^{†}\Vert }_2{\Vert A_k-A{Ṽ}_k{Ṽ}_k^T\Vert }_2{\Vert b\Vert }_2\le \frac{6{\Vert b\Vert }_2}{({\sigma }_k{q}_1/q_2)({\sigma }_k{q}_1/q_2-{\sigma }_{k+1})}·{\sigma }_{k+1}.$$

Thus, x̂ is a good approximation to x* if σ_{k + 1} = ‖E‖₂ is sufficiently small.

Theorem 4.6 suggests that, to correctly determine the effective rank, we need σ_k and σ_{k + 1} well-separated with respect to the distortion q₂/q₁ introduced by G. For LSRN, q₂/q₁ is bounded by a small constant with high probability if we choose the oversampling factor γ to be a moderately large constant, e.g., 2. We note that the distortion of the random normal projection used in Coakley, Rokhlin, and Tygert [3] is around 1000, which reduces the reliability of determining the effective rank of an approximately rank-deficient problem. We verify this claim empirically in section 6.9.

Remark. Theorem 4.6 assumes that G has full rank and the subspace embedding property (4.7). It is not necessary for G to be a random normal projection matrix. The result also applies to other random projection matrices satisfying this condition, e.g., the randomized discrete cosine transform used in Blendenpik [2].

4.4. Complexity

In this section, we discuss the complexity of LSRN. For space complexity, a careful implementation of LSRN should only use 𝒪(m + n²) RAM instead of 𝒪(mn + n²), because we can generate G and compute GA in blocks. Note that LSRN does not alter the input data. This is different from, for example, LAPACK’s DGELSD, which modifies the input data to store right singular vectors. For DGELSD, we might need to create a copy of the input data, which costs 𝒪(mn) RAM.

Next, we analyze the time complexity of LSRN (Algorithm 1) in terms of floating-point operations (flops). Note that we need only Σ̃ and Ṽ, but not Ũ or a full SVD of à in step 4 of Algorithm 1. In step 6, we assume that the dominant cost per iteration is the cost of applying AN and (AN)^T. Then the total cost is given by

$$\begin{array}{ccc}\hfill \hfill & \hfill sm\times \text{flops}(\text{randn})\hfill & \text{for generating}G\hfill \\ \hfill +\hfill & \hfill s\times \text{flops}(A^{T}u)\hfill & \text{for computing}Ã\hfill \\ \hfill +\hfill & \hfill 2s{n}^2+11n^3\hfill & \text{for computing}\mathrm{\Sigma ̃}\text{and}Ṽ[11,\mathrm{p}.254]\hfill \\ \hfill +\hfill & \hfill N_{\text{iter}}\times (\text{flops}(A\upsilon )+\text{flops}(A^{T}u)+4nr)\hfill & \text{for solving}\underset{y}{\text{min}}{\Vert ANy-b\Vert }_2,\hfill \end{array}$$

where lower-order terms are ignored. Here, flops(randn) is the average flop count to generate a pseudorandom number from the standard normal distribution, while flops(Aυ) and flops(A^Tu) are the flop counts for the respective matrix-vector products. If A is a dense matrix, we have flops(Aυ) = flops(A^Tu) = 2mn. The total cost becomes

$$\text{flops}(\mathtt{L}\mathtt{S}\mathtt{R}{\mathtt{N}}_{\text{dense}})=sm\text{flops}(\text{randn})+2smn+2s{n}^2+11n^3{N}_{\text{iter}}\times (4mn+4nr).$$

Comparing this with the SVD approach, which uses 2mn² + 11n³ flops, we find LSRN requires more flops, even if we only consider computing à and its SVD. However, the actual running time is not fully characterized by the number of flops. It is also affected by how efficiently the computers can do the computation. We empirically compare the running time in section 6. If A is a sparse matrix, we generally have flops(Aυ) and flops(A^Tu) of order 𝒪(m). In this case, LSRN should run considerably faster than the SVD approach. Finally, if A is an operator, it is hard to apply SVD, while LSRN still works without any modification. If we set γ = 2 and ε = 10⁻¹⁴ and assume that n is sufficiently large, we know N_iter ≈ 100 with high probability by Theorem 4.5, and hence LSRN needs approximately 2n + 200 matrix-vector multiplications.

One advantage of LSRN is that the stages of generating G and computing à = GA are embarrassingly parallel. Thus, it is easy to implement LSRN in parallel. For example, on a shared-memory machine using p cores, the total running time decreases to

$$T_{\mathtt{L}\mathtt{S}\mathtt{R}\mathtt{N}}^{\mathrm{m}\mathrm{t},p}=T_{\text{randn}}/p+T_{\text{mult}}/p+T_{\mathrm{s}\mathrm{v}\mathrm{d}}^{\mathrm{m}\mathrm{t},p}+T_{\text{iter}}/p,$$ (4.12)

where T_randn, T_mult, and T_iter are the running times for the respective stages if LSRN runs on a single core, $T_{\mathrm{s}\mathrm{v}\mathrm{d}}^{\mathrm{m}\mathrm{t},p}$ is the running time of SVD using p cores, and communication cost among threads is ignored. Hence, multithreaded LSRN has very good scalability with near-linear speedup on strongly over- or underdetermined problems.

Alternatively, let us consider a cluster of size p using MPI, where each node stores a portion of rows of A (with m ≫ n). Each node can generate random projections and do the multiplication independently; then an MPI_Reduce operation is needed to obtain Ã. Since n is small, the SVD of à and the preconditioner N are computed on a single node and distributed to all the other nodes via an MPI_Bcast operation. If LSQR is chosen as the iterative solver, we need two MPI_Allreduce operations per iteration in order to apply A^T and to compute a vector norm, while if the CS method is chosen as the iterative solver, we need only one MPI_Allreduce operation per iteration to apply A^T. Note that all the MPI operations that LSRN uses are collective. If we assume the cluster is homogeneous and has perfect load balancing, the time complexity to perform a collective operation should be 𝒪(log p). Hence the total running time becomes

$$T_{\mathtt{L}\mathtt{S}\mathtt{R}\mathtt{N}}^{\mathrm{m}\mathrm{p}\mathrm{i},p}=T_{\text{randn}}/p+T_{\text{mult}}/p+T_{\mathrm{s}\mathrm{v}\mathrm{d}}+T_{\text{iter}}/p+(C_1+C_2{N}_{\text{iter}})𝒪(\text{log}p),$$ (4.13)

where C₁ corresponds to the cost of computing à and broadcasting N, and C₂ corresponds to the cost of applying A^T at each iteration. Therefore, the MPI implementation of LSRN still has good scalability as long as T_svd is not dominant, i.e., as long as à is not too big. In our empirical evaluations typical values of n (or m for underdetermined problems) are around 1000, and thus this is the case.

5. Tikhonov regularization

We point out that it is easy to extend LSRN to handle certain types of Tikhonov regularization, also known as ridge regression. Recall that Tikhonov regularization involves solving the problem

$$\text{minimize}\frac{1}{2}{\Vert Ax-b\Vert }_2^2+\frac{1}{2}{\Vert Wx\Vert }_2^2,$$ (5.1)

where W ∈ ℝ^{n × n} controls the regularization term. In many cases, W is chosen as λI_n for some value of a regularization parameter λ > 0. It is easy to see that (5.1) is equivalent to the following LS problem, without any regularization:

$$\text{minimize}\frac{1}{2}{\Vert \left(\begin{array}{c}\hfill A\hfill \\ \hfill W\hfill \end{array}\right)x-\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right)\Vert }_2^2.$$ (5.2)

This is an overdetermined problem of size (m + n) × n. If m ≫ n, then we certainly have m + n ≫ n. Therefore, if m ≫ n, we can directly apply LSRN to (5.2) in order to solve (5.1). On the other hand, if m ≪ n, then although (5.2) is still overdetermined, it is “nearly square” in the sense that m + n is only slightly larger than n. In this regime, random sampling methods and random projection methods like LSRN do not perform well. In order to deal with this regime, note that (5.1) is equivalent to

$$\begin{array}{cc}\hfill \text{minimize}& \frac{1}{2}{\Vert r\Vert }_2^2+\frac{1}{2}{\Vert Wx\Vert }_2^2\hfill \\ \hfill \text{subject to}& Ax+r=b,\hfill \end{array}$$

where r = b − Ax is the residual vector. (Note that we use r to denote the matrix rank in a scalar context and the residual vector in a vector context.) By introducing z = Wx and assuming that W is nonsingular, we can rewrite the above problem as

$$\begin{array}{cc}\hfill \text{minimize}& \frac{1}{2}{\Vert \left(\begin{array}{c}\hfill z\hfill \\ \hfill r\hfill \end{array}\right)\Vert }_2^2\hfill \\ \hfill \text{subject to}& (A{W}^{-1}{I}_m)\left(\begin{array}{c}\hfill z\hfill \\ \hfill r\hfill \end{array}\right)=b;\hfill \end{array}$$

i.e., as when computing the min-length solution to

$$(A{W}^{-1}{I}_m)\left(\begin{array}{c}\hfill z\hfill \\ \hfill r\hfill \end{array}\right)=b.$$ (5.3)

Note that (5.3) is an underdetermined problem of size m × (m + n). Hence, if m ≪ n, we have m ≪ m + n, and we can use LSRN to compute the min-length solution to (5.3), denoted by $(\begin{array}{c}\hfill z^{*}\hfill \\ \hfill r^{*}\hfill \end{array})$. The solution to the original problem (5.1) is then given by x* = W⁻¹z*. Here, we assume that W⁻¹ is easy to apply (e.g., if W = λI_n), so that AW⁻¹ can be treated as an operator. The equivalence between (5.1) and (5.3) was first established by Herman, Lent, and Hurwitz [15].

In most applications of regression analysis, the optimal regularization parameter is unknown and needs to be estimated, e.g., by cross-validation. This requires solving a sequence of LS problems where only W differs. For overdetermined problems, we need to perform a random normal projection on A only once. The marginal cost to solve for each W is the following: a random normal projection on W, an SVD of size ⌈γn⌉ × n, and a predictable number of iterations. Similar results hold for underdetermined problems when each W is a multiple of the identity matrix.

6. Numerical experiments

We implemented our LS solver LSRN and compared it with competing solvers: DGELSD/DGELSY from LAPACK [1], spqr_solve (SPQR) from SuiteSparseQR [5, 6], and Blendenpik [2]. Table 1 summarizes the properties of those solvers. It is impossible to compare LSRN with all of the LS solvers. We choose solvers from LAPACK and SuiteSparseQR because they are the de facto standards for dense and sparse problems, respectively. DGELSD takes the SVD approach, which is accurate and robust to rank-deficiency. DGELSY takes the orthogonal factorization approach, which should be almost as robust as the SVD approach but less expensive. SPQR uses multifrontal sparse QR factorization. With the “min2norm” option, it computes min-length solutions to full-rank underdetermined LS problems. However, it does not compute min-length solutions to rank-deficient problems. Note that the widely used MATLAB’s backslash calls LAPACK for dense problems and SuiteSparseQR for sparse problems.¹ But it does not call the functions that return min-length solutions to rank-deficient or underdetermined systems. We choose Blendenpik out of several recently proposed randomized LS solvers, e.g., [22] and [3], because a high-performance implementation is publicly available and it is easy to adapt it to use multithreads. Blendenpik assumes that A has full rank.

Table 1.

LS solvers and their properties.

solver	min-len solution to		Taking advantage of
	underdet?	rank-def?	sparse A	operator A
DGELSD/DGELSY	yes	yes	no	no
SPQR	yes	no	yes	no
Blendenpik	yes	no	no	no
LSRN	yes	yes	yes	yes

6.1. Implementation and system setup

The experiments were performed on either a local shared-memory machine or a virtual cluster hosted on Amazon’s Elastic Compute Cloud (EC2). The shared-memory machine has 12 Intel Xeon CPU cores at clock rate 2GHz with 128GB RAM. The virtual cluster consists of 20 m1.large instances configured by a third-party tool called StarCluster.² An m1.large instance has two virtual cores with two EC2 Compute Units³ each. To attain top performance on the shared-memory machine, we implemented a multithreaded version of LSRN in C, and to make our solver general enough to handle large problems on clusters, we also implemented an MPI version of LSRN in Python with NumPy, SciPy, and mpi4py. Both packages are available for download.⁴ We use the multithreaded implementation to compare LSRN with other LS solvers and use the MPI implementation to explore scalability and to compare iterative solvers under a cluster environment. To generate values from the standard normal distribution, we adopted the code from Marsaglia and Tsang [19] and modified it to use threads; this can generate a billion samples in less than two seconds on the shared-memory machine. For both the multi-threaded version and the MPI version, the random seeds for each thread/process is determined by its rank, which works well in practice. We compiled SuiteSparseQR with Intel Threading Building Blocks (TBB) enabled, as suggested by its author. We also modified Blendenpik to call multithreaded FFTW routines. Blendenpik’s default settings were used. All of the solvers were linked against the BLAS and LAPACK libraries shipped with MATLAB R2011b. This is a fair setup because all the solvers can use multithreading automatically and are linked against the same BLAS and LAPACK libraries. The running times were measured in wall-clock times.

6.2. κ(AN) and number of iterations

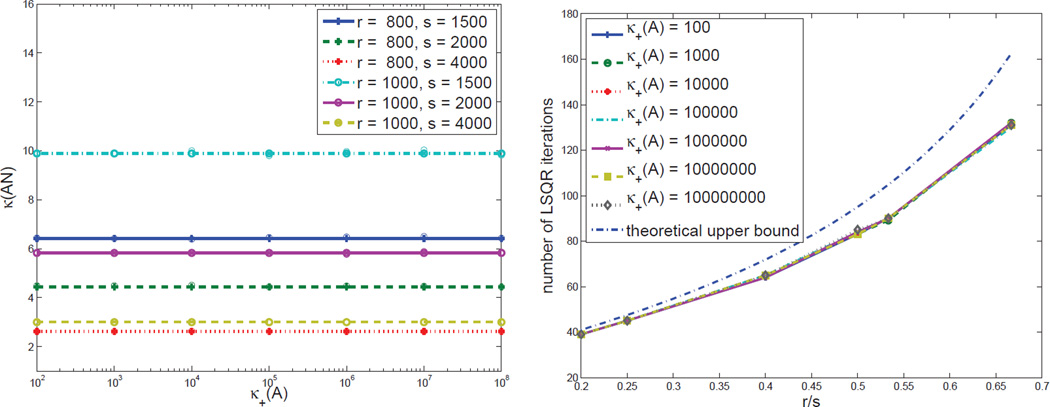
Recall from Theorem 4.4 that κ(AN), the condition number of the preconditioned system, is roughly bounded by $(1+\sqrt{r/s})/(1-\sqrt{r/s})$ when s is large enough such that we can ignore α in practice. To verify this statement, we generate random matrices of size 10⁴ × 10³ with condition numbers ranging from 10² to 10⁸. The left figure in Figure 1 compares κ(AN) with κ₊(A), the effective condition number of A, under different choices of s and r. We take the largest value of κ(AN) in ten independent runs as the κ(AN) in the plot. For each pair of s and r, the corresponding estimate $(1+\sqrt{r/s})/(1-\sqrt{r/s})$ is drawn in a solid line of the same color. We see that $(1+\sqrt{r/s})/(1-\sqrt{r/s})$ is indeed an accurate estimate of the upper bound on κ(AN). Moreover, κ(AN) is not only independent of κ₊(A), but it is also quite small. For example, we have $(1+\sqrt{r/s})/(1-\sqrt{r/s})<6$ if s > 2r, and hence we can expect super fast convergence of CG-like methods. Loss of orthogonality is not an issue here because of extremely good conditioning and small iteration counts. Based on Theorem 4.5, the number of iterations should be less than $(\text{log}\epsilon -\text{log}2)/\text{log}\sqrt{r/s}$, where ε is a given tolerance. In order to match the accuracy of direct solvers, we set ε = 10⁻¹⁴. The right figure in Figure 1 shows the number of LSQR iterations for different combinations of r/s and κ₊(A). Again, we take the largest iteration number in ten independent runs for each pair of r/s and κ₊(A). We also draw the theoretical upper bound $(\text{log}\epsilon -\text{log}2)/\text{log}\sqrt{r/s}$ in a dotted line. We see that the number of iterations is basically a function of r/s, independent of κ₊(A), and the theoretical upper bound is very good in practice. This confirms that the number of iterations is fully predictable given γ.

Fig. 1.

Left: κ₊(A) versus κ(AN) for different choices of r and s. A ∈ ℝ^{104 × 103} is randomly generated with rank r ∈ {800, 1000} and effective condition number κ₊(A) ∈ {10², 10³, …, 10⁸}. For each (r, s) pair, we take the largest value of κ(AN) in ten independent runs for each κ₊(A) and plot them using circle marks. The estimate $(1+\sqrt{r/s})/(1-\sqrt{r/s})$ is drawn using a solid line for each (r, s) pair. Right: Number of LSQR iterations versus r/s. The number of LSQR iterations is merely a function of r/s, independent of the condition number of the original system.

6.3. Tuning the oversampling factor γ

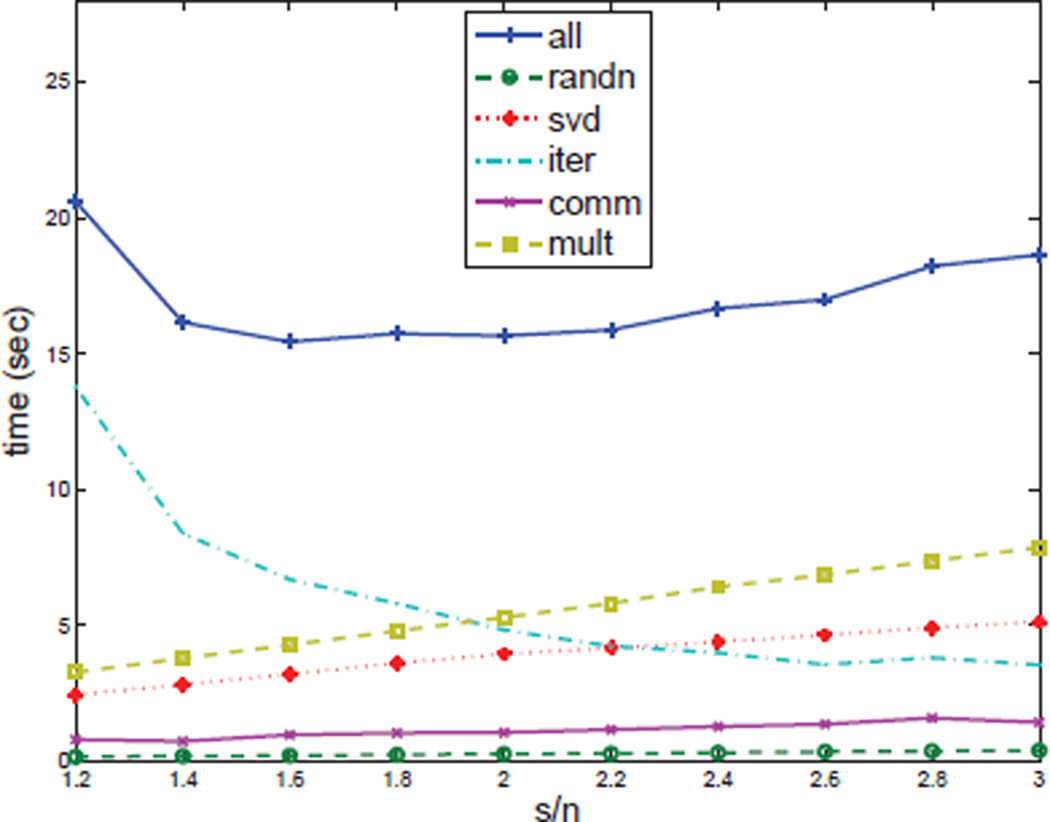
Once we set the tolerance and maximum number of iterations, there is only one parameter left: the oversampling factor γ. To demonstrate the impact of γ, we fix the problem size to 10⁵ ×10³ and the condition number to 10⁶, set the tolerance to 10⁻¹⁴, and then solve the problem with γ ranged from 1.2 to 3. Figure 2 illustrates how γ affects the running times of LSRN’s stages: randn for generating random numbers, mult for computing à = GA, svd for computing Σ̃ and Ṽ from Ã, and iter for LSQR. We see that the running times of randn, mult, and svd increase linearly as γ increases, while iter time decreases. Therefore, there exists an optimal choice of γ. For this particular problem, we should choose γ between 1.8 and 2.2. We experimented with various LS problems. The best choice of γ ranges from 1.6 to 2.5, depending on the type and the size of the problem. We also note that, when γ is given, the running time of the iteration stage is fully predictable. Thus we can initialize LSRN by measuring randn/sec and flops/sec for matrix-vector multiplication, matrix-matrix multiplication, and SVD, and then determine the best value of γ by minimizing the total running time (4.13). For simplicity, we set γ = 2.0 in all later experiments; although this is not the optimal setting for all cases, it is always a reasonable choice.

Fig. 2.

The overall running time of LSRN and the running time of each LSRN stage with different oversampling factor γ for a randomly generated problem of size 10⁵ × 10³. For this particular problem, the optimal γ that minimizes the overall running time lies in [1.8, 2.2].

6.4. Solution accuracy

Under the default settings γ = 2.0 and ε = 10⁻¹⁴, we test LSRN’s solution accuracy on three types of LS problems: full rank, rank-deficient, and approximately rank-deficient. As mentioned in section 4.3, LSRN uses the common approach to determine the effective rank of Ã, whose singular values smaller than cσ₁(Ã) are treated as zeros, where c is a user input. A is generated by constructing its SVD. For full-rank problems, we use the following MATLAB script:

• U = orth(randn(m, n)); S = diag (linspace (1, 1/kappa, n));

• V = orth(randn(n, n)); A = U*S*V’; x = randn(n, 1);

• b = A*x; err = randn(m, 1); b = b + 0.25*norm(b)/norm(err) * err;

For rank-deficient problems, we use

• U = orth(randn(m, r)); S = diag (linspace (1, 1/kappa, r)); V = orth(randn(n, r));

The script for approximately rank-deficient problems is the same as for the full rank one except that

• S = diag ([linspace (1, 1/kappa, r), 1e−8 * ones (1, n−r)]);

We choose m = 10⁵, n = 100, r = 80, and κ = 10⁶. DGELSD is used as a reference solver with c (RCOND) set as 10⁻⁷. The metrics are relative differences in ‖x‖₂ and ‖Ax − b‖₂ and ‖A^T (Ax − b)‖₂, all scaled by 1/κ, which is generally more informative (see [3, Remark 5.3]), and computed using quad precision. Table 2 lists the average values of those metrics from 50 independent runs. We see that LSRN is accurate enough to meet the accuracy requirement of most applications.

Table 2.

Comparing LSRN’s solution accuracy to DGELSD. DGELSD’s solution is denoted by x*, and LSRN’s denoted by x̂. The metrics are computed using quad precision. We show the average values of those metrics from 50 independent runs. LSRN should be accurate enough for most applications.

	$\frac{{\Vert \mathrm{x̂}\Vert }_2-{\Vert x^{*}\Vert }_2}{c{\Vert x^{*}\Vert }_2}$	$\frac{{\Vert A\mathrm{x̂}-b\Vert }_2{\Vert A{x}^{*}-b\Vert }_2}{c{\Vert A{x}^{*}-b\Vert }_2}$	$\frac{{\Vert A^T(A{x}^{*}-b)\Vert }_2}{c}$	$\frac{{\Vert A^T(A\mathrm{x̂}-b)\Vert }_2}{c}$
Full rank	−8.5e-14	0.0	3.6e-18	2.5e-17
Rank-def	−5.3e-14	0.0	8.1e-18	1.5e-17
Approx. rank-def	9.9e-12	−7.3e-16	2.5e-17	2.7e-17

6.5. Dense least squares

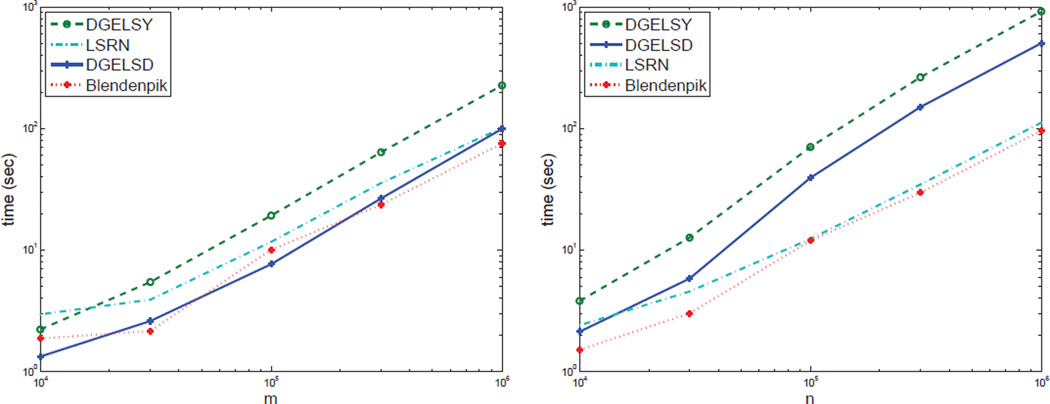
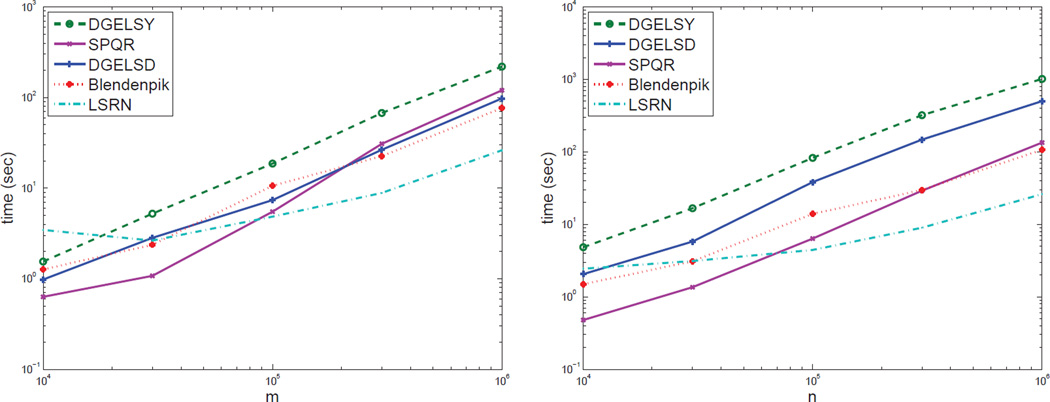
Though LSRN is not designed for dense problems, it is competitive with DGELSD/DGELSY and Blendenpik on large-scale strongly over- or underdetermined LS problems. Figure 3 compares the running times of LSRN and competing solvers on randomly generated full-rank LS problems. We use the script from section 6.4 to generate test problems. The results show that Blendenpik is the overall winner. The runners-up are LSRN and DGELSD. We find that the SVD-based DGELSD actually runs much faster than the QR-based DGELSY on strongly over- or underdetermined systems on the shared-memory machine. It may be because of better use of multithreaded BLAS, but we do not have a definitive explanation. The performance of LAPACK’s solvers decreases significantly for underdetermined problems. We monitored CPU usage and found that LAPACK could not fully use all of the CPU cores; i.e., it could not effectively call multithreaded BLAS. The performance of Blendenpik also decreases, while that of LSRN does not change much, making LSRN’s performance very close to Blendenpik’s.

Fig. 3.

Running times on m × 1000 dense overdetermined problems with full rank (left) and on 1000 × n dense underdetermined problems with full rank (right). On the problem of size 10⁶ × 10³, we have Blendenpik > DGELSD ≈ LSRN > DGELSY in terms of speed. On underdetermined problems, LAPACK’s performance decreases significantly compared with the overdetermined cases. Blendenpik’s performance decreases as well, while LSRN does not change much.

Remark. The performance of DGELSD/DGELSY varies greatly, depending on the LAPACK implementation. When we use the LAPACK library shipped with MATLAB R2010b, the DGELSD from it takes nearly 150 seconds to solve a 10⁶ × 10³ LS problem, which is slower than LSRN. However, after we switch to MATLAB R2011b, it runs slightly faster than LSRN does on the same problem.

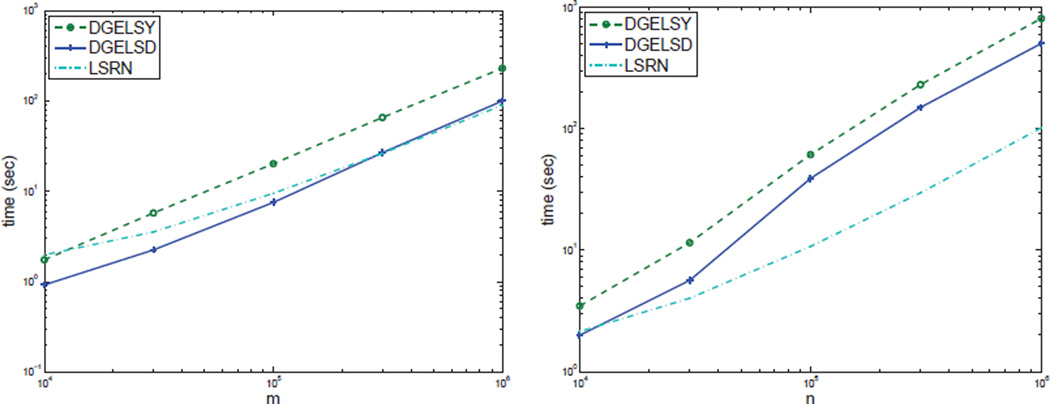
LSRN is also capable of solving rank-deficient problems, and in fact it takes advantage of any rank-deficiency (in that it finds a solution in fewer iterations). Figure 4 shows the results on over- and underdetermined rank-deficient problems generated the same way as in previous experiments, except that we set r = 800. Blendenpik is not included because it is not designed to handle rank deficiency. DGELSY/DGELSD remains the same speed on overdetermined problems as in full-rank cases, and runs slightly faster on underdetermined problems. On the problem of size 10⁶ × 10³, DGELSD spends 99.5 seconds, almost the same as in the full-rank case, while LSRN’s running times reduce to 89.0 seconds, from 101.1 seconds on its full-rank counterpart.

Fig. 4.

Running times on m × 1000 dense overdetermined problems with rank 800 (left) and on 1000 × n dense underdetermined problems with rank 800 (right). LSRN takes advantage of rank-deficiency. We have LSRN > DGSLS/DGELSD > DGELSY in terms of speed.

We see that, for strongly over- or underdetermined problems, DGELSD is the fastest and most reliable routine among the LS solvers provided by LAPACK. However, it (or any other LAPACK solver) runs much slower on underdetermined problems than on overdetermined problems, while LSRN works symmetrically on both cases. Blendenpik is the fastest dense least squares solver in our tests. Though it is not designed for solving rank-deficient problems, Blendenpik should be modifiable to handle such problems following Theorem 3.2. We also note that Blendenpik’s performance depends on the distribution of the row norms of U. We generate test problems randomly so that the row norms of U are homogeneous, which is ideal for Blendenpik. When the row norms of U are heterogeneous, Blendenpik’s performance may drop. See Avron, Maymounkov, and Toledo [2] for a more detailed analysis.

6.6. Sparse least squares

The running time and flop count of SPQR depend upon the fill-reducing ordering it finds (itself a heuristic for an NP-hard problem), and thus the memory usage and factorization time are strongly dependent on the sparsity pattern of A. LSRN relies instead on matrix-matrix and matrix-vector multiplications involving A, and hence its flop count and memory usage are independent of how the nonzero entries are distributed in A. LAPACK does not have any direct sparse LS solver. Blendenpik uses fast transforms, which treat the input matrix as a dense matrix in order to apply fast transforms.

We generated sparse LS problems using MATLAB’s “sprandn” function with density 0.01 and condition number 10⁶. All problems have full rank. Figure 5 shows the results. DGELSD/DGELSY and Blendenpik basically perform the same as in the dense case. For overdetermined problems, we see that SPQR handles sparse problems very well when m < 10⁵. As m grows larger, the factor R becomes increasingly dense in general and SPQR slows down. For our test cases, SPQR runs even longer than DGELSD when m ≥ 3 × 10⁵. LSRN becomes the fastest solver among the five when m ≥ 10⁵. It takes only 26.1 seconds on the overdetermined problem of size 10⁶ ×10³. On large underdetermined problems, LSRN still leads by a huge margin.

Fig. 5.

Running times on m × 1000 sparse overdetermined problems with full rank (left) and on 1000 × n sparse underdetermined problems with full rank (right). DGELSD/DGELSY and Blendenpik perform almost the same as in the dense case. SPQR performs very well for small and medium-scaled problems, but it runs slower than the dense solver Blendenpik on the problem of size 10⁶ × 10³. LSRN starts to lead as m goes above 10⁵, and it leads by a huge margin on the largest problem. The underdetermined case is very similar to its overdetermined counterpart.

LSRN makes no distinction between dense and sparse problems. The speedup on sparse problems is due to faster matrix-vector and matrix-matrix multiplications. Hence, although no test was performed, we expect a similar speedup on fast linear operators as well. Also note that, in the multithreaded implementation of LSRN, we use a naive multithreaded routine for sparse matrix-vector and matrix-matrix multiplications, which is far from optimized and thus leaves room for improvement.

6.7. Real-world problems

In this section, we report results on some real-world large data problems. The problems are summarized in Table 3, along with running times. DGELSY is not included because it is inferior to DGELSD.

Table 3.

Real-world problems and corresponding running times in seconds. DGELSD does not take advantage of sparsity, with its running time determined by the problem size. Though SPQR may not output min-length solutions to rank-deficient problems, we still report its running times (marked with “ * ”). Blendenpik either does not apply to rank-deficient problems or runs out of memory (OOM). LSRN’s running time is mainly determined by the problem size and the sparsity.

Matrix	m	n	nnz	Rank	Cond	DGELSD	SPQR	Blendenpik	LSRN
landmark	71952	2704	1.15e6	2671	1.0e8	18.64	4.920*	-	17.89
rail4284	4284	1.1e6	1.1e7	full	400.0	> 3600	505.9	OOM	146.1
tnimg_1	951	1e6	2.1e7	925	-	510.3	72.14*	-	41.08
tnimg_2	1000	2e6	4.2e7	981	-	1022	168.6*	-	82.63
tnimg_3	1018	3e6	6.3e7	1016	-	1628	271.0*	-	124.5
tnimg_4	1019	4e6	8.4e7	1018	-	2311	371.3*	-	163.9
tnimg_5	1023	5e6	1.1e8	full	-	3105	493.2	OOM	197.6

landmark and rail4284 are from the University of Florida Sparse Matrix Collection [7]. landmark originated from a rank-deficient LS problem. rail4284 has full rank and originated from a linear programming problem on Italian railways. Both matrices are very sparse and have structured patterns. Though SPQR runs extremely fast on landmark, it does not guarantee to return the min-length solution. Blendenpik is not designed to handle the rank-deficient landmark, and it unfortunately runs out of memory (OOM) on rail4284. LSRN takes 17.55 seconds on landmark and 136.0 seconds on rail4284. DGELSD is slightly slower than LSRN on landmark and much slower on rail4284.

tnimg is generated from the TinyImages collection [24], which provides 80 million color images of size 32 × 32. For each image, we first convert it to grayscale, compute its two-dimensional DCT (Discrete Cosine Transform), and then keep only the top 2% largest coefficients in magnitude. This gives a sparse matrix of size 1024 × 8e7 where each column has 20 or 21 nonzero elements. Note that tnimg does not have apparent structured pattern. Since the whole matrix is too big, we work on submatrices of different sizes. tnimg_i is the submatrix consisting of the first 10⁶ × i columns of the whole matrix for i = 1, …, 80, where empty rows are removed. The running times of LSRN are approximately linear in n. Both DGELSD and SPQR are slower than LSRN on the tnimg problems. More importantly, their running times show that DGELSD and SPQR do not have linear scalability. Blendenpik either does not apply to the rank-deficient cases or runs OOM.

We see that, though both methods take advantage of sparsity, SPQR relies heavily on the sparsity pattern and its performance is unpredictable until the sparsity pattern is analyzed, while LSRN does not rely on the sparsity pattern and always delivers predictable performance and, moreover, the min-length solution.

6.8. Scalability and choice of iterative solvers on clusters

In this section, we move to the Amazon EC2 cluster. The goals are to demonstrate that (1) LSRN scales well on clusters, and (2) the CS method is preferred to LSQR on clusters with high communication cost. The test problems are submatrices of the tnimg matrix in the previous section: tnimg_4, tnimg_10, tnimg_20, and tnimg_40, solved with 4, 10, 20, and 40 cores, respectively. Each process stores a submatrix of size 1024 × 1e6. Table 4 shows the results, averaged over five runs. Ideally, from the complexity analysis (4.13), when we double n and double the number of cores, the increase in running time should be a constant if the cluster is homogeneous and has perfect load balancing (which we have observed is not true on Amazon EC2). For LSRN with CS, from tnimg_10 to tnimg_20 the running time increases 27.6 seconds, and from tnimg_20 to tnimg_40 the running time increases 34.7 seconds. We believe the difference between the time increases is caused by the heterogeneity of the cluster, because Amazon EC2 does not guarantee the connection speed among nodes. From tnimg_4 to tnimg_40, the problem scale is enlarged by a factor of 10 while the running time only increases by a factor of 50%. The result still demonstrates LSRN’s good scalability. We also compare the performance of LSQR and CS as the iterative solvers in LSRN. For all problems LSQR converges in 84 iterations and CS converges in 106 iterations. However, LSQR is slower than CS. The communication cost saved by CS is significant on those tests. As a result, we recommend CS as the default LSRN iterative solver for cluster environments. Note that to reduce the communication cost on a cluster, we could also consider increasing γ to reduce the number of iterations.

Table 4.

Test problems on the Amazon EC 2 cluster and corresponding running times in seconds. When we enlarge the problem scale by a factor of 10 and increase the number of cores accordingly, the running time only increases by a factor of 50%. It shows LSRN’s good scalability. Though the CS method takes more iterations, it is faster than LSQR by saving communication cost.

Solver	Ncores	Matrix	m	n	nnz	Niter	Titer	Ttotal
LSRN w/ CS	4	tnimg_4	1024	4e6	8.4e7	106	34.03	170.4
LSRN w/ LSQR						84	41.14	178.6
LSRN w/ CS	10	tnimg_10	1024	1e7	2.1e8	106	50.37	193.3
LSRN w/ LSQR						84	68.72	211.6
LSRN w/ CS	20	tnimg_20	1024	2e7	4.2e8	106	73.73	220.9
LSRN w/ LSQR						84	102.3	249.0
LSRN w/ CS	40	tnimg_40	1024	4e7	8.4e8	106	102.5	255.6
LSRN w/ LSQR						84	137.2	290.2

6.9. Comparison with Coakley, Rokhlin, and Tygert

Coakley, Rokhlin, and Tygert [3] introduced a least squares solver, referred to as CRT11, based on pre-conditioned normal equation, where the preconditioning matrix is computed via a random normal projection G, with G ∈ ℝ^{(n + 4) × m}. We implemented a multithreaded version of CRT11 that shares the code base used by LSRN and uses 𝒪(m + n²) RAM by computing in blocks. In this section, we report some comparison results between CRT11 and LSRN.

It is easy (and thus we omit details) to derive the time complexity of CRT11, which requires applying A or A^T 3n + 6 times, while from section 4.4 we know that LSRN needs roughly 2n + 200 matrix-vector multiplications under the default setting. So LSRN is asymptotically faster than CRT11 in theory. We compare the running times of LSRN and CRT11 on dense strongly overdetermined least square problems, where m is fixed at 10⁶ while n ranges from 1000 to 3000, and A has full rank. The test problems are generated the same way as in section 6.5. We list the running times in Table 5, where we see that LSRN is slightly slower than CRT11 when n = 1000 and becomes faster when n = 2000, 3000, and 4000.

Table 5.

Running times (in seconds) on full-rank dense overdetermined problems of size 10⁶ × n, where n ranges from 1000 to 4000. LSRN is slightly slower than CRT 11 when n = 1000 and becomes faster when n = 2000, 3000, and 4000, which is consistent with our theoretical analysis.

	n = 1000	n = 2000	n = 3000	n = 4000
CRT11	98.0	327.7	672.3	1147.9
LSRN	101.1	293.1	594.0	952.2

Hardware limitations prevented testing larger problems. We believe that the difference should be much clearer if A is an expensive operator, for example, if applying A or A^T requires solving a partial differential equation. Based on the evaluation result, we would recommend CRT11 over LSRN if n ≤ 1000, and LSRN over CRT11 otherwise.

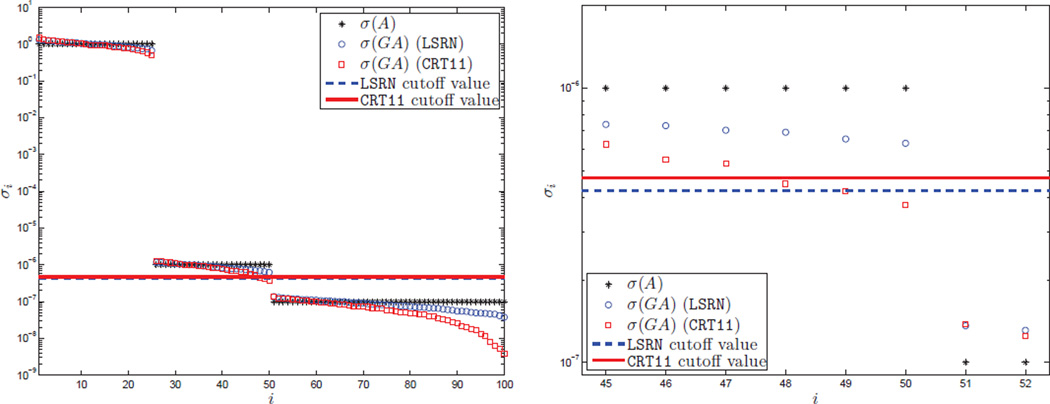
In [3], the authors showed that, unlike the original normal equation approach, CRT11 is very reliable on a broad range of matrices because the condition number of the preconditioned system is not very large (≈ 1000). This is true for full-rank matrices. However, the authors did not show how CRT11 works on approximately rank-deficient problems. Based on our analysis in section 4.3, we need σ_k and σ_{k + 1} well-separated with respect to the distortion introduced by G in order to determine the effective rank correctly. In LSRN we choose G ∈ ℝ^{2n × m}, which leads to a small constant distortion (with high probability), while in CRT11 we have G ∈ℝ^{(n + 4) × m}, which leads to a relatively large distortion. It suggests CRT11 might be less reliable than LSRN in estimating the rank of an approximately rank-deficient problem. To verify this, we use the following MATLAB script to generate a test problem:

• sigma = [ones (1, n/4), 1/kappa*ones (1, n/4), e*ones (1, n/2)];

• U = orth(randn(m, n)); A = U*diag (sparse (sigma)).

where we choose m = 10000, n = 100, κ = 10⁶, and e = 10⁻⁷. Thus we have A’s effective rank k = 50, σ₁(A) = 1, σ_k = 10⁻⁶, and σ_{k + 1} = 10⁻⁷; To estimate the effective rank, we set $c=\sqrt{{\sigma }_k{\sigma }_{k+1}}/{\sigma }_1={10}^{-6.5}$, and singular values of à = GA that are smaller than cσ₁(Ã) are treated as zeros. Figure 6 compares the singular values of A and GA for both CRT11 and LSRN (rescaled by $1/\sqrt{s}$ for better alignment, where s = n + 4 for CRT11 and s = 2n for LSRN). We see that CRT11 introduces more distortion to the spectrum of A than LSRN. In this example, the rank determined by CRT11 is 47, while LSRN outputs the correct effective rank. We note that LSRN is not risk-free for approximately rank-deficient problems, which still should have sufficient separation between σ_k and σ_{k + 1}. However, it is more reliable than CRT11 on approximately rank-deficient problems because of less distortion introduced by G.

Fig. 6.

Left: Comparison of the spectrum of A and GA for both CRT11 and LSRN (rescaled by $1/\sqrt{s}$ for better alignment, where s = n + 4 for CRT11 and s = 2n for LSRN) and the cutoff values in determining the effective rank of A. Right: Zoomed in to show that the effective rank estimated by CRT11 is 47, while LSRN outputs the correct effect rank, which is 50.

7. Conclusion

We developed LSRN, a parallel solver for strongly over- or underdetermined and possibly rank-deficient systems. LSRN uses random normal projection to compute a preconditioner matrix for an iterative solver such as LSQR or the Chebyshev semi-iterative (CS) method. The preconditioning process is embarrassingly parallel and automatically speeds up on sparse matrices, fast linear operators, and rank-deficient data. We proved that the preconditioned system is consistent and extremely well-conditioned, and derived strong bounds on the number of iterations of LSQR or the CS method, and hence on the total running time. On large dense systems, LSRN is competitive with the best existing solvers, and runs significantly faster than competing solvers on strongly over- or underdetermined sparse systems without sparsity patterns that can be exploited to reduce fill-in. LSRN is easy to implement using threads or MPI, and scales well in parallel environments. The LSRN package can be downloaded from http://www.stanford.edu/group/SOL/software/lsrn.html.