Alteration of neural action potential patterns by axonal stimulation: the importance of stimulus location

Abstract

Objective

Stimulation of peripheral nerves is often superimposed on ongoing motor and sensory activity in the same axons, without a quantitative model of the net action potential train at the axon endpoint.

Approach

We develop a model of action potential patterns elicited by superimposing constant frequency axonal stimulation on the action potentials arriving from a physiologically activated neural source. The model includes interactions due to collision block, resetting of the neural impulse generator, and the refractory period of the axon at the point of stimulation.

Main Results

Both the mean endpoint firing rate and the probability distribution of the action potential firing periods depend strongly on the relative firing rates of the two sources and the intersite conduction time between them. When the stimulus rate exceeds the neural rate, neural action potentials do not reach the endpoint and the rate of endpoint action potentials is the same as the stimulus rate, regardless of the intersite conduction time. However, when the stimulus rate is less than the neural rate, and the intersite conduction time is short, the two rates partially sum. Increases in stimulus rate produce non-monotonic increases in endpoint rate and continuously increasing block of neurally generated action potentials. Rate summation is reduced and more neural action potentials are blocked as the intersite conduction time increases.. At long intersite conduction times, the endpoint rate simplifies to being the maximum of either the neural or the stimulus rate.

Significance

This study highlights the potential of increasing the endpoint action potential rate and preserving neural information transmission by low rate stimulation with short intersite conduction times. Intersite conduction times can be decreased with proximal stimulation sites for muscles and distal stimulation sites for sensory endings. The model provides a basis for optimizing experiments and designing neuroprosthetic interventions involving motor or sensory stimulation.

1. Introduction

Peripheral nerve stimulation is widely used as a basic science tool, a therapeutic intervention, or a neuroprosthetic technique to restore lost function, e.g., muscle nerve stimulation to assess voluntary muscle activation during maximal voluntary contractions, sensory stimulation to ameliorate pain, or Functional Electrical Stimulation (FES) to restore motor or sensory function in cases of neural injury or disease (Peckham and Kilgore, 2013). In some cases, there is no ongoing physiological activity during the stimulation, but in many circumstances, stimulation is superimposed on action potential trains generated by physiological mechanisms, such as stimulation of muscle to augment voluntary muscle force, with potential application in stroke rehabilitation (Knutson et al., 2012, Langzam et al., 2007, Perumal et al., 2010, Makowski et al., 2013, Yeom and Chang, 2010a), or stimulation of sensory nerves with intact sensory receptors, e.g. to restore bladder function (Bruns et al., 2009).

Interactions between action potentials elicited at the neuron and at the stimulation site can occur through three mechanisms: collision block in the axonal segment between the neuron and the stimulation site, failure of a stimulus to generate action potentials because the axon is refractory after a neural action potential passes the stimulation site, and phase resetting of the neural source by an antidromic action potential invading the neuron. We have not found previous studies of the expected patterns of action potential trains created by simultaneous electrical nerve stimulation and physiological activity, but experimental and modeling studies have demonstrated basic interaction patterns of action potentials arising from multiple encoder sites of sensory endings. Collision block and resetting can occur naturally in branched sensory fibers with multiple encoding sites if action potentials originating in one branch invade the other branch (Lindblom and Tapper, 1966, Eagles and Purple, 1974, Goldfinger, 1984), which has been exploited as an intervention to artificially block unwanted neural activity (van den Honert and Mortimer, 1981).

Phase resetting occurs in neural action potential generators when an antidromic action potential invades the physiological action potential generation site. Resetting has been observed for sensory receptors with branches innervating multiple encoding sites (Fukami, 1980) and in motor neurons undergoing repetitive discharge (Eccles, 1955), and is the mechanism that underlies switching between action potential sources in the case of multiple impulse initiation sites (Lin and Crago, 2002, Mileusnic et al., 2006). The site with the higher rate will continually reset the site with lower rate and provide all of the action potentials reaching the endpoint (i.e., winner take all).

In this simulation study, we examine the effect of constant frequency stimulation at different rates and locations along a peripheral axon relative to the neuronal action potential source. We show that stimulation can alter the mean frequency of endpoint action potentials, but can also alter the probability distribution of the action potential periods without substantially changing the mean frequency. These effects depend strongly on the intersite conduction time between the neuronal action potential source and the stimulation site, as well as on their relative firing periods and the axonal refractory period. Therefore, the physiological effects of stimulation will depend on both the stimulus pattern, and the location along the axon where the stimulation takes place.

2. Methods

2.1. Interaction mechanisms in a peripheral nerve

Figure 1 illustrates the basic patterns of action potentials generated by a neuron and stimulation along the axon. The schematics at the left depict the example of stimulation close to the endpoint, such as motor point stimulation of a distal limb muscle, but the same interactions would also occur with the neuron replaced by a sensory encoder site with stimulation between the sensory receptor and the CNS.

Figure 1.

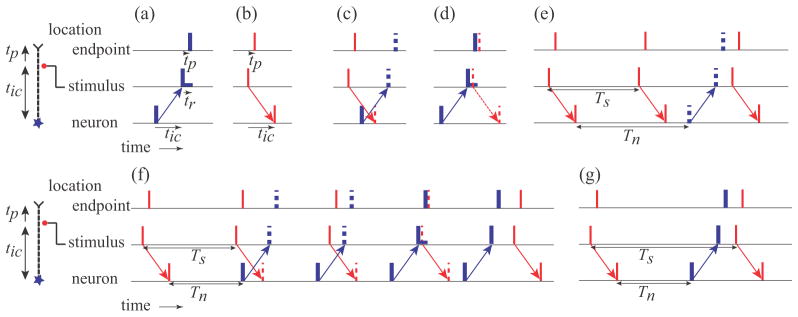
Interactions of action potentials originating at cell body of a neuron and action potentials elicited by stimulation at a location along the axon before the endpoint. The same interactions would occur for stimulation along an axon connecting a sensory encoder to the CNS. The intersite conduction time between the neuron and the stimulation site and from the stimulation site to the muscle endpoint are given by t_ic and t_p respectively. (a,b) Thin red and thick blue vertical bars indicate timing of action potentials originating from the stimulation and the neuron respectively. The refractory period t_r is shown by the horizontal bar following the action potential at the stimulus site. (c) Example of collision block. Dashed vertical bars indicate when action potentials would have occurred if they had not been blocked. (d) Example of stimulation during the refractory period. (e) Example of resetting of neural firing by an antidromic action potential arriving at the neuron before the next neural firing. T_n and T_s are the neuronal firing period and the stimulation period respectively. This pattern illustrates the pattern of firing in Range 1. (f) Example of multiple sequential interactions that can take place in Range 2. (g) An example of resetting when the neural rate is greater than the stimulus rate, which occurs in Range 3. Ranges are defined in Results.

In the absence of interactions, an action potential generated by the neuron, shown in figure 1(a), travels past the stimulation site after the intersite conduction time t_ic, and arrives at the endpoint after an additional delay t_p. A stimulus elicits a pair of action potentials that travel both antidromically and orthodromically, as shown in figure 1(b). The orthodromic action potential arrives at the endpoint after time t_p, and the antidromic action potential arrives at the neuron after time t_ic.

Collision block, illustrated in figure 1(c), occurs when action potentials travelling in opposite directions arrive at the same point on the same axon – both action potentials are abolished. The safety factor for one action potential to excite the membrane segment that carried the other action potential is insufficient to generate an action potential in the membrane beyond the collision point because it is in a refractory state.

Collision block can occur in the section of the axon between the neuron and the stimulating electrode if the neuron generates an action potential within time t_ic either before or after the stimulation, i.e. a 2t_ic window. In the illustrations in figure 1, collision block will occur whenever the two arrows cross, which will happen if the neuron fires or the stimulus occurs within t_ic of each other.

The stimulus can also be blocked from generating action potentials if the axon is refractory, which would occur if an action potential originating from the neuron passes the stimulation site a short period of time (refractory period, t_r) prior to the stimulus, as illustrated in figure 1(d). Action potentials generated by the stimulus will also create refractory periods, but in this configuration, the interactions would never occur due to collision block.

We assume complete phase resetting when an antidromic action potential generated by a stimulus pulse arrives at the neuron prior to the time when the next neural action potential would normally occur. With complete phase resetting, the neuron behaves as if it had just generated a normal action potential, and the next action potential is generated after the regular period, i.e., the generation process is reset, as illustrated in figure 1(e). When antidromic action potentials propagate to a motor neuron cell body, and that cell is being excited by synaptic activity, the action potential is conducted into the initial segment and then into the soma-dendritic space in spite of the low safety factor (Lloyd, 1943, Eccles, 1955, Lipski, 1981). Thus, complete resetting is likely in contrast to partial phase shifting that would occur with passive conduction into an encoding site. Complete phase resetting has also been demonstrated experimentally with sensory receptors (Fukami, 1980).

2.2. Simulation protocols

Endpoint action potential trains in a single axon were created by implementing independent neuronal and stimulation sources, and simulating the interactions described above. Neuronal sources were modeled as pulse trains with normally distributed firing periods described by the mean (T_n) and coefficient of variation (CV). The neuronal firing period was reset if an antidromic action potential from the stimulation arrived at the neuron before the next neuronal action potential was generated. The stimulation had a fixed period (T_s) and generated both orthodromic and antidromic action potentials. Stimulus action potentials always occurred except during the refractory period following the passage of a neuronal action potential at the stimulation site. Both orthodromic neuronal action potentials and antidromic stimulation action potentials were annihilated by collision block if they occurred in the time window described above.

We chose parameter values typical of human Group A motor and sensory peripheral axons. Intersite conduction times ranged from 0 to 0.02 s and stimulation rates ranged from 1 to 35 s⁻¹. The mean neural firing period was fixed at T_n = 0.05 s (R_n = 20 s⁻¹) with CV = 0 or 0.2, a value typical of motor neuron firing periods (Nordstrom et al., 1992, De Luca et al., 1982). Note that the results can be normalized, as described in the Results. The refractory period t_r of a stimulated axon varies with the strength of the stimulus relative to the activation threshold. Borg reported values ranging from 0.88 +/− 0.26 to 1.83 +/− 0.26 ms (mean +/− Std. Dev.) for stimulation intensities of 2 to 1.1 times threshold respectively (Borg, 1984). We chose a fixed value of 1.5 ms for this study.

All simulations and analyses were performed in Matlab. Action potentials were modeled as events, controlled by the designated firing periods and by the modeled interactions. We recorded vectors of event times (neural, stimulation, endpoint) along with the endpoint action potential sources (neural or stimulation). We also recorded the numbers of each type of interaction (resetting, collision, refractory).

The statistical properties of action potential trains arriving at the endpoint of the axon were estimated by simulating long periods of firing (10³ s) to reduce statistical fluctuations in the outcome measures. The resulting action potential trains were analyzed to calculate the mean endpoint action potential rates, the fraction of endpoint action potentials that originated from the stimulation as opposed to the neuron, the fractions of stimuli that resulted in resets, collisions, or refractory blocks, and the probability distributions of the action potential firing periods. We systematically examined the dependence of the behavior on intersite conduction time, and the mean neuronal and stimulus firing periods.

3. Results

3.1. Interaction patterns of constant frequency action potential trains

The pattern of action potentials arriving at the endpoint depends on the relative neural and stimulation periods, T_n and T_s respectively. The patterns also depend on the intersite conduction time, t_ic, between the neuron and the stimulation site, and the axonal refractory period t_r.

For constant firing rates, the patterns are repetitive and are synchronized to a stimulus that results in neuronal resetting. The patterns can be organized into ranges, defined by the ratio of firing periods, T_n/T_s. The inverse ratio R_s/R_n provides an equivalent definition, but the following explanations and figure 1 are described in terms of the periods because they are based on timing.

Range 1: If the stimulus period is less than the neural firing period, a second antidromic action potential will arrive at the neuron before it would initiate its own action potential, as illustrated in figure 1(e). In this range, the neuron never initiates any action potentials, and the pattern of action potentials at the endpoint consists of a constant period train at the stimulus period, but delayed relative to the stimulation by t_p. The endpoint behavior of 1:1 stimulus tracking is defined as being in Range 1, when the condition defined by (1) is true.

$$\frac{T_n}{T_s}=\frac{R_s}{R_n}>1$$ (1)

Range 2: As T_n becomes shorter than T_s, the next stimulus following neuronal resetting occurs during the collision block window, as illustrated in figure 1(f). As a result, the neuronal action potential generator is not reset and the orthodromic stimulated action potential travels to the endpoint. Since T_n < T_s, the times of successive stimuli will increase relative to the time of neuronal firing. Collisions will continue to occur until a stimulated action potential arrives after the collision block window, but perhaps during the refractory period, preventing both stimulation and resetting. A stimulus will eventually arrive after the refractory period, at which time the neuron will be reset and the pattern will repeat. The pattern of action potentials arriving at the endpoint will consist of a series of action potentials at the stimulus period when stimulation results in collisions, followed by a series of action potentials at the neuronal firing period when stimulation occurs during the refractory period, followed by a single period shorter than either T_s or T_n just prior to resetting. The exact number of each period will decrease as T_s increases. The conditions for the mixed interactions observed in Range 2 are given by (2).

$$\frac{R_s}{R_n}<1<\frac{R_s}{R_n}+R_s(2t_c+t_r)$$ (2)

Range 3: If the next stimulus following resetting occurs after the neuronal action potential passes the stimulus site and the refractory period is over, the neuron will be reset by the antidromic action potential, as illustrated in figure 1(g). For each stimulus, the endpoint will receive two action potentials, one generated by the neuron, alternating with one generated by the stimulation. Thus, the net average period at the endpoint will be half the period of stimulation, although the pattern will consist of two alternating periods defined by T₁ = T_n + 2t_c, and T₂ = T_s − T₁. The conditions for the stimulus doubling behavior observed in Range 3 are given by (3).

$$\frac{R_s}{R_n}>\frac{1}{2}>\frac{R_s}{2R_n}+\frac{R_s}{2}(2t_c+t_r)$$ (3)

For even lower stimulus frequencies, R_s/R_n < ½, the endpoint activation patterns are repeated versions of Range 2 and 3, and will not be elaborated here.

3.2. Endpoint action potential trains during constant frequency stimulation

The action potential trains arriving at the endpoint are characterized by a series of action potentials with period P_n, P_s, and other periods that make up the difference when switching between action potentials from one source to action potentials from the other source. The pattern depends on four parameters: the neuronal and stimulus firing periods, the intersite conduction time and the refractory period.

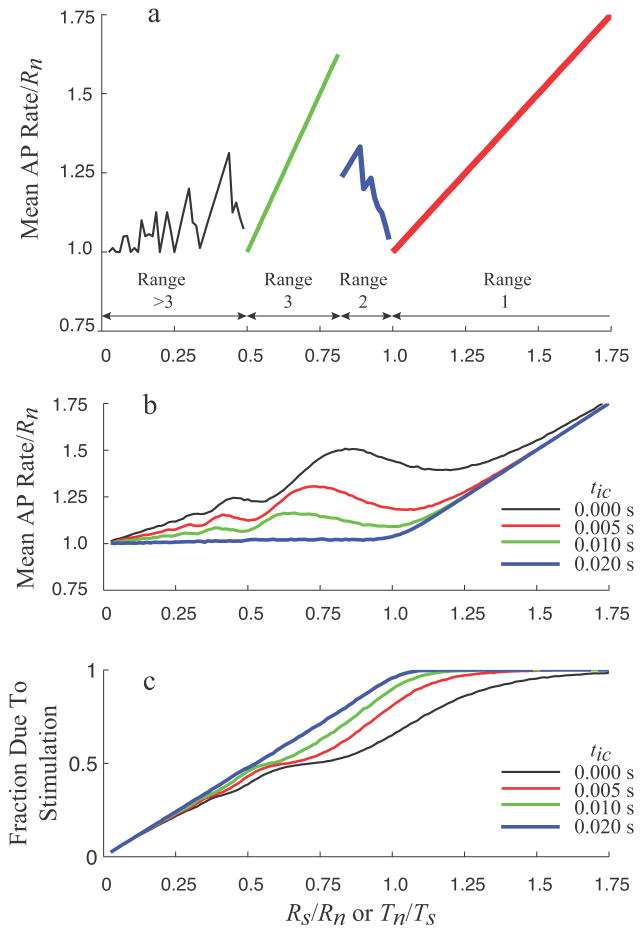
The mean rate of endpoint action potentials during constant rate neuronal firing and constant rate stimulation shows a complex, non-monotonic behavior, as shown in figure 2(a). When the stimulus rate exceeds the neural rate (Range 1), the endpoint rate is equal to the stimulus rate. At stimulus rates beginning at half the neural rate (beginning of Range 3), the mean rate increases as twice the stimulus rate, due to the behavior illustrated in figure 1(g). As the stimulation frequency exceeds the limit defined by (2), the behavior transitions from Range 3 to Range 2, and the mean endpoint rate starts to decrease irregularly, due to the mixed interaction behavior illustrated in figure 1(f). Analogous patterns are seen in the range of stimulus rates below half of the neural rate.

Figure 2.

(a) Normalized mean rate of action potentials at the endpoint for a constant neural rate and a varying stimulation rate. In this example, the neural rate is fixed at 20 s⁻¹, the intersite conduction time is fixed at 0.005 s, the refractory period is fixed at 0.0015 s, and the stimulus rate is stepped from 0.5 to 35 s⁻¹. Pattern Ranges for this parameter set are indicated by different symbols. (b) Mean endpoint action potential rate as a function of normalized stimulus rate and period during normally distributed neural firing (T_n mean = 0.05 s, CV = 0.2) at four different intersite conduction times. (c) Fraction of the endpoint action potentials that are generated by the stimulation as a function of normalized stimulus rate or period.

3.3. Endpoint action potential trains during variable neural firing periods and different intersite conduction times

Similar patterns can be seen when the variability of neural firing is included, and when the conduction time is increased, as shown in figure 2(b). For long intersite conduction times, e.g., t_ic=0.02s, the mean action potential rate is relatively flat for stimulus frequencies below the neural firing rate, but then tracks the stimulus rate when it exceeds the neural rate. For stimulation directly at the neural source, i.e., t_ic=0.0s, the mean endpoint rate increases with stimulus rate, but non-monotonically, with periods of alternating slope until well above the neural firing rate, where the endpoint firing rate approaches the stimulus rate, and becomes independent of intersite conduction time. For intermediate intersite conduction times, the behavior is also intermediate between the two examples, with some reduction in endpoint rate with increasing t_ic, and gradual scaling of the fluctuations to lower stimulus rates.

The stimulus rate and intersite conduction time also influence whether the action potentials arriving at the endpoint originate from the neuron or from the stimulus, as shown in figure 2(c). For the longest intersite conduction time, t_ic=0.02s, the fraction of the endpoint action potentials due to stimulation increases nearly linearly with stimulus rate until saturating at unity when the stimulus rate is greater than the neural rate. At zero intersite conduction time, the slope of the dependence is lower and fluctuates similarly to the mean rates, but the fraction of stimulus generated action potentials increases monotonically. At intermediate intersite conduction times, the behavior is intermediate between the two extremes described above.

3.4. Relative distribution of action potential interaction mechanisms

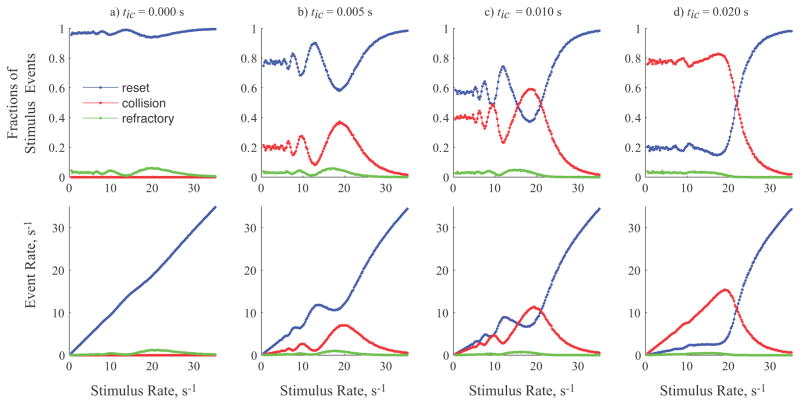
The mechanisms of interaction between action potentials from the neural and stimulation sources vary with relative frequencies and intersite conduction times, as illustrated in figure 3. The top row shows the fraction of stimuli that produce resets, collisions, and refractory blocks. The bottom row shows the overall rates for the different events, taking into account the actual stimulus rate.

Figure 3.

Fractions of stimulus events (top row) and overall event rates (bottom row) for resets, collisions, and refractory blocks as a function of the stimulus rate during normally distributed neural firing (T_n mean = 0.05 s, CV = 0.2). Each column shows the stimulus fractions and event rates at four different intersite conduction times ranging from 0 to 0.02 s, as in figure 2(b, c).

Regardless of intersite conduction time, stimulation rates greater than the neural rate yields high rates of resetting, low rates of collisions, and virtually no refractory blocks since resetting prevents any neural action potentials from being generated. For stimulus rates below the neural firing rate, there is a strong dependence on conduction time. For stimulation at the neural site, figure 3 column (a), there are no opportunities for collisions and so interaction is dominated by resets since the refractory period is short relative to the stimulus period. Therefore, the rate of resets increases in proportion to stimulus rate. As intersite conduction time increases, figures 3 columns (b–d), resetting decreases due to increasing rates of collision events. At t_ic=0.01 s, the fractions of stimuli and the rates of collision and resetting events are similar, but complementary. Comparing the plots for the longest value of intersite conduction time in column 3(d) to the plots for zero intersite conduction time in column 3(a) shows a near reversal of the importance of collision and resetting events for rates below the mean neural firing rate.

3.5. Distribution of endpoint firing periods

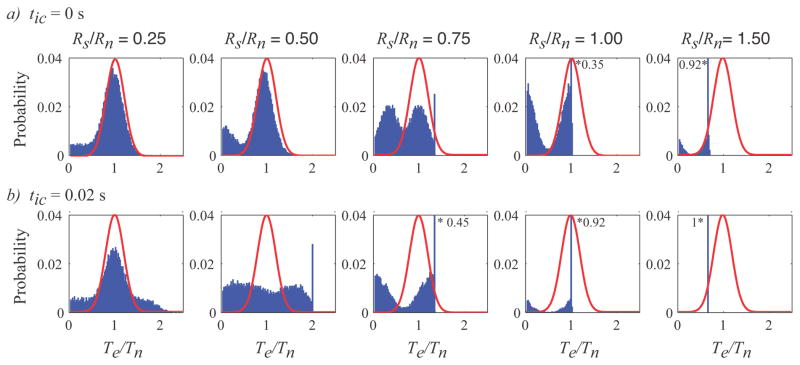
Stimulation also changes the probability distribution of endpoint firing periods. The probability distributions in figure 4 show the dependence of the normalized endpoint firing period on the intersite conduction time and the ratio of stimulus rate to mean neural firing rate. At stimulus rates significantly higher than the neuronal firing period, e.g. R_s/R_n = 1.5, the periods of the action potentials arriving at the endpoint are dominated by the stimulus period, due to the high fraction of resetting, as shown in figure 3. As the stimulus rate decreases, the distribution shifts from being dominated by the stimulus to being bimodal, e.g. at R_s/R_n = 0.5 or 0.75, to eventually being dominated by the neural source, e.g., at R_s/R_n = 0.25. The shift occurs more rapidly as the intersite conduction time increases, since there is more time for collision block interactions. The distribution of action potential periods can be much broader than the distribution without stimulation. Stimulation, even at low rates, can increase the fraction of both shorter periods and longer periods. At long intersite conduction times, the periods can exceed twice the mean neuronal firing period. The refractory interaction prevents any of the distributions from including periods less than the refractory time.

Figure 4.

Probability distribution of endpoint action potential periods normalized to the mean neuronal firing period (T_e/T_n) as functions of stimulus rate and intersite conduction time. Each row (a, b) is for a fixed intersite conduction time of 0 and 0.02s respectively. Each column is for a different ratio of stimulus rate to mean neuronal firing rate. For reference, the continuous red lines show the probability of the action potential period in the absence of any stimulation. Each histogram bin is 1 ms wide. All histograms have the same scale to facilitate comparison, and the bins marked by * give the value when it exceeds the scale.

4. Discussion

To our knowledge, this is the first systematic study of the interactions between neurally generated and stimulated action potential trains that combines all three mechanisms of collision block, neural source resetting, and refractory periods. We found that the average action potential period and probability distribution at the axon endpoint depends not only on the relative firing rates of the two sources, but also on the intersite conduction time between the two sources. For short intersite conduction times relative to the neural firing period, the mean action potential rate and variance increase, and the interactions are dominated by resetting. As the intersite conduction time approaches half the neural firing period, the average action potential rate approaches the higher of the two sources, the variance is reduced, and the interactions are dominated by collision block. Overall, the fraction of the endpoint action potentials originating from the stimulation increases continually with stimulus rate until none of the neurally generated action potentials reach the endpoint when the stimulus rate meets or exceeds the high end of the neural rate distribution.

4.1. Contributions of action potential interaction mechanisms

The mechanisms of action potential interaction included in this model are well known, and have been demonstrated in various experimental and theoretical studies. Refractory blockage played a small role, typically accounting for 2% – 5% of the interactions in figure 3, and primarily for R_s/R_n<1. The rate of refractory blockage for random timing would be expected to be 3% for the examples shown in figure 4 (t_r/T_n = 0.0015s/0.05s = 0.03). The fraction of refractory blocks would increase if the stimulus intensity was reduced to near threshold and the relative refractory period was included in the model, but would still remain a small percentage of the total events at typical peripheral nerve firing rates.

Collision block requires a length of axon for the collisions to occur, and the longer the conduction time between action potential sources, the higher the fraction of collisions, as shown in figure 3. Interestingly, conduction time is twice as significant as the stimulus period in determining the fraction of collisions (see figures 1(f), 3 and eqns. 2, 3) since the colliding stimulus action potential can be generated either before or after the neural action potential is generated. The intersite conduction time is affected both by the distance from the neural source, and by the conduction velocity. Thus, collisions will be more frequent for small diameter, slow conducting axons than for large diameter, fast conducting axons even at the same action potential source rates.

Resetting occurs more frequently at high R_s/R_n ratios and with short intersite conduction times, as seen in figure 3. In contrast to symmetrical resetting observed in multiple encoder sites, resetting by stimulation is asymmetrical. The stimulus can reset the neuron but the neuron cannot reset the stimulus. Resetting and collision block have opposing dependencies on the intersite conduction time. With the shortening of intersite conduction time, the opportunities for collisions are lost, increasing the rate of resetting.

The three interaction mechanisms have different effects on the fraction of endpoint action potentials that originate from the neuron or from the stimulus. Refractory blocks have no effect on the conduction of neural action potentials, since a collision block precedes any stimulus induced refractory period. However neural action potentials can occlude the stimulation.

Collisions and resetting events are complementary in number, but both contribute to loss of neuronal information reaching the endpoint. Collision blocks do not change the number of endpoint action potentials, but shorten the time of arrival and switch the action potential source from the neuron to the stimulus. Thus, the mean endpoint rate will stay the same and the neuron will fire at the same rate, but the fraction of endpoint action potentials from the neuron will decrease. In contrast, resetting delays the generation of the next neuronal action potential, while sending a stimulus generated action potential to the endpoint. Thus, the net endpoint rate is increased above the neural rate, with the simultaneous loss of neuronal information.

4.2. Consequences and implications of interactions

The choice of stimulus rate has traditionally been used as a design variable for optimizing experimental or clinical outcomes of stimulation. The choice of electrode design and stimulus location along the nerve has also received some attention with regard to convenience, selectivity (Tyler and Durand, 2002, Grill and Mortimer, 1998), and recruitment order (Lertmanorat et al., 2006, Bergquist et al., 2011, Gregory and Bickel, 2005, Knaflitz et al., 1990). The effect of location on endpoint action potential patterns has not been considered before, and offers another opportunity to optimize stimulation protocols.

Our results show that the net effect of the stimulation is to block (occlude) neural activity from reaching the endpoint and to add activity that is generated by the stimulation. The gradual increase in occlusion with increasing stimulus rate replaces the neural activity with stimulus-linked activity, removing the information content in the neural code, while maintaining or even increasing the mean rate of endpoint action potentials. This is the equivalent of de-efferenting muscles or de-afferenting the sensory neurons, while maintaining or increasing the rate of endpoint firing.

In the case of muscle nerve stimulation, the switch of the action potential from the neural to the stimulated pool would remove its contribution to the voluntary EMG and add it to the M-wave. In the case of sensory stimulation, the temporal coding of the sensation would be disrupted and it would likely interfere with perception. This may contribute to paresthesias during stimulation. Similarly, resetting decreases the number of action potentials arising from the neuron by lengthening the neural firing period. However, each resetting is accompanied by an endpoint action potential from the stimulation site. The combination of asymmetrical resetting and short intersite conduction times allows stimulation to increase the mean rate of endpoint action potentials even when the neuron is firing faster than the stimulus.

The loss of neural modulation increases progressively with both stimulus rate and intersite conduction time. Thus, stimulation close to the neural source can increase the mean firing rate and preserve a higher fraction of neural information reaching the endpoint than stimulation applied closer to the endpoint. To achieve the same mean endpoint rate with a long intersite conduction time requires a higher stimulation rate and a greater loss of neuronal information.

This study was motivated in part by the goal of augmenting voluntary contraction strength in individuals with impaired movement poststroke. Several experimental studies demonstrated that the contractions elicited by stimulation during voluntary effort do not add linearly, i.e., there is partial occlusion (Langzam et al., 2006, Yeom and Chang, 2010a, Perumal et al., 2010, Makowski et al., 2013). In a separate study, we demonstrate that the occlusion arises in part from the interactions shown here, but that there are additional mechanisms that lie in the physiological response properties of muscle (Crago and Makowski, 2012). Thus, optimization of stimulation for specific applications must also consider the physiological response properties of the systems receiving the endpoint action potential trains.

For motor efferent stimulation, reducing the intersite conduction time implies stimulating proximally rather than distally. Motor point stimulation with surface, epimysial or intramuscular electrodes or nerve cuff stimulation on specific muscle nerve branches is usually employed to achieve muscle selectivity (Peckham and Kilgore, 2013). For distal limb muscles such as those controlling the wrist or ankle, this means that the intersite conduction times are relatively long given typical motor unit firing rates. However, for proximal muscles such as those controlling the shoulder or hip, motor point or muscle nerve stimulation would have low intersite conduction times. To achieve low intersite conduction times for distal muscles, stimulation would have to be applied to compound nerves containing axons innervating multiple muscles and probably also containing cutaneous sensory nerves. Activating specific muscles while stimulating a compound nerve requires selective nerve stimulation technologies (Grill and Mortimer, 1996, Fisher et al., 2013, Badia et al., 2011).

For afferent stimulation, the intersite conduction time is lowest for stimulation near the sensory receptors, which is also the location that offers the most spatial selectivity. As with motor stimulation, proximal receptors will have intrinsically short intersite conduction times.

Experimental validation of the model predictions could be carried out directly in reduced preparations. Alternatively, the predictions could be validated indirectly in human subjects by measuring the physiological effects of stimulation and their dependence on stimulus rate and intersite conduction time. Interpretation of experimental outcomes will require models of the physiological effects of altering the endpoint action potential trains, including possible interactions due to reflexes. A modeling study of motor stimulation superimposed on neurally driven contractions predicts greater net force and a larger fraction of neural action potentials reaching the muscle at low stimulus rates for proximal compared to distal stimulation sites (Crago and Makowski, 2014). The greater force reflects higher motor unit firing rates, while the higher fraction of neural action potentials will produce a larger neural component of the EMG with proximal stimulation. Several investigators have performed similar stimulation experiments during voluntary contractions in multiple muscle groups, demonstrating the feasibility of these experiments, although all of the studies reported to date include relatively high stimulus rates and employ motor point stimulation of relatively distal muscles with long intersite conduction times (Langzam et al., 2006, Yeom and Chang, 2010b, Perumal et al., 2010, Makowski et al., 2013).

4.3. Limitations of the current study

The paradigms investigated in our study always included stimulation applied at a constant rate and neural rates with fixed means and normally distributed firing periods. However, the action potential pattern is as important as the mean rate in determining which action potentials will arrive at the endpoint and how the physiological system will respond. The same mean rate can be obtained with an infinite range of firing patterns. Stimulation is generally carried out at a constant frequency, but in some cases, bursts or variable patterns of stimuli are more effective in eliciting a physiological response, e.g., (Bruns et al., 2009 Bruns et al., 2009). Similarly, neural firing is characterized by high variability of firing periods, with bursts of motor neuron activity during dynamic motor activity, and with bursts of afferent firing in response to the onset of a physiological stimulus (phasic response), or as part of the normal phasic nature of a natural stimulus (e.g., touch, locomotion). High frequency bursts from either source would tend to dominate lower rate firing from the other source. The consequences of action potential interactions in these dynamic situations could be similarly analyzed using the interaction model developed in this study.

The duration of the refractory period varies with the amplitude of the stimulus relative to the minimum value that is required in the absence of prior activity. The absolute refractory period is followed by a relative refractory period when a second action potential can be elicited by a stronger stimulus. We did not model the relative refractory period in this study, so the results represent what would be expected with a strong (suprathreshold) stimulus on single axons. In peripheral nerve stimulation, there will be a range of axonal diameters and therefore relative thresholds, and thus including the relative refractory period will require knowledge of the stimulus amplitudes.