General Recognition Theory with Individual Differences: A New Method for Examining Perceptual and Decisional Interactions with an Application to Face Perception

Abstract

A common question in perceptual science is to what extent different stimulus dimensions are processed independently. General recognition theory (GRT) offers a formal framework via which different notions of independence can be defined and tested rigorously, while also dissociating perceptual from decisional factors. This article presents a new GRT model that overcomes several shortcomings with previous approaches, including a clearer separation between perceptual and decisional processes and a more complete description of such processes. The model assumes that different individuals share similar perceptual representations, but vary in their attention to dimensions and in the decisional strategies they use. We apply the model to the analysis of interactions between identity and emotional expression during face recognition. The results of previous research aimed at this problem have been disparate. Participants identified four faces, which resulted from the combination of two identities and two expressions. An analysis using the new GRT model showed a complex pattern of dimensional interactions. The perception of emotional expression was not affected by changes in identity, but the perception of identity was affected by changes in emotional expression. There were violations of decisional separability of expression from identity and of identity from expression, with the former being more consistent across participants than the latter. One explanation for the disparate results in the literature is that decisional strategies may have varied across studies and influenced the results of tests of perceptual interactions, as previous studies lacked the ability to dissociate between perceptual and decisional interactions.

A common goal in perceptual science is to determine whether some stimulus dimensions or components are “special,” in the sense of being processed and represented independently from other types of information. In vision, for example, much research has focused on determining whether there is independent processing of object and spatial visual information (e.g., Ungerleider & Haxby, 1994), different kinds of shape properties (e.g., Blais, Arguin, & Marleau, 2009; Stankiewicz, 2002; Vogels, Biederman, Bar, & Lorincz, 2001), different semantic categories of objects (e.g., Beeck, Haushofer, & Kanwisher, 2008; Kanwisher, 2000), identity and expression in faces (e.g., Bruce & Young, 1986; Haxby, Hoffman, & Gobbini, 2000), etcetera.

In the behavioral literature, a variety of concepts have been proposed to describe interactions in the processing of sensory dimensions (see Ashby & Townsend, 1986), each of them related to one or more operational definitions of dimensional interaction. Much behavioral research on the independence of stimulus dimensions has been performed by testing interactions through such operational definitions.

The best current framework for the analysis and interpretation of studies aimed at testing different forms of independence between stimulus dimensions is offered by general recognition theory (GRT; Ashby & Townsend, 1986). GRT is an extension of signal detection theory to cases in which stimuli vary on more than one dimension. GRT inherits from signal detection theory the ability to dissociate perceptual from decisional processes in perception, while also offering a formal framework in which different forms of dimensional interaction can be defined and studied.

Unfortunately, several severe restrictions of the GRT model used in the past greatly limit its usefulness. For the most popular experimental designs, GRT has more free parameters than there are degrees of freedom in the data. Thus, it is impossible to fit the full model to these data and so some restrictive assumptions must be imposed. Even with such assumptions, the small number of degrees of freedom increases the risk of over-fitting. Another restriction is that the model must be fit separately to the confusion matrix of each individual participant. For each fit, one can ask whether two dimensions interact, but what conclusion can be drawn if the data of 13 participants show some form of interaction and the data of 7 participants do not show such interaction? Finally, recent research has shown that traditional GRT analyses can not clearly distinguish between decisional and perceptual interactions between dimensions (Mack, Richler, Gauthier, & Palmeri, 2011; Silbert & Thomas, 2013).

This article describes a generalization of GRT that solves all of these problems. Briefly, the model we describe was inspired by individual-differences multidimensional scaling (INDSCAL; Carroll & Chang, 1970). The model simultaneously fits the data of all participants. It assumes that all participants share the same perceptual distributions, but like INDSCAL, it allows each participant to divide his or her attention differently between the two stimulus dimensions. In addition, unlike INDSCAL, the new model allows each participant to use unique decision bounds. As we will see, the model gives a remarkably accurate simultaneous account of the data from many different participants, and as a result, we believe it offers the strongest method currently available for studying perceptual and decisional interactions.

The following sections provide a more detailed description of GRT, of the types of interactions defined within GRT, and of the problems with traditional GRT approaches. Then the new generalized GRT model is presented and applied to the analysis of interactions between identity and emotional expression in face perception.

General Recognition Theory

Overview

As in signal detection theory, GRT assumes that the perceptual effects of a stimulus are not fixed, but vary across stimulus presentations according to some probability distribution. Some applications of GRT do not make any assumptions about the shape of such perceptual distributions (e.g., Ashby & Maddox, 1994; Ashby & Townsend, 1986), but most assume that they are multivariate normal.

The most common applications of GRT are to tasks in which stimuli are constructed from the factorial combination of two levels of two stimulus components, A and B, resulting in four stimuli: A₁B₁, A₂B₁, A₁B₂ and A₂B₂. In an identification experiment, participants are shown one of these four stimuli (chosen randomly) on each trial and are then required to identify uniquely which stimulus was presented. The data from this experiment are typically collected in a 4 × 4 confusion matrix, with a row for each stimulus and a column for each response. The entry in row i and column j lists the number of trials that the participant responded with the jth response when stimulus i was presented. This matrix has 12 degrees of freedom (4 × 3) because the sum of entries in each row is constrained to equal the number of times the associated stimulus was presented in the experiment.

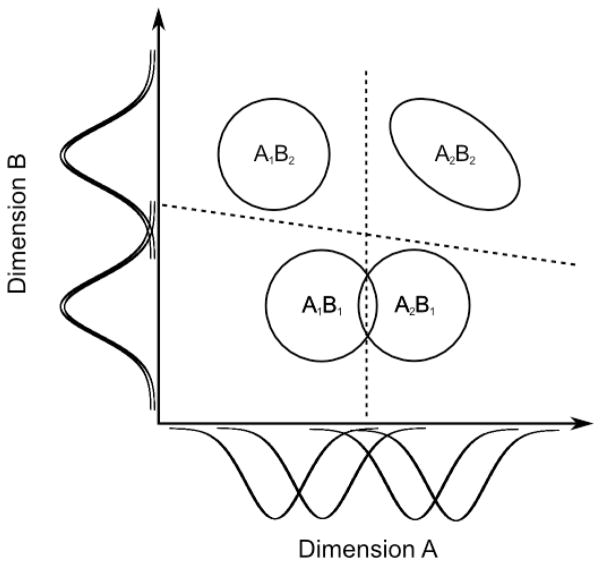
Figure 1 shows an example of a multivariate normal GRT model for such a typical 2×2 design. Each stimulus has a different distribution of perceptual effects, represented by an ellipse. The ellipse describes the shape that a scatterplot would take if many random samples were drawn from the associated perceptual distribution. The lines are the decision bounds that separate the perceptual plane into four response regions. GRT can be used to make inferences about perceptual and decisional interactions by studying the perceptual distributions and decision bounds of the best-fitting model.

Figure 1.

Example of a multivariate normal GRT model for an experiment with 2 dimensions and two levels in each dimension (2×2 design). Ellipses represent contours of equal likelihood for the perceptual distribution of a specific stimulus. The univariate normal distributions represent marginal distributions.

GRT rigorously defines a number of different types of dimensional interaction (Ashby & Townsend, 1986), the most popular of which are perceptual separability, perceptual independence and decisional separability. Dimension A is perceptually separable from dimension B if the perception of A does not depend on the level of dimension B. In GRT, this condition holds if and only if the marginal distribution of perceptual effects along dimension A does not depend on the level of B. Marginal distributions for dimensions A and B are depicted at the bottom and left of Figure 1, respectively. It can be seen that the marginal distributions for B₁ are the same for both levels of A. Similarly, the marginal distributions for B₂ are also the same for both levels of A. This means that dimension B is perceptually separable from dimension A. On the other hand, the marginal distributions for dimension A are closer for level 1 of dimension B than for level 2 of dimension B. Thus, dimension A is not perceptually separable from dimension B.

Dimension A is decisionally separable from dimension B if the decision about the level of A does not depend on the perceived value of component B. In GRT this condition holds if and only if the decision bounds are vertical and horizontal lines. In Figure 1, dimension A is decisionally separable from dimension B, but dimension B is not decisionally separable from dimension A.

Perceptual and decisional separabilities deal with interactions between dimensions that are manifest by comparing perceptual representations across stimuli. Perceptual independence, on the other hand, deals with dependencies that occur when a single stimulus is perceived. Two dimensions are perceived independently for stimulus A_iB_j if the perceived value on dimension A is statistically independent of the perceived value on dimension B. In the multivariate normal model, which considers only linear relations between dimensions, this means that two dimensions are independent for stimulus A_iB_j if their correlation is zero. For example, perceptual independence holds for all stimuli in Figure 1 except A₂B₂, which is the only one in which the contour of equal likelihood is diagonally oriented, representing a negative correlation between dimensions.

Once identification data are collected, two approaches can be used to analyze the resulting empirical confusion matrix. The summary statistics approach (Ashby & Townsend, 1986; Kadlec & Townsend, 1992a, 1992b) consists of computing various summary statistics from the confusion matrix and then checking whether these satisfy certain conditions that are diagnostic for perceptual separability, decisional separability, or perceptual independence. The model-based approach (Ashby & Lee, 1991; Thomas, 2001) consists of fitting one or more GRT models to the empirical confusion matrix and selecting the model that describes the data best. The focus of the present work is on expanding and improving the model-based approach.

Problems with GRT

As mentioned above, despite its usefulness, GRT suffers from several weaknesses when applied to the 2 × 2 identification experiment. These weaknesses are not inherent to the theory. They either arise exclusively when the 2×2 design is used or they stem from current practice in the application of GRT. Even so, these problems are not trivial, as the 2×2 design is the smallest design (in terms of numbers of stimuli and responses) that allows an evaluation of the most important types dimensional interaction. The task is simple and easy to learn, and the experiment does not need to be overly long to sample enough data to estimate each of the 16 cells in the confusion matrix accurately. The ease with which a 2×2 experiment can be run and analyzed has made it very popular among researchers.

A number of the weaknesses vanish when GRT is applied to data from a 3×3 identification experiment (e.g., Ashby & Lee, 1991), which requires training 9 stimulus-response assignments and estimating 81 entries in the confusion matrix. However, this requires a long experiment (5 days in Experiment 1 of Ashby & Lee, 1991) and the possibility of disrupting processing due to high working memory requirements (i.e., since the participant must memorize 9 response labels). A further advantage of the 2×2 design over the 3×3 design is that only the former allows testing separability of stimulus “components” that cannot be ordered along continuous dimensions (e.g., there is no correct way of ordering two faces along an “identity” dimension). In this case, the GRT model for a 2×2 design is not influenced by the way in which we choose to order the levels of each component; that is, levels 1 and 2 in one dimension can be reversed without changing conclusions about dimensional interactions. This is not true of the GRT model for a 3×3 design, in which altering the order of the levels along a dimension is likely to alter the results of our analyses.

As mentioned above, the first problem with applications of GRT is that the number of degrees of freedom provided by the data in a 2×2 experiment is too small to fit the full model. The full model has 20 free parameters, but the 4 × 4 empirical confusion matrix that results from the Figure 1 experiment has only 12 degrees of freedom. Thus, experimenters using the 2×2 design must fix some parameters to constant values in order to fit a GRT model to data. In general, fixing any parameter in the model will constrain the researcher’s ability to evaluate a specific form of dimensional interaction. For example, constraining the decision bounds to be horizontal or vertical lines has been common in previous applications (e.g., Silbert, 2012; Thomas, 2001) and doing so is equivalent to making the assumption that decisional separability holds for the task under study. Similarly, fixing all variances to the same value (e.g., Fitousi & Wenger, 2013; Silbert, 2012) assumes a form of perceptual separability in which perceptual noise along each dimension does not depend on the level of the other dimension. Ideally, a full characterization of the interactions between two dimensions should not rely on any a priori assumptions about how the dimensions interact (Silbert, 2012).

A second, related problem is that the small number of data points available from a 2×2 design, relative to the number of parameters that need to be fit, means that there is always a risk of model over fitting. When several models are fit to the data, as we fit increasingly complex models we increase the likelihood that the model is fit to random error instead of describing real properties of perceptual and decisional processes. This can lead to variability in the results across participants in aspects that we might not expect to be variable, such as perceptual independence and separability (e.g., Fitousi & Wenger, 2013; Mestry et al., 2012; Silbert, 2012).

A third problem is that systematic methods for pooling results across participants have rarely been explored. The interpretation of the overall pattern of results from each experiment is usually left to the researcher’s judgment, instead of having a statistically sound basis. One solution to this problem has been provided by Silbert (2012), who proposed a hierarchical model in which the parameters governing each individual’s perceptual and decision processes are drawn from normal distributions, each with a different mean and variance hyper-parameter. This allows examining group effects by estimating the values of such hyper-parameters. This model, however, does not solve the first two problems mentioned earlier.

Finally, two recent publications have called into question the validity of conclusions about decisional separability that can be reached using GRT analyses. Mack and colleagues (Mack, Richler, Gauthier, & Palmeri, 2011) have shown through simulated data that, when the summary statistics approach is used, some cases of violations of perceptual separability are misclassified as violations of decisional separability. This issue is not critical when one considers that most applications of GRT use the summary statistics approach in conjunction with model-based analyses or other tests. A more serious challenge has been raised by Silbert and Thomas (2013), who showed analytically that a failure of decisional separability is non-identifiable in the 2×2 identification experiment. That is, if the data from an experiment can be fit by a GRT model in which decisional separability fails, then it is always possible to find a different GRT model in which decisional separability holds and that predicts the exact same data pattern. This result is explained schematically in Figure 2. In the left panel, we see four perceptual distributions for the stimuli in a 2×2 identification experiment. The solid lines represent the decision bounds used by a participant in this experiment (the dotted lines should be ignored for now). It can be seen that decisional separability fails for this participant. The right panel shows that a simple transformation of the perceptual space (rotating and shearing) leads to a model producing the exact same response probabilities, but in which now decisional separability does hold. Furthermore, the transformation also goes from a model with perceptual separability and independence (left) to a model without perceptual separability or independence (right).

Figure 2.

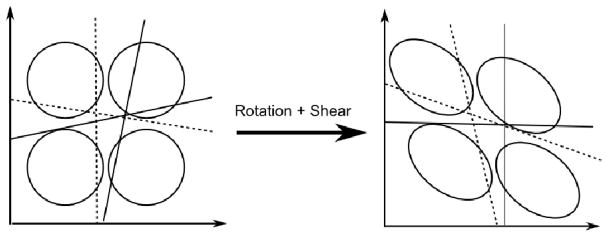
Example of how, in the 2×2 design, a simple transformation of the perceptual space can render a GRT model with violations of decisional separability into a different GRT model yielding the same response probabilities and no violations of decisional separability. A second set of decision bounds is included to show why the same is not true for GRT-wIND.

GRT with Individual Differences (GRT-wIND): An extension to General Recognition Theory

The GRT-wIND model is inspired by three-way multidimensional scaling models (for a review, see chapters 21 and 22 in Borg & Groenen, 2005). Data analysis using these models is also known as individual differences scaling, or INDSCAL, after a popular algorithm used to find solutions (Carroll & Chang, 1970). These models assume that the similarity data from a number of individuals can be explained by a common perceptual space, but that the relative weight or saliency of the dimensions of this space might be different for different people.

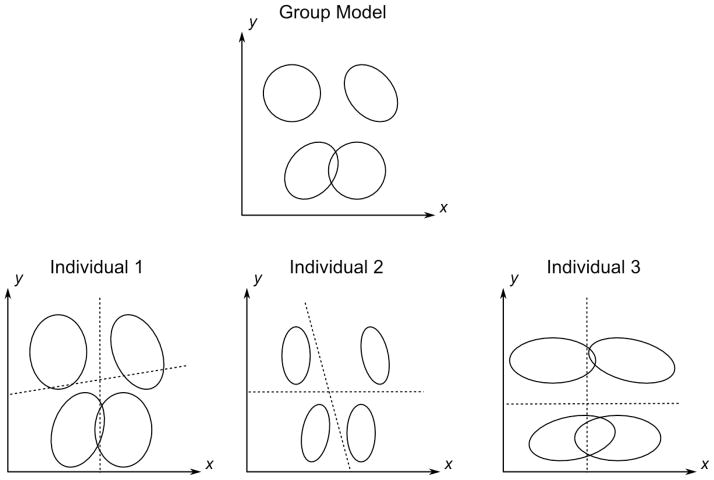
A schematic representation of the new GRT-wIND model is shown in Figure 3. The model assumes that the structure of the perceptual distributions is the same for all participants; that is, some aspects of perception are universal, in particular the relations between dimensions within stimuli (covariance of each distribution) and across stimuli (the means of each distribution and the ratio of their variance along a dimension). This is represented by a single set of perceptual distributions in the “Group model” at the top of Figure 3. On the other hand, it is also assumed that attentional and decisional processes could vary across individuals. This is represented by the three models at the bottom of Figure 3. Note first how all perceptual interactions are the same across individual models. On the other hand, each individual model has a different scaling of the variances along a particular dimension, representing individual attentional processes. For example, in Participant 1, variances are extended in the direction of the y-axis, representing the fact that this participant is paying little attention to dimension B. Participant 2 shows a different pattern, in which variances are shrunk in the direction of the x-axis, representing higher attention to dimension A. Each individual participant model also has a different set of two decision bounds that divide the perceptual space into response regions, instantiating the assumption that decision processes might vary across participants. For example, for Participant 3, both bounds are orthogonal to the dimension they divide, whereas this is not true for Participants 1 and 2.

Figure 3.

Schematic representation of the GRT-wIND model.

Within the framework of GRT-wIND, perceptual separability and perceptual independence are phenomena that should hold or fail for all participants in any given experiment. Although attention might change how well an individual can discriminate a dimension, it should not affect the structure of perceptual interactions. On the other hand, decisional separability is a phenomenon that can hold in some individuals and fail in others, or even vary for a single individual as a function of factors such as training with a task.

To describe the model more specifically, assume we have run a 2×2 identification experiment, in which stimuli vary along two dimensions A and B, each with two levels indexed by i=1, 2, and j=1, 2, respectively. Suppose there are N participants in the experiment, indexed by k=1, 2, … N. The GRT-wIND model for this experiment has 16 group parameters, which control the distributions of perceptual effects. These distributions are assumed to be bivariate normal and common to all participants. Each distribution is described by a mean vector:

$${\underset{\_}{\mu }}_{A_i{B}_j}=\left[\begin{array}{c}{\mu }_{A_i{B}_{j}1}\\ {\mu }_{A_i{B}_{j}2}\end{array}\right],$$ (1)

and a covariance matrix:

$${\mathbf{\sum }}_{A_i{B}_j}=\left[\begin{array}{cc}{\sigma }_{A_i{B}_{j}1}^2& {\rho }_{A_i{B}_j}{\sigma }_{A_i{B}_{j}1}{\sigma }_{A_i{B}_{j}2}\\ {\rho }_{A_i{B}_j}{\sigma }_{A_i{B}_{j}1}{\sigma }_{A_i{B}_{j}2}& {\sigma }_{A_i{B}_{j}2}^2\end{array}\right],$$ (2)

where ρ_AiBj is a correlation parameter. We can arbitrarily set μ_A1B1 = [0, 0] and σ_A1B11 = σ_A1B12 = 1, which fix the position and scale of the final solution. The remaining group parameters are two means and two variances for each of the other perceptual distributions (4 × 3 = 12), plus a correlation parameter for each distribution (4).

The model also has 6 parameters that describe processes unique to each individual. Two of these parameters, κ_k and λ_k, control the level of attention that participant k allocates to each dimension. We assume that the effect of attention to one dimension is to increase the discriminability of stimuli along that dimension. Within the GRT framework, this can be done by either increasing the distance between means of distributions along the relevant dimension or by decreasing the variances of the distributions along the relevant dimension. Here, we implement attention as affecting variances, because this is consistent with previous modeling of attention using GRT (Maddox, Ashby & Waldron; 2002) and because it seemed more straightforward and easier to interpret than modifying the distances between means across subjects. The parameter κ_k > 0 represents a global level of attention. High values of κ_k decrease the values of all variances, leading to fewer confusion errors in general. The parameter λ_k is a selective attention parameter that ranges from 0 to 1. A value of λ_k = 0.5 represents equal attention to each dimension. High values of λ_k decrease the variances on dimension A and increase the variances on dimension B, representing selective attention to A. The opposite is true for low values of λ_k. The covariance matrix for the distribution of perceptual effects of A_iB_j in participant k is equal to:

$${\mathit{\sum }}_{A_i{B}_{j}k}=\left[\begin{array}{cc}\frac{{\sigma }_{A_i{B}_{j}1}^2}{{\kappa }_k{\lambda }_k}& {\rho }_{A_i{B}_j}\frac{{\sigma }_{A_i{B}_{j}1}{\sigma }_{A_i{B}_{j}2}}{\sqrt{{\kappa }_k^2{\lambda }_k(1-{\lambda }_k)}}\\ {\rho }_{A_i{B}_j}\frac{{\sigma }_{A_i{B}_{j}1}{\sigma }_{A_i{B}_{j}2}}{\sqrt{{\kappa }_k^2{\lambda }_k(1-{\lambda }_k)}}& \frac{{\sigma }_{A_i{B}_{j}2}^2}{{\kappa }_k(1-{\lambda }_k)}\end{array}\right]$$ (3)

It can be seen that both parameters together determine the ability of a subject at discriminating each dimension relative to the group’s ability. When κ_kλ_k is greater than 1, the variance along dimension A is smaller than in the group model, leading to less overlap between perceptual distributions, representing higher individual discriminability on dimension A. A value of κ_kλ_k less than 1 increases the variance along dimension A relative to the group model, leading to more overlap between perceptual distributions on that dimension, and lower individual discriminability. Similarly, κ_k(1−λ_k) > 1 decreases the variance along dimension B and κ_k(1−λ_k) < 1 increases the variance along dimension B relative to the group solution.

The other four individual parameters describe the linear decision bounds that are assumed to be unique to each participant. Each single bound can be written as a discriminant function:

$$h_{Ak}(x_1,x_2)=b_{Ak1}{x}_1+b_{Ak2}{x}_2+c_{Ak},$$ (4)

where h_Ak represents the discriminant function used to classify component A by the kth subject. A similar equation can be used to describe h_Bk, the discriminant function used to classify component B by the kth subject. Only two of the three parameters b_Ak1, b_Ak2, and c_Ak are free however, because any line can be described by two parameters. Thus, the parameters b_Ak1 and b_Bk2 were fixed to a value of 1.0. The discriminant function has the property that it returns positive values for points (x₁, x₂) falling on one side of the bound (the first response area) and negative values for points on the other side of the bound (the second response area). Because the two-dimensional model has two linear bounds (h_Ak and h_Bk), four parameters are required to describe those bounds for each individual.

In the appendix, we describe procedures to estimate the parameters of a GRT-wIND model from identification data using maximum likelihood estimation. We also describe how to run statistical tests for perceptual independence, perceptual separability and decisional separability once the model has been fit to data. Traditionally, these tests are performed by fitting different GRT models to the same data and comparing them through a likelihood ratio test or through information criteria (Thomas, 2001; see Ashby & Soto, in press). The large number of parameters in a GRT-wIND model can make this strategy inconvenient, because fitting each single model to the data is computationally expensive. Here we recommend a different strategy, described in more detail below, in which maximum-likelihood parameter estimates are tested against expected values from null hypotheses using a Wald test (Wald, 1943).

The GRT-wIND model solves all the problems with the traditional application of GRT that were identified in the introduction. First, the full model can be fit to the data from any identification experiment, as long as the number of participants is large enough. This is because each additional participant in the experiment contributes more data points than the number of new parameters that must be estimated for that individual, increasing the total number of degrees of freedom. For the 2×2 design, each new participant adds data with 12 new degrees of freedom and requires the estimation of only 6 new parameters, so with N ≥ 3 it is possible to fit the full model, including the 16 group parameters.

Second, there is less risk of over-fitting using an GRT-wIND model than using a traditional GRT model, especially with small designs such as the popular 2×2 experiment. This is because in most cases it is feasible to gather data from many participants and obtain a large number of degrees of freedom. Using the 2×2 design, a sample size of 10 leads to 44 degrees of freedom after fitting the full model. A sample size of 20 leads to 104 degrees of freedom after fitting the full model.

Third, because perceptual distributions are assumed to be universal, all conclusions about perceptual factors are shared by the whole group of participants. Thus, analyses of perceptual separability and independence do not lead to disparate results for different individuals. Furthermore, individual differences in behavior are modeled as differences in attention and decision processes instead of as random error (Silbert, 2012). This allows us to study these individual differences and perhaps to test the model’s assumptions.

Finally, GRT-wIND does not suffer from the problem of non-identifiability of decisional separability in the 2×2 identification experiment, except in the extreme and unlikely case in which all participants in the study use decision bounds that are parallel to one another. If violations of decisional separability are found and individual decision bounds have slightly different slopes, then it is not possible to find an equivalent model (i.e., producing the same response probabilities) in which decisional separability holds for all participants, unless the assumption of universal perception is violated. This can be seen in Figure 2, where the dotted line represents the decision bound for a second participant in the experiment. Note how the transformation applied in the right panel, leading to decisional separability for the first participant does not lead to the same result for the second participant. The result would be the same with any other pair of decision bounds, unless they are parallel. Two separate transformations can be found that would independently lead to decisional separability for each participant, but the resulting model would assume different perceptual representations across participants. In the appendix, we offer a formal proof of the proposition that decisional separability is non-identifiable in the Gaussian GRT model with two or more bounds per dimension if and only if all bounds for each dimension are parallel to one another. We note that this condition for non-identifiability applies not only to GRT-wIND, but also to the traditional GRT model for designs larger than 2×2.

In the rest of this article, we apply GRT-wIND to study interactions between identity and emotional expression in face perception, with two goals in mind. The first is to explore how well GRT-wIND can describe data from an identification experiment compared to the traditional application of GRT. If the assumptions of the model are correct, then it should fit the data as well or better than individual GRT models, and deviations from a perfect fit should be randomly distributed. The second goal is to determine whether and how identity and expression interact during face perception, using for the first time an approach that clearly dissociates between different forms of independence and between perceptual and decisional factors.

An application to face perception

Researchers in face perception have shown much interest in the issue of whether or not identity and emotional expression are processed independently. This interest is largely due to the fact that influential theories of face recognition have proposed either completely independent (Bruce & Young, 1986) or partially independent (Haxby et al., 2000) processing of these important dimensions.

Most studies addressing this issue have not found complete independence of identity and emotion. Some studies that used the Garner filtering task (Garner, 1974) found an asymmetric pattern of interactions, in which identity is separable from expression, but expression is not separable from identity (Baudouin, Martin, Tiberghien, Verlut, & Franck, 2002; Schweinberger, Burton, & Kelly, 1999; Schweinberger & Soukup, 1998; for a comparative/evolutionary analysis of this effect, see Soto & Wasserman, 2011). This asymmetric interaction is also supported by the overall pattern of results from experiments using a face adaptation paradigm (Ellamil, Susskind, & Anderson, 2008; Fox & Barton, 2007; Fox, Oruç, & Barton, 2008; Pell & Richards, 2013). However, other studies have found interference in the processing of each dimension when there are variations in the other (Fitousi & Wenger, 2013; Ganel & Goshen-Gottstein, 2004; for facilitation effects, see Yankouskaya, Booth, & Humphreys, 2012), or a lack of such interference effects (Etcoff, 1984).

One problem with these previous studies is that they did not dissociate between different types of perceptual and decisional interactions. Furthermore, it has been shown that only some forms of integrality lead to an interference effect in the filtering task, whereas others cannot be observed using this test (Ashby & Maddox, 1994). Recently, Fitousi and Wenger (2013) applied GRT to the analysis of interactions between emotional expression and identity, and found no violations of perceptual independence in any of their participants, but violations of either perceptual or decisional separability in all participants. However, these results were obtained using the traditional GRT framework, so they are prone to all the shortcomings outlined previously.

Here, we take a new look at this problem by analyzing data from a 2×2 identification design using GRT-wIND. This is done with two goals in mind: (1) to evaluate the performance of GRT-wIND in describing real identification data, and (2) to analyze interactions between identity and emotional expression while distinguishing among different types of independence and dissociating perceptual from decisional processes.

Method

Participants

Twenty-six undergraduates at the University of California Santa Barbara were recruited to participate in this experiment. Each participant was given class credit for participation.

Stimuli and apparatus

The stimuli were four grayscale images of male faces (see Figure 8), part of the California Facial Expression (CAFE) database (Dailey, Cottrell, & Reilly, 2001). Images in this database were obtained from individuals trained to produce correct expressions according to the Facial Action Coding System (FACS; Ekman, Friesen, & Hager, 1978). Each face showed one of two identities with either a neutral or sad emotional expression. The identities were chosen in an attempt to avoid differences in discriminability between the two identities and the two emotions (Ganel & Goshen-Gottstein, 2004). The faces were shown through an elliptical aperture in a homogeneous gray screen; this presentation revealed only inner facial features and hid non-facial information, such as hairstyle and color.

Figure 8.

Scatterplot showing the values of the estimated attentional parameters. Kernel density estimates for the distribution of values of each parameter estimate are shown at the top and right of the scatterplot.

Stimulus presentation, feedback, response recording and response time measurement were controlled using MATLAB augmented with the Psychophysics Toolbox (Brainard, 1997), running on a Macintosh computer. Responses were given on a standard Macintosh keyboard: the “d” key for identity one with sad expression, the “f” key for identity one with neutral expression, the “j” key for identity two with sad expression, and the “k” key for identity two with neutral expression.

Procedures

The experiment lasted about 45 minutes and was composed of 12 blocks of 50 trials for a total of 600 trials. Participants were told that there were 4 stimuli and each stimulus corresponded to one of the assigned response keys; their task was to learn the mapping between stimuli and response keys. Participants were not verbally instructed about the correct response for each stimulus because, in our experience, instruction is of little help to master difficult discrimination tasks such as the one used here. Furthermore, participants still need to go through a practice period in order to eliminate the effects of initial perceptual learning from the data (see Lehky, 2000) and they could learn the stimulus-response mapping during this period. A trial proceeded as follows: a crosshair appeared on the screen for 200 ms prior to stimulus presentation. The stimulus was presented for 16.667 ms (at the refresh rate of the monitor, 60 Hz). After the presentation participants were to give a response using one of the four assigned response keys. Feedback was displayed in the middle of the screen beginning 500 ms after the response was collected and consisted of the word “Correct” in green font color or “Incorrect” in red font color. If a response was too late (more than 5 seconds), participants saw the words “Too Slow”. Feedback remained on screen for 500 ms, after which there was a 1 second intertrial interval. The participants were allowed to rest between blocks if they wished.

Results

The data from two participants were excluded from the analysis because their performance was at chance by the end of the experiment. GRT is a model of asymptotic performance, not of learning, so it is important to discard data during the learning period when estimating individual participant confusion matrices. Toward this end, learning curves were obtained by averaging performance within a moving window of 101 trials, starting with the average of trials 1 to 101, moving the window one trial up in each step (2–102, 3–103, and so on), and ending with the average of trials 500 to 600. An exponential function was fit to the resulting 500 average points that comprised the learning curves using least-squares estimation. The point in the best-fitting exponential curve where the slope was smaller than 0.001 for the first time was used as a cutoff: only data after this point were used to build individual confusion matrices. This cutoff ranged from trial 53 to 320 across participants, with a mean of 150.5.

Table 1 shows the average confusion matrix, obtained by transforming individual confusion matrices into response proportions and averaging those proportions across participants (individual confusion matrices can be found in the supplementary material). The numbers in parentheses represent the minimum and maximum proportion found across subjects.

Table 1.

Average confusion matrix. Numbers in cells represent average response proportions and ranges (min/max).

Stimuli	Responses
	Neutral-ID1	Sad-ID1	Neutral-ID2	Sad-ID2
Neutral-ID1	0.888 (0.711/1.0)	0.051 (0.0/0.235)	0.04 (0.0/0.184)	0.021 (0.0/0.103)
Sad-ID1	0.049 (0.0/0.196)	0.895 (0.707/0.992)	0.019 (0.0/0.081)	0.037 (0.0/0.131)
Neutral-ID2	0.047 (0.0/0.25)	0.018 (0.0/0.098)	0.879 (0.607/0.974)	0.056 (0.007/0.2)
Sad-ID2	0.051 (0.0/0.419)	0.092 (0.0/0.419)	0.131 (0.0/0.403)	0.727 (0.147/0.964)

Model fit to the data

GRT-wIND was fit to the data from individual confusion matrices using the procedures outlined in the appendix. To facilitate finding the global maximum of the likelihood function instead of a local maximum, the optimization was run 60 times, each time with different random starting values for the parameters. The solution with highest maximum likelihood was chosen as the best-fitting GRT-wIND model.

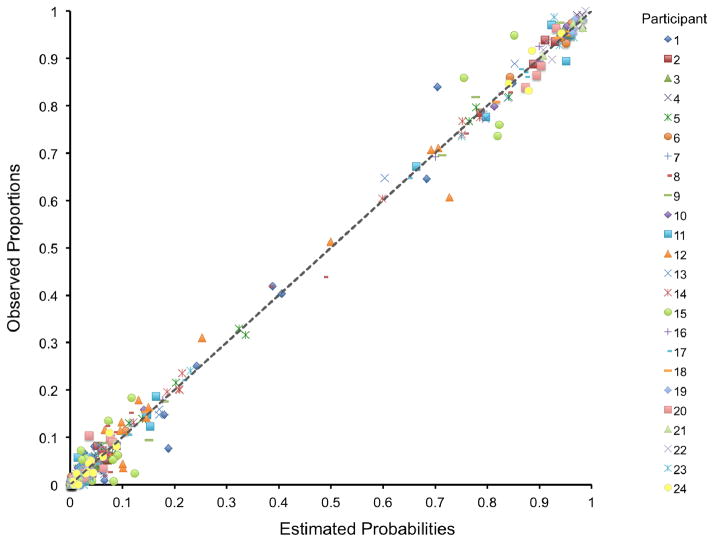
The best-fitting GRT-wIND model was used to estimate response probabilities for each cell in each participant’s confusion matrix. Figure 4 shows these estimated probabilities plotted against the corresponding observed response proportions. The data from each participant is plotted using a different symbol. The diagonal dotted line represents a perfect fit. It can be seen that there is a high level of correspondence between the 384 (i.e., 24 participants × 16 values in each matrix) observed and estimated values. In fact, the model accounted for 99.52% of the variance in the data (r = .9976). More importantly, the deviations from a perfect fit shown in Figure 4 (i.e., the differences between observed and predicted values, or residuals) seem to be randomly distributed around the dashed line across all values of the estimated probabilities. This observation was statistically confirmed by the results of a Durbin-Watson test, which indicated that the serial correlation in the residuals was not significantly different from zero, DW = 1.976, p > 0.5. A non-random distribution of residuals should produce a serial correlation different from zero. This suggests that all systematic variability in the data was captured by the model.

Figure 4.

Scatterplot depicting observed response proportions against predicted response probabilities. The data from different participants is plotted with different symbols. The diagonal line represents a model with perfect fit.

An important goal of the present experiment was to compare how well GRT-wIND would explain identification data compared to traditional GRT models. Unfortunately, a straightforward comparison is difficult in this case because, as indicated earlier, the full traditional GRT model cannot be fit to the data from a 2×2 identification experiment. Perhaps the best comparison would then be between the best-fitting GRT-wIND model found using the procedures proposed here and the best-fitting traditional GRT model found using the procedures commonly used in the literature. In the traditional model-based application of GRT (e.g., Ashby & Lee, 1991; Ashby, Waldron, Lee, & Berkman, 2001; Thomas, 2001), a number of different GRT models are fit to the data of each participant in a study. The different models are obtained by fixing different parameters to specific values, representing assumptions about perceptual independence, perceptual separability and decisional separability. For example, a model assuming perceptual independence would have all correlation parameters fixed to zero. Once the models are fit to data, model selection procedures are used to decide which one best describes the data for that particular individual (for a review, see Ashby & Soto, in press). Thus, in traditional GRT applications the perceptual representations are allowed to vary across individuals. GRT-wIND imposes the constraint that such representations should be the same for all people. If the assumption of universal perception is not true, then we would expect that using different models for different individuals would provide a better fit to data than using the GRT-wIND model.

To compare GRT-wIND to the traditional model-based approach, we fit the hierarchy of models shown in Figure 5 to the data from each participant, using maximum likelihood estimation. The hierarchy shown in Figure 5 was recommended previously to perform model-based GRT analyses (Ashby & Soto, in press) and is similar to those found in previous studies that have applied GRT to the 2×2 identification experiment (e.g., Thomas, 2001). Because there are only 12 degrees of freedom in the data, some parameters were fixed for all models: variances were set to one and decisional separability was assumed for both dimensions. In Figure 5, m represents the number of free parameters in the model, PS stands for perceptual separability, PI for perceptual independence, DS for decisional separability and 1_RHO describes a model with a single correlation parameter for all distributions. To facilitate finding the global maximum of the likelihood function, the optimization was run 20 times for each model, each time with different random starting values for the parameters, and the solution with highest maximum likelihood was chosen as the best solution.

Figure 5.

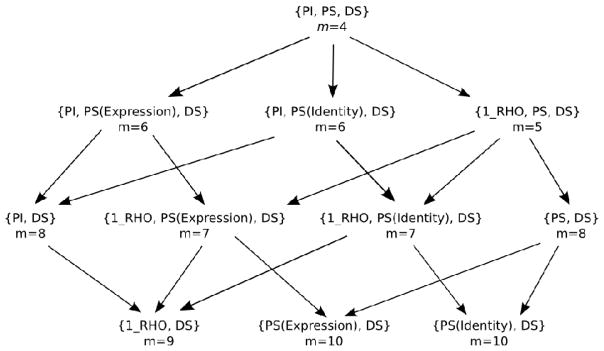
Hierarchy of GRT models fitted to individual confusion data. The number of free parameters is symbolized by m. PI stands for perceptual independence, PS for perceptual separability, DS for decisional separability and 1_RHO for a single correlation in all distributions.

Arrows in Figure 5 connect models that are nested within each other. The model selection procedure starts at the top of the hierarchy and compares nested models through a likelihood ratio test (see Appendix). If this test indicates significant differences in fit, the lower model is selected and the process continues. This process results in a small set of candidate non-nested models, which are compared using the corrected Akaike Information Criterion (AIC_C, see Appendix).

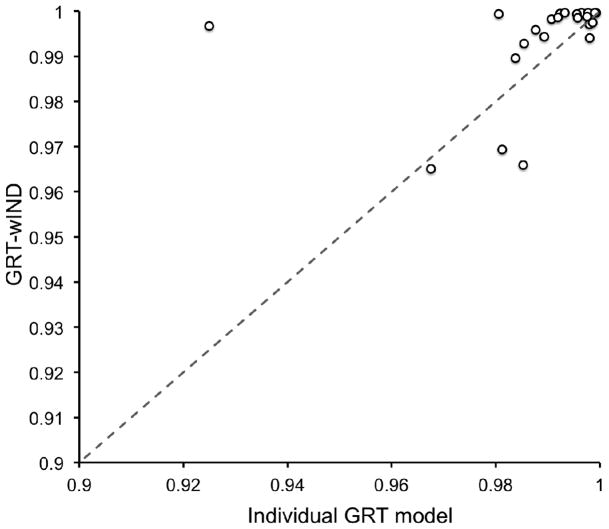
To compare how well GRT-wIND accounted for the data in each individual confusion matrix compared to the best-fitting traditional GRT model, we computed estimated response probabilities from both models and correlated them with the observed response proportions of each participant. From these correlations we computed the percentage of variance in the individual data explained by each model. Figure 6 shows the results of this analysis in the form of a scatterplot, with each dot representing one participant. The position of the dot along the abscissa represents the fit of the traditional GRT model, whereas the position along the ordinate represents the GRT-wIND fit. The diagonal represents equal fits for both models. Both models account for a high percentage of variance, but GRT-wIND provides a better fit than the best-fitting traditional GRT model for 18 out of the 24 participants. This number of successes is significantly higher than chance according to a sign test, p < .05, Cohen’s g = .25. The success of GRT-wIND is especially impressive here, given that the number of free parameters in GRT-wIND (i.e., 160) was less than the sum of the number of parameters of the best-fitting traditional GRT models (i.e., 166, see Table 2).

Figure 6.

Comparison of percentage of variance in the data from each individual confusion matrix explained by GRT-wIND and the best individual GRT model. Each circle represents results from a single participant.

Table 2.

Best-fitting GRT model (from those shown in Figure 5) for each participant in the experiment. PI stands for perceptual independence, PS for perceptual separability, DS for decisional separability and 1_RHO for a single correlation in all distributions.

Participant	Best-fitting model	Number of free parameters
1	{PS(Identity), DS}	10
2	{PS, DS}	8
3	{1-RHO, PS(Identity), DS}	7
4	{1-RHO, PS(Identity), DS}	7
5	{PS, DS}	8
6	{1-RHO, PS, DS}	5
7	{1-RHO, PS, DS}	5
8	{1-RHO, PS(Emotion), DS}	7
9	{PS, DS}	8
10	{1-RHO, PS(Identity), DS}	7
11	{1-RHO, DS}	9
12	{1-RHO, PS, DS}	5
13	{PS, DS}	8
14	{1-RHO, PS(Emotion), DS}	7
15	{PS, DS}	8
16	{PI, PS(Identity), DS}	6
17	{1-RHO, PS, DS}	5
18	{PS, DS}	8
19	{1-RHO, PS(Identity), DS}	7
20	{1-RHO, PS, DS}	5
21	{1-RHO, PS(Identity), DS}	7
22	{1-RHO, PS, DS}	5
23	{1-RHO, PS(Identity), DS}	7
24	{1-RHO, PS(Emotion), DS}	7

To complement the previous analysis, which focused on model fits to each individual confusion matrix, we also computed a global AIC_C measure for the best-fitting traditional GRT model using the sum of the log-likelihoods of all 24 models (one for each confusion matrix), and the sum of their number of free parameters. This allowed a direct comparison of the overall fit of traditional GRT models against GRT-wIND, taking into account both fit to the data and model flexibility. The AIC_C for the the traditional GRT models was 11,439, much higher than the AIC_C of 11,216 obtained for the GRT-wIND model. The probability that GRT-wIND is a better model than the traditional GRT models to describe these data, computed using AIC weights (Burnham & Anderson, 2004), was ≈1.0. In sum, we conclude that GRT-wIND provided a better fit to the data than the best-fitting traditional GRT models. Note here that although many traditional GRT models were not tested, the best-fitting GRT models were found using a model hierarchy (Figure 5) and procedures that are representative of applications found in the literature.

Table 2 lists the best-fitting GRT model for each participant, together with the corresponding number of free parameters of each model. On average, the GRT-wIND model has 6 free parameters for each participant (160 parameters / 24 participants). It can be seen from Table 2 that the best-fitting GRT model for most participants (17) had a larger number of degrees of freedom than this average. Note also how violations of perceptual independence are found consistently across participants (except for Participant 16), but conclusions about perceptual separability resulting from fitting individual models are highly variable. Twelve participants show no violations of perceptual separability for both dimensions, eight participants show violations only for emotion, three participants show violations only for identity, and one participant shows violations for both dimensions. Thus, GRT-wIND can fit the data from the present experiment better than individual GRT models, using fewer free parameters and, as we will see in the following section, avoiding the problem of inconsistent conclusions about perceptual separability.

Tests of perceptual interactions

There are several approaches that allow testing hypotheses about dimensional interactions within the framework of maximum likelihood estimation. One approach that has been used in the past with GRT is to fit several versions of the model and then select the one that offers the best account of the data according to some criterion (such as likelihood ratio tests or AIC, see Appendix). This is the approach that we used in the previous section to find the best traditional GRT model for each participant. Unfortunately, fitting GRT-wIND is computationally intensive (each model fit took 48–72 hours in a single processor of our computer cluster), as it involves solving an optimization problem in a very high-dimensional space (160 parameters in the present study), so fitting as many models as shown in Figure 5 is not feasible.

However, one of the main reasons for using such a large number of models in the past has been that the full GRT model could not be fit, precluding researchers from testing a single hypothesis about dimensional interaction without making additional assumptions. Fitting many models is a way to select the best set of assumptions among the models that can be fit. In the framework of GRT-wIND, it is possible to fit the full model and then test in isolation any assumptions of interest by focusing only in the restrictions imposed by those assumptions. Thus, testing as many models as in Figure 5 is not only unfeasible within the framework of GRT-wIND, but also unnecessary.

In sum, we can focus on a few restricted models, one for each type of dimensional interaction that we want to test. Again, one way to proceed is by fitting each model to the data and performing model selection against the full GRT-wIND model. However, this strategy would still take considerable computing time and resources. More importantly, in our experience the likelihood function of GRT-wIND has many local maxima, and fitting multiple GRT-wIND models increases the risk of getting stuck in these local maxima for at least one of these models. This could lead to the unfair comparison of a true maximum-likelihood model against a local-maximum model. Local maxima should be avoided for each model, by running the optimization algorithm with as many starting parameter values as possible (here we used 60), or through other means that also demand additional computing resources. To test for the most important forms of dimensional interaction, this would mean fitting six different GRT-wIND models many times.

We believe that a better use of limited computing resources is trying to find the true maximum likelihood for the full model and then directly testing estimated parameters. In the appendix, we describe methods to do exactly this using a Wald test. This test can be computed after fitting only the full model to data and is easy for most researchers to interpret, as it relies on p-values and the familiar Chi-Square distribution. Thus, this test has the additional advantage of being familiar to most experimental psychologists, more so than performing model selection through AIC and related methods.

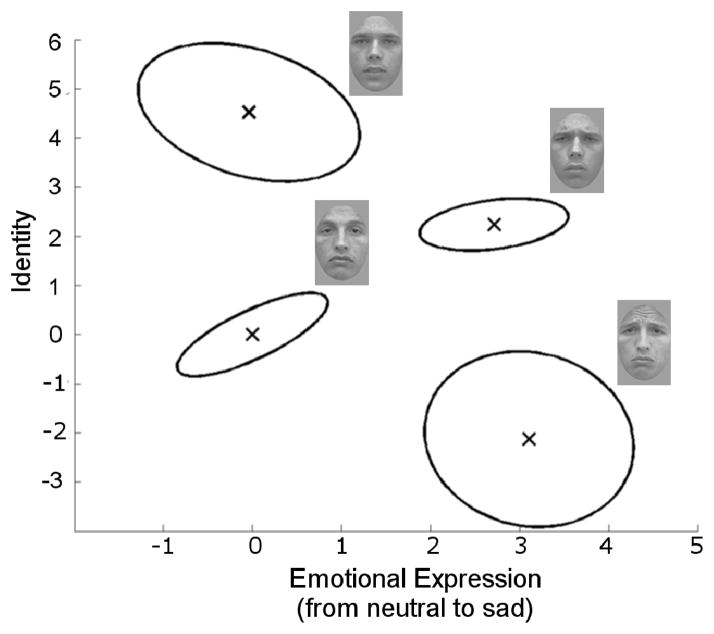
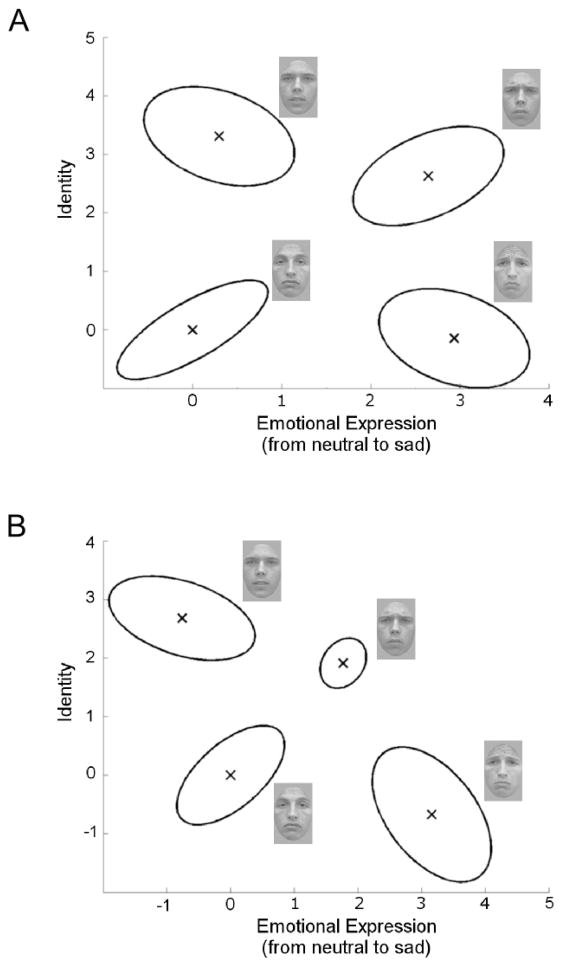
Figure 7 shows the group perceptual distributions obtained from the best-fitting GRT-wIND model. The face corresponding to each distribution is shown next to its contour of equal likelihood. As described above, the shape of the contours give important information about dimensional interactions.

Figure 7.

Best-fitting configuration of perceptual distributions from the experiment reported here. Ellipses are contours of equal likelihood. Face images associated with each perceptual distribution are shown.

First note that three of the four perceptual distributions seem to have a correlation parameter considerably different from zero (i.e., the contours are tilted), indicating violations of perceptual independence. The Wald test of perceptual independence confirmed that these violations were significant, χ²(4) =49.68, p < .001.

Next, note that violations of perceptual separability are also apparent in Figure 7. Specifically, there are clear violations of perceptual separability of identity from emotion. Figure 7 shows what seems to be a mean-shift integrality: the means of the distributions for both identities are shifted down for the sad emotional expression compared to the neutral emotional expression. Furthermore, the variance of the distribution of identity 1 seems much higher for the sad expression than for the neutral expression, and vice-versa for the distribution of identity 2. These results were confirmed by the Wald test, which indicated significant violations of perceptual separability of identity from expression, χ²(4) =803.63, p < .001.

On the other hand, violations of perceptual separability of emotional expression from identity are less clear. The means for each level of emotion are aligned across levels of identity, but the variances seem to differ, especially the variances of the distributions for the sad expression. The Wald test indicated that deviations of perceptual separability of emotional expression from identity were not significant, χ²(4) =.67, p > .5.

Analysis of attentional and decisional factors

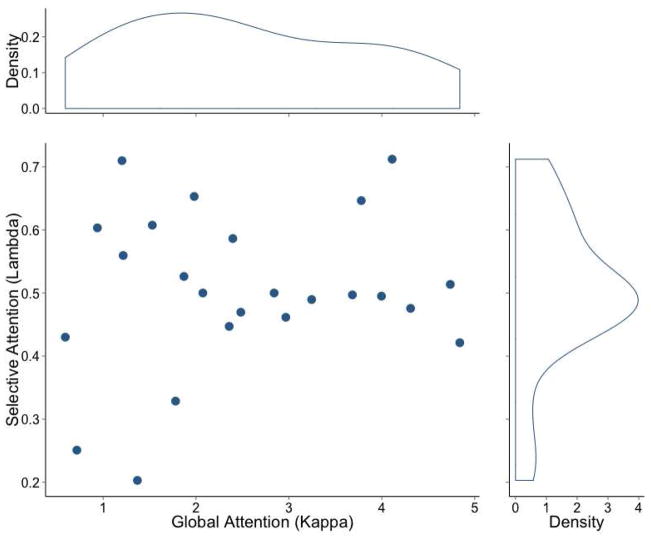
Figure 8 shows a scatterplot in which the coordinates of each dot represent the estimates of the two attention parameters for each participant. The figure also shows estimates of the probability distribution of each attention parameter (i.e., kernel estimates). Note that if a participant was using exactly the distributions depicted in Figure 7, then κ_k should be equal to 2.0 and λ_k should be equal to 0.5. The level of global attention, represented by the parameter κ_k, varies widely across participants without a clear mode in the distribution. The level of selective attention to emotional expression, represented by λ_k, has a clear mode around 0.5 and is asymmetric around that mode, with more subjects showing selective attention to emotional expression (λ_k > 0.5) than subjects showing selective attention to identity (λ_k < 0.5). The difference between the distributions of κ_k and λ_k suggests that there was more variability in the general attention of participants to the task than in the selective attention to one dimension versus the other. In other words, most participants allocated roughly equal amounts of attention to the two dimensions, but they differed wildly in their overall discriminability. This difference could be motivational, but it could also reflect differences in the ability of participants to discriminate among different faces.

Finally, the Pearson correlation between the two attentional parameters was not significant: r = .16, t(22) = 0.78, p > .1). This suggests that the two parameter estimates captured different aspects of a participant’s performance in the task.

An interesting question is whether the variability in individual parameters is the outcome of a single distribution of attentional and decisional strategies, or alternatively whether it is the outcome of two or more clearly distinguishable subgroups of people using different strategies in the task. If the second alternative was true, perhaps a better way to model these data would be through a mixture model (Lee & Wetzels, 2010; Navarro, Griffiths, Steyvers, & Lee, 2006), which would be more parsimonious (i.e., fewer free parameters) and less prone to overfitting than GRT-wIND. The presence of subgroups of participants using a common attentional or decisional strategy should be detectable from the parameter distribution: subgroups should result in multimodal distributions for these parameters. The distributions observed in Figure 8 appear unimodal, which was confirmed by dip tests of unimodality (Hartigan & Hartigan, 1985) that were non-significant both for the distribution of global attention, D = .05, p > .5, and the distribution of selective attention, D = .04, p > .5.

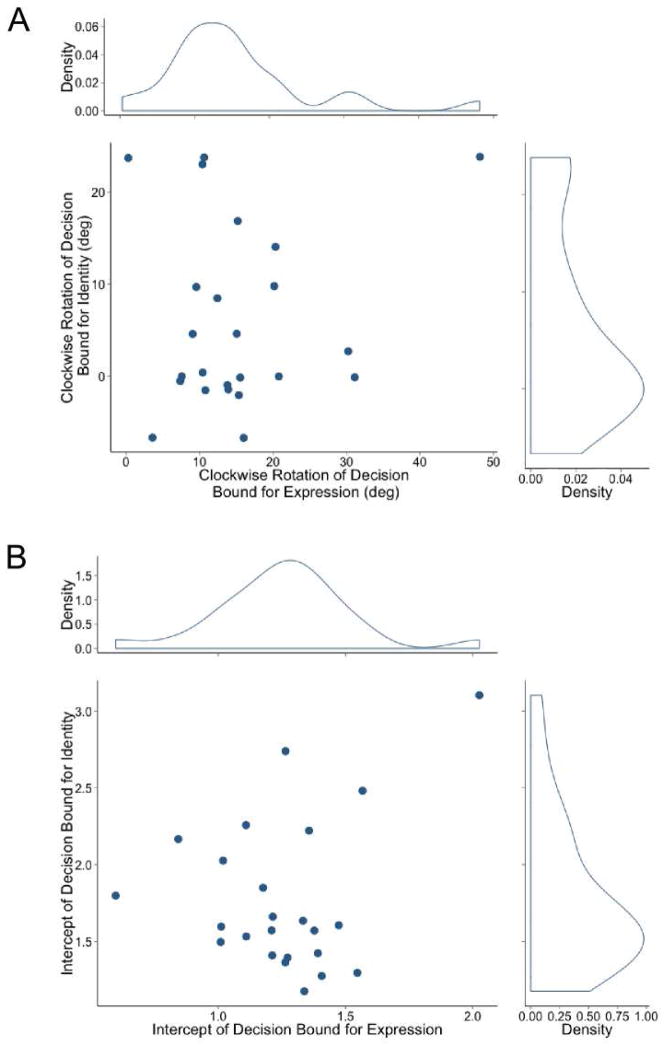
To analyze individual decision strategies, the parameters from the best-fitting discriminant functions (Equation 4) were used to compute, for each dimension, the intercept of the decision bound and its degrees of clockwise rotation from vertical (on the emotional expression dimension) or horizontal (on the identity dimension). Note that these rotation values both equal zero when decisional separability holds, with values higher or lower than zero representing deviations from decisional separability. Similarly, the intercept represents the point where the decision bound crosses the relevant dimension; that is, its position along the relevant dimension.

Figure 9A shows a scatterplot in which the coordinates of each dot represent the degrees of clockwise rotation from the decisional separability bound for a single participant. Decision bounds for emotional expression cluster around 10 degrees of clockwise rotation from vertical, with all of them being greater than zero. The results from Figure 9A suggest that deviations from decisional separability of expression from identity were common and similar across participants. The results of Wald tests (α = .05) on each individual slope indicated that the observed violations of decisional separability were significant in 22 of the 24 participants. A dip test of unimodality for the distribution of slopes was not significant, D = .07, p > .5, suggesting a single underlying distribution of decisional strategies across the group of participants.

Figure 9.

Scatterplots summarizing the best-fitting GRT-wIND bounds. Panel A shows degrees of clockwise rotation from the decisional separability bounds, and Panel B shows the intercepts of each bound. Kernel density estimates for the distribution of values of each parameter are shown at the top and right of the corresponding scatterplot.

Decision bounds for identity are more heterogeneous, with many of them clustering around zero degrees of rotation from horizontal, but others having quite high positive values. The results suggest deviations from decisional separability of identity from expression for some, but not all participants. The results of Wald tests (α = .05) on individual slopes revealed significant violations of decisional separability in only 4 of the 24 participants. The dip test for unimodality was not significant, D = .08, p > .1.

The scatterplot in Figure 9A shows that there was no relation between the orientation of the two decision bounds across participants, which was confirmed by a non-significant Pearson correlation between these values, r = .15, t(22) =.69, p > .1. This result suggests that the decisional strategies employed by participants to classify each dimension were independent from each other.

Figure 9B shows a scatterplot where the coordinates of each dot represent intercepts of the decision bounds for a single participant. These values were not significantly correlated across participants, r = .25, t(22) =1.19, p > .1. The distributions observed in Figure 9B appear unimodal, which was confirmed by non-significant dip tests of unimodality for the distribution for expression, D = .06, p > .5, and the distribution for identity, D = .05, p > .5.

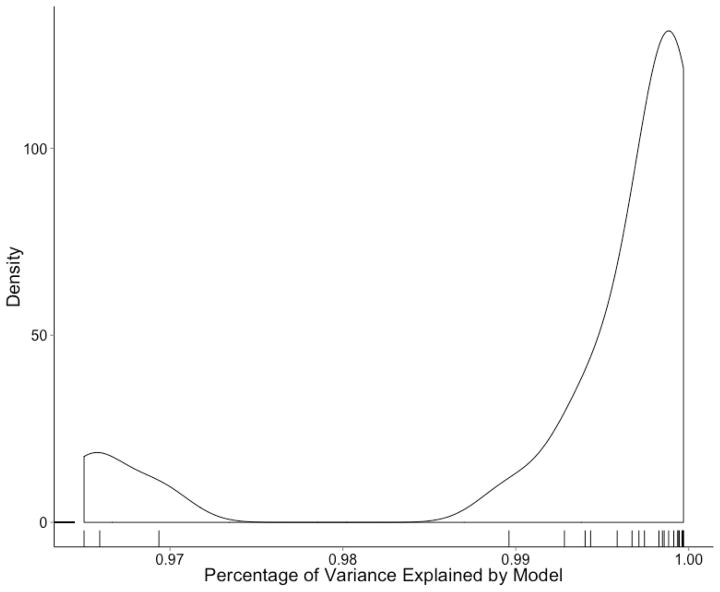
Although the analyses presented in this section did not find evidence of subgroups of participants using different decisional or attentional strategies, it is still possible that subgroups exist which differ in other aspects of processing, such as perception of identity and expression. The existence of such subgroups would violate one of the most important assumptions behind GRT-wIND: that perceptual representations have a similar structure across individuals. If subgroups exist, then they should produce a multimodal distribution for measures of model-fit, with one mode having a high fit value, representing participants whose behavior is well-explained by the model, and one or more modes having a lower fit value, representing participants whose behavior is not well-explained by the model. Figure 10 shows the percentage of the variance in each participant’s data explained by GRT-wIND, together with a kernel density estimate for the distribution of measures of fit. The distribution seems to be bimodal, with most participants clustering between 0.99 and 1.00, but a small group of three participants having a lower value of model-fit between .96 and .97. However, the distribution was not significantly different from unimodal according to a dip test, D = .05, p > .5.

Figure 10.

Kernel density estimate for the distribution of percentage of variance explained by GRT-wIND.

A closer examination of the results for these three subjects gave clues as to exactly what was different about them in relation to the rest of the group. A look at Figure 6 reveals that for at least one of these participants (participant 12), whose point in the plot lies right next to the diagonal, the individual GRT model did not provide a substantially better fit than GRT-wIND. This suggests that perhaps there was something about this participant’s data that violated the assumptions of GRT in general and not GRT-wIND in particular.

The other two participants (participants 1 and 15) showed a clearly higher fit value for the individual GRT model than for GRT-wIND. For participant 1, this was likely the result of over-fitting: the individual GRT model required 10 parameters to provide such good fit to the data, which is considerably more than the average of 6 parameters required by GRT-wIND.

Participants 1 and 12 showed rather poor performance in the task (see supplementary material), which was reflected in the two lowest values for κ_k in the sample (below 1.0, see Figure 8). One possibility is that some of the data from these participants comes from an early learning stage that could not be detected by our criteria for data exclusion. Such learning performance cannot be captured by any GRT model, as these are models of asymptotic performance.

The results of participant 15 are more difficult to explain this way, which suggests that perhaps this participant did use processes that could not be captured by GRT-wIND. This participant showed a good fit by an individual GRT model without an extremely high number of degrees of freedom (8). None of the estimated parameters for this participant were outliers, and there are patterns in his/her data that seem different from most other participants, such as a high frequency of responding “identity 2 neutral” when presented with “identity 1 neutral” (see supplementary material).

Evaluation of common assumptions in previous GRT models

As indicated previously, traditional GRT analyses for the 2×2 identification design require making a number of assumptions in order to evaluate dimensional interactions. An advantage of GRT-wIND is that the full model and restricted models that incorporate assumptions can be fit to the same data. As a consequence, the GRT-wIND framework allows us to evaluate, for a given dataset, how valid different assumptions are and how they can affect conclusions about dimensional interaction. Here, we perform such analysis for two of the most common assumptions in previous applications of GRT: equal variances for all distributions and decisional separability in both dimensions (e.g., Ashby & Soto, in press; Thomas, 2001; Fitousi & Wenger, 2013).

To determine the validity of the assumption of equal variances, we performed a Wald test of the null hypothesis that all variances in the model were equal to one, as the variances for the first distribution were fixed to this value. The test did not show significant violations of the assumption that the variances were equal to one, χ²(6) =.84, p > .5.

To evaluate the consequences of assuming equal variances for tests of dimensional interactions, a restricted model with all variances fixed to 1.0 was fitted to the data. The optimization was performed 20 times, each time with a different set of starting parameter values. Then the analysis of interactions using Wald tests was performed on the obtained maximum likelihood estimates. The AIC_C for this restricted model was equal to 11,257, which is higher than the AIC_C of 11,216 found for the full model. Thus, the full model does seem to capture structure in the data that cannot be captured by a model assuming equal variances.

There are several explanations for the contradictory results of the Wald test and the AIC comparison in this analysis. The most obvious explanation is that the two methods were developed with different goals in mind: the Wald test was designed to test null hypotheses about maximum likelihood estimates, whereas the AIC was designed to choose among a set of models the one that yields the best balance between fit to the data and model complexity. This, combined with the fact that the AIC comparison does not take into account sampling variability (see Preacher & Merkle, 2012) means that there is no reason to expect the two methods to yield the same results in all applications. A more practical issue is that estimation error could have affected the covariance values that were input to the Wald test, or the maximum likelihood estimates for the restricted model.

Regardless of whether or not the assumption about equal variances was violated by our data, an important question is to what extent making this assumption could affect the estimates of other parameters in the model and the results of tests of separability and independence.

Figure 11A displays the maximum likelihood solution for the restricted model. It can be seen that violations of perceptual separability that are apparent in the full model, such as the mean-shift integrality described earlier, almost disappear in the restricted model. Furthermore, the assumptions have an effect on the analysis of interactions through the Wald test. Using the full model, we found significant violations of perceptual separability of identity from expression, but such violations were not found using the restricted model, χ²(4) =0.78, p > .5. As with the full-model analysis, there were no significant violations of perceptual separability of expression from identity, χ²(4) =3.79, p > .1, but the violations of perceptual independence were significant, χ ²(4) =51.02, p < .001.

Figure 11.

Best-fitting configuration of perceptual distributions for the restricted GRT-wIND models fitted to the experimental data. Panel A shows the restricted model in which all variances are equal to one. Panel B shows the restricted model that assumes decisional separability for both dimensions. Ellipses are contours of equal likelihood. Face images associated with each perceptual distribution are shown.

The tests of violations of decisional separability of expression from identity led to the same result for the full and restricted model in 18 participants, but 6 participants who showed such violations with the full model did not show them with the restricted model. The tests of violations of decisional separability of identity from expression were consistent for the full and restricted model in only 10 participants, with 13 participants who did not show violations with the full model showing them with the restricted model and one participant who did show violations with the full model not showing them with the restricted model. In sum, the model assuming equal variances led to less apparent violations of decisional separability of expression from identity, and to more apparent violations of decisional separability of identity from expression.

The results of Wald tests of decisional separability carried out with the full model were presented earlier. They indicated that individual bounds for emotional expression deviated significantly from decisional separability in most participants, whereas bounds for identity deviated significantly from decisional separability in only a few participants (see Figure 9). What is left is determining to what extent this assumption could affect the results of tests of other forms of interaction.

We fitted a restricted GRT-wIND model that assumed decisional separability in both dimensions to the data. As before, the optimization was performed 20 times, each time with a different set of starting parameter values. The AIC_C for this restricted model was equal to 11,267, which is higher than the AIC_C of 11,216 found for the full model. Thus, in this case the AIC comparison confirms the results of the Wald tests, showing reliable evidence that the full model captures structure in the data that cannot be captured by a model assuming decisional separability.

Figure 11B displays the maximum likelihood solution for the restricted model. In this case, violations of perceptual separability of identity from emotion are still present in the restricted model and are significant according to the Wald test, χ²(4) =171.77, p < .001. Furthermore, the restricted model shows violations of separability of emotion from identity that are less apparent in the full model. Such violations turned out to be statistically significant, χ²(4) =2,239.27, p < .001. As with the full model, violations of perceptual independence were also statistically significant, χ²(4) =163.11, p < .001.

To summarize the most important results of this section, both the assumption of equal variances and the assumption of decisional separability led to changes in the conclusions reached through GRT-wIND about perceptual separability and decisional separability. Perceptual independence, on the other hand, was consistently violated in all analyses. These results suggest that common assumptions made in model-based analyses using GRT can have an important influence in the results of such analyses. As GRT-wIND does not require such assumptions, we recommend its use over traditional GRT models to analyze the data from 2×2 identification designs.

Discussion

This article presents an extension to GRT that overcomes many of the weaknesses that result from the traditional method via which GRT is applied to the analysis of dimensional interactions. This new GRT-wIND model assumes that the structure of perceptual representations for a set of stimuli is shared among all people, whereas attention to specific stimulus dimensions and decision strategies vary across individuals. The model was successfully applied to the analysis of new data from an identification experiment in which facial stimuli varied in identity and emotional expression. The model was able to describe these data better than traditional GRT models, despite having fewer free parameters, while also allowing tests of all types of independence defined within GRT. The results from our analyses of dimensional interactions revealed that identity is not perceptually separable from emotional expression, whereas deviations of perceptual separability of expression from identity were both small and not statistically significant. There were also clear violations of perceptual independence. Violations of decisional separability for both dimensions were common, but more participants showed statistically reliable violations in the case of expression than in the case of identity.

All GRT analyses of dimensional interactions require assumptions. For example, decisional separability is usually assumed when there are not enough degrees of freedom to fit a full GRT model. Assuming decisional separability is also a way to deal with the non-identifiability in the 2×2 identification experiment (Silbert & Thomas, 2013). Modeling identification data with GRT-wIND offers the advantage that no assumptions are required regarding perceptual separability, decisional separability, or perceptual independence. Instead, an assumption is made that all experimental participants share the same perceptual distributions. This assumption is not only plausible; without it, the analysis of perceptual independence would be a trivial endeavor: if different individuals perceived a set of stimuli in fundamentally different ways, then there would be no answer (or rather, multiple answers) to the question of whether or not two dimensions are processed independently.

A second assumption of GRT-wIND is that there is variability across people in their attention to stimulus dimensions and in their decisional strategies. This is fundamentally different from a recent hierarchical GRT model that, like GRT-wIND, incorporates group parameters (Silbert, 2012). This hierarchical model proposes that individual differences are due to random variability around group parameters, not reflecting a psychologically meaningful process. More research is necessary to understand which model is correct in this regard. If individual attentional and decisional strategies discovered through GRT-wIND can predict individual differences in other parameters, then it would be possible to make a case for its assumptions. On the other hand, GRT-wIND offers a practical advantage over the hierarchical GRT model: the latter suffers from a number of the shortcomings with traditional GRT models identified in the introduction, including being unable to dissociate all types of dimensional interaction identified in the theory (Ashby & Townsend, 1986).

The analysis of interactions between identity and expression in face perception using GRT-wIND suggested that expression is perceptually separable from identity, but identity is not perceptually separable from expression. This result is particularly important, because perceptual separability is the concept that seems more similar to the idea of “independence” evaluated by previous studies. Most of those previous studies have found the opposite result, with identity having a large influence in processing of expression and expression having a small or nonexistent influence in processing of identity (e.g., Baudouin et al., 2002; Ganel & Goshen-Gottstein, 2004; Schweinberger et al., 1999; Schweinberger & Soukup, 1998; Soto & Wasserman, 2011). An important difference between previous studies and the present experiment is that using GRT-wIND allowed us to dissociate perceptual and decisional factors in dimensional interaction. One explanation for prior experimental results is that they might reflect the outcome of decisional rather than perceptual processes. In the present study, violations of decisional separability were common for both face dimensions, and more consistent across participants in the case of expression. Such consistent violations of decisional separability might be what most previous studies captured. Furthermore, decision strategies can vary depending on instructions and experimental procedures (e.g., Ashby et al., 2001), which could explain the variability in the results of previous research.

On the other hand, an important limitation of the present experiment is that it included only two identities and a single emotional expression. Perhaps a different pattern of results will arise with other expressions or with different identities; more research will be necessary to reach a strong conclusion about the interaction between identity and emotion. Such research should include comparisons between familiar and non-familiar identities (e.g., Ganel & Goshen-Gottstein, 2004), manipulation of the discriminability of each dimension (e.g., Schweinberger & Soukup, 1998) and testing the generality of the results by using several different identities and emotional expressions. However, because the present experiment established that violations of decisional separability can be easily found in a face identification task, all future research should aim to dissociate decisional factors from the analysis of perceptual separability and independence.

Another limitation of the present study is that the application of GRT-wIND to an identification design only allows an analysis of response frequencies. This is different from most previous studies using the Garner interference task, which focus on the analysis of response times. Analysis of response times is possible within the framework of GRT-wIND, but it would require both additional assumptions and additional experiments. Perhaps the simplest way to incorporate response times into any GRT model is to assume that response time decreases with the distance between the perceptual effect of a stimulus and the decision bound (see Ashby & Maddox, 1994). Unfortunately, this results in a well-defined model only for experiments with a single decision bound per participant, where each response time corresponds to a single distance-to-bound. For the identification experiment reported here, one decision bound is required for each dimension, so a single response time would be some function of two distances-to-bound. In order to model response times using GRT, one strategy is to run both an identification and a speeded-categorization experiment using the same stimuli and participants (Maddox & Ashby, 1996). The data from the identification experiment is used to find parameters of the perceptual distributions for a set of stimuli, as we have done here. These parameters are then used to build a model of response times for the classification experiment. An advantage of GRT-wIND is that, because it assumes common perceptual distributions across participants, it allows these two experiments to be performed on two separate groups, making it much easier to perform such two-stage studies. We are currently working on implementing this extension of GRT-wIND, which is beyond the scope of the present work.

The only previous study addressing dimensional interactions between identity and expression using GRT (Fitousi & Wenger, 2013) found that, for unfamiliar faces such as those studied here, perceptual separability of emotional expression was violated whereas perceptual separability of identity was not violated. This is the opposite to what we found here. One possible explanation for these disparate results is that the limited degrees of freedom in the data forced Fitousi and Wenger to make some simplifying assumptions that could have biased their results. These authors assumed equal variances in all the GRT models that they tested. We found that this assumption was invalid for our data and that it affected the outcome of tests of perceptual separability. Furthermore, the most general model that Fitousi and Wenger could have tested, given the small number of degrees of freedom in their data, must have included additional simplifying assumptions. Unfortunately, we do not know what those assumptions are, because the authors do not report what models they included in their analysis.

More generally, it seems important at this point to give some guidance as to how researchers should interpret disparate conclusions about separability and independence reached through traditional GRT models and GRT-wIND. A GRT model for the 2×2 identification design requires a number of parameters to explain the data from a single participant. Traditional GRT models do not allow estimation of all these parameters, so many of them must be fixed by the researcher. On the other hand, GRT-wIND allows estimation of all the parameters necessary to explain the data from a single participant. When the same parameters that are held fixed in GRT models are allowed to vary in GRT-wIND, this affects the values estimated for the parameters shared by both models. For example, given a specific data set from a single participant, if the slope parameter for the bound in dimension B is fixed to 1 in a GRT model, but the estimated value in GRT-wIND is 2, then the values of other parameters (in particular, the means and variances along dimension B) will differ for the two models, to accommodate the fact that different slopes must explain the same data. This will happen to varying degrees, regardless of whether or not our estimate of the slope in GRT-wIND turns out to be significantly different from the value of 1 assumed in the GRT model.

Fixed parameters in traditional GRT models are equivalent to assumptions about separability and independence. GRT-wIND is free of such assumptions, at the cost of assuming that different people perceive a set stimuli in a fundamentally similar way. In practice, when a researcher finds that GRT and GRT-wIND lead to different conclusions about a particular data set, if the assumptions of GRT-wIND can be justified, then the conclusions reached through GRT-wIND should be preferred. As we have shown here, analysis of the distribution of parameters and measures of fit can help to determine whether the main assumptions of GRT-wIND are violated in a given data set.

The experiment reported here used extremely short presentation times (about 16.67 ms), which might raise the concern that participants did not base their responding on high-level facial features, but on low-level differences among the images such as large areas with different contrast. There are at least three reasons to believe that this was not the case in the present study. First, images were standardized in several ways to avoid use of low-level image properties. The original images were histogram-equalized and we eliminated non-facial features by showing faces through an oval window. Second, previous research suggests that faces can be discriminated with presentation times as short as 100 ms at the same level of performance as with presentation times of 1,000 ms, and they can still be discriminated to a good level well below 100 ms (e.g., Lehky, 2000). Furthermore, such results were obtained using a more difficult task than the one used here, involving stimulus masking (which disrupts visual processing after presentation of the mask), smaller differences between faces (achieved through morphing) and no feedback. Third, our own personal experience with the task confirmed that identification is easily achieved on the basis of identity and emotion after a short adaptation time.

In recent years, researchers have showed increasing interest in using GRT to analyze dimensional interactions in face perception (e.g., Cornes, Donnelly, Godwin, & Wenger, 2011; Fitousi & Wenger, 2013; Mestry et al., 2012; Richler, Gauthier, Wenger, & Palmeri, 2008). Such applications are promising, because GRT offers a number of advantages over other approaches, including a dissociation between perceptual and decisional processes and the possibility of defining vague concepts–such as configural and holistic face processing–within a formal framework.

These advantages of GRT might prove to be extremely useful to answer important open questions about the interaction among face dimensions. For example, the structural reference hypothesis (Ganel & Goshen-Gottstein, 2004; Ganel, Valyear, Goshen-Gottstein, & Goodale, 2005) proposes that emotional expression is coded as dynamic variations from the invariant structure of faces. This invariant structure influences the way in which each individual expresses emotion. Because familiarity with a face should lead to better knowledge of the structure of a face, the structural reference hypothesis predicts that familiarity should lead to a larger interference of identity on expression processing, a prediction that has been confirmed using a Garner filtering task (Ganel & Goshen-Gottstein, 2004). However, familiarity with a face can also lead to changes in decisional bias, particularly if a face has been experienced more times showing one particular expression (e.g., Jim Carrey is typically happy, whereas Tommy Lee Jones is typically serious). Thus, the results from a filtering task are difficult to interpret unless it can be shown that the effect of familiarity is on perceptual representations instead of decisional biases.

The increased interest in the application of GRT to the study of face perception and other areas of perceptual science has been undermined recently by papers reporting shortcomings with the GRT framework (Mack et al., 2011; Silbert & Thomas, 2013). An important contribution of the present work is the description of an extended GRT framework, GRT-wIND, which overcomes most shortcomings in traditional applications of GRT. This new framework can easily be applied to analyze data from the most commonly used experimental designs without sacrificing the ability to test any forms of independence defined by GRT, which makes it an important addition to the toolbox available to researchers in perceptual science.

Appendix

Here we prove that the problem of non-identifiability of decisional separability described by Silbert and Thomas (2013) only occurs in GRT-wIND in the special case in which the decision bounds of all participants for each dimension are parallel to each other. We also describe procedures to: (1) estimate the parameters of a GRT-wIND model from identification data using maximum likelihood estimation, (2) run statistical tests for perceptual independence, perceptual separability and decisional separability, and (3) estimate parameters and test different types of independence as in previous applications of GRT.

Identifiability of decisional separability in the 2×2 GRT-wIND model

Silbert and Thomas (2013) showed analytically that a failure of decisional separability is non-identifiable in the Gaussian GRT model for a 2×2 identification experiment. That is, if the data from an experiment can be fit by a GRT model in which decisional separability fails, then it is always possible to find a different GRT model in which decisional separability holds and that predicts the exact same data pattern. We call this result the Silbert-Thomas non-identifiability, or STn for short.

We start by summarizing the proof offered by Silbert and Thomas (2013). Their theorem states that “Any perceptually separable but decisionally nonseparable configuration can be transformed to a configuration that is perceptually nonseparable, decisionally separable, and equivalent with respect to predicted response probabilities” (p. 17). Thus, they focus on the case in which the original configuration exhibits perceptual separability but violations of decisional separability. However, the more general result is that decisional separability is nonidentifiable in this model. As the authors indicate, “Any arbitrary (and, in general, not perceptually separable) linear bound model without decisional separability can be rotated and sheared to produce a model with decisional separability […], failure of decisional separability is never identifiable in this model” (pp. 4–5).

The proof for this theorem starts with a configuration without decisional separability and that has been translated so that the origin of the xy-plane coincides with the intersection of the two decision bounds h_A and h_B. The angle between h_B and the x-axis is represented by ϕ and the angle between the bounds h_A and h_B is represented by ω. Decisional separability holds when ϕ = 0 and ω = π/2. Rotation of the original configuration by ϕ degrees brings h_B to be parallel to the x-axis (and orthogonal to the y-axis), achieving decisional separability of component B from A. The horizontal shear transformation has the property of changing the angle between all lines in the plane except those parallel to the x-axis. Thus, for any value of ω, a horizontal shear transformation can be found that brings this angle to π/2 while keeping h_B parallel to the x-axis, thus achieving decisional separability of component A from B while also keeping decisional separability of component B from A.

The rotation and shear transformations can be represented by the transformation matrices L₁ and L₂, respectively, which combine to produce:

$$\mathbf{L}={\mathbf{L}}_2{\mathbf{L}}_1=\left[\begin{array}{cc}1& -\frac{1}{tan\omega }\\ 0& 1\end{array}\right]\left[\begin{array}{cc}cos\varphi & -sin\varphi \\ sin\varphi & cos\varphi \end{array}\right]=\left[\begin{array}{cc}cos\varphi -\frac{sin\varphi }{tan\omega }& -sin\varphi -\frac{cos\varphi }{tan\omega }\\ sin\varphi & cos\varphi \end{array}\right]$$ (A1)

This is an area-preserving affine transformation. The change-of-variables theorems for densities guarantees that probabilities will be preserved under such transformation (Billingsley, 2013). This means that the predicted probabilities of correct responses in the original configuration and the decisionally-separable configuration are the same, as the values of the integrals involved do not change. The means and covariance matrices in the decisionally-separable configuration can be computed from the original means and covariance matrices by using the formulas:

$${\underset{\_}{\mu }}_T=\mathbf{L}\underset{\_}{\mu }$$ (A2)

$${\mathbf{\sum }}_T=\mathbf{L}\mathbf{\sum }{\mathbf{L}}^{\mathrm{T}}$$ (A3)

In the remainder of this section, we show the conditions under which decisional separability is non-identifiable in GRT models with more than one bound per dimension. GRT-wIND and n×m GRT models with n>2 and m>2 are special cases of this general class. We start by identifying the conditions under which STn holds for a model with 2 bounds per dimension. It is then straightforward to see that the same conditions apply for any larger number of bounds per dimension.

Theorem

In a Gaussian GRT model with two dimensions and two linear bounds per dimension, where the ith bound for dimension A is represented as h_Ai and the jth bound for dimension B as h_Bj, the non-identifiability of decisional separability identified by Silbert and Thomas (2013) is true if and only if h_A1 || h_A2 and h_B1 || h_B2.

Proof

We first prove that if h_A1 || h_A2 and h_B1 || h_B2, then STn holds. As with the proof of STn, we start with a configuration without decisional separability that has been translated so that the origin of the xy-plane coincides with the intersection of h_A1 and h_B1. We represent the angle between h_Bj and the x-axis as ϕ_j and the angle between of h_Ai and h_Bj as ω_ij. Because h_B1 and h_B2 are parallel to each other, but not parallel to the x-axis, they intersect the latter at congruent angles; that is, ϕ₁ = ϕ₂. Thus, rotation of the original configuration by ϕ₁ degrees brings both h_B1 and h_B2 to be parallel to the x-axis and orthogonal to the y-axis, achieving decisional separability of component B from A. After rotation, it is still true that h_A1 || h_A2 and h_B1 || h_B2, because rotation preserves parallelism. This means that ω_ij = ω for all i and j. Thus, a single shear tranformation can bring this angle to π/2, achieving decisional separability of component A from B while also keeping decisional separability of component B from A.

To complete the proof, we must show that if STn holds, then h_A1 || h_A2 and h_B1 || h_B2. For STn to hold, a decisionally-separable configuration must exist that can be found by applying an affine transformation L to an original configuration without decisional separability. By definition, in this decisionally-separable configuration h_A1 ⊥ x, h_A2 ⊥ x, h_B1 ⊥ y and h_B2 ⊥ y. Because two lines that are both perpendicular to a third line are parallel to each other, with all lines in the same plane, h_A1 || h_A2 and h_B1 || h_B2 in the decisionally-separable configuration. To go from the decisionally-separable configuration to the original configuration, we must apply the transformation L⁻¹. This inverse transformation exists because both shear and rotation are invertible transformations. The inverse of an affine transformation is itself an affine transformation that conserves parallelism, so application of L⁻¹ to the decisionally-separable transformation conserves the property that h_A1 || h_A2 and h_B1 || h_B2. Thus, if STn holds, then bounds must be parallel in the decisionally-separable configuration as well as in the original configuration.

This completes the proof for the case in which there are two linear bounds per dimension. A corollary is that for models with more than two bounds per dimension, STn holds if and only if each bound in one dimension is parallel to each of the other bounds in that specific dimension.

Here we have exclusively dealt with part (i) of the theorem proposed by Silbert and Thomas (2013). Part (ii) of this theorem proposes that a configuration with mean shift integrality and decisional separability is unidentifiable from a configuration with perceptual separability and without decisional separability. This theorem also deals with the non-identifiability of decisional separability, so as before it only holds for models with more than one bound per dimension if those bounds are parallel. Furthermore, an additional condition for this theorem to hold is that all covariance matrices in the model must be identical (Thomas & Silbert, in press). This in general is not the case in GRT-wIND or in traditional GRT models for designs larger than 2×2, which allow for estimation of different variances and covariances for each perceptual distribution.

In conclusion, STn is not generally true in GRT-wIND or any other model with more than one bound per dimension. The non-identifiability of decisional separability arises in such models only under very specific circumstances.

Maximum likelihood estimation for GRT-wIND

The data from each participant in an identification experiment are summarized in a confusion matrix, with rows corresponding to each stimulus in the experiment, columns corresponding to each response, and response frequencies reported in each cell of the matrix. Let S₁, S₂, …, S_n denote the n stimuli in an identification experiment and let R₁, R₂, …, R_n denote the n responses. Let r_ij denote the frequency with which the participant responded R_j on trials when stimulus S_i was presented. Finally, there are N participants in the experiment, indexed by k=1, 2, …,N. Given a set of parameter values for the model, the likelihood of this confusion data is computed in two steps.

In the first step, the predicted confusion matrix of each participant is computed using standard methods. For example, the predicted probability that a participant responds R_j on trials when stimulus S_i was presented, denoted by P(R_j|S_i), is computed by integrating the volume of the S_i perceptual distribution in response region R_j. A numerical approximation to this multiple integral can be computed efficiently using Cholesky factorization (Ennis & Ashby, 2003; for a tutorial overview, see Ashby & Soto, in press).

The second step is to compute the log of the likelihood function for participant k:

$$log{L}_k=\sum _{i=1}^n\sum _j^n{r}_{ij}logP\left(R_j|S_i\right)$$ (A4)

These log-likelihoods are then summed across all participants:

$$logL=\sum _{k=1}^{N}log{L}_k$$ (A5)

The maximum likelihood estimates of the parameters in a GRT-wIND model are those that maximize the expression in Equation A5.

Statistical tests of independence with GRT-wIND

The large number of parameters in a GRT-wIND model makes the computational cost of using likelihood ratio tests and model selection procedures prohibitive. Thus, we recommend a deviation from the custom of computing such tests in GRT analyses. The strategy used here consists of fitting the full GRT-wIND model and testing maximum-likelihood parameter estimates against expected values from null hypotheses using a Wald test (Wald, 1943).

Let θ̂ be a column vector containing the maximum likelihood parameter estimates. The Wald test can be used to test any null hypothesis that can be expressed in the form of linear restrictions on θ̂:

$$\begin{array}{l}{H}_0:\mathbf{R}\underset{\_}{\widehat{\theta }}-\underset{\_}{q}=0\\ H_1:\mathbf{R}\underset{\_}{\widehat{\theta }}-q\ne 0\end{array}$$

where R is a matrix with number of columns equal to the number of parameters and number of rows equal to the number of restrictions being tested, and q is a column vector with number of rows equal to the number of restrictions being tested. For example, if we wanted to test the hypothesis that θ̂₁ = 0, then R would have a single row (we are testing a single restriction) with a +1 in the first cell of that row and zeros in all other cells, while q would have a single cell with a zero in it. If we want to additionally test the hypothesis that θ̂₂ − θ̂₃ = 10, then we would add a second row to R with a +1 in the second column (corresponding to +θ̂₂) and −1 in the third column (corresponding to −θ̂₂), while q would now have a second cell with the value 10 in it.

Null hypotheses are tested using the Wald statistic:

$$W={\left[\mathbf{R}\underset{\_}{\widehat{\theta }}-\underset{\_}{q}\right]}^{\mathrm{T}}{\left[\mathbf{R}{\mathbf{\sum }}_{\underset{\_}{\widehat{\theta }}}{\mathbf{R}}^{\mathrm{T}}\right]}^{-1}\left[\mathbf{R}\underset{\_}{\widehat{\theta }}-\underset{\_}{q}\right]$$ (A6)

where []^T represents matrix transpose. The statistic W has a chi-squared distribution with degrees of freedom equal to the number of restrictions being tested (the length of q). Computing W requires the covariance matrix of the maximum likelihood estimates, which can be estimated using the Hessian of the log-likelihood function at the solution:

$${\mathbf{\sum }}_{\underset{\_}{\widehat{\theta }}}=H{(\underset{\_}{\widehat{\theta }})}^{-1}$$ (A7)

Usually the Hessian in Equation A4 can be obtained from the same optimization software that is used to obtain the parameter estimates that maximize the log-likelihood, but better estimates are obtained from numerical differentiation software. In this study, we used the DERIVEST suite (D’Errico, 2006) to obtain estimates of the Hessian.

For the 2×2 identification design used here, the restrictions imposed on the model by perceptual separability of dimension A from dimension B are the following:

$$\begin{array}{l}{\mu }_{A_1{B}_{2}1}=0\\ {\sigma }_{A_1{B}_{2}1}=1\\ {\mu }_{A_2{B}_{1}1}-{\mu }_{A_2{B}_{2}1}=0\\ {\sigma }_{A_2{B}_{1}1}-{\sigma }_{A_2{B}_{2}1}=0\end{array}$$

The restrictions imposed in the model by perceptual separability of dimension B from dimension A are the following:

$$\begin{array}{l}{\mu }_{A_2{B}_{1}2}=0\\ {\sigma }_{A_2{B}_{1}2}=1\\ {\mu }_{A_1{B}_{2}2}-{\mu }_{A_2{B}_{2}2}=0\\ {\sigma }_{A_1{B}_{2}2}-{\sigma }_{A_2{B}_{2}2}=0\end{array}$$

The restrictions imposed in the model by perceptual independence in each of the perceptual distributions are the following:

$$\begin{array}{l}{\rho }_{A_1{B}_1}=0\\ {\rho }_{A_1{B}_2}=0\\ {\rho }_{A_2{B}_1}=0\\ {\rho }_{A_2{B}_2}=0\end{array}$$

The Wald test allows tests of decisional separability for the whole group or for each participant individually. Here, we focus on the latter kind of test. Testing whether decisional separability of dimension A from dimension B holds in participant k involves a single restriction:

$$b_{A_{k2}}=0$$

Testing whether decisional separability of dimension B from dimension A holds in participant k involves the following restriction:

$$b_{B_{k1}}=0$$

Model fit and selection in the traditional GRT approach

To fit any GRT model to data (e.g., the models in the hierarchy shown in Figure 5), the confusion matrix from a single participant is used to find the values of the free parameters that maximize Equation A1.

A popular method to test assumptions about independence and separability is to fit a restricted and an unrestricted version of the model to data. The restricted model contains a number of parameters that are set to values reflecting the assumption under test. For example, testing perceptual independence would require setting all ρ parameters to zero. The same parameters would be free to vary in the unrestricted model. Once both models are fit to data, the likelihood of the data at the solutions (L_U and L_R for the unrestricted and unrestricted versions, respectively) can be used to run a likelihood ratio test, by computing the following statistic:

$$\mathbf{\Lambda }=-2(log{L}_R-log{L}_U),$$ (A8)

which follows a Chi-squared distribution with degrees of freedom equal to the difference in number of free parameters between the two models.

The likelihood ratio test can only be applied to select between two nested models. To select between two non-nested models, it is possible to use the Akaike information criterion (AIC, Akaike, 1974) for model comparison. Here we use a version of AIC corrected for a bias problem present when the number of data points is small compared to the number of free parameters (see Burnham & Anderson, 2004):

$${\mathit{AIC}}_C=-2logL+2m+2m(m+1)/(n^2-m-1),$$ (A7)

where m is the number of free parameters in the model and n² is the number of cells in the confusion matrix. The first two terms in Equation A7 correspond to the traditional definition of AIC and the last term corresponds to the correction factor. A smaller value of AIC represents a better fit of the model to the data.

In the present study, as in previous model-based applications of GRT (e.g., Ashby & Lee, 1991; Ashby et al., 2001; Fitousi & Wenger, 2013; Thomas, 2001), a hierarchy of models was fit to the data from each participant (see Figure 5). The procedure starts at the top of the hierarchy and compares nested models through likelihood ratio tests until the test results in a non-significant increase in fit. If more than one candidate model survives this process, the model with the smallest AIC_C is selected.