Discovering chemistry with an ab initio nanoreactor

Abstract

Chemical understanding is driven by the experimental discovery of new compounds and reactivity, and is supported by theory and computation that provides detailed physical insight. While theoretical and computational studies have generally focused on specific processes or mechanistic hypotheses, recent methodological and computational advances harken the advent of their principal role in discovery. Here we report the development and application of the ab initio nanoreactor – a highly accelerated, first-principles molecular dynamics simulation of chemical reactions that discovers new molecules and mechanisms without preordained reaction coordinates or elementary steps. Using the nanoreactor we show new pathways for glycine synthesis from primitive compounds proposed to exist on the early Earth, providing new insight into the classic Urey-Miller experiment. These results highlight the emergence of theoretical and computational chemistry as a tool for discovery in addition to its traditional role of interpreting experimental findings.

Experimental chemistry often plays the principal role in discovering new compounds and proposing new reaction mechanisms, while computational chemistry provides valuable support by arbitrating between competing proposed mechanisms. Recent algorithmic and computational advances, including those that leverage graphics processing unit (GPU) architectures^{1, 2, 3, 4} could open the door to using computation not only to arbitrate different hypotheses, but also as a discovery tool to reveal new fundamental chemical mechanisms. Our experimentally-inspired⁵ ab initio nanoreactor accomplishes this using an ab initio molecular dynamics (AIMD) simulation of freely reacting molecules, coupled with automatic analysis and refinement methods to build a quantitatively accurate reaction network. By seeding the nanoreactor with diverse reactants available in various environments, such as the early Earth or the upper atmosphere, we explore reactivity and discover new reaction schemes. This approach will help guide experiment by posing new hypotheses and suggesting novel experiments.

The statistical rarity of activated chemical reactions restricts most AIMD studies to specific transformations along a chosen reaction coordinate or collective variable.^{6, 7, 8} A promising approach to overcome the rarity of reactive events has been the application of predefined heuristic rules^{9, 10, 11} or geometric searching^{12, 13} to generate new molecules and reaction networks. In contrast, the nanoreactor discovers molecules and reactions based only on the fundamental equations of quantum and classical mechanics. Reactions occur freely without preordained reaction coordinates or elementary steps.

Although recent advances in AIMD provide much computational relief, these simulations nevertheless remain costly for sampling large numbers of reactive events. We overcome this difficulty by incorporating new acceleration techniques in the nanoreactor. A virtual piston enhances reactivity by periodically pushing molecules toward the center of the nanoreactor, greatly increasing the frequency of collisions and barrier crossings (see Supplementary Figure 1). This evokes ideas from high-pressure and shock wave simulations,^{14, 15, 16} with the key difference that the periodic forcing increases the number of barrier crossings through ballistic collisions rather than inducing an equilibrium high-pressure regime. Furthermore, we use an approximate Hartree-Fock (HF) ansatz to access large simulation sizes (hundreds of atoms) and long time scales (hundreds of picoseconds). Sampling of chemical space at this approximate level is augmented by subsequent energy refinement of the discovered reaction pathways using more quantitative methods such as density functional theory (DFT). This strategy exploits the fact that the qualitative topography of the energy landscape is well-described with methods that may not provide quantitative estimates of reaction rates. For example, HF is well known to predict chemically reasonable molecular structures,¹⁷ even though DFT¹⁸ and more sophisticated wavefunction methods¹⁹ are more accurate for thermochemistry and barrier heights.

The nanoreactor achieves its goal of broadly exploring reaction pathways by taking an intermediate stance between physically realistic simulation and rule-based enumeration approaches. The ab initio simulation ensures that reaction trajectories obey physical equations of motion and avoids a combinatorial explosion of possibilities, while the occurrence of reactions is accelerated by explicitly not aiming to replicate the physicochemical conditions of any one environment. The pathways resulting from energy refinement are applicable to any thermodynamic setting by providing reaction parameters (e.g. concentration, temperature) as input variables to a kinetic model. This approach is valid as long as the relevant reactions are sampled at least once and included in the knowledge base. Ensuring complete sampling can be difficult and it would be premature to claim that we have achieved this for the prototypical cases presented in this paper. Here we focus on introducing the nanoreactor, presenting some newly discovered pathways from nanoreactor simulations, and discussing the broader implications of discovery-based theoretical methods.

RESULTS AND DISCUSSION

Insight into the synthesis of a diverse set of products

We discuss two nanoreactor simulations on contrasting systems. The first starts with a homogeneous collection of acetylene molecules, which we chose due to the well-known tendency of acetylene to polymerize into larger molecules. The second one is an idealization of the classic “Urey-Miller” experiment,²⁰ including several compounds postulated to exist in the early Earth atmosphere (hydrogen, ammonia, methane, carbon monoxide and water). The “Urey-Miller” simulation differs from the experimental conditions in that the virtual piston is used in place of electric sparks, though both methods provide an energy input to accelerate barrier crossings. Both simulations consist of many initial reactant molecules (50 – 100) in order to sample a large reaction space.

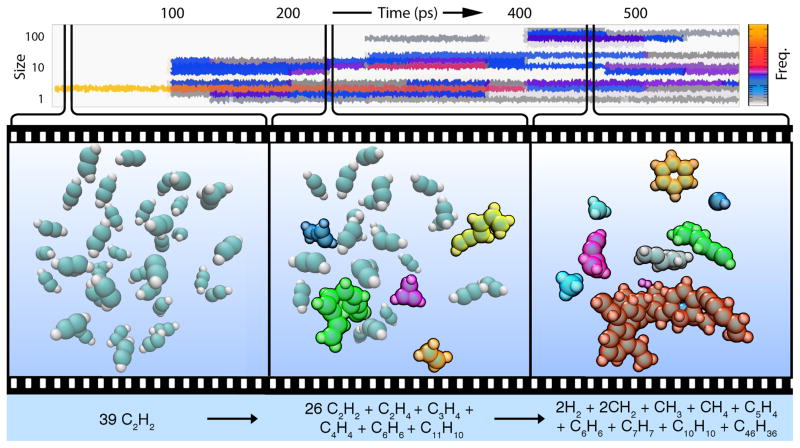
Figure 1 illustrates the acetylene nanoreactor simulation (movie clip in Supplementary Video 1). Molecules freely react with each other over the course of the simulation. The piston accelerates the reaction rate, oscillating with a period of 2 ps (4000 time steps). Nearly one hundred distinct products are formed after ~500 ps simulation time (1 million time steps) including methane, ethylene, cyclopropene, benzene, and larger polymeric species with both aliphatic and aromatic character (Supplementary Figure 3). We visualized the simulation trajectory using a machine-learning algorithm to identify new products and automatically highlight them in molecule-specific colors.

Figure 1.

Timeline of a nanoreactor simulation trajectory (movie clip in Supplementary Video 1). Top: Molecular size distribution as a function of simulation time. Left: Simulation begins with a collection of acetylene molecules (C = teal, H = white). New molecules are automatically highlighted with molecule-specific colors to indicate observed reactivity. Middle: Simple products appear first, including short polymeric species (green, yellow) as well as ethylene (orange) and cyclopropene (violet). Right: At longer simulation times the molecular size distribution becomes considerably wider; more than half of the atoms form a large molecule containing multiple aromatic rings (red). A long-lived, inert benzene molecule is also formed (gold, top right).

The diversity of discovered compounds is surprisingly rich. Previous experiments on acetylene reactivity at high pressure^{21, 22} indicate an increase in the number of single and double C–C bonds and a decrease in the number of triple bonds; a combination of linear and branched conjugated chains are formed rather than a covalently bonded single crystal. The nanoreactor produces some linear and branched conjugated chains similar to the experiment, but there are also many new motifs including aromatic rings, allenes and a smaller number of antiaromatic and highly strained rings. Since the goal of the nanoreactor is to discover new reactivity independently of specific experimental conditions, it is encouraging that we not only reproduced some of the observed chemistry from the high-pressure experiment but also found a greater diversity of chemical species which may be important in other settings. This is in part due to the high kinetic energy imparted by the piston, corresponding to instantaneous temperatures as high as ~10,000 K; at such temperatures, electronic excitations may be thermally accessible. Although the resulting multistate nonadiabatic dynamical effects could be included,²³ the nanoreactor currently ignores them, consistent with its primary goal to sample reaction space rather than realistically modeling a particular physical process.

The “Urey-Miller”-inspired simulation generated a starkly different collection of molecules, with much smaller products. Among the discovered products were the natural amino acid glycine, the unnatural amino acids α-hydroxyglycine and α-aminoglycine, and a reduced analogue of alanine with a geminal diol replacing the carboxyl group (see Supplementary Fig. 4). Additional discovered products include urea, ethylene glycol, and isocyanic acid, all of which have also been detected in meteorites that may have delivered organic molecules to the early Earth.²⁴ A few illustrative examples of discovered reactions are provided in Supplementary Figs. 5–9. These examples include reactions catalyzed by surrounding ammonia or water molecules that act as proton shuttles.

A complex web of reaction pathways

In addition to the high diversity of products, the nanoreactor simulation also offers insight into how the products were formed. The molecular dynamics pathway that connects stable reactant and product species is used to locate a corresponding minimum energy path (MEP). Using these MEPs, we build a network of reaction mechanisms linking products with reactants. More than 700 distinct reactions are found in the Urey-Miller simulation, with a wide distribution of reaction energies and barrier heights (see Supplementary Fig. 2). A significant fraction of the reactions occur with barriers < 50 kcal/mol, indicating they may be kinetically viable under ambient conditions.

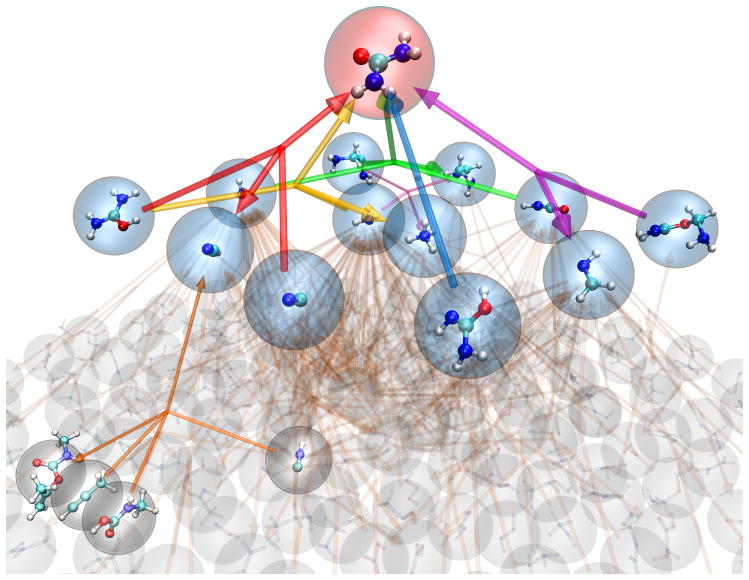
Deriving chemical insight from a complex web of reactions can be challenging. If we are mainly interested in a particular compound, we can map out the local network of closely related compounds – i.e. the molecules that appear on either side of chemical equations leading to the compound of interest. To do this, we focus on a particular molecule in the reaction network and investigate the energetics of the reactions it is involved in. Figure 2 shows one such representation of a reaction network derived from the “Urey-Miller” nanoreactor (3D view in Supplementary Video 2), which includes hundreds of products. Here we focused on a particular molecule (urea, red sphere) and visualized the reactions that it was involved in, leading to a second tier of molecules (blue spheres). Colored arrows indicate chemical reactions; arrowheads indicate one side of the chemical equation, though reactions can occur in either direction. Since each molecule is involved in reactions with so many others, the third tier of molecules (gray spheres) numbers in the hundreds and cannot be clearly represented. In the foreground, carbamimidic acid, H₂NC(NH)OH, tautomerizes to urea, CO(NH₂)₂, via proton transfer (blue arrows). Formaldimine, H₂CNH, also reacts with urea to form an ester adduct (violet arrows, right). Many of these molecules are found in interstellar clouds, and the pathways outlined here may be instructive for reactions that happen in a variety of environments including interstellar space.^{25, 26}

Figure 2.

Pyramid representation of reaction network with focus on a product molecule of interest (3D view in Supplementary Video 2); the initial reactants were H₂, H₂O, NH₃, CH₄ and CO. Compounds (C = teal, H = white, N = blue, O = red) are shown in spheres, and reactions (i.e. chemical equations) are indicated using colored arrows. Arrowheads indicate one side of the chemical equation, though reactions can occur in either direction. The chosen molecule (urea) is highlighted in red, and molecules directly involved in reactions with urea are highlighted in blue. Reactions more than one step removed from urea are mostly blurred out to show the high connectivity and complexity in the overall graph, with a single reaction highlighted (gray spheres, bottom left).

Following a specific reaction

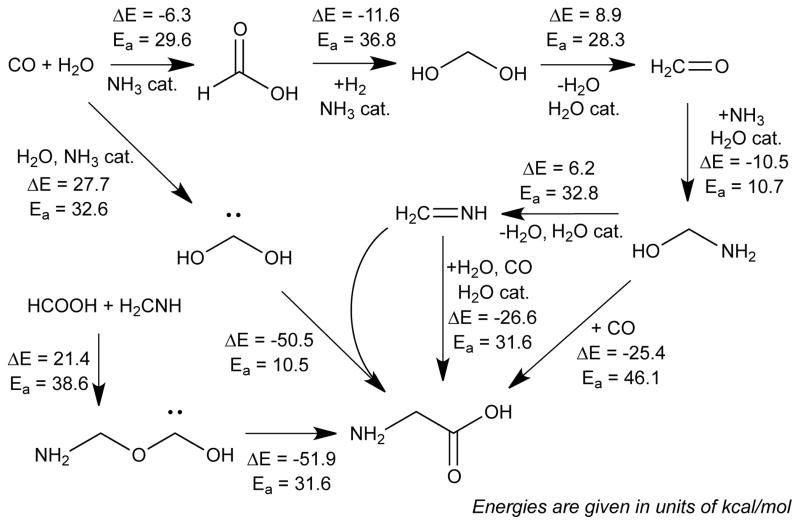
Focusing on a specific molecule allows us to trace the synthetic pathways leading from the starting materials. Figure 3 shows such a collection of pathways leading to glycine. Here glycine was formed with several distinct pathways involving reaction barriers of less than 40 kcal/mol. Formaldimine (Figure 3 center) is a key intermediate that participates in three of the four pathways. In one pathway, formaldimine combines with H₂O and CO in a termolecular reaction, and in the other two pathways it combines with formic acid, HCOOH, and proceeds through a singlet carbene intermediate. Aminomethanol (H₂NCOH, Figure 3 right) is another key intermediate—it is a precursor to formaldimine, but it can also react with CO directly to yield glycine.

Figure 3.

Sequence of elementary reaction steps derived from the nanoreactor simulation that begins with the fundamental reactants (CO, H₂, H₂O, and NH₃) and ends with the amino acid glycine. Glycine (bottom center) is formed via four different pathways, three of which involve formaldimine (center) and two of which involve singlet carbene intermediates. Reaction energies (ΔE) and activation barriers (E_a) calculated using DFT are provided in kcal/mol.

Formaldimine, formaldehyde and formic acid are among the most highly connected compounds in the reaction network, participating in more than 40 reactions with other species (the other two species with such high connectivity are methanol and hydrogen cyanide, plus the initial reactants). These highly connected compounds have in common the ability to react via several different types of pathways; for example, formic acid is found to participate in proton transfer, nucleophilic addition and dehydration reactions. Formic acid is easily formed from the starting materials by addition of water to carbon monoxide, whereas formaldimine requires several more elementary steps due to the need to form a C=N double bond. The C=N double bond of formaldimine participates in many addition reactions as either the nucleophile or electrophile, and leads to a diverse collection of primary amines and secondary imines. We note that the glycine synthesis pathways involve H₂ only once in the hydrogenation of formic acid to yield methanediol, and CH₄ never appears (it is highly inert). This supports previous proposals that biomolecules may have formed with little participation from these highly reducing compounds.²⁴

Emergence of higher-order chemical principles

Higher-order chemical principles emerge naturally from simulation and analysis in the nanoreactor. For example, the acetylene nanoreactor formed a large number of C-C bonds whereas the “Urey-Miller” nanoreactor did not. Many alternate pathways competing with C-C bond formation are available in the “Urey-Miller” system, most notably carbon-heteroatom bond formation via nucleophilic addition which involves a lower activation energy.

Another interesting observation is that the acetylene simulation forms very large molecules including a single large species comprised of more than 70 atoms, whereas the “Urey-Miller” simulation forms much smaller molecules (up to 16 atoms). This is because the sum total of bond orders across the entire simulation is roughly conserved, a natural consequence of electron conservation. The acetylene nanoreactor starts with a large number of triple bonds that can be traded to make more single bonds between molecules, whereas most of the “Urey-Miller” reactants are fully saturated molecules. Without double and triple bonds, a bimolecular reaction of two molecules that yields a larger product must also eliminate a smaller product, leading to quasi-equilibrium in the molecular size distribution.

The essential catalytic role of water and ammonia illustrates the importance of solvent in reducing the barrier of important pathways where hydrogen atoms or protons are transferred. In Figure 3, more than half of the elementary steps involve one or two catalytic water/ammonia molecules which participate by acting as a proton wire. For example, the barrier to the dehydration of methanediol (to yield formaldehyde) is lowered by more than 15 kcal/mol by the presence of a catalytic water molecule (from 43.5 to 28.3 kcal/mol). In the three elementary steps where carbon monoxide is hydrogenated to yield formaldehyde (Figure 3 top) a water molecule is temporarily incorporated and the highest barrier is 36.8 kcal/mol; the direct hydrogenation is much less favorable, with a barrier of 69.5 kcal/mol. In an aqueous environment, the presence of many solvent molecules would further facilitate such chemistry by stabilizing highly polar or temporarily charged species (for example, H₃O⁺ or NH₄⁺). Thus hydrogen-bonding solvents such as water play both an implicit and explicit role; we plan to include implicit solvent effects to improve the accuracy of the energy refinement for condensed phase conditions.

The future of the nanoreactor approach

The provided examples demonstrate that: (1) The ab initio nanoreactor not only finds many reactions that are well-known from experimental chemistry, but also discovers new pathways not previously characterized. (2) Many of these reactions proceed through low to moderate reaction barriers, in spite of simulation conditions. Finally, (3) some of the reactivity is complex and highly concerted, and is thus unlikely to be discovered through heuristic rule-based approaches. The termolecular reaction to yield glycine in Figure 3 and the acid-catalyzed ring opening in Supplementary Fig. 9 are examples of complex mechanisms, since three bonds are broken and two bonds are formed in a single barrier crossing. The nanoreactor discovers many termolecular reactions due to how it accelerates molecular collisions; although these reactions are rare in the gas phase, they can become relevant when two or more reactants form a pre-associated complex.²⁷

Here we showed two nanoreactor simulations with dramatically different results; the acetylene simulation underwent massive polymerization, whereas the “Urey-Miller” simulation generated a complex network of reactions including several pathways to glycine that pass through formaldimine, formic acid and aminomethanol as intermediates. Many of the discovered reactions are complex and concerted, highlighting the unique utility of the nanoreactor as a purely discovery-based means of generating chemically interesting elementary steps and supplementing existing methods reliant on hypotheses and prior expectations. More recent studies in prebiotic chemistry argue that the early Earth atmosphere was likely much less reducing, containing N₂, CO₂, possibly even some O₂;^{28, 29} thus, the prebiotic significance of this study should be taken in the context of the original Urey-Miller experiment rather than more modern hypotheses of the ancient Earth’s atmospheric composition. We anticipate that the nanoreactor will contribute to our future understanding of complex reactivity in natural systems by providing novel hypotheses for reaction pathways and elementary steps in arenas as diverse as catalysis, prebiotic chemistry, and astrochemistry.

METHODS

The nanoreactor AIMD simulations were performed with the TeraChem quantum chemistry and ab initio molecular dynamics software package,^{1, 2, 3, 4, 30, 31, 32, 33, 34} using the Hartree-Fock (HF) electronic wavefunction and a 3-21G Gaussian basis set to calculate the Born-Oppenheimer potential energy surface. The acetylene simulations used unrestricted Hartree-Fock and employed level-shifting³⁵ to allow for open-shell states, whereas the Urey-Miller simulation used restricted Hartree-Fock. The acetylene simulation used a single initial configuration whereas the Urey-Miller simulation used four different initial configurations with the same molecules. The equations of motion were numerically integrated using Langevin dynamics with an equilibrium temperature of 2000 K (also the starting temperature) and a friction coefficient of 7 ps⁻¹. The temperature corresponds to an average kinetic energy of 4.0 kcal/mol per degree of freedom; the thermal motion rapidly breaks apart noncovalent interactions without breaking the covalent bonds. The calculations were feasible due to the efficiency of TeraChem, which dramatically accelerates the calculation of the Fock operator – especially the Coulomb and exchange operators – by evaluating the two-electron integrals on the graphics processing unit (GPU). The self-consistent field (SCF) calculation at each AIMD step was made more robust by using the augmented direct inversion in the iterative subspace (ADIIS) algorithm³⁶ as a backup in cases where the default DIIS algorithm³⁷ failed to converge. A total of 560/1296 ps of time evolution was followed for the acetylene (156 atoms) and Urey-Miller (228 atoms) simulations, respectively. The total computational cost of these calculations was 41,700 (acetylene) and 132,400 (Urey-Miller) CPU/GPU hours; TeraChem uses one CPU core per GPU.

The molecules were restrained to move inside a spherical volume by a boundary potential, with a time-dependent component to increase the occurrence of reaction events:

$$\begin{array}{c}V(r,t)=f(t)U(r,r_1,k_1)+(1-f(t))U(r,r_2,k_2);\\ U(r,r_0,k)=\frac{mk}{2}{(r-r_0)}^2\theta (r-r_0);f(t)=\theta \left(\lfloor \frac{t}{T}\rfloor -\frac{t}{T}+\frac{\tau }{T}\right),\end{array}$$

where k₁ = 1.0 kcal mol⁻¹ Å⁻², r₁ = 14.0 Å, k₂ = 0.5 kcal mol⁻¹ Å⁻², r₂ = 8.0 Å, τ = 1.5 ps, T = 2.0 ps, ⌊ ⌋ is the floor function and θ is the Heaviside step function. f(t) is a rectangular wave that oscillates between 1 (duration τ) and 0 (duration T−τ), and U(r,r₀,k) is a radial potential that is zero inside the prescribed radius r₀ and harmonic outside. The force constant is multiplied by the atomic mass (in a.m.u) such that all atoms at the same radial coordinate were subject to equal acceleration. The rectangular waveform switches the restraint potential between U(r,r₁,k₁) and U(r,r₂,k₂), forcing atoms with radial position 8.0 < r < 14.0 Angstrom toward the center and causing them to collide. When the sphere is expanded again, the molecules in the simulation rapidly diffuse (due to the high temperature) to fill the larger volume. The rectangular waveform spans a broad frequency range, and thus the applied energy does not preferentially drive any specific mode in the system.

The simulation analysis was performed using graph-theoretical and machine-learning routines in the networkx³⁸ and scikit-learn³⁹ Python modules. The atomic connectivity for each frame in the nanoreactor AIMD trajectory is determined using covalent radii, and graphs representing individual molecules are constructed from the connectivity matrix. We identified chemical reactivity in the nanoreactor simulation by searching for changes in the connectivity graphs (i.e. molecules) as a function of time. A major challenge in this procedure is the transient appearance of spurious connectivity graphs due to high frequency bond vibrations and close contacts during molecular collisions. We addressed this problem by applying a two-state hidden Markov model (HMM) to each time series, in which the observed time series of a given connectivity graph is modeled using an underlying lower-frequency signal:

$$P(Y)=\sum _{X=0,1}P(Y\mid X)P(X);P(Y\mid X)=\{\begin{array}{c}0.6,Y=X\\ 0.4,Y\ne X\end{array};X_{i+1}=\left(\begin{array}{cc}0.999& 0.001\\ 0.001& 0.999\end{array}\right)X_i,$$

where Y is the observed time series and X is the underlying lower-frequency signal described by a Markov process. The HMM is parameterized by: (1) the probability of correctly observing the hidden signal (60% of the time), and (2) the transition probability matrix for the Markov process (0.1% per time step). The HMMs allowed the algorithm to recognize molecules despite transient disruptions of their connectivity graphs. A reaction in the nanoreactor trajectory is recognized as a sequence of frames in which a set of complete connectivity graphs transforms into a different complete set. The atoms involved in the reaction are extracted from the trajectory, which includes the reactant and product, as well as certain catalytic species which chemically participate but do not change their compositions (e.g. a catalytic water molecule in proton transfer). The reactive trajectory segments are used to perform subsequent energy refinements via minimum energy path (MEP) search.

In order to accurately determine the thermochemistry and barrier heights (which can be used to infer reaction rates), the MEP search is performed using more accurate (and more computationally expensive) electronic structure methods; the increased cost is largely mitigated by the much smaller size of these calculations, as they only include the atoms that participate in an individual reaction. We chose to use the B3LYP three-parameter density functional approximation and the larger 6-31+G(d,p) basis set for its ability to reproduce experimental heats of formation and activation energies in organic chemistry,^{40, 41} but even more accurate and computationally expensive methods such as coupled cluster^{42, 43, 44} could also be used. Importantly, the reactive AIMD trajectory segments used to initiate the MEP search contain numerous large amplitude and high frequency motions that are orthogonal to the reaction coordinate. Therefore, we carried out the path refinement in several stages, which we briefly summarize here and will cover in detail in an upcoming publication.

First, the AIMD path endpoints are energy-minimized in order to obtain optimized reactant and product structures; the sequences of optimization coordinates are joined with the AIMD segment to create a continuous path that connects minimized reactants and products. Next, the path is smoothed with an interpolation algorithm in internal coordinates, which ensures a smooth connecting path that avoids unphysical structures (e.g. atoms passing through each other). The interpolated path is used as an initial guess to the string method⁴⁵ which provides an estimate of the transition state. From here, the transition state is located using a partitioned rational function optimization algorithm, followed by an intrinsic reaction coordinate (IRC) calculation to reconnect the transition state with the reactant and product. In cases where the IRC calculation results in different molecules from the initial reactant and product, the IRC-derived endpoints are used in the reaction network. The Q-Chem quantum chemistry software package⁴⁶ was used in the refinement calculations.