Randomised P-values and nonparametric procedures in multiple testing

Abstract

The validity of many multiple hypothesis testing procedures for false discovery rate (FDR) control relies on the assumption that P-value statistics are uniformly distributed under the null hypotheses. However, this assumption fails if the test statistics have discrete distributions or if the distributional model for the observables is misspecified. A stochastic process framework is introduced that, with the aid of a uniform variate, admits P-value statistics to satisfy the uniformity condition even when test statistics have discrete distributions. This allows nonparametric tests to be used to generate P-value statistics satisfying the uniformity condition. The resulting multiple testing procedures are therefore endowed with robustness properties. Simulation studies suggest that nonparametric randomised test P-values allow for these FDR methods to perform better when the model for the observables is nonparametric or misspecified.

1. Introduction

Consider the problem of testing a pair of hypotheses H₀: θ = θ₀ versus H₁: θ ≠ θ₀ based on the realisation x, called data, of a random observable X whose distribution F is assumed, possibly incorrectly, to belong to a known class of distributions = {F (x; θ): θ ∈ Θ}. The class is said to be a model for F. Assume further that the test rejects H₀ for large values of a statistic S(X). Given data X = x, the P-value or significance value is defined by

$$P(x)=\mathbf{P}\{S(X)\ge S(x)\mid X~F(·;{\theta }_0)\}.$$

The P-value statistic is P (X). Given an α ∈ [0, 1], the test which rejects H₀ whenever P (X) ≤ α, which we shall denote by δ(X; α), is called an α-level test. The size of δ(X; α) is the probability of rejecting H₀ when in fact θ = θ₀.

For the size of δ(X; α) to be α for any α ∈ [0, 1], it is necessary and sufficient that P (X) have a uniform distribution under θ = θ₀. However, this condition will only be true when S(X) has a continuous distribution and the assumed model is correct. If S(X) has a discrete or mixed-type distribution or the model is misspecified, i.e. F ∉ , then this uniformity condition does not hold and the size of δ(X; α) need not be α. The impact of the breakdown of this uniformity condition may be deemed acceptable for a single hypothesis test. However, when testing many hypotheses simultaneously, the breakdown of this uniformity condition may cause multiple testing procedures to perform poorly.

Benjamini and Hochberg (1995) introduced a method for controlling the false discovery rate (FDR), which is the expected proportion of erroneously rejected null hypotheses (false discoveries) among rejected null hypotheses (discoveries). FDR methods are useful in situations when it is acceptable for a small proportion of discoveries to be false discoveries. Many other methods have been developed to estimate the FDR for specified rejection regions or observed P-values (see Efron, Tibshirani, Storey, and Tusher 2001; Storey 2002, 2003; Efron 2004; Genovese and Wasserman 2004; Jin and Cai 2007; Ruppert, Nettleton, and Hwang 2007; Sun and Cai 2007). However, many FDR methods are developed under the assumption that each P-value statistic P_i (X_i) for testing the ith pair of hypotheses H_0i versus H_1i is uniformly distributed under H_0i. But in many practical situations calling for FDR control or estimation, this uniformity condition does not hold. For example, in a standard microarray analysis, T-tests or Wilcoxon rank-sum tests are employed to test the null hypotheses that gene expression levels are not differentially expressed across two treatment groups. However, the Wilcoxon rank-sum test statistic has a discrete distribution, while the T-test is valid only if a normal model is correct for each of the F_i s.

The fact that the uniformity condition may not be satisfied has been partly addressed. Some FDR methods allow for the estimation of the distribution of the P-value statistics under the null hypotheses (see, e.g. Yekutieli and Benjamini 1999; Korn, Troendle, McShane, and Simon 2004; Pollard and van der Laan 2004; van der Laan and Hubbard 2006; Efron 2007; Dudoit and van der Laan 2008; Efron 2008), and hence do not require that P-value statistics satisfy the uniformity condition. However, as noted in Efron (2008), these methods will lead to FDR estimators with a larger standard error. In Section 5, we will see that these methods may also lead to biased FDR estimators. Other FDR methods have been developed for P-value statistics with discrete distributions (see, e.g. Gilbert 2005; Kulinskaya and Lewin 2009).

In this paper, rather than modifying or developing an FDR method, we focus on the P-value statistics themselves that are being used in many of these FDR methods. The idea is to augment the observable x by an independently generated uniform random variate u, and to view the doubleton (x, u) as full data. The collection of decision functions given by Δ = {δ(X, U; α): α ∈ [0, 1]} is viewed as a stochastic process. The decision process Δ will then induce a well-defined P-value statistic, denoted P_Δ(X, U), which is uniformly distributed, under H₀, for a model if and only if the size of δ(X, U; α) is α under model for each α in [0,1]. This framework provides an avenue for generating P-value statistics that satisfy the uniformity condition when test statistics have discrete distributions. These P-value statistics are then the statistics on which existing FDR methods will operate. If P_Δ(X, U) depends in a nontrivial manner on U, it will be said to be a randomised P-value statistic. This framework will allow for robust nonparametric procedures to be used to generate P-value statistics that are uniformly distributed under the null hypotheses. Hence, those FDR methods which assume the uniformity condition are endowed with robustness properties.

In Section 2, the definitions of a valid decision process and a randomised P-value statistic are given. A discussion regarding randomisation in multiple testing is in Section 3. In Section 4, the randomised Wilcoxon rank-sum test P-value statistic is defined and compared with the nonrandomised Wilcoxon P-value and T-test P-value statistics. In Section 5, the P-values discussed in Section 4 are applied to an FDR-controlling and an FDR-estimating procedure. Simulation studies suggest that if F is non-normal, these procedures perform much better when using the randomised Wilcoxon P-values rather than the T-test P-values and comparable when F is normal. Procedures always perform better when using the randomised Wilcoxon P-values as compared with the nonrandomised Wilcoxon P-values. In Section 6, a real microarray data set is used to illustrate the methods in this paper and to demonstrate that the set of null hypotheses that are declared false will depend on the type of P-value and FDR procedure used to test the null hypotheses. Concluding remarks are in Section 7.

2. Randomised P-value statistics

2.1. Decision processes and P-values

In this section, we introduce the notion of a randomised P-value statistic associated with a randomised decision or test function. Recall that a randomised test function for testing H₀ versus H₁ based on X ∈ 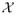is a function ϕ: 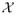→ [0, 1], with the interpretation that ϕ(x) is the probability of rejecting H₀ when X = x. Let U be uniformly distributed over the unit interval and independent of X. We define a decision function δ: 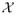× [0, 1] → {0, 1} via δ(x, u) = I {u ≤ ϕ(x)}. The important point is that this δ is a nonrandomised decision function with respect to the augmented random observable (X, U). The decision function δ has the interpretation that if δ = 1 (0), then H₀ is rejected (not rejected).

Let us suppose that X ~ F with F ∈ , and consider the problem of testing H₀: F ∈ ⊂ versus H₁: F ∈ \ = based on X and U. For the decision function δ(X, U), its size is defined by η = E{δ(X, U)|(X, U) ~ F ⊗ λ}, where (X, U) ~ F ⊗ λ means that X ~ F, U ~ λ with λ being Lebesque or uniform probability measure on [0, 1], and with X and U independent. For brevity, we write E_F {δ(X, U)} ≡ E{δ(X, U)|(X, U) ~ F ⊗ λ} for the remainder of the paper. We could specify the size of η to determine the complete specification of δ(X, U). Thus it will be beneficial to indicate this symbiotic interplay by writing δ(X, U; η). The stochastic process indexed by η and defined by Δ = {δ(X, U; η): η ∈ [0, 1]} will be called a decision process provided it satisfies the condition that for every F ∈ , the mapping η ↦ δ(x, u; η) is nondecreasing, right-continuous, and with δ(x, u; 0) = 0 and δ(x, u; 1) = 1 for almost all (x, u) ∈ 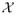× [0, 1] with respect to F ⊗ λ. The index η will be referred to as the size index.

For a given decision process Δ, we define its induced P-value statistic by

$$P_{\mathrm{\Delta }}(X,U)=inf\{\eta \in [0,1]:\delta (X,U;\eta )=1\}.$$ (1)

This will be referred to as a randomised P-value statistic when it depends nontrivially on U. A realised P-value P_Δ(x, u) can be interpreted as the smallest size index η allowing for the rejection of H₀ given the augmented data (x, u) using the decision process Δ.

2.2. Examples of decision processes and P-value statistics

The definition of the P-value statistic in Equation (1) is quite general since the form of the decision process could be quite general. Therefore, before proceeding we demonstrate this definition more concretely by obtaining the specific forms of P_Δ(X, U) for three commonly encountered decision processes. For each decision process, suppose that S(X) is a one-dimensional test statistic. Let Q be a distribution function on the range space of S(X). Define q(s) = ΔQ(s) = Q(s) − Q(s−) and the quantile function Q⁻¹(u) = inf{s: Q(s) ≥ u}.

Let us first consider a ‘lower-tailed’ decision or test function. This type of decision function is used when small values of S(x) are evidence against the null hypothesis. The decision function has the form, for η ∈ [0, 1],

$${\delta }^{-}(X,U;\eta )=I\{S(X)<Q^{-1}(\eta )\}+I\{S(X)=Q^{-1}(\eta )\}I\{U\le {\gamma }^{-}(\eta )\},$$

where

$${\gamma }^{-}(\eta )=\frac{\eta -Q(Q^{-1}(\eta )-)}{q(Q^{-1}(\eta ))},$$

with the convention that 0/0 = 0. Observe that E{δ⁻(X, U; η)|S(X) ~ Q} = η.

Form the decision process Δ⁻ = {δ⁻(X, U; η): η ∈ [0, 1]}. Note that {η: δ(x, u; η) = 1} = {η: η ≥ Q(S(x)−) + uq(S(x))}. Thus, by Equation (1), the associated P-value statistic for the decision process Δ⁻ is

$$P_{{\mathrm{\Delta }}^{-}}(X,U)=inf\{\eta \in [0,1]:{\delta }^{-}(X,U;\eta )=1\}=Q(S(X)-)+Uq(S(X)).$$ (2)

Analogously, consider an ‘upper-tailed’ decision function. This decision function is used when large values of S(x) are evidence against a null hypothesis. The decision function has the form, for η ∈ [0, 1],

$${\delta }^{+}(X,U;\eta )=I\{S(X)>Q^{-1}(1-\eta )\}+I\{S(X)=Q^{-1}(1-\eta )\}I\{U\le {\gamma }^{+}(\eta )\},$$

where

$${\gamma }^{+}(\eta )=\frac{\eta -[1-Q(Q^{-1}(1-\eta ))]}{q(Q^{-1}(1-\eta ))}.$$

Again, note that E{δ⁺(X, U; η)|S(X) ~ Q} = η.

Form the upper-tailed decision process Δ⁺ = {δ⁺(X, U; η): η ∈ [0, 1]} and observe that {η: δ⁺(x, u; η) = 1} = {η: η ≥ 1 − Q(S(x)) + uq(S(x))}. It follows from Equation (1) that the P-value statistic for Δ⁺ is

$$P_{{\mathrm{\Delta }}^{+}}(X,U)=inf\{\eta \in [0,1]:{\delta }^{+}(X,U;\eta )=1\}=1-Q(S(X))+U_q(S(X)).$$ (3)

The P-value expressions in Equations (2) and (3) are the forms obtained according to the P-value definition of Cox and Hinkley (1974), so their definition is subsumed by the P-value definition in Equation (1).

The ‘two-sided’ decision function has the form given by, for η ∈ [0, 1] and for a fixed c ∈ [0, 1],

$$\begin{array}{l}{\delta }_c^0(X,U;\eta )=max\{{\delta }^{-}(X,U;(1-c)\eta ),{\delta }^{+}(X,U;c\eta )\}\\ ={\delta }^{-}(X,U;(1-c)\eta )+{\delta }^{+}(X,U;c\eta ),\end{array}$$

with the second form following since it is easy to see that the probability that δ⁻(X, U; (1 − c)η) and δ⁺(X, U; cη) simultaneously take the value of one is zero. Note that this decision function is a combination of the lower- and upper-tailed test functions where the lower-tailed test is allocated a size of (1 − c)η and the upper-tailed test is allocated a size of cη. Form the decision process ${\mathrm{\Delta }}_c^0=\{{\delta }_c^0(X,U;\eta ):\eta \in [0,1]\}$. It is important to point out that c should not depend on η and (X, U), otherwise ${\mathrm{\Delta }}_c^0$ need not satisfy some of the conditions of a decision process.

As to be expected, the P-value statistic induced by ${\mathrm{\Delta }}_c^0$ is closely related to the P-value statistics for Δ⁺ and Δ⁻. We present the form of this P-value statistic in Theorem 2.1 and then present some distributional equivalences in Corollary 2.2.

Theorem 2.1

Fix a c ∈ [0, 1] and let Δ⁻, Δ⁺, and ${\mathrm{\Delta }}_c^0$ be defined as above. Then,

$$P_{{\mathrm{\Delta }}_c^0}(X,U)=min\left\{\frac{P_{{\mathrm{\Delta }}^{-}}(X,U)}{1-c},\frac{P_{{\mathrm{\Delta }}^{+}}(X,U)}{c}\right\}.$$ (4)

Proof

Note that

$$\begin{array}{l}\{\eta :{\delta }_c^0(x,u;\eta )=1\}=\{\eta :{\delta }^{+}(x,u;c\eta )=1\}\cup \{\eta :{\delta }^{-}(x,u;(1-c)\eta )=1\}\\ =\{\eta :c\eta \ge 1-Q(S(x))+uq(S(x))\}\cup \{\eta :(1-c)\eta \ge Q(S(x)-)+uq(S(x))\}\\ =\left\{\eta :\eta \ge \frac{P_{{\mathrm{\Delta }}^{+}}(x,u)}{c}\right\}\cup \left\{\eta :\eta \ge \frac{P_{{\mathrm{\Delta }}^{-}}(x,u)}{1-c}\right\}\\ =\left\{\eta :\eta \ge min\left[\frac{P_{{\mathrm{\Delta }}^{+}}(x,u)}{c},\frac{P_{{\mathrm{\Delta }}^{-}}(x,u)}{1-c}\right]\right\}.\end{array}$$

Hence, the result follows from Equation (1).

Corollary 2.2

For Δ⁺, Δ⁻, and ${\mathrm{\Delta }}_c^0$ defined as above,

$$P_{{\mathrm{\Delta }}_c^0}(X,U)\stackrel{d}{=}min\left\{\frac{1-P_{{\mathrm{\Delta }}^{+}}(X,U)}{1-c},\frac{P_{{\mathrm{\Delta }}^{+}}(X,U)}{c}\right\}\stackrel{d}{=}min\left\{\frac{P_{{\mathrm{\Delta }}^{-}}(X,U)}{1-c},\frac{1-P_{{\mathrm{\Delta }}^{-}}(X,U)}{c}\right\},$$

where ‘ $\stackrel{d}{=}$’ means equal in distribution.

Proof

It suffices to show that $1-P_{{\mathrm{\Delta }}^{-}}(X,U)\stackrel{d}{=}{P}_{{\mathrm{\Delta }}^{+}}(X,U)$ since this would imply that $1-P_{{\mathrm{\Delta }}^{+}}(X,U)\stackrel{d}{=}{P}_{{\mathrm{\Delta }}^{-}}(X,U)$. But since $U\stackrel{d}{=}1-U$ and Q(s−) = Q(s) − q(s), we have

$$\begin{array}{l}1-P_{{\mathrm{\Delta }}^{-}}(X,U)=1-\{Q(S(X)-)+Uq(S(X))\}\\ =1-\{Q(S(X))-Q(S(X))+Uq(S(X))\}\\ =1-Q(S(X))+\{1-U\}q(S(X))\\ \stackrel{d}{=}1-Q(S(X))+Uq(S(X))=P_{{\mathrm{\Delta }}^{+}}(X,U).\end{array}$$

The constant c can be viewed as a weight between the lower- and upper-tailed tests. If it is more desirable, or perhaps optimal, to reject the null hypothesis for large values of S(x) rather than small values of S(x), then c can be chosen to be close to 1. Observe, also, that when c = 1/2, which may be preferable under symmetry considerations, then we obtain from expression (4) the usual P-value statistic in two-sided hypotheses testing, given by $P_{{\mathrm{\Delta }}_{1/2}^0}(X,U)=2min\{P_{{\mathrm{\Delta }}^{+}}(X,U),P_{{\mathrm{\Delta }}^{-}}(X,U)\}$.

2.3. Properties of P-value statistics

It is desirable to have a decision process in which the size index η coincides with the size of δ(X, U ; η) for any η. Since the size of δ(X, U ; η) will depend on , it is important to emphasise that the validity of a test is relative to the sub-model . We shall therefore say that the decision function δ(X, U ; η) is -size-valid at η if E_F δ(X, U ; η) = η, and the decision process Δ is -size-valid if, for every η ∈ [0, 1], δ(X, U ; η) is -size-valid at η. Likewise, we say that δ is -level-valid at η if E_F δ(X, U ; η) ≤ η, and Δ is -level-valid if δ(X, U ; η) is -level valid at η for every η ∈ [0, 1].

Next we consider the distribution of the P-value statistic under . We say that P_Δ(X, U) is -uniform if P_F {P_Δ (X, U) ≤ t} = t for every t ∈ [0, 1]. Likewise, we say that P_Δ(X, U) is -uniformly bounded if P_F {P_Δ(X, U) ≤ t} ≤ t for every t ∈ [0, 1].

The size and level validity of Δ are tied-in to each other. In Theorem 2.3, we see that P_Δ(X, U) is -uniform if and only if Δ is -size-valid and P_Δ(X, U) is -uniformly bounded if and only if Δ is -level-valid.

Theorem 2.3

Let Δ = {δ(X, U ; η) : η ∈ [0, 1]} be a decision process for H₀ : F ∈ versus H₁: F ∈ . Then P_Δ(X, U) is -uniformly bounded if and only if Δ is -level-valid, and P_Δ(X, U) is -uniform if and only if Δ is -size-valid.

Proof

Let F ∈ . Then there exists an N ⊂ × [0, 1], dependent on F, with w ↦ δ(x, u; w) right-continuous and nondeceasing for (x, u) ∈ N^c and with (F ⊗ λ)(N) = 0. We first show that

$$\{(x,u):P_{\mathrm{\Delta }}(x,u)\le t\}=\{(x,u)\in N^c:\delta (x,u;t)=1\}\cup \{(x,u)\in N:P_{\mathrm{\Delta }}(x,u)\le t\}.$$ (5)

Consider an (x, u) ∈ N^c. If w ≥ P_Δ(x, u), then w ≥ inf{w′ : δ (x, u; w′) = 1} implying that δ(x, u; w) = 1 since δ(x, u; ·) is right-continuous and nondecreasing for (x, u) ∈ N^c. Conversely, if δ(x, u; w) = 1, then since δ(x, u; ·) is right-continuous and nondecreasing for (x, u) ∈ N^c and takes values in {0, 1}, then w ≥ inf{w′: δ(x, u; w′) = 1} = P_Δ(x, u). This proves Equation (5). From Equation (5) and since (F ⊗ λ)(N) = 0, it follows that P_F {P_Δ(X, U) ≤ t} = P_F {δ(X, U ; t) = 1} for every F ∈ , so that

$$\begin{array}{l}\underset{F\in {\mathcal{F}}_0}{sup}{\mathbf{P}}_F\{P_{\mathrm{\Delta }}(X,U)\le t\}=\underset{F\in {\mathcal{F}}_0}{sup}{\mathbf{P}}_F\{\delta (X,U;t)=1\}\\ =\underset{F\in {\mathcal{F}}_0}{sup}{E}_F\{\delta (X,U;t)\}\le t\end{array}$$

for every t ∈ [0, 1] if and only if Δ is -level-valid, and with equality if and only if Δ is -size-valid.

Theorem 2.3 suggests that the P-value uniformity condition can be verified by checking that Δ is -size-valid, which in some situations can be verified by verifying that the model is valid. For example, Δ_T in Section 5 is -size-valid if a normal model for F is appropriate. However, if the sample size of the data for testing a null hypothesis is small, model validation techniques may be considered unpalatable, thus warranting the use of a randomised nonparametric type test to ensure that the P-value statistic satisfies the uniformity condition. Such types of P-values will be studied in greater detail in Section 4. For now, we use Theorem 2.3 to examine the relationship among decision processes Δ⁺, Δ⁻, and ${\mathrm{\Delta }}_c^0$ and P-values P_Δ⁺, P_Δ⁻, and $P_{{\mathrm{\Delta }}_c^0}$.

Corollary 2.4

Let Δ⁺ and Δ⁻ be defined as in Section 2.2 and let c ∈ [0, 1] be fixed. If Δ⁺ and Δ⁻ are both -level-valid, then ${\mathrm{\Delta }}_c^0$ is also -level-valid, hence $P_{{\mathrm{\Delta }}_c^0}(X,U)$ is -uniformly bounded.

Proof

The second implication follows from the first assertion. The first assertion follows immediately by noting that

$$\begin{array}{l}\underset{F\in {\mathcal{F}}_0}{sup}{E}_F{\delta }_c^0(X,U;\eta )=\underset{F\in {\mathcal{F}}_0}{sup}\{E_F{\delta }^{+}(X,U;c\eta )+E_F{\delta }^{-}(X,U;(1-c)\eta )\}\\ \le \underset{F\in {\mathcal{F}}_0}{sup}\{E_F{\delta }^{+}(X,U;c\eta )+\underset{F\in {\mathcal{F}}_0}{sup}{E}_F{\delta }^{-}(X,U;(1-c)\eta )\}\\ \le c\eta +(1-c)\eta =\eta ,\end{array}$$

with the last inequality arising from the -level-validity of Δ⁺ and Δ⁻.

Corollary 2.5

Assume the conditions of Corollary 2.4. If, furthermore, there exists an F₀ ∈ such that S(X) ~ Q when X ~ F₀, then ${\mathrm{\Delta }}_c^0$ is -size-valid, hence $P_{{\mathrm{\Delta }}_c^0}(X,U)$ is -uniform.

Proof

Using the additional condition, we have that

$$E_{F_0}{\delta }_c^0(X,U;\eta )=E_{F_0}{\delta }^{-}(X,U;(1-c)\eta )+E_{F_0}{\delta }^{+}(X,U;c\eta )=\eta .$$

Coupling this with the result of Corollary 2.4, we obtain that ${sup}_{F\in {\mathcal{F}}_0}{E}_F{\delta }_c^0(X,U;\eta )=\eta$, thereby proving that ${\mathrm{\Delta }}_c^0$ is -size-valid.

3. Discussion on randomised testing

Before considering more concrete examples, we discuss the use of a randomiser U in multiple testing. Such a device is usually considered unpalatable or undesirable (cf. Randles and Wolfe 1979, p. 34) in the single-pair hypothesis testing problem. There are two major arguments against randomised tests or decision functions. The first is our uneasy feeling that we are relinquishing the decision-making to a ‘biased coin’ when we randomise, while the second is the common-sensical objection that, when using a randomised multiple testing procedure, we may end up rejecting one null hypothesis and not another even if the observed data for these tests are identical. Certainly, both of these concerns are quite compelling, but let us try to clarify the relevant issues.

3.1. An implementation perspective

The notion of randomised testing or decision-making is clearly not new as this is critical in the Neyman and Pearson (1933) hypothesis testing framework and is also central in decision and game theory. In fact, optimal strategies are usually randomised, also called mixed, strategies. Let us examine how we operationally implement a randomised test function, ϕ(x), which takes values in [0, 1]. Given data x, H₀ is rejected with probability ϕ(x). If ϕ(x) ∈ {0, 1}, then our decision is clear. However, if ϕ(x) ∈ (0, 1), we then generate a U ~ U [0, 1], and if U ≤ ϕ(x) we reject H₀, otherwise we fail to reject H₀. This protocol, however, leads to a very-human psychological difficulty since the ‘coin flip’ (U) acquires a very central role in the decision-making process, eliciting the strident cry ‘Why should I let a coin make my final decision?’

However, suppose that for every experiment leading to data x we simultaneously generate a uniform variate u independently of x, and call (x, u) the full data. We then let the decision function δ depend immediately on (x, u) and make it nonrandomised, that is, taking {0, 1}-values only. In this paper, this is done by defining δ(x, u) = I{u ≤ ϕ(x)} where the ϕ(·) is the usual randomised test function depending only on data x. Then, the psychological difficulty mentioned above disappears, or is at least diminished, since with the full data (x, u) at hand, an unequivocal decision can be made. Since the u-component of the data was obtained together with the experimental component x, we may view the randomisation experiment as simply a data-gathering experiment. In essence, at the moment of generating the randomiser u, no Sword of Damocles is hanging over our heads to make an immediate decision. This is a crucial difference with the standard protocol, so the ‘coin flip’ in this revised protocol does not acquire a ‘door-die’ quality. In essence, defining a decision function in such a manner emphasises that any randomised decision function could be viewed as nonrandomised, so long as we view (x, u) as the full experimental data.

3.2. Whither common sense or mathematical metric?

As mentioned earlier, another objection to randomised multiple testing procedures is the potential to end up with two conflicting conclusions for two genes even when they possess the same data or rank vectors. This clearly runs counter to our intuition. However, our intuition is based on our common sense, whereas a mathematical metric of assessing such procedures should be utilised. To elaborate on this matter in a concrete manner, let us suppose that we have 10,000 genes and for the mth gene we observe the value of a random variable X_m which has a binomial distribution with parameters 10 and θ_m, and suppose that we want to test for gene m the pair of hypothesis H_0m : θ_m = 0.5 versus H_1m : θ_m = 0.7. We may assume that the X_ms are independent of each other. For the mth pair of hypotheses, the most powerful Neyman–Pearson test of size α = 0.05 (of course, in a multiple testing setting we actually need to adjust this value, e.g. using the Sidak sizes, but for illustrative purpose, let us stick with 0.05) is a randomised test which rejects H_0m if X_m > 7, while if X_m = 7, we reject H_0m with a probability of 0.89. The difficulty alluded to above is the possibility that, for example, genes 1 and 2 may have observed values x₁ = 7 and x₂ = 7. When using this multiple testing procedure there is a probability of (2)(0.89)(0.11) = 0.1958 that we will end up with different decisions for these genes, even though they have exactly the same data. We could certainly have used the nonrandomised 0.05-level tests for each of these genes where H_0m is rejected if and only if X_m > 7. If this multiple testing procedure is used, then we will never encounter the common-sensical impasse described above.

But, the question is, which of these two multiple testing procedures is better, mathematically speaking? Let us now assume that among these 10,000 genes, 20% have their alternative hypotheses being correct. Since the probability of observing the value of 7 for a Bin(10, 0.7) distribution is 0.2668, then we would expect that among the 2000 genes with θ_m = 0.7, about 534 of them will get a value of x_m = 7. Among these 534 cases, if we use the randomised multiple testing procedure, we expect to find 475 of them to have correct alternative hypotheses, whereas if we used the nonrandomised multiple testing procedure, in all of these 534 cases we will fail to reject their null hypotheses. Thus, many more real discoveries will be achieved by using the randomised multiple decision function, with potential practical, important, and even ethical implications such as improving the odds of discovering new and effective drugs. But then, one may still wonder how we could justify making different decisions for these genes where the observed values of X_ms are equal to 7. However, statistics, at least from the frequentist viewpoint, is never about individual cases (‘genes’), but rather it is always about the ensemble of cases. Thus, from this perspective, we feel that the afore-mentioned common-sensical objection to randomised multiple testing procedures is more of a mirage.

3.3. Alternatives to randomised testing

The goal of this paper is to provide a general definition of a P-value statistic, and to further demonstrate that the type of P-value statistic being used in a multiple testing method will have an impact on the performance of the method, especially if the procedure is developed under the uniformity condition. However, not all methods are developed under this uniformity condition. Let us pause to discuss some of these alternative methods.

Others have considered modifying the nonrandomised (crisp) P-value, defined by P(x) = P_H0 {S(X) ≥ S(x)}, but without making use of a randomiser. Lancaster (1961) defined the mid-P-value via P_mid = P_H0{S(X) > S(x)} +(1/2)P_H0 {S(X) = S(x)}. Westfall and Soper (1998) considered weighting the nonrandomised P-values, while Westfall and Soper (2001) considered constructing P-values with weighted test statistics. Both methods were designed to control the family-wise error rate (the probability of making one or more false discoveries). Geyer and Meeden (2005) used fuzzy set theory to develop the ‘fuzzy’ P-value, and show that it can be uniformly distributed under the null hypothesis. Here, the test function ϕ(x) is viewed as a fuzzy set membership function. Berger and Casella (2005) show that, for a realisation of the data x, the corresponding fuzzy P-value can be viewed as a uniform random variable over the interval (p_l(x), p_u(x)] where p_l(x) = P_H0{S(X) > S(x)} and p_u(x) = P_H0{S(X) ≥ S(x)}. That is, the fuzzy P-value (which we should point out is not actually a ‘value’ in the traditional sense) is P_fuzzy ~ U(p_l(x), p_u(x)). Hence, fuzzy P-values are not directly applicable to multiple testing methods that require P-values to be realisations of a random variable. For example, Kulinskaya and Lewin (2009) modify the BH procedure, to allow for fuzzy P-values.

As pointed out by a referee, some multiple testing methods (see Westfall and Young 1989; Tarone 1990; Westfall and Wolfinger 1997; Hommel and Krummenauer 1998; Roth 1999; Gilbert 2005; Gutman and Hochberg 2007; Westfall and Troendle 2008) exploit the discreteness of the nonrandomised P-values. For example, consider testing the pairs of hypotheses H_0m : p_1,m = p_2,m versus H_1m : p_1,m ≠ p_2,m for m = 1, 2, …, M with data X_1,m ~ Bin(10, p_1,m),X_2,m ~ Bin(10, p_2,m) using Fisher’s exact tests. Recall that the P-value for Fisher’s exact test is based on the conditional distribution P(X_1,m = x_1,m|X_m = x_m, p_1,m = p_2,m), where X_m = X_1,m + X_2,m. For brevity, we write P₀(X_1,m = x_1,m|X_m = x_m) = P(X_1,m = x_1,m|X_m = x_m, p_1,m = p_2,m). Note that if X_m = 0, for example, then X_1,m = 0. Hence, P₀(X_1,m = 0|X_m = 0) = 1, so the (nonrandomised) P-value for this test is 1. Even if X_m = 1, then P₀(X_1,m = 0|X_m = 1) = P₀(X_1,m = 1|X_m = 1) = 1/2 which again results in a (nonrandomised) P-value of 1. In Tarone (1990) (other procedures mentioned operate in a similar manner), the standard Bonferroni (1936) procedure is adapted by automatically accepting those null hypotheses whose X_m is small (or large), and testing the remaining M^* ≤ M null hypotheses at level α/M^*. It is shown that the procedure controls the family-wise error rate at level α.

Now, let us consider an interesting example posed by a referee, and briefly compare two multiple testing methods. Method 1 is the method described above, which automatically accepts some null hypotheses and tests the remaining M^* null hypotheses at level α/M^* using nonrandomised P-values from Fisher’s exact test. Method 2 simply tests all M null hypotheses at level α/M using randomised P-values from Fisher’s exact test. Now, suppose that p_1,m = p_2,m = 0.0001 for m = 1, 2, …, 4999, p_1,5000 = 0.25 and p_2,5000 = 2p_1,5000. Then method 1 will likely automatically accept the first 4999 true null hypotheses (note that P(X_m ≤ 1|p_1,m = p_2,m = 0.0001)⁴⁹⁹⁹ = 0.99) and it will test H_0,5000 at level α/1. On the other hand, method 2 tests all 4999 true null hypotheses and the false null hypotheses at level α/5000. Clearly, in this scenario, method 1 is superior to method 2 since it will likely test the false null hypothesis at level α rather than α/5000, and automatically accept the true null hypotheses. However, let us consider the other side of the coin. Suppose that, for m = 1, 2, …, 4999, p_1,m = 0.0001 and p_2,m = 2p_1,m, while for m = 5000, p_1,m = p_2,m = 0.25. Method 1 will likely erroneously accept all of the false null hypotheses (note P(X_m ≤ 1|p_1,m = 0.0001, p_2,m = 0.0002)⁴⁹⁹⁹ = 0.98), and test the true null hypothesis at level α. On the other hand, method 2 will test the 4999 false null hypotheses at level α/5000, rather than automatically (erroneously) accepting them. Further, it will test the true null hypothesis at level α/5000 rather than α, so that the probability of making a false discovery is also much lower for method 2. Thus, each of these methods have certain situations in which they would be expected to perform well. It would be interesting to compare these two methods in more detail, but our goal in this present paper is limited to just comparing P-value statistics rather than different multiple testing methods.

4. Concrete examples

Observe that the formulation in the preceding section is general in that the observable X may reside in a complicated sample space 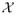. In particular, it could be a discrete, continuous, or mixed-type random vector. It could even be a collection of stochastic processes. Thus, the notion of a randomised P-value statistic carries over to these complicated data structures.

In our concrete examples, we consider the two-group location-shift model. Let $\mathit{X}=(X_1,\dots ,X_{n_1})\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }F(x)$, and $\mathit{Y}=(Y_1,\dots ,Y_{n_2})\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }F(y-\theta )$ where F(·) ∈ = {H : H is a continuous distribution function on ℝ}, θ ∈ ℝ, and X and Y are independent. We also let U ~ U[0, 1] which is independent of (X, Y). The problem is to test H₀ : (θ, F) ∈ versus H₁ : (θ, F) ∈ where = {(θ, F) : θ ≥ 0, F ∈ } and = {(θ, F) : θ < 0, F ∈ }. The decision functions will be of form δ : ℝ_n1× ℝ_n2× [0, 1] × [0, 1] → {0, 1}, where δ(x, y, u; η) = 1(0) means reject (do not reject)H₀ at size index η with augmented data (x, y, u). We now describe the specific decision processes of interest.

4.1. Decision processes

The standard two-sample T -test for a shift in location could be invoked to test H₀ versus H₁. Define the decision function δ_T by

$${\delta }_T(\mathit{x},\mathit{y},u;\eta )=I\{T(\mathit{x},\mathit{y})\le {\mathcal{T}}_{n_1+n_2-2}^{-1}(\eta )\}$$

with

$$T(\mathit{x},\mathit{y})=\frac{\overline{y}-\overline{x}}{s_p\sqrt{1/n_1+1/n_2}};s_p=\sqrt{\frac{(n_1-1)s_x^2+(n_2-1)s_y^2}{(n_1+n_2-2)}},$$

where x̄, ȳ, s_x, and s_y are the sample means and standard deviations of x and y, respectively, and (·) is the cumulative distribution function of Student’s central T-distribution with k degrees-of-freedom. Form the decision process Δ_T = {δ_T (X, Y,U; η) : η ∈ [0, 1]}. The well-known two-sample T -test P-value can be recovered from Equation (1) since

$$\begin{array}{l}{P}_{{\mathrm{\Delta }}_T}(\mathit{X},\mathit{Y},U)=inf\{\eta \in [0,1]:{\delta }_T(\mathit{X},\mathit{Y},U;\eta )=1\}\\ =inf\{\eta \in [0,1]:I[T(\mathit{X},\mathit{Y})\le {\mathcal{T}}_{n_1+n_2-2}^{-1}(\eta )]=1\}\\ =inf\{\eta \in [0,1]:I[{\mathcal{T}}_{n_1+n_2-2}(T(\mathit{X},\mathit{Y}))\le \eta ]=1\}\\ ={\mathcal{T}}_{n_1+n_2-2}(T(\mathit{X},\mathit{Y})).\end{array}$$

Observe that since T (X, Y) has a continuous distribution, there is no need for randomisation. Hence Δ_T and P_ΔTcould be viewed as nonrandomised.

Next we consider the validity of the T-test under a normal model and the more general model . Denote the family ${\mathcal{F}}_0^{\text{Norm}}=\{(\theta ,F):\theta \ge 0,F=N(\mu ,{\sigma }^2),\mu \in ℝ,{\sigma }^2>0\}$ where N(μ, σ²) is a normal distribution function with mean μ and variance σ². It is well-known that T (X, Y) has distribution function if and only if $(\theta ,F)\in {\mathcal{F}}_0^{\text{Norm}}$ and θ = 0. Further, P_(θ,F){T (X, Y) ≤ t} < (t) for every θ > 0, t ∈ ℝ, and $F\in {\mathcal{F}}_0^{\mathit{Norm}}$. Hence

$$\begin{array}{l}\underset{(\theta ,F)\in {\mathcal{F}}_0^{\text{Norm}}}{sup}{E}_{(\theta ,F)}\{{\delta }_T(\mathit{X},\mathit{Y},U;\eta )\}=\underset{(\theta ,F)\in {\mathcal{F}}_0^{\text{Norm}}}{sup}{\mathbf{P}}_{(\theta ,F)}\{T(\mathit{X},\mathit{Y})\le T_{n_1+n_2-2}^{-1}(\eta )\}\\ ={\mathcal{T}}_{n_1+n_2-2}({\mathcal{T}}_{n_1+n_2-2}^{-1}(\eta ))=\eta \end{array}$$

for every η ∈ [0, 1]. Thus, Δ_T is ${\mathcal{F}}_0^{\mathit{Norm}}$-size-valid, and by Theorem 2.3, P_Δ (X, Y,U) is ${\mathcal{F}}_0^{\mathit{Norm}}$-uniform. On the other hand, T (X, Y) is not distributed according to a distribution for many (θ, F) ∈ even when θ = 0 (for instance, take F to be an exponential cumulative distribution function F(x) = (1 − e^−x)I (x > 0)). Hence, Δ_T need not be -size-valid and, by Theorem 2.3, P_ΔT need not be -uniform.

Next we consider a nonrandomised Wilcoxon decision process. Define

$${\delta }_{\mathrm{W}}(\mathit{x},\mathit{y},u;\eta )=I\{W(\mathit{x},\mathit{y})<{\mathcal{W}}_{n_1,n_2}^{-1}(\eta )\},$$

where $W(\mathit{x},\mathit{y})={\sum }_{j=1}^{n_2}{R}_j(\mathit{x},\mathit{y})$ and R_j (x, y) = rank of y_j among (x, y), and (·) is the cumulative distribution function of a Wilcoxon rank-sum statistic for vectors of length n₁ and n₂ and θ = 0. The decision process corresponding to δ_W is given by Δ_W = {δ_W(X, Y,U; η) : η ∈ [0, 1]} and the associated P-value statistic is

$$\begin{array}{l}{P}_{{\mathrm{\Delta }}_{\mathrm{W}}}(\mathit{X},\mathit{Y},U)=inf\{\eta \in [0,1]:{\delta }_{\mathrm{W}}(\mathit{X},\mathit{Y},U;\eta )=1\}\\ =inf\{\eta \in [0,1]:I[W(\mathit{X},\mathit{Y})<{\mathcal{W}}_{n_1,n_2}^{-1}(\eta )]=1\}\\ ={\mathcal{W}}_{n_1,n_2}(W(\mathit{X},\mathit{Y})).\end{array}$$

Again, Δ_W and P_ΔW do not depend on u and could therefore be considered to be nonrandomised.

We can again use Theorem 2.3 to examine the distribution of P_ΔW. By Theorem 4.2.13 in Randles and Wolfe (1979), for every F ∈ and θ > θ′, P_(θ,F) {W(X, Y) ≤ w} ≤ P_(θ′,F){W(X, Y) ≤ w} for every w ∈ {n₂(n₂ + 1)/2, …, n₂(2n₁ + n₂ + 1)/2}, the range of W(X, Y). Hence,

$$\begin{array}{l}\underset{(\theta ,F)\in {\mathcal{F}}_0}{sup}{E}_{(\theta ,F)}\{{\delta }_{\mathrm{W}}(\mathit{X},\mathit{Y},U;\eta )\}=\underset{(\theta ,F)\in {\mathcal{F}}_0}{sup}\mathbf{P}\{W(\mathit{X},\mathit{Y})<{\mathcal{W}}_{n_1,n_2}^{-1}(\eta )\}\\ ={\mathcal{W}}_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta )-)\\ \le \eta \end{array}$$

for every η ∈ [0, 1]. Therefore, Δ_W is -level-valid. Thus, by Theorem 2.3, P_ΔW (X, Y,U) is -uniformly bounded. However, by the discreteness of we have ${\mathcal{W}}_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta )-)<\eta$ for some η. For example, take η ∈ ( (w), (w + 1)) with w and w + 1 being possible values of W(X, Y). Thus, Δ_W is not -size-valid, and again by Theorem 2.3, P_ΔW (X, Y,U) is not -uniform.

Now let us consider the randomised Wilcoxon rank-sum test. Define decision function δ_WR by

$${\delta }_{\text{WR}}(\mathit{x},\mathit{y},u;\eta )=I\{W(\mathit{x},\mathit{y})<{\mathcal{W}}_{n_1,n_2}^{-1}(\eta )\}+I\{u\le \gamma (\eta )\}I\{W(\mathit{x},\mathit{y})={\mathcal{W}}_{n_1,n_2}^{-1}(\eta )\},$$

where $\gamma (\eta )=[\eta -{\mathcal{W}}_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta )-)]/[w_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta ))]$ and w_n1,n2(·) is the probability mass function of a Wilcoxon rank-sum statistic for vectors of length n₁ and n₂ when θ = 0 and F ∈ . Form the decision process Δ_WR = {δ_WR(X, Y,U; η) : η ∈ [0, 1]}. It can be verified that {(x, y, u, η) : δ_WR(x, y, u; η) = 1} = {(x, y, u, η) : η ≥ (W(x, y)−) + uw_n1,n2 (W(x, y))}. Hence

$$\begin{array}{l}{P}_{{\mathrm{\Delta }}_{\text{WR}}}(\mathit{X},\mathit{Y},U)=inf\{\eta \in [0,1]:{\delta }_{\text{WR}}(\mathit{X},\mathit{Y},U;\eta )=1\}\\ =inf[\eta \in [0,1]:I\{W(\mathit{X},\mathit{Y})<{\mathcal{W}}_{n_1,n_2}^{-1}(\eta )\}+I\{U\le \gamma (\eta )\}I\{W(\mathit{X},\mathit{Y})={\mathcal{W}}_{n_1,n_2}^{-1}(\eta )\}=1]\\ ={\mathcal{W}}_{n_1,n_2}(W(\mathit{X},\mathit{Y})-)+U{w}_{n_1,n_2}(W(\mathit{X},\mathit{Y})).\end{array}$$

Though the null hypotheses in this section are stated in terms of the location-shift null model , it can be shown that Δ_WR is size-valid under a less restrictive null model, , and hence P_ΔWRis -size-valid. Similar arguments can be used to show that Δ_WR is -size-valid and that P_ΔWR is -uniform.

Theorem 4.1

Suppose that $X_1,\dots ,X_{n_1}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }F$ and $Y_1,\dots ,Y_{n_2}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }G$ and F,G ∈ . For testing H₀ : (F,G) ∈ ≡ {(F,G) ∈ : F(t) ≥ G(t), ∀t ∈ ℝ} versus H₁ : (F,G) ∈ = {(F,G) ∈ : F(t) < G(t), ∀t ∈ ℝ}, the decision process Δ_WR is -size-valid and P_ΔWR (X, Y,U) is -uniform.

Proof

It follows from Theorem 2.3 that P_ΔWR (X, Y,U) is -uniform if Δ_WR is -size-valid. Hence, it suffices to show that E_F,G{δ_WR(X, Y,U; η)} = η for any η ∈ [0, 1]. For any F and G and for any F′ ∈ such that F′ (t) ≥ F(t), ∀t ∈ ℝ, we have, by Theorem 4.3.3 in Randles and Wolfe (1979), that P_(F′,,G){W(X, Y) ≤ w} ≤ P_(F,G){W(W, Y) ≤ w} for any w ∈ ℝ. Further, P_(G,G){W(X, Y) ≤ w} does not depend on G for G ∈ . Hence, P_(F,G){W(X, Y) ≤ w} = P_(G,G){W(X, Y) ≤ w} = (w) for any G ∈ . Hence,

$$\begin{array}{l}\underset{(F,G)\in {\mathcal{H}}_0}{sup}{E}_{(F,G)}\{{\delta }_{\text{WR}}(\mathit{X},\mathit{Y},U;\eta )\}={\mathcal{W}}_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta )-)+\gamma (\eta )w_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta ))\\ ={\mathcal{W}}_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta )-)+\left\{\frac{\eta -{\mathcal{W}}_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta )-)}{w_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta ))}\right\}{w}_{n_1,n_2}({\mathcal{W}}_{n_1,n_2}^{-1}(\eta ))=\eta \end{array}$$

for any η ∈ [0, 1]. Thus, Δ_WR is -size-valid and P_ΔWR(X, Y, U) is -uniform.

Let us also examine the densities of the three P-value statistics for several different data generating distributions F. Figure 1 displays the simulated densities of P_ΔT(X, Y, U), P_ΔW(X, Y, U), and P_ΔWR(X, Y, U) when F is a normal, a Cauchy, or a Laplace distribution function and n₁ = n₂ = 5. Notice that P_ΔT is uniformly distributed only when F is normal, while P_ΔWR is uniformly distributed for every F considered. Observe that P_ΔW is not uniformly distributed for any F considered, though the distribution-free property of Δ_W is manifested by noting that the density plot for P_ΔW is invariant with respect to F.

Figure 1.

Density plots of 100,000 simulated P-values for each of P_ΔT (X, Y,U), P_ΔW (X, Y,U), and P_ΔWR (X, Y,U) when X₁, …, X₅, $Y_1,\dots ,Y_5\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }F$, and F (location, scale) are normal(0, 1), Cauchy(0, 1), and Laplace(0, 1) distribution functions.

5. Application to FDR-controlling procedures

The framework from Section 2 easily extends to the multiple testing setting. However, it now becomes possible to define decision functions and P-values in more general ways. We briefly present a framework for this multiple testing setting for clarity.

For each m ∈ = {1, 2, …, M}, let observable random entity X_m ∈ have (marginal) distribution function F_m. Further, let be a model for F_m and a nonempty subset of . Consider testing H_0m : F_m ∈ with observable random entities X_m and U_m, where X_m is independent of U_m, and the U_ms are independent standard uniform random variables. Define decision functions δ_m : × [0, 1] → {0, 1} by δ_m(X_m, U_m). Again we write δ_m(X_m, U_m; η) for δ_m(X_m, U_m) when δ_m has size index η. The size of δ_m is η = E_Fm {δ(X_m, U_m)}. Assume that for every F_m ∈ , δ_m(x_m, u_m; η) is nondecreasing and right-continuous in η with δ_m(x_m, u_m; 0) = 0 and δ_m(x_m, u_m; 1) = 1 for almost all (x_m, u_m) ∈ × [0, 1] with respect to F_m ⊗ λ_m, where λ_m is a uniform probability measure on [0, 1]. Define decision processes Δ_m = {δ_m(X_m, U_m; η) : η ∈ [0, 1]}. The P-value statistic for Δ_m is defined via

$$P_{{\mathrm{\Delta }}_m}(X_m,U_m)=inf\{\eta \in [0,1]:{\delta }_m(X_m,U_m;\eta )=1\}.$$

There are currently many FDR methods that assume P-values from true null hypotheses are uniformly distributed. However, we restrict our study of the impact of the use of randomised P-values on just two of these methods. The methods considered are the BH procedure developed in Benjamini and Hochberg (1995) and Efron’s empirical Bayes procedure developed in Efron et al. (2001) and Efron (2004, 2007, 2008).

5.1. Simulation setup

The simulation study is designed to mimic a small-scale microarray analysis. That is, the number of hypotheses to be tested is large, the sample size for each test is small, and most null hypotheses are true. Specifically, we consider the two-sample location shift model for each m ∈ = {1, 2, …, 1000}. Assume that ${\mathit{X}}_m=(X_{1m},\dots ,X_{n_{1}m})\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }{F}_m(x)$; and ${\mathit{Y}}_m=(Y_1,\dots ,Y_{n_{2}m})\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }{F}_m(y-{\theta }_m)$, where F_m ∈ , θ_m ∈ ℝ, and X_m, Y_m, and U_m are independent. Define decision processes Δ_T,m = Δ_T, Δ_W,m = Δ_W, and Δ_WR,m = Δ_WR for m ∈ , where Δ_T, Δ_W, and Δ_WR are defined as in Section 4. The P-values for each of the decision processes are then defined via P_ΔT (X_m, Y_m, U_m), P_ΔW (X_m, Y_m, U_m), and P_ΔWR (X_m, Y_m, U_m). The problem is to test H_0m : (θ_m, F_m) ∈ versus H_1m : (θ_m, F_m) ∈ , where and are defined as in Section 4.

Data are generated as follows. For a single data set, H_0m is tested with independent X_1m, …, X_5m, Y_1m, …, Y_5m and U_m for m ∈ {1, 2, …, 1000}. For m ∈ {1, 2, …, 900} X_1m, …, X_5m, $Y_{1m},\dots ,Y_{5m}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }{F}_m(·-0)$. For m = 901, 902, …, 1000, $X_{1m},\dots ,X_{5m}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }{F}_m(·-0)$, while $Y_{1m},\dots ,Y_{5m}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}}{\sim }{F}_m(·-(-2))$. We consider the same three different data generating distributions from the last section. That is, F_m is a normal, a Cauchy, or a Laplace distribution with scale 1 and location −2 or 0. The number of simulation replications is 5000.

5.2. Benjamini and Hochberg (1995) procedure

The BH procedure is designed to control the FDR. Let random variable V be the total number of falsely rejected null hypotheses (false discoveries) and let random variable R be the total number of rejected null hypotheses (discoveries). In our notation, $V={\sum }_{m=1}^{M}I(H_{0m}\text{is}\text{true}){\delta }_m$ and $R={\sum }_{m=1}^M{\delta }_m$. Let random variable Q be defined by Q = V/max{R, 1}. The FDR is defined via FDR = E[Q], where the expectation operator E(·) is with respect to the (true) joint distribution governing the random observables. The BH procedure is defined as follows. Let p_m be realised P-values for testing null hypotheses H_0m, m ∈ , and let p₍₁₎ ≤ p₍₂₎ ≤ ··· ≤ p_(M) be the ordered P-values with H_0(j) being the null hypothesis associated with p_(j). The procedure rejects H₀₍₁₎, …, H_0(k), where k is defined via

$$k=max\left\{m\in ℳ:p_{(m)}\le \frac{m\alpha }{M}\right\}.$$

Benjamini and Hochberg (1995) showed that if the P-value statistics from the true null hypothesis are uniformly distributed and independent, then the FDR for this procedure is less than or equal to M₀α/M, where $M_0={\sum }_{m=1}^{M}I$ (H_0m is true), the number of ‘true’ null hypotheses. Benjamini and Yekutieli (2001) and Sarkar (2002) showed that the procedure controls the FDR under certain dependency structures as well.

P-values for the j th replicated data set are computed via P_ΔT (x_mj, y_mj, u_mj), P_ΔW(x_mj, y_mj, u_mj), and P_ΔWR (x_mj, y_mj, u_mj) for j = 1, 2, …, 5000. The procedure is applied at α = (0.01, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5). For a given α and for data set j, the true false discovery proportion q_j(α) and the number of discoveries r_j(α) are recorded. Plots of (α, $\overline{q(\alpha )}$) and (α, $\overline{r(\alpha )}$), where $\overline{q(\alpha )}={\sum }_{j=1}^{5000}{q}_j(\alpha )/5000$ and $\overline{r(\alpha )}={\sum }_{j=1}^{5000}{r}_j(\alpha )/5000$ are the average false discovery proportion and the average number of discoveries, respectively, are presented in Figure 2.

Figure 2.

The average FDR and average number of discoveries over 5000 replications for the BH procedure with α ∈ [0.01, 0.5]. F_m(location, scale) are N(θ_m, 1), Cauchy(θ_m, 1), and Laplace(θ_m, 1) distributions, where θ_m = 0 for m = 1, …, 900 and θ_m = 2 for m = 901, …, 1000. P-values P_ΔT, P_ΔW, and P_ΔWR are denoted by ‘+’,‘△’, and ‘○’, respectively.

Simulation studies suggest that the BH procedure controls the FDR at level M₀α/M = 0.9α when invoking randomised Wilcoxon P-values when F_m is a normal, Laplace, or Cauchy distribution function. When making use of the T-test P-values, however, the FDR is not necessarily controlled at 0.9α. The procedure is conservative in that the FDR is often less than 0.9α when using nonrandomised Wilcoxon P-values. The randomised Wilcoxon P-values always allow for more discoveries than the nonrandomised Wilcoxon P-values, and typically allow for more discoveries than the T-test P-values, the exception being when F is normal, which is to be expected since both tests are valid but with the T-test being more powerful than the Wilcoxon test.

5.3. Efron’s empirical Bayes procedure

The procedure studied in this section, which was introduced in Efron et al. (2001) and further developed in Efron (2004, 2007, 2008), makes use of Z-values, which are typically computed via z_m = Φ⁻¹(Q(s_m)), where Φ⁻¹(·) is the standard normal quantile function and s_m ≡ s_m(x_m) is a test statistic with distribution Q under H_0m. It is then assumed that the Z-values have marginal mixture density

$$f(z_m)={\pi }_0{f}_0(z_m)+(1-{\pi }_0)f_1(z_m),$$

so that Z_m has density f₀ under H_0m and density f₁ under H_1m. The weight π₀ can be viewed as the proportion of true null hypotheses or as the prior probability that H_0m is true. Notice that f₀ is a standard normal distribution by the probability integral transformation if the statistic Q(S_m) has a uniform distribution under H_0m. However, as noted in the previous section, Q(S_m) will not have a uniform distribution when Q is discrete or when $S_m\stackrel{d}{\ne }Q$ under H_0m. We will consider computing Z-value statistics via

$$Z_m(X_m,U_m)={\mathrm{\Phi }}^{-1}(Q(S_m(X_m)-1)-U_m\mathrm{\Delta }Q(S_m(X_m))),$$

where ΔQ(s) = Q(s) − Q(s−). Observe that Z_m(X_m, U_m) can be equivalently expressed Z_m(X_m, U_m) = Φ⁻¹(P_Δ−(X_m, U_m)). Note that even if Q is a discrete distribution, Z_m has a standard normal density so long as P_Δ−(X_m, U_m) has a uniform distribution under H_0m.

The local fdr at Z_m = z (Efron 2004) is defined via

$$\text{fdr}(z)=\frac{{\pi }_0{f}_0(z)}{f(z)}=\mathbf{P}(H_{0m}\text{is}\text{true}\mid Z_m=z).$$

Sun and Cai (2007) have shown that decision rules of form δ_m(z_m) = I (fdr(z_m) < γ) possess certain optimality properties. However, since the local fdr depends on the unknown quantities f₀(z), f₁(z), and π₀, these quantities need to be estimated in order to implement such a decision rule.

If a local fdr estimator is developed under the assumption that f₀ is a standard normal density, it shall be referred to as a type 1 estimator, while if f₀ is estimated by f̂₀ (Efron 2004 calls f̂₀ the empirical null distribution), the local fdr estimator is called a type 2 estimator. These estimators are denoted by

$$\widehat{{\text{fdr}}_1(z)}=\frac{{\widehat{\pi }}_0{f}_0(z)}{\widehat{f}(z)}\text{and}\widehat{{\text{fdr}}_2(z)}=\frac{{\widehat{\pi }}_0{\widehat{f}}_0(z)}{\widehat{f}(z)}.$$

It is important to note that though it can be assumed that Z_m has a standard normal density under H_0m (and hence estimate fdr(z) by $\widehat{{\text{fdr}}_1(z)}$), it is not necessary to make use of such an assumption. One may make use of the empirical null distribution and estimate fdr(z) with $\widehat{{\text{fdr}}_2(z)}$. However, as stated in Efron (2008), ‘the empirical null is an expensive luxury from the point of view of estimation efficiency’. That is, it is desirable to use type 1 estimators if indeed f₀ is a standard normal density since type 2 local fdr estimators tend to have a larger standard error.

We investigate both the bias and variability of these local fdr estimators relative to the type of Z-value considered using the simulated data sets described in Section 5.1. For each set of 1000 hypotheses tests, Z-values are computed z_WRm = Φ⁻¹(P_ΔWR (x_m, y_m, u_m)) and z_Tm = Φ⁻¹(P_ΔT (x_m, y_m, u_m)). The two types of estimates of the local fdr are computed for z = (−4, −3.8, …, −2.2, −2) using the software locfdr available in R (Efron, Turnbull, and Narasimhan 2009). The discrete Z-values Φ⁻¹(P_ΔW(x_m, y_m)) are omitted from consideration because the estimation algorithms fail to converge. The true local fdr at z for simulated data set j is approximated by

$${\text{fdr}}_j(z)=\frac{{\sum }_{m=1}^{M}I({\theta }_{mj}=0)I(z-0.1<z_{mj}\le z+0.1)}{max\{{\sum }_{m=1}^{M}I(z-0.1<z_{mj}\le z+0.1),1\}},$$

where z_mj is the Z-value for testing H_0m from simulated data set j. The type i local fdr estimate for data set j is denoted $\widehat{{\text{fdr}}_{ij}(z)}$. All default parameters were used in the R function locfdr (Efron et al. 2009) for computing $\widehat{{\text{fdr}}_1(z)}$ and $\widehat{{\text{fdr}}_2(z)}$. The maximum likelihood method was used to estimate f̂₀ for type 2 local fdr estimators. The average bias and standard deviation of the local fdr estimators over the 5000 replications are computed via

$$\text{bias}(\widehat{{\text{fdr}}_i(z)})=\overline{\widehat{{\text{fdr}}_i(z)}}-\overline{\text{fdr}(z)}\text{and}s(\widehat{{\text{fdr}}_i(z)})=\sqrt{\sum _{j=1}^{5000}\frac{{[\widehat{{\text{fdr}}_{ij}(z)}-\overline{\widehat{{\text{fdr}}_i(z)}}]}^2}{4999}}$$

where $\overline{\widehat{{\text{fdr}}_i(z)}}={\sum }_{j=1}^{5000}\widehat{{\text{fdr}}_{ij}(z)}/5000$ and $\overline{\text{fdr}(z)}={\sum }_{j=1}^{5000}{\text{fdr}}_j(z)/5000$.

Figure 3 has plots of ( $\overline{\text{fdr}(z)},\text{bias}(\widehat{{\text{fdr}}_1(z)})$), and ( $\overline{\text{fdr}(z)},s(\widehat{{\text{fdr}}_1(z)})$) when Z-values are z_WRm and z_Tm. We see that $\widehat{{\text{fdr}}_1(z)}$ performs well in terms of bias and variability when considering the randomised Wilcoxon-type Z-values for each data-generating distribution considered. On the other hand, this estimator tends to be biased when F_m is non-normal, when considering T-test-type Z-values. As for $\widehat{{\text{fdr}}_2(z)}$, we see that it is more biased and variable than $\widehat{{\text{fdr}}_1(z)}$ regardless of which Z-value statistic is considered. However, when using the randomised Wilcoxon Z-values, recall that f₀ is standard normal so long as the F_m are continuous since P_ΔWR is -uniform. Hence, the less biased and less variable local fdr estimator can be used to define a decision rule if making use of the randomised Wilcoxon Z-values regardless of F_m. On the other hand, when computing Z-values with a T-test statistic, if F_m is not normal then f₀ need not be a standard normal density since P_ΔT need not be uniformly distributed when θ_m = 0. In short, the simulation study suggests that the type 2 local fdr estimator is indeed an ‘expensive luxury’, and also demonstrates that it is unnecessary if we make use of the randomised Wilcoxon Z-values.

Figure 3.

Plots of average bias and standard deviation of $\widehat{{\text{fdr}}_1(z_{T_m})}(+),\widehat{{\text{fdr}}_1(z_{{\text{WR}}_m})}(\mathrm{o}),\widehat{{\text{fdr}}_2(z_{T_m})}(\mathrm{x})$, and $\widehat{{\text{fdr}}_2(z_{{\text{WR}}_m})}$ versus $\overline{\text{fdr}(z)}$. z-values are computed z_WRm = Φ⁻¹(P_ΔWR (x_m, y_m, u_m)) and z_Tm = Φ⁻¹(P_ΔT (x_m, y_m, u_m)). Data are generated as in Section 5.1.

6. Application to a microarray data set

Methods in Sections 4 and 5 are applied to the microarray data set in Timmons et al. (2007), where five Affymetrix chips from brown fat cells and eight Affymetrix chips from white fat cells yielded a total of 13 gene expression measurements for each of M = 12, 488 genes. The goal is to determine, for each gene, if a gene’s expression level is related to fat cell type. The form of the data for testing H_0m is in Table 1.

Table 1.

Illustration of the observed gene expression measurements along with uniform variates and P-values.

m	x1m	x2m	…	x5m	y1m	y2m	…	y8m	um	PΔT	PΔW	PΔWR
1	1.22	1.66	…	2.33	5.64	1.79	…	4.05	0.210	0.317	0.177	0.150
2	3.57	19.22	…	11.89	5.17	29.49	…	11.26	0.766	0.193	0.362	0.350
⋮	⋮	⋮	…	⋮	⋮	⋮	…	⋮	⋮	⋮	⋮	⋮
12,488	2.52	10.91	…	22.67	10.70	7.35	…	12.81	0.872	0.505	0.528	0.521

We assume that $X_{1m},\dots ,X_{5m}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }{F}_m(x)$ and $Y_{1m},\dots ,Y_{8m}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }{F}_m(y-{\theta }_m)$ for θ_m ∈ ℝ and F_m ∈ for each m ∈ {1, 2, …, M}. The goal is to test H_0m : θ_m = 0, F_m ∈ against H_1m : θ_m ≠ 0, F_m ∈ for each m.

We first test the null hypotheses with Efron’s empirical Bayes procedure using Z-values from T-tests and randomised Wilcoxon tests, which we again denote by z_Tm = Φ⁻¹(P_ΔT (x_m, y_m, u_m)) and z_WRm = Φ⁻¹(P_ΔWR (x_m, y_m, u_m)), respectively. The software locfdr is used to perform the analysis (Efron et al. 2009). The decision rule

$$\text{Reject}{H}_{0m}\text{if}\widehat{{\text{fdr}}_i(z_m)}<0.2$$

is used to determine which H_0ms are declared false. Note that, as mentioned in Efron (2004) and Sun and Cai (2007), the FDR defined in Section 5, which is referred to as the ‘tail area FDR’ in Efron (2004, 2007), can be considerably less than 0.2 for this decision rule. In Figure 4, we see that $\widehat{{\text{fdr}}_1(z)}<\widehat{{\text{fdr}}_2(z)}$ whether Z-values are computed from T-test or the randomised Wilcoxon test. In fact $\widehat{{\text{fdr}}_2(z_{T_m})}>0.2$ and $\widehat{{\text{fdr}}_2(z_{{\text{WR}}_m})}>0.2$ for every m allowing for no null hypotheses to be rejected (genes to be ‘discovered’). On the other hand, $\widehat{{\text{fdr}}_1(z_{T_m})}<0.2$ for 1881 z_Tms and $\widehat{{\text{fdr}}_1(z_{{\text{WR}}_m})}<0.2$ for 2026 z_WRms. Clearly, whether or not f₀ is assumed to be a standard normal distribution under H_0m, and which type of Z-value is used in the analysis, has a major impact on the alternative hypotheses that are ‘discovered’.

Figure 4.

Plots of the local fdr estimates arising from microarray data in Timmons et al. (2007). Notes: $\widehat{{\text{fdr}}_1(z_T)}=(\dots .),\widehat{{\text{fdr}}_1(z_{\text{WR}})}=(-),\widehat{{\text{fdr}}_2(z_T)}=(-.-.-),\widehat{{\text{fdr}}_2(z_{\text{WR}})}=(---)$.

Next we analyse the data with the BH procedure at FDR levels of α = 0.05, 0.1, and 0.2. This procedure requires that P-values for testing H_0m : θ_m = 0, F_m ∈ against H_1m : θ_m ≠ 0, F ∈ be calculated so that small P-values are evidence against H_0m. Note that in the empirical Bayes analysis above, Z-values are computed using lower-tailed P-value statistics even though the alternative hypotheses are two sided. The form of the two-sided P-value for testing H_0m with a T-test or Wilcoxon rank-sum test is well known. From Theorem (2.1) with c = 1/2, we define the two-sided randomised Wilcoxon P-value via

$$P_{{\mathrm{\Delta }}_{\text{WR}}^2}({\mathit{x}}_m,{\mathit{y}}_m,u_m)=2min\{P_{{\mathrm{\Delta }}_{\text{WR}}}({\mathit{x}}_m,{\mathit{y}}_m,u_m),1-P_{{\mathrm{\Delta }}_{\text{WR}}}({\mathit{x}}_m,{\mathit{y}}_m,u_m)\},$$

where Δ_WR is defined as in Section 4 with n₁ = 5 and n₂ = 8. It can be verified that this P-value statistic is ${\mathcal{F}}_0^0$-uniform where ${\mathcal{F}}_0^0=\{(\theta ,F):\theta =0,F\in \mathcal{F}\}$ using arguments in Section 4 and Corollary 2.5. The BH procedure was applied at alpha levels of 0.05, 0.1, and 0.2 using the two-sided T-test P-values, Wilcoxon P-values, and randomised Wilcoxon P-values. Again, we see that the set of genes declared differentially expressed will depend on how the P-value for each test is calculated, as can be seen in Table 2. For α = 0.05, the BH procedure allows for 812, 863, and 908 discoveries when using P-values from T-tests, Wilcoxon tests, and randomised Wilcoxon tests, respectively (columns 2–4). Only 637 hypotheses were rejected by the BH procedure at α = 0.05 for all three P-value types (row 2, column 5) even though 1065 null hypotheses are rejected at α = 0.05 for at least one of the P-value types (row 2, column 6). Of course, we cannot know the true false discovery proportion for any of the three sets of rejected null hypotheses. However, the uniformity condition will always be satisfied for the randomised Wilcoxon P-values if it is satisfied for the T-test P-values. On the other hand, it may be the case that the uniformity condition is satisfied for the randomised Wilcoxon P-values but is not satisfied for the T-test P-values.

Table 2.

The number of discoveries when using T-test P-value (T), Wilcoxon P-value (W), and randomised Wilcoxon P-value (WR) for FDR control at level α are displayed for α ∈ {0.05, 0.1, 0.2}.

α	T	W	WR	T ∩ W ∩ WR	T ∪ W ∪ WR
0.05	812	863	908	637	1065
0.10	1483	1499	1609	1200	1834
0.20	2758	2304	2749	2141	3121

The number of null hypotheses that were rejected using T-test, Wilcoxon, and randomised Wilcoxon P-values are in column 4 and the number of null hypotheses that were rejected when using at least one of the three P-values are in column 5.

7. Concluding remarks

Many multiple testing procedures, especially those designed to control or estimate the FDR, are defined in terms of the P-values of the individual tests. We have provided a framework for generating a P-value that is uniformly distributed under the null hypothesis even in situations when the test statistic is discrete. This framework views a decision function δ(x, u; α) as an element of the decision process {δ(x, u; α) : α ∈ [0, 1]}. Though we call a P-value depending on uniform variate u as randomised, we believe this terminology may be slightly misleading, for when viewing u as part of data, the P-value is in fact not randomised with respect to augmented data (x, u).

Methods in this paper make nonparametric distribution-free test procedures usable for FDR methods, providing an alternative to a parametric model for the random observables. As an example, we defined a nonparametric randomised Wilcoxon decision process to test for a shift in location across two treatment groups. It was demonstrated that the nonparametric randomised P-value statistic generated from this process is uniformly distributed under the null hypothesis so long as the data generating distribution is continuous, while the T-test P-value statistic is uniformly distributed under the null hypothesis provided the data generating distribution is normal. If data are non-normal, a situation common in microarray analysis, we have illustrated that those FDR methods requiring the uniformity assumption perform better when using a nonparametric randomised Wilcoxon P-value rather than a T-test P-value or nonrandomised Wilcoxon P-value. Methods in this paper could also be used to construct P-values for FDR methods when random observables have discrete distributions, such as when data are dichotomous.

Not all FDR methods assume the uniform model for P-value statistics from true null hypothesis. In the future, it would be interesting to compare some of these methods with some FDR methods requiring the uniform assumption. The goal of this paper, however, was to compare P-value statistics, and to demonstrate that the manner in which P-value statistics are calculated needs to be carefully considered, especially when applied to FDR methods that require P-value statistics to have uniform distributions under the null hypotheses.