Prediction of paraquat exposure and toxicity in clinically ill poisoned patients: a model based approach

Abstract

Aims

Paraquat poisoning is a medical problem in many parts of Asia and the Pacific. The mortality rate is extremely high as there is no effective treatment. We analyzed data collected during an ongoing cohort study on self-poisoning and from a randomized controlled trial assessing the efficacy of immunosuppressive therapy in hospitalized paraquat-intoxicated patients. The aim of this analysis was to characterize the toxicokinetics and toxicodynamics of paraquat in this population.

Methods

A non-linear mixed effects approach was used to perform a toxicokinetic/toxicodynamic population analysis in a cohort of 78 patients.

Results

The paraquat plasma concentrations were best fitted by a two compartment toxicokinetic structural model with first order absorption and first order elimination. Changes in renal function were used for the assessment of paraquat toxicodynamics. The estimates of toxicokinetic parameters for the apparent clearance, the apparent volume of distribution and elimination half-life were 1.17 l h⁻¹, 2.4 l kg⁻¹ and 87 h, respectively. Renal function, namely creatinine clearance, was the most significant covariate to explain between patient variability in paraquat clearance.This model suggested that a reduction in paraquat clearance occurred within 24 to 48 h after poison ingestion, and afterwards the clearance was constant over time. The model estimated that a paraquat concentration of 429 μg l⁻¹ caused 50% of maximum renal toxicity. The immunosuppressive therapy tested during this study was associated with only 8% improvement of renal function.

Conclusion

The developed models may be useful as prognostic tools to predict patient outcome based on patient characteristics on admission and to assess drug effectiveness during antidote drug development.

What is already known about this subject

• Although heavily restricted, paraquat remains widely used in the developing world.

• There is currently limited information on paraquat pharmacokinetics and pharmacodynamics in humans.

• Available prognostic tools for patient outcome after paraquat poisoning were not developed based on pharmacology and do not account for differences in treatment effects.

What this study adds

1. This is the first report on population pharmacokinetic and pharmacokinetic/pharmacodynamic analyses of paraquat in humans.

2. The developed models can be used to characterize quantitatively treatment effects and therefore optimize prognostic tools dedicated to predict patient outcome after poisoning.

Introduction

Paraquat is a commonly used herbicide that causes many deaths from accidental or intentional ingestion. Although heavily restricted, it remains widely used in the developing world, especially in Asia. Ingestion of more than 15–30 ml of a 20% (w/v) paraquat can result in death from multiple organ failure or respiratory failure within a month of intoxication. Due to the lack of effective treatment 1–5, the mortality rate after paraquat ingestion is around 60%, which is much higher than that of other commonly used herbicides such as glyphosate and chlorophenoxy herbicides (both around 5–30%) 6,7.

Understanding the disposition of paraquat in humans is important for evaluating treatments that aim to reduce paraquat concentrations and/or effects. Animal studies indicate that paraquat, a cation of a strong base, is rapidly but poorly absorbed from the gastrointestinal tract. Only 5–15% reaches the blood stream where the peak concentration is obtained within 2–6 h 3. Protein binding of paraquat is very low and paraquat is not metabolized 8. Small amounts of paraquat have been found in bile (post-mortem), indicating that some excretion via bile occurs 8. However, up to 98% of paraquat is excreted unchanged in the urine indicating that renal function is a key factor in the elimination of paraquat 9–11. Paraquat toxicokinetics (TK) have been studied in several animal species including dogs, rats and rabbits 11–15. To date, only a few studies have focused on paraquat TK in humans 16,17. Moreover, the relationship between human TK and toxicodynamics (TD) has not been studied. Over decades, many procedures and treatments have been used to modify toxicity of paraquat without any great success 1,18–20. The best predictors of outcome are volume of ingestion, kidney function and age.

Acute kidney injury (as measured by a change in creatinine) is very common and very strongly predicts death after paraquat poisoning 21,22. However, a rise in creatinine is a good predictor because it is both an indicator of the extent of ongoing toxicity and of the ability to eliminate paraquat. It would be useful to determine the relative contribution of these two factors as they have different implications for improving management.

We report on a non-linear mixed effects approach to characterize better paraquat kinetics and toxicity in a paraquat intoxicated population (population TK/TD or pop TK/TD), the uncertainty around TK and TD and the potential covariates that could explain variability in paraquat disposition in intoxicated patients.The aims of the present study were 1) to predict the time course of paraquat exposure based on information recorded on admission such as the initial kidney function and the ingested volume, 2) to understand better the relationship between paraquat exposure and toxicity in humans and 3) to assess the influence of patient characteristics on paraquat exposure and toxicity, including the effects of commonly used treatment approaches.

Methods

Patients

The subjects (n = 78) included in the present analysis were from two different sources: 1) an ongoing cohort study on self-poisoning and 2) a nested randomized controlled trial (RCT) assessing the efficacy of immunosuppressive therapy on paraquat poisoning (ISRCTN85372848) in Sri Lankan tertiary hospitals. Demographic and clinical data were collected prospectively from all consenting patients. The studies were approved by the Ethics Review Committee of the Faculty of Medicine, University of Peradeniya, Sri Lanka, and the Human Research Ethics Committee of the Australian National University. Informed written consent was obtained from the patients or, where this was not possible, from relatives.

Paraquat ingestion was initially diagnosed based on patient's or relative's history and/or by examination of the bottle or label brought to the hospital. Paraquat ingestion was then confirmed via the mi-quantitative urine dithionate test (done at least 4 h after ingestion). The amount of paraquat ingested was estimated from the volume described by the patients or their relatives. A ‘little’ or ‘a teaspoon’ was interpreted as equivalent to 5 ml, a ‘mouthful’ to 25 ml, a ‘small cup’ to 100 ml, a ‘glass’ to 300 ml and a ‘bottle’ to 400 ml of a commercial product containing 20% paraquat. If the patient reported a range of volumes of ingestion, the mean volume was used 23.

Sixty-eight patients were included in the TD study. The patients were grouped by treatment regimen as standard care (n = 19), standard care plus placebo (n = 26) and standard care plus immunosuppressive therapy (comprising pulse therapy with methylprednisolone and cyclophosphamide/MESNA, and dexamethasone) (n = 23) as described elsewhere 20. Standard care consisted of resuscitation (assessment and management of airway, breathing and circulation), decontamination using charcoal or Fuller's earth and intravenous fluids. Haemoperfusion/haemodialysis were not used in any patients.

Blood and urine sampling

Serial blood and urine samples were collected for the quantification of paraquat concentrations at admission (t = 0), 4, 8, 16 and 24 h (post-admission) and then daily until discharge. After discharge, all patients were followed up at 1 month and 3 months at the clinic or their home. At follow-up, some clinical data, blood and urine samples were collected. Around 6–8 ml blood were withdrawn at each time point and transferred to two EDTA tubes and mixed thoroughly. Then soon after collection, blood samples were centrifuged for 10 min at 3000 rev min^–1 and plasma was separated. Urine volumes were not recorded, but where possible 20 ml of urine was also collected at these time points, and centrifuged at 2000 rev min^–1 for 10 min. Clear supernatant was then transferred into small tubes. Plasma and urine samples were then carefully labelled and immediately transferred to a −20°C freezer, and later shipped to Australia for further analysis.

Paraquat analysis

Paraquat concentrations in plasma and urine were determined using the LC–MS/MS system consisting of an SLC-10AVP system controller, two LC-10AD pumps, an SIL-20AC-HT autosampler (Shimadzu, Kyoto, Japan) and an API2000 triple quadrupole (Applied Biosystems Inc., Foster City, CA, USA), a mass spectrometer coupled with an electrospray ionization (ESI) source and a divert valve. 24 Briefly, analysis of plasma and urine samples was carried out by one step protein precipitation using cold acetonitrile (−20 to −10°C). After centrifugation, an aliquot of 10 μl of supernatant was injected into a Kinetex™ hydrophilic interaction chromatography (HILIC) column with a KrudKatcher™ Ultra in-line filter. The chromatographic separation was achieved using the mobile phase mixture of 250 mm ammonium formate (with 0.8% aqueous formic acid) in water and acetonitrile at a flow rate of 0.3 ml min⁻¹. The calibration curve was linear over the concentration range of 10–5000 μg l⁻¹, with an LLOQ of 10 μg l⁻¹. The inter- and intra-day precision (% RSD) was <8.5% with accuracy within the range of 95.1–102.8%. Paraquat in plasma and urine samples was stable when stored at −20°C for three freeze–thaw cycles.

Descriptive statistics and graphic generation

Graphics and descriptive statistics were generated using GraphPad Prism version 6.01 (GraphPad Solfware, San Diego, USA). The relationship between paraquat plasma and urine concentration over time was also plotted to provide a rough model-independent assessment of the expected change over time in renal paraquat clearance (CL).

Population TK–TD analysis

Pop TK: Structural model

The concentration–time data for paraquat in plasma were analyzed by a non-linear mixed effect modelling approach using Phoenix NLME version 1.2 Build 6.3.0.395 (Pharsight Corporation, Mountain View, CA, USA). Initial TK model selection was performed using graphical analysis. Plots of paraquat plasma concentration vs. time were generated for each individual and examined to determine the appropriate descriptive model. During this analysis, it was assumed that the renal function modified by paraquat had already reached a steady-state at the time most of the plasma paraquat concentrations were measured. This was based on the fact that renal function has been shown to decrease exponentially after paraquat ingestion before reaching a steady-state impaired renal function within the first 48 h 13. Based on the graphical analysis and the known physicochemical and TK properties of paraquat, a two compartment model with first order absorption and first order elimination was used as the TK structural model. Data were fitted using the extended least squared first order conditional estimation method (FOCE ELS) as implemented in Phoenix software. The model was parameterized in terms of paraquat apparent oral CL (CL_PQ/F), apparent volume of distribution of the central compartment after oral administration (V₁/F), apparent volume of distribution of the peripheral compartment after oral administration (V₂/F), inter-compartmental CL after oral administration (Q/F), absorption rate constant (K_a) and bioavailability factor (F). K_a was fixed to 1 h⁻¹ given the lack of data during the absorption phase and given that the reported mean t_max in humans was 3 h 3. As the ingested dose was estimated from volume of ingestion, the varying doses were imputed as covariates on the bioavailability factor and the median dose of paraquat (10 g) was given as the amount administered to each patient. In order to avoid numerical issues due to boundaries of F between 0 and 1, the logit of bioavailability factor (XF) was first estimated, and the the bioavailability factor was subsequently regenerated using the following formula:

(1)

Pop TK: Stochastic model

Inter-individual variability (IIV) in TK parameters were modelled using an exponential model as illustrated below:

(2)

where P_i is the parameter estimate of the i^th individual, P is the typical value for the population and η_i is the random effect for individual i, η was assumed to be normally distributed with a mean value of 0 and a variance of ω². 25 IIV terms were added on all the TK parameters.

Residual errors were best described using a combined model (additive and proportional) as depicted below:

(3)

where C_ji and C_0ji are the i^th measured (observed) and model predicted paraquat plasma concentrations for the j^th patient, respectively. ε_1jiand ε_2ji denote the proportional and the additive terms for random residual error, respectively. They were assumed to be normally distributed with a mean of 0 and variances of and .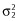

Pop TK: Covariate model

A stepwise approach was used for TK covariate model building with forward inclusion followed by backward exclusion. The following covariates were assessed for their effects on paraquat disposition: body weight (BW, kg), gender, age (years), amount ingested (g) and renal function markers: serum creatinine concentration (Cr_s, mg dl^–1) and estimated creatinine clearance (eCL_cr, l h⁻¹). eCL_cr was estimated using the Cockcroft–Gault equation 26. Covariates were first tested separately according to their biological plausibility and where considered to be significant when their addition to the base model led to a decrease of at least 3.84 points in the objective function value (OFV) (P value < 0.05 in the approximate χ² distribution with 1 degree of freedom) 27,28. The continuous covariates were normalized to their corresponding medians and introduced into the model as shown by Equation 4:

(4)

where P_k is the TK parameter, θ_k1 is the typical value of the TK parameter in the population, θ_k2 is the effect coefficient of the covariate, Cov is the value of the covariate and Cov_median is the median of the covariate in the population under investigation.

Categorical covariates were entered into the model using an exponential model. For example, the following model was used to assess gender effect on PD parameters:

(5)

where X_1j = 0 and 1 for males and females respectively, θ₀ is the typical value of the TD parameter in the population and θ_1j is the effect coefficient for females.

TK model evaluation

Criteria for selecting the final model included change in the OFV, precision of parameter estimation (coefficient of variation (CV) estimates smaller than 50%) 29, graphical analysis and quality of goodness of fit plots. All of these criteria were taken into account when evaluating alternate models.

Lead TK models were evaluated with regards to their accuracy and their stability using non-parametric bootstrapping and visual predictive check (VPC) methods 30. A non-parametric bootstrapping method was used to assess the stability and uncertainty of the final model and estimate the confidence intervals (CI) around parameter estimates in order to characterize the precision of their estimation 31,32. One thousand replicates of the data sets were generated by randomly sampling the patient data, and the final model was fitted individually to each of them. All of the model parameters were estimated, and their median and 95% CIs were generated. The VPCs were performed using the final model parameters to simulate TK data for 1000 virtual subjects. The 95% prediction interval of simulated concentrations or effects was computed and plotted against the observed values. Bayesian estimates of parameters for individual patients were also computed from the final model. The final TK model was used to generate individual predicted concentrations at times of TD measurements. These individual predicted concentration values were used as input for the TD model. TD parameters and their associated variability were estimated in a subsequent step as described below.

Population TD model development

TD: Structural model

Acute renal failure is a common and important acute toxic effect, and the extent of injury predicts death in severe paraquat poisoning 3,21. eCL_cr was used as the marker of paraquat renal toxicity. Initial pop TD model selection was carried out using graphical analysis. Plots of paraquat plasma concentration and TD effect (eCL_cr) were constructed for each individual and examined to determine the appropriate descriptive model. Based on this graphical analysis, the inhibitory fractional sigmoid E_max model including the baseline was chosen and is described as follows:

(6)

where E_(t) is the TD effect (eCL_cr) at time t, E₀ is the baseline eCL_cr of each patient at admission, E_max is the maximal fractional decrease of eCL_cr caused by paraquat, IC₅₀ is the concentration of paraquat causing a 50% of maximum paraquat induced eCL_cr decrease, and γ is a shape factor characterizing the slope of the response. 25

TD: Stochastic model

Inter-individual variability in TD parameters was also assumed to be log-normally distributed and was also modelled using an exponential model. IIV terms were imputed on all TD parameters.

The residual errors were best described using a log-additive error model as depicted below:

(7)

where Eo_ij is the observed effect (eCL_cr) for the i^th individual at concentration j, E_ji is the individual predicted effect (eCL_cr) for the i^th individual at concentration j, ε_ji is the residual error term. ε_ji is assumed to be normally distributed with a mean of 0 and a variance equal to σ².

TD: Covariate model

The following covariates were tested on the baseline parameter given that they plausibly affected baseline CL_cr: age, gender, body weight. The effects of different treatments were tested as covariate on E_max, IC₅₀ and γ. Continuous covariates were entered using power models and categorical covariates were entered into the model using exponential models as previously described.

When the covariate had more than two categories, such as treatment groups, the following equations were used:

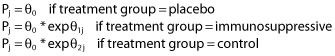(8)

θ_1j and θ_2j are the effect coefficients of the covariate.

TD model evaluation

Lead TD models were also evaluated by a bootstrapping approach and VPC as previously described. Bayesian estimates of parameters for individual patients were also computed from the final model.

Results

Patient demographics and plasma: urine paraquat ratios

A total of 698 plasma concentrations from 78 paraquat poisoned patients were included in the TK analysis. The demographics of the patients in this study are shown in Table 1. Most paraquat plasma concentrations were proportional to urine concentrations with a median ratio (plasma : urine) of 0.17 (Figure 1) in this population. The plasma : urine paraquat ratio was variable but overall did not change significantly over time.

Table 1.

Demographics of the patients enrolled in the population toxicokinetic and toxicodynamic studies

Characteristics	Toxicokinetic study (n = 78) Median (range)	Toxicodynamic study (n = 68) Median (range)
Male/female (n)	52/26	45/23
Age (years)	28 (14–76)	30 (14–76)
Weight (kg)	51 (35–66)	51 (35–66)
Crs (mg dl–1)	2 (0.3–12.6)	2 (0.3–12.6)
CLcr (l h−1)	1.89 (0.29–13.25)	2.05 (0.29–13.25)
Ingestion volume (ml)	50 (5–750)	–
Ingestion dose (g)	10 (1–150)	–

CL_cr, creatinine clearance; Cr_s, serum creatinine.

Figure 1.

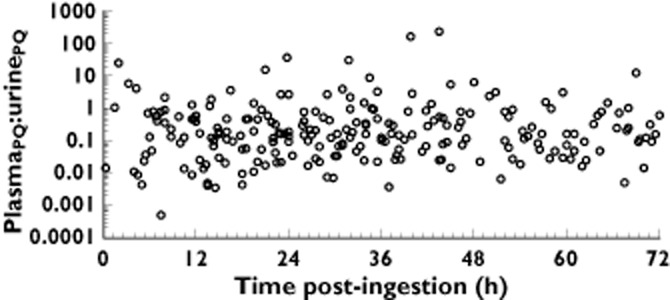
Scatter plot of plasma : urine paraquat concentrations

Population TK model

As described in the methods section, a two compartment TK structural model with first order absorption and first order elimination was fitted to the data. Parameter estimates for the TK base model are presented in Table 2. Given the lack of data in the early distribution phase, the V₂/F value was fixed to 0.17 l kg⁻¹ based on a sensitivity analysis and taking into account previously reported values of paraquat volume of distribution and patient body weights.

Table 2.

Toxicokinetic model for paraquat

Description of model	OFV	Parameter (RSE (%))			Covariate effect (RSE (%))			IIV % (RSE (%))
		V1/F	CL/F	Q/F	V1/F	CL/F	XF	V1/F	CL/F	XF
Base model with mixed error model	9496	16.46 (16)	0.58 (15)	1.74 (8)	–	–	–	91 (20)	125 (44)	142 (38)
Final model with ingestion dose effect on F, CLcr effect on CLPQ, BW on V1	9449	13.63 (16)	0.15 (31)	0.84 (11)	BW: 1.0	CLcr: 1.57 (10)	Dose: 6.93E-8 (42)	89 (18)	124 (57)	142 (37)

%CV, coefficient of variation; %SE, standard error; BW, body weight; CL/F, clearance; F, bioavailability;V₁/F, apparent volume of central compartment; IIV, Inter-individual variability; OFV, objective function value; Q/F, apparent inter-compartmental clearance; XF, the logit of bioavailability.

Parameter estimates for the final model are also shown in Table 2. Ingested dose and renal function markers were found to be significant covariates on the paraquat F and apparent paraquat clearance (CL_PQ), respectively. Estimated CL_cr or Cr_s were tested to assess which marker performed better in reflecting renal contribution to CL_PQ. Even though smaller standard error estimates were obtained when Cr_s was used (data not shown) as a renal function marker, the OFV was significantly higher than when CL_cr was used (Table 2). Inclusion of body weight in the model also significantly reduced the OFV. The goodness of fit plots obtained from the final TK model are shown in Figure 2, which indicate the model satisfactorily fitted the data.

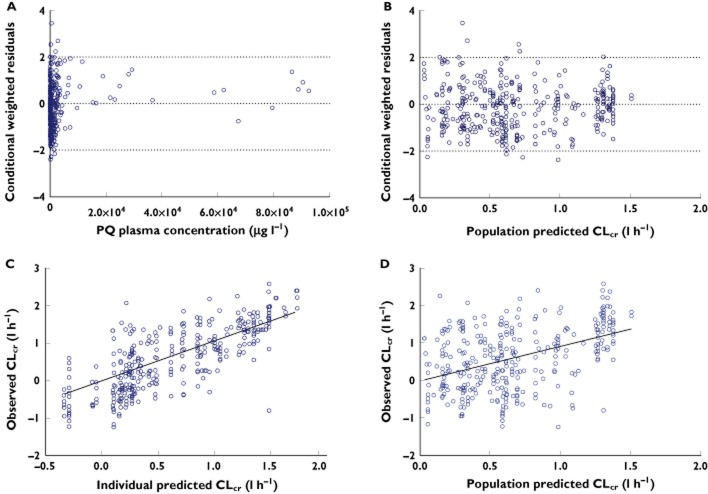
Figure 2.

Diagnostic goodness of fit plots from the final population toxicokinetic model: Conditional weighted residuals vs. time after ingestion (A), conditional weighted vs. population predicted concentration (B), observed vs. individual predicted concentrations (C) and observed vs. population predicted concentrations (D). The open circles are the observed data and the plotted line is the line of identity (y = x)

Population TD model

The final TK model was used to predict individual paraquat concentrations at times of TD measurement. Based on graphical analysis, an inhibitory fractional sigmoid E_max model including the baseline as shown in equation (5) was chosen as the structural TD model. Parameter estimates for the base TD model are presented in Table 3. Parameter estimates for the final model are also included in Table 3.

Table 3.

Toxicodynamic model of paraquat

Description of model	OFV	Parameter (RSE(%))				Covariate effect (RSE(%))		IIV % (RSE(%))
		IC50	γ	E0	Emax	E0	Emax	IC50	γ	E0	Emax
Base model with log-additive error model	745	346 (3)	24.02 (2)	3.35 (2)	0.55 (2)	–	–	373 (62)	4 (0.01)	38 (1)	6 (0.02)
Final model with age, gender and BW effect on E0,Treatment effect on Emax	727	207 (1)	5.02 (0.7)	3.23 (0.7)	0.62 (0.7)	Age: −0.07 (0.7) Male: 0.14 (0.7) BW: 1.39 (0.7)	Active: −0.08 (0.7) Control: −0.27 (0.7)	369 (20.2)	31 (0.1)	27 (0.1)	6 (0.01)

%CV, coefficient of variation; %SE, standard error; BW, body weight; E₀, the baseline creatinine clearance; E_max, the maximum fractional decrease of creatinine clearance; IC₅₀, the concentration of PQ causing a 50% of maximum PQ induced-creatinine clearance reduction; IIV, Inter-individual variability; OFV, objective function value; γ, a shape factor characterising the slope of the response.

The final pop TD model (model 7) included age, gender and body weight as covariates on baseline eCL_cr and method of treatment as covariate on maximum reduction of eCL_cr (E_max) (Table 3). Immunosuppression treatment slightly lowered the E_max, by 8% compared with the placebo group. The E_max was 24% lower in the patients treated with standard treatments outside the RCT compared with the placebo group (suggesting these two standard treatment only groups may differ due to the inclusion criteria for the RCT, in a way not accounted for by measured covariates). Goodness of fit plots were generated for the final model and the weighted residuals showed no apparent visual bias for the prediction (Figure 3).

Figure 3.

Diagnostic goodness of fit plots from the final population toxicodynamics model: Conditional weighted residuals vs. paraquat plasma concentrations (A), conditional weighted residuals vs. population predicted CL_cr (B), observed versus individual predicted CL_cr (C) and observed vs. population predicted CL_cr (D). The open circles are the observed data and the plotted line is the line of identity (y = x)

Model evaluation

The accuracy and stability of these models were assessed by non-parametric bootstrap and VPCs. As shown in Table 4, the mean population parameters estimated from the bootstrapping were stable and comparable with the estimates from the final model. The estimates of the parameters from the final model all fell within the 95% CIs of the corresponding parameters obtained with the 1000 bootstraps, indicating that the final model was fairly robust. The VPCs showed that approximately 95% of the observed data appeared to fall within the 95% CI (Figure 4), suggesting that the final model accurately described the observed data. The estimated TK and TK/TD parameters of the individual patients are listed in Table 5.

Table 4.

Results of non-parametric bootstrap analysis of paraquat population toxicokinetics and toxicodynamics

Parameter	Final model				Bootstrap
	Mean	%CV	2.5% CI	97.5% CI	Mean	%CV	Median	2.5% CI	97.5% CI
Toxicokinetics
θV (l)	13.63	16	9.28	17.98	14.64	36	13.59	6.62	27.32
θCL (l h−1)	0.15	31	0.06	0.24	0.22	86	0.16	0.02	0.73
θQ (l h−1)	0.84	11	0.67	1.02	0.87	27	0.85	0.48	1.35
Proportional residual error (%)	0.48	39	0.12	0.84	0.80	148	0.44	0.11	4.38
Additive residual error (μg l−1)	0.89	2	–	–	1.26	77	0.98	0.1	3.7
Toxicodynamics
θIC50 (μg l−1)	207	1.04	202.91	211.36	286	80	208	126	806
θγ	5.02	0.74	4.94	5.09	5.49	15	5.15	3.97	6.84
θE0 (l h−1)	3.23	0.73	3.18	3.27	3.17	9	3.17	2.69	3.77
θEmax (l h−1)	0.62	0.72	0.61	0.63	0.62	7	0.62	0.54	0.71
Log additive residual error(l h−1)	0.58	–	–	–	0.58	6	0.58	0.51	0.64

%CV, coefficient of variation; θ_CL, typical value of the clearance; θ_E0, typical value of the baseline creatinine clearance; θ_Emax, typical value of the maximum fractional decrease of creatinine clearance; θ_IC50, typical value of the concentration of PQ causing a 50% of maximum PQ induced-creatinine clearance reduction; θ_Q, typical value of the inter-compartmental clearance; θ_V, typical value of the volume distribution; θ_XF, typical value of the logit of bioavailability; θ_γ, typical value of a shape factor characterising the slope of the response; CI, confidence interval.

Figure 4.

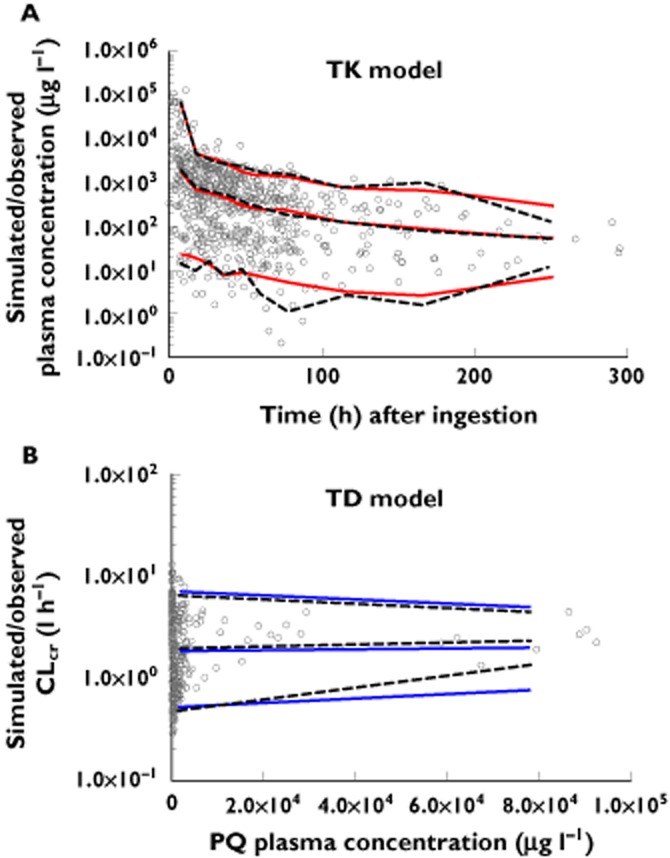
Scatter plots for visual predictive check: observed and simulated concentrations vs. time (A) and observed and simulated CL_cr vs. paraquat plasma concentrations (B). Percentiles (5, 50 and 95) were calculated using the final pop TK and TD model. (A) , observed quantiles, 5, 50, 95%; , predicted quantiles, 5, 50, 95%; (B) , observed quantiles, 5, 50, 95%; , predicted quantiles, 5, 50, 95%

Table 5.

Distribuion of empirical Bayes estimates of population toxicokinetic and toxicodynamic parameters

Model	Parameter	Mean	SD	2.5%	97.5% CI
Toxicokinetics (n = 78)	V1 (l kg−1)	0.34	0.21	0.28	0.38
	V2 (l kg−1)	2.06	1.73	1.67	2.44
	Ka(h−1)	0.93	0.40	0.84	1.0
	CLPQ (l h−1)	1.17	3.52	0.32	2.01
	t1/2,z (h)	86.98	189.2	41.53	132.4
Toxicodynamics (n = 68)	IC50(μg l−1)	429	893	213	645
	Emax(l h−1)	0.62	0.006	0.61	0.62

%CI, confidence interval; CL_PQ, paraquat clearance; E_max, the maximum fractional decrease of creatinine clearance; IC₅₀, the concentration of PQ causing a 50% of maximum PQ induced-creatinine clearance reduction; K_a, absorption rate constant; SD, standard deviation; t_1/2,z, elimination half-life; V₁, volume of distribution of central compartment; V₂, volume of distribution of peripheral compartment.

Clinical usefulness of the model

The change of estimated CL_PQ over time is shown in Figure 5 indicating that after an initial rapid decrease, the CL_PQ was stable over time. The resulting median paraquat concentrations and CL_cr were simulated for three different values CL_cr at admission: the minimum, the median and the maximum values (0.3, 6 and 13 l h⁻¹, respectively) in this cohort of patients. The results displayed in Figure 6 show that the model is able to predict paraquat exposure and toxicity given patient characteristics on admission. It could therefore serve to optimize prognostic tools dedicated to predict patients' outcome on admission and could serve as a tool to evaluate treatment options and candidate antidotes.

Figure 5.

Time course of empirical Bayes estimates of CL_PQ in PQ-poisoning patients

Figure 6.

Time course of median predicted PQ concentrations for initial CL_cr of 0.3, 6 and 13 l h⁻¹

Discussion

We used a population approach to describe paraquat disposition and its effects on renal function in poisoned patients. A two compartment TK model with rapid absorption fitted the data well. Renal function was the most important factor influencing paraquat CL. As a function of paraquat concentration, there was a variable but rapid reduction in paraquat CL within 24 to 48 h, which then was constant and low (around 10 ml min⁻¹). The time at which most of paraquat samples were collected was estimated to be more than 48 h after ingestion. Whilst paraquat does induce an immediate and variable change in renal function, this renal function appears to reach an impaired new steady-state renal function within 48 h 13. Accordingly, the PK model used in this work used the simpler constant impaired renal function after paraquat ingestion and did not consider the time variant changes in renal function at early times. Renal injury occurred with relatively low concentrations of paraquat (IC₅₀ = 429μg l⁻¹). This analysis has implications for the development of better prognostic tools, for evaluation of candidate antidotes and for the design of the optimal methods to enhance elimination.

In humans, there are limited data on absorption of paraquat. Any uncertainty on the ingestion dose and time of ingestion in our study would be expected to propagate into uncertainty on TK and TD parameter estimates. There is only one study that has reported the complete recovery of paraquat after oral dosing 16, and they estimated a V of 1.4 l kg⁻¹. If this value is substituted into our V/F estimated, F is estimated to be around 0.58.

Other studies have estimated values for V/F ranging from 1.2 to 2.75 l kg⁻¹ 33,34. and thus the V/F of about 2.4 l kg⁻¹ estimated from our TK model is in the range of estimates. Several factors are known to influence paraquat distribution. The extent to which the herbicide is actively taken up by lungs, liver, kidney and other tissues determines V/F. Therefore, if tissue binding of paraquat increased over time, V/F will increase as well. However, a high V/F estimation could be due to the over-estimation of the ingested doses. A limitation of this study is the lack of any way to quantify accurately ingestion volume, which impacts on estimated TK and TK/TD parameters (in both our and all other human studies). Moreover, the uncertainty in the estimation of some key covariates (e.g. renal function) also affects the degree of precision in these models.

The deep compartment consists of tissues where the toxic effects are manifested (in particular lungs and kidneys) and other tissues which act as a reservoir. Paraquat is actively taken up into type II pneumocytes resulting in slow elimination of paraquat from the lungs compared with other tissues 1. Active renal uptake and excretion of paraquat is also concentration dependent and saturable 35. Consequently, high concentrations of paraquat are seen in kidney. Impairment of kidney function in turn leads to higher concentrations of paraquat in the plasma 12. Muscle is an important paraquat reservoir explaining the persistence of paraquat in plasma and urine for several weeks after exposure 16. The long elimination half-life (t_1/2,z) of 3–4 days in our study reflects the combined effects of reduced CL from the decline in renal function and the slow release of paraquat from tissues into the circulation.

An obvious large change in paraquat renal CL in these patients was not observed and the plasma : urine paraquat ratio changed little over time (Figure 1) which could wrongly suggest a simple and static first order elimination process. Modelling individual patient concentrations did demonstrate a progressive decline in CL. Several previous reports also indicate that paraquat renal CL (and total CL) is a non-linear function of time. A large decrease over time in CL_PQ occurs with nephrotoxicity 8,13. At low doses, CL_PQ may exceed 12 l h⁻¹ in humans with normal kidney function 36. The mean estimate for CL_PQ/F (1.17 l h⁻¹) obtained from our pop TK model is considerably lower than that reported in some previous human case reports (mean = 4.39 l h⁻¹) 34, and they showed a rapid change in CL_PQ/F from 8.77 to 2.72 l h⁻¹ within 12 h. Substituting F = 0.58 into CL_PQ/F yields an estimated mean CL_PQ of 0.68 l h⁻¹ (11.33 ml min⁻¹) in our study. This CL_PQ is similar to those reported by Houze et al. which ranged from 0.47 to 0.59 l h⁻¹ (7.9 to 9.9 ml min⁻¹) 16. It seems likely we and Houze et al. have missed a very short early phase of high CL_PQ reported by others 34,36. The low CL_PQ reflects the very rapid onset of paraquat induced renal impairment 12,13,35,37–39. Therefore, the low estimated CL_PQ/F in the present study reflects that most blood samples were collected 6 or more h post-paraquat ingestion when renal damage was already established. While a further modest decline in estimated CL_PQ/F was found over 24 to 48 h (Figure 5), thereafter the estimated CLs were constant over time.

In our analysis, the effect of the eCL_cr, (reflecting GFR), on CL_PQ was lower than one would expect. This probably reflects errors in the estimate of GFR rather than the model 40. The Cockcroft–Gault equation has at least a 30% variance around actual renal function in the chronic kidney disease population with Cr^s ≤ 1.5 mg dl^–1 41. It also performs very poorly when Cr is changing (i.e. it assumes steady-state). However, other estimation methods perform equally poorly (when compared with gold standard methods such as iohexol CL). Future studies should ideally use more accurate direct measurements of GFR or CL_cr.

The model suggested a very small effect of immunosuppressive treatment (8% lower E_max compared with the placebo group). This is consistent with the clinical outcome reported in this trial 20 which was a very small favourable treatment effect that was not statistically significant. However, this difference was less than that seen in the non-RCT patients (24% lower E_max), which might be a result of the RCT inclusion criteria aiming to select people who had significant poisoning but also who would survive long enough to measure renal injury. Further, another RCT has also reported that immunosuppressive therapy did not improve renal function 2,42, so, these results should not be used to imply that immunosuppressive treatment has substantial effects on renal injury.

Model predictions may serve a number of purposes. From a clinical perspective, they can identify patients on admission who are very likely to develop kidney dysfunction. Using the TK model developed in this study, a paraquat plasma concentration–time profile can be predicted for individual patients on admission. Thereafter, a combination of the TK and the TD model could predict kidney function, namely CL_cr, changes over time. Prediction of TK and acute kidney injury might in turn be used to identify patients most likely to benefit from enhanced elimination or who are most suitable for inclusion into clinical trials of strategies to prevent kidney injury and other manifestations of paraquat toxicity.

In conclusion, renal function was the most significant covariate to explain between patient variability in paraquat CL. Renal injury occurred with relatively low concentrations of paraquat (IC₅₀ = 429 μg l⁻¹). A reduction in paraquat CL occurred over 24 to 48 h after paraquat ingestion, and afterwards the CL was constant and low. The low CL (around 10 ml min⁻¹) and long half-life (3–4 days) in these cases suggest further studies of extracorporeal elimination would be worth exploring, as it is clear much greater CL can be obtained by such methods 39. After optimal methods for enhancing elimination have been developed, large clinical trials will still be needed to determine if such methods can improve clinical outcomes.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare no support from any organization for the submitted for the submitted work; no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years and no other relationships or activities that could appear to have influenced the submitted.

The authors acknowledge the usefulness of approaches to modelling used in unpublished similar work (PKPD modelling of human chlorpyrifos poisoning) conducted by Jacqueline M. Anderson and colleagues.

Author contributions

K. Wunnapuk and F.T. Musuamba designed experiments and conducted the analyses; K. Wunnapuk, M.S. Roberts, N.A. Buckley and F.T. Musuamba wrote the paper; F. Mohammed and I. Gawarammana collected human plasma and urine samples and edited the paper; I. Gawarammana performed the randomized controlled trial study; X. Liu edited the paper; N.A. Buckley, M.S. Roberts and R.K. Verbeeck supervised the project.