Comparative Performance Analysis of Intel Xeon Phi, GPU, and CPU: A Case Study from Microscopy Image Analysis

Abstract

We study and characterize the performance of operations in an important class of applications on GPUs and Many Integrated Core (MIC) architectures. Our work is motivated by applications that analyze low-dimensional spatial datasets captured by high resolution sensors, such as image datasets obtained from whole slide tissue specimens using microscopy scanners. Common operations in these applications involve the detection and extraction of objects (object segmentation), the computation of features of each extracted object (feature computation), and characterization of objects based on these features (object classification). In this work, we have identify the data access and computation patterns of operations in the object segmentation and feature computation categories. We systematically implement and evaluate the performance of these operations on modern CPUs, GPUs, and MIC systems for a microscopy image analysis application. Our results show that the performance on a MIC of operations that perform regular data access is comparable or sometimes better than that on a GPU. On the other hand, GPUs are significantly more efficient than MICs for operations that access data irregularly. This is a result of the low performance of MICs when it comes to random data access. We also have examined the coordinated use of MICs and CPUs. Our experiments show that using a performance aware task strategy for scheduling application operations improves performance about 1.29× over a first-come-first-served strategy. This allows applications to obtain high performance efficiency on CPU-MIC systems - the example application attained an efficiency of 84% on 192 nodes (3072 CPU cores and 192 MICs).

I. Introduction

Scientific computing using co-processors (accelerators) has gained popularity in recent years. The utility of graphics processing units (GPUs) has been demonstrated and evaluated in several application domains [1]. As a result, hybrid systems that combine multi-core CPUs with one or more co-processors of the same or different types are being more widely employed to speed up expensive computations. The architectures and programming models of co-processors may differ from CPUs and vary among different co-processor types. This heterogeneity leads to challenging problems in implementing application operations and obtaining the best performance. The performance of an application operation will depend on its data access and processing patterns and may vary widely from one co-processor to another. Understanding the performance characteristics of classes of operations can help in designing more efficient applications, choosing the appropriate co-processor for an application, and developing more effective task scheduling and mapping strategies.

In this paper, we investigate and characterize the performance of operations in an important class of applications on GPUs and Intel Xeon Phi Many Integrated Core (MIC) architectures. Our primary motivating application is digital Pathology involving the analysis of images obtained from whole slide tissue specimens using microscopy image scanners. Digital Pathology is a relatively new application domain compared to magnetic resonance imaging and computed tomography. It is an important application domain because investigation of disease morphology at the cellular and sub-cellular level can reveal important clues about disease mechanisms that are not possible to capture by other imaging modalities. Analysis of a whole slide tissue image is both data and computation intensive because of the complexity of analysis operations and data sizes – a three-channel color image captured by a state-of-the-art scanner can reach 100K 100K×pixels in resolution. Compounding this problem is the fact that modern scanners are capable of capturing images rapidly, enabling research studies to gather thousands of images. Moreover, an image dataset may be analyzed multiple times to look for different features or quantify sensitivity of analysis to input parameters.

Although microscopy image analysis is our main motivating application, we expect that our findings in this work will be applicable in other applications. Microscopy image analysis belongs to a class of applications that analyze low-dimensional spatial datasets captured by high resolution sensors. This class of applications include those that process data from satellites and ground-based sensors in weather and climate modeling; analyze satellite data in large scale biomass monitoring and change analyses; analyze seismic surveys in subsurface and reservoir characterization; and process wide field survey telescope datasets in astronomy [2], [3], [4], [5]. Datasets in these applications are generally represented in low-dimensional spaces (typically a 2D or 3D coordinate system); typical data processing steps include identification or segmentation of objects of interest and characterization of the objects (and data subsets) via a set of features. Table I lists the categories of common operations in these application domains and presents examples in microscopy image analysis. Operations in these categories produce different levels of data products that can be consumed by client applications. For example, a client application may request only a subset of satellite imagery data covering the east coast of the US. Operations from different categories can be chained to form analysis workflows to create other types of data products. Data access and processing patterns in these operation categories range from local and regular to irregular and global access to data. Local data access patterns correspond to accesses to a single data element or data elements within a small neighborhood in a spatial and temporal region (e.g., data cleaning and low-level transformations). Regular access patterns involve sweeps over data elements, while irregular accesses may involve accesses to data elements in a random manner (e.g., certain types of object classification algorithms, morphological reconstruction operations in object segmentation). Some data access patterns may involve generalized reductions and comparisons (e.g., aggregation) and indexed access (e.g., queries for data subsetting and change quantification).

Table I.

Operation Categories

Operation Category	Microscopy Image Analysis
Data Cleaning and Low Level Transformations	Color normalization. Thresholding of pixel and regional gray scale values.
Object Segmentation	Segmentation of nuclei and cells.
Feature Computation	Compute texture and shape features for each cell.
Aggregation	Aggregation of object features for per image features.
Classification	Clustering of nuclei and/or images into groups.
Spatio-temporal Mapping and Registration	Deformable registration of images to anatomical atlas.
Data Subsetting, Filtering, and Subsampling	Selection of regions within an image. Thresholding of pixel values.
Change Detection and Comparison	Spatial queries to compare segmented nuclei and features within and across images.

Our work examines the performance impact of different data access and processing patterns on application operations on CPUs, GPUs, and MICs. The main contributions of the paper can be summarized as follows: (1) We define the data access and computation patterns of operations in the object segmentation and feature computation categories for a microscopy image analysis application. (2) We systematically evaluate the performance of the operations on modern CPUs, GPUs, and MIC systems. (3) We experimentally show that the data access pattern and parallelization strategy employed by the operations strongly affect their performance. While the performance on a MIC of operations that perform regular data access is comparable or sometimes better than that on a GPU. GPUs are significantly more efficient than MICs for operations and algorithms that irregularly access data. This is a result of the low performance of the latter when it comes to random data access. We also show that applications can achieve high performance efficiency by coordinated use of MICs and CPUs. The example application attained an efficiency of 84% on 192 nodes (3072 CPU cores and 192 MICs). This efficiency was achieved by using a performance aware task scheduling strategy, which improved performance about 1.29× over a first-come-first-served strategy.

II. Example Application and Core Operations

In this section we provide a brief overview of microscopy image analysis as our example application. Presently our work is focused on the development of operations in the object segmentation and feature computation categories, since these are the most expensive categories (or stages) in this application. We describe the operations in these stages, and present the operations’ data access and processing patterns.

A. Microscopy Image Analysis

Advances in tissue scanning technologies have made it more feasible to capture images from whole slide tissues extracted from humans or animals. This in turn has facilitated the utility of whole slide tissue specimens in research as well as clinical settings. Morphological changes in tissues at the cellular and sub-cellular scales provide valuable information about tumors, complementing genomic and clinical information, and can lead to a better understanding of tumor biology and clinical outcome [6].

Use of whole slide tissue images (WSIs) in large scale studies, involving thousands of high resolution images, is a challenging problem because of the computational requirements and sizes of WSIs. The segmentation and feature computation stages may operate on images of 100K×100K pixels in resolution and may identify about millions of micro-anatomic objects in an image. Cells and nuclei are detected and outlined during the segmentation stage. This stage applies a cascade of operations that include pixel value thresholds and morphological reconstruction to identify candidate objects, fill holes to remove holes inside objects, area thresholding to filter out objects that are not of interest. Distance transform and watershed operations are applied to separate objects that overlap. The feature computation stage calculates a set of spatial and texture properties per object that include pixel and gradient statistics, and edge and morphometry features. The next section describes the set of core operations in these two stages and their data and processing patterns.

B. Description of Core Operations

The set of core operations in the segmentation and feature computation stages is presented in Table II. These operations are categorized according to the computation stage in which they are used (segmentation or feature computation), data access pattern, computation intensity, and the type of parallelism employed for speeding up computation. Whenever available, we used sequential implementations of the operations available with OpenCV [7] or from other research groups as presented in column CPU Source from Table II.

Table II.

Core operations in segmentation and feature computation phases from microscopy image analysis. IWPP stands for Irregular Wavefront Propagation Pattern.

Operations	Description	Data Access Pattern	Computation	Parallelism	CPU Source
Segmentation Phase
Covert RGB to grayscale	Covert a color RGB image into grayscale intensity image	Regular, multi-channel local	Moderate	Data	OpenCV
Morphological Open	Opening removes small objects and fills small holes in foreground	Regular, neighborhood (13×13 disk)	Low	Data	OpenCV
Morphological Reconstruction	Flood-fill a marker image that is limited by a mask image.	Irregular, neighborhood (4-/8-connected)	Low	IWPP	vincent [8]
Area Threshold	Remove objects not within an area range	Mixed, neighborhood	Low	Reduction	Implemented
FillHolles	Fill holes in objects using a flood-fill starting at selected points	Irregular, neighborhood (4-/8-connected)	Low	IWPP	Vincent [8]
Distance Transform	Compute distance to the closest background pixel for each foreground pixel	Irregular, neighborhood (8-connected)	Moderate	IWPP	Implemented
Connected Compo- nents Labeling	Label with the same value pixels in components (objects) of a mask image	Irregular, global	Low	union-find	Oliveira [9]
Feature Computation Phase
Color Deconvolution [10]	used for separation of multi-stained biological images into different channels	Regular, multi-channel local	Moderate	Data	Implemented
pixel statistics	Compute vector of statistics (mean, median, max, etc) for each object in the input image	Regular, access a set of bounding-boxed areas	High	Object	Implemented
Gradient statistics	Calculates magnitude of image gradient in x,y and derives same per object features	Regular, neighborhood and bounding-boxed areas	High	Object	Implemented OpenCV(Grad)
Sobel Edge	Compute vector of statistics (mean, median, max, etc) for each object in the input image	Regular, access a set of bounding-boxed areas	High	Object	Implemented OpenCV(Sobel)

The operations in the segmentation stage carry out computations on elements from the input data domain (pixels in the case of an image), while those in the feature computation stage additionally perform computations associated with objects. The operations can be first classified based on data access patterns as: 1) regular operations that access data in contiguous regions such as data scans; or 2) irregular operations in which data elements to be processed are irregularly distributed or accessed in the data domain. For some operations, data elements to be processed are only known during execution as runtime dependencies are resolved. Examples of such operations include those that perform flood-fill and irregular wave front propagations.

Data accessed in the computation of a given data element may be: 1) local in operations in which the computation of a data element depends only on its value; 2) multi-channel local, which is a variant of the former in operations that independently access data elements with the same index across multiple layers of the domain (e.g., multiple channels in an image); 3) within a neighborhood, in operations that perform computations on data elements in a spatial and/or temporal neighborhood. The neighborhood is often defined using structure elements such as 4-/8-connected components or discs; and 4) areas in a bounding-box, which are used in the feature computation phase in operations on objects that are defined within minimum bounding boxes.

Parallel execution patterns exhibited by the core operations are diverse: 1) Data parallelism; 2) Object parallelism; 3) MapReduce [11] or generalized reduction; 4) Irregular wavefront propagation pattern (IWPP) [12]; 5) Union-find [13]. The data parallel operations are those that concurrently and independently process elements of the data domain. The Object parallelism exists in operations that process multiple objects concurrently. A MapReduce-style pattern is employed in the “Area Threshold” operation. This operation maps elements from the input data according to their values (labels) before a reduction is performed to count the number of elements with the same label value (area of components). The area is then used to filter out components that are not within the desired size range.

The IWPP pattern is characterized by independent wave-fronts that start in one or more elements of the domain. The structure of the waves is dynamic, irregular, data dependent, and only known at runtime as expansions are computed. The elements forming the front of the waves (active elements) work as sources of propagations to their neighbors, and only active elements are the ones that contribute to the output. Therefore, the efficient execution of this pattern relies on using a container structure, e.g., a queue or a set, to maintain the active elements and avoid computing areas of the data domain that are not effectively contributing to the output. This pattern is presented in Algorithm 1. A set of (active) elements from a multi-dimensional grid space (D) is selected to compose the wavefront (S). During the propagations, an element (e_i) from S is extracted and the algorithm tries to propagate e_i value to its neighbors (N_G) in a structure G. If a propagation condition between the active element and each of the neighbors (e_j ∈ Q) is evaluated true, the propagation occurs and that neighbor receiving the propagation is added to the set of active elements (S). This process occurs until the set S is not empty. The parallelization of this pattern heavily relies on an efficient parallel container to store the wavefront elements. In the parallel version of IWPP multiple elements from the active set may be computed in parallel as long as race conditions that may arise due parallel propagations that update the same element e_j in the grid are avoided. Applications that use this pattern, in addition to our core operations, include: Watershed, Euclidean skeletons, skeletons by influence zones, Delaunay triangulations, Gabriel graphs and relative neighborhood graphs.

The union-find pattern [13] is used for manipulating disjoint-set data structures and is made up of three operations: 1) Find: determines the set in which a component is stored; 2) Union: merges two subsets into a single set; and 3) MakeSet: creates an elementary set containing a single element. This is the processing structure of the connected components labeling (CCL) operation in our implementation. The CCL first creates a forest in which each element (pixel) from the input data is an independent tree. It iteratively merges trees from adjacent elements in the data domain such that one tree becomes a branch in another tree. The condition for merging trees is that the neighbor elements must be foreground pixels in the original image. When merging two trees (Union), the label values of the root of the two trees are compared, and the root with the smaller value is selected as the root of the merged tree. After this process is carried out for all pixels, each connected component is assigned to a single tree, and the labeled output can be computed by flattening the trees and reading labels.

III. Implementation of Core Operations

A. Architectures and Programming Models

We have implemented the operations listed in Table II for the new Intel Xeon Phi (MIC), CPUs, and GPUs. We briefly describe the MIC architecture only, because of space constraints. The MIC used in the experimental evaluation (SP10P) is built with 61 light-weight x86 cores clocked at 1090 MHz, with cache coherency among all cores that are connected using a ring network. The cores process instructions in-order, support a four-way simultaneous multi-threading (SMT), and execute 512-bit wide SIMD vector instructions. The MIC is equipped with 8GB of GDDR5 DRAM with theoretical peak bandwidth of 352GB/s.

The programming tools and languages employed for code development for a MIC are the same as those used for CPUs. This is a significant advantage as compared to GPUs that alleviates code migration overhead for the co-processor. The MIC supports several parallel programming languages and models. In this work, we have implemented our operations using OpenMP on the MIC and CPU; we used CUDA¹ for the GPU implementations. The MIC supports two execution modes: native and offload. In the native mode the application runs entirely within the co-processor. This is possible because MICs run a specialized Linux kernel that provides the necessary services and interfaces to applications. The offload mode allows for the CPU to execute regions of the application code with the co-processor. These regions are defined using pragma tags and include directives for transferring data. The offload mode also supports conditional offload directives, which may be used to decide at runtime whether a region should be offloaded to the coprocessor or should be executed on the CPU. This feature is used in our dynamic task assignment strategy for application execution using the CPU and the MIC cooperatively.

B. Parallel Implementation of Operations

We present the details of the MIC and GPU implementations only, because the CPU runs the same code as the MIC. The Data parallel operations were trivial to implement, since computing threads may be assigned for independent computation of elements from the input data domain. However, we had to analyze the results of the auto vectorization performed by the compiler for the MIC, since it could not vectorize some of the loops when complex pointer manipulations were used. In these cases, however, we annotated the code with (#pragma simd) to guide the vectorization when appropriate.

The parallelization of operations that use the IWPP pattern heavily relies on the use of parallel containers to store the wavefront elements. The parallel computation of elements in the wavefront requires those elements be atomically updated, as multiple elements may concurrently update a third element e_j. In order to implement this operation in CUDA, we developed a complex hierarchical parallel queue to store wavefront elements [12]. This parallel queue exploits the multiple GPU memory levels and is implemented in a thread block basis, such that each block of threads has an independent instance of the queue to avoid synchronization among blocks. The implementation of the IWPP on the MIC was much simpler. The standard C++ queue container used in the sequential version of IWPP is also available with the MIC coprocessor. The IWPP code instantiates one copy of this container per computing thread, which independently carries out propagations of a subset of wavefront elements. In both cases, atomic operations were used to update memory during a propagation to avoid race conditions and, as a consequence, the MIC vectorization was not possible since vector atomic instructions are not supported.

The MapReduce-style pattern, or reduction, is employed in object area calculations. The MIC and GPU implementations use a vector with an entry per object to accumulate its area, and threads concurrently scan pixels in the input data domain to atomically increment the corresponding entry in the reduction vector. Because the number of objects may be very high, it is not feasible to create a copy of this vector per thread and eliminate the use of atomic instructions.

In the Union-find pattern a forest is created in the input image, such that each pixel stores its neighbor parent pixel or itself when it is a tree root. For the parallelization of this pattern, we divided the input data into tiles that may be independently processed in parallel. A second phase was then executed to merge trees that cross tile boundaries. The MIC implementation assigns a single tile per thread and avoids the use of atomic instructions in the first phase. The GPU implementation, on the other hand, computes each tile using a thread block. Since threads computing a tile are in the same block, they can take advantage of fast shared-memory atomic instructions. The second phase of Union-find was implemented similarly for the MIC and the GPU. It uses atomic updates to guarantee consistency during tree merges across tile boundaries.

Finally, the operations with Object Parallelism can be independently carried out for each segmented object. A single thread in the MIC or a block of threads in the GPU is assigned for the computation of features related to each object. All of the operations with this type of parallelism were fully vectorized.

IV. Cooperative Execution on Clusters of Accelerators

The strategy for execution of a pipeline of segmentation and feature computation stages on a cluster system is based on a Manager-Worker model that combines a bag-of-tasks style execution with coarse-grain dataflow and makes use of function variants. A function variant represents multiple implementations of a function with the same signature. In our case, the function variant of an operation is the CPU, GPU, and MIC implementations. One Manager process is instantiated on the head node. Each computation node is designated as a Worker. The Manager creates tasks of the form (input image tile, processing stage), where processing stage is either the segmentation stage or the feature computation. Each of these tasks is referred to as a stage task. The Manager also builds the dependencies between stage task instances to enforce correct execution. The stage tasks are scheduled to the Workers using a demand-driven approach. A Worker may ask for multiple tasks from the Manager in order to keep all the computing devices on a node busy.

A local Worker Resource Manager (WRM) on each computation node controls the CPU cores and co-processors (GPUs or MICs) used by a Worker. When the Worker receives a stage task, the WRM instantiates the operations in the stage task. It dynamically creates operation tasks, represented by tuples (input data, operation), and schedules them for execution as it resolves the dependencies between the operations – note that the segmentation and feature computation stages consist of pipelines of operations; hence there are dependencies between the operations. The set of stage tasks assigned to a Worker may create many operation tasks. The operations may have different performance characteristics on different computing devices. In order to account for this variability, a task scheduling strategy, called Performance Aware Task Scheduling (PATS), was employed in our implementation [14], [15]. PATS assigns tasks to CPU cores or co-processors based on an estimate of each task’s co-processor speedup and on the computational loads of the co-processors and CPUs. When an accelerator requests a task, PATS assigns the tasks with higher speedup to this processor. If the device available for computation is a CPU, the task to attain lower speedup on the accelerator is chosen. We refer reader to [14], [15] for a more detailed description of the PATS implementation. PATS also implements optimizations such as data reuse and overlap of data copy and computations to further reduce data processing overheads.

V. Experimental Evaluation

We performed the experimental evaluation using a distributed memory Linux cluster called Stampede². Each compute node has dual socket Intel Xeon E5-2680 processors, an Intel Xeon Phi SE10P co-processor, and 32GB of main memory. We also used a node equipped with a single NVIDIA K20 GPU. The nodes are connected using Mellanox FDR InfiniBand switches. The codes were compiled using Intel Compiler 13.1 with “-O3” flag. Since we execute the codes on the MIC using the offload mode, a computing core is reserved to run the offload daemon, and a maximum of 240 computing cores are launched. The images for the experiments were collected from brain tumor studies [6]. Each image is divided into 4K×4K tiles which are processed concurrently on the cluster system.

A. Scalability of Operations on MIC

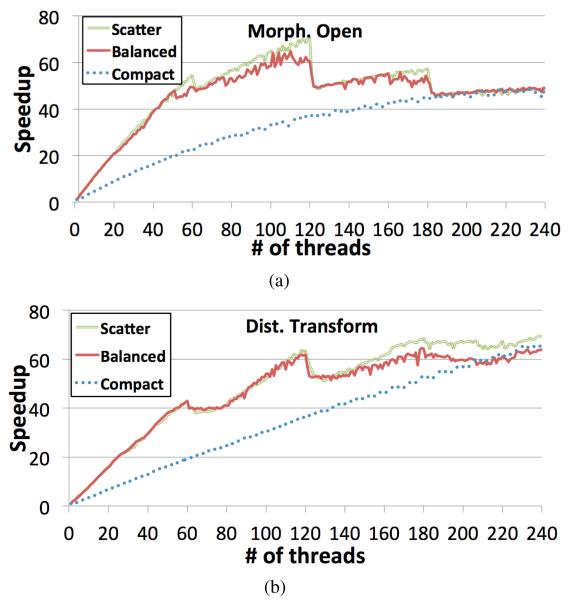
This section evaluates the performance and scalability of the operations on the MIC. This analysis also considers the effects of thread affinity that determines the mapping of computing threads to computing cores. We examined three affinity strategies: compact, balanced, and scatter. Compact assigns threads to the next free thread context n + 1, i.e., all four contexts in a physical core are used before threads are placed in the contexts of another core. Balanced allocates threads to new computing cores before contexts in the same core are used. Threads are balanced among computing cores and subsequent thread IDs are assigned to neighbor contexts or cores. Scatter allocates threads in a balanced way, like the balanced strategy, but it sets thread IDs such that neighbor threads are placed in different computing cores. We selected two operations with different data access and computation intensities for the experiments: (1) Morphological Open has a regular data access pattern and low computation intensity; (2) Distance Transform performs irregular data access and has a moderate computation intensity. OpenMP static loop scheduling was used for execution, because the dynamic version resulted in lower performance.

The scalability results with respect to thread affinity are presented in Figure 1. There is a great variability in speedups with different operations and different thread affinity strategies. Morphological Open and Distance Transform achieved the best performances when 120 and 240 threads were used, respectively (Figures 1(a) and 1(b)). The graphs show that peaks in performance are reached when the number of threads is a multiple of the number of computing cores, i.e., 60, 120, 180, and 240 threads. In these cases, the number of threads per computing core is the same, allowing better computational balance among the physical cores.

Figure 1.

Evaluation of scalability with respect to thread affinity type for selected operations on the MIC.

The performance of the Morphological Open operation scales until 120 threads are employed. It significantly degrades when more threads are used. This behavior is a consequence of the MIC’s performance with memory intensive applications. As reported in [16], [17], the maximum memory bandwidth on the MIC is reached, measured using the STREAM benchmark [16] (regular data access), when one or two threads are instantiated per computing core (a total of 60 or 120 threads). When the number of threads increases to 180 and 240, there is a reduction in memory throughput due to congestion on the memory subsystem. Since Morphological Open is memory bound, this property of the MIC is a limiting factor on the performance of the operation when 120 and more threads are executed.

The scalability of Distance Transform is presented in Figure 1(b). This operation fully benefited from the MIC’s 4-way hyperthreading and attained the best performance with 240 threads. Memory bandwidth also plays an important role in the scalability of this operation. However, this operations performs irregular access to data. Since random memory bandwidth is not typically included in devices specifications, we created a micro-benchmark to the MIC’s performance with random data access in order to better understand the operation’s performance. This benchmark consists of a program that randomly reads and writes elements from/to a matrix in parallel. The positions to be accessed in this matrix are stored into a secondary vector of indices, which is equally initialized in the CPU for all the devices. We observed that bandwidth attained by the MIC with random data access increases until the number of threads is 240. We conclude that this is the reason for the observed performance behavior of the Distance Transform operation.

The scatter and balanced thread affinity strategies achieve similar performance, but the compact strategy fails to attain good performance with the Morphological Open operation. The compact strategy uses all the 60 physical cores only when close to 240 threads are instantiated. On the other hand, Morphological Open achieves best performance with 120 threads. With this many threads the compact affinity uses only 30 physical cores.

B. Performance Impact of Vectorization on MIC

This section analyzes the impact of using the Intel Xeon Phi SIMD capabilities. For this evaluation, we used the Gradient Stats operation, which makes full use of SIMD instructions to manipulate single-precision floating-point data. The scatter affinity strategy is used in the experiments because it was more efficient. Gradient Stats achieved speedups of 16.1× and 39.9×, respectively, with the non-vectorized and vectorized versions, as compared to the single-threaded vectorized execution. The performance gains with vectorization are higher with lower number of threads − 4.1× for the single-threaded configuration. The performance gap between the two versions is reduced as the number of threads increases because of the better scalability of the non-vectorized version. At best, vectorization results in an improvement of 2.47× on top of the non-vectorized version.

C. Comparative Performance of MIC, GPU, and CPU

This section evaluates the performance of the operations on the MIC, GPU, and CPU. The speedup values were calculated using the single core CPU execution as the base-line. While the CPU and MIC executables were generated from the same C++ source code annotated with OpenMP, the GPU programs were implemented using CUDA. The same parallelization strategy was employed in all of the implementations of an operation.

The overall performance of the operations on different processors is presented in Figure 2. There is high variability in the speedup attained by each of the operations even when a single device is considered. In addition, the relative performance on the CPU, MIC, and GPU varies among the operations, which suggests that different computing devices are more appropriate for specific operations. In order to understand the reasons for the performance variations, we divided the operations into three disjoint groups that internally have similarities regarding the memory access pattern and execution strategy. The groups are: (1) Operations with regular data access: RGB2Gray, Morphological Open, Color Deconvolution, Pixel Stats, Gradient Stats, and Sobel Edge; (2) Operations with irregular data access: Morphological Reconstruction, FillHoles, and Distance Transform; (3) Operations that heavily rely on the use of atomic functions, which include the Area Threshold and Connected Component Labeling (CCL). To understand the performance of these operations, we measured their computation intensity and correlated it with each device’s capabilities using the notions of the Roofline model [18].

Figure 2.

Speedups achieved by operations on the CPU, MIC, and GPU, using the single core CPU version as a reference. The number above each dash refers to the number of threads that lead to the best performance on the MIC.

1) Regular Operations

The peak memory bandwidth and computation power of the processors are important to analyze the operations performance on each of them. The memory bandwidth with regular data access was measured using the STREAM benchmark [16] in which the K20 GPU, the CPU, and the MIC reached peak throughputs of 148GB/s, 78GB/s (combined for the two CPUs), and 160GB/s, respectively, with a single thread per core. Increasing the number of threads per core with the MIC results in a reduction of the bandwidth. Moreover, while the K20 GPU and the MIC are expected to deliver peak double precision performance of about 1 TFLOPS, the 2 CPUs together achieve 345 MFLOPS.

The Morphological Open, RGB2Gray and Color Deconvolution operations are memory bound operations with low arithmetic-instruction-to-byte ratio. As presented in Figure 2, their performance on the GPU is about 1.25× higher than that on the MIC. Furthermore, the CPU scalability with this operations is low, because the memory bus is rapidly saturated. The improvements of the GPU on top of the CPU are consistent with their differences in memory bandwidth. The Color Deconvolution operation attains better raw speedups than other operations due to its higher computation intensity. While Morphological Open attains maximum performance with 120 threads because of its ability of reusing cached data (neighborhood in computation of different elements may overlap), the other two operations use 180 threads in order to hide the memory access latency. The remaining of the regular operations (Pixel Stats, Gradient Stats, and Sobel Edge) are compute bound due to their higher computation intensity. These operations achieve better scalability with all the devices. The performances of the GPU and MIC are similar with improvements of about 1.9× on top of the multicore CPU execution because of their higher computing capabilities. This set of compute intensive operations obtained the best performance with the MIC using 120 threads. Using more threads does not improve performance because the MIC threads can launch a vector instruction each two cycles, and compute intensive operations should maximize the hardware utilization with a 2-way hyperthreading.

2) Irregular Operations

The operations with irregular data access patterns are Morphological Reconstruction, FillHoles, and Distance Transform. This set of operations strongly relies on the device performance to execute irregular (random) accesses to data. We used the same micro-benchmark described in Section V-A to measure each of the systems’ throughput in this context.

The results are presented in Table III. The experiments were carried out by executing 10 million random reading or writing operations in a 4K×4K matrix of integer data elements. As shown, the bandwidth attained by the processors is much lower than those with regular data access. The GPU significantly outperforms the other devices. The random writing bandwidth of the MIC processors is notably poor. This is in fact expected because this processor needs to maintain cache consistency among its many cores, which will result in a high data traffic and competition in its ring bus connecting caches. Due the low bandwidth attained by all the processors, the irregular operations are necessarily memory bound.

Table III.

Device Bandwidth with Random Data Accesses (MB/s).

	CPU	MIC	GPU
Reading	305	399	895
Writing	74	16	126

As presented in Figure 2, the Distance Transform operation on the GPU is about 2× faster than on the MIC, whereas the MIC performance is not better than that of the CPU. This operation performs only irregular data access in all phases of its execution, and the differences in the random data access performances of the devices are crucial to its performance.

The other two operations (Morphological Reconstruction and Fill Holes) in this category have a mixed data access patterns. These operations are based on the irregular wave front propagation pattern, and their most efficient execution is carried out with an initial regular propagation phase using raster/anti-raster scans, before the algorithm migrates to the second phase that irregularly access data and uses a queue to execute the propagations. Since the first phase of these operations is regular, it may be efficiently executed on the MIC. In the MIC execution, the algorithm will iterate several times over the data using the regular (initial) phase, before it moves to the irregular queue based phase. The MIC execution will only migrate to the irregular pattern after most of the propagations are resolved, which reduces the amount of time spent in the irregular phase. Hence, the performance gains on the GPU as compared to those on the MIC are smaller for both operations: about 1.33×. We want to highlight that the same tuning regarding the appropriate moment to migrate from the regular to the irregular phase is also performed with the GPU version.

3) Operations that Rely on Atomic Instructions

The Area Threshold and CCL operations heavily rely on the use of atomic add instructions to execute a reduction. Because the use of atomic instructions is critical for several applications and computation patterns, we analyze the performance of the evaluated devices with regard to execution of atomic instructions and its implications to the Area Threshold and CCL operations. To carry out this evaluation, we created a micro-benchmark in which computing threads concurrently execute atomic add instructions in two scenarios: (1) using a single variable that is updated by all threads and (2) an array indexed with the thread identifier. The first configuration intends to measure the worst case performance in which all threads try to update the same memory address, whereas the second case assesses performance with threads updating disjoint memory addresses.

The results are presented in Table IV. The GPU once again attained the best performance, and it is at least 5× faster than the other processors in both scenarios. The reduction in the GPU throughput from the configuration with an array to the single variable, however, is the highest among the processors evaluated. This drastic performance penalty occurs because a GPU thread warp executes in a SIMD way and, hence, the atomic instructions launched by all threads in a warp will be serialized. In addition, the GPU launches a larger number of threads. This results in higher levels of concurrency and contention for atomic instructions.

Table IV.

Device Throughput with Atomic Adds (Millions/sec).

	CPU	MIC	GPU
single Variable	134	55	693
Array	2,200	906	38,630

The CPU is about 2.4× faster than the MIC in both scenarios. The MIC is equipped with simpler computing core and typically relies on the use of vectorized operations to achieve high performance. However, it lacks support for vector atomic instructions, which poses a serious limitation. The introduction of atomic vector instructions, such as those proposed by Kumar et. al. [19] for other multiprocessors, could significantly improve the MIC performance. Because the Area Threshold and CCL operations greatly depend on atomic instructions, they attained better performance on the GPU. In both cases, the execution on the CPU is more efficient than on the MIC (Figure 2).

D. Multi-node Execution using CPUs and MICs

This section evaluates application performance in using CPUs and MICs cooperatively on a distributed memory cluster. The example application is built from the core operations and is implemented as a hierarchical pipeline in which the first level is composed of segmentation and feature computation stages, and each of these stages is created as a pipeline of operations as described in Section IV. We evaluated four versions of the application: (1) CPU-only refers to the multi-core CPU version that uses all CPU cores available; (2) MIC-only uses a MIC per node to perform computations; (3) CPU-MIC FCFS uses all CPU cores and the MIC in coordination and distributes tasks to processors in each node using FCFS (First-Come, First-Served) fashion; (4) CPU-MIC PATS also uses all CPU cores and the MIC in coordination, but the tasks are scheduled to devices based on the expected speedup of each task on each device. The speedup estimates are those presented in Figure 2.

The weak scaling evaluation in which the dataset size and the number of nodes increase proportionally is presented in Figure 3. The experiments with 172 nodes used an input dataset with 68,284 4K×4K image tiles (3.27TB of uncompressed data). All versions of the application scaled well as the number of nodes is increased from 4 to 192. The MIC-only execution was slightly faster than the multi-core CPU-only version. The cooperative CPU-MIC executions attained improvements of up to 2.06× on top of the MIC-only version. The execution using PATS is 1.29× faster than using FCFS. This is a result of PATS being able to map tasks to the more appropriate devices for execution. The efficiency of the fastest CPU-MIC PATS version is about 84%, when 192 computing nodes are used. The main factor limiting performance is the increasing cost of reading the input image tiles concurrently from disk as the number of nodes (and processes) grows.

Figure 3.

Multi-node weak scaling evaluation: dataset size and the number of nodes increase proportionally.

VI. Related Work

Efficient utilization of computing systems with co-processors requires the implementation of efficient and scalable application computing kernels, coordination of assignment of work to co-processors and CPUs, minimization of communication, and overlapping of communication and computation. Mars [20] and Merge [21] are designed to enable efficient execution of MapReduce computations on shared memory machines equipped with CPUs and GPUs. Qilin [22] implements an automated methodology to map computation tasks to CPUs and GPUs. PTask [23] provides OS abstractions for task based applications on GPU equipped systems. Other frameworks to support execution on distributed memory machines with CPUs and GPUs were also proposed [24], [25], [26], [27], [28], [29], [30]. DAGuE [24] and StarPU [30] support execution of regular linear algebra applications. They express the application tasks dependencies using a Directed Acyclic Graph (DAG) and provide different scheduling policies, including those that prioritize execution of tasks in the critical path. Ravi [25] and Hartley [26] proposed runtime techniques to auto-tune work partitioning among CPUs and GPUs. OmpSs [28] supports execution of dataflow applications created via compilation of annotated code.

More recently, research groups have focused on applications that may benefit from Intel’s Xeon Phi co-processor [31], [32], [33], [34], [17]. Joó et al. [31] implemented a Lattice Quantum Chromodynamics (LQCD) method using Intel Phi processors. Linear algebra algorithms were also ported to MIC [32], [34]. Hamidouche et al. [35] proposed an automated approach to perform computation offloads on remote nodes. The use of OpenMP based parallelization on a MIC processor was evaluated in [33]. That work analyzed the overheads of creating and synchronizing threads, processor bandwidth, and improvements with the use of vector instructions. Saule et al. [17] implemented optimized sparse matrix multiplication kernels for MICs, and provided a comparison of MICs and GPUs for this operation.

In our work, we perform a comparative performance evaluation of MICs, multi-core CPUs, and GPUs using an important class of operations. These operations employ diverse computation and data access patterns and several parallelization strategies. The comparative performance analysis correlates the performance of operations with co-processors characteristics using co-processor specifications or performance measured using micro-kernels. This evaluation provides a methodology and clues for application developers to understand the efficacy of co-processors for a class of applications and operations. We also investigate coordinated use of MICs and CPUs on a distributed memory machine and its impact on application performance. Our approach takes into account performance variability of operations to make smart task assignments.

VII. Conclusions

Creating efficient applications that fully benefit from systems with co-processors is a challenging problem. Application developers often have little information about which co-processors are more suitable for their applications. In this paper we provide a comparison of CPUs, GPUs, and MICs using operations that exhibit different data access patterns (regular and irregular), computation intensity, and types of parallelism, from a class of applications. An array of common parallelization strategies for these operations are also studied. The experimental results show that different types of co-processors are more appropriate for specific data access patterns and types of parallelism, as expected. The MIC’s performance compares well with that of the GPU when regular operations and computation patterns are used. The GPU is more efficient for those operations that perform irregular data access and heavily use atomic operations. Our work also shows that a strong performance variability exists among different operations, as a result of their computation patterns. This performance variability needs to be taken into account to efficiently execute pipelines of operations using co-processors and CPUs in coordination.