Compensation for red-green contrast loss in anomalous trichromats

Abstract

For anomalous trichromats, threshold contrasts for color differences captured by the L and M cones and their anomalous analogs are much higher than for normal trichromats. The greater spectral overlap of the cone sensitivities reduces chromatic contrast both at and above threshold. But above threshold, adaptively nonlinear processing might compensate for the chromatically impoverished photoreceptor inputs. Ratios of sensitivity for threshold variations and for color appearance along the two cardinal axes of MacLeod-Boynton chromaticity space were calculated for three groups: normals (N = 15), deuteranomals (N = 9), and protanomals (N = 5). Using a four-alternative forced choice (4AFC) task, threshold sensitivity was measured in four color-directions along the two cardinal axes. For the same participants, we reconstructed perceptual color spaces for the positions of 25 hues using multidimensional scaling (MDS). From the reconstructed color spaces we extracted “color difference ratios,” defined as ratios for the size of perceived color differences along the L/(L + M) axis relative to those along the S/(L + M) axis, analogous to “sensitivity ratios” extracted from the 4AFC task. In the 4AFC task, sensitivity ratios were 38% of normal for deuteranomals and 19% of normal for protanomals. Yet, in the MDS results, color difference ratios were 86% of normal for deuteranomals and 67% of normal for protanomals. Thus, the contraction along the L/(L + M) axis shown in the perceptual color spaces of anomalous trichromats is far smaller than predicted by their reduced sensitivity, suggesting that an adaptive adjustment of postreceptoral gain may magnify the cone signals of anomalous trichromats to exploit the range of available postreceptoral neural signals.

Introduction

Normal trichromatic color vision requires input from three types of photoreceptors: short- (S), medium- (M), and long- (L) wavelength–sensitive cones. Anomalous trichromacy is an inherited abnormality of color vision in which one or more of the cone photopigments is altered in its spectral sensitivity (Nathans, Piantanida, Eddy, Shows, & Hogness, 1986). In deuteranomaly, affecting about 5% of males, the normal L photopigment is usually retained (MacLeod & Hayhoe, 1974), but the M photopigment is replaced by an anomalous photopigment that we refer to as L′, close in sensitivity to the normal L (Alpern & Moeller, 1977; Alpern & Wake, 1977; Merbs & Nathans, 1992b). Protanomals (1% of males) correspondingly have two photopigments maximally sensitive in the middle-wave part of the spectrum, the normal M and an anomalous M′ photopigment that replaces the normal L (Merbs & Nathans, 1992b).

Molecular analysis of the genes for the M and L opsins has revealed a wide variety of alternative alleles, many or most of which could be considered “hybrids,” containing genetic elements from the ancestral genes for both M and L opsins (see Neitz & Neitz, 2011, for review). Anomalous trichromats express two different genes for the same opsin, which overlap with the variant alleles for the M and L opsins observed in normals (Neitz & Neitz, 2011). The variety of different anomalous genotypes lends corresponding variety to the spectral sensitivities of the anomalous cones (Merbs & Nathans, 1992b; Asenjo, Rim, & Oprian, 1994). Consequently, there are many phenotypes of anomalous trichromacy. The spectral separation between the two cone types sensitive to medium and long wavelengths of light may, in different individuals, be as small as 1 nm or as large as 12 nm. Variation in spectral separation predicts a proportion (but not all) of the wide variation among individual anomalous trichromats in color discrimination (Deeb et al., 1992; Neitz, Neitz, & Kainz, 1996; Sanocki, Teller, & Deeb, 1997; Crognale, Teller, Motulsky, & Deeb, 1998; Shevell, He, Kainz, Neitz, & Neitz, 1998; Barbur et al., 2008).

Because there is a greater spectral overlap between the two cone types in anomalous trichromacy than in normal color vision, threshold contrasts for color differences in the medium- and long-wavelength part of the spectrum are much higher than for normals. The greater spectral overlap between the medium- and long-wavelength sensitive cones in anomalous trichromacy inevitably results in a smaller difference between the excitations of the two operative classes of cone.

The postreceptoral representation of color in the anomalous visual system will depend both on the cone absorption spectra and on the postreceptoral neural connectivities. If those connectivities are the same as in the normal trichromat—the most natural and economical hypothesis—the “red-green” opponent neurons of the anomalous visual system will be greatly understimulated and would make use of much less neural capacity than is available (MacLeod, 2003). Regan and Mollon (1997) and others (MacLeod, 2003; Bosten, Robinson, Jordan, & Mollon, 2005; Webster, Juricevic, & McDermott, 2010) have suggested that anomalous trichromats might benefit from an increase in postreceptoral gain that compensates for the reduced color-difference signals received from the cones. Regan and Mollon based their suggestion on results of experiments measuring the relative salience of chromatic variation along the two cardinal axes of MacLeod-Boynton chromaticity space, S/(L + M) and L/(L + M). They found that for some anomalous trichromats, the relative salience of L/(L + M) modulation was in the normal range. However, because Regan and Mollon did not measure sensitivity at threshold, it was unclear whether all anomalous trichromats show greater salience for L/(L + M) modulations than would be predicted from their reduced thresholds.

Long-term shifts in color appearance have been observed following long-term alterations in the chromatic environment, either induced experimentally (Neitz, Carroll, Yamauchi, Neitz, & Williams, 2002) or by removal of cataracts (Delahunt, Webster, Ma, & Werner, 2004). We here investigate the possibility that, in addition to such shifts, adaptive alterations in postreceptoral gain allow the sensitivity of postreceptoral color signals to be adjusted to best represent environmental stimuli. Thus, in normal vision, adaptive gain control might decide the relative signal strengths of the S/(L + M) and L/(L + M) channels: For each observer, they would be optimized to best represent the range of chromaticities present in the natural environment (von der Twer & MacLeod, 2001; MacLeod, 2003). It might also help achieve consistency of color appearance between the eyes (MacLeod, 2003) and within the same eye despite changes in macular pigment density between the fovea and the periphery (Beer, Wortman, Horwitz, & MacLeod, 2005; Webster, Halen, Meyers, Winkler, & Werner, 2010). For the anomalous trichromat, gain control should ideally be adapted to the input from the anomalous cones. If postreceptoral gain is adjusted in anomalous trichromats to compensate for the greater spectral overlap of their cones, the appearance of colors might not be as different from the norm as would otherwise be expected.

We used multidimensional scaling (MDS) to reconstruct perceptual color spaces for anomalous trichromats. We chose MDS because we were specifically interested in color appearance in anomalous trichromacy rather than in the suprathreshold contrast response function (e.g., Krauskopf & Gegenfurtner, 1992; Sankeralli & Mullen, 1999) or in suprathreshold color salience (Regan & Mollon, 1997). MDS has been used to map subjective color space to a coordinate system, in which the distance between the positions of two colors in the reconstructed space corresponds to the perceptual difference between them (Indow & Uchizono, 1960). MDS has revealed that subjective color space is at least two-dimensional with dimensions roughly corresponding to the “red-green” and “blue-yellow” opponent systems (Helm, 1964; Cavonius & Mollon, 1984). For anomalous trichromats, the red-green dimension is compressed relative to that of normals (Helm, 1964; Paramei, Izmailov, & Sokolov, 1991; Paramei & Cavonius, 1999; Paramei, Bimler, & Cavonius, 2001), and the size of the compression along the red-green axis is indicative of the degree of color deficiency (Paramei et al., 1991; Paramei et al., 2001). However, it is not clear whether the degree of compression along the red-green axis is predictable from the degree of reduction in sensitivity to color discrimination along the same axis. To test this point was the aim of our investigation.

In a simple model, in which postreceptoral processing is fixed and not optimized for the anomalous photopigment, the relative compression along the red-green axis in an anomalous trichromat's MDS-reconstructed color space should be predicted by the relative reduction in sensitivity at threshold along the same axis. Roughly speaking, compared to the normal color space, the color space of the anomalous trichromat would be compressed along the red-green axis relative to the blue-yellow axis with a reduction of the perceived relative differences between red and green stimuli equal to the factor of reduction in the red-green sensitivity at threshold. However, if the anomalous cone signal is magnified postreceptorally to compensate for the reduced signal from the spectrally altered photopigment, the relative compression of the red-green axis in the anomalous trichromats' perceptual color space reconstructed using MDS would be less than the reduced threshold sensitivity suggests.¹

We compare the degree to which anomalous trichromats have reduced sensitivity for red-green color differences with the degree to which their perceptual color space is contracted along the same axis. To measure thresholds for chromatic discrimination, we used a four-alternative forced choice (4AFC) task. We calculated mean “sensitivity ratios” (the ratio of red-green sensitivity to blue-yellow sensitivity) for normals, deuteranomals, and protanomals. Using the same subjects, we used MDS to reconstruct a map of subjective color space for each group based on averaged dissimilarity ratings for pairs of 25 different colors. We found “color difference ratios,” defined as ratios of the mean size of perceived color differences along the L/(L + M) axis to those along the S/(L + M) axis for the subjective color spaces and then compared them with the analogous sensitivity ratios from the 4AFC task.

Methods

General methods

Color space

We use in this paper a scaled version of the MacLeod-Boynton (1979) chromaticity diagram as a color metric. The MacLeod-Boynton chromaticity diagram is an isoluminant plane with the ratio L/(L + M) along the x-axis and the ratio S/(L + M) along the y-axis, where S, M, and L are the activations of the three classes of normal cone. We constructed our version of the MacLeod-Boynton chromaticity diagram differently from the original, using, instead of the Smith and Pokorny (1975) cone fundamentals, the Stockman, MacLeod, and Johnson (1993) cone fundamentals scaled so that for equal-energy white S/(L + M) = 1 and L/(L + M) = 0.7.

The MacLeod-Boynton chromaticity diagram is physiologically valid only for the standard normal observer (who has the cone spectral sensitivities used to construct the diagram). In anomalous observers, it does not accurately represent the conditions for metameric matches but remains useful as an index of color differences generated using fixed primaries as in the present experiments. A color space based on anomalous cone activations would be different from the standard MacLeod-Boynton diagram and would need to be constructed using their own cone fundamentals. We attempt to do this below in the Models section. Elsewhere in the paper, we use our scaled MacLeod-Boynton color diagram as a color metric, a coordinate system in which to represent color. We could equally have chosen the CIE diagram. In using the MacLeod-Boynton coordinates as a metric to compare color differences across observers, we require only that coordinate differences be proportional to the differences in the amounts of the fixed red, green, and blue primaries, a condition necessarily satisfied for any fixed primaries.

Equipment

Experimental stimuli were presented on a Diamond Pro 2070SB monitor (Mitsubishi, Tokyo, Japan). The gamma functions of the monitor were linearized using measurements made with a UDT photometer (United Detector Technologies, Hawthorne, CA), and the color calibration was achieved using a SpectraScan PR650 spectroradiometer (Photo Research, Inc., Chatsworth, CA). Visual stimuli were generated using a Visual Stimulus Generator (VSG) 2/4 graphics card (Cambridge Research Systems, Rochester, UK). For the 4AFC task, responses were gathered using a Cambridge Research Systems CT3 Response Box. For the MDS task, responses were gathered using a numerical keypad.

Anomaloscope

The anomaloscope was a two-channel optical system. Subjects matched a monochromatic orange light of 588 nm, passed through a diffuser, with a mixture of red and green. Our red and green primaries were displayed on a DreamColor LP2480ZX monitor (Hewlett Packard, Palo Alto, CA), chosen for its enhanced gamut. To reduce the level of S-cone stimulation by the DreamColor's green primary, we passed the light from the matching stimulus, presented on the DreamColor, through a yellow long-wavelength transmitting dichroic filter (LINOS AG, Göttingen, Germany) having half-maximum transmission at 525 nm and less than 1% transmission below 520 nm. The spectra of the three primaries are shown in Figure 1c. Subjects were able to adjust the ratio of red/green displayed on the DreamColor's matching field by using a mouse trackball. They were able to adjust the luminance of the matching field using mouse buttons.

Figure 1.

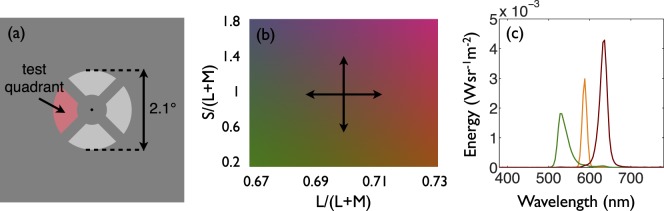
Stimulus for the forced-choice discrimination task (a and b) and for the anomaloscope (c). (a) The spatial structure of the stimulus for the forced-choice discrimination task. (b) A diagram of the MacLeod-Boynton chromaticity space with arrows pointing from equal-energy white in four directions along the cardinal axes, showing the possible S/(L + M) and L/(L + M) coordinates of the test quadrant. (c) The radiance spectra of the three primaries of the anomaloscope. The monochromatic orange (orange line) peaks at 588 nm. The green primary (green line) peaks at 530 nm, and the red primary (red line) peaks at 636 nm.

Subjects made five matches in the presence of the experimenter. To investigate the possibility of dichromacy, the experimenter adjusted the red/green ratio of the matching field to both extremes of the range available and asked subjects to attempt to match the monochromatic orange field and the matching field by adjusting only the luminance of the matching field. If subjects were unable to find matches at both extremes of the range, dichromacy was excluded, and they were allowed to make five matches by adjusting both the red-green ratio and the luminance of the matching field. We predicted matches for normals using the Smith and Pokorny (1975) cone fundamentals and also predicted the loci of matches for protanopes and deuteranopes who lack either the medium- or long-wavelength cones. We classified color vision as normal, protanopic, deuteranopic, deuteranomalous, or protanomalous by comparing subjects' matches with the predictions. If a subject accepted matches over an extended range (but not the whole range) of red/green ratios that included an anomalous match and a normal match, they were classed as extreme anomalous trichromats.

Subjects

Twenty-nine subjects participated in the experiments. All subjects were either undergraduates at the University of California, San Diego, or lab members. All subjects gave written informed consent for their participation in this study, which adhered to the tenets of the Declaration of Helsinki.

Anomalous subjects were identified by screening approximately 350 candidates using the anomaloscope. Extreme anomalous trichromats were excluded from our sample.

Subjects were divided into three groups corresponding to their type of color vision: normals (N = 15), deuteranomals (N = 9), and protanomals (N = 5). All subjects with anomalous color vision were males, and of the subjects with normal color vision, nine were males and six were females. All subjects were naïve to the purposes of the experiment except for two of the authors (AB and DM), one with normal and one with deuteranomalous color vision.

All subjects had normal or corrected-to-normal visual acuity. Subjects with normal color vision passed all of the plates in Ishihara's Tests for Color-Blindness, Concise Edition (1987).

Forced-choice discrimination thresholds

The stimulus consisted of four quadrants of a disc (inner diameter 0.8°, outer diameter 2.1°) with a black fixation dot at the center (Figure 1a). Each quadrant was separated by a gap of 0.15°. The background was metameric with equal-energy white with a luminance of 17.5 cd/m².

The chromaticity of the three distractor quadrants was metameric with equal-energy white, and the chromaticity of the test quadrant was either an increment or a decrement along one of the cardinal axes of the MacLeod-Boynton chromaticity space (Figure 1b). To ensure that both the test and distractor quadrants were isoluminant for both the normal and anomalous subjects, each subject completed a minimum motion task available in Psychtoolbox (PTB-3: Brainard, 1997; Pelli, 1997; Kleiner, Brainard, & Pelli, 2007), similar to that described by Anstis and Cavanagh (1983). Data from this was used to calculate the stimulus intensities required to achieve isoluminance for individual subjects.

Because we used the minimum motion task to generate perceptually isoluminant stimuli, the luminance of the test and distractor quadrants were slightly different for each subject. The average luminance of the stimulus quadrants was 37.1 cd/m² for normals, 36.1 cd/m² for deuteranomals, and 41.6 cd/m² for protanomals.

In the 4AFC discrimination task, subjects indicated which of four stimulus quadrants appeared to be of a different color from the other three. The test stimulus was presented for up to 3 s and was removed immediately after the subject responded to the trial using the response box. Subjects were given audio feedback on each trial: A relatively high-pitched tone indicated a correct response, and a lower tone indicated an incorrect response.

Two interleaved ZEST staircases (Watson & Pelli, 1983; King-Smith, Grigsby, Vingrys, Benes, & Supowit, 1994) were used to track 81% points on the psychometric functions. The experiment was repeated over two sessions with each session separated by at least 1 day.

Multidimensional scaling

Selection of stimuli

Stimuli for the MDS experiment were selected on the basis of group mean unique and intermediate hue settings made by 58 subjects who did not go on to participate in the experiments described in the present paper and who had normal color vision, assessed using the Ishihara plates. The methods and results for the unique and binary hue measurements have been published elsewhere (Bosten & Lawrance-Owen, 2014), but we provide them briefly here.

Subjects were presented with circles of 90 selectable colored segments on a CRT monitor covered with a touch-sensitive screen (Figure 2a). The colored segments were isoluminant with a luminance of 28 cd/m². The background on which the segments were presented was metameric with D65 and was 17 cd/m² in luminance. A scaling factor of 2.8 was applied to the L/(L + M) axis, maintaining the chromaticity of the background. Stimuli were presented on a Diamond Pro 2070SB CRT monitor, calibrated using a UDT photometer and a SpectraScan PR650 spectroradiometer. To gather subjects' responses, a Keytec Magic Touch ProE-X touch screen (model number ET2032C) was used, attached to the CRT monitor.

Figure 2.

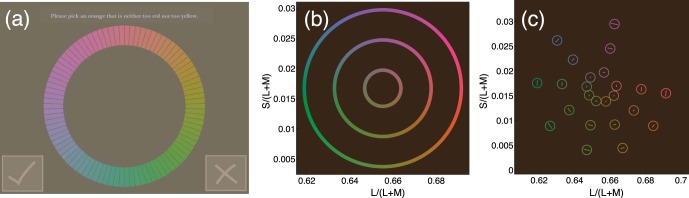
Selection of stimuli for the MDS experiment. (a) Stimulus. The subject selected the segment he or she thought best matched the instructions, in this case, “Please pick an orange that is neither too red nor two yellow.” The subject could change the selection or confirm it by tapping the check symbol. (b) Loci of chromaticities allowed for the selections. Unique and binary hue selections were measured for stimuli of three different saturations, represented by the three circles. (c) Results. Mean hue selections are given by the open circles with 95% CIs indicated by the bars inside the data points.

According to the block, subjects were asked to choose, for example, “a red that is neither too orange nor too purple” or “an orange that is neither too red nor too yellow” (Malkoc, Kay, & Webster, 2005). The subject selected the segment he or she thought best matched the instruction by tapping it with a stylus. There were 16 blocks, each of 15 trials. In each block, settings were gathered for one of the four unique hues (red, green, blue, and yellow) or one of the four intermediate hues (orange, purple, blue-green, and yellow-green). In each block, three different saturations were tested. For the first five trials, the saturation was high; for the second five trials, it was medium; and for the third five trials, it was low (the saturations tested are shown in Figure 2b). In the first eight blocks, all eight hues were measured in a random order, and they were measured again in a different random order in the second eight blocks.

Median hue settings for the 24 colors were found for each subject. A group average for each color was calculated by taking the mean of 58 subjects' median settings. The group mean hue settings, shown in Figure 2c with 95% confidence intervals (CIs), were used as stimuli in the MDS experiment.

Procedure for MDS

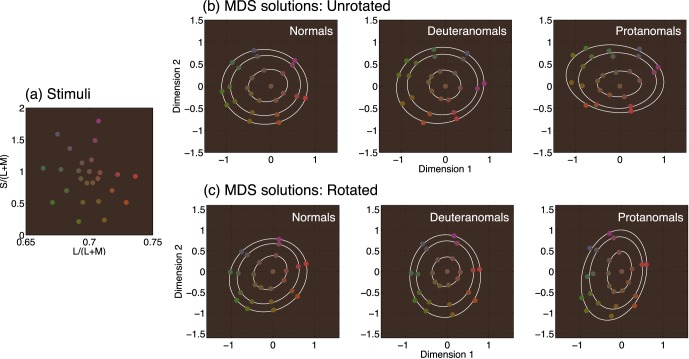
The chromaticities of the 25 stimuli used in Experiment 2 are shown in Figure 4a. One stimulus was metameric with equal-energy white. The other 24 stimuli were eight unique and intermediate hues of three different saturations. All stimuli were made isoluminant for individual observers using the results of the minimum motion procedure but were approximately 40% greater in luminance than the background. The background was metameric with equal-energy white and had a luminance of 17.5 cd/m².

Figure 4.

(a) Positions of the 25 stimuli in the MacLeod-Boynton chromaticity space used for the MDS experiment. (b) Raw group average MDS results. Best-fitting ellipses are shown through the set of eight data points corresponding to each of the three different saturations included in the set of stimuli. (c) Results of the Procrustes analysis. Group average MDS solutions were rotated to best coincide with the MacLeod-Boynton chromaticity diagram shown in (a).

On each trial, a pair of stimuli was presented. The stimuli were discs of diameter 2° with chomaticities that were selected from the set shown in Figure 4a. Subjects were instructed that they should rate the difference between the two members of each pair on a scale of 0–9, and 0 was to be used if the pair was identical. Subjects entered a number corresponding to their rating on a numerical keypad. The number then appeared on the screen, and then they could either change their response or press the enter key to confirm the rating. There was no time limit for each trial, and they were free to move their eyes from one stimulus to the other.

Before starting the experiment, a palette showing all 25 stimuli was presented so that subjects could judge the full range of color differences. They then completed a training phase in which nine randomly selected stimulus pairs were presented, and their consistency at rating the dissimilarities was monitored. The nine pairs were continuously cycled in a random order until subjects had rated all nine pairs within one unit of their rating on the previous presentation.

Subjects then began the experiment. There were 325 possible pairings of colors, and each pair was presented in random order. This was repeated so that all possible pairs of colors were presented twice.

Results

4AFC discrimination

Thresholds were measured for discriminating color differences from equal-energy white in both directions along each cardinal axis of MacLeod-Boynton chromaticity space. Figure 3 shows thresholds along each axis for individual subjects.

Figure 3.

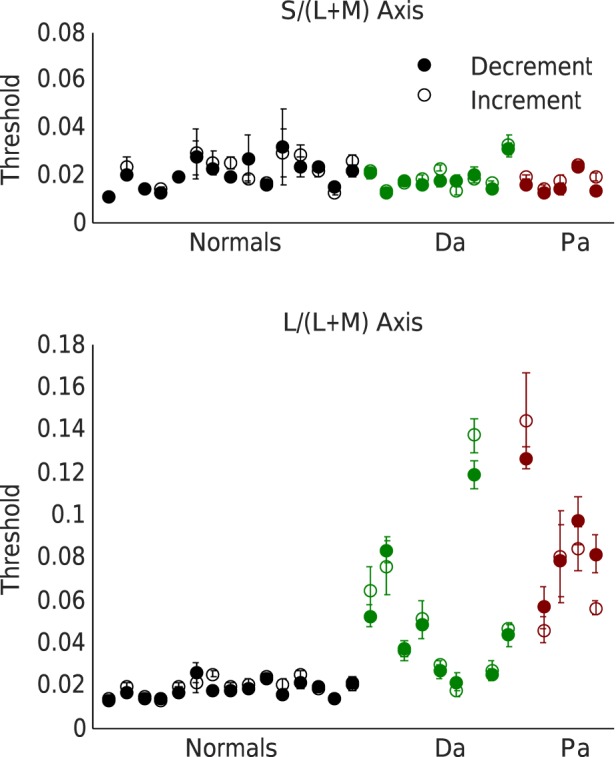
Thresholds for discrimination along the S/(L + M) and the L/(L + M) axes, shown for individual subjects. Thresholds for increments are shown by open circles and thresholds for decrements by filled circles. Data for normals are shown in black, for deuteranomals (Da) in green, and for protanomals (Pa) in red. Errors bars are plus or minus one standard error of the mean. Individual subjects' results are shown in the same order in both upper and lower panels.

Thresholds for discrimination along each axis were converted to units of log sensitivity (log of inverse threshold). Individual subjects' log sensitivities for increments and decrements along each axis were averaged to find group means for log sensitivity along each cardinal axis and to calculate a sensitivity ratio (red-green sensitivity:blue-yellow sensitivity) for each group. To find 95% CIs we used a bootstrap procedure with 1,000 recalculations of group mean sensitivity ratios. The mean sensitivity ratios were 1.08 for normal (95% CI 0.93–1.21), 0.41 for deuteranomals (95% CI 0.31–0.54), and 0.21 for protanomals (95% CI 0.16–0.27). Mean sensitivity ratios were 38% of normal for deuteranomals and 19% of normal for protanomals.

To compare groups, we did an analysis of variance (ANOVA) on the log difference in sensitivity between the L/(L + M) axis and the S/(L + M) axis. A one-way, repeated-measures ANOVA revealed a significant main effect of group (p = 1.88 × 10⁻⁸). A post hoc Tukey test showed significantly smaller sensitivity ratios for deuteranomals (p < 0.001) and protanomals (p < 0.001) compared to normals. The sensitivity ratios of deuteranomals and protanomals were not significantly different from one another.

Association with settings on anomaloscope

We correlated sensitivity ratios for individual subjects with anomaloscope mean match and matching range. For deuteranomals, both correlations were significant (ρ = 0.82, p = 0.01 for mean match and ρ = 0.73, p = 0.03 for matching range). The correlations were in the expected directions; greater matching ranges and matches further from normal were associated with lower sensitivity ratios. For protanomals neither correlation was significant (ρ = 0.5, p = 0.45 for mean match and ρ = 0.2, p = 0.78 for matching range), but the correlations were in the expected direction. Conclusions about protanomals cannot be drawn owing to our small sample (N = 5).

Multidimensional scaling

For each subject, we collected a matrix of the dissimilarity ratings of all possible pairs of stimuli, in which each cell contained the mean of two ratings for a particular pair. The data were combined within each group (normals, deuteranomals, and protanomals) to create matrices of dissimilarity judgments that reflected group averages. For averaging, each subject's data were transformed to have unit mean and standard deviation. Data were then averaged for each group by taking the mean normalized rating for each cell. After averaging, matrices of dissimilarity ratings were translated so that the minimum value in the matrix was zero.

Metric MDS was applied to the group average matrices. Metric MDS produces a set of coordinates for the stimuli that minimizes the difference between the input dissimilarity matrix and the Euclidian distances between corresponding stimulus pairs in the solution (Torgerson, 1958). Group average two-dimensional metric MDS solutions are shown in Figure 4b. The residual stresses (stress 1) of the two-dimensional solutions were 0.139 for normals, 0.121 for deuteranomals, and 0.176 for protanomals. Because stress is higher for metric than nonmetric MDS solutions, but goodness-of-fit criteria are better established for nonmetric MDS (Hair, Anderson, Tatham, & Black, 1998), we report that the stresses of nonmetric two-dimensional solutions were 0.062 for normals (good), 0.079 for deuteranomals (good), and 0.120 for protanomals (fair).

Average MDS solutions for the different groups are rotated differently because of group differences in the relative saliences of the cardinal axes of MacLeod-Boynton space. For normals, both dimension 1 and dimension 2 correlate significantly with both L/(L + M) and S/(L + M): For dimension 1, ρ = 0.75 with L/(L + M), and ρ = 0.45 with S/(L + M); for dimension 2, ρ = 0.59 with L/(L + M), and ρ = 0.87 with L/(L + M); p < 0.05 in all cases. That both MDS dimensions correlate with both cardinal axes of the MacLeod-Boynton space indicates that the MDS solution has a rotation intermediate to that of the MacLeod-Boynton chromaticity diagram. For deuteranomals and protanomals, dimension 1 correlates significantly with S/(L + M) (ρ = 0.93 for deuteranomals, and ρ = 0.93 for protanomals), and dimension 2 correlates significantly with L/(L + M) (ρ = 0.97 for deuteranomals, and ρ = 0.89 for protanomals). Although MDS solutions are rotationally invariant, the first dimension of the output corresponds to that containing the greatest perceptual distances. Unsurprisingly, this corresponds to the S-axis for anomalous trichromats. We note that our results do not imply that anomalous trichromats are using L/(L + M) or S/(L + M); they must be using their own equivalent color dimensions, which are only slightly rotated from normal (see the Models section).

To compare the ratios of perceived dissimilarity along the cardinal axes of MacLeod-Boynton space for each group, we transformed the three group average solutions so that they were all oriented the same way. We did this by applying Procrustes analysis (Dryden & Mardia, 1998) to each group average solution to find the transformation that best matched the solution to the map of the input stimuli in MacLeod-Boynton chromaticity space (Figure 4a). Procrustes analysis finds the optimal superimposition of two sets of coordinates by applying linear transformations: rotation, translation, and scaling. It minimizes the sum of squares of the coordinate differences when the three arbitrary transformations are combined. The optimal translation from the Procrustes analysis was not retained; instead, the “white” stimulus was taken as the origin for each of the MDS solutions. Results are shown in Figure 4c. Here, the three group average MDS solutions are each rotated to best coincide with the map of the stimuli in MacLeod-Boynton chromaticity space (Figure 4a), and isotropic scaling factors are applied so that the sum of the horizontal and vertical variances is the same for all three subject groups.

For the rotated MDS solutions, dimension 1 correlates significantly with L/(L + M) for all three groups (ρ = 0.96 for normals, ρ = 0.97 for deuteranomals, and ρ = 0.91 for protanomals). Dimension 2 correlates significantly with S/(L + M) (ρ = 0.95 for normals, ρ = 0.95 for deuteranomals, and ρ = 0.96 for protanomals).

We extracted color-difference ratios from the transformed MDS solutions by finding the intersections of best-fitting ellipses through the set of eight data points for each saturation and the x- y-axes. For each ellipse, we took the distance between the two x-intercepts as an estimate of the size of the perceived color difference arising from the stimulus differences along the corresponding axis in the chromaticity diagram, L/(L + M), and the distance between the two y-intercepts as the equivalent for the S/(L + M) axis. We calculated a color difference ratio for each ellipse (the ratio of the distance between the x-intercepts to the distance between the y-intercepts) and then for each group took the mean of the color difference ratios of the three ellipses for the three different saturations. The mean color difference ratios (x/y) were 1.04 for normals, 0.90 for deuteranomals, and 0.69 for protanomals. Thus, mean color difference ratios for deuteranomals were 86% of normal and for protanomals were 67% of normal.

Response times for each dissimilarity judgment were recorded. A Mann-Whitney-Wilcoxon test showed no significant difference in mean response times between normal and anomalous subjects (p = 0.81), and an Ansari-Bradley test for homogeneity of variance indicated that there was no significant difference between the dispersions of normal and anomalous response times (p = 0.82).

Individual differences

We also analyzed MDS data for individual subjects. For each subject, we found the two-dimensional MDS solution and then transformed it using Procrustes analysis to bring the solution in optimal alignment with the MacLeod-Boynton chromaticity diagram (Figure 4a). Figure 5 shows individual MDS solutions with ellipses fit to data points for the three different saturations. In four cases, for three normals and one protanomal, the best-fitting curves to the data were hyperbolae and not ellipses. Two of these normal subjects (normal panels 2 and 9) appear to exhibit a minority strategy, producing solutions in which one dimension is red-green or warm-cold, and the other dimension is saturation. The third normal subject (normal panel 14) appears to have produced a categorical solution with the different saturations intermingled. The protanomalous subject (protanomal panel 1) has produced a c-shaped solution with variation along the S/(L + M) dimension (compare to Figure 4a). This is consistent with a one-dimensional solution (Shepard, 1974; Rodieck, 1977). It is possible that this subject was a protanope misclassified as a protanomal.

Figure 5.

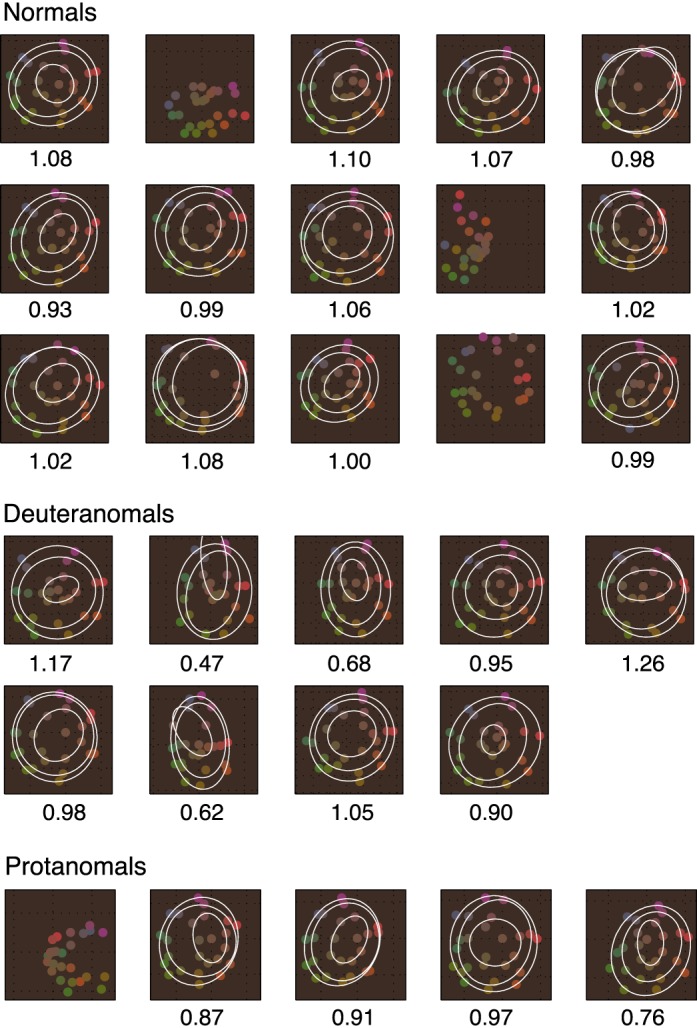
Two-dimensional MDS solutions for individual subjects. Where ellipses could be fit to the positions of the eight stimuli of a particular saturation, they are shown in white. Mean color difference ratios (averaged across three fitted ellipses) are given below each panel. The order (left to right) of subjects within each group is the same as in Figure 3.

Most subjects produced two-dimensional solutions that resembled the MacLeod-Boynton chromaticity diagram. Mean color-difference ratios for individual subjects were extracted from the three ellipses fit to the eight data points for each saturation. These ranged from 0.93 to 1.10 for normals, from 0.47 to 1.26 for deuteranomals, and from 0.76 to 0.97 for protanomals. Although particular anomalous subjects have smaller color-difference ratios than normals (lowering the mean color-difference ratio for group average data), other anomalous subjects have color-difference ratios that are within the normal range.

Association with settings on anomaloscope

We correlated color-difference ratios calculated from two-dimensional MDS solutions for individual subjects with mean match and matching range from the anomaloscope. Correlations were nonsignificant for deuteranomals (ρ = 0.43, p = 0.25 for mean match; ρ = 0.42, p = 0.27 for matching range) but in the expected direction (smaller color-difference ratios were associated with larger matching ranges and more extreme mean matches). For protanomals, the correlation between mean match and color-difference ratio was ρ = 1, but this was nonsignificant (p = 0.08) owing to our small sample size (N = 4 because we were unable to fit ellipses to the data from one subject). The correlation between matching range and color-difference ratio for protanomals was ρ = 0.

Comparison between results of 4AFC and results of MDS

Figure 6 shows the mean sensitivity ratios of deuteranomals and protanomals as percentages of the mean ratio of normal trichromats in the 4AFC task and mean color-difference ratios as a percentage of normal for the MDS task.

Figure 6.

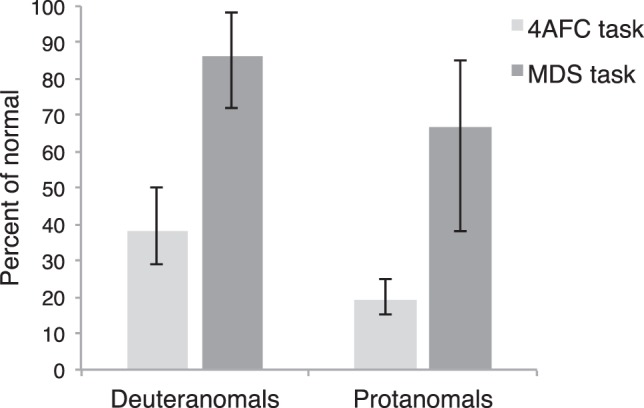
Percentage of normal mean sensitivity ratio for deuteranomals and protanomals in the 4AFC task (light gray bars) and percentage of normal mean color difference ratio for deuteranomals and protanomals in the MDS task (dark gray bars). Error bars are bootstrapped 95% CIs.

Protanomals tend to have worse red-green discrimination compared to deuteranomals overall, which likely results from the fact that protanomals, on average, have a higher degree of spectral overlap between their long wavelength–sensitive cones (Neitz & Neitz, 2011). Although our data do not show a significant difference between the thresholds of deuteranomals and protanomals, this is likely because of the low statistical power resulting from our small sample of protanomals. Our data reflect a lower mean sensitivity for protanomals than for deuteranomals and a larger factor of compression along the red-green axis of their MDS-reconstructed perceptual color space.

We used data from individual subjects to look for an association between performance at threshold and color appearance. We correlated sensitivity ratios calculated for individuals in the forced-choice discrimination task with the equivalent color-difference ratios extracted from individual two-dimensional MDS solutions. For deuteranomals, Spearman's ρ was 0.62. This was nonsignificant (p = 0.086), but we had limited power to detect a correlation of medium size due to our small sample of nine. The correlation of 0.62 was in the expected direction: Larger sensitivity ratios were associated with larger color-difference ratios.

Models

To what degree are our results at threshold and for color appearance expected given the spectral sensitivities of the anomalous trichromats' medium and long wavelength–sensitive cones? We constructed models of anomalous color spaces to compare the cone-opponent representations of our stimuli for deuteranomals, protanomals, and normals. Specifically, we constructed color stimulus spaces for anomalous trichromats equivalent to the MacLeod-Boynton space and then considered the relationship between those and (a) color discrimination thresholds for anomalous trichromats based on the results of normals and (b) the positions in perceptual color space of the 25 stimuli used in the MDS experiment.

To model each anomalous cone fundamental of a given peak sensitivity (λ), we first used Lamb's (1995) formula:

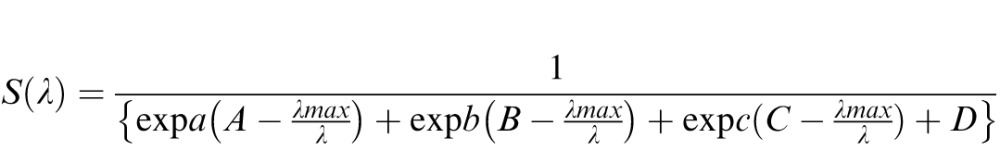where S(λ) is the simulated sensitivity as a function of wavelength, a = 70, b = 28.5, c = −14.1, A = 0.880, B = 0.924, and C = 1.104. We then accounted for self-screening (Brindley, 1953), assuming an optical density of 0.5. We accounted for macular pigment using data provided by Bone, Landrum, and Cains (1992) and for the lens using data provided by van Norren and Vos (1974).

Discrimination thresholds

We used simulated cone fundamentals to model discrimination thresholds for deuteranomals and protanomals. We first created a model for normal observers, inserting into the Lamb equation peak sensitivities of 426.3 nm, 529.7 nm, and 556.7 nm. These are the peak sensitivities of the normal opsins in an in vitro suspension (for the L-cones with serine at site 180) (Merbs & Nathans, 1992a). We transformed the coordinates of the stimuli at the mean normal threshold from our scaled MacLeod-Boynton space to an equivalent space based on the modeled cone fundamentals. The transformation was achieved by modeling cone responses to reconstructed spectra of the stimuli at threshold. The spectra of the red, green, and blue primaries were available, having been measured with a PR650 spectroradiometer as part of the color calibration of the monitor. Similarly, we transformed the coordinates of stimuli at the mean threshold for normals into color spaces simulated for deuteranomals and protanomals with spectral separations of the medium and long wavelength–sensitive photopigments ranging from 1 nm to 20 nm.

We assumed that the thresholds of deuteranomals and protanomals are reciprocally related to the difference in cone chromaticity between the red and green primaries for the observer in question.

That difference is (L_red − L_green)/(L + M) or r_red − r_green (using the original notation of MacLeod and Boynton, 1979); here the cone excitations L and M are the ones computed for the individual observer (in our case, the ones derived as described above). The rationale for this relationship between cone chromaticity and threshold is as follows: Let p be the proportion of red in a stimulus, and 1 − p the proportion of green, each in units of luminance so that the combined luminance from both primaries, L + M, is constant as p varies. Then the cone chromaticity corresponding to r is (p × L_red + (1 − p) × L_green)/(L + M) for each observer (putting in primes as needed for the anomalous observers). This changes linearly with p between the values for the two primaries as p goes from 0 to 1. Accordingly, the gradient of cone chromaticity as p changes is dr/dp = (L_red − L_green)/(L + M) or r_red − r_green; the L and M cone contrasts for all isoluminant mixtures of red and green phosphors are multiplied by this observer-dependent scaling factor. If threshold requires a criterion change in cone chromaticity or cone excitation (as expected if postreceptoral connectivities are the same for all observers), the necessary change in p will be inversely related to dr/dp or r_red − r_green. The factor by which these primary chromaticity differences go down is the factor by which the threshold is expected to go up. The threshold may be expressed directly as a difference in the proportion of the primaries or equivalently as a difference in the standard observer's cone chromaticity because these two vary together. In Figure 7a, we show how threshold computed on this basis changes with the separation between the medium- and long-wavelength sensitive photopigments. The predicted thresholds are based on the assumption that for detection, anomalous trichromats require a difference in L′/(L′ + L) or in M′/(M′ + M) as large as the difference in L/(L + M) required by the average normal. As expected, the theoretical thresholds of Figure 7a vary inversely with spectral separation; correspondingly, predicted chromatic sensitivity, the reciprocal of threshold, is proportional to spectral separation.

Figure 7.

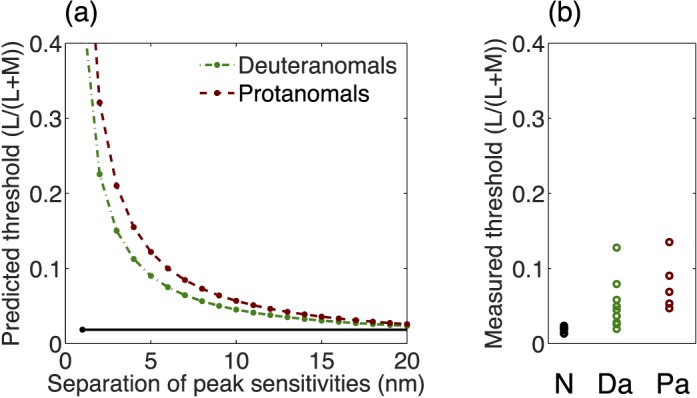
(a) Model of thresholds for deuteranomals and protanomals. This figure shows predicted thresholds for the two groups as a function of the separation of the peak spectral sensitivities of the medium and long wavelength–sensitive cones, assuming that anomalous trichromats require for detection the same ratio of medium to long wavelength–sensitive cone activation as normals. The measured mean normal threshold is shown for comparison in black. (b) Measured L/(L + M) thresholds for normals (N), deuteranomals (Da), and protanomals (Pa). These thresholds are averaged across increments and decrements.

Predicted thresholds can be compared with the ranges of measured thresholds shown in Figure 7b. Our threshold results are compatible with cone spectral separations in our anomalous subjects ranging upward from 4 nm. This is plausible because we excluded extreme anomalous trichromats, who may have the smallest cone spectral separations. However, we note that some anomalous trichromats with very small cone spectral separations have surprisingly good discrimination (Hurvich, 1972) perhaps because of variation between cone types in optical density (He & Shevell, 1995; Thomas, Formankiewicz, & Mollon, 2011). The model may overestimate thresholds for nearly dichromatic observers when the long-wave cone spectral separation is very small if their S cones can distinguish between the compared stimuli.

Multidimensional scaling

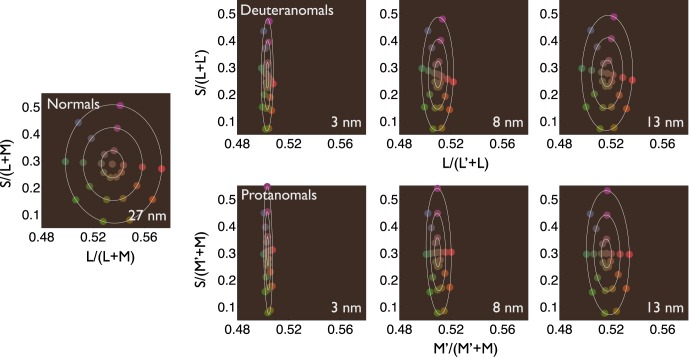
We also used our model of the cone fundamentals of anomalous trichromats to predict performance on the MDS task. We plotted the positions of the stimuli in a MacLeod-Boynton diagram for our simulated normal, with a 27-nm separation between the peak sensitivities of the L and M cones. We plotted the positions of the stimuli in equivalent spaces constructed for deuteranomals and protanomals having spectral separations between medium and long wavelength–sensitive cones of 3 nm, 8 nm (the separation between the DeMarco, Pokorny, & Smith [1992] anomalous cone fundamentals), and 13 nm. Results are shown in Figure 8 with the simulated cone spectral separations indicated in each panel.

Figure 8.

MacLeod-Boynton diagrams showing the positions of the MDS stimuli for simulated normal, deuteranomalous, and protanomalous observers. In each panel, the separation between the peak sensitivities of the simulated medium and long wavelength–sensitive cones is indicated in the lower right. Ellipses fit to each set of eight stimuli of a given saturation are shown in white.

These figures predict performance on the MDS task if anomalous trichromats require the same ratio of activation of the medium and long wavelength–sensitive cones as the normal for a given distance in perceptual color space. To calculate predicted color-difference ratios from the model, we transformed the modeled stimulus spaces for protanomals and deuteranomals using Procrustes analysis to align the modeled spaces with the MacLeod-Boynton chromaticity diagram (the same procedure as used for the MDS results). We fit ellipses to the points representing the three different stimulus saturations in the transformed spaces and took the ratio of the distance between x-intercepts to the distance between y-intercepts. Like the threshold sensitivities of Figure 7a, this ratio proved to be approximately proportional to the spectral separation of the long-wavelength cones, justifying the use of threshold ratios to predict MDS color-difference ratios. Yet, experimentally, the MDS color-difference ratios are much closer to normal than the threshold ratios: 86% of normal (deuteranomals) and 67% of normal (protanomals) for our measured group mean MDS results in contrast to the threshold ratios of 38% and 19% of normal, respectively.

Discussion

We have found that although anomalous trichromats have substantially reduced sensitivity for detecting differences between red and green stimuli at threshold, color appearance along a red-green dimension is relatively preserved. We quantified our results by taking ratios of performance along the two cardinal axes of MacLeod-Boynton chromaticity space. At threshold, sensitivity ratios compared sensitivity along the L/(L + M) axis to sensitivity along the S/(L + M) axis. For color appearance, we compared the perceived difference between stimuli along the L/(L + M) axis to the perceived difference between stimuli along the S/(L + M) axis from the MDS results. For deuteranomals and protanomals, sensitivity ratios were 38% of normal and 19% of normal, respectively. Color-difference ratios were 86% and 67% of normal (Figure 6).

An individual analysis revealed large individual differences as we might expect from the range of different opsins that different anomalous trichromats express. Sensitivity ratios ranged from 14% to 72% of the normal mean for deuteranomals and 12% to 25% of the normal mean for protanomals (Figure 3). For the MDS results, color-difference ratios ranged from 45% to 121% of the normal mean for deuteranomals and from 73% to 93% of the normal mean for protanomals although one subject (perhaps a misclassified protanope) produced a probably one-dimensional MDS solution, showing no differentiation in color appearance between red and green (Figure 5).

What could explain our results? Consider the minimal model of anomalous trichromacy, in which postreceptoral processing is the same as in normal trichromacy, and only the photopigment swap differentiates anomalous from normal observers. As noted in the Introduction, on this view, we might naively expect that the reduced sensitivity for red-green color differences will be expressed as a simple scaling of the red-green axis of subjective color space. Our model of the performance of anomalous trichromats with different cone sensitivities makes this assumption. The model accounts fairly well for anomalous trichromats' performance at threshold if our subjects have a 4-nm or greater separation between the peak sensitivities of their medium- and long-wavelength sensitive cones. The same model applied to MDS performance predicts color-difference ratios ranging from 13% to 54% of the normal mean for deuteranomals and from 8% to 43% of the normal mean for protanomals as the separation between the peak sensitivities of the medium and long wavelength–sensitive photopigments increases from 3 nm to 13 nm (Figure 8). These ranges hardly overlap with the results of our MDS experiment, in which individual color difference ratios for anomalous trichromats range from 45% to 121% of the normal mean.

A simple pigment swap can account for discrimination thresholds in anomalous trichromats but not color appearance. Our results are, however, compatible with an alternative hypothesis that postreceptoral signal amplification partially compensates for the impoverished red-green contrast occasioned by the pigment swap.

The theoretical picture developed thus far neglects a known complication. The function relating chromatic contrast sensitivity to chromatic contrast shows a compressive nonlinearity with reduced sensitivity for detecting chromatic differences at higher chromatic contrasts (Le Grand, 1949). If the neural signals evoked by the MDS stimuli in normals are severely compressed, while the reduced chromatic signal received from anomalous trichromats' medium- and long-wavelength sensitive cones makes them less subject to compression, this could help explain why anomalous subjects experience less attenuation of large color differences than expected on the simple pigment swap model. But the MDS results themselves provide evidence against such an interpretation. They do support the postulated compressive nonlinearity in a mild form: Figure 9 shows that successive increases in colorimetric saturation (Δ(L/(L + M))) lead to successively smaller increments in perceived (MDS-based) color difference for L/(L + M) chromatic contrasts. The figure shows the compressive nonlinearity for L/(L + M) increments, but functions were similar for all other axes tested. But importantly, both groups of anomalous trichromats show a compressive nonlinearity along the L/(L + M) axis to the same degree as normal. This is evidence against the idea that the relative expansion of the perceptual color spaces of anomalous trichromats that we find can be explained merely by an escape from suprathreshold nonlinearity. Rather, the results do require a postreceptoral amplification, operating prior to the compressive transformation, that makes the normal and anomalous postreceptoral representations of color quantitatively comparable and hence subject to comparable magnitudes of nonlinear compression.

Figure 9.

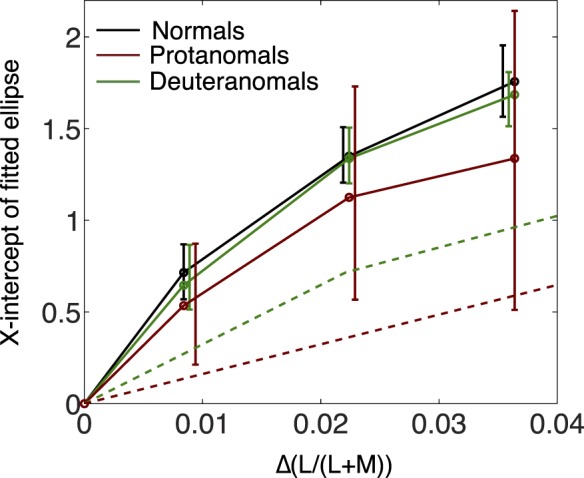
Nonlinearity of contrast response function for L/(L + M) increments. Data points connected by the solid lines represent the x-intercepts of the ellipses fitted to the MDS solutions for stimuli of the three different saturations. For all three groups, equal successive increments in colorimetric saturation (Δ(L/(L + M))) lead to successively smaller displacements in subjective color space as reflected in the MDS structure. Error bars are bootstrapped 95% CIs, drawn staggered in the figure for visibility. The large bootstrapped CIs for protanomals reflect the small sample size (N = 5). The dashed lines show predictions for deuteranomals and protanomals based on the sensitivity ratios measured at threshold without any postreceptoral compensation. If anomalous trichromats require the same difference in ratio of long- to middle-wave cone activities as normals to perceive a given color difference, this is equivalent to a horizontal scaling to the normal (solid black) curve, based on the factor of sensitivity reduction at threshold for each group.

Once compressive nonlinearity is incorporated into the theoretical picture, it becomes possible in principle to distinguish between postreceptoral compensation by sensitivity scaling (a postreceptoral boosting of chromatic sensitivity equivalent to a multiplication of the effective chromatic contrast) and compensation by response scaling (a perceptual boosting of perceived color differences). In the absence of any compensation of either type, the curves of Figure 9 would be horizontally scaled in proportion to the threshold whether the relationship between MDS distance and colorimetric saturation is linear or not. This prediction is shown by the dashed curves in Figure 9, in which the normal stimulus contrasts that define the horizontal coordinates for each experimental stimulus have been scaled up enough to compensate for the reduced anomalous cone contrast. At any vertical coordinate in Figure 9, the rightward-displaced dashed curves define what might be considered an interobserver metameric match between anomalous and normal observers: When the higher chromatic saturation is delivered to the anomalous retina, the cones respond as the normal cones do to the lower saturation shown on the continuous black curve. If the anomalous and normal nervous systems differ only by the pigment swap, the match between their photoreceptor excitations would not be upset by later processing, and the horizontally displaced pairs of stimuli would elicit identical judgments when presented to the respective observers.

If we assume nonlinear compression to a common maximum for all curves, the “zero compensation” model still predicts curves for the anomalous observers that differ radically from those of normals, being horizontally stretched by factors of roughly 2.5 for deutans and five for protans, so that the anomalous observers never approach the common asymptote; this contrasts sharply with the experimental similarity of MDS results for normal and anomalous groups.

Even for normal observers, though, the relationship between MDS distance and chromaticity difference in Figure 9 deviates only mildly from linearity. Consequently, the data cannot distinguish decisively between the sensitivity-scaling and response-scaling types of postreceptoral compensation. A compensatory postreceptoral boosting of chromatic sensitivity—a horizontal scaling in Figure 9—could (by definition) compensate precisely for loss of chromatic contrast at the photoreceptors, producing superimposed curves in Figure 9. A perceptual response scaling equivalent to a scaling of MDS distances (a vertical scaling in Figure 9) would have a broadly similar effect, appropriate to compensate approximately—although not in this case precisely—for the horizontal scaling introduced at the photoreceptors. Thus, either compensatory sensitivity scaling or compensatory response scaling can provide a defensible model for the nearly normal MDS behavior of the anomalous subjects, but a model without any compensation fails to account for that result even when the observed nonlinearity is taken into account.

Admittedly, the judgments of similarity that underlie the MDS results are subject to many influences besides the low-level neural amplification that we have invoked to explain them. Indeed, one example of a response scaling would be that anomalous trichromats calibrate themselves to the linguistic descriptions of differences between reds and greens that they find the normal majority making. Although it may be impossible to rule out such a “cognitive compensation” mechanism, we think it is unlikely. Observers were asked to rate the dissimilarity between each pair of colors in the MDS task relative to the maximum color differences in the stimulus set. To encourage this strategy, they were shown the entire stimulus set before the experiment began and asked to identify the largest and smallest differences. For anomalous trichromats, the S-cone opponent color dimension is preserved, so we would expect them to judge L/(L + M) color differences (which might be diminished) relative to S/(L + M) color differences (which should be normal). To explain our results, any cognitive expansion must be selectively applied to the L/(L + M) axis of color space. Such a selective amplification seems implausible, particularly because the cardinal axes that must be selectively spared or amplified on this hypothesis are not easily subjectively separated or identified.

On the other hand, one might consider the possibility that a compensatory amplification is made at the very first stage of visual processing at the photoreceptors themselves. But such an increase would seem maladaptive in relation to luminance processing, and if applied only to the L and M cones would change the balance of S and L cone inputs to the redness of violets and to a skewing of the unique blue locus that is not observed. Moreover, to explain the rough agreement between the anomalous observers' losses of chromatic sensitivity and expectations based on pigment spectral overlap, the random noise that generates errors in our forced-choice discrimination task must be injected prior to the compensatory gain adjustment that we postulate, implying that the gain adjustment is downstream from the predominant sources of noise.

Conclusions

Without postreceptoral amplification, we would expect that the factor of reduction (compared to normals) in the sensitivity ratios of anomalous trichromats at threshold would equal the factor of reduction in their color difference ratios extracted from the MDS solutions. However, we find that the factor of reduction in color-difference ratios is much smaller than the factor of reduction in sensitivity ratios (see Figure 6). Thus, our results are in support of an alternative model in which adaptive nonlinear processing magnifies postreceptorally the impoverished cone signals to compensate for the greater spectral overlap of the anomalous photopigments.

The MDS color space of anomalous trichromats is not as compressed along the red-green axis as might be expected from their poor discrimination thresholds, suggesting that reddish and greenish colors lose little of their normal vividness in anomalous trichromacy. The adaptive postreceptoral gain that we invoke to explain our results has been introduced into simulations of anomalous color vision by Webster, Juricevic, et al. (2010). Their simulations provide visual confirmation that postreceptoral gain can almost normalize color appearance for deuteranomals and protanomals (see Webster et al., 2010, figures 3 and 4).

In conclusion, our results indicate that although red-green color appearance in anomalous trichromats is not the same as that of normals, it is recovered to large degree.