On the Mechanics of Fatigue and Fracture in Teeth

Short abstract

Tooth fracture is a major concern in the field of restorative dentistry. However, knowledge of the causes for tooth fracture has developed from contributions that are largely based within the field of mechanics. The present manuscript presents a technical review of advances in understanding the fracture of teeth and the fatigue and fracture behavior of their hard tissues (i.e., dentin and enamel). The importance of evaluating the fracture resistance of these materials, and the role of applied mechanics in developing this knowledge will be reviewed. In addition, the complex microstructures of tooth tissues, their roles in resisting tooth fracture, and the importance of hydration and aging on the fracture resistance of tooth tissues will be discussed. Studies in this area are essential for increasing the success of current treatments in dentistry, as well as in facilitating the development of novel bio-inspired restorative materials for the future.

1. Introduction

From a mechanical perspective, teeth are very resilient structures. They have been designed to withstand the loads of mastication, reaching values of 700 N and greater [1–3], and over lifetimes that involve tens of millions of cycles [4]. Although they are able to withstand the demands of most oral activities, tooth failure is not uncommon, and thus, is a major concern in the field of restorative dentistry. While dental caries are the primary cause of “failure” overall, tooth fracture resulting from mechanical forms of degradation, or potential synergism between participating chemical and mechanical modes, is among the top three contributors [5–8]. The mechanics behind these failures and the relevance of fatigue and fracture to the incidence of these failures is the primary topic of this review.

In the discussion of teeth as a mechanical structure, it is important to provide details regarding the materials and their roles. Each tooth is comprised of multiple hard tissues including enamel, dentin, and cementum as shown in Fig. 1(a). Enamel is the most highly calcified tissue in the body (roughly 90% apatite mineral by volume), and serves as a stiff and wear-resistant outermost layer occupying the tooth crown. The underlying tissue is dentin, one of much lower mineral content (roughly 50% by volume) and is connected to enamel by the dentin-enamel junction (DEJ). That interface is highly complex and is perhaps worthy of its own review [9]. Dentin occupies the major part of tooth by both weight and volume. It serves as the elastic foundation for enamel and as a protective enclosure for the dental pulp, the innermost tissue. The pulp is a living (vital) soft tissue, which contains nerves, blood vessels, and other organic constituents. Located beneath the anatomic tooth crown, the root also consists primarily of dentin and is covered by a thin layer of cementum, which provides connection between the tooth and jaw bone via the periodontal ligament [10]. Details regarding the microstructure of dentin and enamel, as well as the importance to their mechanical behavior will be discussed later in this review.

Fig. 1.

Tooth anatomy. (a) Schematic of human tooth. (reprinted from Ref. [10] with permission from the publisher) (b) micrograph of the dentin's microstructure. T, IT, and PT represent tubule, intertubular, and peritubular dentin, respectively, (c) micrograph of enamel microstructure.

In discussing the mechanical forms of tooth failure it is important to address whether the tooth is intact (i.e., without evidence of prior dental work) or the tooth has been restored (i.e., having received treatment to repair the tooth and its integrity). Teeth that have undergone attack by oral bacteria (i.e., dental caries) will require that the affected dentin and enamel are excavated and that a dental material is placed within the cavity that restores the tooth's overall form and function. This process is the staple of restorative dentistry and has served the profession since its inception in the 18th century [11]. The nature of damage and propensity for bulk fracture of the tooth are different for unrestored and restored teeth. For example, unrestored teeth often exhibit cracks on the surface (Fig. 2(a)). These cracks propagate about the tooth's surface depending on various parameters such as the amount and condition of contact loading, tooth morphology, the microstructure of subunits of the teeth, etc. [12,13]. Nevertheless, cracks located in unrestored teeth generally do not cause bulk fracture or require extraction. That does not diminish the importance of this form of structural degradation. Understanding what causes the initiation of cracks and the mechanisms responsible for crack arrest is relevant to development of new dental materials that are inspired by the biological systems they replace.

Fig. 2.

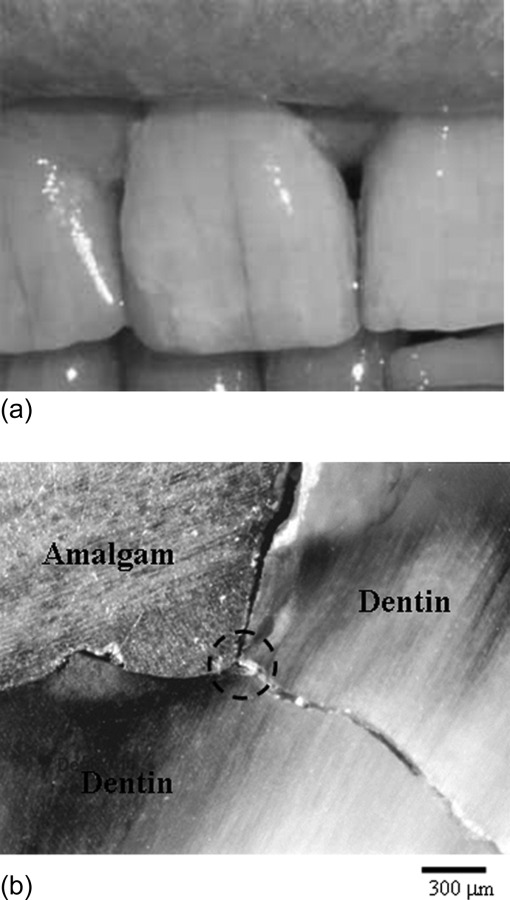
Cracks in human teeth. (a) Cracks in unrestored anterior teeth, (b) crack development in tooth restored with amalgam restoration. The crack initiated at the interface of the restoration and tooth structure in the region where there is a large stress concentration (the encircled area). Note that the crack extension is perpendicular to the tubule orientation in dentin.

Restored teeth generally undergo failure due to cracks that cannot be seen. These cracks develop within the dentin, at the interface between the restoration and surrounding hard tissue as shown in Fig. 2(b). The failure of restored teeth due to cracks of this type is a major obstacle to the success of restorative dentistry [14–19], and has been termed the “cracked tooth syndrome” [20]. Mechanical failures of restored teeth are likely to result from large stresses and/or fatigue, a cumulative process of damage development and its propagation. The importance of cavity size and design [21,22], the amount of damage introduced to the tissue by excavations e.g., Refs. [23–26] and the type of restoration e.g., Refs. [27,28] are some of factors which have been studied over the past decades. Failures also occur within the restorative materials. Failure of the restoration generally involves sub-critical fracture (i.e., chipping and indentation fractures) and degradation of the restorative margins [5,6,29]. These failures are equally important as they most often result in secondary caries within the adjacent dental hard tissues. This topic is beyond the scope of the present review. For those interested in this topic, a review of recent advancements in restorative materials with a more detailed description of mechanical performance and future enhancements was recently presented by Ferracane [8].

More recently a number of investigations have been conducted to understand the mechanics of tooth failure, as well as to determine the importance of fatigue and fracture mechanics in the failure process. Results from these studies are providing a greater understanding of the tooth as a mechanical structure, as well as the fatigue and fracture resistance of dentin and enamel. They are also distinguishing important physiological factors that render the tooth more susceptible to failure.

The overall objective of this review is to present the work in this area, with an emphasis on the importance of applied mechanics to the development of knowledge. The manuscript is organized in the following manner. Section 2 describes the work that has been performed to assess the fracture resistance of the tooth as a structure. As studies performed to evaluate the fracture behavior of tooth tissues have largely required nonstandardized approaches, Sec. 3 presents the developed methods and their application. Section 4 reviews studies performed to determine the fracture behavior of dentin and enamel, and that is followed by a description of studies evaluating the fatigue crack growth resistance in Sec. 5. The influence of important oral conditions and physiological factors on the fatigue and fracture resistance is discussed in Sec. 6. Lastly, Sec. 7 offers a summary, and addresses challenges and future work that is needed in this area.

2. On the Fracture Resistance of Teeth

Contact between teeth and food particles, or simply with opposing teeth, can cause damage at the tooth's surface and result in degradation of tooth functionality. Cumulative microscale contact with hard small food particles and under low contact forces can cause wear on the tooth's surface. Yet, macroscale contacts involving teeth and larger food particles and under higher load ranges (100–1000 N) can cause damages in the form of cracks [30]. By virtue of its high mineral content, tooth enamel is a brittle material. As such, some of the aforementioned mechanical forms of damage that are observed in teeth may be expected. Nevertheless, despite the development of cracks on the surface of teeth as a result of function, these cracks seldom result in bulk fracture of the tooth. That raises questions such as: “What prevents tooth fracture from originating from the visible external cracks in enamel?” or “How does the tooth geometry and enamel thickness contribute to the tooth's ability to maintain its integrity over the range of oral functions?”. Those and similar questions have stimulated research in this area.

The capacity for teeth to withstand the loads of mastication without causing tooth fracture is of substantial interest in the field of dentistry and to biological evolution e.g., Refs. [30–33]. Hertzian mechanics has been used to evaluate the nature of contact that takes place between teeth and/or restorative materials used for tooth replacement for some time [34]. Hertzian mechanics can offer new insights into the load-bearing capacity of teeth, their “strength” and the modes of failure. Robust empirical models have been developed to predict the critical loads for the initiation of cracks, and for tooth failure, as a function of characteristic tooth dimensions such as tooth base radius, enamel thickness, and material toughness. Details of the models can be found in Lawn and Lee [35]. Research in this area has distinguished that the initiation of damage begins in enamel and is distributed within a greater part of the volume with increasing load. Most of the cracks are limited to the enamel layer and do not influence tooth functionality. Only at high load ranges does fracture of the entire tooth occur (by either tooth chipping or splitting).

In general, two modes of cracking have been observed to develop in teeth under contact loading, including longitudinal cracks and margin cracks. Longitudinal cracks can also be sub-categorized as radial cracks and median cracks as described in Figs. 3(a) and 3(b). Radial cracks initiate from pre-existing flaws at the base of the enamel and extend upward to the occlusal surface. Median cracks start from shear-nucleated flaws within the quasi-plastic yield zone directly beneath the contact load at the occlusal surface, and then extend downward through the enamel thickness. Margin cracks initiate from intrinsic defects (i.e., the protein-rich tufts) at the DEJ and propagate to the occlusal surface of the teeth. Further loading causes other modes of failure such as chipping, cone cracking outside the contact zone, as well as delamination failure at the DEJ or progression into dentin [12,33].

Fig. 3.

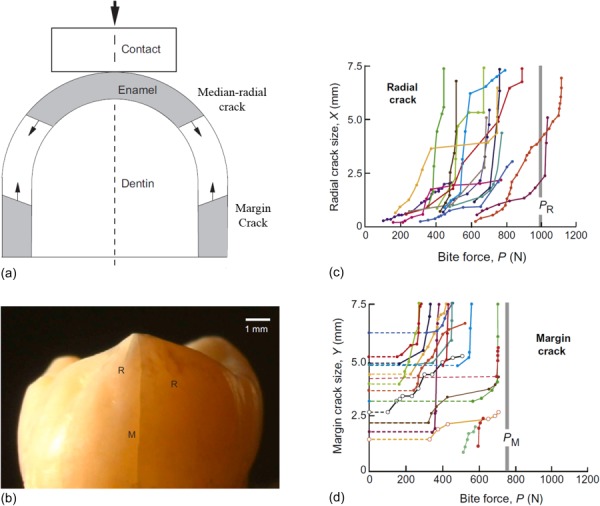
Contact loading failures in human molar teeth. (a) Schematic of various cracks types on tooth surface, (b) crack formation on a human molar due to contact with a flat indenter on the top of the cusp (reprinted from Ref. [38] with permission from the publisher). M and R in the figure stand for margin and radial cracks, respectively (reprinted from Ref. [95] with permission from the publisher). (c) Measured radial crack size as a function of indentation load (reprinted from Ref. [37] with permission from the publisher), (d) measured margin crack size as a function of indentation load (reprinted from Ref. [37] with permission from the publisher). P_R and P_M are the estimated critical loads from developed contact models.

The influence of various dietary-related parameters and tooth geometry on the failure modes of teeth has been examined. The nature of tooth failures is associated with the dietary habits and food characteristics such as the food particles size and their mechanical properties. Mastication involving small, hard objects is likely to induce local deformation at the occlusal surface, which causes generation of radial cracks, whereas large, soft food particles are less likely to cause cracking [35]. Tooth size and morphology are other important factors in the evaluation of critical failure load. A comparison of failure loads in a study of different primate teeth showed that the general mechanical properties (elastic modulus and hardness) of primates' enamel are not significantly different and that the critical failure loads are only a function of teeth morphology and enamel thickness [36].

Differences in the failure modes that develop in teeth of different mammals and the importance of tooth geometry have also been studied. During the generation of biting forces a hoop stress concentration develops at the cervical base of the tooth and creates margin cracks [35]. Based on the work of Chai et al. [13], margin cracks are more likely to initiate in smaller teeth sizes with large enamel thickness in contact with soft objects. This crack type is predominant in teeth, but very stable, as the path length is very large—it extends from the margins to propagate about the occlusal surface. A map of radial crack sizes in teeth as a function of bite force is shown in Fig. 3(c). The minimum contact load required to initiate the growth of dormant margin cracks using a flat hard indenter in human molars is about 200 N; the cracks initiate from the cervical base and traverse roughly 8 mm toward the occlusal surface [37]. The critical load required for the cracks to grow from the cervical margin to the occlusal surface ranged from 400 to 600 N (Fig. 3(d)) [37]. Similar evaluations for longitudinal cracks, including radial, and median cracks, showed higher loads ranges as shown in Fig. 3(c). Considerable scatter is generally observed in experimental results involving contact induced fracture of teeth and is attributed to variations in the tooth dimensions, contact area (cuspal radius of curvature), and the enamel microstructure among the teeth evaluated.

In more recent studies, efforts have been focused on validating experimental results obtained for cracking of the enamel encasement using finite element analyses [37–39]. Simulations involving different sizes of teeth and enamel thickness have been performed to estimate the loads required to develop and propagate cracks in teeth. Assuming that enamel exhibits both homogenous and isotropic fracture toughness, simulations showed that margin cracks grow under lower load ranges when compared to radial cracks under the same starting crack size [37]. The authors also discussed the role of the “starter defect” for crack initiation and conveyed that while the initial defect size was not considered in their models for the tooth failure predictions, a minimum defect size is necessary for stable crack extension. Although the minimum defect size required for crack extension requires further assessment, it is believed that enamel microstructure is definitely the source for the “starter defect.”

Chai et al. [40] described the enamel “tufts” as intrinsic defects within the microstructure that serve as the starting point for the development of radial and margin cracks in teeth. These natural cracks, which can be found in the enamel, extend from the DEJ toward the occlusal surface over tens of micrometers and at the interface of the rods [41]. Not all cracks that initiate at the DEJ undergo progression to reach the occlusal surface; some are arrested along their path through the enamel thickness. Section 4.1 provides an explanation of why the progression of some cracks in enamel are arrested, and the importance of this observation.

3. Methods of Evaluating Fatigue and Fracture in Tooth Tissues

Characterizing the durability of the tooth with regards to the forces of mastication requires an understanding of the mechanical behavior of the individual tissues. Indeed, evaluations on the fatigue and fracture properties of dentin and enamel are an important requisite to the study of tooth fractures. While simple in concept, these investigations involve many complications, much of which is due to the relatively limited volume of human dental tissues that enable such evaluations. Animal teeth (e.g., bovine or ovine) are occasionally adopted as a substitute for human teeth in an attempt to obtain larger sample volumes, but that raises questions regarding the consistency in microstructure between the teeth of humans and other mammals, and the corresponding validity of the results. Even in the adoption of substitutes for human tissue, the maintenance of mineral content and hydration of the tissue are important concerns.

Miniaturized specimens have often been considered as an alternative to using standardized approaches for measuring the fracture properties of biomaterials. There are several methods developed to estimate the fracture properties of dental materials and tissues of the tooth. Pilliar et al., [42–44] adopted a short rod specimen for determining the fracture toughness of dental materials and later used this approach to evaluate the fracture toughness of bonded interfaces [45]. Wang et al., [46] developed a compact sandwich specimen for evaluating the fracture toughness of bone and prosthetic materials, which has been adopted for evaluating the fracture properties of dental materials as well e.g., Refs. [47–49]. Furthermore, Ruse et al. [50] developed a novel notchless triangular prism (NTP) specimen for evaluating the fracture toughness of dental materials, adhesive interfaces and hard tissues [51–53]. Flexural loading of beams has been employed to measure the fracture toughness of natural materials such as nacre e.g., Refs. [54,55] and bone e.g., Refs. [56–58] and has also been used for evaluating the fatigue and fracture properties of dentin and enamel e.g., Refs. [59–62]. The compact tension configuration has been adopted for evaluating the fracture properties of hard tissues as well [63]. Nevertheless, constraints in tissue volume have limited this configuration to studies of dentin from the tooth crown e.g., Refs. [64–66]. A schematic description of the more common specimen configurations that have been adopted is presented in Fig. 4.

Fig. 4.

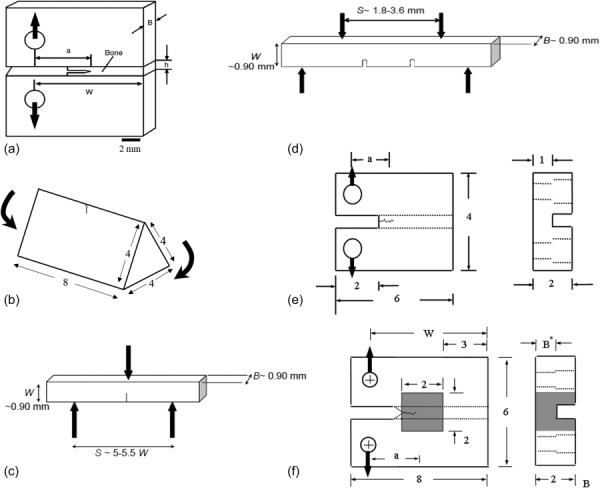
Schematic of various testing configurations used for dental materials. (a) Compact sandwich specimen (reprinted from Ref. [46] with permission from the publisher), (b) NTP specimen (reprinted from Ref. [50] with permission from the publisher), (c) three point bending specimen (reprinted from Ref. [61] with permission from the publisher), (d) four point bending specimen (reprinted from Ref. [61] with permission from the publisher), (e) miniature CT specimen (reprinted from Ref. [64] with permission from the publisher), (f) inset CT specimen (reprinted from Ref. [63] with permission from the publisher).

As the specimen size decreases, the specimen geometry can be more difficult to prepare precisely, which can reduce the level of confidence in the estimated properties. There are other concerns in the evaluation of the fatigue and fracture behavior of teeth. Many earlier evaluations suffered from the lack of a precrack in the samples, or alternatively achieved fracture from a notch rather than a well-defined crack. Variations in the initial flaw geometry have been identified to contribute to scatter in the responses and a greater potential for over-estimation of the fracture toughness [59]. Yet, advances in the methods of specimen preparation and testing over the last decade have largely overcome these issues and are resulting in a better understanding of the fracture resistance and fatigue properties of dental tissues.

One additional concern regarding evaluations on the fracture of these materials is the potential for inadvertent mixed-mode loading rather than pure Mode I. Three-point and four-point flexural configurations have been one of the most common formats for estimate the fatigue and fracture properties of dentin and enamel. However, unlike evaluations performed on ceramics and metals, crack propagation in biological materials often follows an oblique path in flexural configurations and causes a combination of Mode I and Mode II driving forces in these specimens. A recent study by Bechtle et al. [62] addressed the possible effects from mixed-mode conditions on the reported fracture toughness of dentin under the flexure configuration, and presented new geometric function solutions for kink cracks in bending specimens.

Regarding investigations of dental enamel, most of the early studies on the fracture resistance of this tissue were based on indentation methods rather than a traditional fracture mechanics approach involving crack extension e.g., Refs. [67–71]. Indentation techniques have become quite common for evaluating the apparent fracture toughness of brittle materials, ceramics in particular, as it is relatively easy and can be performed on a small volume of material. In addition, unlike the standard methods it does not require a precrack. Yet, there are significant concerns regarding the use of the indentation approach for estimating fracture toughness [72–74], especially in evaluations involving biomaterials or hard tissues [75]. One consideration is that there are over 30 different models for estimating the fracture toughness from indentation cracks [74,76], and many of these have been developed from curve fits to data rather than from physical models for fracture [74]. Even when comparing two highly brittle materials of nearly identical composition, the indentation fracture test has been shown to give highly misleading results when compared to other methods [77]. Some consider indentation techniques unsuitable for quantifying the fracture toughness of materials [74,75]. Thus, while the indentation approach can be used to achieve a relative comparison between the fracture behavior of selected materials, there are strong arguments that it should not be used in characterizing the fracture toughness of both engineering materials and hard tissues.

The aforementioned techniques for evaluating the crack growth resistance of dental materials utilize a specimen with major dimension of l ≥ 4 mm. That value is quite large for application to the dentin and enamel of teeth. Zhang et al. [63] proposed a miniature “inset” CT specimen (Fig. 4(f)) for evaluating the crack growth resistance of dentin and enamel, or for materials where the available material volume is a strict constraint. This specimen utilizes a small piece of tissue, with major dimension of 2 mm. In this configuration, the material of interest is embedded (or molded) within another. For hard tissues, the molding material is generally a resin composite that is used in dentistry for placing direct restorations. The inset CT specimen presently requires the smallest volume of material that has been reported for evaluating fracture behavior using a conventional crack growth approach. A recent investigation reported a generalized equation for the K_I in the inset CT specimen as function of crack length. The model considers a wide range of inset materials, with elastic modulus range from 10 GPa to 100 GPa [78]. The generalized equation describing the stress intensity distribution was also validated from an analysis of the fracture behavior for a commercial resin composite using both the inset CT specimen and the standard geometry defined by ASTM E399 [79]. Results obtained for the fracture toughness of the calibration material estimated using both specimen types were within 2%. As such, the inset CT specimen can serve as a viable approach for studying the fracture behavior of small volumes of structural materials.

4. Evaluations on the Fracture Resistance of Tooth Tissues

The fracture resistance of hard tissues of the tooth has been studied for decades and a relatively wide range in fracture properties has been reported for dentin and enamel. Some of this variation can be attributed to relevant factors including differences in the testing methods, variations in the microstructure, structural anisotropy, the potential influence of age, etc. [80]. Variations in the tensile properties of tooth tissues suggest that inherent flaws contribute to the failure of tooth tissues and that a damage mechanics approach is potentially warranted for evaluating failure of these materials [81]. This section focuses on experimental evaluations that have been performed to determine the fracture resistance of enamel and dentin, and addresses the importance of relevant contributing factors on the fracture properties of these tissues.

4.1. Fracture Properties of Enamel.

As cracks are commonly found within the enamel on the surface of teeth, and clinical evidence of tooth fracture is not uncommon, the fracture toughness of this tissue is highly relevant to the field of dentistry. Although classical brittle materials generally have a single-value of fracture toughness, some materials exhibit an increase in the fracture resistance with crack extension (i.e., rising R-curve behavior). Work with other material systems has shown that this behavior develops as a result of the microstructure, constitutive behavior and the contributing toughening mechanisms e.g., Refs. [56,82,83]. While the R-curve is not an intrinsic material property due to its dependence on crack size and specimen geometry [84], it can provide substantial information on the importance/effectiveness of a material's microstructure on resisting crack extension.

Enamel has been primarily regarded as a brittle material, which is largely attributed to its high mineral content and the frequent identification of cracks on the surface of teeth. Furthermore, several studies have credited the DEJ for arresting cracks on the occlusal surface of teeth and preventing them from continuing into the dentin [51,59,85–87]. As such, there has been comparatively little attention on the fracture properties of enamel, especially in comparison to that for bone and dentin. The difficulty in conducting such evaluations has served as an additional obstacle. Nevertheless, recent studies have shown that enamel has an interesting behavior and that it is an important contributor to the tooth's overall resistance to fracture [37,39,88–90].

A description of the fracture resistance of enamel requires a more detailed description of its microstructure. Enamel is the most highly mineralized tissue in the human body. The minerals largely exist as crystallites of carbonated hydroxyapatite and are in the form of nanoscale rods. They are systematically assembled together with an interfacial thin film of noncollagen proteins to form “keyhole” shaped rods, also referred to as the enamel prisms (Fig. 1(c)) [91]. The enamel rods extend from the DEJ to the occlusal surface of the tooth. At the occlusal surface the enamel exhibits an amorphous microstructure (i.e., without well-defined rods). There are variations in the microstructure through the thickness as well. In the “outer” enamel (close to the tooth's surface), the rods extend inwards in a nearly parallel arrangement from just beneath the occlusal surface. In the inner enamel (closest to the DEJ), the rods are assembled in sub-units and bands that deviate from one another. Each band of rods follows a sinusoidal path that results in a complex decussating structure, which is responsible for the “Hunter-Schreger bands” evident from visual inspections of the enamel. There are also spatial variations in the geometry of the individual rods. Specifically, the effective diameter decreases from roughly 8 μm at the tooth's surface to almost 4 μm at the DEJ [10,91]. Furthermore, at the nanolevel there is a variation in the orientation of the hydroxyapatite crystals. At the center of the rods (or prism head) the crystals are oriented parallel to the longitudinal axis of the tooth, while in the inter-rod region (about the prism tail) the crystals are more oblique to the rod axis [10,92]. It is believed that this small variation in crystal orientation has an important influence on the mechanical properties of enamel at both the micro and macro levels [93]. There are also spatial variations in the organic content. The protein content in enamel increases from the occlusal surface toward the DEJ where the natural defects “tufts” exist [94]. The tufts are believed to occur because of abrupt changes in the rod orientation that exist at the DEJ, and there is larger amount of protein content in this region [10]. It has been reasoned that enamel tufts serve to aid in resisting enamel failure by promoting stress shielding and increasing the compliance of the enamel structure e.g., Ref. [95].

The first evaluation on the fracture properties of enamel was reported by Rasmussen et al. [96] in terms of the work to fracture (W_f: defined as the work required to form a new surface of unit area) of dental beams loaded in flexure. The estimated W_f for enamel specimens was 13 J/m² and 200 J/m² for crack growth parallel and perpendicular to the rod direction, respectively, indicating a substantial degree of anisotropy [96]. Over the last three decades the fracture behavior of enamel has been primarily evaluated using the indentation approach. According to the results of these studies, the average indentation fracture resistance (or apparent toughness) ranges between roughly 0.5 and 1 MPa·m^0.5 [67,71,97–99].

Due to limitations of the indentation fracture approach, Bajaj and Arola [88,89] evaluated the crack growth resistance of human enamel using a conventional fracture mechanics approach employing the enamel inset CT specimen (Fig. 4(f)) after Zhang et al., [63]. A representative R-curve obtained for crack extension from the occlusal surface toward the DEJ is shown in Fig. 5(a). As evident in this figure, the fracture resistance curves shows that human enamel exhibits rising R-curve behavior, with increase in crack growth resistance over nearly the entire thickness of the enamel layer. For cracks growing from the occlusal surface toward the DEJ, the average initiation toughness (K_o) was 0.55 ± 0.06 MPa·m^0.5, which is in the range of estimated values from indentation technique. However, there is a substantial rise in the crack growth resistance of enamel with extension (beyond a factor of 3), with the fracture toughness (at plateau; Kc) reaching an average of over 2 MPa·m^0.5. As evident in Fig. 5(a), the largest extent of toughening occurs after 1 mm of crack growth, which results from the crack entering the region of decussated enamel.

Fig. 5.

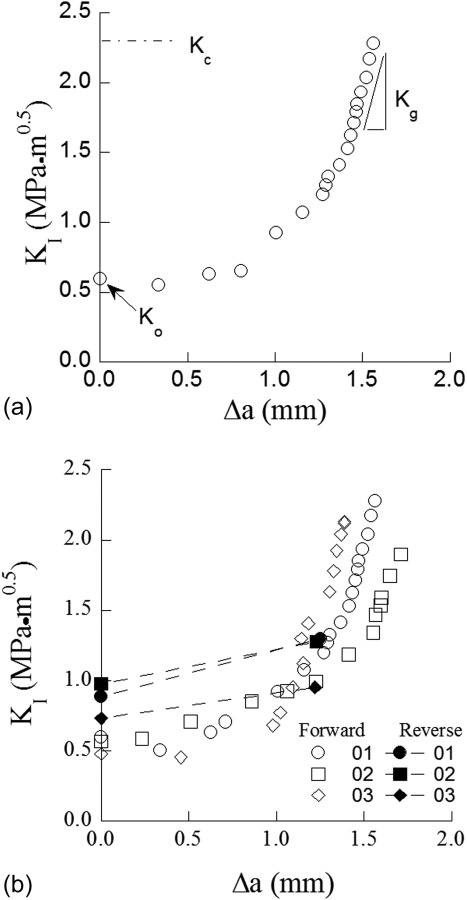
R-curve response of human enamel. (a) Typical R-curve response of enamel for cracks growing from occlusal surface toward the DEJ (reprinted from Ref. [88] with permission from the publisher), (b) comparison of R-curve response of enamel for forward and reverse crack growth directions (reprinted from Ref. [88] with permission from the publisher).

A comparison of the crack growth resistance has been performed for cracks extending from the occlusal surface inward toward to the DEJ (regarded as the forward direction) and in the opposite direction from the DEJ to the occlusal surface (regarded as the reverse direction). Representative crack growth responses in the forward and reverse directions are shown in Fig. 5(b) [89]. The fracture resistance curves revealed that enamel exhibits an increase in the crack growth resistance in both directions, but there are unique aspects to the responses. Those cracks growing from the DEJ toward the occlusal surface (reverse direction) are clearly less stable with respect to those in the forward direction. In the reverse direction, the average initiation toughness (K_o) was 0.87 ± 0.13 MPa·m^0.5, and there is only a mild rise in the crack growth resistance with extension; the reported fracture toughness (K_c) for this direction was 1.17 ± 0.13 MPa·m^0.5 [89]. The larger growth toughness for the forward direction suggests that the microstructure of enamel has been designed through the course of evolution to resist cracks that initiate at the occlusal surface.

Cracks that initiate at the tooth's surface may extend toward the DEJ (i.e., longitudinally along the rods) or about the occlusal surface (i.e., in-plane with the rods but transverse to their axis). Comparisons of the crack growth resistance in these two directions have been performed to understand the orientation dependence. Bechtle et al. [62,90] prepared flexure specimens from bovine incisors and subjected them to three-point loading to achieve Mode I growth. The reported initiation toughness in the longitudinal direction ranged from 0.8 to 1.5 MPa·m^0.5 and increased up to 3.0 MPa·m^0.5. For cracks with transverse orientation, the initiation toughness was equivalent to that in the longitudinal direction, but an increase in toughness of up to 4.4 MPa·m^0.5 was documented over only 0.5 mm crack extension [90]. A similar evaluation was performed by Yahyazadehfar et al. [100] on sections of occlusal enamel obtained from human molars. That study concentrated on the role of the microstructure and rod orientation to the fracture resistance of enamel. Similar to the finding reported for bovine enamel, the initiation toughness of enamel was not dependent on the orientation of crack growth. However, in evaluations on the human enamel there was relatively little difference observed in the R-curves obtained for crack growth in the longitudinal and transverse directions (Fig. 6(a)). Nevertheless, there was evidence that there was an important contribution of the microstructure to the fracture behavior. Consequently, a new concept was introduced for describing the enamel microstructure termed “the degree of decussation (D)” (Fig. 6(b)), which is simply the ratio of fracture area composed of decussated enamel to the total fracture surface area. According to this definition the samples comprised mostly of uniformly oriented parallel rods (prisms) and low value of D (comprised mostly outer enamel), exhibited the lowest toughness. The largest extent of toughening was observed in samples of inner enamel resulting from contributions of the decussation.

Fig. 6.

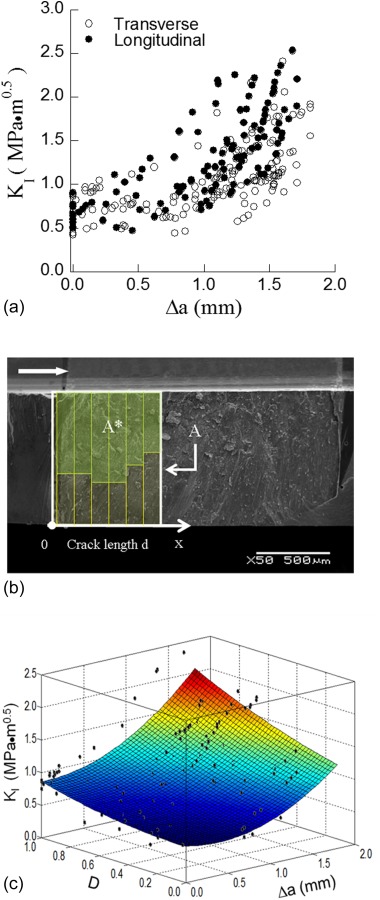
The influence of prism decussation on the crack growth resistance of human enamel. (a) A comparison of crack growth resistance of enamel in the transverse and longitudinal directions (reprinted from Ref. [100] with permission from the publisher. (b) characterization of the degree of decussation of enamel from fracture surface (reprinted from Ref. [100] with permission from the publisher). The arrow is indicative of crack growth in the specimen. (c) Crack growth resistance of enamel in the transverse direction as a function of degree of decussation (D) (reprinted from Ref. [100] with permission from the publisher).

Characteristics of the fracture resistance curves for enamel in Figs. 5 and 6 are reflective of the toughening mechanisms participating in the fracture process. The most common toughening mechanisms observed contributing to crack growth resistance in enamel include ligament bridging, crack deflection and microcracking (loosening of prisms) [88,90,101]. These mechanisms occur across length scales, from the nanoscale to the macroscale. Observation of the crack path in the transverse direction showed that the preferred crack path is along the rod boundary and the mechanisms associated with crack growth in the inner and outer enamel are slightly different. In the outer enamel crack branching and crack bifurcation are evident, which results in the formation of unbroken ligaments (Fig. 7(a)). Within the inner enamel the crack path appears more tortuous, and crack bridging serves a more dominant role as a result of the crack's interaction with the decussated microstructure (Fig. 7(b)) [100].

Fig. 7.

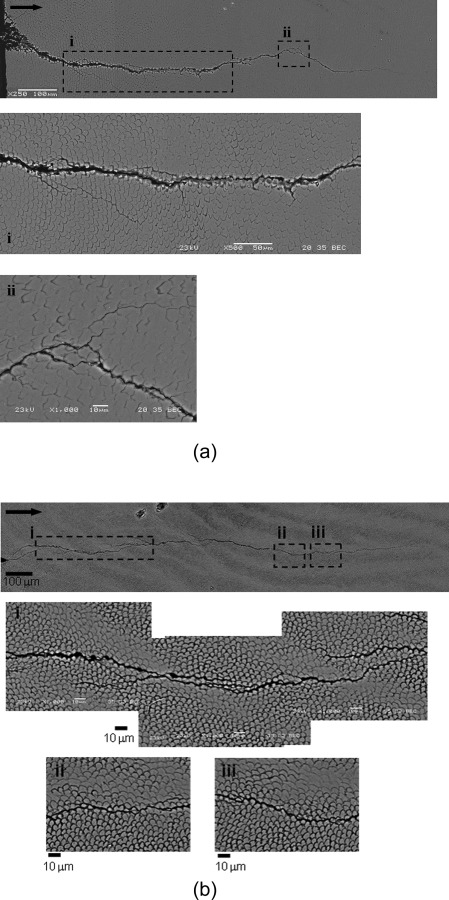
Crack path within human enamel resulting from incremental crack growth from the notch in the transverse direction. (a) Crack path in outer enamel (reprinted from Ref. [100] with permission from the publisher), (b) crack path in inner enamel (reprinted from Ref. [100] with permission from the publisher) . Note that the crack growth is from left to right.

The aforementioned investigations adopted linear elastic fracture mechanics for characterizing the fracture properties of enamel. However, the size of the process zone and inelastic contributions to the fracture process (presence of microcracks and bridging ligaments) substantiates the use of elastic-plastic fracture mechanics or development of a cohesive traction law for a more complete characterization. Some efforts have been made in this regard. Bajaj and Arola [88] estimated the contribution of selected mechanisms to the toughening of enamel based on theoretical models developed to characterize the toughening mechanisms in ceramics and natural materials (after the work of Evans and Faber [83], Evans and McMeeking [102], Shang and Ritchie [103], Sigl [104], Ji and Gao [105]). Unbroken ligament bridges were identified to have the largest contribution to toughening of enamel, with bridging stress intensity between 0.2 and 0.6 MPa·m^0.5, which is up to approximately 25% of the global toughness. The importance of protein bridging and microcracking were also assessed, with contributions of up to 0.1 MPa·m^0.5 and 0.5 MPa·m^0.5, respectively.

Ang et al. [101] estimated the “crack-tip” toughness of bovine enamel from an analysis of cracks induced by Vicker's indentations using a cohesive zone law. Their assessment adopted the cohesive zone solution of the Dugdale–Muskhelishvili crack model, which assumes that toughening is only based on bridging stresses behind the crack tip. In this model, the crack opening displacement (COD) for very short crack lengths (less than 10 μm) was correlated to the size of the cohesive zone and active bridging stresses, which were presumed constant through the cohesive zone. The estimated bridging stresses ranged from roughly 160 to 800 MPa over a cohesive zone length of 1 to 10 μm [101]. The small cohesive zone size and relatively large bridging stresses suggest that the participating bridging ligaments acting on the microcracks consisted of proteins, crystallites, and multiple rods. Overall, the aforementioned studies accounting for the fracture process zone in enamel provide greater insight, but they do not provide understanding of the isolated contributions of the various toughening mechanisms, or the effects of the spatial variations in microstructure. Future studies in this direction appear warranted.

Results of the studies by Yahyazadehfar et al. [100] showed that the growth toughness of human enamel is lowest in the transverse direction. The dissimilarity in crack growth resistance between the longitudinal and transverse directions serves to deflect cracks at the occlusal surface to propagate transversely about the tooth's crown. That process acts to restrict cracks to the outer enamel, thereby preventing progression toward the DEJ. This is an interesting process, and one that is only apparent from evaluating the fracture behavior through the crack growth characteristics. A finite element study by Barani et al. [38] simulated crack propagation in enamel on the tooth's surface considering both radial and margin cracks. The simulations, which included the R-curve response of enamel and through-thickness variation in elastic modulus, confirmed that cracks in enamel prefer to propagate at the surface and about the periphery of the tooth. Therefore, results of these two studies collectively establish that the tooth's resistance to fracture and penetration of cracks initiating at the occlusal surface comes from a combination of the microstructure of the enamel and the tooth geometry. The DEJ may still play an important role. When the driving force is large enough to exceed the mechanisms of toughening and the crack proceeds in the longitudinal direction from the occlusal surface, the DEJ will serve as the second defense in preventing bulk fracture [9,51,85,87,106]. It appears that the microstructure of enamel may possess many valuable secrets that are applicable to increasing the fracture resistance of engineering structures.

4.2. Fracture Properties of Dentin.

As cracks located at the tooth's surface are deflected by the microstructure of enamel and then arrested within the decussated zone or at the DEJ, they are not likely to cause tooth failure. Tooth fracture is more likely to originate from cracks that initiate and grow within the dentin. Flaws in the form of cracks can be introduced within the dentin during the restorative process as a result of material removal [25,26]. As an alternative, cracks may develop in dentin from incipient flaws as a result of fatigue, particularly in regions of stress concentration posed by the restoration geometry [21]. In recognition of the significance of fracture to the field of dentistry, many investigations have been conducted to characterize the fracture properties of dentin. Reviews on this topic have been presented earlier [107,108].

Similar to the discussion of fracture in enamel, a more detailed description of dentin's microstructure is warranted. Dentin possesses a much higher organic content than enamel with a composition of approximately 45% mineral, 33% organic material (collagen type I), and 22% water by volume [10]. The microstructure of dentin is illustrated in Fig. 1(b). The most distinct feature of the microstructure is the dentin tubules, which are a network of microscopic channels extending radially outward from the pulp toward the DEJ and cementum. The number, diameter, and orientation of the tubules vary with distance from the pulp. The tubule density and size of tubules are lowest at the DEJ and there is an increase in both of these parameters with increasing proximity to the pulp region [109]. Each tubule is surrounded by a highly mineralized cuff of apatite crystals known as the peritubular dentin. The intertubular dentin occupies the region between the tubules and comprised of mineralized collagen fibers, which are oriented in planes that are roughly perpendicularly to the tubules [80,110]. The mineralized collagen fibers are comprised of collagen fibrils with diameter of 50–100 nm. The fibrils are reinforced by apatite crystals, existing in plate form with roughly 5 nm thickness [111], and located in both interfibrillar and intrafibrillar sites.

The first reported evaluation on the fracture properties of dentin consisted of estimates of the work to fracture (W_f) for dentin beams under flexure loading [96]. The average W_f for fracture perpendicular and parallel to the tubules was 270 J/m² and 550 J/m² estimated, respectively [96,112]. The orientation dependence of W_f was attributed to the organization of the collagen fibrils surrounding the tubules. For crack growth perpendicular to the tubules the fracture surface was in the plane with the collagen fibril network, whereas in the parallel orientation the fracture plane was oriented perpendicular to the fibrils. But due to the lack of a well-defined crack, an estimate for the fracture toughness could not obtained. El Mowafy and Watts [113] obtained the first estimate for the plane strain fracture toughness (K _Ic) of human dentin using CT specimens. They reported an average value for K _Ic of 3.08 MPa·m^0.5 for crack growth parallel to the tubules; there is some concern with these results as the crack was started from a notch and not a precrack, which may have caused an overestimation [53,59].

One of the most important topics regarding the fracture properties of dentin has been the importance of tubule orientation [53,59,60,80,96,112,114]. Using the NTP specimen (Fig. 2(b)), Iwamoto and Ruse [53] confirmed that dentin exhibits direction-dependence in the resistance to fracture. For crack extension parallel and perpendicular to the tubules, the fracture toughness K _Ic was estimated to be approximately 2.0 MPa·m^0.5 and 1.1 MPa·m^0.5, respectively. Nalla et al. [60] also evaluated anisotropy in the fracture behavior of dentin from elephant tusks, which enabled the use of larger specimen sizes. Results were in agreement with those obtained for human dentin, with estimated fracture toughness being lowest for cracks growing perpendicular to the tubules (K_c ≈ 1.6 MPa·m^0.5) and with regards to the condition where cracks extension occurs parallel to the tubules (K_c ≈ 2.5 MPa·m^0.5) [60].

Due to the spatial variations in the microstructure of dentin in human teeth, the fracture resistance is potentially location dependent. Indeed, Wang [115] reported that the fracture toughness of root dentin (4.8 MPa·m^0.5) was substantially greater than that for tissue of the crown (2.1 MPa·m^0.5). They postulated that the differences in fracture resistance are related to properties of the collagen fibrils in coronal and radial dentin and the anisotropy in the tissue cause by the fibril orientation in the root [116].

In the previous studies a single value of crack growth resistance was reported. Yet, more recent studies on dentin have evaluated the fracture behavior in terms of the R-curves. Typical fracture resistance curves for human dentin obtained using the CT specimen configuration are shown in Fig. 8(a); representative responses are shown for crack growth in-plane and perpendicular to the tubules. As evident in this figure, human dentin exhibits rising R-curve behavior regardless of the tubule orientation. In both orientations the growth response develops a well-defined plateau after approximately 0.5 mm of crack extension, indicating that the fracture process has reached a steady-state.

Fig. 8.

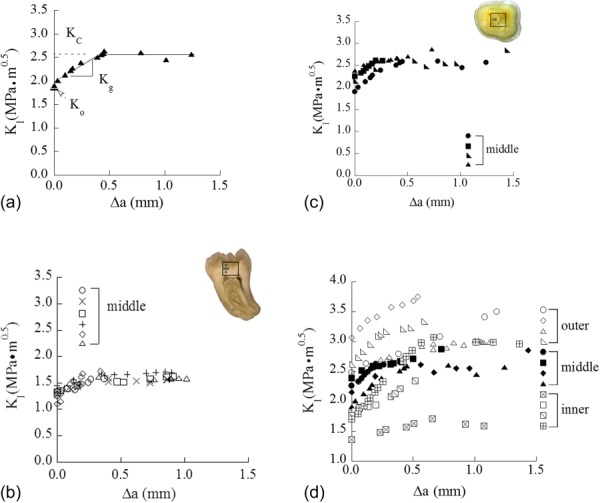
Crack growth response of human coronal dentin obtained from miniaturized CT specimen. (a) Typical R-curve response in dentin (reprinted from Ref. [66] with permission from the publisher), (b) R-curve response for the crack growing perpendicular to the tubules (90 deg orientation) (reprinted from Ref. [120] with permission from the publisher), (c) R-curve response for the crack growing parallel to the tubule plane (0 deg orientation) (reprinted from Ref. [66] with permission from the publisher). (d) A comparison of the crack growth resistance of dentin in 0 deg orientation as a function of spatial distance with respect to occlusal surface (reprinted from Ref. [66] with permission from the publisher). Note that the results presented in both Figs. 8(b) and 8(c) achieved from middle dentin.

R-curves have been obtained from experiments on dentin using the single crack in flexural and CT specimen geometry [62,117–120]. A direct quantitative comparison of the responses across these studies is not possible due to the influence of specimen geometry on the toughening behavior [73,84]. For the CT specimen configuration, the average initiation (K_o), growth (K_g), and fracture toughness (K_C) for cracks extending perpendicular to the plane of tubules were 1.34 ± 0.06 MPa·m^0.5, 0.93 ± 0.39 MPa·m^0.5/mm, and 1.65 ± 0.10 MPa·m^0.5, respectively (Fig. 8(b)) [120]. Toughening was attributed to the development of crack bridging behind the crack in addition to inelastic deformation promoted by the mineralized collagen and generation of microcracks within the peritubular cuffs (Fig. 9) [118,120]. For cracks in-plane with the tubules, the average initiation 2.2 MPa·m^0.5, growth 1.2 MPa·m^0.5/mm) and plateau toughness 2.7 MPa·m^0.5 are greater than those values for the transverse direction (Fig. 8(c)) [66]. The mechanisms contributing to the toughening behavior in this orientation are similar, except perhaps for a larger contribution of the mineralized collagen caused by its orientation.

Fig. 9.

Toughening mechanisms in human coronal dentin for cracks oriented perpendicular to the tubules. (a) The development of unbroken ligaments in the intertubular dentin (reprinted from Ref. [120] with permission from the publisher). Note that the crack is growing from right to left. (b) Bridging ligaments formed by dentin collagen (reprinted from Ref. [120] with permission from the publisher) (c) microcracks and separation in the peritubular cuffs as shown with the white arrows (reprinted from Ref. [120] with permission from the publisher).

Spatial variations in the fracture resistance of human dentin have been evaluated [66], and results obtained for cracks extending in-plane with the tubules are shown in Fig. 8(d). The fracture resistance curves shown here are for 3 regions, namely from tissue that is closest to the DEJ (outer dentin), closest to the pulp cavity of the tooth (i.e., inner dentin) and midway between those two locations (middle dentin). As evident in this figure, the fracture resistance behavior is similar across the crown of the tooth, but there is a distinct decrease in toughness with increasing proximity to the pulp. This finding is of substantial importance to the field of dentistry as it establishes the larger potential for tooth fracture with increasing depth of restorative work (cutting, etching, etc.,) that may introduce flaws. One interesting finding that was noted in comparing the fracture resistance across the regions is that the toughening mechanisms were actually dependent on location. Within the inner dentin, which exhibits the largest tubule density, toughening was achieved by meandering of the crack to nearby lumens (Figs. 10(a) and 10(b)). This process results in a reduction of the stress intensity at the crack tip via blunting as the crack tip is located within the lumen and via the microcracking process in the K-dominant zone, as well as by crack curving [66,119]. Within the specimens of middle dentin microcracking of peritubular cuffs were also dominant (Fig. 10(c)). However, in the outer dentin the toughening behavior appeared to be largely attributed to the development of unbroken ligaments behind the crack tip (Fig. 10(d)). Thus, in addition to exhibiting anisotropy in the fracture resistance, human dentin also exhibits spatial variations. It is quite interesting to note that the microstructure of dentin appears to have been graded in such a manner that, in case of failure of the enamel and the DEJ to achieve crack arrest, can serve as the “third” defense.

Fig. 10.

Toughening mechanisms during crack growth in human coronal dentin in the direction parallel to the tubules. (a) Crack extension in inner dentin. The crack primarily extends from lumen to lumen as shown with the white arrows. Some degree of peritubular microcracking is also observed at the crack tip as outlined (white encircled area) (reprinted from Ref. [141] with permission from the publisher). (b) Micrograph showing the presence of ligaments bridging the crack in inner dentin (arrows) (reprinted from Ref. [141] with permission from the publisher), (c) microcracking of the peritubular cuffs is predominant in central dentin (reprinted from Ref. [141] with permission from the publisher), (d) example of ligaments bridging the crack and microcracks observed during crack growth in outer dentin (reprinted from Ref. [141] with permission from the publisher).

One obvious limitation of the aforementioned studies is that they have treated the fracture resistance assuming linear elastic behavior. Due to the presence of a fracture process zone and the capacity of these material to undergo inelastic deformation, a rigorous evaluation of the fracture resistance must account for these factors. Indeed, Yan et al., [121] applied elastic-plastic fracture mechanics to human dentin and found that inelastic processes contributed significantly to the fracture toughness of this tissue, resulting in an increases of the estimated toughness by more than 30%. Toughening mechanisms have been identified operating in front and behind the crack tip, which function to resist fracture differently. While a cohesive zone could be adopted to evaluate their combined affect (e.g., as performed by Yang et al., [122] for bone), a hybrid approach could also be used. This process involves experiments and numerical modeling and enables greater isolation of the contributions from the extrinsic and intrinsic toughening mechanisms to the fracture resistance. In this case the COD achieved from experimental measurements serve as the benchmark solution for the numerical simulations. In the study by Ivancik and Arola [66], the hybrid process was used with the numerical model incorporating elastic-plastic constitutive behavior, and a cohesive zone behind the crack tip developed to account for the unbroken ligaments of tissue operating in the crack wake. According to this approach, it was found that extrinsic toughening contributed an average of 26% of the total energy for fracture, intrinsic toughening was roughly 3%. In comparing the spatial variations in toughening (i.e., within the inner, middle, and outer regions), the contributions of extrinsic toughening were 2.5 times greater in the outer dentin than close to the pulp. The differences are expected to be due to the greater collagen content near the DEJ, which increases the crack closure stresses caused by the unbroken ligaments and fibrils.

5. Evaluations on the Fatigue Properties of Tooth Tissues

In this section, the fatigue response of enamel and dentin are discussed. Overall, fatigue failures can involve the initiation of damage or well-defined flaw, propagation of that damage or flaw to a critical state, and then followed by rupture. The process of mastication results in cyclic loading of teeth and generally occurs at a frequency of just below 2 Hz [123,124]. Estimates for the number of cycles resulting from daily routines indicate that the average tooth may experience up to 750 k cycles annually [4]. The number of cycles that any one tooth experiences, and the magnitude of cyclic stress are dependent on many factors, which may include the presence of prior restorations, tooth recruitment in mastication, patient age, dental health, etc. Nevertheless, finite element evaluations of the stress distribution within restored and unrestored teeth suggest that the cyclic stresses are within the elastic range [27,125].

According to the stresses borne by mastication, teeth are subjected to high-cycle fatigue and both the stress-life and fatigue crack growth approaches are applicable for analyzing fatigue failures in tooth tissues. The stress-life fatigue behavior is commonly described in terms of the stress amplitude (σ) of the fatigue cycle and number of cycles to failure (N_f), and modeled using a power law description after Basquin [126] according to

$$\mathit{\sigma }=\mathit{A}{\left({\mathit{N}}_{\mathit{f}}\right)}^{\mathit{B}}$$ (1)

where A and B are empirical constants that are developed from a best-fit to the experimental data. In conditions in which the life of the material/component is governed by the growth of a crack, the fatigue crack growth rate is generally interpreted in terms of the stress intensity range (ΔK). Assuming that the driving force promotes a ΔK that is greater than the stress intensity threshold (ΔK _th) of the material, then the steady state fatigue crack growth response can be described using a power law form after Paris et al., [127] according to

$$\frac{\mathit{da}}{\mathit{dN}}=\mathit{C}{\left(\Delta \mathit{K}\right)}^{\mathit{m}}$$ (2)

where C and m are scaling constants termed as Paris Law coefficient and exponent, respectively. The incremental fatigue crack growth rate da/dN is quantified by the ratio of incremental fatigue crack extension (Δa) to the number of cycles associated with the period of growth (ΔN) and the stress intensity range (ΔK) is simply (ΔK = K _max − K _min). Both the stress-life behavior and fatigue crack growth resistance of enamel and dentin have been studied. Detailed reviews of the fatigue behavior of hard tissues of the human body have been reported [108,128]. Thus, this portion of the review is focused on new results and only highlights previous findings.

5.1. Fatigue Properties of Enamel.

Although cracks are often observed in the enamel of vital teeth and have been noted to develop under cyclic temperature changes [129], studies on the fatigue behavior of enamel are scant. Undoubtedly, the largest obstacle to these studies is the limited volume of enamel that is available, and the corresponding restrictions to specimen size and geometry. However, in a recent investigation aimed at evaluating the durability of adhesive bonds to enamel [130], the stress-life fatigue response of enamel was evaluated for the first time. In this study small sections of cuspal enamel were bonded to a resin composite in a beam configuration (Fig. 11(a)). The specimens were evaluated under cyclic flexure loading and a finite element analysis was performed to estimate the stress state with the enamel, resin adhesive and composite, as required due to the presence of the interface. Results showed that there was a large variability in the fatigue performance of the enamel-bonded interface beams (Fig. 11(b)), and that fatigue failure occurred within the enamel, not within the adhesive joint. In fact, all fatigue failures occurred in the enamel and adjacent to the adhesive interface. A fractographic analysis showed that both the initiation of failure and propagation occurred at the interface of adjacent enamel rods. Accounting for the stress concentration that develops at the interface due to the elastic mismatch between the three materials, the estimated endurance limit of enamel was approximately 12 MPa. That value is much smaller (far less than half) than the apparent endurance limit of the resin composite and dentin.

Fig. 11.

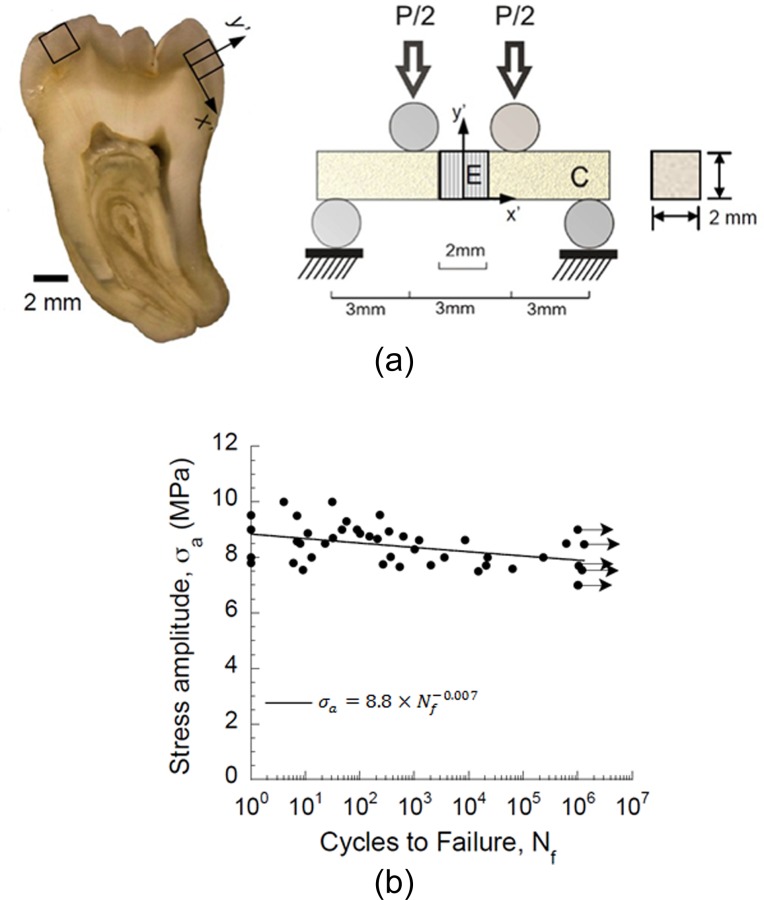
Fatigue life response of human enamel. (a) Schematic of enamel specimen preparation and testing (b) fatigue life response of enamel (reprinted from Ref. [130] with permission from the publisher). Note that the enamel cubes were oriented in specimens in such a manner that the occlusal surface was always subjected to tension (reprinted from Ref. [130] with permission from the publisher). Arrows represent those samples that did not fail within 1.2 × 10⁶ cycles.

Studies on the fatigue crack growth response of enamel are equally scant. Bajaj et al. [131] evaluated the fatigue crack growth behavior of human enamel and compared the responses to that of sintered hydroxyapatite. Results of that investigation showed that the threshold stress intensity of outer enamel is approximately 0.35 MPa·m^0.5, about three times the value for hydroxyapatite (0.13 MPa·m^0.5). The findings revealed that the microstructure of enamel and the organic proteins act to increase the resistance to crack propagation [131]. Electron microscopy evaluations of the fracture surfaces showed that the enamel exhibited similar extrinsic toughening mechanisms in resisting fatigue cracks as those operating during quasi-static crack growth. The cracks generated in the enamel were close to the occlusal surface of the tooth (i.e., outer enamel) and propagated toward the region of decussation. Upon reaching the decussated rods the crack underwent several toughening mechanisms including crack curving, the development of unbroken ligament bridges and crack bifurcation.

One interesting aspect of the fatigue crack growth response of enamel is that it exhibits both “short” and “long” crack behavior. A representative fatigue crack growth response for enamel is shown in Fig. 12(a). Two regions of distinct behavior are evident. The short crack response refers to crack lengths that are small when compared to the dimensional scale of the microstructure or primary elements contributing to toughening [132]. For short cracks, the resistance to cyclic crack extension increases with crack length as signified by the reduction in incremental growth rate. This behavior is indicative of the increase in the degree of extrinsic toughening that develops behind the crack tip until the process zone reaches a steady-state length behind the crack tip. Thereafter, the crack undergoes an increase in the incremental growth rate with stress intensity range, which is characteristic of long crack behavior. Enamel is not the only hard tissue that exhibits short crack behavior [133].

Fig. 12.

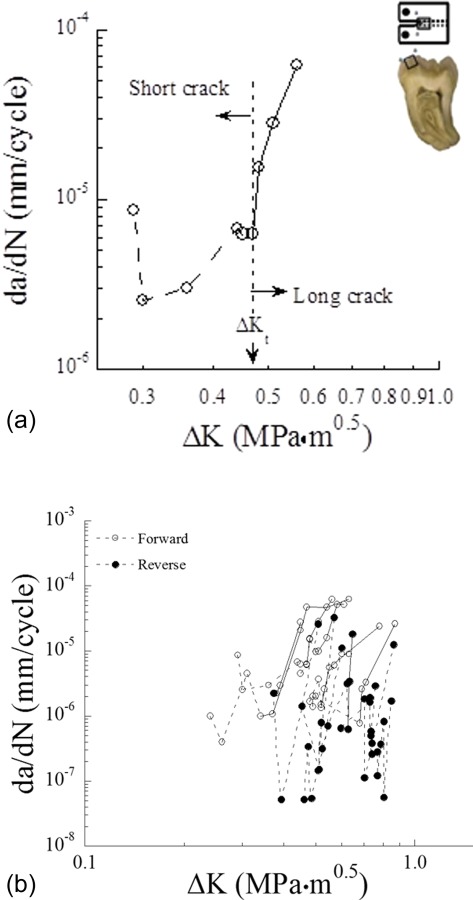
Fatigue crack growth response of human enamel. (a) Typical fatigue crack growth response in enamel from inset CT specimen (reprinted from Ref. [88] with permission from the publisher), (b) comparison of the fatigue crack growth resistance of enamel for crack extension in the forward and reverse directions (reprinted from Ref. [88] with permission from the publisher).

Similar to the evaluation of directional dependence in the R-curve behavior, the fatigue crack growth resistance of enamel has been examined in the forward (from the occlusal surface to the DEJ) and reverse (from the DEJ outwards) directions [89]. Interestingly, steady state “long crack” fatigue crack growth behavior was only achieved in the Forward direction (Fig. 12(b)). Results from that investigation also showed the importance of decussation on the crack growth process. For example, crack initiation within outer enamel occurred at a significantly lower stress intensity range (ΔK = 0.39 ± 0.09 MPa.m^0.5) than that for inner enamel (ΔK = 0.53 ± 0.12 MPa.m^0.5). Stable crack extension in the forward direction occurred over more than a millimeter of crack extension with the stress intensity range of 0.39–0.65 MPa.m^0.5. In contrast, cracks in the reverse directions reached instability over only hundreds of micrometers of growth. These findings reinforce those obtained from monotonic loading, and suggest that the microstructure of enamel appears to have been designed to be most effective in resisting cracks that initiate at the occlusal surface and undergo extension toward the DEJ.

5.2. Fatigue Properties of Dentin.

Fatigue of dentin has received the attention of investigators for more than a decade. Indeed, the failure of teeth with restorations has been identified to occur through a process involving fatigue and fatigue crack growth [21]. Several studies have evaluated the fatigue behavior of dentin and reviews on this topic have been reported previously [108,134]. Therefore, only a brief review of earlier work is presented here along with highlights, and with more emphasis placed on recent findings and their importance.

Investigations on the stress-life fatigue response have distinguished that dentin exhibits “metal-like” fatigue behavior [61,134], i.e., it exhibits a reduction in life with increasing stress amplitude. Dentin exhibits an “apparent” endurance limit that ranges between 20 and 50 MPa and is generally interpreted between 1 × 10⁶ and 1 × 10⁷ cycles; the presence of an endurance response depends on the nature of loading, including the stress ratio and testing frequency. Nalla et al. [134] reported that the fatigue life of human dentin decreases with a reduction in loading frequency and that an increase in the mean stress causes a reduction in the endurance limit [135]. Furthermore, the stress-life behavior is a function of tubule orientation (Fig. 13(a)) [136], with lowest resistance to fatigue occurring when the cyclic normal stresses are directed along the axis of the tubules. More recent work has shown that the processes used for cutting of dentin during the introduction of restorations can cause a substantial reduction in fatigue strength. Specifically, Majd et al. [26] discovered that cutting of coronal dentin with either carbide cutting burs or an abrasive air jet (both clinically relevant) substantially degraded the stress-life fatigue resistance. Cutting with carbide burs reduced the apparent endurance limit by nearly 40% (Fig. 13(b)). Furthermore, development of a Kitagawa-Takahashi diagram for the fatigue responses suggested that the average intrinsic flaw length resulting from bur cutting was approximately 70 μm. Results from that study distinguished that dentin is sensitive to flaws and that the methods presently used for cutting and removing demineralized tissues introduce detrimental defects. Of related importance, a recent preliminary study of dentin obtained from restored teeth, i.e., that underwent a period of oral function after placement of the restoration, showed substantially lower fatigue strength than unrestored tissue [107]. As dentin is not capable of repairing damage through a process of remodeling, the development of tools for minimizing the introduction of damage or the repair damage through remineralization processes are important considerations.

Fig. 13.

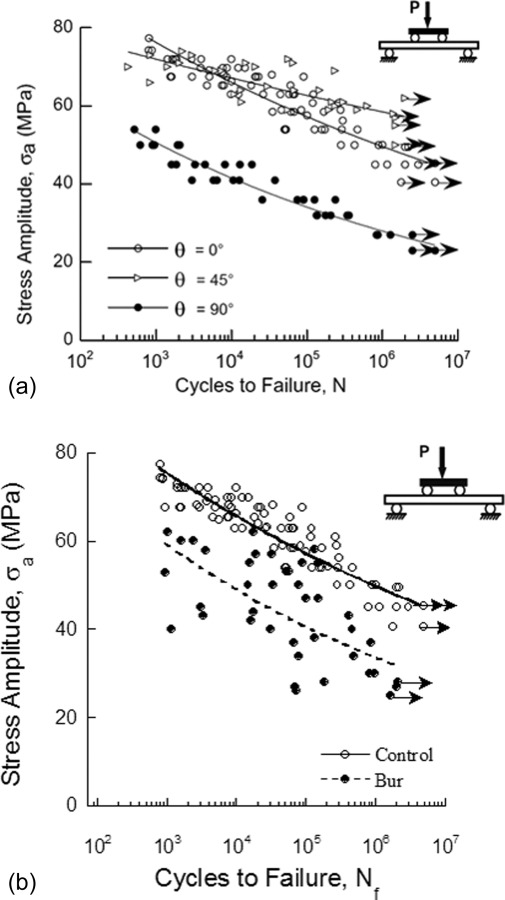
Fatigue life response of human coronal dentin. (a) The role of tubule orientation on the fatigue life response of young coronal dentin (reprinted from Ref. [140] with permission from the publisher), (b) comparison of fatigue life diagram for bur treated dentin beams and control beams (reprinted from Ref. [26] with permission from the publisher) . Arrows indicate those beams that did not fail.

The fatigue response of dentin has also been evaluated in terms of its fatigue crack growth resistance. Similar to the findings obtained from evaluations on the S-N behavior, independent studies on the fatigue crack growth resistance of dentin have shown that it is a function of testing frequency [137], and stress ratio (R) [138]. Higher fatigue crack growth rates occur with lower loading frequency and increasingly positive stress ratios. Moreover, the threshold stress intensity (ΔK _th) of dentin decreases with increasing stress ratio for R > 0, a characteristics that is exhibited by many engineering materials. That behavior is believed to result from dissipation of the tissue's ability to resist damage by viscous processes under the sustained mean stress.

Dentin exhibits anisotropy in the fatigue crack growth resistance with respect to the tubule orientation [139–141]. A comparison of the fatigue crack growth behavior of dentin with cracks extending parallel, oblique and perpendicular to the tubules (0 deg, 45 deg, and 90 deg orientations, respectively) showed that cracks preferred to grow perpendicular to the tubule axis under cyclic loading. Hence, cracks that develop within this tissue have a preferred growth direction, and anisotropy in the growth resistance contributes to the clinical observations that cracks extend from the line angle of restorations (region of maximum stress concentration) and largely extend perpendicular to the tubules (Fig. 2(b)). The larger fatigue crack growth resistance in the 0 deg and 45 deg orientations has been attributed to the arrangement of collagen fibers in relation to the crack orientation. By virtue of the collagen fibril arrangement in the intertubular dentin, the collagen fibrils are believed to play a greater role in resisting crack growth via extrinsic toughening in the 0 deg and 45 deg orientations. A recent study by Ivancik et al. [141] distinguished that the fatigue crack growth resistance of dentin is not only dependent on the tubule orientation but there are also spatial variations. Specifically, there is a significant decrease in the stress intensity threshold, and increase in the incremental rate of cyclic crack extension with an increase in proximity to the pulp cavity [141]. Thus, due to the potential for introducing defects during the cutting of dentin [26], the probability of tooth fracture after the placement of a dental restoration increases with depth of the preparation from the occlusal surface.

A survey of the mechanisms identified in resisting fatigue crack growth shows that they are consistent with those active in quasi-static crack extension, and that extrinsic toughening via crack bridging is believed to be the most potent. Nevertheless, dentin is far less resistant to the initiation of crack extension and fracture under cyclic loading in comparison to under quasi-static loading. A comparison of the critical stress intensity required for the initiation of cyclic crack growth (i.e., K _max estimated from ΔK _th) and the initiation toughness for quasi-static loading (K_o) shows that the resistance to crack extension under cyclic loading is more than 50% lower. In addition, the average fracture toughness of dentin (K_c) is over twice the maximum (i.e., critical) value of stress intensity (K _max) at instability during cyclic loading. Observations of the fracture surfaces from dentin samples suggest that the extrinsic mechanisms of toughening (mainly crack bridging) are substantially less effective during cyclic loading when compared to their contributions in the quasi-static condition [66]. In short, fatigue of the unbroken ligaments reduces their potency. Consequently, the fatigue crack growth properties of tooth tissues, as well as the contribution of clinically relevant factors to changes in the fatigue crack growth resistance, are of substantial importance to incidence of restored tooth fractures.

6. Influence of Aging, Dehydration and Other Factors

Based on the large range in oral conditions and parafunctional habits, there are a number of potential contributors to the fatigue and fracture behavior of teeth. For example, the influence of temperature variations, dehydration and polar solvents are relevant concerns to the fracture resistance of tooth tissues. With regards to thermal variations, increases in temperature up to 60 °C are reportedly not important to the fracture resistance of dentin [112,113]. However, Rasmussen and Patchin [112] reported that a decrease in temperature below 0 °C caused an increase in the work to fracture of dentin. Clearly it is far more convenient to conduct experimental evaluations at room temperature rather than 37 °C, and the majority of reported evaluations are conducted in ambient conditions. But that raises concern as to whether the tissue's response at room temperature is representative of that at body temperature. A comparison of the fatigue crack growth behavior of human dentin at both 22 °C and 37 °C has shown that there is no significant difference (Fig. 14). While no equivalent evaluation has been reported for enamel, the lower relative organic content would be expected to result in less temperature dependence than dentin.

Fig. 14.

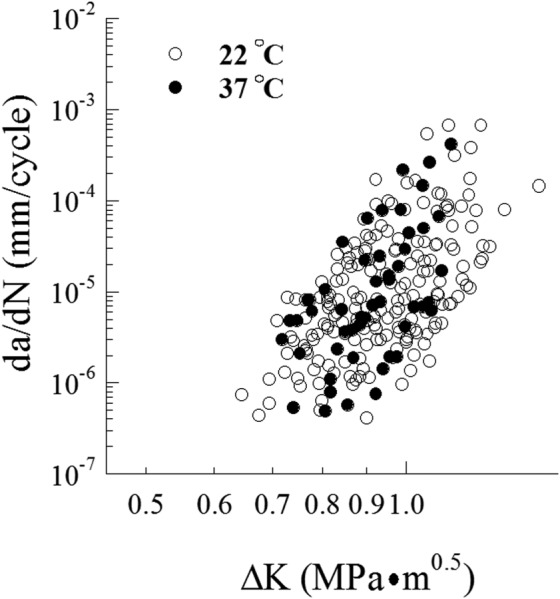
Comparison of fatigue crack growth resistance of human coronal dentin at room and human body temperatures

Changes in the level of hydration is a relevant concern as there can be a reduction in the level of salivary flow rate with aging, as a result of some medications or other conditions e.g., Refs. [142,143]. As expected, dehydration causes a reduction in the crack growth resistance of dentin [118,144]. In evaluating the influence of hydration on the R-curve behavior of dentin, Kruzic et al. [118] showed that removal of water under vacuum resulted in less prominent rise in the R-curve with crack growth. All three components of the response, i.e., the initiation, growth and plateau toughness were reduced by more than 40% of those values for the fully hydrated tissue. One of the most interesting findings is that the degradation in toughness caused by loss of water was temporary. Shortly after rehydration, the R-curve recovered to that of the originally hydrated tissue [118]. A distinct difference between the two conditions was that larger CODs were observed in the hydrated state. Hydrated dentin undergoes more extensive inelastic deformation around the crack tip as a result of the intrafibrillar spaces being occupied by water molecules, which results in “plasticization” of this highly organic system. The viscoplastic nature of the near-tip deformation promotes crack blunting, and results in higher crack growth resistance in the hydrated condition. Apart from the inelastic deformation, which serves as an intrinsic toughening mechanism ahead of the crack tip, crack bridging by unbroken ligaments of tissue was identified to be the major toughening mechanism contributing to the rising R-curve responses in conditions of hydration.

In contrast to the influence of dehydrating dentin by vacuum, chemical dehydration of dentin using polar solvents (e.g., ethanol) causes a marked rise in crack growth resistance. Nalla et al., [145] showed that while the initiation toughness of samples preconditioned in water and ethanol solution were not significantly different, the ethanol treatment caused an increase in the crack growth resistance; the growth toughness and fracture toughness increased by approximately 150% and 70%, respectively. The change in fracture behavior within polar solvent was rationalized to result from the formation of cross-links between the collagen peptides that developed with the removal of water [146]. These covalent cross-links enhance the strength of the briding ligaments behind the crack tip, thereby increasing the potency of bridging stresses that act to shield the crack tip of the opening mode stress intensity [145].

As a result of improvements in oral health, there is an increase in the number of senior dentate patients. This rise in number of elderly patients has become another important concern in dentistry. Interestingly, although bone undergoes a decrease in the degree of mineralization with age, human dentin undergoes an increase [147–149]. The process begins in the third decade of life and is associated with a progressive filling of the dentin tubules with mineral until they become completely filled [10,140]. A comparison of the microstructure of dentin from young and old patients is shown in Fig. 15(a). Dentin undergoes a reduction in the resistance to fatigue with patient age [61,150]. Kinney et al. [61] focused on the properties of dentin from the tooth roots and found that fatigue strength of old dentin (patient age > 65) was significantly lower than that of young dentin (patient age <25) in the low-cycle range (Fig. 15(b)), whereas for high-cycle fatigue (N_f ≥ 100 k cycles) there was no apparent different between the two age groups. In the study of Arola and Reprogel [150] involving tissue from the tooth crown, there was a significant decrease in the fatigue strength of dentin from senior patients (age > 50), and over the entire stress-life regime. The difference in fatigue behavior between the two studies could suggest that there are spatial variations in the rate of physiological aging and/or the degree of degradation in fatigue resistance between tissue of the tooth root and crown.

Fig. 15.

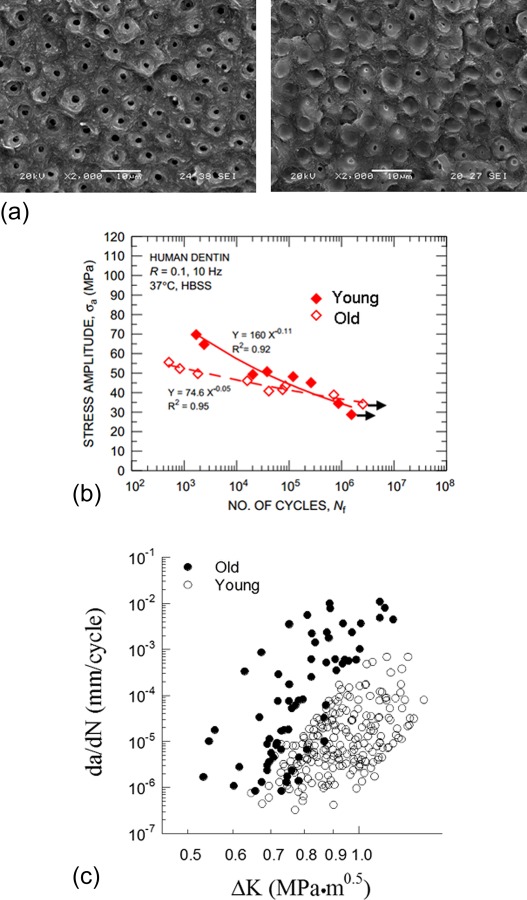
Influence of aging on the microstructure and fatigue response of human dentin. (a) Micrographs of fatigue fracture surfaces of young (left) and old (right) dentin (reprinted from Ref. [141] with permission from the publisher). Note that the tubules in young dentin are open. However, they become occluded with aging. (b) Comparison of the fatigue life responses of old and young dentin (reprinted from Ref. [61] with permission from the publisher) (c) comparison of fatigue crack growth responses of old and young dentin (reprinted from Ref. [141] with permission from the publisher).

Changes in the fatigue crack growth behavior of dentin with aging have also been studied [64]. A comparison of fatigue crack growth in dentin obtained from “young” and “old” patient age groups is shown in Fig. 15(c) for cyclic extension occurring perpendicular to the tubules. Aging of dentin causes a significant reduction in the resistance to the initiation of fatigue crack growth, and significant increase in the rate of incremental extension. Owing to the influence of tubule orientation on the fracture behavior, Ivancik et al. [141] characterized the influence of aging on the degree of anisotropy in the fatigue crack growth resistance of dentin. It was found that the direction of lowest fatigue crack growth resistance is perpendicular to the lumens, regardless of age, and the degree of anisotropy remained nearly constant. Interestingly, the age-related degradation appears to be most severe in the tissue that is located farthest from the pulp [141]. Overall, the fatigue crack growth properties of dentin show the lowest degree of spatial variation in old teeth.

The influence of aging on the fracture toughness of dentin has also been investigated. Koester et al. [119] was among the first to report on the R-curves for human dentin, and showed that the fracture toughness decreases significantly with aging. This evaluation identified that occlusion of the tubules adversely affects the extent of extrinsic toughening. The unfilled lumens in young dentin provide a source for crack initiation and the development of secondary “daughter” cracks. These satellite cracks provide potential for crack deflection, branching, and at larger crack lengths results in occurrence of bridging.

Nazari et al. [120] also investigated the effects of aging on the fracture toughness of human dentin for cracks oriented perpendicular to the tubules. In that orientation there was a significant reduction in the initiation (K_o) and plateau (K_c) toughness with increasing age. In old dentin the crack growth resistance increased with extension from initiation to fracture (K_c = 1.17 MPa·m^0.5) by less than 10%, whereas in young dentin there was a 25% increase from initiation to fracture (K_c = 1.65 MPa·m^0.5). Consistent with the mechanisms noted previously, extrinsic toughening via unbroken ligaments were predominant in young dentin. However, they were only seldom noted in the fracture process zone in the old samples. Collectively, the results of these studies suggest that dentin undergoes a decrease in the resistance to fracture with aging, and that it is largely due to the reduction in extrinsic toughening arising from the development of unbroken ligaments.

7. Challenges and Future Work

A review of research on the mechanics of tooth fractures was presented, including investigations on the fatigue and fracture properties of the dentin and enamel. Results from evaluations on the resistance to fracture of these hard tissues has shown that both are primarily extrinsically toughened, and that it arises from the development of unbroken ligaments that act to shield the crack through the development of bridging stresses. Extrinsic toughening plays a critical role in the fatigue crack growth resistance of dentin and enamel, as is also found in many engineering materials [151]. However, cyclic loading causes extensive degradation in the potency of the bridging elements in hard tissues. And as a result, the crack growth resistance of these materials is considerably lower under cyclic conditions in comparison to that in quasi-static loading. Therefore, fatigue should be recognized as a critically important factor in fragility failures involving hard tissues of the tooth. Recognition of that behavior raises the importance of adopting fatigue as a platform for evaluating tooth tissues in future evaluations.

Despite the contributions from past studies in understanding the fatigue and fracture properties of hard tissues, this field is far from mature. There are a number of challenges and unanswered questions that remain to be addressed. One of the primary concerns is the development of biofilm on the tooth's surface. While tooth fracture is one of the primary causes for restored tooth failures, secondary caries is by far the most common cause of failure [6,152]. Secondary caries result from the acid production of biofilms e.g., Refs. [29,153], which here refers to a colony of bacteria from the oral cavity. Although previous studies have evaluated the degradation of restorative materials under the challenge of biofilms [154–157], the influence of biofilms on the fatigue and fracture resistance of dental hard tissues has not been addressed. Mechanical forms of damage at the tooth's surface and microcracks at bonded interfaces in restored teeth can facilitate the penetration of bacteria. Acid production of biofilms reduces the local pH to a level that promotes demineralization of the dentin and enamel. Do et al. [158] evaluated the stress-life fatigue behavior and fatigue crack growth resistance of dentin within a lactic acid environment having pH = 5, and reported that a pH < 7 causes significant degradation in the fatigue resistance. Nevertheless, a lactic acid solution having constant pH cannot represent the complexity of conditions promoted by the acid production of biofilms. Thus, further work regarding the synergism between cyclic stresses and demineralizing environments on the fatigue behavior of hard tissues may be warranted. In addition, as new dental materials are developed with anticaries resistance and remineralizing capacity, careful and clinically relevant evaluations concerning the mechanical behavior of these materials and their bonded interfaces will be important. This review did not address the elastic properties of dentin and enamel and the potential problems caused by elastic mismatch between the hard tissue and restoratives, which are important issues in the success of restorative dentistry as well. The elastic properties and strength of dentin and enamel have been discussed in previous reviews [80]. The maintenance of their elastic properties and strength over time will be critically important to understand.

In regards to enamel, there are some additional factors that may be valuable to explore. In contrast to the efforts regarding aging of dentin, the effects of aging on the fatigue and fracture resistance of dental enamel have not been fully addressed. Enamel undergoes an increase in the elastic modulus and hardness, as well as an increase in the indentation brittleness with age [97,159]; that is believed to occur due to a loss of proteins. Past studies concerning fracture of enamel have also emphasized the contributions of proteins in the potency of the toughening mechanisms and in crack arrest. However, an investigation on the changes in fracture resistance with removal of proteins, or via a modification of their conformation, has not been reported. As such, while the role of proteins is undoubtedly important, their specific contribution to the fracture resistance of enamel remains a little vague.

As evident from a description of the methods employed for evaluating the fracture behavior of tooth tissues, there are no methods that have been standardized within the size scale of the materials available. That may raise some criticism in the “validity” of the results, which is an issue that has been raised with respect to the methods used in characterizing synthetic dental materials as well e.g., Ref. [160]. The use of different methods of investigation, involving specimen sizes and configurations, also makes it more difficult to compare the findings across investigations. Thus, development of standardized methods for evaluating the fatigue and fracture properties of materials at the size scale necessary for their application to hard tissues of the tooth would make a substantial contribution to the field, and facilitate further progress. The development of standardized methods for this purpose would undoubtedly support their application to biomedical materials in other areas as well.

Growing knowledge on the fracture properties of natural materials has fueled engineers and scientists to develop new bioinspired microstructures with impressive performance e.g., Refs. [161–164]. Dental hard tissues have considerably higher toughness than their fundamental constituent (HAp), which is very brittle and has low resistance to fracture. As previously mentioned, the proteins play a critical role in the toughing mechanisms that contribute to the crack growth resistance of these materials. But the proteins also appear to act in repairing damage within mineralized tissues [12,165]. That topic has not been pursued in detail and has remained controversial. Recent investigations have shown significant advances in the synthesis of enamel, and with nanomechanical properties that are similar to that of dental enamel [166,167]. One limitation of the mechanical evaluations that are adopted for characterizing these synthesized materials is that their fracture behavior is not considered. Resistance to fracture is a vital requirement for most structural materials [168], including those in nature. Perhaps that topic will spark the interests of future scientists in the area of applied mechanics.