Short abstract
Thermal pain arising from the teeth is unlike that arising from anywhere else in the body. The source of this peculiarity is a long-standing mystery that has begun to unravel with recent experimental measurements and, somewhat surprisingly, new thermomechanical models. Pain from excessive heating and cooling is typically sensed throughout the body through the action of specific, heat sensitive ion channels that reside on sensory neurons known as nociceptors. These ion channels are found on tooth nociceptors, but only in teeth does the pain of heating differ starkly from the pain of cooling, with cold stimuli producing more rapid and sharper pain. Here, we review the range of hypotheses and models for these phenomena, and focus on what is emerging as the most promising hypothesis: pain transduced by fluid flowing through the hierarchical structure of teeth. We summarize experimental evidence, and critically review the range of heat transfer, solid mechanics, fluid dynamics, and electrophysiological models that have been combined to support this hypothesis. While the results reviewed here are specific to teeth, this class of coupled thermomechanical and neurophysiological models has potential for informing design of a broad range of thermal therapies and understanding of a range of biophysical phenomena.
Keywords: biomechanics, bioheat transfer, teeth, hierarchical multiscale models, electrophysiology, pain transduction
1. Introduction
Among their many roles, teeth serve as sensory tissue [1–4]. One such sensory role is sensing of temperature: ice cream that is too cold or tea that is too hot can lead to thermal pain sensed by teeth. Pain from excess heating and cooling is transduced via a common pathway involving pain-sensing neurons (nociceptors) that terminate within the intricate structures that exist beneath the enamel of a tooth. Despite being transduced along this common pathway, the pain resulting from excess heating and cooling is perceived very differently: while hot stimuli such as hot tea generally induce a dull, longer and lasting pain, cold stimuli such as ice cream can induce sharper, more transient pain [5,6]. Although the human experience of pain is much more complicated than simply an electrophysiological signal in a nociceptor, in this case the different perceived pain responses have been confirmed in vivo through electrophysiological data from animals [6–9]. The source of this difference is a long-standing debate.
Three hypotheses (i.e., the neural theory, the odontoblastic transduction theory, and the hydrodynamic theory) have been proposed to explain the tooth pain mechanism [10]. Amongst the three hypotheses, the hydrodynamic theory has been widely accepted, which assumes that dentinal fluid flow induced by noxious stimuli may activate mechanoreceptors resulting in pain sensation [1,11–13]. A key piece of evidence motivating this theory is the observation that many pain-inducing external stimuli (e.g., heating, mechanical stimulus, and dental restoration) cause either inward (toward the pulp chamber) or outward (away from the pulp chamber) dentinal fluid flow [14–17]. A key piece of evidence supporting this theory comes from simultaneous recording of dentinal fluid flow and intradental neural discharge evoked in a cat tooth [9,18], showing that fluid flow correlates directly with nociceptor signaling in a range of fluid flow rates.
Pressure applied to the tooth during mastication of high modulus foods can cause high stresses and fluid flow in the teeth. The work of Chang et al. [19] and Paphangkorakit and Osborn [16] show that masticating high elastic modulus foods results in high stress and deformation in the tooth structure, causing faster fluid flow compared to that of soft food. Moreover, fast chewing of hard food particles can induce faster fluid flow, which may evoke pain [19]. Therefore, people often feel tooth pain when masticating a hard substance with a fast chewing rate. Such pain, however, differs from that associated with thermal pain in teeth because deformation of the relatively soft foundation underlying teeth might be expected to evoke pain in parallel with or even before that from flow in dentinal microtubules. In addition to hydrodynamic theory, Linsuwanont et al. have recently proposed a possible mechanism for tooth pain sensation [20]. Upon thermal stimulation on the enamel surface, they observed a rapid development of strain at the pulpal wall before a notable temperature change could be detected at the dentine-enamel junction. These results indicate that mechanical deformation may directly evoke nerve impulses, or may induce dentinal fluid flow that triggers nerve impulse.
This review begins with a brief description of the structure of a tooth, emphasizing the various hierarchical anatomical features that play a role in the leading hypotheses about the sources of these differences. The review continues with a summary of key experimental observations, and critically reviews several of the leading hypotheses. The review then expounds upon what is emerging as the most promising hypothesis: pain transduced by fluid flowing through the hierarchical structure of teeth due to heat transfer and thermomechanical effects.
1.1. Tooth Structure and Innervation.
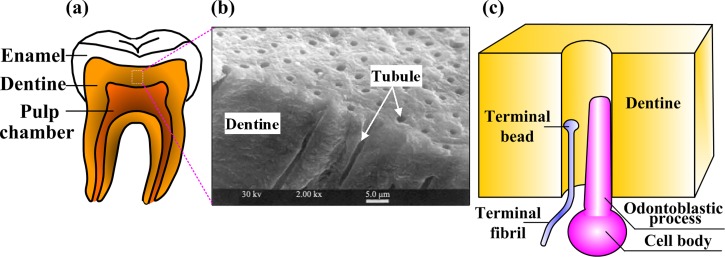
We begin with an introduction to the anatomy of a tooth as a whole (Fig. 1(a)). The crown of the tooth possesses a translucent white cap of enamel, a highly mineralized tissue, and the root of the tooth is covered by a thinner layer of highly mineralized cementum. Beneath these is a layer of dentin that surrounds the pulp. The pulp contains vasculature, connective tissue, and several classes of cells. These cells include fibroblasts that manage connective tissue; odontoblasts that generate dentin and nerve fibers. The nerve fibers within the tooth that are of primary interest having pain-sensing units are called nociceptors. The function and spatial distribution of these are believed to be of primary importance to the sensing of thermal pain, and will be discussed in detail below.
Fig. 1.
Tooth structure and neuron innervation. (Reprinted Quintessence International with permission from Europe PubMed Center.) (a) Cut-away image of a human tooth illustrating several key composite layers; (b) SEM image of dentine showing solid dentine material and dentinal microtubules running perpendicularly from the pulpal wall toward dentine-enamel junction; (c) schematic of the innervation of a dentinal microtubule. The pulpal terminus of a dentinal microtubule usually contains the terminus of a nociceptor and a process extended by an odontoblast. The terminal fibril of the nociceptor ends with a terminal bead that is rich in ion channels that are sensitive to noxious stimuli including heat and shear stress.
Nociceptors come in two major varieties that govern many differences between fast and slow pain throughout the body. Signals associated with fast, sharp pain reaching the trigeminal and dorsal root ganglia of the brain through thinly myelinated A-delta fibers. Slower, duller, more sustained pain reaches these regions of the brain through slower, unmyelinated C-fibers [21]. Each nociceptor has at its terminus a terminal fiber, and this fiber has a terminal bead that hosts a range of ion channels activated by stimuli such as heat, acidity, and mechanical stress.
The tooth innervation system mainly includes both A-delta and C fibers [22]. The positioning of these within the tooth has long been suspected as an important factor in sensing differences between pain from heating and cooling. Dentinal microtubules radiate from the pulp wall to the exterior mineralized tissue of the tooth and contain micrometer diameter channels. Dentinal microtubules associated with the root extend from the pulp to the dentine-cementum junction, and those associated with the crown extend from the pulp to the dentine-enamel junction (Fig. 1(b)) [23]. Some A-delta fiber terminals are oriented perpendicular to odontoblast processes penetrating into dentinal microtubules (Fig. 1(c)) [24–26], while C fibers are located exclusively within the pulp [8,27]. This difference offers an attractive hypothesis about differences in pain response to heating and cooling, especially given the fundamental differences between A-delta and C fibers. Peripheral A-delta fibers are responsible for sharp, shooting pain sensations occurring after short latency, while C-fibers are responsible for dull, burning pain following considerably longer latency [8,22,28]. However, the simple explanation that A-delta fibers cool down sooner because they are closer to the crown proves not to be supported by the models described in this review. Instead, thermal pain might involve signal transduction across a number of hierarchies. Stimuli must pass through tooth enamel to dentine (macroscale level), dentinal microtubules (microscale level), and nociceptor ion channels (molecular level). The following sections will describe ways that this hierarchical structure might contribute to sensations of pain.
2. Physiological Responses of a Tooth to Heating and Cooling
The sensations of hot and cold on a tooth are likely familiar to many, with cold ice cream triggering pain that is relatively rapid and sharp pain, and hot tea triggering pain that is more gradual and dull. These sensations are transduced via C-fibers in the teeth. Like all nociceptors, these C-fibers deliver pain signals in the form of repeating voltage spikes whose frequency corresponds to increasing levels of pain.
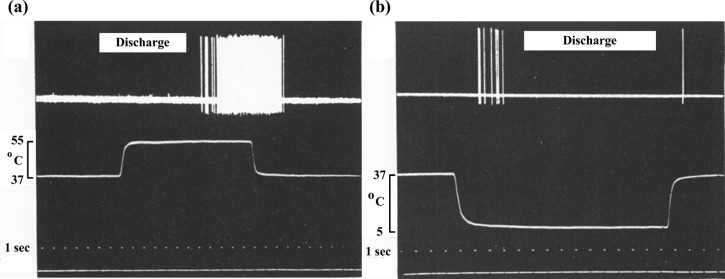
The voltage spike trains are measurable in a dog model. The classic experiment involves direct measurement neuron discharge in the intrapulpal nerve of a dog's tooth that is covered with a sheath through which temperature-controlled saline flows. For heating, the classic results of neuron discharge for a heating response show a voltage spike train arising after a relatively long latency period (>10 s) following the application of noxious heat, then an increase in frequency (Fig. 2(a)) [6]. The high frequency spike train endures a few seconds after the hot saline is replaced with body temperature saline, then ceases. Such long latency in neural discharge characteristics may be attributed to neural hypothesis where temperature rise/decrease around the nociceptors requires relative long time.
Fig. 2.
Experimentally recorded neural discharge patterns under hot or cold stimulations. (Reprinted from Archives of Oral Biology with permission from Elsevier.) (a) Neural discharge pattern (voltage trace, top) following heating from 37 °C to 55 °C for 12 s (temperature trace, middle) and a cooling back to 37 °C; (b) neural discharge pattern following cooling from 37 °C to 5 °C for 15 s and a re-warming to 37 °C.
The neurophysiologic response to cold stimulus is starkly different, with a rapid transient tooth pain response widely reported in daily life and dentistry [5,28,29]. Following cold stimulus in an analogous experiment, Matthews [6] showed that voltage spikes are sharper and occur much more rapidly. Voltage spikes appear within a second after cold stimulation, but then cease after a few seconds despite the continued application of cold saline (Fig. 2(b)) [6,8,9]. In one experiment, a single spike is observed following return to physiologic temperature.
The mechanisms underlying these differences between the responses to heating and cooling have been a long-standing source of debate. In the following section, we review major hypotheses about the sources of these differences.
3. Critical Review of the Three Dominant Hypotheses for Differences in the Sensation of “Hot” and “Cold” in Teeth
The mechanisms underlying these differences between sensations of hot and cold stimuli remain unclear, partly because of complexity of tooth innovation system that is composed of odontoblasts, nerve endings, and the liquid content of dentinal microtubules [30]. Here, we review from an engineering perspective the three dominant hypotheses suggested to explain the mechanism underlying the transduction process of teeth pain sensation [10].
3.1. The Neural Theory.
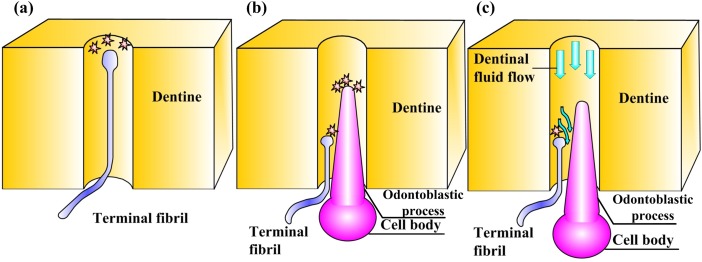
The simplest hypothesis is that the ion channels or nociceptors transducing heating and cooling behave differently (Fig. 3(a)). Two different types of nociceptors exist with different speeds of transduction, so the idea that ion channels sensitive to heating and cooling simply exist on different nociceptors is an attractive explanation for our mystery. Additionally, such nociceptors could be located differently within the tooth, with cold nociceptors placed nearer the surface.
Fig. 3.
The three dominant hypotheses explaining differences between pain associated with heating and cooling. (a) The neural theory, in which differences arise from hot- and cold-sensitive ion channels on the terminal fibril of a nociceptor; (b) the odontoblastic transduction theory, in which signals transduced by odontoblasts are conveyed to the terminal fiber of a nociceptor; (c) the hydrodynamic theory, in which thermally induced dentinal fluid flow over the terminal bead of a nociceptor plays an important role in thermal pain transduction.
In an alternative version of the neural theory, nociceptors are identical, but the ion channels for heating and cooling behave differently. This is a particularly attractive hypothesis because we now know that heating and cooling are indeed transduced by different ion channels (see, for example, the review of Woolf and Ma [31]). Heating is sensed by the TRPV1, TRPV2, TRPV3, and TRPV4 channels. The TRPV1 channel's probability of opening increases significantly at ∼43 °C, the threshold for thermal pain. Cooling is sensed by the TRPM8 and possibly TRPA1 channels.
These hypotheses have never been falsified definitively, but engineering analysis is paving the way for their testing, and the current evidence is stacked against them. The hypothesis that different nociceptors are primarily responsible for transducing heating and cooling has not been tested fully, although we note that careful histological analysis of this hypothesis is possible now that channels for sensing cooling have been identified. A problem with this hypothesis is that it conflicts with initial engineering analysis of heat transfer within a tooth. Although the temperature rise near the nociceptor endings in the dentine-enamel junction [32] corresponds with the initiation of nociceptor voltage spikes associated with noxious heating as in Fig. 2(a), the temperature response in cooling seems inconsistent with the involvement of the TRPM8 or TRPA1 channels. The challenge is that, following cooling of the type applied in the experiment of Fig. 2(b), the dentine-enamel junction temperature is predicted to be still within the normal physiologic range at the time that a voltage spike train is measured [6,8,9,33–35]. This suggests that other pathways are likely involved, but further engineering analysis is needed. Specifically, once adequate models for the temperature-dependent opening probability of TRPM8 and TRPA1 channels are developed, coupled thermomechanical and neurophysiological modeling will be of value in definitive testing the neural hypothesis.
3.2. The Odontoblastic Transduction Theory.
A second hypothesis is motivated by the presence of odontoblasts, some of whose processes penetrate into the dentinal microtubules. Although following cooling, the temperature at the dentine-enamel junction changes slowly compared to the timescale of the initiation of the voltage spike train, subtle changes to the shape of the dental microtubules occur relatively rapidly due to the thermomechanical constriction of the tooth as a whole [2]. Some dentine microtubules contain both a process extending from an odontoblast and the sensory nerve fiber. Could this construction be sensed in some way by odontoblasts and could this information be transferred to the nociceptors?
The thought is quite appealing from many perspectives. Cells similar to odontoblasts are known to be quite compliant relative to dentine [36], and, therefore, would be expected to deform in registry with the dentine microtubules [37,38]. The odontoblastic transduction theory (Fig. 3(b)) postulates that odontoblasts may sense external stimuli and transduce the signal to nearby nociceptors on nerve fiber through one of several pathways. These include paracrine signaling, direct electrical connections, or synaptic junctions [25,39–43]. Although such transmission has not yet been observed, odontoblasts are suspected to play a role as sensory cells in tooth pain transmission due to their close relationship with nerve fiber. While this theory relies upon anatomical features that are not yet certain, evidence exists of adhesion between sensory nerve fibers and odontoblasts [25,39–44]. Arguing against this hypothesis is an experiment conducted on a tooth following the elimination of odontoblasts, where, the tooth retains sensitivity in the absence of odontoblasts [1,45]. However, this does not falsify the hypothesis, but rather shows that at the very least multiple sources of a pain signal might exist. Further, additional research is required to determine whether as yet unidentified cellular processes that connect odontoblasts to nociceptors are retained in these experiments.
Further supporting this more complicated and multiply sourced view of tooth thermal pain transduction, Magliore and co-workers have recently demonstrated that the odontoblast process itself can act as a sensory unit that directly mediates tooth pain sensation [40,46]. Recent studies confirm the existence of mechanosensitive ion channels on odontoblasts, suggesting that odontoblasts may be able to convert pain-evoking dentinal fluid flow within dentinal tubules into electrical signals via mechanosensitive ion channels [41,47,48]. Additional evidence is the discovery of functional TRP channels expressed by odontoblasts [43,49]. Although these findings support a role for the odontoblast itself in sensory transduction in teeth, the precise mechanisms through which these cells detect nociceptive stimuli have yet to be fully elucidated.
3.3. The Hydrodynamic Theory.
An additional theory related to thermomechanical constriction or expansion of dentinal microtubules implicates the fluid flow that these shape changes induce. The hydrodynamic theory (Fig. 3(c)) postulates that this fluid flow stimulates mechanosensitive ion channels on nociceptors within a dentinal microtubule or at the pulp dentine junction [1,11–13]. This hypothesis is bolstered by observations of relatively rapid increases in dentinal fluid flow following heating or cooling of a tooth [2,17]. Additionally, intradental nociceptors in a cat model are known to respond differently to inward flow (into the pulp) and outward flow (away form the pulp), with signals much stronger and more rapidly transduced for outward flow [9,18,50]. Since inward flow and outward flow are associated with heating and cooling, respectively, this provides an attractive potential basis for the different nociceptor responses to heating and cooling [9,10,17,18].
Support for this hypothesis is broad and derives largely from coupled engineering and electrophysiological analysis of the tooth. This story and the hierarchical and multiphysical models that comprise its main players are the focus of the remainder of this review.
The idea underlying these models is that flow over nociceptors is sufficient during outflow (cooling) to activate stress-sensitive ion channels on nociceptors; this activates voltage spikes that are transduced as pain long before dentine-enamel junction temperature deviates significantly from the physiologic range [2]. Central to this is the way that odontoblastic processes residing in dentine microtubules displace in response to flow, further constricting the area available for flow; this can amplify or reduce the fluid velocity and, hence, shear stress over stress activated channels [3].
The hydrodynamic theory is not without its detractors as well. Arguing against the hydrodynamic theory is the same experiment that weighs against the odontoblastic theory: if odontoblasts play an important role in differences between pain transduced in cooling and heating, then why are these differences observed in teeth from which odontoblasts have been removed? Testing the hydrodynamic hypothesis against these experimental data will require a modeling effort that has not yet been undertaken.
However, a hierarchy of models has been assembled to quantitatively connect heating and cooling of tooth enamel to the electrophysiological responses of nociceptors. These models and their validation against experiment is discussed, along with insight that the models offer into the hierarchical, multiphysical sensing functions of teeth in general.
4. The Hierarchy of Models Supporting the Hydrodynamic Theory
Relating the heating or cooling of a tooth to signals produced by intradental nociceptors requires the linking of several models across multiple structural hierarchies. Enamel and dentine are both highly anisotropic tissues [51–53]. This anisotropy is known to have a strong effect on stress distributions in the tooth [53]. However, in the analyses discussed here that have been applied to pain transduction across hierarchies, enamel and dentine have been approximated as isotropic materials with different mechanical properties. Improving upon this approximation is an important area for future inquiry.
The steps involved are first to model how heating of a tooth surface relates to heating and deformation of dentinal microtubules, and how this in turn induces fluid flow. Thereafter, the shear stresses on nociceptors must be estimated, and the effect of this shear stress on nociceptor response modeled. Models that have been shown to be suitable for this purpose are described in the following sections.
4.1. Time-Varying Temperature Distribution Within a Tooth.
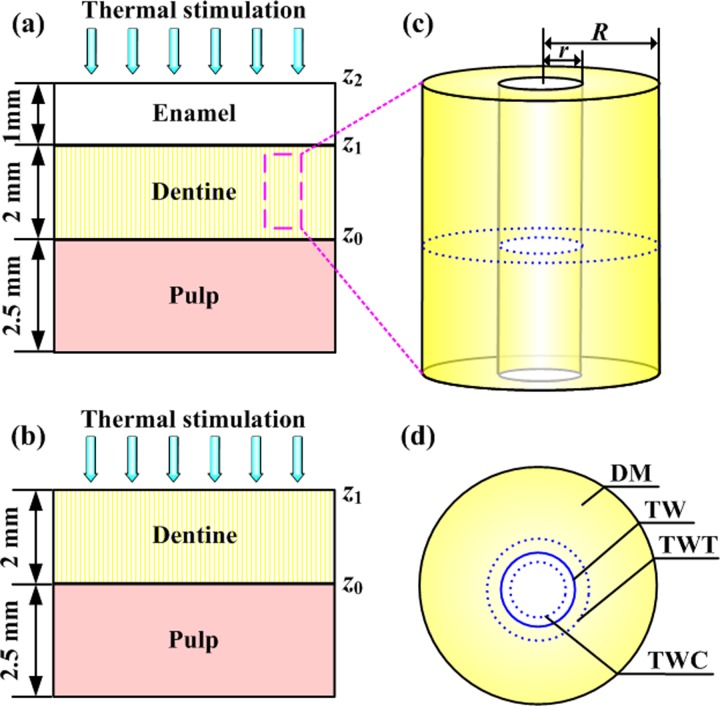
The largest of the hierarchical length scales considered in this analysis is that of an entire tooth. A unit cell approach modeling the tooth as a one-dimensional layered structure (Figs. 4(a) and 4(b)) has been shown to approximate the temperature distribution and thermomechanical deformation of a tooth adequately [2,20].
Fig. 4.
Idealized models for the thermomechanics of tooth heating. (Reprinted from Archives of Oral Biology with permission from Elsevier.) (a) One-dimensional, three-layer tooth model; (b) one-dimensional, two-layer tooth model; (c) individual dentinal microtubule; (4) representative area sectioned from (c) illustrating deformation of the dentinal microtubule wall. DM: dentine matrix; TW: microtubule wall before deformation; TWC: microtubule wall following compressive thermal stress induced deformation; TWT: microtubule wall following tensile thermal stress induced deformation.
Heat transfer within each layer i of this model is governed by the one-dimensional 1D Fourier heat transfer equation
| (1) |
where the index i = 1, 2, and 3 represents the enamel, dentine, and pulp layers, respectively; T is the temperature, dependent on time t(s) and location z(m); and ki (W m−1 K−1), ci (J kg−1 K−1), and ρi (kg m−3) are the effective thermal conductivity, specific heat1 and mass density of each layer i. Appropriate physical properties of each layer are listed in Table 1 . Solving these equations relates an applied surface temperature change to distributions of temperature T(z, t) across a tooth.
Table 1.
Physical properties of teeth
| Property | Tooth component | Values | Ref. |
|---|---|---|---|
| K | Enamel | 0.81 | [54] |
| Thermal conductivity | Dentine | 0.48 | [54] |
| (W m−1 K−1) | Pulp a | 0.63 | [55] |
| cp | Enamel | 0.71 | [56] |
| Specific heat | Dentine | 1.59 | [56] |
| (× 10−3 J kg−1 K−1) | Pulp a | 4.2 | [55] |
| ρ | Enamel | 2.80 | [56] |
| Density | Dentine | 1.96 | [56] |
| (× 10−3 kg m−3) | Pulp a | 1.00 | [55] |
| E | Enamel | 94 | [57] |
| Young's modulus (GPa) | Dentine | 20 | [57] |
| ν | Enamel | 0.30 | [58] |
| Poisson ratio | Dentine | 0.25 | [57] |
| λ | Enamel | 1.696 | [59] |
| Coefficient of thermal expansion (× 10−5K−1) | Dentine | 1.059 | [59] |
Values taken from water following de Vree et al. [85].
4.2. Time-Varying Thermal Stresses Within a Tooth.
Relating the model of time-varying temperature distribution to the time course of dentine microtubule deformation requires a stress analysis. The tooth has been modeled at the largest hierarchical level as a three-layer structure [2,60] consisting as a layer of enamel, a layer of dentine, and a layer of pulp. Thermal stresses in the pulp layer have been shown to be negligible: the pulp layer is highly permeable and compliant relative to the other layers and has been modeled as a liquid layer that contributes to heat transfer without restraining the solid layers (enamel and dentine) from thermal deformation. The thermomechanical behavior of enamel and dentine can give rise to thermal stress in two ways. First, a nonuniform distribution of temperature even in a single layer can lead to stressing through frustrated expansion/contraction. Second, restriction of thermal expansion or contraction due to the property mismatch of the bonded of enamel and dentine leads to stressing and (frustrated) flexure even in the case of a uniform change of temperature.
Stresses were approximated here by assuming that single enamel layers or enamel-dentine composite layers remain flat while bearing in-plane stresses. The standard plate theory equations governing the in-plane stresses in a single layer of such a model (Fig. 4(b)) show a dependence of stresses at position z and time t on the spatial-temporal distribution of temperature [61]
| (2) |
where , . E (Pa), ν, λ(K−1) are the Young's modulus, Poisson ratio, and coefficient of thermal expansion of the layer, respectively. T 0 is the temperature at the base of the pulp. Note that in several key experiments, the enamel layer is removed prior to heating of the tooth and this equation is, thus, adequate on its own for modeling the dentine layer.
Incorporating an enamel layer (Fig. 4(b)) (z 2 ≤ z < z 1) [61]
| (3) |
where subscripts e and d refer to the enamel and dentine layers; ; , in which Ei and are the elastic modulus and Poisson ratio of layer i; , in which is the coefficient of thermal expansion of layer i; and the constants , and are properties of the unit cell as a whole, defined below. For the dentine layer (z 1 ≤ z < z 0),
| (4) |
The in-plane extensional, coupling, and bending stiffness of the overall laminate of structure are governed by the 3 × 3 matrices A, B, and D, respectively, whose elements are given by
| (5) |
where the indices i, j = {1, 2, 6} represent in-plane normal and shear terms in the usual way [61]; k = 1, 2 represent the enamel and dentine layers, respectively; and is the stiffness matrix of layer i, defined by
| (6) |
The elements , , , , , and can be determined by
| (7) |
Solving these equations relates distributions of temperature T(z, t) to thermal stresses σ(z, t) across the tooth.
4.3. Dentinal Fluid Flow Within Microtubules Associated With Thermal Stresses.
The next hierarchical level involves study of a single representative dentinal microtubule. The distributions of temperature T(z, t) and thermal stress σ(z, t) within the dentine layer can be passed down to this hierarchical level from a tooth-level thermomechanical analysis. The dentinal microtubule is well modeled as a cylinder with inner and outer radii of r and R (Fig. 4(c)). The goal is then to obtain an estimate of the velocity of dentinal fluid flow at the pulpal end of the microtubule resulting from the heating or cooling of the tooth.
Within Eq. (8) is an assumption that pressure exerted by the fluid on the dentinal microtubule is negligible, which appears to be a reasonable approximation because dentinal microtubules open to the pulp chamber. However, the resistance to fluid flow has not yet been measured and it is possible that the pressure can sustain an appreciable transient. Two factors will affect this velocity. The first factor is thermal stress within the dentine layer. Assuming that the outer surface of the cylinder is subjected to the thermal stress (through dentine layer) in the radial direction (Fig. 4(d)), the displacement of dentinal microtubule wall could be expressed as [2]
| (8) |
where υd is Poisson's ratio for the dentine layer.
Noting that the volume change of microtubule is given by
| (9) |
The dentinal fluid flow velocity at the pulpal end of microtubule due to thermal deformation of microtubule is obtained
| (10) |
where ′ represents a total derivative with respect to time.
The second factor is volume change of dentinal fluid caused by thermal expansion or contraction. This is governed by
| (11) |
where α is the coefficient of thermal expansion of the dentinal fluid. The fluid flow velocity at the pulpal end of microtubule due to thermal expansion or contraction of dentinal fluid is then
| (12) |
As described by Eq. (13), the total dentinal fluid flow velocity at the pulpal end of microtubule consists of two parts: flow due to microtubule volume change induced by thermal deformation, and flow due to thermally induced volume change of the dentinal fluid itself. These are average volumetric flow rates over the entire microtubule and can, thus, be added
| (13) |
Solving these equations yields an estimate of the volumetric flow from an individual dentinal microtubule as a function of time following a prescribed change of the temperature of the enamel (or dentine) surface.
4.4. Shear Stress on a Nociceptor Associated With Dentinal Fluid Flow.
Relating dentinal fluid flow velocities to signals traveling through nociceptors involves two more modeling steps. The first is a mechanics model to estimate shear stresses experienced by the terminal end of a nociceptor within a dentinal microtubule. This shear stress is then incorporated into a modified Hodgkin–Huxley model that accounts for the action of stress-activated mechanosensitive ion channels.
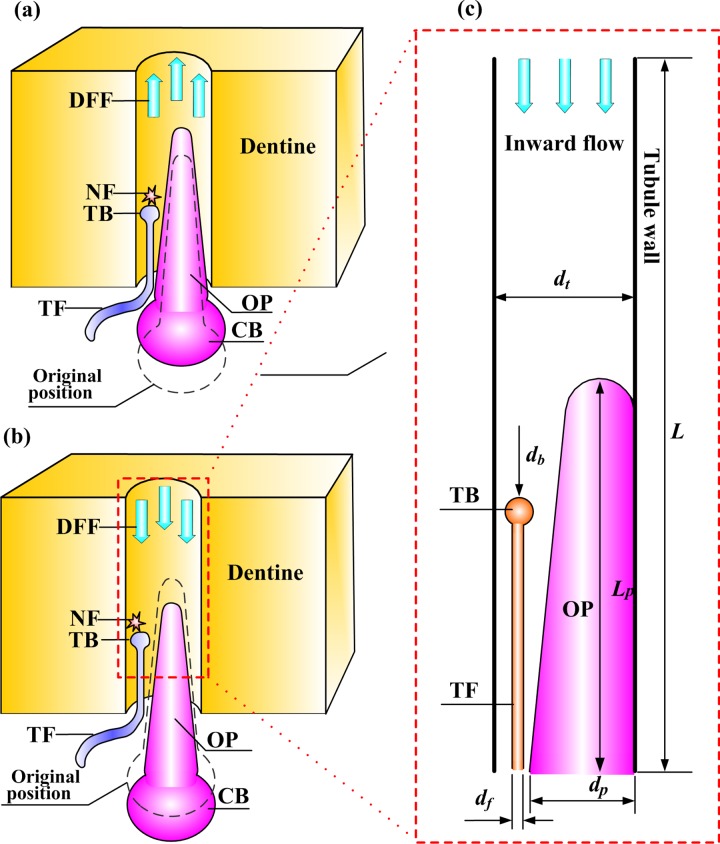
A typical dentinal microtubule contains a single terminal nociceptive fibril and a single odontoblastic process, with the remaining volume occupied by dentinal fluid [26] (Figs. 5(a) and 5(b)). Dentinal fluid flowing away from the pulp can displace an odontoblastic process into the dentinal microtubule (Fig. 5(a)), while flow into the pulp can displace such processes toward the pulpal exit of the dentinal microtubule (Fig. 5(b)) [9]. The goal of the model in this section is to predict shear stresses that arise on the terminal bead on the terminal fiber of a nociceptor as this occurs.
Fig. 5.
Microscale model of tooth physiology. (Reprinted from PLoS ONE with permission from PLoS.) (a) A slightly outward displacement of an OP and its CB in response to “outward” flow from the dentinal microtubule into the pulpal space; (b) a slightly inward displacement of an odontoblastic process and its cell body in response to “inward” flow from the pulpal space into the dentinal microtubule; (c) an idealization used to estimate fluid shear stresses on the TB of a nociceptor TF associated with DFF. NF: nerve firing.
A simplified two-dimensional computational fluid dynamics model has been developed for this purpose (Fig. 5(c)) and appears to capture the relevant physics [3,62]. The model involves an odontoblastic process and terminal fiber of a nociceptor residing in the pulpal along a portion of a dentine microtubule at the junction. The odontoblastic process is idealized roughly as a rounded cone that protrudes from the cell body in the pulp and narrows into the dentinal microtubule [26,63]. This cone displaces in the dentinal fluid flow direction by an amount that is approximated as varying linearly with mean fluid velocity.
With these assumptions and using parameters listed in Table 2, an estimate of the maximum shear stress around the terminal bead has been made using the flow field calculated from steady-state incompressible Navier–Stokes equations:
Table 2.
Physiological parameters of the dental innervation system
| Parameters | Value | Ref. |
|---|---|---|
| Dentinal microtubule (cat canine) diameter, dt (μm) | 0.73 | [9] |
| Dentinal fluid viscosity, μ (Pa·s) | 1.55 × 10−3 | [64] |
| Dentinal fluid density, ρ (kg/m3) | 1010 | [64] |
| Terminal fibril diameter, df (μm) | 0.1 | [65] |
| Terminal bead diameter, db (μm) | 0.2 | [25] |
| Odontoblastic process diameter, dp (μm) | <1 | [63] |
| (14) |
| (15) |
where V(m/s), p (Pa), ρ (kg/m3), and μ (Pa·s) are the velocity vector field, pressure field, mass density, and viscosity of the dentinal fluid, respectively. Constant fluid velocity boundary conditions are appropriate in these conditions for the proximal and distal boundaries [3]. The entrance or exit velocity can be scaled to data for dentinal fluid flow velocity Vc and associated nociceptor signals measured in a feline tooth model [9]; the boundary velocity V at the distal boundary of an individual dentinal microtubule scales with Vc according to the number density N of dentinal microtubule per unit area and the fraction of dentinal microtubules that are in free communication with the pulp, which is approximately 30% [66]
| (16) |
where dd is the nominal diameter of a dentinal microtubule. In a feline model, N ≈ 2200/mm2 and d d ≈ 0.73 μm have been reported [9].
Since the local channel diameter in the vicinity of the terminal bead (that is, the gap between the terminal bead and the odontoblastic process) is less than 1 μm, the slip boundary effect on the simulation results should be considered by using the following equation [62]:
| (17) |
where τ slip (Pa) and τ nonslip (Pa) are the wall shear stress when slip and nonslip boundary conditions are applied, respectively; δ (μm) is the slip length at the wall (∼0.1 μm); and h (μm) is the distance between two parallel walls (i.e., the local channel diameter of ∼0.12 μm). The final outcome of these simulations is an estimate of change of the maximum shear stress on a terminal bead.
4.5. Electrophysiological Response of a Nociceptor in Response to Fluid Shear Stress.
In response to noxious stimuli, nociceptors generate action potentials due to transport of ions through the cell membrane via nominally stimulus-specific ion channels situated on their terminal beads [21,67]. These channels are gated by three major classes of stimuli: mechanical, thermal, and chemical stimuli. These have been modeled as resulting in three distinct transmembrane currents that are induced accordingly [68]. Following the well-established model of Hodgkin and Huxley [68], the total stimulus-induced current, I st (μA/cm2), can then be calculated as the sum of the three currents in view of the parallel distributions of the ion channels in the membranes of nociceptors
| (18) |
where I mech, I heat, and I chem are the currents generated by the opening of the mechanically, thermally, and chemically gated ion channels, respectively (all in μA/cm2). In the following, equations are specialized to the case of intradental nociceptor terminals stimulated by shear stress from the dentinal fluid flow, so that only I mech is nonzero.
Since I mech from mechanically gated ion channels shows an approximately exponential scaling with the magnitude of mechanical stimulus [69], the quantitative relationship between the maximum shear stress and the stimulus current can be modeled as [3]
| (19) |
where I st is the mechanically evoked current; τ MSS is the maximum shear stress on the nociceptor terminal bead; τ thr is the threshold level of τ MSS required for activation of the mechanically gated ion channels; H(x) is the Heaviside function accounting for the threshold process; C h1 and C h3 constants with units of current density (e.g., μA/cm2); C h2 is a dimensionless constant; I shift (μA/cm2) is the shift current. Thus, action potential is generated only if τ MSS ≥ τ thr [3]. Reasonable values of C h1, C h2, and C h3 are 2.0 μA/cm2, 2.0, and −1.0 μA/cm2, respectively [3].
All neurons have been found to behave in a way quantitatively similar to that described by the Hodgkin–Huxley model [68]. Hence, a modified Hodgkin–Huxley model has been proposed to model multiple K + channels in the frequency modulation of nociceptors [3,70,71]
| (20) |
where V mem is the membrane potential (mV), which is positive when the membrane is depolarized and negative when the membrane is hyperpolarized; t (ms) is the neural discharge time; Cm (μF/cm2) is the membrane capacitance per unit area; I Na, IK, and IL are the Na+, K + and leakage current components (μA/cm2), respectively; IK 2 is an additional current (the fast transient K + current component, μA/cm2). The ionic currents I Na, IK, IL, and IK 2 are driven by the potential difference and governed by the permeability coefficient, or conductance [68,70]
| (21) |
| (22) |
| (23) |
| (24) |
where m, n, and h are gating variables; A and B are factors having the same functional significance as the factors m and h; V Na, VK, VL, and VK 2 are the reversal potentials for the Na+, K +, leakage, and fast transient K + current components (mV), respectively; and g Na, gK, gL, and gA are the associated maximal ionic conductances (mS/cm2), respectively. The conductance of the ionic current can be regulated by voltage dependent activation and inactivation variables (gating variables) [68]
| (25) |
where x can be any one of the three gating variables, m, n, and h; αx and βx are rate constants (s−1) that can be approximated from voltage clamp experiment [68]
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
The factors A and B can be estimated using the model of Connor et al. [72]
| (32) |
| (33) |
| (34) |
| (35) |
A major gap in the experimental literature is electrophysiological characterization of these constants for intradental nociceptors. However, parameters measured for squid axons [70] have proven adequate for replicating experimental observation for tooth nociceptor electrophysiology: gA = 47.7 mS/cm2, Cm = 2.80 μF/cm2, g Na = 120 mS/cm2, gK = 36 mS/cm2, gL = 0.3 mS/cm2, A fac = B fac = 7.0, m fac = H fac = 0.263, and n fac = 2.63. Two free parameters remaining are V Na and VK, which have been chosen to fit experimental data for a feline canine tooth: V Na = 57.2 mV and VK = –78.8 mV [73]. The remaining parameter, the reversal potential of leakage current VL, has been estimated by adjusting VL to reach the equilibrium membrane potential, resulting in VL = –63.8 mV [70,71]. This model, in combination with those above, can test the entire hydrodynamic hypothesis by predicting action potential arising from intradental nociceptors as a function of heating of the surface of a tooth.
5. The Role of Modeling in Testing Hypotheses for Thermal Pain Transduction in Teeth
The hierarchical multiscale models presented in this review applied to predict experimentally measured nociceptor signals arising from controlled conditions of fluid flow across dentine in living animals and from heating of teeth, and have been used to make additional predictions as well. We describe here efforts to link models with experiment and discuss what the integrated model predicts for the responses of teeth.
We begin with a discussion of thermally induced dentinal fluid flow in dentinal microtubules, and show results indicating that the effects of the dentinal fluid flow velocity and direction on the shear stress experienced by nociceptors have strong correlation with experimental observations related to thermal pain in teeth. We then link fluid flow to nociceptor input and to output signals predicted by a modified Hodgkin–Huxley model for intradental nociceptors. The model, with its integration of several hierarchies and classes of physics, performs quite well and suggests promise for such integrated models both in predicting and describing a broad range of physiologies and pathologies. We discuss some of these at the end of this section.
5.1. Heating at the Dentine-Enamel Junction.
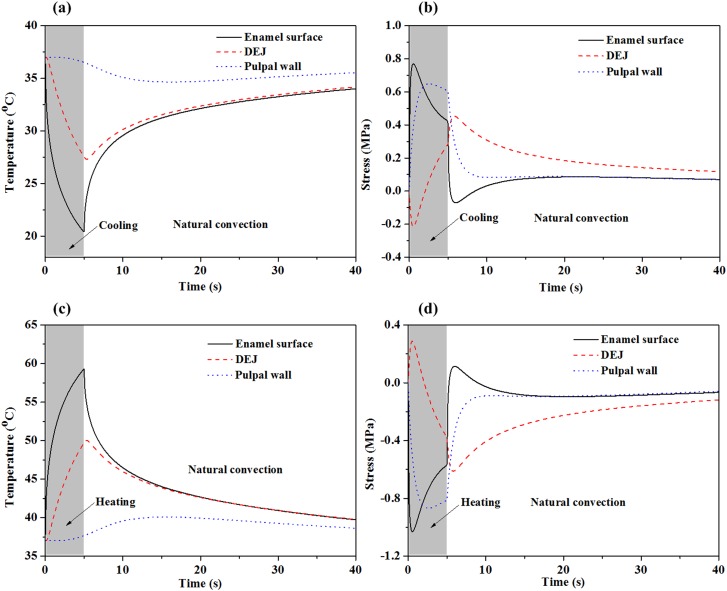
The time course of the temperature distribution in a heated tooth has proven to be useful not only as a first stage of the modeling of the hydrodynamic theory but also as a first order assessment of the feasibility of the neural hypothesis. Following cold stimulation, the temperature distribution near the dentine-enamel junction shows little deviation from the physiologic range at the time when nociceptor activation initiates (Fig. 6(a)). This calls into question the neural theory, but as mentioned above, does not falsify it because no model for the temperature activation of cold-sensing ion channels has yet been proposed.
Fig. 6.
Simulated temperature and thermal stress change as a function of time at the enamel surface, the DEJ and the pulpal wall following 5 °C cold saline ((a) and (b)) and 80 °C hot saline ((c) and (d)) stimulation on an enamel surface. (Reprinted from Archives of Oral Biology with permission from Elsevier.) Thermal stimulation for 5 s was followed by natural convection for35 s in a 25 °C room temperature. The heat transfer coefficient in the simulations was 10 W/(m2K). Initial condition: entire tooth at body temperature (37 °C). Boundary condition: bottom of pulp layer kept at body temperature (37 °C).
However, mechanical effects are predicted to reach the dentine-enamel junction and dentine-pulp junction much more quickly. This has been demonstrated by Linsuwanont et al. [20]. They found by finite element analysis that a rapid mechanical response could be observed before temperature changes reached the dentino-enamel junction. Cold stimulation induces contraction of the outer layer resulting in bending stresses in the layered tooth structure. Peak tensile stresses (positive) at the enamel surface and compressive stresses (negative) at the dentine-enamel junction (Fig. 6(b)) occur less than 1 s after initiation of cooling [2,74]. As the temperature change reaches deeper into the inner layer, the tensile stresses at the pulpal wall decrease, causing thermal contraction of the structure and counteracting the initial flexure. Although these deformation characteristics are consistent with the experimental observations by Linsuwanont et al. [20], we emphasize that this qualitative agreement serves only to suggest that the posited biophysical mechanisms are capable of predicting experimentally observed trends. Given the current state of the field and the relatively limited validation of models and parameters for all of the phenomena that contribute to these trends, this agreement serves as tenuous support. Much additional experimentation is still needed at all levels.
Hot stimulus of the enamel surface results in a similar time course of heating and stressing (Figs. 6(c) and 6(d)), weighing further against the neural hypothesis.
5.2. Thermally Induced Dentinal Fluid Flow.
It has been demonstrated that mechanical loading can result in dentinal fluid flow [16]. By fluid-structure interaction (FSI) simulation, Chang et al. found that the dentinal fluid flow velocity in the coronal pulp varies with different loading angles [75]. The dentinal fluid flow velocity increased as the mechanical loading angle decreased to 0 deg (approached the horizontal). They also found that mechanical loading as an effect of food mastication is able to induce dentinal fluid flow [19]. Their FSI simulation showed that dentinal fluid flow velocity depends on elastic modulus of masticated food particles and chewing rate. Masticating food with a high elastic modulus and faster chewing rate result in higher dentinal fluid flow, which may probably result in pain sensation.
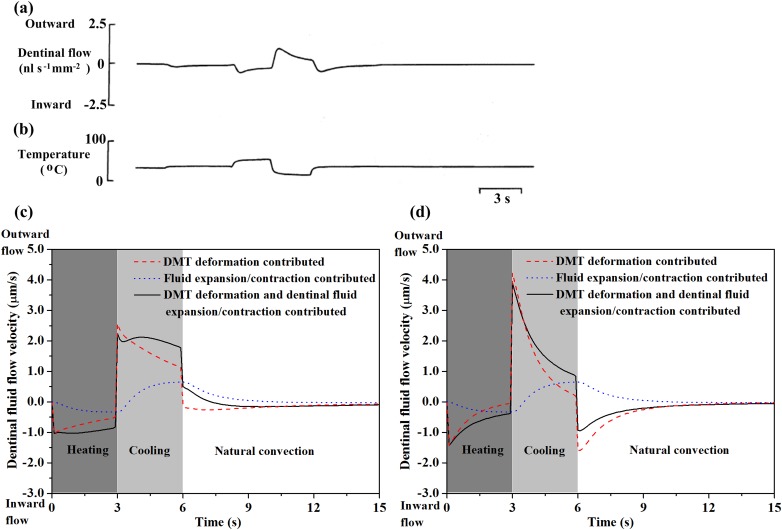
In addition to mechanical stimuli and some dental restorative processes [15,16], thermal stimulation has also been found to cause dentinal fluid flow in dentinal microtubules. This review will focus mainly on thermal induced dentinal fluid flow. Thermal stressing causes fluid flow within dentinal microtubules. Experiments conducted on teeth with exposed dentine (enamel layer removed) [9] provide a time course of this flow (Figs. 7(a) and 7(b)). Modeling efforts have helped identify the relative importance of the two sources of this flow: deformation of the dentinal microtubules and dilatation of the dentinal fluid [2]. Predictions (solid line, Fig. 7(c)) agree qualitatively with experiment and indicate a stronger role for dentinal microtubule thermal deformation (dashed line, Fig. 7(c)) than for dilatation of dentinal fluid (dotted line, Fig. 7(c)). Dentinal microtubule deformation causes an initially rapid inward flow (into the pulp) under heating and outward flow (away form the pulp) under cooling. Dentinal fluid dilatation opposes these flows, but acts much more slowly and with a lower magnitude. Dentinal microtubule deformation is, thus, most likely responsible for initially rapid, thermally induced fluid flow. Although experimental data do not exist, inclusion of the enamel surface is predicted to yield similar results (Fig. 7(d)) [2].
Fig. 7.
Estimates of how dentinal fluid flow velocity changes following thermal stimulation. Experimentally measured time course of dentinal fluid flow velocity (a) and corresponding temperature variation (b), (reprinted from Archives of Oral Biology with permission from Elsevier); simulated dentinal fluid flow velocity as a function of time for thermal stimulation on exposed dentine surface (c) and enamel surface (d). Heating: 55 °C, 3 s duration; cooling: 5 °C, 3 s duration, rewarming: 37 °C, (reprinted from Ref. [2] with permission from Elsevier).
Although the qualitative trends predicted by the simulations cited above are correct, we emphasize that these trends represent a major gap in the understanding of tooth mechanics: the predicted flow rates are nearly two orders of magnitude lower than measured flow rates. Reported cold stimulus (0–5 °C)-induced outward dentinal fluid flow velocities range between 530 and 850 μm/s [9,29], while those reported for hot stimulus (55 °C)-induced inward dentinal fluid flow range between 350 and 780 μm/s [9]. This certainly is an area that requires additional experimentation and analysis, and some discussion here of promising areas for future inquiry is warranted. An important difference to be analyzed is the way that fluid flow velocity was recorded by Andrew and Matthews [9]. These investigators used sectioned tooth root and their measured fluid flow rates, thus, included effects of expansion and fluid dilatation within the entire pulpal chamber rather than in the dentinal microtubules alone. Although the models seem to capture the main features of the responses of dentinal fluid under thermal stimulation, much more work is needed in this area.
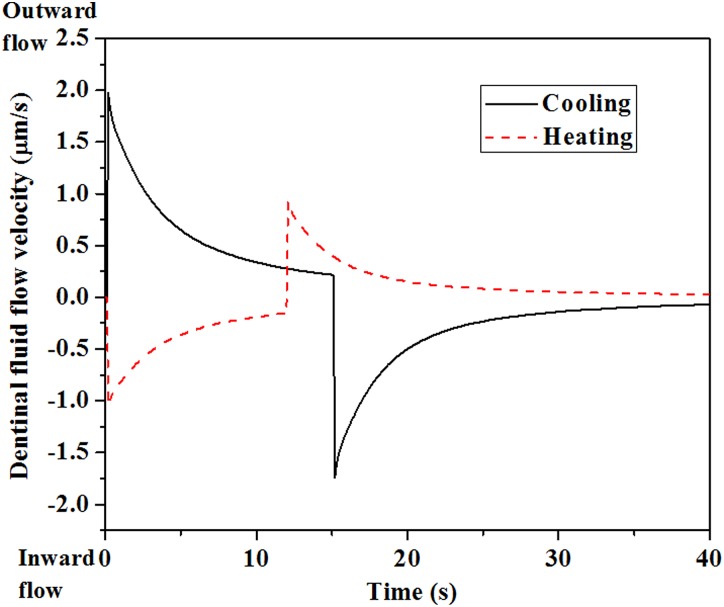
Flow of dentinal fluid within dentinal microtubules following cold stimulus correlates with the time courses of nociceptor signaling reported in Refs. [6,8,9] (solid line, Fig. 8). The initially high rate of outward dentinal fluid flow during the first ∼1 s may induce large shear stresses in the terminal beads of nociceptors within dentinal microtubules, resulting in activation of mechanosensitive ion channels and, consequently, neural discharge and pain [9,50,63,76]. The subsequent decay in dentinal fluid flow rate may, hence, reduce and eventually eliminate neural discharges and the associated sensations of pain (Fig. 2(b)). These observations leave one remaining mystery, however. Following heating of teeth to 55 °C, a much longer (>10 s) latent interval is observed in nociceptor response, over which no neural discharge can be detected (Fig. 2(a)) [6,8]. However, predictions of dentinal fluid flow within dentinal microtubules show no such latency period during heating, with thermomechanically induced dentinal microtubules deformation leads to rapid (<1 s) inward dentinal fluid flow (dashed line, Fig. 8). If the dentinal fluid flow responds just as quickly following heating as it does following cooling, how can dentinal fluid flow-induced nociceptor responses be so different following hot and cold stimuli?
Fig. 8.
Simulated dentinal fluid flow velocity as a function of time during thermal stimulation. (Reprinted from Archives of Oral Biology with permission from Elsevier.) Solid line: cooling at 5 °C, 15 s duration, followed by rewarming at 37 °C. Dashed line: heating at 55 °C, 12 s duration, followed by rewarming at 37 °C.
The explanation for this is suggested by experimental observations that nociceptors are much “less sensitive” to inward dentinal fluid flow, as arises from heating, than to outward dentinal fluid flow, as arises from cooling [9,50]. As we review in Sec. 5.3, the hierarchical models presented in this review uncover a mechanism for this difference, showing that the rate of inward dentinal fluid flow required to evoke responses through mechanosensitive ion channels on intradental nociceptors is much higher than the rate of outward dentinal fluid flow.
5.3. Mechanosensitive Ion Channels, Nociceptor Discharge, and the Differences Between Hot and Cold Tooth Pain.
The unresolved question of Sec. 5.2 is how very similar inward and outward dentinal fluid flow velocities, occurring over approximately the same time interval, can lead to very different signals from intradental nociceptors. We review in this section evidence that the question can be resolved through combined modeling of dentinal fluid flow over microscale anatomy, stress-activated ion channel activity, and nociceptor electrophysiology.
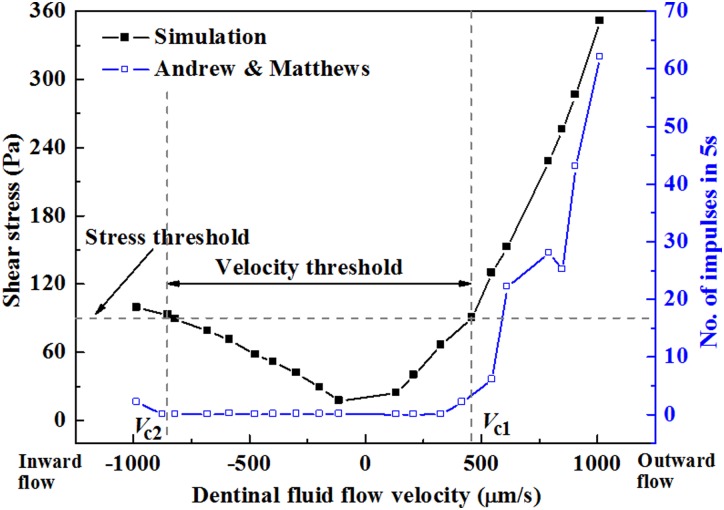
At the level of fluid flow over microscale anatomy, very similar inward and outward dentinal fluid flow velocities lead to very different shear stresses over the terminal beads of nociceptors [3]. As an example, Fig. 9 shows the maximum shear stresses predicted to occur on the surfaces of intradental nociceptor terminal beads for several inward (negative) and outward (positive) dentinal fluid flow velocities; the velocities chosen are those reported in Ref. [9]. The key result is that inward dentinal fluid flow produces much smaller shear stress on the terminal bead of the nociceptor fiber than does outward dentinal fluid flow of the same speed. Models suggest that this arises from differences in the constriction of the channel resulting from movement of odontoblastic process relative to the relatively rigid dentinal microtubule wall [3].
Fig. 9.
Estimated shear stress on a terminal bead compared to experimentally measured neural discharge rates. (Reprinted from PLoS ONE with permission from PLoS.) Dentinal fluid flow induces shear stress over the terminal bead of a nociceptor. The maximum estimated shear stress experienced by the terminal bead (line with, filled symbols) correlates with neural discharge rate (line with, open symbols) over a range of dentinal fluid flow velocities (negative for inward flow from the dentinal microtubules into the pulp; positive for outward flow from the pulp into the dentinal microtubules).
Mechanical modeling supports the contention that these differences in shear stress is transduced into significant differences in mechanical activation of nociceptors that terminate within dentinal microtubules. A key factor is that the mechanosensitive channels on the terminal beads of nociceptors have a threshold shear stress below which they are unlikely to become activated [9]. Although direct measurements have not yet been made, back-calculation of the threshold value by fitting predictions to experiment yields a reasonable threshold of approximately 90 Pa [3].
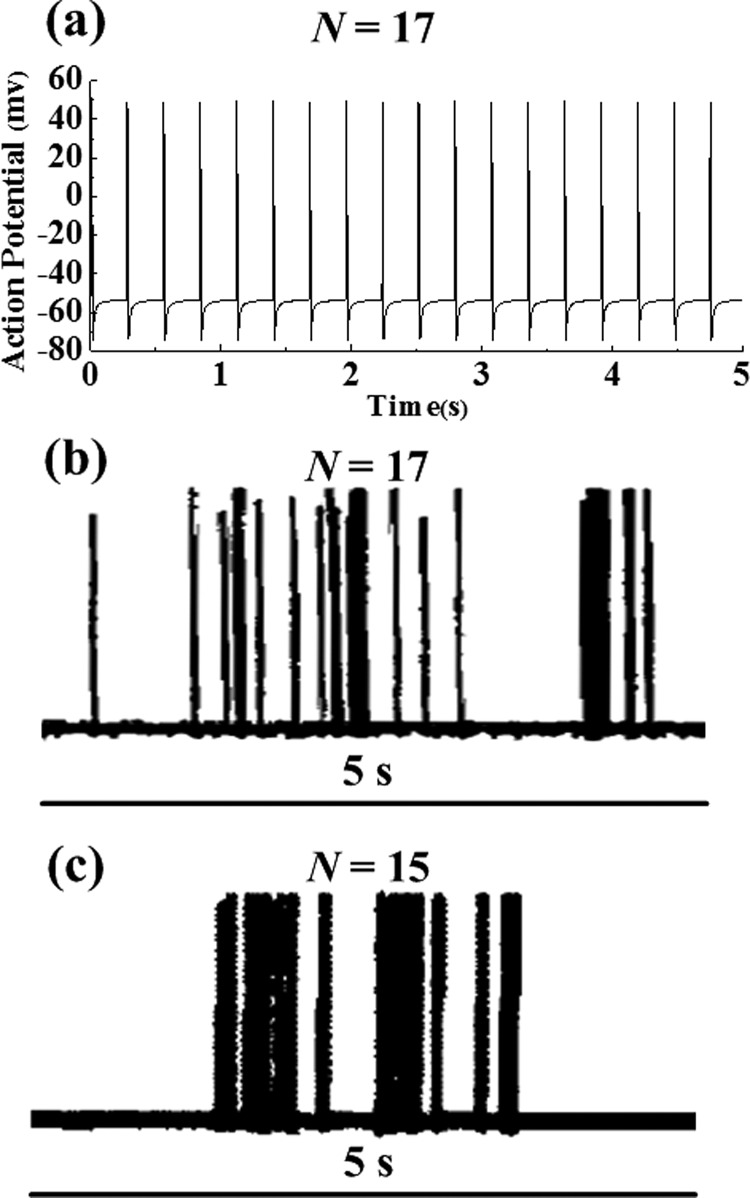
With this single parameter fitted, along with V Na and VK from Sec. 4. 5, models and experiment match quite well [3]. Simulated membrane potential (with frequency response of N = 7 impulses per 5 s interval (1.4 Hz), Fig. 10(a) [3]) at an outward flow velocity of ∼610 μm/s agrees well with experimental recordings of Vongsavan and Matthews [18] (N = 17 in Fig. 10(b)) and Andrew and Matthews [9] (N = 15 in Fig. 10(c)).
Fig. 10.
Variations in nociceptor membrane potential induced by an outward flow velocity (from the pulp into the dentinal microtubules) of 611.6 m/s. (Reprinted from PLoS ONE, Archives of Oral Biology, and The Journal of Physiology with permission from PLoS, Elsevier, and John Wiley and Sons respectively). (a) Simulated action potential; ((b) and (c)) experimental measurements by Vongsavan and Matthews [18] and Andrew and Matthews [9], respectively. N is the number of neural firing impulses in 5 s.
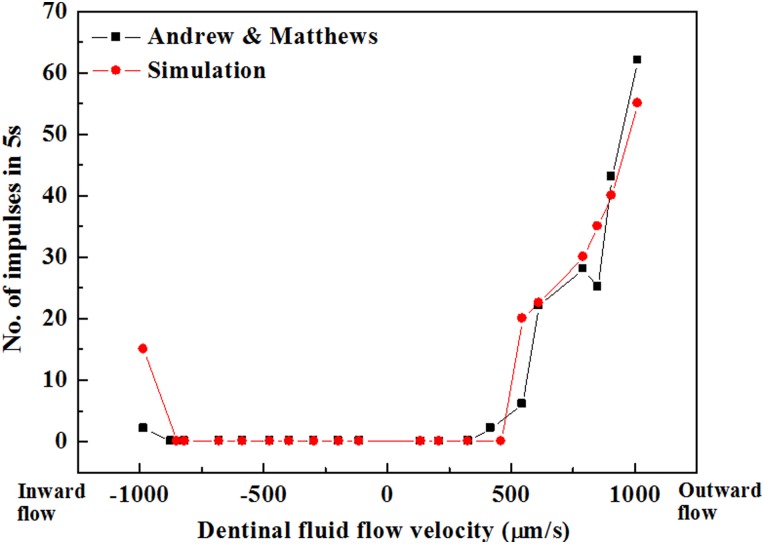
But what about the directionality of nociceptor response? Experimental observations show that the relationship between nociceptor discharge rate and dentinal fluid flow velocity is significantly different for dentinal fluid flow in different directions (Fig. 11) [9]. The nociceptor discharge rate increases progressively as outward dentinal fluid flow velocity increases above a threshold.
Fig. 11.
Comparison of simulated and measured nociceptor frequency responses. (Reprinted from PLoS ONE and The Journal of Physiology with permission from PLoS and John Wiley and Sons respectively). The data of Andrew and Matthews [9] can be well predicted by a the series of models reviewed in this article that embody the hydrodynamic theory.
Simulations can capture this and the fact that nociceptors appear much less sensitive to inward dentinal fluid flow (Fig. 11) [3]. The primary source of this in the models is odontoblastic process displacement: as described above, this displacement is different for inward and outward flows, and the resulting changes to shear stresses on the terminal bead of the nociceptor result in dramatically different pain responses [3]. Although much work is left to do, these correlations provide strong support for the hydrodynamic theory.
The story supported by the models is, thus, the following. The latency of the neural response following cold stimulus [6,8] is too short for the local temperature at the terminal beads of nociceptors within dentinal microtubules to activate temperature sensitive channels such as the TRPM8 channel [6], making these channels an unlikely source of the rapid response; however, outward dentinal fluid flow can be detected long before a temperature change at the dentine-enamel junction [9,17]. The models described here suggest that mechanoreceptors with physiologically reasonable threshold stresses may be activated by outward dentinal fluid flow and account for the initial sharp, shooting pain following noxious cooling of teeth.
The fluid mechanics models described here constitute tremendous simplifications of the tooth anatomy, including both the architecture of the tooth and the placement, shape, and interactions of odontoblasts and nerve fibers. Much more work is needed to identify the actual physiology of these cells and their interactions, and the state of the art in biomechanical modeling as we see it represents only crude guesses. However, these simplifications nevertheless enable a qualitative picture of how fluid flow and odontoblastic retraction might combine to enable rapid transduction of cold stimulus and slower transduction of hot stimulus.
Within this context, however, many possibilities arise for this signaling. The details of the way that nociceptors interact with odontoblastic processes and indeed the cell bodies themselves are in need of attention from the biomechanics community. Of particular interest is the emerging evidence supporting the possibility of odontoblasts themselves acting as sensory cells for tooth pain, either alone or in concert with membrane-bound nerve cells [40,41,43,46,47,49]. Biomechanical models that could be useful in testing the possibility of odontoblasts as sensing units are an important need.
5.4. Observations that Cannot be Explained by the Hydrodynamic Theory.
The above sections review support for the hydrodynamic hypothesis in explaining a central difference between hot and cold pain in teeth. However, other factors play roles in the wide range of thermal pain experienced, and for many of these the mathematical models described above show that hydrodynamic effects likely play only a minor role.
The first of these is a second sensation has been reported following sustained cold stimulus of teeth: a dull, burning pain that arises after a long latency (∼30 s) [28]. This latter pain sensation arises when predicted dentinal fluid flow velocities are much lower, and as a steady state temperature distribution is reached. Because at that time the temperature around the receptors may drop below the threshold for temperature-sensitive channels, this may be attributable to the activation of cold-sensitive receptors [28,77].
In the case of hot stimuli (55 °C), a relatively long latency (>10 s) of the nociceptor response can be observed, with no detectable discharge signal [6,8]. The models suggest that the relatively lower shear stresses evoked by the inward dentinal fluid flow are inadequate to activate mechanosensitive channels on nociceptors [3,9]. As above, these long latency and persistent pain signals might be due to activation of channels such as TRPV1 that can be activated after sufficient time for heat transfer [6,8]. For sustained heating of this magnitude, the pain signal transduced in nociceptors subsides, but this as well is unlikely to be due to hydrodynamic effects due to slower fluid flow near steady state. Instead, this may due to thermal denaturation of heat-sensitive ion channels on nociceptors.
6. Concluding Remarks
The models presented in this review bridge a broad range of biophysical phenomena and hierarchical length scales to connect the thermomechanics of teeth to nociceptor signals. In the problem presented here, a thermomechanical model of a tooth connects to a thermomechanical model of a dentinal fluid flow. A computational fluid dynamics simulation of flow around a single nociceptor terminal bead is introduced. Finally, by coupling this computational fluid dynamics model to a modified Hodgkin–Huxley model, a mechanistic insight is gained into long-standing questions regarding thermal pain in teeth. In the case of cold stimulus of teeth, an initially high rate of thermally induced outward dentinal fluid flow may activate intradental nerve terminals mechanically, thereby producing experimentally induced nociceptor discharge with short latency. This is a possible explanation for why cold stimuli seem to cause transient higher pain intensity than do hot stimuli.
The models open a number of interesting and important questions, many of which are outlined above. Further work is required to test and possibly falsify the neural hypothesis, and careful electrophysiological characterization of intradental nociceptors is warranted. Observation of cell dynamics during fluid flow would be quite valuable, and would help answer questions about some of the approximate models used above. For example, is it possible that nociceptor terminal bead motion is an important factor in hydrodynamic pain transduction? Does surface tension, known to drive some cellular migratory phenomena [78], play a role? Additionally, careful characterization of the tissue and flow field at the dentine/pulp interface is needed, as in a number of other hard-to-soft tissue transitions gradients and other mechanisms play important roles [78–81].
Beyond the teeth, transduction of mechanically induced fluid flow may underlie a great number of physiologic and pathophysiologic phenomena, and hierarchical, multiphysical models presented in this review have potential for application in a number of these areas. Indeed, fluid-induced mechanical stimuli to many cells are well known to be important in a range of pathologies such as cerebral aneurysm (e.g., Refs. [82,83]).
Of great relevance to the class of models presented here are other cases in which mechanically induced fluid flow may serve as an indirect but effective mechanism for physiologic or pathologic signal transduction. A possible example of physiologic signal transduction of this review is mechanotransduction by bone. The mechanism by which mechanical loading in bones is transduced by the osteoblasts, osteoclasts, and osteocytes that maintain and remodel bone are an area of ongoing debate. The transduction of fluid flow induced by mechanical constriction of narrow channels within bone is an intriguing candidate for this [84–86], and may potentially have overlap with the transduction of thermal pain in teeth.
A potential example of pathologic signal transduction is chronic back pain. Chronic back pain likely results from a very broad range of causes. A cerebrospinal fluid flow obstruction known as syringomyelia is an especially common occurrence following spinal cord injury, occurring in 28% of patients, and can result in pain that is poorly understood and is difficult to treat [87]. Mechanically induced fluid flow is a potential source of pain in this instance and in many other types of back pain.
Pain therapies themselves can benefit from the mechanistic understanding and quantitative predictive abilities that models like that developed in this review. The mechanisms underlying nonpharmacological therapies for low back pain are poorly understood at best. As one of many examples, the American College of Physicians and the American Pain Society both recommend traditional Chinese medicine (acupuncture) as a proven therapy for low back pain [88], but the reasons for acupuncture's efficacy and are not understood. Consensus is building that electrical stimulation in acupuncture operates through soluble factors [89], and the pathway for release of these factors may well involve ionic gradients, diffusion, and mechanotransduction by the central nervous system. Understanding pain and pain treatments is highly important, and motivate continued development of coupled biophysical models such as those described in this review.
Acknowledgment
This research was supported by the National 111 Project of China (B06024), the Major International Joint Research Program of China (11120101002), the Natural Science Foundation of Shaanxi Province (2012JQ1006), the Fundamental Research Funds for the Central Universities (2012jdhz46) and the National Institutes of Health (R01HL109505). F.X. was supported by the Program for New Century Excellent University Talents (NCET-12-0437) and the China Young 1000-Talent Program.
Contributor Information
Min Lin, The Key Laboratory of Biomedical Information, Engineering of Ministry of Education, School of Life Science and Technology, Xi'an Jiaotong University, Xi'an 710049, China;; Bioinspired Engineering, and Biomechanics Center, Xi'an Jiaotong University, Xi'an 710049, China
Guy M. Genin, Department of Neurological Surgery, and School of Engineering, Washington University, St. Louis, MO 63110; Department of Mechanical Engineering, and Materials Science, Washington University, St. Louis, MO 63130
Feng Xu, The Key Laboratory of Biomedical Information, Engineering of Ministry of Education, School of Life Science and Technology, Xi'an Jiaotong University, Xi'an 710049, China;; Bioinspired Engineering, and Biomechanics Center, Xi'an Jiaotong University, Xi'an 710049, China, e-mail: fengxu@mail.xjtu.edu.cn
TianJian Lu, Bioinspired Engineering, and Biomechanics Center, Xi'an Jiaotong University, Xi'an 710049, China, e-mail: tjlu@mail.xjtu.edu.cn.
References
- [1]. Brännström, M. , 1986, “The Hydrodynamic Theory of Dentinal Pain: Sensation in Preparations, Caries, and the Dentinal Crack Syndrome,” J. Endod., 12(10), pp. 453–45710.1016/S0099-2399(86)80198-4 [DOI] [PubMed] [Google Scholar]
- [2]. Lin, M. , Liu, S. B. , Niu, L. , Xu, F. , and Lu, T. J. , 2011, “Analysis of Thermal-Induced Dentinal Fluid Flow and Its Implications in Dental Thermal Pain,” Arch. Oral. Biol., 56(9), pp. 846–85410.1016/j.archoralbio.2011.02.011 [DOI] [PubMed] [Google Scholar]
- [3]. Lin, M. , Luo, Z. Y. , Bai, B. F. , Xu, F. , and Lu, T. J. , 2011, “Fluid Mechanics in Dentinal Microtubules Provides Mechanistic Insights Into the Difference Between Hot and Cold Dental Pain,” PLoS One, 6(3), p. e18068.10.1371/journal.pone.0018068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Ahn, D. K. , Doutova, E. A. , Mcnaughton, K. , Light, A. R. , Närhi, M. , and Maixner, W. , 2012, “Functional Properties of Tooth Pulp Neurons Responding to Thermal Stimulation,” J. Dent. Res., 91(4), pp. 401–40610.1177/0022034511435703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Brännström, M. , and Johnson, G. , 1970, “Movements of the Dentine and Pulp Liquids on Application of Thermal Stimuli. An in Vitro Study,” Acta Odontol. Scand., 28(1), pp. 59–7010.3109/00016357009033132 [DOI] [PubMed] [Google Scholar]
- [6]. Matthews, B. , 1977, “Responses of Intradental Nerves to Electrical and Thermal Stimulation of Teeth in Dogs,” J. Physiol. (London), 264, pp. 641–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Matthews, B. , 1968, “Cold-Sensitive and Heat-Sensitive Nerves in Teeth,” J. Dent. Res., 47, pp. 974–975. [Google Scholar]
- [8]. Jyvasjarvi, E. , and Kniffki, K. D. , 1987, “Cold Stimulation of Teeth: A Comparison Between the Responses of Cat Intradental a Delta and C Fibres and Human Sensation,” J. Physiol. (London), 391, pp. 193–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Andrew, D. , and Matthews, B. , 2000, “Displacement of the Contents of Dentinal Tubules and Sensory Transduction in Intradental Nerves of the Cat,” J. Physiol. (London), 529(3), pp. 791–80210.1111/j.1469-7793.2000.00791.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Sessle, B. J. , 1987, “Invited Review: The Neurobiology of Facial and Dental Pain: Present Knowledge, Future Directions,” J. Dent. Res., 66(5), pp. 962–98110.1177/00220345870660052201 [DOI] [PubMed] [Google Scholar]
- [11]. Brännström, M. , and Aström, A. , 1972, “The Hydrodynamics of the Dentine; Its Possible Relationship to Dentinal Pain,” Int. Dent. J., 22(2), pp. 219–227. [PubMed] [Google Scholar]
- [12]. Brännström, M. , and Johnson, G. , 1978, “The Sensory Mechanism in Human Dentin as Revealed by Evaporation and Mechanical Removal of Dentin,” J. Dent. Res., 57(1), pp. 49–5310.1177/00220345780570012001 [DOI] [PubMed] [Google Scholar]
- [13]. Brännström, M. , Linden, L. A. , and Astrom, A. , 1967, “The Hydrodynamics of the Dental Tubule and of Pulp Fluid. A Discussion of Its Significance in Relation to Dentinal Sensitivity,” Caries Res., 1(4), pp. 310–31710.1159/000259530 [DOI] [PubMed] [Google Scholar]
- [14]. Ratih, D. N. , Palamara, J. E. A. , and Messer, H. H. , 2007, “Dentinal Fluid Flow and Cuspal Displacement in Response to Resin Composite Restorative Procedures,” Dent. Mater., 23(11), pp. 1405–141110.1016/j.dental.2006.11.029 [DOI] [PubMed] [Google Scholar]
- [15]. Kim, S. Y. , Ferracane, J. , Kim, H. Y. , and Lee, I. B. , 2010, “Real-Time Measurement of Dentinal Fluid Flow During Amalgam and Composite Restoration,” J. Dent., 38(4), pp. 343–35110.1016/j.jdent.2009.12.008 [DOI] [PubMed] [Google Scholar]
- [16]. Paphangkorakit, J. , and Osborn, J. W. , 2000, “The Effect of Normal Occlusal Forces on Fluid Movement Through Human Dentine in Vitro,” Arch. Oral. Biol., 45(12), pp. 1033–104110.1016/S0003-9969(00)00090-X [DOI] [PubMed] [Google Scholar]
- [17]. Linsuwanont, P. , Palamara, J. E. A. , and Messer, H. H. , 2007, “An Investigation of Thermal Stimulation in Intact Teeth,” Arch. Oral. Biol., 52(3), pp. 218–22710.1016/j.archoralbio.2006.10.009 [DOI] [PubMed] [Google Scholar]
- [18]. Vongsavan, N. , and Matthews, B. , 2007, “The Relationship Between the Discharge of Intradental Nerves and the Rate of Fluid Flow Through Dentine in the Cat,” Arch. Oral. Biol., 52(7), pp. 640–64710.1016/j.archoralbio.2006.12.019 [DOI] [PubMed] [Google Scholar]
- [19]. Su, K. C. , Chuang, S. F. , Ng, E. K. , and Chang, C. H. , 2013, “An Investigation of Dentinal Fluid Flow in Dental Pulp During Food Mastication: Simulation of Fluid–Structure Interaction,” Biomech. Model. Mechanobiol., 12(4), pp. 1–910.1007/s10237-012-0464-x [DOI] [PubMed] [Google Scholar]
- [20]. Linsuwanont, P. , Versluis, A. , Palamara, J. E. , and Messer, H. H. , 2008, “Thermal Stimulation Causes Tooth Deformation: A Possible Alternative to the Hydrodynamic Theory?,” Arch. Oral. Biol., 53(3), pp. 261–27210.1016/j.archoralbio.2007.10.006 [DOI] [PubMed] [Google Scholar]
- [21]. Julius, D. , and Basbaum, A. I. , 2001, “Molecular Mechanisms of Nociception,” Nature, 43(13), pp. 203–21010.1038/35093019 [DOI] [PubMed] [Google Scholar]
- [22]. Närhi, M. , Jyväsjärvi, E. , Virtanen, A. , Huopaniemi, T. , Ngassapa, D. , and Hirvonen, T. , 1992, “Role of Intradental A- and C-Type Nerve Fibres in Dental Pain Mechanisms,” Proc. Finn. Dent. Soc., 88 (Suppl. 1), pp. 507–516. [PubMed] [Google Scholar]
- [23]. Grayson, W. , and Marshall, J. , 1993, “Dentin: Microstructure and Characterization,” Ouint. lnt. 24(9), pp. 606–617. [PubMed] [Google Scholar]
- [24]. Byers, M. R. , 1994, “Dynamic Plasticity of Dental Sensory Nerve Structure and Cytochemistry,” Arch. Oral. Biol., 39(Suppl. 1), pp. S13–S2110.1016/0003-9969(94)90183-X [DOI] [PubMed] [Google Scholar]
- [25]. Byers, M. R. , 1984, “Dental Sensory Receptors,” Int. Rev. Neurobiol., 25, pp. 39–9410.1016/S0074-7742(08)60677-7 [DOI] [PubMed] [Google Scholar]
- [26]. Carda, C. , and Peydro, A. , 2006, “Ultrastructural Patterns of Human Dentinal Tubules, Odontoblasts Processes and Nerve Fibres,” Tissue & Cell, 38(2), pp. 141–15010.1016/j.tice.2006.01.002 [DOI] [PubMed] [Google Scholar]
- [27]. Närhi, M. V. O. , 1985, “The Characteristics of Intradental Sensory Units and Their Response to Stimulation,” J. Dent. Res., 64, pp. 564–571. [DOI] [PubMed] [Google Scholar]
- [28]. Mengel, M. K. , Stiefenhofer, A. E. , Jyväsjärvi, E. , and Kniffki, K. D. , 1993, “Pain Sensation During Cold Stimulation of the Teeth: Differential Reflection of A [δ] and C Fibre Activity?,” Pain, 55(2), pp. 159–16910.1016/0304-3959(93)90145-F [DOI] [PubMed] [Google Scholar]
- [29]. Chidchuangchai, W. , Vongsavan, N. , and Matthews, B. , 2007, “Sensory Transduction Mechanisms Responsible for Pain Caused by Cold Stimulation of Dentine in Man,” Arch. Oral. Biol., 52(2), pp. 154–16010.1016/j.archoralbio.2006.09.009 [DOI] [PubMed] [Google Scholar]
- [30]. Gillam, D. G. , Mordan, N. J. , and Newman, H. N. , 1997, “The Dentin Disc Surface: A Plausible Model for Dentin Physiology and Dentin Sensitivity Evaluation,” Adv. Dent. Res., 11(4), pp. 487–50110.1177/08959374970110041701 [DOI] [PubMed] [Google Scholar]
- [31]. Woolf, C. J. , and Ma, Q. , 2007, “Nociceptors—Noxious Stimulus Detectors,” Neuron, 55(3), pp. 353–36410.1016/j.neuron.2007.07.016 [DOI] [PubMed] [Google Scholar]
- [32]. Mummery, J. H. , 1924, “The Nerve Supply of the Dentine,” Proc. R. Soc. Med., 17, pp. 35–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Trowbridge, H. O. , Franks, M. , Korostoff, E. , and Emling, R. , 1980, “Sensory Response to Thermal Stimulation in Human Teeth,” J. Endod., 6(1), pp. 405–41210.1016/S0099-2399(80)80216-0 [DOI] [PubMed] [Google Scholar]
- [34]. Naylor, M. N. , 1963, “Sensory Mechanisms in Dentine,” Studies on the Mechanism of Sensation to Cold Stimulation of Human Dentine, Anderson D. J., ed., Pergamon Press, Oxford, p. 73. [Google Scholar]
- [35]. Kollmann, W. , and Matthews, B. , 1982, “Anatomical, Physiological and Pharmacological Aspects of Trigeminal Pain,” Anatomical, Physiological and Pharmacological Aspects of Trigeminal Pain, Matthews B. and Hill R. G., eds,., Excerpta Medica, Amsterdam, pp. 51–65. [Google Scholar]
- [36]. Marquez, J. P. , Elson, E. L. , and Genin, G. M. , 2010, “Whole Cell Mechanics of Contractile Fibroblasts: Relations Between Effective Cellular and Extracellular Matrix Moduli,” Philos. Trans. R. Soc. A, 368, pp. 635–65410.1098/rsta.2009.0240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Marquez, J. P. , Genin, G. M. , Zahalak, G. I. , and Elson, E. L. , 2005, “Thin Bio-Artificial Tissues in Plane Stress: The Relationship Between Cell and Tissue Strain, and an Improved Constitutive Model,” Biophys. J., 88(2), pp. 765–77710.1529/biophysj.104.040808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. Marquez, J. P. , Genin, G. M. , Zahalak, G. I. , and Elson, E. L. , 2005, “The Relationship between Cell and Tissue Strain in Three-Dimensional Bio-Artificial Tissues,” Biophys. J., 88(2), pp. 778–78910.1529/biophysj.104.041947 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Maurin, J. C. , Couble, M. L. , Didier-Bazes, M. , Brisson, C. , Magloire, H. , and Bleicher, F. , 2004, “Expression and Localization of Reelin in Human Odontoblasts,” Matrix Biol., 23(5), pp. 277–28510.1016/j.matbio.2004.06.005 [DOI] [PubMed] [Google Scholar]
- [40]. Allard, B. , Magloire, H. , Couble, M. L. , Maurin, J. C. , and Bleicher, F. , 2006, “Voltage-Gated Sodium Channels Confer Excitability to Human Odontoblasts: Possible Role in Tooth Pain Transmission,” J. Biol. Chem., 281(39), pp. 29002–2901010.1074/jbc.M601020200 [DOI] [PubMed] [Google Scholar]
- [41]. Magloire, H. , Allard, B. , Couble, M. L. , Maurin, J. C. , and Bleicher, F. , 2008, “Mechanosensitivity in Cells and Tissues,” Mechanosensitive Ion Channels in Odontoblasts, A. Kamkin and I. Kiseleva, eds., Springer, New York. [Google Scholar]
- [42]. El Karim, I . A. , Linden, G. J. , Curtis, T. M. , About, I. , Mcgahon, M. K. , Irwin, C. R. , Killough, S. A. , and Lundy, F. T. , 2011, “Human Dental Pulp Fibroblasts Express the “Cold-Sensing” Transient Receptor Potential Channels Trpa1 and Trpm8,” J. Endod., 37(4), pp. 473–47810.1016/j.joen.2010.12.017 [DOI] [PubMed] [Google Scholar]
- [43]. El Karim, I. A. , Linden, G. J. , Curtis, T. M. , About, I. , Mcgahon, M. K. , Irwin, C. R. , and Lundy, F. T. , 2011, “Human Odontoblasts Express Functional Thermo-Sensitive TRP Channels: Implications for Dentin Sensitivity,” Pain, 152(10), pp. 2211–222310.1016/j.pain.2010.10.016 [DOI] [PubMed] [Google Scholar]
- [44]. Holland, G. R. , 1985, “The Odontoblast Process: Form and Function,” J. Dent. Res., 64, pp. 499–514. [DOI] [PubMed] [Google Scholar]
- [45]. Hirvonen, T. J. , and Narhi, M. V. , 1986, “The Effect of Dentinal Stimulation on Pulp Nerve Function and Pulp Morphology in the Dog,” J. Dent. Res., 65(11), pp. 1290–129310.1177/00220345860650110101 [DOI] [PubMed] [Google Scholar]
- [46]. Magloire, H. , Couble, M. L. , Thivichon-Prince, B. , Maurin, J. C. , and Bleicher, F. , 2009, “Odontoblast: A Mechano-Sensory Cell,” J. Exp. Zool., Part B, 312(5), pp. 416–42410.1002/jez.b.21264 [DOI] [PubMed] [Google Scholar]
- [47]. Magloire, H. , Lesage, F. , Couble, M. L. , Lazdunski, M. , and Bleicher, F. , 2003, “Expression and Localization of Trek-1 K+ Channels in Human Odontoblasts,” J. Dent. Res., 82(7), pp. 542–54510.1177/154405910308200711 [DOI] [PubMed] [Google Scholar]
- [48]. Allard, B. , Couble, M. L. , Magloire, H. , and Bleicher, F. , 2000, “Characterization and Gene Expression of High Conductance Calcium-Activated Potassium Channels Displaying Mechanosensitivity in Human Odontoblasts,” J. Biol. Chem., 275(33), pp. 25556–2556110.1074/jbc.M002327200 [DOI] [PubMed] [Google Scholar]
- [49]. Son, A. R. , Yang, Y. M. , Hong, J. H. , Lee, S. I. , Shibukawa, Y. , and Shin, D. M. , 2009, “Odontoblast Trp Channels and Thermo/Mechanical Transmission,” J. Dent. Res., 88(11), pp. 1014–101910.1177/0022034509343413 [DOI] [PubMed] [Google Scholar]
- [50]. Charoenlarp, P. , Wanachantararak, S. , Vongsavan, N. , and Matthews, B. , 2007, “Pain and the Rate of Dentinal Fluid Flow Produced by Hydrostatic Pressure Stimulation of Exposed Dentine in Man,” Arch. Oral. Biol., 52(7), pp. 625–63110.1016/j.archoralbio.2006.12.014 [DOI] [PubMed] [Google Scholar]
- [51]. Wang, R. , and Weiner, S. , 1998, “Human Root Dentin: Structural Anisotropy and Vickers Microhardness Isotropy,” Connect Tissue Res., 39(4), pp. 269–27910.3109/03008209809021502 [DOI] [PubMed] [Google Scholar]
- [52]. Kinney, J. H. , Marshall, S. J. , and Marshall, G. W. , 2003, “The Mechanical Properties of Human Dentin: A Critical Review and Re-Evaluation of the Dental Literature,” Crit. Rev. Oral Biol. Med., 14(1), pp. 13–2910.1177/154411130301400103 [DOI] [PubMed] [Google Scholar]
- [53]. Spears, I . R. , Van Noort, R. , Crompton, R. H. , Cardew, G. E. , and Howard, I . C. , 1993, “The Effects of Enamel Anisotropy on the Distribution of Stress in a Tooth,” J. Dent. Res., 72(11), pp. 1526–153110.1177/00220345930720111101 [DOI] [PubMed] [Google Scholar]
- [54]. Lin, M. , Liu, Q. D. , Kim, T. , Xu, F. , Bai, B. F. , and Lu, T. J. , 2010, “A New Method for Characterization of Thermal Properties of Human Enamel and Dentine: Influence of Microstructure,” Infrared Phys. Technol., 53(6), pp. 457–46310.1016/j.infrared.2010.09.004 [Google Scholar]
- [55]. De Vree, J. H. , Spierings, T. A. , and Plasschaert, A. J. , 1983, “A Simulation Model for Transient Thermal Analysis of Restored Teeth,” J. Dent. Res., 62(6), pp. 756–75910.1177/00220345830620061401 [DOI] [PubMed] [Google Scholar]
- [56]. Brown, W. S. , Dewey, W. A. , and Jacobs, H. R. , 1970, “Thermal Properties of Teeth,” J. Dent. Res., 49(4), pp. 752–75510.1177/00220345700490040701 [DOI] [PubMed] [Google Scholar]
- [57]. Xu, H. H. , Smith, D. T. , Jahanmir, S. , Romberg, E. , Kelly, J. R. , Thompson, V . P. , and Rekow, E. D. , 1998, “Indentation Damage and Mechanical Properties of Human Enamel and Dentin,” J. Dent. Res., 77(3), pp. 472–48010.1177/00220345980770030601 [DOI] [PubMed] [Google Scholar]
- [58]. Fenner, D. N. , Robinson, P. B. , and Cheung, P. M. Y. , 1998, “Three-Dimensional Finite Element Analysis of Thermal Shock in a Premolar With a Composite Resin Mod Restoration,” Med. Eng. Phys., 20(4), pp. 269–27510.1016/S1350-4533(98)00011-3 [DOI] [PubMed] [Google Scholar]
- [59]. Xu, H. C. , Liu, W. Y. , and Wang, T. , 1989, “Measurement of Thermal Expansion Coefficient of Human Teeth,” Aust. Dent. J., 34(6), pp. 530–53510.1111/j.1834-7819.1989.tb04660.x [DOI] [PubMed] [Google Scholar]
- [60]. Jakubinek, M. B. , O'Neill, C. , Felix, C. , Price, R. B. , and White, M. A. , 2008, “Temperature Excursions at the Pulp-Dentin Junction During the Curing of Light-Activated Dental Restorations,” Dent. Mater., 24(11), pp. 1468–147610.1016/j.dental.2008.03.012 [DOI] [PubMed] [Google Scholar]
- [61]. Xu, F. , Wen, T. , Seffen, K. A. , and Lu, T. J. , 2008, “Biothermomechanics of Skin Tissue,” J. Mech. Phys. Solids, 56(5), pp. 1852–188410.1016/j.jmps.2007.11.011 [Google Scholar]
- [62]. Lin, M. , Luo, Z. Y. , Bai, B. F. , Xu, F. , and Lu, T. J. , 2011, “Fluid Dynamics Analysis of Shear Stress on Nerve Endings in Dentinal Microtubule: A Quantitative Interpretation of Hydrodynamic Theory for Tooth Pain,” J. Mech. Med. Biol., 11(1), pp. 205–21910.1142/S0219519411003983 [Google Scholar]
- [63]. Pashley, D. H. , 1996, “Dynamics of the Pulpo-Dentin Complex,” Crit. Rev. Oral Biol. Med., 7(2), pp. 104–13310.1177/10454411960070020101 [DOI] [PubMed] [Google Scholar]
- [64]. Berggren, G. , and Brännström, M. , 1965, “The Rate of Flow in Dentinal Tubules Due to Capillary Attraction,” J. Dent. Res., 44(2), pp. 408–41510.1177/00220345650440021701 [DOI] [PubMed] [Google Scholar]
- [65]. Holland, G. R. , Matthews, B. , and Robinson, P. P. , 1987, “An Electrophysiological and Morphological Study of the Innervation and Reinnervation of Cat Dentine,” J. Physiol., 386, pp. 31–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66]. Pashley, D. H. , Livingston, M. I. , Reeder, O. W. , and Horner, J. A. , 1978, “Effects of the Degree of Tubule Occlusion on the Permeability of Human Dentine, in Vitro,” Arch. Oral. Biol., 23, pp. 1127–113310.1016/0003-9969(78)90119-X [DOI] [PubMed] [Google Scholar]
- [67]. McCleskey, E. W. , and Gold, M. S. , 1999, “Ion Channels of Nociception,” Annu. Rev. Physiol., 61, pp. 835–85610.1146/annurev.physiol.61.1.835 [DOI] [PubMed] [Google Scholar]
- [68]. Hodgkin, A. L. , and Huxley, A. F. , 1952, “A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve,” J. Physiol., 117, pp. 500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69]. Francois, R. , Liam, J. D. , and John, N. W. , 2010, “Kinetic Properties of Mechanically Activated Currents in Spinal Sensory Neurons,” J. Physiol., 588(2), pp. 301–31410.1113/jphysiol.2009.182360 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70]. Xu, F. , Wen, T. , Lu, T. J. , and Seffen, K. A. , 2008, “Modeling of Nociceptor Transduction in Skin Thermal Pain Sensation,” ASME J. Biomech. Eng., 130(4), p 041013.10.1115/1.2939370 [DOI] [PubMed] [Google Scholar]
- [71]. Xu, F. , Lu, T. J. , and Seffen, K. A. , 2008, “Skin Thermal Pain Modeling—A Holistic Method,” J. Therm. Biol., 33(4), pp. 223–23710.1016/j.jtherbio.2008.01.004 [Google Scholar]
- [72]. Connor, J. A. , Walkter, D. , and McKown, R. , 1977, “Neural Repetitive Firing Modifications of the Hodgkin–Huxley Axon Suggested by Experimental Results From Crustacean Axons,” Biophys. J., 18, pp. 81–10210.1016/S0006-3495(77)85598-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73]. Hodgkin, A. L. , 1964, The Conduction of the Nervous Impulses, Liverpool University Press, Livepool. [Google Scholar]
- [74]. Llyod, B. A. , McGinley, M. B. , and Brown, W. S. , 1978, “Thermal Stress in Teeth,” J. Dent. Res., 57(4), pp. 571–58210.1177/00220345780570040701 [DOI] [PubMed] [Google Scholar]
- [75]. Su, K. C. , Chang, C. H. , Chuang, S. F. , and Ng, E. Y. K. , 2013, “The Effect of Dentinal Fluid Flow During Loading in Various Directions—Simulation of Fluid–Structure Interaction,” Arch. Oral. Biol., 58(6), pp. 575–58210.1016/j.archoralbio.2012.10.004 [DOI] [PubMed] [Google Scholar]
- [76]. Brännström, M. , and Astroem, A. , 1964, “A Study on the Mechanism of Pain Elicited From the Dentin,” J. Dent. Res., 43, pp. 619–62510.1177/00220345640430041601 [DOI] [PubMed] [Google Scholar]
- [77]. Chul-Kyu, P. , Mi Sun, K. , Zhi, F. , Hai, Y. L. , Sung, J. J. , Se-Young, C. , Sung, J. L. , Kyungpyo P., Kim, J. S. , and Oh, S. B. , 2006, “Functional Expression of Thermo-Transient Receptor Potential Channels in Dental Primary Afferent Neurons: Implication for Tooth Pain,” J. Biol. Chem., 281(25), pp. 17304–1731110.1074/jbc.M511072200 [DOI] [PubMed] [Google Scholar]
- [78]. Polak, S. , Rustom, L. , Genin, G. , Talcott, M. , and Wagoner Johnson, A. , 2013, “A Mechanism for Effective Cell-Seeding in Rigid, Microporous Substrates,” Acta Biomater., 9(8), pp. 7977–798610.1016/j.actbio.2013.04.040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79]. Liu, Y. , Birman, V . , Chen, C. , Thomopoulos, S. , and Genin, G. M. , 2011, “Mechanisms of Bimaterial Attachment at the Interface of Tendon to Bone,” J. Eng. Mater. Technol., 133(1), pp. 76–8510.1115/1.4002641 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80]. Liu, Y. , Thomopoulos, S. , Birman, V . , Li, J.-S. , and Genin, G. , 2012, “Bi-Material Attachment Through a Compliant Interfacial System at the Tendon-to-Bone Insertion Site,” Mech. Mater., 44, pp. 83–9210.1016/j.mechmat.2011.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81]. Thomopoulos, S. , Birman, V . , and Genin, G. M. , 2013, Structural Interfaces and Attachments in Biology, Springer, New York. [Google Scholar]
- [82]. Xiang, J. , Natarajan, S. K. , Tremmel, M. , Ma, D. , Mocco, J. , Hopkins, L. N. , Siddiqui, A. H. , Levy, E. I. , and Meng, H. , 2011, “Hemodynamic–Morphologic Discriminants for Intracranial Aneurysm Rupture,” Stroke, 42(1), pp. 144–15210.1161/STROKEAHA.110.592923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [83]. Meng, H. , Metaxa, E. , Gao, L. , Liaw, N. , Natarajan, S. K. , Swartz, D. D. , Siddiqui, A. H. , Kolega, J. , and Mocco, J. , 2011, “Progressive Aneurysm Development Following Hemodynamic Insult,” J. Neurosurg., 114(4), pp. 1095–110310.3171/2010.9.JNS10368 [DOI] [PubMed] [Google Scholar]
- [84]. Fritton, S. P. , and Weinbaum, S. , 2009, “Fluid and Solute Transport in Bone: Flow-Induced Mechanotransduction,” Annu. Rev. Fluid. Mech., 41, pp. 347–37410.1146/annurev.fluid.010908.165136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85]. Wang, Y. , Mcnamara, L. M. , Schaffler, M. B. , and Weinbaum, S. , 2007, “A Model for the Role of Integrins in Flow Induced Mechanotransduction in Osteocytes,” Proc. Natl. Acad. Sci., U. S. A., 104(40), pp. 15941–1594610.1073/pnas.0707246104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86]. Cowin, S. C. , and Weinbaum, S. , 1998, “Strain Amplification in the Bone Mechanosensory System,” Am. J. Med. Sci., 316(3), pp. 184–18810.1097/00000441-199809000-00006 [DOI] [PubMed] [Google Scholar]
- [87]. Robert, R. , Perrouin-Verbe, B. , Albert, T. , Bussel, B. , and Hamel, O. , 2009, “Chronic Neuropathic Pain in Spinal Cord Injured Patients: What is the Effectiveness of Surgical Treatments Excluding Central Neurostimulations?,” Annal. Phys. Rehabil. Med., 52(2), pp. 194–20210.1016/j.rehab.2008.12.016 [DOI] [PubMed] [Google Scholar]
- [88]. Chou, R. , Qaseem, A. , Snow, V . , Casey, D. , Cross, J. T. J. , Shekelle, P. , and Owens, D. K. , 2007, “Diagnosis and Treatment of Low Back Pain: A Joint Clinical Practice Guideline from the American College of Physicians and the American Pain Society,” Ann. Intern. Med., 147(7), pp. 478–49110.7326/0003-4819-147-7-200710020-00006 [DOI] [PubMed] [Google Scholar]
- [89]. Ulett, G. A. , Han, S. , and Han, J.-S. , 1998, “Electroacupuncture: Mechanisms and Clinical Application,” Biol. Psychiatry, 44(2), pp. 129–13810.1016/S0006-3223(97)00394-6 [DOI] [PubMed] [Google Scholar]