Abstract
The present study addresses the prediction of apple tree development, taking into account both the number and within‐tree position of tree components. The architectural development of two trees per scion cultivar, ‘Fuji’ and ‘Braeburn’, was studied by describing all shoots over 6 years. Flowering and fruiting were observed over 3 years. The description included different scales [entire trees, axes, growth units (GUs) and metamers], and the analysis compared all axes of the trees as a function of their branching order and age. Three main aspects of vegetative development were investigated: the quantity of primary growth; the number and nature of developing axillary shoots; and meristem death. Results confirm the existence of within‐tree morphological gradients, and show that the decrease in growth was comparable in magnitude for all axes and GUs, irrespective of their position. This decrease results from a reduction in the number of metamers per GU, which was modelled by an exponential function. The decrease in growth involved changes in the number and nature of the axillary shoots, which could be described by simple functions. The probability of spur death was constant over the years but differed according to cultivar and type of bearing shoot. The within‐tree probability of flowering and fruiting was predictable for ‘Braeburn’ because axes, regardless of their position and type, had a high probability of flowering and a low probability of fruit set which led to a regular bearing habit. In contrast, ‘Fuji’ had an alternating bearing behaviour that was more complex to predict. This appeared to result from a synchronized increase in the probability that all GUs at tree scale are floral, combined with a high probability of fruit set. The consequences of these results for both yield prediction and architectural simulations are discussed.
Key words: Malus × domestica Borkh, tree architecture, morphological gradients, vegetative development, shoot types, growth units, metamers, branching, flowering, fruit set, synchrony, multi‐scale
INTRODUCTION
Apple tree production has been studied extensively from both quantitative and qualitative points of view. Tree and orchard productivities have been investigated in relation to many agronomic factors such as training systems, rootstocks and crop management practices. Within‐tree fruit position has been demonstrated to have a marked effect on fruit size and maturity. Spatial and topological fruit locations have been investigated: (1) in relation to spatial coordinates (x, y, z); and (2) fruit position with regard to other plant components in the branching system. On one hand, the effect of spatial position on fruit colour has been interpreted as being a result of the light environment (Robinson et al., 1983; Wünsche et al., 1996). On the other hand, the effect of topological position on fruit quality (especially its size and sugar content) has been interpreted as being the result of competition between organs for resources produced by physiological processes occurring simultaneously. In particular, fruiting and vegetative growth have often been considered as antagonistic processes (Jackson and Palmer, 1977; Evequoz et al., 1982). However, prediction of fruit production in these studies was based on total fruit weight per tree as correlated with trunk cross‐sectional area (Robinson and Lakso, 1991), or with regard to the type of shoot produced (Tustin et al., 1988; Volz et al., 1994). No predictions have yet been made of the within‐tree fruiting position.
In annual plants, the amount of crop produced can be predicted from the development of individual plants and responses to environmental conditions (Gauthier et al., 1999; Noffsinger et al., 2000). Such detailed predictions have yet to be developed for perennial plants, probably because of their structural complexity, which increases with time. Despite this, quantitative analyses of the architecture of several perennial species have shown that vegetative and floral shoot development is linked to its position in the tree (de Reffye et al., 1991b; Barthélémy et al., 1997). The link between shoot development and position has been described as ‘architectural gradients’ and has been used to simulate plant development by the use of the reference axis concept (de Reffye et al., 1991a; Blaise et al., 1998). As yet, the existence of architectural gradients has not been quantified in the apple tree. In addition, previous studies that have addressed the architectural development of fruit trees have not been able to predict productivity in terms of fruit number or position.
From a qualitative point of view, the architectural development of the apple tree results from rhythmic growth and monopodial branching until the apical meristem differentiates into an inflorescence (Crabbé, 1984). At that stage the morphogenetic activity of the meristem terminates. Several previous studies have described floral differentiation in the apple tree (Abbott, 1970, 1977; Luckwill, 1974). This occurs in the resting buds, either in terminal or axillary positions on 1‐year‐old wood. Thus, the floral growth unit (GU) that develops from the resting bud is a mixed unit composed of vegetative organs in its proximal part and floral organs in its distal part. This floral growth unit, called a ‘bourse’, usually bears an axillary vegetative GU that develops immediately (without any resting period) and is called a ‘bourse shoot’ (Escobedo‐Alvarez, 1990; Crabbé and Escobedo‐Alvarez, 1991). Because of this developmental pattern, the axes of the apple tree are made up of successive sympodial units. Growth remains rhythmic throughout tree ontogeny.
Quantitative investigations of plant architecture have recently been facilitated by improvements in measuring methodologies (Godin et al., 1997a, b; Hanan and Room, 1997; Sinoquet et al., 1997). These methods can be used to build architectural databases in which all organs of a tree can be located individually, without a priori sampling. In the present study, a method which deals with multi‐scale descriptions of plant topology (Godin and Caraglio, 1998; Godin et al., 1999) was used to investigate the developmental rules of individual apple trees. The aim was to predict vegetative development and the occurrence of flowering and fruiting within trees in relation to tree age and shoot type, as well as to compare the type of shoot development according to within‐tree position. Therefore, the multi‐scale topology of entire trees, i.e. the number, nature and relative position of tree components, was described. Owing to the time taken to acquire these datasets, only two trees per scion cultivar, ‘Fuji’ and ‘Braeburn’, were described. The analysis focused on within‐tree organization of the tree components and possible synchrony between events.
MATERIALS AND METHODS
Plant material
Forty trees per scion cultivar ‘Fuji’ and ‘Braeburn’, grafted on Lancep Pajam®1 (type M9), were planted at Melgueil INRA experimental station (south‐east France) in two blocks of 20 trees each, at 1·8 × 6 m spacing, in the winter of 1994–1995. During the first year of growth, trees were trained in a vertical axis by selecting the long axillary shoots along the main axis, which was maintained without pruning. In spring 1997, long and medium shoots were bent according to the ‘Solaxe’ training system (Lespinasse and Lauri, 1999). In June 1997, 1998 and 1999, young fruits were thinned manually, removing all axillary fruits on 1‐year‐old wood. Architectural data were collected on two trees per cultivar selected at random from each block of 20 trees. Fruit yields after thinning are given in Table 1 for these four trees for 1998 and 1999 (years 5 and 6).
Table 1.
Fruit yield after thinning of two ‘Fuji’ and two ‘Braeburn’ trees
| Number of fruit/TCSA (fruits cm–2) | ||
| Tree | Year 5 | Year 6 |
| ‘Fuji’1 | 8·2 | 11·8 |
| ‘Fuji’2 | 6·4 | 9·5 |
| ‘Braeburn’1 | 9·2 | 13·7 |
| ‘Braeburn’2 | 16·9 | 11·9 |
TCSA, Trunk cross‐sectional area.
Tree topology
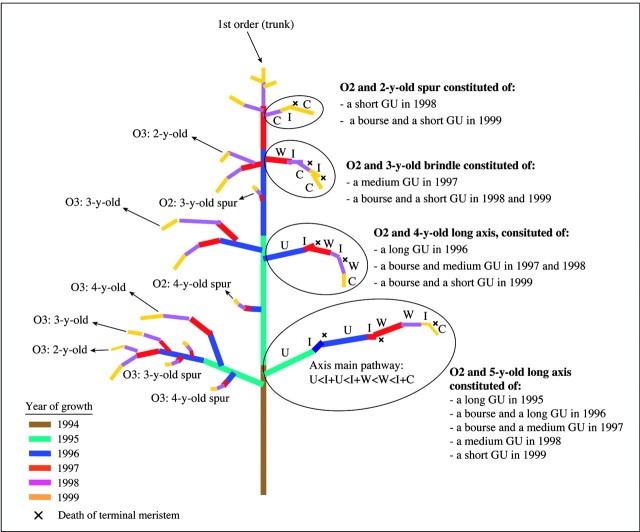
Two trees per cultivar were first described in 1997, when the trees were 4 years old. The method used, and the simplifications and codes chosen to describe tree topology have been described previously by Costes et al. (1999) and Godin et al. (1999). In brief, each tree was broken down into three levels of organization (Table 2; Fig. 1) corresponding to the axes, growth units and metamers (as defined by White, 1979). Two types of link between plant components were considered: succession and branching, denoted by < and +, respectively. Decomposition of a plant component into smaller components defined at a finer scale was denoted by / (Table 2). Three axis types were considered: long shoots, brindles and spurs (labelled R, W and S, respectively, in the database). All were pluri‐annual and sympodial axes. They were thus constituted of a succession of floral and vegetative GUs (examples of axis decomposition in GUs are given on the right‐hand side of Fig. 1). The definition of these three axis types was based on their composition in terms of GUs (Fig. 1): a long shoot is constituted of at least one long GU; a brindle is constituted of at least one medium GU but does not contain any long GUs; and a spur is constituted of a short GU only.
Table 2.
Scales, class symbols, and topological relationships used to describe apple tree architecture
| Scale | Symbol | Description | / = Decomposition | < = Succession | + = Branching |
| 1 Trees | f | ‘Fuji’ tree | R, W, S | ||
| b | ‘Braeburn’ tree | R, W, S | |||
| 2 Axis | R | Long shoot | U, B, D, I | R, W, S | |
| W | Brindle | B, D, I | W, S | ||
| S | Spur | D, I | S | ||
| 3 GU | I | Bourse | E | D, B, U | |
| U | Long GU (length > 20 cm) | E | I, D, B, U | I, D, B, U | |
| B | Medium GU (5 cm < length ≤ 20 cm) | E | I, D, B, U | I, D, B | |
| D | Short GU (length ≤ 5 cm) | E | I, D, B, U | I, D | |
| 4 Metamer | E | Internode | E, F | E, F | |
| F | Fruit |
GU, Growth unit.
Fig. 1. Schematic representation of an apple tree trained with the Solaxe system showing the location of the different axes and growth units (GUs) used for data extraction, sampling and statistical analysis. Examples of axes decomposition into GUs are illustrated on the right‐hand side. The left‐hand side illustrates the relationship between axis age and branching order. O2, Order 2; O3, order 3; O4, order 4.
Growth units were divided into four types: long GUs (labelled U) more than 20 cm in length; medium GUs (labelled B) more than 5 cm but less than 20 cm in length; and short GUs (labelled S) less than 5 cm in length. The fourth GU type corresponds to the floral GU or ‘bourse’ (labelled I) that results from floral differentiation of the apical meristem. Bourse shoots can develop into short, medium or long GUs, and were categorized in the same manner as vegetative GUs. Thus, in spring, the three vegetative GUs (long, medium and short) can develop either from the terminal bud if this has not differentiated into a bourse, or as a bourse shoot. Since the vegetative development of these GUs did not depend on the presence of a bourse (the difference was estimated to be less than 10 % on average; data not shown), we did not distinguish between these two categories in the rest of this paper.
Metamers were counted on the long and medium GUs only. Bud scale scars and the metamers whose axillary buds were not visible to the naked eye were ignored. Final fruit set was observed over three successive years: 1997–1999. When a bourse bore a fruit, it was considered as a different component, labelled F at the metamer scale.
In 1997, descriptions of each tree took 1 d; in 1998 and 1999, when the trees were 5 and 6 years old, 5–7 d were required to describe one tree. The main difficulty was the visual identification of each woody plant component recorded in the previous database and the description of the new growth both in axillary and terminal positions. New lines corresponding to the newly developed shoots and new variables were inserted into the database. This insertion was partly done as a post‐treatment of the database back in the laboratory, and was partly automated using a MicroSoft Visual Basic® program.
Variable extraction
The architectural database was explored using AMAPmod software (Godin et al., 1997a, b). Vegetative components, bourses and fruits were counted and located within the tree for each year of growth. The position of each component refers to its branching order (with order 1 corresponding to the trunk, order 2 to axillary shoots along the trunks, etc.) and to tree age, which also corresponds to calendar years, denoted 1 to 6 (Fig. 1). In some particular cases mentioned in the text, age refers to shoot age (which also corresponds to the insertion rank along its bearer shoot for a given branching order; Fig. 1). Axillary shoots that had a sylleptic development along the trunk (i.e. feathers) or along branches (which occurred only rarely) were not considered in this analysis. Thus, axis age corresponds to the year of growth of the bearer shoot minus one. To quantify tree development, tree components were counted on the three defined scales, taking into account their breakdown into finer scales.
Tree scale.
The total number of long shoots, brindles and spurs was counted by selecting components at scale 2 according to their label, R, W or S, and their branching order. The number of GUs, i.e. bourses and long, medium and short GUs, was counted by selecting, for each tree and each year, the components at scale 3 according to their label (I, U, B, D).
Axis scale.
Long shoots, brindles and spurs were grouped together relative to their branching order and age (Fig. 1). The different types of GU developing along the main pathway of these axes were then counted relative to the successive years of growth (Fig. 1). The probability of the three vegetative GUs (long, medium or short) was investigated. Because their sum is equal to 1 (Fig. 2), only two probabilities have to be calculated, the probability that a GU is medium (denoted by p1) or long (denoted by p2).
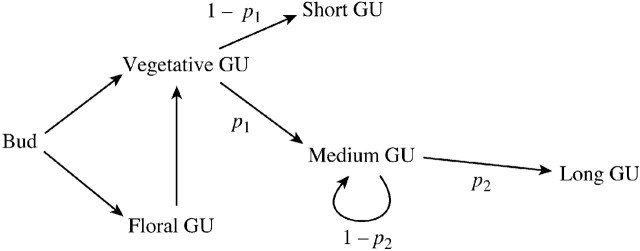
Fig. 2. Schematic representation of the different fates of a GU developing from a resting bud. Because three possible types of vegetative GU were considered, if p1 and p2 are, respectively, the probability that a given GU becomes a medium GU or continues its development to become a long GU, then: p(short GU) = 1 – p1, p(medium GU) = p1(1 – p2) and p(long GU) = p1p2, with p(short GU) + p(medium GU) + p(long GU) = 1.
For each year, the probability that a GU along the main pathway would be floral was calculated as the ratio between the number of bourses and the total number of first GUs that developed that year at that position. Indeed, when they develop, bourses are always the first GU within the annual shoots. After a bourse develops, a bourse shoot develops almost systematically on long shoots and brindles, but in a more variable manner for spurs. On spurs, the absence of a bourse shoot led to the spur death (or ‘extinction’ according to Lauri et al., 1997). The probability of a spur remaining alive was calculated for: (1) different types of bearing shoot (long shoots or brindles), and (2) different positions and spur ages within the trees and along the bearer shoots.
GU scale.
The number of metamers per GU was counted for each year of growth along axes and brindles. In the case of rhythmic growth within a year of growth, the number of metamers was summed. Branching was analysed for successive GUs of axes and brindles grouped together as previously described, according to branching order and age. Only long and medium GUs were considered since spurs usually produce only one new shoot (either terminal or a bourse shoot). When two bourse shoots developed on the same bourse, this was considered as a reiteration. For each year of growth the number of developed axillary shoots was compared with the number of metamers of the GU. The proportion of the three axillary shoot types (long shoots, brindles or spurs) was then calculated with reference to the total number of axillary shoots.
Finally, fruit set was calculated as the percentage of bourses bearing at least one fruit. In the same manner as previously, three axis types were considered and sorted according to their branching order and age.
Statistical analyses
All statistical analyses were performed using Statistica software (Kernel version 5.1, StatSoft, Inc., Tulsa, OK, USA). Owing to the small number of trees observed, results on the tree scale were analysed qualitatively, and the numbers of axes and GUs per tree were compared by χ2 tests. On the axis and GU scales, mean values for the different variables (number of GU types, number of metamers, number of axillary shoots) were computed. Their changes over the years or according to within‐tree positions were fitted as simply as possible using linear or exponential regressions. Mean values were compared using the non‐parametric Kruskall–Wallis analysis of variance since these variables were not normally distributed. In addition, the experimental design did not allow us to study interactions between the factors (axis type, branching order, age, year of growth) since the number of shoots and GUs were not similar for these different factors. Thus, each factor was analysed separately, considering the other factors as covariables in order to take account of, and suppress, the possible interactions.
RESULTS
Tree scale
‘Braeburn’ trees produced about 30 % more axes than ‘Fuji’ trees (Table 3), mainly due to a larger number of spurs in ‘Braeburn’ trees, although ‘Fuji’ trees developed more brindles. The distribution of brindles and spurs per branching order differed between cultivars but the distribution of long shoots did not differ significantly. For both cultivars, the number of long shoots reached a maximum at order 3, while the number of brindles was maximal at orders 3 and 4 in ‘Braeburn’ and ‘Fuji’, respectively. For both cultivars, spurs were more numerous when the branching order was ≥3, being maximal at order 4. Compared with ‘Fuji’ trees, there were more spurs in ‘Braeburn’ trees regardless of the branching order, but particularly at orders 4 and 5.
Table 3.
Mean number of long shoots, brindles and spurs per tree (n = 2), according to branching order, on ‘Fuji’ and ‘Braeburn’ apple trees
| Branching order | χ2 test | ||||||||
| Axis type | Cultivar | 1 | 2 | 3 | 4 | 5 | 6 | Total | (p) |
| Long shoots | ‘Braeburn’ | 1 | 20 | 38·5 | 12·5 | 72 | |||
| ‘Fuji’ | 1 | 17 | 30 | 15 | 3 | 66 | 0·845 | ||
| Brindles | ‘Braeburn’ | 0 | 18 | 102 | 97·5 | 33 | 3·5 | 254 | |
| ‘Fuji’ | 0 | 16 | 78 | 153 | 110 | 35·5 | 394 | <0·001 | |
| Spurs | ‘Braeburn’ | 0 | 52 | 570 | 963 | 616 | 117 | 2321 | |
| ‘Fuji’ | 0 | 30 | 447 | 542 | 387 | 89·5 | 1500 | 0·002 | |
| Total | ‘Braeburn’ | 1 | 90 | 710 | 1073 | 649 | 120 | 2646 | |
| ‘Fuji’ | 1 | 63 | 555 | 710 | 500 | 125 | 1959 | ||
In both cultivars, the mean number of long GUs per tree increased from the first to the fourth year of growth, then decreased in years five and six, whereas the number of bourses and short GUs increased each year (Table 4). By contrast, the number of medium GUs increased in ‘Braeburn’ trees until year 5, then decreased suddenly, whereas their number increased until year 6 in ‘Fuji’ trees. The total number of short GUs per tree also differed between the cultivars, being lower in ‘Fuji’ than in ‘Braeburn’. A similar difference was observed in the number of bourses per tree, but the difference was less in year 6. This suggests that entrance into productivity is slower in ‘Fuji’.
Table 4.
Mean number of long, medium and short growth units (GUs) per tree (n = 2) according to the year of growth, on ‘Fuji’ and ‘Braeburn’ apple trees
| Year of growth | χ 2 test | ||||||||
| GU type | Cultivar | 1 | 2 | 3 | 4 | 5 | 6 | Total | (p) |
| Long | ‘Braeburn’ | 1 | 8 | 37·5 | 52 | 7 | 7·5 | 113 | <0·001 |
| ‘Fuji’ | 1 | 5·5 | 33 | 50 | 31 | 16 | 136·5 | ||
| Medium | ‘Braeburn’ | 0 | 1 | 55 | 166 | 237 | 96·5 | 555·5 | <0·001 |
| ‘Fuji’ | 0 | 0·5 | 35 | 83·5 | 167·5 | 243 | 529·5 | ||
| Short | ‘Braeburn’ | 0 | 9 | 111 | 482·5 | 960·5 | 1642 | 3205 | <0·001 |
| ‘Fuji’ | 0 | 4 | 26·5 | 237 | 608·5 | 804·5 | 1680·5 | ||
| Bourse | ‘Braeburn’ | 0 | 11 | 146·5 | 576·5 | 1115·5 | 1382 | 3231·5 | <0·001 |
| ‘Fuji’ | 0 | 2·5 | 32 | 185 | 238 | 799 | 1256·5 | ||
Thus, the number of tree components and their development within trees differed between the two cultivars: ‘Braeburn’ trees developed most of their long shoots and long GUs over the first 4 years of growth, with the number being maximal at order 3; in ‘Fuji’, growth was less intense during the first years of tree development, but continued after year 4 with the development of medium GUs at higher branching orders. Over 6 years, twice as many GUs were produced on ‘Braeburn’ trees than on ‘Fuji’ trees.
Axis scale: bourse development
Along the main pathway of the three axis types, the probability of GUs being floral was higher in ‘Braeburn’ than in ‘Fuji’ (Table 5). This was studied in relation to three factors: (1) axis type, (2) branching order and (3) year of growth. On both cultivars, long shoots and brindles had a similar probability of being floral. In ‘Braeburn’, spurs were more likely to be floral than were long shoots or brindles, whereas in ‘Fuji’ spurs were less often floral. Among the total number of bourses per tree, those belonging to spurs (also called axillary flowers) represented 81 and 72 % in ‘Braeburn’ and ‘Fuji’, respectively (data not shown). Since long shoots and brindles had the same probability of being floral they were grouped in the same category for further analyses.
Table 5.
Probability of a GU being floral, according to axis type
| Cultivar | Long shoot | Brindle | Spur | Cultivar effect |
| ‘Braeburn’ | 0·75b | 0·76b | 0·82a | ** |
| ‘Fuji’ | 0·55a | 0·58a | 0·46b |
Within rows, different superscript letters indicate significant differences according to the Kruskall–Wallis non‐parametric test (P < 0·05). ** indicates significant effect of the cultivar according to the same test (P < 0.01).
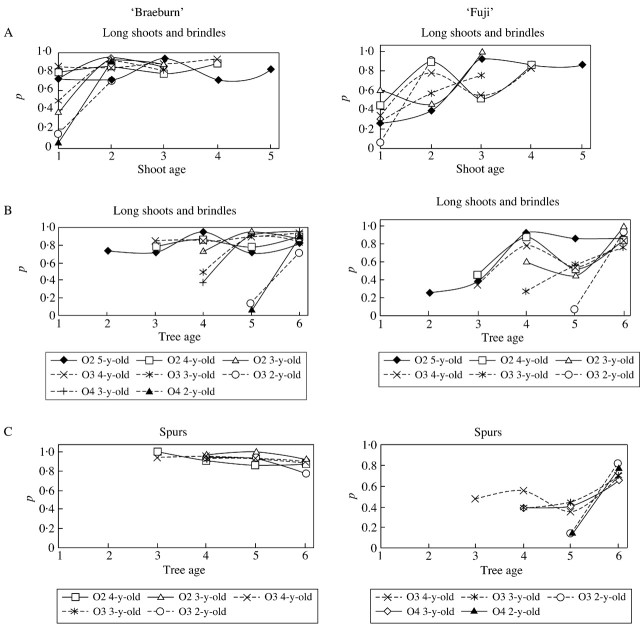
In both cultivars the probability of being floral was significantly affected by tree age, shoot age and branching order (Fig. 3A and B). In ‘Braeburn’, irrespective of whether tree age or axis age was chosen as the index, long shoots and brindles exhibited a similar behaviour: the oldest (5 and 4 years old), which began to develop when the tree was less than 4 years old, had a relatively high initial probability of flowering and this probability remained stable in the following years. Some fluctuations were observed, but their amplitude was low (the probability was always between 0·7 and 0·95). By contrast, the 2‐ and 3‐year‐old shoots that began to develop later, when the trees were 5 or 6 years old, showed a lower probability during their first year of growth. This was observed regardless of the branching order (order 3 and 4). However, once these shoots were 2 years old, the probability increased and thereafter did not differ from that of the older shoots.
Fig. 3. Probability that a GU will become floral, according to axis type on ‘Fuji’ and ‘Braeburn’ apple trees. The probability of the GU belonging to a long shoot or brindle was considered according to shoot age (A) and tree age (B), while that of the GU belonging to spurs was considered according to tree age only (C). O2, Order 2; O3, order 3; O4, order 4.
‘Fuji’ trees showed different behaviour according to age and branching order. On the one hand, when the shoots were sorted according to age, they exhibited markedly different and desynchronized behaviour (Fig. 3A). On the other hand, when sorted according to tree age, similar and synchronized behaviour was noted (Fig. 3B). As previously observed in ‘Braeburn’, the younger the shoot, the lower was its initial probability of flowering. But the oldest long shoots and brindles that began to develop when the trees were 2 and 3 years old had a relatively low initial probability of flowering. This probability increased until year 4. In year 5 a broad fluctuation in the probability of flowering was observed. The same occurred in year 5 for both order 2 and 3 shoots. The new shoots developing when the trees were 5 and 6 years old had a lower initial probability of flowering than older shoots. Their probability of flowering increased in the following year of growth, but this increase was less regular than that in ‘Braeburn’. Finally, considering all the shoots in year 5, shoots showing a high flowering probability in the previous year exhibited a low flowering probability, with the exception of the oldest shoots which maintained a high probability from years 4 to 6. In year 6 the situation was reversed. These results highlight the alternating floral behaviour of ‘Fuji’ trees.
A similar difference between cultivars was observed for the floral behaviour of spurs (Fig. 3C). In ‘Braeburn’, the flowering probability was close to 1 for all spurs, regardless of their age and position. The probability was slightly more variable for higher branching orders but remained high (0·9–1 for order 2 spurs; 0·8–0·9 for order 3 spurs). By contrast, the probability was fairly low for ‘Fuji’ spurs (0·1–0·5) over their first years of growth and increased with spur age. This increase was more rapid when the spurs were located at higher branching orders. During the growth of the oldest spurs much variation in flowering probability was observed, synchronized with that of long shoots and brindles. This indicates that the low flowering probability observed in year 5 was a general feature of all shoots within the trees, except the oldest long shoots.
Finally, these results highlight differences between cultivars in terms of their floral differentiation. In ‘Braeburn’, floral differentiation was regular from the second year of tree growth, and remained regular as the shoot aged. The spurs flowered regularly from their first year of growth, regardless of their position. In ‘Fuji’, axes seemed to acquire floral capability as the tree and shoot aged, and this phenomenon was faster for the axes at higher branching orders. Large variations in floral probability of all shoot types were observed as the axes aged. This variation was synchronous for all axes in the tree.
Axis scale: vegetative GUs
Successive analyses focused on: (1) the proportion of the three vegetative GU types along long shoots; (2) the proportion of medium and short GUs along brindles; and (3) the probability of the spurs remaining alive for different bearing axes (long shoot or brindle) and spur ages.
In both cultivars, the proportion of vegetative GUs depended on tree age (i.e. the year of growth) (Fig. 4A). Consequently, probabilities p1 and p2 (the probability of a GU being medium or long, respectively) were not constant values but were related to tree age in ‘Braeburn’ and to shoot age in ‘Fuji’. In ‘Braeburn’, long GUs were more numerous during the first 3 years of tree growth. In year 5, the proportion of long GUs decreased drastically for all long shoots within trees, i.e. regardless of their order and age. This decrease was compensated by a proportional increase in medium GUs, while the number of short GUs was fairly stable or decreased (Fig. 4B and C). In year 6, the proportion of medium GUs also decreased, while short GUs became the most numerous in the trees. This evolution was similar and synchronous for all long shoots, whatever their order and age.
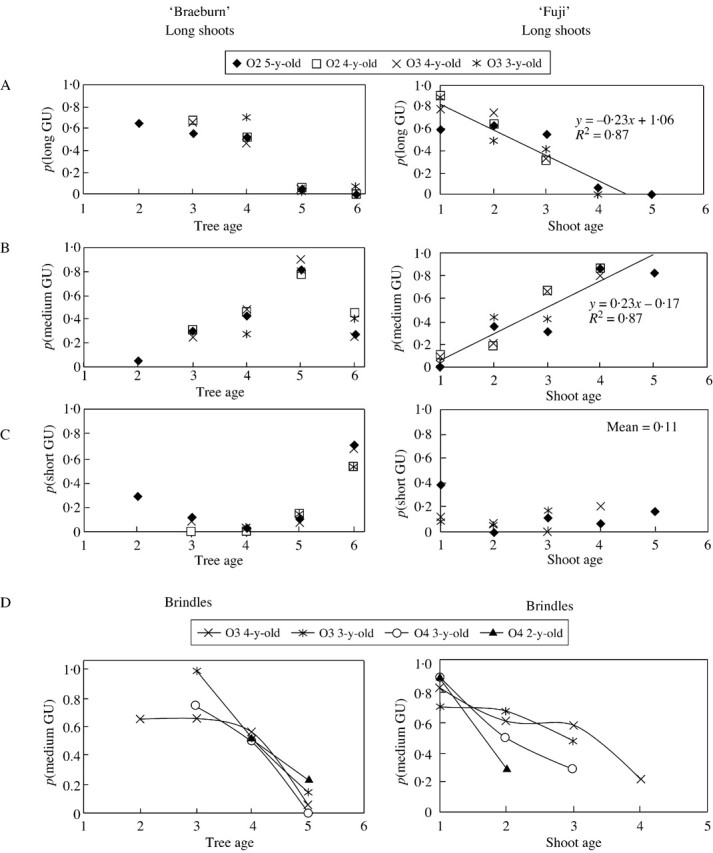
Fig. 4. Probability of the successive GUs of long shoots being long (A), medium (B) or short (C) according to the year of growth and the location of the shoot within the tree, on ‘Fuji’ and ‘Braeburn’ apple cultivars. D, Probability of the successive GUs of brindles being medium according to the year of growth and the location of the shoot within the tree. The x‐axis refers to the calendar years for ‘Braeburn’ (year 1 being 1995) and to shoot age for ‘Fuji’ (year 1 corresponds to the first year of growth of the shoot: 1995 if the shoot is 5 years old; 1996 if the shoot is 4 years old, etc.). O2, Order 2; O3, order 3; O4, order 4.
In ‘Fuji’, the proportion of long GUs also decreased with time, but the decrease was more gradual than that in ‘Braeburn’ (Fig. 4). This decrease was similar for all long shoots in the trees, irrespective of shoot age. It was proportionally compensated by the increase in medium GUs, whereas the proportion of spurs remained constant (Fig. 4B and C). The decrease in long GUs and the increase in medium GUs were fitted by linear regressions, whose parameters were identical but reversed in sign (±0·23). In this case, given that the proportion of spurs is constant and approximately equal to 0·11, it can be deduced that p1 = 0·89 and p2 ≈ –0·27a + 1·19, where a is tree age (in years), and p2 = 0 when a > 5.
Along the brindles, the number of medium GUs also decreased with tree age in ‘Braeburn’ trees, and with shoot age in ‘Fuji’ trees (Fig. 4D). This decrease was compensated by a corresponding increase in short GUs (data not shown). In both cultivars, the higher the branching order, the more rapid the decrease in medium GUs. In the same manner, in year 6, all GUs were short in ‘Braeburn’ while 20–30 % were medium in ‘Fuji’.
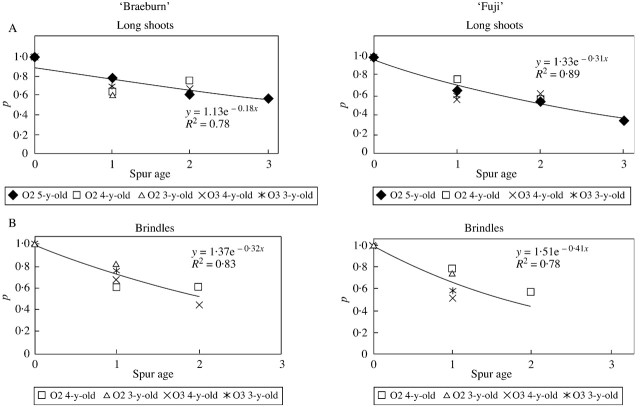
The proportion of spurs remaining alive after floral differentiation was investigated according to their age and bearing axis type (long shoot or brindle). This proportion decreased exponentially with spur age in both cultivars, regardless of shoot type (Fig. 5). The coefficient of the fitted exponential function corresponds to the death probability (or the absence of bourse shoot), which was constant over the years. In both cultivars this probability was lower in spurs borne on long shoots than on brindles. The two cultivars differed in the probability of spur death, with spurs dying more rapidly in ‘Fuji’ than in ‘Braeburn’, irrespective of the bearing‐shoot type.
Fig. 5. Proportion of spurs that remained alive according to spur age, on ‘Fuji’ and ‘Braeburn’ apple cultivars. The bearing shoot—long shoots (A) or brindles (B)—was considered according to its order and age. O2, Order 2; O3, order 3; O4, order 4.
GU scale: mean number of metamers per GU
The mean number of metamers was calculated for the successive GUs of trunks and order 2 and 3 long shoots (Fig. 6). Long and medium GUs, for which the number of metamers was observed, were grouped together in these calculations. In both cultivars, mean values decreased over successive years along the trunks and shoots. Along the trunks the GUs had a mean number of metamers that varied from 50 to 60 in the first year of growth, decreasing to an average of ten metamers in year 6. Along the long shoots, the mean number of metamers per GU decreased over 5 years (from year 2 to year 6). After six years of growth, none of the GUs contained more than an average of ten metamers, in either ‘Fuji’ or ‘Braeburn’ trees. In both cultivars, the mean number of metamers per GU in the different shoots was remarkably similar, irrespective of their order and age. Thus, the mean number of metamers that developed per GU did not differ for shoots belonging to the same branching order, but depended only on tree age.
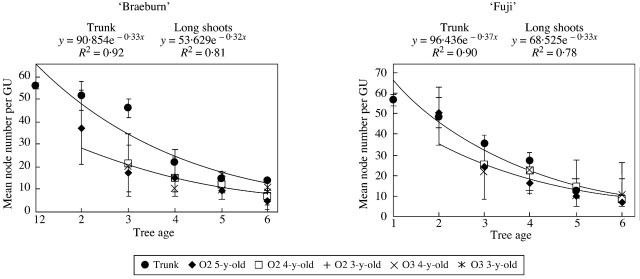
Fig. 6. Changes in the mean number of nodes per GU along the trunk and long shoots of ‘Fuji’ and ‘Braeburn’ apple trees, according to their branching order and insertion rank. O2, Order 2; O3, order 3; O4, order 4.
The decrease in the mean number of metamers per GU over time was fitted by exponential functions, considering successively the trunks and long shoots. In both cultivars, the mean number of metamers per GU could be predicted as a function of tree age with a high r2 coefficient (Fig. 6). The exponential function coefficient corresponds to the rate of decrease in the number of developed metamers over the years. During the first 3 years of growth, the GUs of long shoots of ‘Braeburn’ showed a lower mean number of metamers than those of the trunks. The trunk was thus dominant throughout this period. By contrast, in ‘Fuji’ trees, the mean number of metamers per GU was similar on trunks and long shoots over all 6 years of growth.
By definition, brindles contain only medium or short GUs. The mean number of metamers per medium GU was about ten (data not shown), irrespective of the branching order. As shown previously, the successive GUs are first medium and then rapidly become short. Since no count was made of the number of metamers in the short GUs, it was not possible to study the decrease in the mean number of metamers along the brindles.
Branching: number and type of axillary shoots
These two variables were studied for successive GUs along the trunks and long shoots, taking into account their branching order and age. In both cultivars, a linear relationship was found between the number of metamers and the number of axillary shoots (data not shown). A similar relationship accounted for long shoots at orders 2 and 3, and for trunks (r2 = 0·92 and 0·87 for ‘Braeburn’ and ‘Fuji’, respectively). Thus, the year of growth and the branching order had no direct effect on the relationship between the number of metamers and the number of axillary shoots. All of the variability due to the successive years of growth was accounted for by the number of metamers per GU.
In ‘Braeburn’, 61 % of the metamers bore an axillary shoot, whereas only 38 % of the metamers were branched in ‘Fuji’. In addition, intersections of the linear regressions with the x‐axis showed that no axillary shoots were present when the number of metamers was less than five in ‘Braeburn’, and less than two in ‘Fuji’. Consequently, the percentage of metamers bearing an axillary shoot decreased from the centre to the tree periphery because of the increase in the number of short GUs (data not shown).
To account for these results, the percentage of axillary shoot types (long shoots, brindles or spurs) was calculated for all long shoots, irrespective of their order or insertion rank, but taking into account the year of growth (Fig. 7). For both cultivars, and for all years of growth, spurs were the most numerous axillary shoot type. Their percentage increased until year 4, whereas that of long axillary shoots and brindles decreased rapidly. Thus, the decrease in the number of metamers per GU involved a modification in axillary shoot types. Indeed, the percentage of axillary buds able to develop was constant when the GU contained more than five nodes, but the probability that a given axillary shoot would continue to grow and develop into a brindle or, later, into a long shoot, decreased with the number of nodes of the bearing shoot. Thus, with the exception of a reiteration process, the development of an axillary shoot was equivalent to, or less than, that of its bearer. The decrease in the cumulative number of long axillary shoots and brindles was approximated by an exponential function. The coefficient of the exponential function corresponds to the rate of decrease in the probability of an axillary shoot being a brindle or long shoot. As previously observed at other scales, axillary shoots are more frequent in ‘Braeburn’ than in ‘Fuji’.
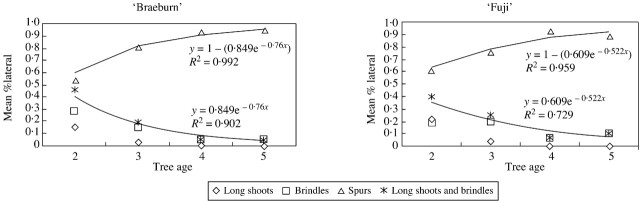
Fig. 7. Proportion of axillary shoot types borne on successive GUs of long shoots, on ‘Fuji’ and ‘Braeburn’ apple cultivars. The proportion of long axillary shoots (including both long shoots and brindles) is fitted by an exponential function, the parameter of which represents the rate of decrease in production of brindles and long axillary shoots.
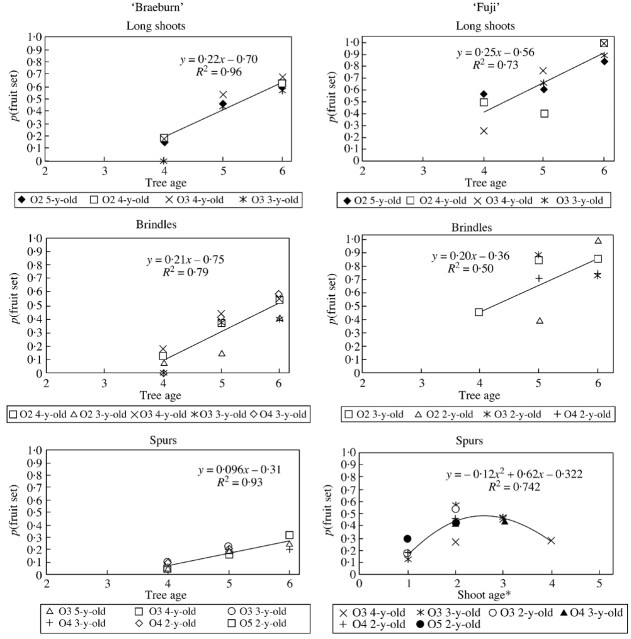
Final fruit set
Mean final fruit set was calculated for the 1997, 1998 and 1999 harvests. For both cultivars, shoot type and year of harvest had a significant effect on fruit set (Table 6), whereas shoot branching order had no effect (data not shown). In addition, regardless of the shoot type and year of harvest, ‘Fuji’ had a higher fruit set than ‘Braeburn’. Spurs always had a lower fruit set than long shoots and brindles. Because thinning had been performed preferentially on 1‐year‐old spurs, this category was removed when comparing fruit set of the different shoot types; this did not alter the results (data not shown). Fruit set in long shoots and brindles was not significantly different in 1998 but did differ in 1999. In 1999, long shoots had a larger fruit set in both cultivars.
Table 6.
Probability of a bourse bearing fruit, according to axis type
| Cultivar | Long | Brindle | Spur | Cultivar effect | |
| Year 5 | ‘Braeburn’ | 0·40a | 0·39a | 0·15b | ** |
| ‘Fuji’ | 0·67a | 0·71a | 0·40b | ||
| Year 6 | ‘Braeburn’ | 0·63a | 0·52b | 0·17c | ** |
| ‘Fuji’ | 0·94a | 0·65b | 0·35c |
Within rows, different superscript letters indicate significant differ ences according to the Kruskall–Wallis non‐parametric test (P < 0·05).
In both cultivars, and both for long shoots and brindles, the increase in fruit set over the years was fitted by a linear regression (Fig. 8). For each cultivar, the parameters were fairly similar between long shoots and brindles even though fruit set was more variable in brindles. This variability was the reason why, in ‘Fuji’, fruit set on long shoots and brindles was not significantly different in 1999. Spur fruit set increased linearly over the years in ‘Braeburn’, whereas that in ‘Fuji’ seemed to depend on spur age (this result requires confirmation since 4‐year‐old spurs were rare).
Fig. 8. Fruit set probability of floral GUs according to axis age and tree age (year of growth), on ‘Fuji’ and ‘Braeburn’ apple cultivars. * In the case of ‘Fuji’ spurs, a better prediction of fruit set probability was obtained with spur age than with tree age. O2, Order 2; O3, order 3; O4, order 4.
Considering all of the axillary shoots borne on a given GU, irrespective of their type and age, the relationship between the mean number of fruits and the mean number of floral GUs can be approximated by a linear regression (r2 = 0·97 and 0·92 for ‘Braeburn’ and ‘Fuji’, respectively; data not shown). The slopes correspond to the probability of fruit set, which was higher in ‘Fuji’ than in ‘Braeburn’.
DISCUSSION
The present study allowed us to quantify how vegetative growth, flowering and fruiting evolve within apple trees over a time span of 6 years. Our data, showing a decrease in vegetative growth with tree age, were consistent with previous observations by other authors (Abbott, 1984), the decline corresponding to a growth reduction and an increase in the probability of flowering from the centre of the tree towards the periphery. This centrifugal gradient is also consistent with results found in other tree species (e.g. Costes et al., 1992; Sabatier and Barthélémy, 2001) and with the definition of a within‐tree ‘physiological age’ of buds (Gatsuk et al., 1980; Barthélémy et al., 1997). Our results confirmed this concept in apple trees. They showed that the decrease in growth was comparable in magnitude for all long shoots in the trees, regardless of their position, and for all GUs of axes. This decrease resulted from a decrease in the number of metamers per GU, which was modelled by an exponential function. A similar function was used for both cultivars, differing solely with regards to parameter values. The use of an exponential function had the advantage of providing an easy interpretation of the biological meaning of the parameter corresponding to the rate of reduction in metamer emergence over time. The metamer scale thus appeared to be suitable for modelling the evolution of vegetative growth. Nevertheless, the GU scale is preferable, especially when measurement time is a limiting factor, because measuring the number of metamers per GU is very time consuming. However, the changes in GU type along shoots over time was not as easy to model as the number of metamers, especially in ‘Braeburn’. Indeed, the sudden and synchronized decrease in GU types in year 5, from long GUs to medium and then short GUs, did not correspond to an easily predictable phenomenon. This could be due to our quite arbitrary classification into GU types, and to the class limits which are likely to vary with the observer.
Although the results of the present study were suitable for predicting the mean number of metamers per GU, they were unable to predict the corresponding distributions. Previous studies have shown that the number of metamers per GU does not generally follow a normal distribution and therefore more complex modelling methods are required (de Reffye et al., 1991a). Models have been developed by combining two functions that represent the proportion of GUs that develop a neoformed part and those that do not (de Reffye et al., 1991b; Costes et al., 1992; Seleznyova et al., 2002). This modelling approach is not an example but presently represents the only solution proposed. It was not possible to develop a similar approach in the present study because our focus on the very detailed description of a small number of trees meant that some GU positions were weakly represented.
As far as branching was concerned, quantitative and simple relationships were found between the number of nodes and the number and type of axillary shoots. Again, the relationships—linear regressions—were similar for both cultivars and for the different shoot positions. The slopes of the regressions differed between cultivars, i.e. cultivars differed in the number of nodes bearing an axillary shoot. In ‘Braeburn’, more axillary buds developed but most of the axillary shoots remained short. In both cultivars the development of axillary shoots was equivalent to or less than that of its bearer (when a reiteration process is ignored). As previously with the number of metamers, modelling could have been developed further, especially accounting for the distribution of axillary shoot types according to node rank, as previous carried out on 1‐year‐old apple tree trunks (Guédon et al., 2001; Costes and Guédon, 2002) and on peach trees, according to three different GU types (Fournier et al., 1998).
Spur death is also an important architectural feature that can be predicted using a simple model. The probability of spur death was estimated using an exponential function, the parameters of which differed between the cultivars and depended on the type of bearing shoot. Spurs had a shorter functional life when borne on brindles compared with those borne on long shoots. This result complements previous studies that took account of spur age but not bearing‐shoot type (e.g. Robinson et al., 1983; Lauri et al., 1997). Spurs were also functional for a shorter time in ‘Fuji’ than in ‘Braeburn’. This difference could result from a lower leaf area per spur in ‘Fuji’ compared with that in ‘Braeburn’, as demonstrated by Lauri and Kelner (2001).
Flowering probability cannot be predicted as easily as vegetative growth. Indeed, the alternating bearing pattern cannot be modelled on the basis of individual shoot position. Irregular bearing of ‘Fuji’ is consistent with previous descriptions (Ferree and Schmid, 2000). In addition, the atypical behaviour of ‘Fuji’ regarding the simultaneous occurrence of irregular bearing, with a high extinction of spurs and low number of developing axillary shoots, has already been reported by Lauri et al. (1997), and was interpreted as being the result of delayed axillary bud development. This was not observed in the present study, probably because the trees were relatively young.
Despite the difficulty in predicting flowering probability, new features were highlighted regarding the within‐tree flowering occurrences. For both cultivars, newly developed long shoots had a lower flowering ability than the older shoots. This was consistent with the ageing of meristems, as described by previous authors (Gatsuk, 1980; Barthélémy et al., 1997; Meilan, 1997). In ‘Braeburn’, the flowering probability of 1‐year‐old long shoots decreased with tree age (Fig. 9); older shoots and spurs had similar probabilities of flowering. This shows that flowering probability depends on both shoot and tree age. This simple relationship was not observed in ‘Fuji’, and a more complex function is needed to predict flowering probability, which takes into account both shoot and tree age, as well as the previous year’s fruit load. Indeed, ‘Fuji’ had a slower entrance into productivity as shown by the progressive increase in flowering probability. Because flowering was synchronized on all axes, irrespective of their type, age and position, a drastic decrease occurred simultaneously in all shoots, except the oldest, in the year following the first high yield.
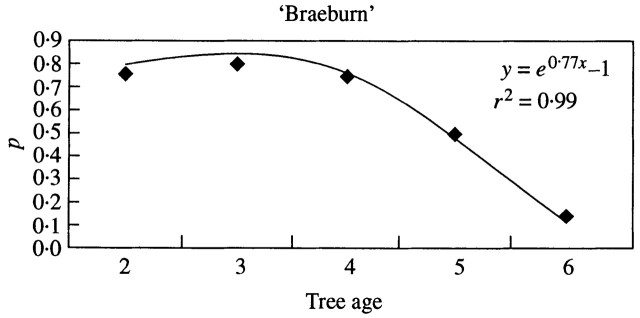
Fig. 9. Probability of the first GU of long shoots and brindles in ‘Braeburn’ being floral, according to tree age (the probability can be considered constant over the following years).
By contrast, fruit number can be easily predicted from the number of bourses that develop in the whole tree or in branching systems. These predictions were equivalent to that performed on the basis of trunk cross‐sectional area (Forshey and Elfving, 1979; Robinson and Lakso, 1991). However, such linear regressions cannot predict the within‐tree fruit position or the bearing‐shoot type, both of which are involved in determining final fruit size and colour (Farhoomand et al., 1977; Tustin et al., 1988). Within‐tree fruit positions can be predicted for both cultivars, by taking account of the differences in the fruit sets of the different shoot types. In ‘Braeburn’, this prediction can be quite precise owing to the relative homogeneity of fruit set on the different shoot types (Fig. 8), whereas it is less precise in ‘Fuji’. In both cultivars, the increase in fruit set observed with shoot age is consistent with previous reports, especially regarding spur ageing (Robbie and Atkinson, 1994).
Finally, our results provide a knowledge database that could be used to develop simulations of apple tree architecture, in particular regarding the topological aspects of architectural development. From a simulation point of view, tree growth is most often viewed as a collection of similar and repeated organs (White, 1979; Porter, 1983). These concepts of repetition and similarity constitute the basis of the models which were first able to simulate plant structure development (Prusinkiewicz and Lindenmayer, 1990; de Reffye et al., 1991a; Fisher, 1992). Our results showed that for most, but not all, of the studied events, axes can be considered as equivalent in their behaviour, in particular if they are sampled according to their age. However, the synchronism of events at the tree scale (such as the synchronized increase in flowering probability in ‘Fuji’ axes and the synchronized decrease in vegetative growth in ‘Braeburn’ axes) and differences in shoot behaviour that depend on the architectural position of the shoot do not argue in favour of strict equivalence between shoots belonging to a given shoot type. Results support the concept of a physiological age for meristems that changes with tree age and within‐tree position, and suggest that positional information has to be taken into account in simulations (Blaise et al., 1998; Prusinkiewicz et al., 2001). Further quantitative investigations of within‐tree shoot similarities are thus required. Methods developed recently for comparing tree topology could be convenient in this regard (Ferraro and Godin, 2000). In addition, our results could be compared with structure–function model outputs (for recent reviews, see Lacointe, 2000; Sievanen et al., 2000). In particular, this class of models could be used to test whether synchronism between axes and alternating bearing behaviour results from between‐organ competition. The comparison between two cultivars showed that the nature and intensity of competition between and within developing shoots can depend on the genotype and the type of process considered, i.e. vegetative growth or flowering. Accounting for genotypic differences in architectural simulations could thus help to explain the apparently contradictory behaviour that has been reported regarding the biennial bearing in different apple cultivars (Jonkers, 1979).
ACKNOWLEDGEMENTS
We are very grateful to G. Cornu (CIRAD Forêt) for his help in VisualBasic programming, and J. C. Salles, G. Garcia and S. Ploquin for their contribution in field measurements. This research was partly supported by INRA AIP AGRAF (1996–1999).
Supplementary Material
Received: 15 May 2002; Returned for revision: 29 July 2002; Accepted: 8 October 2002
References
- AbbottDL 1970. The role of budscales in the morphogenesis and dormancy of the apple fruit bud. In: Luckwill LC, Cutting CV, eds. Physiology of tree crops London: Academic Press, 65–81. [Google Scholar]
- AbbottDL 1977. Fruit‐bud formation in Cox’s Orange Pippin Annual Report Long Ashton Research Station for 1976–1977, 167–176. [Google Scholar]
- Abbott DL 1984. The apple tree: physiology and management. London: Grower Books. [Google Scholar]
- BarthélémyD, Caraglio Y, Costes E.1997. Architecture, gradients morphogénétiques et âge physiologique chez les végétaux. In: Bouchon J, de Reffye P, Barthélémy D, eds. Modélisation et simulation de l’architecture des végétaux Science UpDate. Paris: INRA Editions, 89–136. [Google Scholar]
- BlaiseF, Barczi J, Dinouard P, de Reffye P 1998. Simulation of the growth of plants – modeling of metamorphosis and spatial interactions. In: Kunii TL, Luciani A, eds, Cyberworlds. The architecture and development of plants Tokyo: Springer‐Verlag, 81–109. [Google Scholar]
- CostesE, Guédon Y 2002. Modelling branching patterns in 1‐year‐old trunks of six apple cultivars. Annals of Botany 89: 513–524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CostesE, Sinoquet H, Godin C, Kelner J.1999. 3D digitizing based on tree topology: application to study the variability of apple quality within the canopy. Acta Horticulturae 499: 271–280. [Google Scholar]
- CostesE, de Reffye P, Lichou J, Guédon Y, Audubert A, Jay M.1992. Stochastic modelling of apricot growth units and branching. Acta Horticulturae 313: 89–98. [Google Scholar]
- CrabbéJ.1984. Vegetative vigor control over location and fate of flower buds, in fruit trees. Acta Horticulturae 149: 55–63. [Google Scholar]
- CrabbéJ, Escobedo‐Alvarez JA 1991. Activités méristématiques et cadre temporel assurant la transformation florale des bourgeons chez le Pommier (Malus × Domestica Borkh. cv. Golden Delicious). In: Edelin C, ed. L’arbre: biologie et développement Montpellier: Naturalia Monspeliensa, n° hors série, 369–379. [Google Scholar]
- de ReffyeP, Dinouard P, Barthélémy D 1991a Modélisation et simulation de l’architecture de l’orme du Japon Zelkova serrata (Thunb.) Makino (Ulmaceae): la notion d’axe de référence. In: Edelin C, ed. L’arbre: biologie et développement Montpellier: Naturalia Monspeliensa, n° hors série, 251–266. [Google Scholar]
- de ReffyeP, Elguero E, Costes E 1991b Growth units construction in trees: a stochastic approach. Acta Biotheoretica 39: 325–342. [Google Scholar]
- Escobedo‐AlvarezJA.1990. Etude de la transformation florale des bourgeons de la pousse de ‘bourse’ du pommier. PhD Thesis, Faculté des Sciences Agronomiques de Gembloux, Belgium. [Google Scholar]
- EvequozM, Catzeflis J, Pfammatter W, Ryser JP 1982. Essai sur l’antagonisme entre la végétation et la fructification du pommier. Revue Suisse de Viticulture, d’Arboriculture et d’Horticulture 14: 177–181. [Google Scholar]
- FarhoomandM, Patterson M, Chu C 1977. The ripening pattern of ‘Delicious’ apples in relation to position on the tree. Journal of the American Society for Horticultural Science 102: 771–774. [Google Scholar]
- FerraroP, Godin C 2000. A distance measure between plant architectures. Annals of Forest Science 57: 445–461. [Google Scholar]
- FerreeD, Smid JC 2000. Chemical thinning ‘Fuji’ apple in the Midwest. Journal of the American Pomological Society 54: 61–67. [Google Scholar]
- FisherJB.1992. How predictive are computer simulations of tree architecture. International Journal of Plant Sciences 153: 137–146. [Google Scholar]
- ForsheyCG, Elfving DC 1979. Estimating yield and fruit numbers of apple trees from branch samples. Journal of the American Society for Horticultural Science 104: 897–900. [Google Scholar]
- FournierD, Costes E, Guédon Y.1998. A comparison of different fruiting shoots of peach shoots. Acta Horticulturae 465: 557–565. [Google Scholar]
- GatsukLE, Smirnova OV, Vorontzova LI, Zaugolnova LB, Zhukova LA 1980. Age states of plants of various growth forms: a review. Journal of Ecology 68: 675–696. [Google Scholar]
- GauthierL, Gary C, Zekki H 1999. GPSF: a generic and object‐oriented framework for crop simulation. Ecological Modelling 116: 253–268. [Google Scholar]
- GodinC, Caraglio Y 1998. A multiscale model of plant topological structures. Journal of Theoretical Biology 191: 1–46. [DOI] [PubMed] [Google Scholar]
- GodinC, Costes E, Caraglio Y 1997a Exploring plant topological structure with the AMAPmod software: an outline. Silva Fennica 31: 357–368. [Google Scholar]
- GodinC, Costes E, Sinoquet H 1999. A method for describing plant architecture which integrates topology and geometry. Annals of Botany 84: 343–357. [Google Scholar]
- GodinC, Guédon Y, Costes E, Caraglio Y 1997b Measuring and analyzing plants with the AMAPmod software. In: Michalewicz MT, eds. Advances in computational life science. Vol. I Plants to ecosystems Collingwood, Australia: CSIRO Publishing; 53–84. [Google Scholar]
- GuédonY, Barthélémy D, Caraglio Y, Costes E 2001. Pattern analysis in branching and axillary sequences. Journal of Theoretical Biology 212: 481–520. [DOI] [PubMed] [Google Scholar]
- HananJ, Room P 1997. Practical aspects of virtual plant research. In: Michalewicz MT, ed. Advances in computational life science. Vol. I Plants to ecosystems Collingwood, Australia: CSIRO Publishing, 28–45. [Google Scholar]
- JacksonJE, Palmer JW 1977. Effects of shade on the growth and cropping of apple trees. I. Experimental details and effects on vegetative growth. Journal of Horticultural Science 52: 245–252. [Google Scholar]
- JonkersJ 1979. Biennal bearing in apple and pear: a literature survey. Scientia Horticulturae 11: 303–317. [Google Scholar]
- LacointeA 2000. Carbon allocation among tree organs: a review of basic processes and representation in functional–structural tree models. Annals of Forest Science 57: 521–533. [Google Scholar]
- LauriPE, Kelner JJ 2001. Shoot type demography and dry matter matter partitioning: a morphometric approach in apple (Malus × domestica). Canadian Journal of Botany 79: 1270–1273. [Google Scholar]
- LauriPE, Térouanne E, Lespinasse JM 1997. Relationship between the early development of apple fruiting axes and the regularity of bearing – an approach to the strategies of various cultivars. Journal of Horticultural Science 72: 519–530. [Google Scholar]
- LespinasseJM, Lauri PE 1999. Intégration des nouveaux concepts de conduite dans le système Solaxe. Revue suisse de Viticulture, Arboriculture, Horticulture 31: 167–171. [Google Scholar]
- LuckwillLC.1974. A new look at the process of fruit bud formation in apple. 19th International Horticultural Congress, Warszawa, 237–245. [Google Scholar]
- MeilanR 1997. Floral induction in woody angiosperms. New Forests 14: 179–202. [Google Scholar]
- NoffsingerS, Huyghe C, Van Santen E 2000. Analysis of grain‐yield components and inflorescence levels in winter‐type white lupin. Agronomy Journal 92: 1195–1202. [Google Scholar]
- PorterJR 1983. A modular approach to analysis of plant growth. 1. Theory and principles. New Phytologist 94: 183–190. [Google Scholar]
- PrusinkiewiczPR, Lindenmayer A 1990. The algorithmic beauty of plants. New York: Springer Verlag. [Google Scholar]
- PrusinkiewiczPR, Mündermann L, Karwowski R, Lane B.2001. The use of positional information in the modeling of plants. Proceedings of SIGGRAPH 2001, 289–300. [Google Scholar]
- RobbieFA, Atkinson CJ 1994. Wood and tree age as factors influencing the ability of apple flowers to set fruit. Journal of Horticultural Science 69: 609–623. [Google Scholar]
- RobinsonTL, Lakso AN 1991. Bases of yield and production efficiency in apple orchard systems. Journal of the American Society for Horticultural Science 116: 188–194. [Google Scholar]
- RobinsonTL, Seeley EJ, Barritt BH 1983. Effect of light environment and spur age on ‘Delicious’ apple fruit size and quality. Journal of the American Society for Horticultural Science 108: 855–861. [Google Scholar]
- SabatierS, Barthélémy D 2001. Bud structure in relation to shoot morphology and position on the vegetative annual shoots of Juglans regia L. (Juglandaceae). Annals of Botany 87: 117–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SeleznyovaA, Thorp T, Barnett A, Costes E 2002. Quantitative analysis of shoot development and branching pattern in Actinidia Annals of Botany 89: 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SievanenR, Nikinmaa E, Nygren P, Ozier‐Lafontaine H, Perttunen J, Hakula H 2000. Components of functional–structural tree models. Annals of Forest Science 57: 399–412. [Google Scholar]
- SinoquetH, Rivet P, Godin C 1997. Assessment of the three‐dimensional architecture of walnut trees using digitising. Silva Fennica 31: 265–273. [Google Scholar]
- TustinDS, Hirst PM, Warrington IJ 1988. Influence of orientation and position of fruiting axillary shoots on canopy light penetration, yield and fruit quality of ‘Granny Smith’ apple. Journal of the American Society for Horticultural Science 113: 693–699. [Google Scholar]
- VolzRK, Ferguson IB, Hewett EW, Woolley DJ 1994. Wood age and leaf area influence fruit size and mineral composition of apple fruit. Journal of Horticultural Science 69: 385–395. [Google Scholar]
- WhiteJ 1979. The plant as a metapopulation. Annual Review of Ecological Systems 10: 109–145. [Google Scholar]
- WünscheJN, Lakso AN, Robinson TL, Lenz F, Denning SS 1996. The bases of productivity in apple production systems: the role of light interception by different shoot types. Journal of the American Society for Horticultural Science 121: 886–893. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.