Abstract
We present an all‐inclusive software tool for dealing with the essential core of mathematical and statistical calculations in plant growth analysis. The tool calculates up to six of the most fundamental growth parameters according to a purely ‘classical’ approach across one harvest‐interval. All of the estimates carry standard errors and 95 % confidence limits. The tool is written in Microsoft® Excel 2000 and is available free of charge for use in teaching and research from www.aob.oupjournals.org article supplementary data (http://aob.oupjournals.org/cgi/content/full/90/4/485/DC1).
Key words: Relative growth rate, unit leaf rate, net assimilation rate, specific leaf area, leaf weight fraction, leaf area ratio, allometry
INTRODUCTION
Plant growth analysis is an explanatory, holistic and integrative approach to interpreting plant form and function. It uses simple primary data in the form of weights, areas, volumes and contents of plant components to investigate processes within and involving the whole plant (Evans, 1972; Causton and Venus, 1981; Hunt, 1990). From its origins at the end of the nineteenth century, plant growth analysis first illuminated plant physiology, then agronomy and now physiological and evolutionary plant ecology (e.g. Garnier et al., 1999). In this journal alone, Hoffmann and Poorter (2002) reported that 28 articles since 1993 have drawn upon the approach in one way or another.
This paper presents an up‐to‐date and very comprehensive software tool that deals readily with the essential core of mathematical and statistical calculations in plant growth analysis. These calculations can otherwise be tedious or, particularly in the case of the statistics, neglected.
We take the simplest possible approach, calculating the most fundamental of the growth parameters according to purely ‘classical’ methods across one harvest‐interval (meaning the period of time between two successive harvests). This contrasts with the ‘functional’ or ‘dynamic’ approach, involving the use of many harvests and fitted curves, which can be either parametric (Causton and Venus, 1981; Hunt, 1982) or form‐free (Shipley and Hunt, 1996), and also contrasts with the ‘combined’ approach involving curves fitted to classically derived values (Poorter, 1989). Here, we do not necessarily advocate the classical over the functional approach; we simply facilitate the appropriate calculations for those who have already chosen the former for adequate reasons.
The tool derives relative growth rate in whole plant dry weight (RGR), the central parameter in plant growth analysis, together with its components unit leaf rate (ULR) (the ‘net assimilation rate’, NAR, of many authors), specific leaf area (SLA), and leaf weight fraction (LWF). Instantaneously, these four are defined and related in the following way:
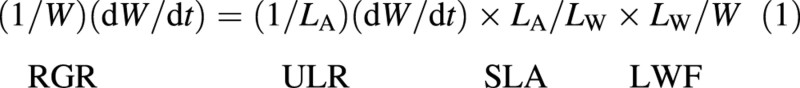
where t is time, W is total dry weight per plant, LA is total leaf area per plant and LW is total leaf dry weight per plant. Leaf weight fraction is synonymous with leaf weight ratio (LWR). The product of SLA and LWF, defined as LA/W and known as leaf area ratio (LAR), is also derived. These growth parameters are generic and many analogues exist that accept other plant variables as inputs (see Hunt, 1990).
The purpose of our tool is to estimate all five parameters, including LAR, as mean values solely across one harvest‐interval (t1 to t2), with a standard error (s.e.) and 95 % confidence limits attached to each estimate. The root–shoot allometric coefficient, and its s.e. and limits, are also derived for the same harvest‐interval.
METHODS
The mathematical and statistical methods follow those of Venus and Causton (1979), as developed by Causton and Venus (1981), whereby harvest‐interval means of the various parameters are obtained without the use of fitted functions and without the ‘pairing’ of plants across the harvest‐interval.
The value of the exact mean RGR across the harvest‐interval t1 to t2 is obtained from the usual formula by Fisher (1921):
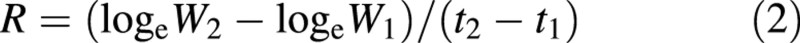
and the statistical estimate of this quantity, R̂, is the same. From Causton and Venus (1981, eqn 2.33), the variance of R is given by:
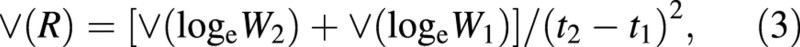
where the symbol ∨ represents variance. In both of these equations, W appears both at harvest 1 and at harvest 2: in eqn (2) it appears as harvest‐means of logeW (not as logs of harvest means of W; see Hoffmann and Poorter, 2002), and in eqn (3) it appears as arrays of replicated measurements. The degrees of freedom associated with the estimate of RGR, and with all the other parameters except the allometric coefficient, are n – 2, where n is the total number of plants for both harvests combined.
For mean ULR (NAR) across the same harvest‐interval, the approximate value is obtained from the usual formula by Williams (1946):
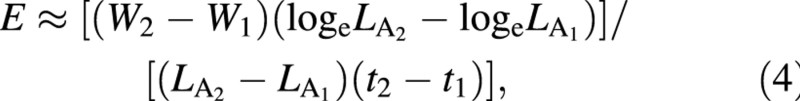
where the symbol ≈ means ‘is approximately equal to’. The statistical estimate of unit leaf rate, Ê, was derived by Causton and Venus (1981, eqn 2.34) and is:
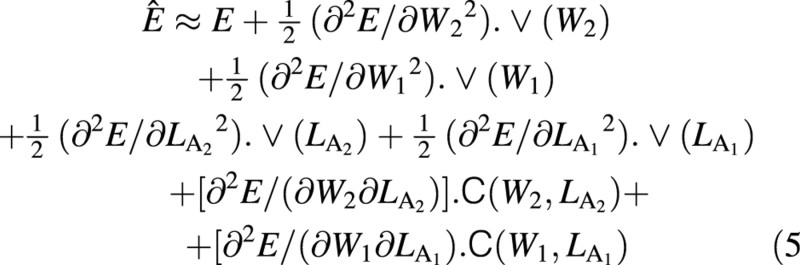
where C represents a covariance term. The variance of this expected mean ULR, again from Causton and Venus (1981, eqn 2.35), is given by:
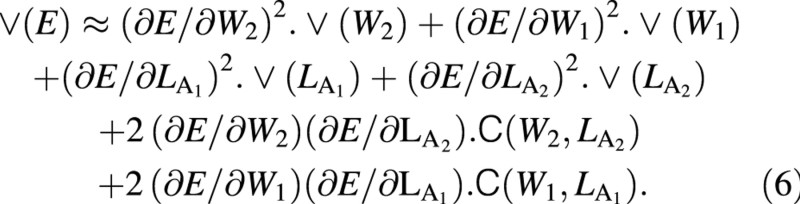
Again, variables W and LA appear both at harvest 1 and harvest 2: as harvest‐means of W, LA and loge LA in eqn (4) and as arrays of replicated measurements in eqns (5) and (6). Using the contractions ΔW = W2 – W1, ΔLA = LA2 – LA1, ΔlogeLA = logeLA2 – logeLA1 and Δt = t2 – t1, the derivatives that appear in eqns (5) and (6) are:
∂E/∂W1 = –ΔlogeLA/(ΔLA. Δt) (7)
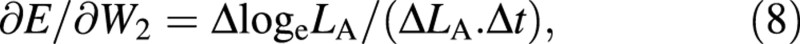
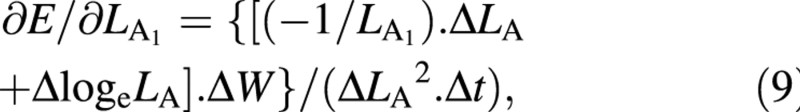
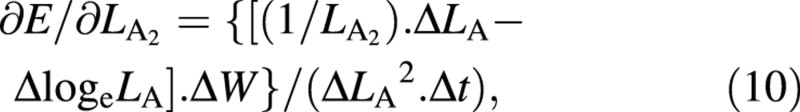
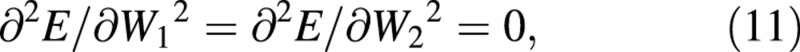
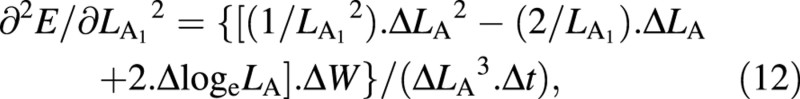
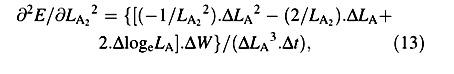

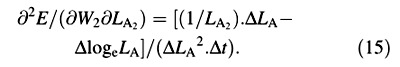
For the LAR, the quotient at either harvest is defined simply as f = LA/W ((Briggs et al., 1920). The statistical estimate of f, and its variance, both after Causton and Venus (1981, eqns 2.13 and 2.14), are then given by:
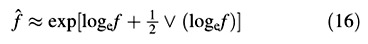
and
∨ (f) ≈ exp[2 loge f + ∨(loge f)]. {exp[∨(loge f)] – 1} (17)
with replicated arrays of quotients being used in eqn (17). Having just two harvests provides no information about the exact relation between f and time, so, from the separate estimates of f on each harvest occasion, the assumed mean value of LAR across the harvest‐interval t2 – t1, and its variance, are simply

and
∨(F) = ½ [∨(f1) + ∨(f2)] (19)
Means of SLA and LWF (Evans and Hughes, 1961), and their variances, are obtained by methods that parallel those used for LAR.
The root‐shoot allometric coefficient (the slope of logeWroot on logeWshoot) and its variance are obtained using a bivariate maximum likelihood estimation (Causton and Venus, 1981, eqns 6.28, 6.29, 6.32 and 6.48; see also Sprent, 1969, Chapter 3). With x as logeWshoot and y as logeWroot, and using the contractions
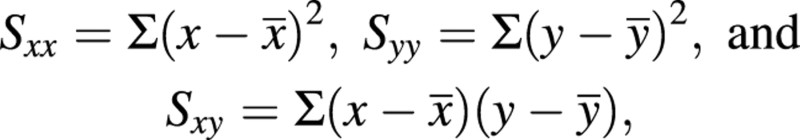
the maximum likelihood estimate of the coefficient of the slope of the straight line joining the two bivariate sets of data is given by:
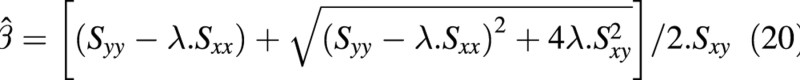
where, assuming that the covariances of the bivariate normal distributions are zero,
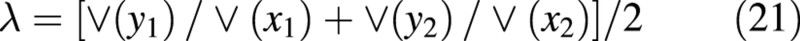
The intercept term is estimated by:

and, since for i = 1, 2
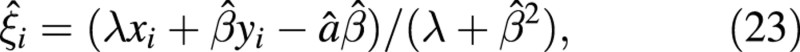
then the variance of the slope is given by:
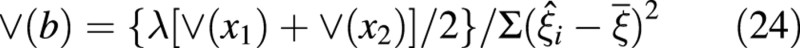
The degrees of freedom associated with the estimate of the allometric coefficient are n – 4.
THE SOFTWARE TOOL
In outline
The tool runs on a PC and is written in Microsoft® Excel 2000. The tool activates every time a suitable matrix of data is copy‐pasted into the input field (in ‘values only’ mode). The outputs comprise a complete set of growth parameters for the one harvest‐interval, all with standard errors and 95 % limits. The tool is liberally supplied with drop‐down comments explaining and advising on each part of the procedure. The tool is available free of charge from R.H. or B.S. Alternatively, it may be downloaded, also free of charge to those with access rights, from the Annals of Botany’s own Internet archive at www.aob.oupjournals.org article supplementary data (http://aob.oupjournals.org/cgi/content/full/90/4/485/DC1).
Inputs
The input matrix is arranged in the usual statistical format, i.e. columns for variables and rows for cases, which are the individual plants. Maximally, the variables are time of harvesting, total root weight per plant, total leaf weight per plant, total non‐leaf above‐ground weight per plant (all weights to be expressed uniformly on a dry‐ or fresh‐weight basis), and total leaf area per plant. Not all of these variables are essential (see below).
Outputs
These are mean values for the specified harvest‐interval of each of RGR, ULR (NAR), LAR, SLA, LWF and the root–shoot allometric coefficient, all with s.e. and a 95 % confidence limit attached. Figure 1 shows the tool displaying a specimen set of input and output data with n = 24.
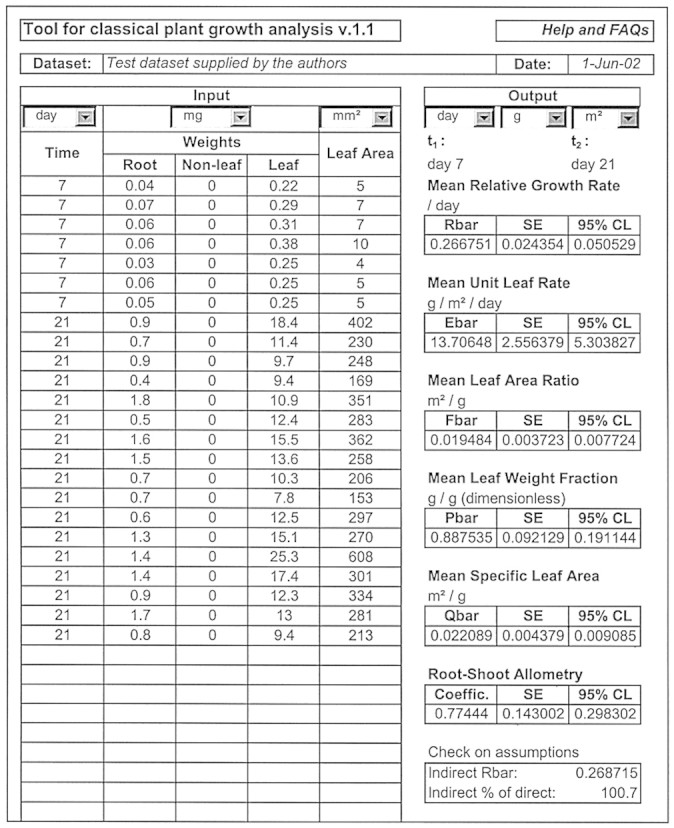
Fig. 1. The spreadsheet tool for classical plant growth analysis, displaying a specimen set of input and output data. The tool is available free of charge from www.aob.oupjournals.org article supplementary data (http://aob.oupjournals.org/cgi/content/full/90/4/485/DC1).
Units
For each of the dimensions time, weight and area, and in both the input and the output fields, the user selects units from extensive drop‐down menus. In any or all of these dimensions, the units selected for the outputs may differ from those used for the inputs (the tool will perform the appropriate conversions). Most of the units offered are metric, but some are non‐SI. It is up to the user to make sensible choices according to the nature of the problem in hand and the eventual use to which the outputs will be put.
‘Frequently asked questions’
Does it matter how far apart the harvests are spaced? No, the time interval presented by the user will be the time interval used for all calculations. Of course, the larger the time interval between harvests, the more the average values of the growth parameters will differ from the instantaneous values if the plants are not growing exponentially.
What if I have more than two harvests? Only two harvests will be recognized from the input data: those occurring at the proffered tmin and tmax. Any data presented with intermediate values of t will be ignored, so it is best to present only two harvests at a time, re‐using the tool for each different harvest‐interval, species and treatment combination. More elaborate methods of analysis involving curve‐fitting might be indicated if harvests form an appreciable series (see Causton and Venus, 1981; Hunt, 1982; Shipley and Hunt, 1996).
Does it matter what units are chosen? No (see above). However, the units chosen must be consistent within any one variable throughout any one use of the tool.
Do there have to be equal numbers of plants at each harvest? No, but sparse or unbalanced replication will adversely affect the statistical results.
What are the lower and upper limits for numbers of replicate plants? Two plants minimum per harvest; five plants minimum for both harvests combined (because the degrees of freedom for the allometric coefficient are n – 4); 100 plants maximum for both harvests combined.
What if a variable contains missing values? The tool will disregard any cases (i.e. rows or single plants) having one or more missing values (empty cells). Missing values will not be equated to zero. Cases can also be deleted temporarily to investigate the effect of eliminating potential data outliers.
What if one whole variable is missing throughout? Fill this variable’s range with zeros. The calculations will proceed wherever possible, but will omit any parameters requiring the missing variable(s), e.g. without LA only RGR, LWF and the allometric coefficient will be calculated. In certain instances some calculations will proceed, but in modified form. For example, without Wroot only SLA will be delivered unaltered; RGR, ULR, LAR and LWF will all be calculated with Wshoot standing‐in alone for total weight W. This facility creates the possibility of deliberate alternative analyses. The only invariably essential datum is time.
What if I want to calculate growth parameters quite other than the five already included? Because the tool is generic, by manipulating the input variables the user can calculate any other growth parameters that have the same mathematical and statistical structure as RGR, ULR or LAR. In such cases the inputs and outputs will not be labelled correctly, but this can be allowed for.
ACKNOWLEDGEMENTS
Peter Mitchell and Eric Garnier commented very helpfully on a draft of this manuscript; Bill Hoffmann kindly allowed us to cite work then in press.
Supplementary Material
Received: 27 March 2002; Returned for revision: 21 May 2002; Accepted: 18 June 2002
References
- BriggsGE, Kidd F, West C.1920. A quantitative analysis of plant growth. II. Annals of Applied Biology 7: 202–223. [Google Scholar]
- CaustonDR, Venus JC.1981. The biometry of plant growth. London: Edward Arnold. [Google Scholar]
- EvansGC.1972. The quantitative analysis of plant growth. Oxford: Blackwell Scientific Publications. [Google Scholar]
- EvansGC, Hughes AP.1961. Plant growth and the aerial environment. I. Effect of artificial shading upon Impatiens parviflora.New Phytologist 60: 150–180. [Google Scholar]
- FisherRA.1921. Some remarks on the methods formulated in a recent article on ‘The quantitative analysis of plant growth’. Annals of Applied Biology 7: 367–372. [Google Scholar]
- GarnierE, Farrar JF, Poorter H, Dale JE, eds.1999. Variation in leaf structure: an ecophysiological perspective. New Phytologist (special issue) 143: 1–221. [Google Scholar]
- HoffmannWA, Poorter H.2002. Avoiding bias in calculations of relative growth rate. Annals of Botany 90: 37–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HuntR.1982. Plant growth curves: the functional approach to plant growth analysis. London: Edward Arnold. [Google Scholar]
- HuntR.1990. Basic growth analysis. London: Unwin Hyman. [Google Scholar]
- PoorterH.1989. Plant growth analysis: towards a synthesis of the classical and the functional approach. Physiologia Plantarum 75: 237–244. [Google Scholar]
- ShipleyB, Hunt R.1996. Regression smoothers for estimating parameters of growth analyses. Annals of Botany 76: 569–576. [Google Scholar]
- SprentP.1969. Models in regression, and related topics. London: Methuen. [Google Scholar]
- VenusJC, Causton DR.1979. Plant growth analysis: a re‐examination of the methods of calculation of relative growth and net assimilation rates without using fitted functions. Annals of Botany 43: 633–638. [Google Scholar]
- WilliamsRF.1946. The physiology of plant growth with special reference to the concept of net assimilation rate. Annals of Botany 10: 41–72. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


