Causal Inference in Latent Class Analysis

Abstract

The integration of modern methods for causal inference with latent class analysis (LCA) allows social, behavioral, and health researchers to address important questions about the determinants of latent class membership. In the present article, two propensity score techniques, matching and inverse propensity weighting, are demonstrated for conducting causal inference in LCA. The different causal questions that can be addressed with these techniques are carefully delineated. An empirical analysis based on data from the National Longitudinal Survey of Youth 1979 is presented, where college enrollment is examined as the exposure (i.e., treatment) variable and its causal effect on adult substance use latent class membership is estimated. A step-by-step procedure for conducting causal inference in LCA, including multiple imputation of missing data on the confounders, exposure variable, and multivariate outcome, is included. Sample syntax for carrying out the analysis using SAS and R is given in an appendix.

Latent class analysis (LCA), a technique for identifying underlying subgroups (i.e., latent classes) in a population, is a statistical method that is now widely accessible to and frequently used by social, behavioral and health researchers. With this technique, a model with a user-specified number of latent classes is fit to a data set, yielding a vector of latent class membership probabilities and a matrix of class-specific probabilities of each response to the set of observed variables used to measure the latent variable. Recent software advances, including PROC LCA (Lanza, Dziak, Huang, Xu, & Collins, 2011) and Mplus (Muthén & Muthén, 1998–2010), make conducting LCA and its extensions straightforward. In addition, finite mixture models more complex than LCA are becoming widely adopted by applied researchers. These models include latent transition analysis (Collins & Lanza, 2010), associative LTA (Bray, Lanza, & Collins, 2010), growth mixture modeling (Muthén & Shedden, 1999 ; Nagin, 2005), and finite mixture regression (Wedel & DeSarbo, 2002). All of these models share the characteristic that underlying heterogeneity is explained by a latent grouping variable, but that individuals’ actual group membership cannot be known with certainty. Rather, each individual has a (typically non-zero) probability of membership in each latent class.

A well-understood extension of finite mixture models that holds great practical importance is the ability to include observed covariates, which serve as predictors of latent class membership. This extension is important in that it allows scientists to better understand the composition of each subgroup. For example, researchers may use LCA to identify latent classes of substance use behavior in adolescence. In this case, the identification of factors that are significantly related to increased odds of membership in classes characterized by high-risk behavior would allow for preventive interventions to be targeted toward individuals with high levels on those factors.

Numerous applications of LCA with covariates have appeared in the literature recently. For example, a study of women’s various healthy and unhealthy weight-control strategies revealed four latent classes: No Weight Loss Strategies (i.e., non-dieters), Dietary Guidelines, Guidelines + Macronutrients (characterized by the inclusion of low-carbohydrate dieting), and Risky Dieting (characterized by strategies such as food restriction and diet pills; Lanza, Savage, & Birch, 2010). The inclusion of five covariates allowed the scientists to assess how body mass index (BMI), weight concerns, desire to be thinner, disinhibited eating, and dietary restraint were related to the weight-control strategy latent class. Results suggested characteristics that were predictive of membership in the Risky Dieting latent class, and ways in which an intervention program could be adapted to meet the unique needs of members of each latent class in order to prevent or reduce unhealthy dieting behaviors.

As with any regression analysis, causality cannot be inferred about associations between predictors and latent class membership due to possible confounders. Fortunately, substantial recent work in the area of causal inference provides guidance for how we might obtain better inference of effects using observational data. We propose the novel but straightforward integration of propensity score methods with LCA in order to draw causal inference about factors that influence latent class membership.

Motivating Example: Effect of College Enrollment on Patterns of Adult Substance Use

Non-college-bound high school students drink more alcohol than their college-bound peers, yet heavy drinking among college youth occurs with a frequency that meets or exceeds that of not-enrolled youth (O’Malley & Johnston, 2002). A great deal of emphasis in research has been placed on the college environment as a high-risk context for heavy drinking (e.g., Sher & Rutledge, 2007; Wechsler, Lee, Kuo, & Lee, 2000), and the consequences that may accompany heavy drinking in college (e.g., Jackson, Sher, & Park, 2005; Perkins, 2002).

Despite what is known about the incidence and consequences of heavy drinking among college students, however, surprisingly few studies have considered the long-term impact of college enrollment on substance use. Such an investigation would require longitudinal data on both the college-enrolled and non-enrolled populations so that comparisons in adult substance use behaviors could be made. One study that drew such comparisons based on latent trajectories in discontinuous patterns of heavy drinking from ages 18 to 30 demonstrated that college-bound youth exhibited lower rates of heavy drinking during high school, similar rates during college ages (ages 19–20), and lower rates in young adulthood (ages 24–25) and adulthood (age 30) (Lanza & Collins, 2006). Yet this study only examined a single-measure outcome in adulthood, an indicator of any recent heavy drinking, as opposed to a more comprehensive examination of alcohol, tobacco and other drug use. Perhaps a more critical limitation, however, is the fact that selection effects for college enrollment prohibit any sort of causal statements to be made about these differences. Selection effects for college enrollment have been well-documented, including parental attitudes and education (Akerhielm, Berger, Hooker, & Wise, 1998), educational expectations (Akerhielm et al., 1998; Beattie, 2002), family income (e.g., Ellwood & Kane, 2000; Klasik, 2011), and race/ethnicity differences (e.g., Cameron & Heckman, 2001; Klasik, 2011; Rivkin, 1995).

In the next section we describe the mathematical model for LCA with covariates, followed by a general overview of propensity score methods that includes a careful presentation of various causal questions that can be addressed using these methods. We then present a step-by-step approach to integrating propensity score methods into LCA in order to adjust for confounding, and demonstrate this approach using an empirical analysis where propensity score techniques were used to adjust for confounding in the effect of college enrollment on adult substance use latent class membership. This is followed by a brief discussion of issues that can arise when integrating propensity score methods with a latent variable model. Sample SAS and R syntax for conducting causal inference in LCA is presented in the Appendix.

LCA with Covariates

Suppose that there are j = 1, …, J observed variables, and that variable j has response categories r_j = 1, …, R_j; suppose also that the latent variable has c = 1, …, C latent classes. Let y represent a particular response pattern (i.e., a vector of possible responses to the observed variables), and let Y represent the array of all possible ys. Each response pattern y corresponds to a cell of the contingency table formed by crosstabulating all of the observed variables, and the length of the array Y is equal to the number of cells in this table. Let us establish an indicator function I(y_j = r_j) that equals 1 when the response to variable j = r_j, and equals 0 otherwise. The probability of observing a particular response pattern or cell in the contingency table cross-classifying the observed variables can be written as

$$P(\mathbf{Y}=\mathbf{y})={\sum }_{c=1}^C{\gamma }_c{\prod }_{j=1}^J{\prod }_{r_j=1}^{R_j}{\rho }_{j,r_j\mid c}^{I(y_j-r_j)},$$ (1)

where γ_c is the probability of membership in latent class c and ${\rho }_{j,r_j\mid c}^{I(y_j=r_j)}$ is the probability of response r_j to observed variable j, conditional on membership in latent class c. The γ parameters represent a vector of latent class membership probabilities that sum to 1. The ρ parameters represent a matrix of item-response probabilities conditional on latent class membership. The model relies on the assumption of conditional independence given latent class. This implies that within each latent class, the J indicators are independent of one another.

Covariates (which also might be referred to as predictors, exogenous variables, or concomitant variables) can be incorporated into the latent class model in order to predict latent class membership (Collins & Lanza, 2010; Dayton & Macready, 1988; van der Heijden, Dessens, & Bockenholt, 1996). Most commonly, covariates are used to predict latent class membership and are added to the latent class model via multinomial logistic regression, although variants of the prediction model are available (e.g., collapsing latent classes to assess the effect of a covariate on membership in one latent class versus the remaining latent classes via binomial logistic regression; see Lanza et al., 2011). As with traditional regression, in LCA covariates can be discrete, continuous, or higher-order terms (e.g., powers or interactions). Indeed, this procedure is equivalent to standard logistic regression analysis, except that here the categorical outcome is latent.

The latent class model including a single covariate X can be expressed as

$$P(\mathit{Y}=\mathit{y}\mid \mathit{X}=\mathit{x})={\sum }_{c=1}^C{\gamma }_c(x){\prod }_{j=1}^J{\prod }_{r_j=1}^{R_j}{\rho }_{j,r_j\mid c}^{I(y_j=r_j)},$$ (2)

where ${\rho }_{j,r_j\mid c}^{I(y_j=r_j)}$ is the probability of response r_j to observed variable j, conditional on membership in latent class c, and γ_c(x) is a standard baseline-category multinomial logistic regression model (e.g., Agresti, 2002)

$${\gamma }_c(x)=P(\mathit{C}=\mathit{c}\mid \mathit{X}=\mathit{x})=\frac{{\mathit{e}}^{{\mathit{\beta }}_{\mathbf{0}\mathit{c}}+{\mathit{\beta }}_{\mathbf{1}\mathit{c}}\mathit{x}}}{1+{\sum }_{{\mathit{c}}^{\prime }=\mathbf{1}}^{\mathit{C}-\mathbf{1}}{\mathit{e}}^{{\mathit{\beta }}_{\mathbf{0}{\mathit{c}}^{\prime }}+{\mathit{\beta }}_{\mathbf{1}{\mathit{c}}^{\prime }}\mathit{x}}}$$ (3)

for c′=1, …, C-1, and where C is the designated reference class. This model can be directly extended to include two or more covariates. Comprehensive technical details on LCA with covariates can be found in the recent literature (e.g., Collins & Lanza, 2010; Lanza, Collins, Lemmon, & Schafer, 2007). Just as with any standard regression analysis, the coefficients linking covariates to latent class membership cannot be interpreted as causal effects without further assumptions.

Propensity Score Methods for Causal Inference

Propensity score methods can be used to address two distinct types of scientific questions. The first is the average causal effect (ACE), which represents the estimated causal effect for the entire population. In our example, the ACE can answer the question: What differences in adult substance use patterns are expected if all individuals in the population had enrolled in college, compared to if no individuals in the population had enrolled in college? The second is the average causal effect among the “treated”, i.e. among the college-enrolled individuals (ACE_C), which represents the effect of the treatment for the population that received it. In our example, the ACE_C can answer the question: Among individuals who enrolled in college, what differences in their adult substance use patterns are expected had they all enrolled in college, compared to if none of them had enrolled in college?

Rosenbaum and Rubin (1983) defined the propensity score as the probability that an individual receives a particular level of a treatment or exposure given measured confounders. A comparison of individuals in one exposure group with individuals in the other exposure group who have the same (or nearly the same) propensity score is the same as a comparison of exposure conditions that were randomly assigned (Rosenbaum, 2002). In other words, they create a random assignment environment even when exposures are not randomized (assuming that the propensity model includes all confounders). Propensity scores are an effective tool for capturing the essence of how the exposure groups differed at the beginning of the study, and equating them in terms of a large set of confounders.

Propensity score estimates, denoted π̂, are typically obtained by logistic or probit regression of the treatment, T_i, on a set of confounders, X_i, although more flexible alternatives such as generalized boosted regression (GBR; McCaffrey, Ridgeway, & Morral, 2004) and classification and regression trees (CART; Luellen, Shadish, & Clark, 2005) have also been used. In the current study, we demonstrate LCA with propensity scores derived using logistic regression; this is an appropriate approach when the treatment is binary. Receiving the “treatment,” which in our observational study corresponds to college enrollment, is modeled as a function of a large set of characteristics that may relate to selection into college. We refer to the college and non-college groups as exposure groups. In this case, the propensity score estimate for individual i is simply the predicted probability

$${\widehat{p}}_i=\frac{\mathit{exp}({X_i}^T\widehat{b})}{1+\mathit{exp}({X_i}^T\widehat{b})}$$ (4)

from the logistic regression,

$$log\left(\frac{{\pi }_i}{1-{\pi }_i}\right)=X_i^T\beta$$ (5)

where X_i = [1, confounders]’ and b̂ are the estimated coefficients from a logistic regression.

Once propensity scores are obtained for the sample, the degree of overlap on the distribution of propensity score estimates for the exposure groups should be assessed. If the distribution of propensity score estimates does not overlap between the groups, then causal inferences are not warranted. In this case it is not feasible to adjust the sample using propensity scores in a way that resembles a randomized controlled trial; this is because there are not comparable individuals in the two groups. If the distribution of scores does overlap, then the propensity score estimates can be used to adjust for confounding in the effect of the exposure to the outcome. The balancing property of the propensity score, described below, has led to many propensity-based techniques for adjusting for selection effects, including matching (Rosenbaum & Rubin, 1985), subclassification (Rosenbaum & Rubin, 1984), and inverse-propensity weighting (IPW; Robins, Rotnitzky, & Zhao, 1995). We focus on matching and IPW, and comment on subclassification in the Discussion.

Inverse propensity weighting (IPW)

The basis for weighting is similar to that of survey weights, in that there is likely an underrepresentation of those who are enrolled in college but had a low propensity to have enrolled and an overrepresentation of those who enrolled in college and in fact had a high propensity to have enrolled. Thus, one solution to estimating the ACE is to up-weight those who are underrepresented and down-weight those who are overrepresented. This is achieved by weighting each individual by the inverse of the estimate of their propensity to be in the group that they were actually in. The weights for individuals who enrolled in college (i.e., received the treatment) are 1/π̂ and the weights for individuals who did not enroll in college (i.e., did not receive the treatment) are 1/(1–π̂). These weights adjust for confounding by weighting the data to mimic a randomized control trial. The weights are then treated like survey weights in all subsequent analysis.

To estimate the ACE_C, a different set of weights are calculated with the goal of weighting the non-enrolled individuals so that they closely resemble the enrolled group. In this case, individuals who enrolled in college are not weighted (this corresponds to weights of 1) and the weights for individuals who did not enroll in college are π̂/(1–π̂).

Matching

There are numerous algorithms for matching individuals based on propensity score estimates in order to be able to form two comparable groups of individuals. In our example, the goal is to match individuals from the non-enrolled group to individuals in the enrolled group in a way such that the two groups are nearly identical in terms of all of the measured confounders. Matching can be done with or without replacement. Another variation of the matching procedure, particularly if there are many more individuals in one exposure group compared to the other, is to do 1:k matching in which an individual in the smaller exposure group is matched with k (e.g., 2) individuals in the larger exposure group. When k is larger than 1, individuals in the larger exposure group are then down-weighted (by 1/k) in the final analysis.

We used a genetic search algorithm and performed 1:1 matching using the MatchIt package for R (Ho, Imai, King, & Stuart, 2011), which calls the Matching package for R (Sekhon, 2011) for the genetic search matching algorithm. The advantage of this algorithm is that it automates the process of achieving balance, an important requirement for causal inference described next.

Balance

The balancing property of propensity scores refers to the fact that all individuals with the same propensity score estimate, regardless of which exposure group they are in, are equivalent on all the measured confounders that were included in the propensity model. Whether or not balance on the measured confounders included in the propensity model has been achieved can be assessed by computing standardized mean differences between the exposure groups on each of the measured confounders before and after adjustment (i.e., weighting or matching). It is generally recommended that the standardized mean differences should not exceed .2 (in absolute value) after weighting or matching because a standardized mean difference of this size is considered a small effect size (Cohen, 1988). If balance is not achieved, then the propensity score model may be revisited to include interaction terms, higher-order terms, and/or additional potential confounders until balance is achieved. This process can be tedious; thus, algorithms that automate this process, such as the genetic search algorithm, can be advantageous.

Methods

Participants

The data for this study were drawn from the National Longitudinal Survey of Youth 1979 (NLSY79 ; Center for Human Resource Research, 1979), a longitudinal study that documents the lives of a representative sample of American youth. The participants were interviewed annually from 1979 through 1994. This study was based on a sample of 1092 adolescents (51% male) who were in Grade 12 at Round 1 of the NLSY79. Among these adolescents, the average age was 17.6 (SD = 0.7) years old in Round 1; 66% of the sample were White, 30% were Black, and 4% were from other race groups. The average annual household income was $18,728 (SD = $13,386), and nearly 82% of the mothers of these adolescents had completed a 12^th grade level of education or less.

Measures

The set of measured confounders to include in this study was derived primarily from the literature on college attendance described above. The following potential confounders were included to adjust for selection effects related to college enrollment: gender, race/ethnicity, household income, single-parent household, residential crowding, maternal education, maternal age, metropolitan status, language spoken at home, educational aspirations of both the adolescent and parent, and type of high school (vocational, commercial, general program, college preparatory). These variables were measured in Round 1.

Full-time college enrollment was assessed in Round 2 (in 1980), one year after the participants’ senior year of high school. In this sample, 423 participants (38.7%) reported being enrolled in college at this time.

Adult use of alcohol, cigarettes, marijuana, crack and cocaine in past month were measured in Round 16 (in 1994) when the participants were approximately 33 years old. Responses to the alcohol use indicator were coded such that 0 represented “No use,” 1 represented “Light use,” defined as having had alcoholic drinks in the past month with no binge drinking, and 2 represented “Binge,” defined as having had 6 drinks or more at one time. An indicator of cigarette use was coded such that 0 reflected “No use” and 1 reflected “Occasional or daily use.” Marijuana use was coded such that 0 represented “No use” and 1 represented “Any use.” A composite item was created for use of either crack or cocaine, where 0 represented “No use” and 1 represented “Any use.”

Analytic Strategy for Causal Inference in LCA

The following seven steps represent a straightforward approach to conducting propensity score analysis in LCA in order to draw causal inference about the effect of a hypothesized causal variable on latent class membership. Because most studies of human behavior, particularly when longitudinal, must be addressed using data that are partially missing, we include analytic steps for using multiple imputation to handle data on confounders, treatment exposure, and the multivariate outcome that are missing at random (MAR). Steps 1 and 2, described below, are to be conducted once. Then, Steps 3 through 6 must be completed within each imputed data set. Finally, Step 7 is completed in order to combine results across imputed data sets, resulting in a final estimate of the causal effect of interest.

Step 1: Variable selection

Variables that are to be included in the analysis must be selected to include items for all measured confounders, an indicator of treatment exposure (in this case, college enrollment), and all indicators of the latent class variable (in this case, all items measuring adult substance use).

Step 2: Multiple imputation

Without addressing missing data with a flexible technique such as multiple imputation, individuals missing a response to even one confounder will receive a missing value on their estimated propensity score. These individuals would necessarily be dropped from any subsequent analysis because those scores form the basis for the inverse propensity weights as well as for the matching procedure. In many applied studies, this can result in a substantially reduced sample and biased estimation of the causal effect. The multiple imputation strategy has the advantage that, once missing values have been filled in, the analyst can proceed with any complete-case analysis technique such as the propensity score techniques described here. Also, missingness in variables relevant for any part of the analysis can be addressed under a single, general imputation model (Schafer, 1997; Rubin, 1996). An excellent discussion of the advantages of multiple imputation appears in Schafer and Graham (2002). By using multiple imputation to handle missing data, the approach described here ensures that the causal inference in LCA is based on the full sample, maximizing statistical power and reducing bias in the estimated effect.

Step 3: Estimate propensity scores and assess overlap (within each imputed data set)

Propensity scores are obtained by predicting college enrollment from a large set of measured confounders, and can include interactions between confounders; the set of predictors should include all variables that relate to selection into college and the outcome. Logistic regression provides a straightforward method for estimating these scores. Once each individual’s propensity score is estimated, overlap must be examined to determine the feasibility of causal inference. The exact level of overlap required depends on whether the ACE or ACE_C is being estimated and whether a matching or weighting strategy is being used. Weighting assumes at least some overlap but since individuals are not actually paired with other individuals, overlap is not as critical as it is for matching. Estimation of the ACE using matching requires that all members of each exposure group have one or more individuals in the other exposure group with nearly equal propensity scores. Overlap requirements for estimation of the ACE_C are slightly less strict, as only individuals in the treatment group must have one or more individuals in the other exposure group with nearly equal propensity scores. The easiest way to assess overlap is to compare box plots of the propensity scores for each group.

Step 4: Calculate weights or conduct matching (within each imputed data set)

To use weighting to adjust for selection effects, two sets of weights can be calculated: one set to estimate the ACE and another to estimate the ACE_C. To estimate the ACE, the weights for individuals who enrolled in college are calculated as 1/π̂ and the weights for individuals who did not enroll are calculated as 1/(1–π̂). To estimate the ACE_C, weights for individuals who enrolled in college are set to 1 and weights for individuals who did not attend are calculated as π̂/(1–π̂).

An alternative to weighting is to create a matched data set that approximates data that might be observed from a randomized controlled trial. There are numerous strategies to implement matching based on the propensity scores derived in Step 3 above; we will rely on an iterative genetic matching method that matches 1:1 with replacement (Diamond & Sekhon, 2012). To create a matched data set using this approach, the current study uses the R package MatchIt (Ho, et al., 2011). The genetic matching algorithm automates the process of achieving optimal balance by minimizing differences on confounders in the matched sample based on paired t-tests and Kolmogorov-Smirnov tests (see Diamond and Sekhon, 2012 for details).

Step 5: Assess balance (within each imputed data set)

Standardized mean differences of confounders across exposure groups should be calculated before and after adjustment for selection, regardless of whether the causal question is ACE or ACE_C and whether the propensity score adjustment is based on weighting or matching. When selection effects are observed, pre-adjusted standardized mean differences may be quite large in absolute value. After adjustment, however, it is desirable for the absolute values of these differences to be less than about 0.2 (in absolute value) for all confounders. When balance (i.e., small or no mean differences between exposure groups on all of the confounders) is achieved, the weighted or matched sample can be considered to mimic a randomized sample assuming that all confounders are measured and included in the propensity model, even though the participants were not randomly selected into college.

Step 6: Conduct LCA using the weighted or matched data set (within each imputed data set)

Selection of the number of latent classes necessary to represent heterogeneity in the outcome of interest should be conducted within each imputed data set in the usual way. Standard approaches include comparing information criteria (e.g., AIC and BIC), calculating the bootstrap likelihood-ratio test p-value, and comparing interpretation of the resultant latent classes. The fact that a measurement model must be selected within each imputed dataset raises issues that are unique to latent variable modeling, and is explored in more detail in the Discussion below. A thorough treatment of model selection in LCA, as well as the issue of model identification, appears elsewhere (see Collins & Lanza, 2010).

All latent class models should be fit using the adjusted data; that is, for IPW all models should include the appropriate set of weights (either to estimate the ACE or the ACE_C), and for matching all models should be fit using the matched data set. Once a latent class model is selected, the exposure indicator (in our example, college enrollment) is then added as a predictor of latent class membership so that the causal effect of interest can be estimated. The estimate of interest is a logistic regression coefficient (in the case of two latent classes) or a set of logistic regression coefficients (in the case of three or more latent classes) representing the association between exposure group and latent class membership. Typically these logistic regression coefficients in LCA are exponentiated, as odds ratios are easier to interpret.

Step 7: Combine results across imputations

The logistic regression coefficients obtained in each imputed data set (see Step 6 above) and their corresponding standard errors can be combined in the usual way using Rubin’s (1987) rules. Specifically, the overall estimate of each logistic regression coefficient is calculated as the mean of the imputation-specific estimates. Each associated standard error estimate represents a weighted sum of the within- and between- imputation variances. Thus, the resultant causal effect of the exposure on latent class membership takes into account both selection effects due to many observed confounders and missing data, including attrition.

Software

SAS PROC MI was used to implement multiple imputation to handle missing data on college enrollment, the latent class indicators, and the confounders considered in this study. SAS PROC GENMOD was used to estimate the propensity scores using logistic regression. PROC LCA (Lanza et al., 2007; 2011) was used to fit all LCA models. In addition, the R package MatchIt (Ho et al., 2011) was used to conduct the propensity score matching. The Appendix shows SAS and R code used to conduct Steps 2 through 7 above.

Results

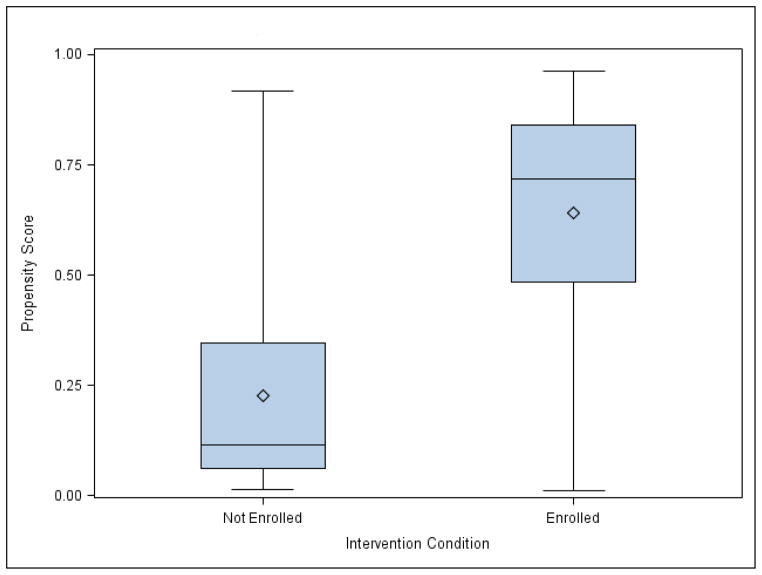
Five imputed data sets were created, where missing responses were replaced with plausible values (Step 2). Variables in the imputation model included all measured confounders, college enrollment, and all indicators of adult substance use behavior. Within each imputation, propensity scores were retained from a logistic regression of college enrollment on the full set of observed confounders (Step 3). Figure 1 shows the overlap of propensity scores across college enrollment groups using side-by-side box plots. Although there was no overlap for the middle 50% of propensity scores for individuals in the enrolled and not enrolled groups, the full distribution showed sufficient overlap for us to proceed to estimate both the ACE and the ACE_C.

Figure 1.

Boxplot of the propensity scores for each college enrollment group (for one imputed dataset).

Causal Question 1: What is the Average Causal Effect (ACE) of College Enrollment on Adult Substance Use?

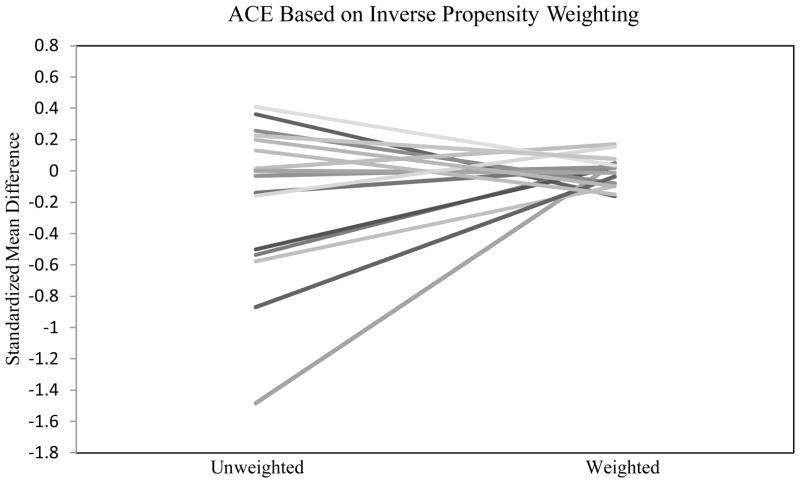
The first causal question was addressed by adjusting for selection effects using weights for the ACE (Step 4). Figure 2 presents the standardized mean differences on confounders before and after adjusting for selection using the ACE weights (Step 5). Prior to adjusting, the differences ranged from approximately −1.5 to 0.4. After adjusting, however, all mean differences were less than 0.2 in absolute value, indicating that balance was achieved using this procedure.

Figure 2.

Standardized mean differences between college enrolled and non-enrolled groups on measured confounders before and after propensity score adjustment based on inverse propensity weights applied to full sample (N=1092) for estimating ACE (for one imputed dataset).

LCA was conducted using the ACE weights (Step 6); we used 100 random sets of starting values to ensure that the maximum-likelihood solution was identified for each model, and compared models with one through three latent classes (see Table 1). The two-class solution, shown in Table 2, best represented the weighted dataset with N=1092 individuals. The first latent class, which comprised 71% of the full weighted sample, was labeled Low-Level Users as it is characterized by very low probabilities of binge drinking, occasional/daily cigarette use, marijuana use, or crack/cocaine use. The second latent class, which comprised 29% of the full weighted sample, was labeled Heavy Drinkers, as those individuals have an elevated probability of reporting binge drinking; individuals in this class were as likely to engage in occasional/daily smoking as not.

Table 1.

Summary of Information for Selecting Number of Latent Classes for Substance Use Behaviors

Method	Number of Classes	G2	df	AIC	BIC	CAIC	aBIC	N
ACE: Weighting	1	104.7	18	114.7	139.7	144.7	123.8	1092
	2	17.0	12	39.0	94.00	104.9	59.0
	3	6.9	6	40.9	125.8	142.8	71.8
ACEC: Weighting	1	111.3	18	121.3	146.3	151.3	130.4	1092
	2	28.0	12	50.0	105.0	116.0	70.0
	3	17.6	6	51.6	136.6	153.6	82.6
ACEC: Matching	1	61.39	18	71.39	93.24	98.24	77.36	584
	2	17.19	12	39.19	87.26	98.26	52.34
	3	7.27	6	41.27	115.56	132.56	61.59

Note. AIC=Akaike Information Criterion; BIC = Bayesian Information Criterion; CAIC = Consistent Akaike Information Criterion; aBIC = Adjusted Bayesian Information Criterion.

Table 2.

Item-Response Probabilities for Two-Class Model While Adjusting for Selection Effects Using Weighting to Estimate ACE, Weighting to Estimate ACE_C, and Matching to Estimate ACE_C

Substance	Response	ACE: Weighting		ACEC: Weighting		ACEC: Matching
		Low-Level Users (71%)	Heavy Drinkers (29%)	Low-Level Users (75%)	Heavy Drinkers (25%)	Low-Level Users (71%)	Heavy Drinkers (29%)
Alcohol	No use	0.58	0.20	0.48	0.03	0.51	0.04
	Light use	0.27	0.36	0.37	0.43	0.38	0.46
	Binge	0.15	0.44	0.15	0.54	0.11	0.50
Cigarettes	No use	0.91	0.50	0.82	0.60	0.87	0.65
	Occasional/Daily	0.09	0.50	0.18	0.40	0.13	0.35
Marijuana	No use	0.98	0.86	0.99	0.77	0.99	0.79
	Any use	0.02	0.14	0.01	0.23	0.01	0.21
Crack/Cocaine	No use	1.00	0.95	1.00	0.91	1.00	0.94
	Any use	0.00	0.05	0.00	0.09	0.00	0.05

Note: Item-response probabilities corresponding to most likely response marked in bold to facilitate interpretation.

College enrollment was then added to the weighted LCA as a covariate. Table 3 reports the parameter estimate and corresponding standard error, p-value, and odds ratio for the effect of college enrollment on membership in the Heavy Drinkers latent class in adulthood. The causal effect of college enrollment was statistically significant, indicating that college attendance leads to significantly reduced odds of adult membership in the Heavy Drinkers class. Specifically, if all individuals in the population were to attend college, the overall odds of membership in the Light Users class is 6.25 times (inverse OR = 1 / 0.16, p-value < .01; see Table 2) more likely than if all individuals in the population were to not attend college. In other words, for the full population, college enrollment considerably reduces adulthood substance use. Thus, college could be considered an effective “treatment” of adulthood substance use on average for the whole population.

Table 3.

Causal Effects of College Enrollment on Latent Classes of Adulthood Substance Use

Causal Question	Estimate	SE	p	Odds Ratio
1) Average Causal Effect (ACE)
Weighting	−1.81	0.63	<.01	0.16
2) Average Causal Effect Among College-Enrolled (ACEC)
Weighting	−0.79	0.59	0.18	0.45
Matching	−0.66	0.70	0.35	0.52

Causal Question 2: What is the Average Causal Effect (ACE_C) of College Enrollment Among those who Attended College?

Method 1: ACE_C based on IPW

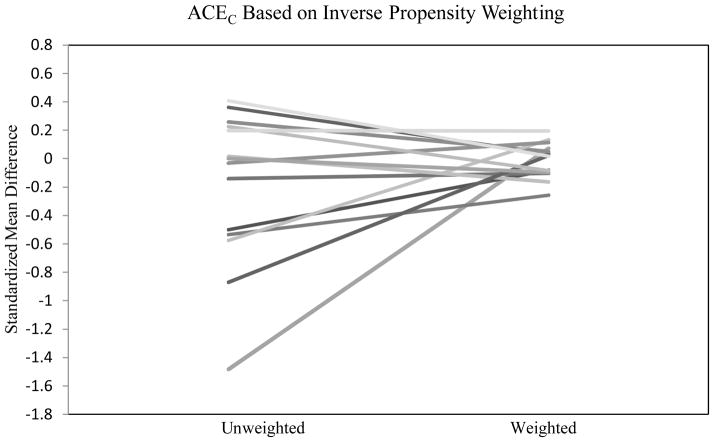
The second causal question was addressed in two ways (Step 4); we first present results based on IPW, and in the next section we present results based on matching. Figure 3 presents the standardized mean differences on confounders before and after adjusting for selection using the ACE_C weights (Step 5). This procedure is identical to the procedure above for estimating the ACE using weights, except that the formula for calculating the weights from the propensity scores varied slightly. As noted above, prior to adjusting, the differences ranged from approximately −1.5 to 0.4. After adjusting using the ACE_C weights, the mean differences for all but one confounder were less than 0.2 in absolute value. The confounder on which balance was not achieved using a 0.2 cut-off did show marked improvement in balance, however, with the mean difference reduced from approximately −0.55 to −0.25.

Figure 3.

Standardized mean differences between college enrolled and non-enrolled groups on measured confounders before and after propensity score adjustment based on inverse propensity weights applied to full sample (N=1092) for estimating ACE_C (for one imputed dataset).

Next, LCA was conducted using the ACE_C weights (Step 6); as before, identification was assessed for each competing model comprising one to three latent classes (see Table 1). Once again a two-class solution was selected; the LCA parameter estimates are shown in Table 2. The latent structure was similar to that of the two-class model using ACE weights. The Low-Level Users latent class, comprising 75% of the sample, is characterized by very low probabilities of binge drinking, occasional/daily cigarette use, marijuana use, or crack/cocaine use. The Heavy Drinkers latent class, comprising the remaining 25%, is characterized by a probability of 0.54 of reporting binge drinking. We emphasize here that despite the fact that both analyses (based on ACE weights and on ACE_C weights) are based on the same sample of N=1092, the latent structure is not necessarily expected to replicate across analyses. This is because we are weighting the data in two different ways, essentially changing the dataset itself.

College enrollment was then added to the weighted (using ACE_C weights) LCA as a covariate. Results for the effect of college enrollment on membership in the Heavy Drinkers latent class in adulthood appear in Table 3. Unlike the model used to assess ACE, in this model the causal effect of college enrollment was not statistically significant, indicating that college attendance does not lead to significantly different odds of adulthood membership in the Heavy Drinking class. This finding may be counterintuitive given the significant results reported above for the ACE, but the causal question posed here is different. Specifically, we find with this analysis that among the individuals who actually enrolled in college, college enrollment did not lead to greater or reduced odds of membership in the Heavy Drinkers class (OR = 0.45, p-value = 0.18).

Method 2: ACE_C based on matching

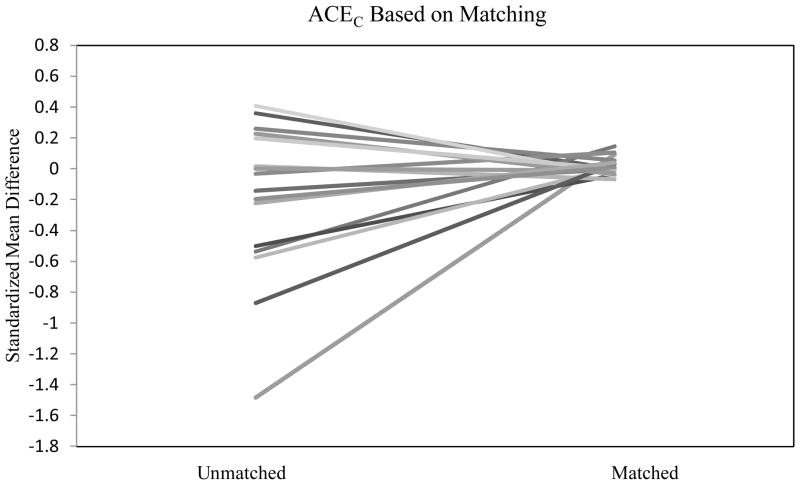
The second causal question was then addressed using MatchIt (Ho et al., 2011) to obtain a new, matched data set (Step 4). The final matched sample had a size of N=584. Figure 4 presents the standardized mean differences on confounders before and after adjusting for selection using this matching approach (Step 5). This procedure is quite different from the first approach to ACE_C (using weights), yet the two approaches address the same exact causal question. Because the matched sample does not contain all study participants, it was important to reassess balance using the new dataset. Prior to adjusting, the mean standardized differences on confounders ranged from approximately −1.5 to 0.4. After matching, the mean differences for all confounders were less than 0.2 in absolute value, indicating that the procedure achieved balance between the college-enrolled and not-enrolled groups.

Figure 4.

Standardized mean differences between college enrolled and non-enrolled groups on measured confounders before and after propensity score adjustment based on matched sample (N=584) for estimating ACE_C (for one imputed dataset).

Next, LCA was conducted using the matched dataset (Step 6). In this study, we implemented genetic matching with replacement, thus the LCA analysis was weighted to account for the repeated selection of observations. Once again identification was assessed for each competing model comprising from one to three latent classes (see Table 1), and a two-class solution was selected; the LCA parameter estimates are shown in Table 2. The latent structure was once again similar to that of the previous two analyses. The Low-Level Users latent class now comprised 71% of the sample and the Heavy Drinkers latent class comprised the remaining 29%. Just as the two weighted analyses were not necessarily expected to reproduce the same measurement model for adulthood substance use, the two analyses designed to address the ACE_C (weighting and matching) were not expected to replicate the measurement model exactly, as they are based on different datasets.

As before, college enrollment was added to the latent class model as a covariate, but instead of applying weights to the full sample, the model was fit to the matched dataset. Results for the effect of college enrollment on membership in the Heavy Drinkers latent class in adulthood appear in Table 3. Just as the estimated ACE_C based on weighting was not statistically significant, the causal effect based on matching also showed no significant effect of college enrollment. Based on matching, we find that among the individuals who actually enrolled in college, college enrollment did not lead to greater or reduced odds of membership in the Heavy Drinkers class (OR = 0.52, p-value = 0.35). Thus, regardless of the approach taken to estimate the ACE_C, we found that college enrollment does not lead to significantly different odds of adulthood membership in the Heavy Drinking class.

Discussion

Propensity score methods have been advanced to the point that social, behavioral, and health scientists are more and more routinely using them to draw causal inferences about effects, such as those reflected in regression coefficients, based on observational data. Integrating these methods into latent class models holds the promise of better understanding the causal mechanisms that lead to behaviors or characteristics that cannot be directly measured. Below we discuss what we feel is perhaps the most important advantage of taking a causal inference approach to estimation – the fact that researchers must think more carefully about the exact question being addressed. We then turn our discussion to the fact that, while in concept propensity score methods can be integrated with structural models in the same way as with more simple models such as linear regression, in practice their application to structural models such as LCA presents unique challenges. We discuss several of these in turn. Finally, we discuss limitations in the current study.

The Appropriateness of Different Causal Questions

One important advantage of taking a causal inference approach to estimating any effect, whether it involves a structural model or not, is that the researcher is required to express a very specific causal question. The ACE and ACE_C reflect very different questions that may or may not be of scientific interest; these two questions fundamentally differ in terms of the population to which the answer can be generalized. We first estimated the ACE: What differences in adult substance use patterns are expected if all individuals in the population had enrolled in college, compared to if no individuals in the population had enrolled in college? Results, which were based in IPW, suggested that in the overall population college enrollment reduced adult substance use behaviors – in particular heavy episodic drinking. We then estimated the ACE_C: Among individuals who enrolled in college, what differences in their adult substance use patterns are expected had they all enrolled in college, compared to if none of them had enrolled in college? Results of analyses relying on both IPW and matching suggested that among the college-enrolled population college enrollment in fact has no impact on adult substance use behaviors. Taken together, we may conclude that college enrollment would reduce adult substance use among non-college-bound youth.

It is important to consider the appropriateness of these two questions in the context of any example. Here, we believe the ACE_C makes more intuitive sense. In concept, to answer this question we are comparing the college-enrolled individuals in terms of their actual substance use behavior to their expected behavior had they not attended college. It may be nonsensical to think about what the expected effect of college enrollment would be, could everyone in the population attend college, because – practically speaking – attending college may not be possible for many individuals in a population, for example due to not meeting academic requirements. If it had been possible to determine who in the population was actually eligible to enroll in college, we could have redefined the ACE for the entire eligible population and answered a compelling research question (for an example of such a causal question see Hong & Raudenbush, 2006).

Propensity Score Techniques and the Measurement Model

In the course of conducting causal inference in LCA, an interesting and important finding emerged. We had initially conducted model selection and interpretation of the latent classes that emerged in an initial analysis of the unadjusted data. That is, we proceeded to conduct LCA with college enrollment as a covariate in the usual way, not adjusting for selection; this is the current practice for fitting structural models with covariates. Based on these results, we selected the three-class model, which included Low-Level Users (64.9%), Heavy Drinkers (33.0%), and a third class characterized by heavy drinking, cigarette smoking, marijuana use, and crack/cocaine use (Poly Drug Users; 2.1%). This last class was more common among non-enrolled individuals. We then incorporated propensity scores in our analysis through IPW and matching, assuming that the three-class model was most appropriate.

The purpose of the propensity score techniques described here is to actually change the data being analyzed so that they more closely resemble a randomized controlled trial – either through reweighting all individuals based on IPW or through matching individuals based on their confounders and eliminating unmatched individuals from the analysis altogether. Because selection effects were very strong, both of these techniques substantially changed the data being analyzed. We then revisited model selection and interpretation within each propensity score method, and found that for answering both the ACE and the ACE_C, the two-class solution was most appropriate. Thus, we emphasize here the importance of studying the structure of latent variables in the context of the causal analysis, as opposed to the traditional naïve (i.e., unadjusted) analysis.

Using Subclassification for Causal Inference in LCA

In addition to matching and IPW, there are several other propensity score techniques that were not discussed in this study. Most notably is the technique of subclassification, where all individuals in a study are divided into, for example, five strata corresponding to the quintiles of the propensity score distribution (Rosenbaum & Rubin, 1984). Then, within each stratum the effect of the exposure variable on the outcome (in this case, the effect of college enrollment on substance use latent class membership) is calculated. The average effect across strata is taken as the average causal effect in the population, i.e. the ACE. Subclassification can be thought of as a sort of coarsened matching procedure; the idea behind it is that individuals in the enrolled and non-enrolled groups within the same propensity score stratum are similar in terms of the entire set of confounders. This implies that balance is achieved within each stratum, something that we were not able to achieve in the current study.

Subclassification for conducting causal inference in LCA is perhaps the simplest propensity score approach to carry out. We relied on multiple-groups LCA where the variable indicating stratum was included as a grouping variable. Despite the apparent ease of use, however, this technique proved to be particularly challenging in this context because it requires an assumption of measurement invariance across strata. Specifically, this means that the item-response probabilities that together quantify the measurement of the latent construct are equal for individuals with very low propensities to attend college, very high propensities, and everything between. Hypothesis tests indicated that this assumption was not plausible in our study.

One additional challenge with using subclassification is that, to the degree that selection effects are strong (as they were in this study), the exposure groups will be highly imbalanced in terms of sample sizes within the lower and higher strata. As an example, individuals with estimated propensity scores between 0.00 and 0.07 represented the lowest quintile. Of these 219 individuals, only 14 (which is 6%) were in the college enrolled group whereas 205 (94%) were in the non-enrolled group. Similarly, among individuals in the next-lowest quintile, only 8% were in the college enrolled group. Thus this approach suffered from severe imbalance in terms of sample sizes for calculating the strata-specific causal effects, failure to achieve balance within strata, and lack of invariance in the measurement of substance use across strata.

Multiple Imputation and Model Selection in LCA

To our knowledge, no previous study has carefully delineated the potential complications that can arise when applying LCA to data after multiple imputation was used to address missingness. While all modern software for LCA can accommodate missingness on the indicators of the latent class variable (assuming that data are missing at random), individuals with missing values on covariates or grouping variables cannot be included in an analysis. This problem is magnified when conducting propensity score analysis, as propensity scores cannot be obtained with logistic regression for individuals with a missing value on even one measured confounder. As an example, household income was an important predictor of college enrollment, yet many participants (17%) refused to answer this question. Therefore, we used multiple imputation to address missingness on all variables involved in the causal analysis.

To the extent that multiple imputed datasets differ from each other, it is conceivable that model selection – which should be conducted on each dataset – could lead to different solutions. Yet to combine results across imputations, researchers must select one structural model and assume that it holds across imputations. An additional consideration is that, even when the same starting values are used across all imputations, it is important to confirm that each model is identified and that the meaning of each latent class is consistent across imputations, even if the ordering of the latent classes disagrees (an issue that can be resolved simply by reordering the classes so that corresponding parameters are combined across imputations).

Limitations

As with any propensity score analysis to estimate causal effects, in this study we assumed that all of the confounders were measured and included in the propensity model. Because there is extensive literature on factors related to college enrollment, many potential confounders are known. For researchers working in a relatively new area, however, it may be more difficult to identify the full set of important confounders. It is possible to examine the impact of possible unmeasured confounders by conducting a sensitivity analysis (Rosenbaum, 2002). Sensitivity analysis has not been well developed in this context and is a point for future development, thus it is beyond the scope of this paper. Certainly, though, even partially adjusting for selection improves any inferences that may be drawn.

Any propensity score technique presented here assumes that measurement invariance for the latent construct holds across exposure groups. This assumption is implied any time a covariate is introduced in structural models. Although the assumption is a testable one, it is unclear how researchers should proceed when measurement invariance does not hold.

We did not use the NLSY-provided survey weights to accommodate the complex survey design. One strategy that has been proposed is to simply multiply the inverse propensity weights by the complex survey weights in order to estimate causal effects for the original population; similarly, one could introduce the survey weights in a matched analysis. There is currently some debate, however, about the appropriateness of this latter approach; we feel this is an important area for future study.

Conclusions

Behavioral researchers often wish to make causal statements about phenomena that cannot be studied using a randomized control trial. In many cases, the phenomenon of interest may best be characterized as a latent variable. Our example involved estimating the effect of college enrollment on adult substance use behavior patterns (i.e., latent class membership). In this example, it would not be feasible to randomly assign high school seniors to attend college; thus, large selection effects may severely bias estimates of the effect of college enrollment on latent classes of adult substance use. Fortunately, statistical techniques for causal inference have advanced to the point that we can now model selection effects in principled ways using observational data to draw better inference. The incorporation of propensity scores in LCA is a novel but straightforward approach to drawing more valid conclusions about factors that influence subsequent latent class membership.

Appendix

SAS and R code for implementing causal inference in LCA using propensity scores

The data set “rawdata” contains the original data with missing values and the data set “imputed1” contains a single imputation of the data set. The variable “college” is a binary variable coded 1 for “enrolled in college” and 0 for “not enrolled in college.” The labels “pretreatment_confounders” and “latent_class_indicators” used below are placeholders for sets of variables to be used as the predictors of college enrollment and the categorical indicators in the latent class model, respectively.

• Step 1: Variable selection (code not shown)

• Step 2: Multiple imputation (SAS code)

  proc mi data=rawdata nimpute= 5 seed=4753262 out=imputed
         (keep = pretreatment_confounders college latent_class_indicators);
    var = pretreatment_confounders college latent_class_indicators;
  run;
  

• Step 3: Estimate propensity scores and assess overlap (SAS code)

  *estimate propensity scores using logistic regression;
  proc genmod data=imputed1 descending;
    model college = pretreatment_confounders/dist=binomial;
    output out=temp1 predicted=propensity_score;
  run;
  *assess overlap;
  proc boxplot data = temp1;
    plot propensity_score * college ;
  run;
  *inverse propensity weights for ACE and ACE_C, respectively;
  data final;
    set temp1;
    if college=1 then psweight_ACE=1/propensity_score;
    else if college=0 then psweight_ACE=1/(1-propensity_score);
    if college=1 then psweight_ACE_C=1;
    else if college=0 then psweight_ACE_C= propensity_score/(1-propensity_score);
  run;
  

• Step 4: Conducting matching (R code)

  #R code for creating matched sample;
  library(MatchIt)
  library(foreign)
  final <- read.csv(file = “path\\final.csv”, header = TRUE)
  attach(final)
  matched <-matchit(college ~ pretreatment_confounders, data = final, method = “genetic”)
  #export matched files into SAS;
  matcheddata <- match.data(matched, group=“all”, distance = “distance”, weights = “psweight_ACECgenetic”, subclass = “ “)
  write.foreign(matcheddata, “path/matcheddata.txt”, “path/matcheddata.sas”, package = “SAS”)
  

• Step 5: Assess balance

  #R code for standardized mean differences after matching;
  summary(matched, standardize=TRUE)
  /*SAS code for standardized mean differences after weighting.
  Standardized mean differences prior to weighting can be computed
  using the code below without the weight statements in proc means*/
  proc means data=final(where=(college=1));
    var pretreatment_confounders;
    weight psweight_ACE;
    output out=ipw1tx1(drop=_FREQ_ _TYPE_ );
  proc transpose data=ipw1tx1 out=tipw1tx1(rename=(_NAME_=NAME));
    id _STAT_;
  proc means data=final(where=(college =0));
    var pretreatment_confounders; weight psweight_ACE;
    output out=ipw1tx2(drop=_FREQ_ _TYPE_ );
  proc transpose data=ipw1tx2 out=tipw1tx2(rename=(_NAME_=NAME) rename=(MEAN=M2) rename=(STD=STD2) rename=(N=N2) rename=(MIN=MIN2) rename=(MAX=MAX2));
    id _STAT_;
  proc sort data = tipw1tx1;
    by NAME;
  run;
  proc sort data = tipw1tx2;
    by NAME;
  run;
  data ipw1;
   merge tipw1tx1 tipw1tx2;
   by NAME;
  stdeff=(M2-MEAN)/STD2;
  run;
  proc print data = ipw1;
    var NAME N MEAN STD N2 M2 STD2 STDEFF;
  run;
  

• Step 6: Conduct LCA using the weighted or matched data set (SAS code)

  *LCA model for ACE/ACE_C for weighted sample;
  *ACE_C can be estimated by changing the statement ‘weight psweight_ACE;’ to ‘weight psweight_ACE_C;’
  proc lca data=final;
    nclass 2;
    items latent_variable_indicators;
    categories 3 2 2 2;
    covariates college;
    reference 2;
    weight psweight_ACE;
    seed 861551;
    run;
  *LCA model for ACE_C using matched sample;
  proc lca data=matcheddata;
    nclass 2;
    items latent_variable_indicators;
    categories 3 2 2 2;
    covariates college;
    weight psweight_ACECgenetic;
    reference 2;
    seed 3563446;
  run;
  

• Step 7: Combine results across imputations (SAS code)

  *repeat Step 3 to Step 6 for m replicated data sets;
  *using Proc Mianalyze to summarize the results;
  *finalmi is a rectangular data set in which a row represents the statistics from one imputed data set and a column represents the estimate (estlc2) or its standard error (serrlc2);
  proc mianalyze data = finalmi;
    modeleffects estlc2;
    stderr serrlc2;
  run;