Why and When “Flawed” Social Network Analyses Still Yield Valid Tests of no Contagion

Abstract

Lyons (2011) offered several critiques of the social network analyses of Christakis and Fowler, including issues of confounding, model inconsistency, and statistical dependence in networks. Here we show that in some settings, social network analyses of the type employed by Christakis and Fowler will still yield valid tests of the null of no social contagion, even though estimates and confidence intervals may not be valid. In particular, we show that if the alter’s state is lagged by an additional period, then under the null of no contagion, the problems of model inconsistency and statistical dependence effectively disappear which allow for testing for contagion. Our results clarify the setting in which even “flawed” social network analyses are still useful for assessing social contagion and social influence.

In his paper, Lyons (2011) offers a number of criticisms of social network analyses that attempt to estimate contagion effects, such as those of Christakis and Fowler (2007, 2008). A number of his criticisms, and a number of other critiques (Cohen-Cole and Fletcher, 2008; Shalizi and Thomas, 2011; Noel and Nyhan, 2011), are important and need to be taken seriously in the conduct and interpretation of such studies. Some progress has been made in addressing or working around some of these critiques (Fowler and Christakis, 2008; Ver Steeg and Galstyan, 2010; Christakis and Fowler, 2011; VanderWeele, 2011). However, many of the issues raised have arguably not yet been dealt with adequately. In this paper, we offer further discussion on several points raised by Lyons (2011), focusing specifically on model consistency and inference. We argue that, although the issues raised by Lyons (2011) can lead to biased estimates and invalid inference, social network analyses like those of Christakis and Fowler (2007, 2008) will, in some circumstances, still suffice as a valid test of the null hypothesis of no contagion (no social influence) in the social network.

On p. 13 of his paper, Lyons (2011) considers a model like that used in Christakis and Fowler (2007, 2008) in which the log odds of the state of a “focal participant” or “ego” at time t, Y_i,t, is modeled as a linear function of the state of the “linked participant” or “alter” at time t, Y_j,t, and at time t − 1, Y_j,t−1, of the ego’s state at time t −1, Y_i,t−1, and of the covariates for the ego, X_i. In this model, β₁ is the coefficient for Y_j,t (the alter’s state at time t) and β₂ is the coefficient for Y_j,t−1 (the alter’s state at time t −1):

$$log\left(\frac{P(Y_{i,t}=1\mid Y_{j,t},Y_{j,t-1},Y_{i,t-1},X_i)}{P(Y_{i,t}=0\mid Y_{j,t},Y_{j,t-1},Y_{i,t-1},X_i)}\right)={\beta }_0+{\beta }_1{Y}_{j,t}+{\beta }_2{Y}_{j,t-1}+{\beta }_3{Y}_{i,t-1}+{\beta }_4^{\prime }{X}_i$$

Christakis and Fowler (2007, 2008) interpret the estimate of β₁ as their “contagion effect” or causal estimate of social influence. Lyons (2011) argues that, if, in the network, there is a person i with a tie to person k and that person k has a tie to person m ≠ i then the models themselves imply that β₁ = 0. The models themselves effectively contradict the existence of the very effect Christakis and Fowler want to assess. Lyons further argues that when the state is continuous and linear regression is used as in the loneliness social network analyses of Cacioppo et al. (2009) then if person i has a tie with person j and person j with person i, and if likewise person j has a tie with person k and person k with person j with k ≠ i then it follows from the models that β₁= β₂ =0.

This issue raised by Lyons is essentially that there are more equations than unknowns. This arises because the state of the ego at time t is regressed on the current state of the alter at the same time t, rather than only on the lagged state of the alter. When there is reciprocation between persons with regard to their ties, this creates modeling problems. Intuitively, the problem develops because the same variable at the same time period, e.g. the ego’s state at time t, is the dependent variable in one regression and the independent variable in another regression.

As noted by Lyons, the models themselves then effectively contradict the conjecture of social influence that Christakis and Fowler want to assess. An important exception, however, arises when the null hypothesis of no contagion is true. In this case, provided that homophily and environmental confounding have been properly controlled for, β₁ does indeed equal 0 (cf. Shalizi and Thomas, 2011). And, if β₁ = 0, then the models may be correctly specified, provided e.g. the log odds of the ego’s state is indeed linear in the covariates. Under the null hypothesis of no contagion, the problem of model inconsistency effectively vanishes¹. Thus, under the null hypothesis of no contagion, a statistical test for β₁ = 0 would provide a joint test of (i) no contagion, (ii) no homophily or environmental confounding conditional on the covariates and (iii) correct model specification with regard to the covariates. The estimate and confidence interval for β₁ would not constitute a valid estimate of the contagion effect, even if there is no homophily or environmental confounding conditional on the covariates. However, whether the confidence interval for β₁ contained 0 would constitute a valid test of the null hypothesis of no contagion, again provided the assumptions of no homophily and no environmental confounding conditional on the covariates and that of correct model specification with respect to the covariates held. Under these assumptions, we can in theory do testing, but not estimation.

This brings us to yet another critique offered by Lyons (2011), that of statistical modeling under the dependence structures that are generated by a social network. Christakis and Fowler (2007, 2008) use a method referred to as generalized estimating equations, clustering on the ego, to take into account the use of multiple time points for the ego. Unfortunately, as Lyons (2011) notes, this is not the only source of dependence in the data. If there is social influence (contagion) then the clusters defined by the ego will not be independent of one another. Moreover, even under the null of no contagion, when contemporaneous ego-alter data is used, the generalized estimating equations standard error is not always valid. Christakis and Fowler (2007, 2008) consider social influence for different types of relationships including ego-nominated friends, alter-nominated friends, mutual friends, spouses, neighbors and siblings. We show in the Appendix that because Christakis and Fowler (2007, 2008) use contemporaneous data for the ego and the alter, and because one person’s state at time t is thus both an outcome in one regression and an independent variable in another, the standard errors for β₁ obtained by Christakis and Fowler (2007, 2008) are anti-conservative whenever relationships are reciprocal e.g. for mutual friends, spouses, siblings and neighbors. In these cases, even under the null hypothesis of no contagion, the standard errors will be invalid and the confidence intervals will be too narrow. One could derive a valid estimator of the standard error under the null but unfortunately the generalized estimating equation standard error used by Christakis and Fowler (2007, 2008) is not valid. However, we also show that for relationships which are not reciprocal, e.g. ego-nominated friendships or alter-nominated friendships (that are not mutual friendships), the generalized estimating equation standard error used by Christakis and Fowler (2007, 2008) is valid under the null hypothesis of no contagion and thus whether their confidence interval includes 0 does constitute a valid test for the null of no contagion, provided control has been made for homophily and environmental confounding.²

For the purposes of testing, both the problem of model inconsistency and the problems of statistical dependence and standard error estimation can be easily addressed if the alter’s state is lagged by an additional period in the regressions. The argument used by Lyons (2011) to show that the models are inconsistent in the presence of contagion is no longer applicable. Moreover, under the null of no contagion, and provided adequate control has been made for homophily and environmental confounding, the clusters defined by the ego are independent of one another, avoiding statistical dependence throughout the network. Finally, by lagging the alter’s state by an additional period, the same variable is no longer an outcome in one regression and a dependent variable in another regression at the same period time t, circumventing the issue of obtaining, under the null, valid standard errors when using generalized estimating equations. The generalized estimating equation standard error will be valid, under the null of no contagion. Thus, if a researcher lags the alter’s state by an extra time period so that the log odds of the ego’s state at time t, Y_i,t, is modeled as a linear function of the alter’s state at time t − 1, Y_j,t−1, and at time t − 2, Y_j,t−2, the ego’s state at time t − 1, Y_i,t−1, and the covariates for the ego:

$$log\left(\frac{P(Y_{i,t}=1\mid Y_{j,t-1},Y_{j,t-2},Y_{i,t-1},X_i)}{P(Y_{i,t}=0\mid Y_{j,t-1},Y_{j,t-2},Y_{i,t-1},X_i)}\right)={\beta }_0+{\beta }_1{Y}_{j,t-1}+{\beta }_2{Y}_{j,t-2}+{\beta }_3{Y}_{i,t-1}+{\beta }_4^{\prime }{X}_i$$

then, whether the generalized estimating equation confidence interval for the coefficient of Y_j,t−1 contains 0 will constitute a valid test of the null of no contagion. We can at least still do testing using the same approach of Christakis and Fowler (2007, 2008) but simply lagging the alter’s state by an additional period.

All of our discussion thus far has assumed that adequate control has been made for homophily and environmental confounding. As noted by Lyons (2011) and by Shalizi and Thomas (2011), this is, of course, a very strong assumption. VanderWeele (2011) proposed a sensitivity analysis technique to assess the extent to which an unmeasured factor responsible for homophily or environmental confounding would have to be related to both the ego’s and the alter’s state in order to substantially alter qualitative and quantitative conclusions. The technique itself made simplifying parametric assumptions but a more general approach could alternatively be used (VanderWeele, 2011; VanderWeele and Arah, 2011). Unfortunately, however, it is not clear that this technique would apply in the context of inconsistent models when contemporaneous data for the ego and the alter are used. This is because the sensitivity analysis parameters in VanderWeele (2011) related the observed expectation for the ego’s state, controlling for observed covariates, to the expectation that would have been obtained had control also been possible for an unobserved covariate; however, when the models are inconsistent then it is no longer clear that the estimates, e.g. in Christakis and Fowler (2007, 2008), using the observed data, provide a consistent estimate of the expectation conditional on the observed covariates, for the very reasons raised by Lyons. The sensitivity analysis technique could, however, be applied to estimates obtained by lagging the alter’s state by an additional period because, once again, the problem of model inconsistency then no longer arises.

We have given numerous arguments for lagging the alter’s state by an additional period: (1) the problem of model inconsistency raised by Lyons (2011) does not arise, (2) the analyses using generalized estimating equations clustering by ego as in Christakis and Fowler (2007, 2008) will give valid tests of the null of no contagion, and (3) the sensitivity analysis technique of VanderWeele (2011) can be applied to the estimates obtained from such analyses.

In fact, Christakis and Fowler (2007, 2008) report, in the online supplement to their papers, that they ran such analyses in which the alter’s state was lagged by an additional period and that the results of such analyses were similar to those of their main analyses using contemporaneous data for the ego and alter, i.e. they once again find evidence of significant contagion effects for smoking and obesity. Moreover, with these lagged social network analyses, the sensitivity analysis techniques to assess that the extent to which latent homophily and unmeasured environmental confounding could explain away the estimates are again applicable and suggest the contagion effect for smoking cessation between spouses and obesity between mutual friends are quite robust to potential latent homophily and unmeasured environmental confounding (VanderWeele, 2011).

A few further caveats are, however, in order. First, the sensitivity analysis techniques, in their present form, are not applicable to dynamic forms of homophily, such as “unfriending”, as considered by Noel and Nyhan (2011). However, this unfriending problem in the Framingham Heart Study data used by Christakis and Fowler (2007, 2008) does not seem, by Noel and Nyhan’s own simulations, sufficiently common to result in substantial biases. Second, even with the alter’s state lagged an additional period, the sensitivity analysis technique of VanderWeele (2011) is applicable to the estimates, but may not be to the limits of the confidence interval obtained by using generalized estimating equations, because, under the alternative hypothesis that contagion effects are present, the standard error for the supposed contagion effect still may not be valid because of statistical dependence in outcomes across the network. If valid confidence intervals were obtained the sensitivity analysis technique of VanderWeele (2011) would be applicable to the limits of the confidence interval as well. Finally, although some progress can be made with testing the null of no contagion, ultimately, we would also like to be able to obtain valid inferences and confidence intervals, not just tests and estimates. Doing so will require the development of statistical theory to handle the sorts of dependence structures that arise on social networks. In our view, this should be one of the central priorities in subsequent work that aims to provide a more rigorous foundation for the types of social network analyses for contagion effects exemplified by the studies of Christakis and Fowler (2007, 2008).

Appendix

Consider outcome data Y_i,t, t = 1, …, T; i = 1, …n; let X_i,t denote p covariates for person i observed up to time t. If X_i,t is time-invariant then we could also write X_i,t = X_i. Let 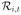denote the set of all Y_j,t with a specific type of tie to person i at time t, i ≠ j, which can be of Type A for an “alter-nominated tie”, of type E for an “ego-nominated tie”, or of type M for a “mutually-nominated tie” (or similarly for any other type of tie which is reciprocal e.g. spouse, neighbor, sibling). To test for contagion we may test the null hypothesis H₀ that Y_i,t is jointly independent of {Y_j,t: Y_j,t ∈ 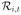} given (X_i,t, Y_i,t−1, Y_j,t−1). We make the following assumptions:

1. The cardinality of 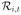remains bounded as n goes to infinity.

2. The support of X_i,t is bounded.

3. Y_i,t is the independent of ({X_j,t′ : t′ ≤ t}, {Y_j,t′ : t′ < t −1}, {X_j,t′ : t′ < t}) given (X_i,t, Y_i,t−1, Y_j,t, Y_j,t−1).

   $$\begin{array}{l}\text{logit}{P}_{i,j,t}(\beta ):=\text{logit}Pr(Y_{i,t}=1\mid Y_{j,t},X_{i,t},Y_{i,t-1};\beta )\\ ={\beta }_0+{\beta }_1{Y}_{j,t}+{\beta }_2{Y}_{j,t-1}+{\beta }_3{Y}_{i,t-1}+{\beta }_4^{\prime }{X}_{i,t},\\ \text{for}\text{all}{Y}_{j,t}\in {\mathcal{R}}_{i,t},\text{where}{\beta }_1=0\text{encodes}\text{the}\text{null}\text{effect}\text{of}{Y}_{j,t},\\ \text{and}\beta ={[\begin{array}{ccccc}{\beta }_0& {\beta }_1& {\beta }_2& {\beta }_3& {\beta }_4^T\end{array}]}^T={[\begin{array}{ccccc}{\beta }_0& 0& {\beta }_2& {\beta }_3& {\beta }_4^T\end{array}]}^T.\end{array}$$ (1)

Christakis and Fowler (2007, 2008) estimate β by maximizing the objective function

$$log\prod _i\prod _t\prod _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}^{Y_{i,t}}{P}_{i,j,t}{({\beta }^{\ast })}^{Y_{i,t}(1-Y_{i,t})}{(1-P_{i,j,t}({\beta }^{\ast }))}^{(1-Y_{i,t})}$$

with respect to β^* which produces β̂, the solution to the estimating equation:

$$\begin{array}{l}\sum _i\sum _t\sum _{j\ne i:Y_{j,t}\in {\mathcal{R}}_{i,t}}{U}_{i,j,t}\left(\widehat{\beta }\right)=0\\ \text{where}{U}_{i,j,t}\left(\widehat{\beta }\right)=W_{i,j,t}{\epsilon }_{it}\\ W_{i,j,t}={[\begin{array}{ccccc}1& Y_{j,t}& Y_{j,t-1}& Y_{i,t-1}& X_{i,t}^T\end{array}]}^T\\ {\epsilon }_{it}=\left\{Y_{i,t}-P_{i,j,t}\left(\widehat{\beta }\right)\right\}\end{array}$$ (2)

this set of equations define a standard GEE for correlated outcomes with a logit link, and the independence working correlation matrix. In this setting, the large sample variance of β̂ is typically approximated by Σ_emp =

$$\begin{array}{l}{\left\{n^{-1}\sum _i\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\frac{\partial U_{i,j,t}({\beta }^{\ast })}{\partial {\beta }^{\ast T}}{\mid }_{\beta }\right]\right\}}^{-1}\\ \times n^{-1}\left\{\sum _i\mathbb{E}{\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}{U}_{i,j,t}(\beta )\right]}^{\otimes 2}\right\}\\ \times {\left\{n^{-1}\sum _i\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\frac{\partial U_{i,j,t}({\beta }^{\ast })}{\partial {\beta }^{\ast T}}{\mid }_{\beta }\right]\right\}}^{-1}\end{array}$$

We now state the main result.

Result

Suppose assumptions 1-4 hold, then, under H₀, the following hold:

1. if for all i and for all t, R_i,t is strictly of type E or A only, then Σ_emp is, when n is large, approximately equal to the large sample variance-covariance of β̂.

2. if for all i and for all t, R_i,t is strictly of type M only, then Σ_emp is guaranteed, when n is large, to be anti-conservative; that is Σ_emp is generally smaller (in the semipositive definite sense) than the variance-covariance of β̂.

Proof

Under H₀ it can be verified that under Assumption 4, $\beta ={[\begin{array}{ccccc}{\beta }_0& 0& {\beta }_2& {\beta }_3& {\beta }_4^T\end{array}]}^T$ solves the equation

$$\mathbb{E}\{U_{i,j,t}(\beta )\}=0$$

which in turn implies that under mild regularity conditions, β̂ is consistent for β. Furthermore, a Taylor series expansion of equation (2) can be used to establish that in large samples, under Assumptions 1-4:

$$\sqrt{n}\left(\widehat{\beta }-\beta \right)\approx {\left\{n^{-1}\sum _i\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\frac{\partial U_{i,j,t}({\beta }^{\ast })}{\partial {\beta }^{\ast T}}{\mid }_{\beta }\right]\right\}}^{-1}\frac{1}{\sqrt{n}}\sum _i\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}{U}_{i,j,t}(\beta )$$

This further implies that in large samples, the variance of $\sqrt{n}\left(\widehat{\beta }-\beta \right)$ is approximately equal to

$$\begin{array}{l}{\left\{n^{-1}\sum _i\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\frac{\partial U_{i,j,t}({\beta }^{\ast })}{\partial {\beta }^{\ast T}}{\mid }_{\beta }\right]\right\}}^{-1}\times n^{-1}\mathbb{E}{\left\{\sum _i\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}{U}_{i,j,t}(\beta )\right\}}^{\otimes 2}\\ \times {\left\{n^{-1}\sum _i\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\frac{\partial U_{i,j,t}({\beta }^{\ast })}{\partial {\beta }^{\ast T}}{\mid }_{\beta }\right]\right\}}^{-1}\end{array}$$

where A^⊗2 = AA^T. The middle factor reduces to

$$\begin{array}{l}{n}^{-1}\mathbb{E}{\left\{\sum _i\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}{U}_{i,j,t}(\beta )\right\}}^{\otimes 2}\\ =n^{-1}\sum _i\mathbb{E}{\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}{U}_{i,j,t}(\beta )\right]}^{\otimes 2}\\ +n^{-1}\sum _{i\ne j}\mathbb{E}\left[\left\{\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}{U}_{i,j,t}(\beta )\right\}\left\{\sum _t\sum _{k:Y_{k,t}\in {\mathcal{R}}_{j,t}}{U}_{j,k,t}^T(\beta )\right\}\right]\end{array}$$

and

$$\begin{array}{l}{n}^{-1}\sum _{i\ne s}\mathbb{E}\left[\left\{\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}{U}_{i,j,t}(\beta )\right\}\left\{\sum _{t^{\prime }}\sum _{k:Y_{k,t^{\prime }}\in {\mathcal{R}}_{s,t^{\prime }}}{U}_{s,k,t^{\prime }}^T(\beta )\right\}\right]\\ =n^{-1}\sum _{i\ne s}\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\sum _{k:Y_{k,t}\in {\mathcal{R}}_{s,t}}{U}_{i,j,t}(\beta )U_{s,k,t}^T(\beta )\right]\end{array}$$

since under Assumption 3, for t < t′, Y_j,t ∈ 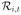, Y_k,t′ ∈ 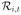and i ≠ s

$$\mathbb{E}\{U_{i,j,t}(\beta )U_{s,k,t^{\prime }}^T(\beta )\}=0.$$

Furthermore, Assumption 3 implies that:

$$\begin{array}{l}{n}^{-1}\sum _{i\ne s}\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\sum _{k:Y_{k,t}\in {\mathcal{R}}_{s,t}}{U}_{i,j,t}(\beta )U_{s,k,t}^T(\beta )\right]=n^{-1}\sum _{i\ne s}\sum _{t}1(Y_{s,t}\in {\mathcal{R}}_{i,t})1(Y_{i,t}\in {\mathcal{R}}_{s,t})\mathbb{E}\{U_{i,j,t}(\beta )U_{s,k,t}^T(\beta )\}\\ =n^{-1}\sum _{i<s}\sum _{t}1(Y_{s,t}\in {\mathcal{R}}_{i,t})1(Y_{i,t}\in {\mathcal{R}}_{s,t})[\mathbb{E}\{U_{i,s,t}(\beta )U_{s,i,t}^T(\beta )\}+\mathbb{E}\{U_{s,i,t}(\beta )U_{i,s,t}^T(\beta )\}]\\ =n^{-1}\sum _{i<s}\sum _{t}1(Y_{s,t}\in {\mathcal{R}}_{i,t})1(Y_{i,t}\in {\mathcal{R}}_{s,t})[\mathbb{E}\{W_{i,s,t}{W}_{s,i,t}^T{\epsilon }_{it}{\epsilon }_{st}\}+\mathbb{E}\{W_{s,i,t}{W}_{i,s,t}^T{\epsilon }_{it}{\epsilon }_{st}\}]\end{array}$$

where

$$\begin{array}{l}\mathbb{E}\{W_{i,s,t}{W}_{s,i,t}^T{\epsilon }_{it}{\epsilon }_{st}\}=\left[\begin{array}{cc}{0}_{(p+2)\times (p+2)}& 0_{(p+2)\times 1}\\ 0_{1\times (p+2)}& P_{i,s,t}(\beta )(1-P_{i,s,t}(\beta ))P_{s,i,t}(\beta )(1-P_{s,i,t}(\beta ))\end{array}\right]\\ :={\mathrm{\Gamma }}_{i,s,t}\end{array}$$

Therefore the variance of $\sqrt{n}\left(\widehat{\beta }-\beta \right)$ is approximately equal to

$$\begin{array}{l}{\left\{n^{-1}\sum _i\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\frac{\partial U_{i,j,t}({\beta }^{\ast })}{\partial {\beta }^{\ast T}}{\mid }_{\beta }\right]\right\}}^{-1}\\ \times n^{-1}\mathbb{E}\left\{\begin{array}{c}{\sum }_i\mathbb{E}{\left[{\sum }_t{\sum }_{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}{U}_{i,j,t}(\beta )\right]}^{\otimes 2}\\ +{\sum }_{i<s}{\sum }_{t}1(Y_{s,t}\in {\mathcal{R}}_{i,t})1(Y_{i,t}\in {\mathcal{R}}_{s,t}){\mathrm{\Gamma }}_{i,s,t}\end{array}\right\}\\ \times {\left\{n^{-1}\sum _i\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\frac{\partial U_{i,j,t}({\beta }^{\ast })}{\partial {\beta }^{\ast T}}{\mid }_{\beta }\right]\right\}}^{-1}.\end{array}$$

The standard sandwich estimator implemented by Christakis and Fowler (2007, 2008) is under H₀ approximately equal to Σ_emp and therefore the bias of their estimator is approximately equal to

$$\begin{array}{l}{\left\{n^{-1}\sum _i\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\frac{\partial U_{i,j,t}({\beta }^{\ast })}{\partial {\beta }^{\ast T}}{\mid }_{\beta }\right]\right\}}^{-1}\\ \times n^{-1}\sum _{i<s}\sum _{t}1(Y_{s,t}\in {\mathcal{R}}_{i,t})1(Y_{i,t}\in {\mathcal{R}}_{s,t}){\mathrm{\Gamma }}_{i,s,t}\\ \times {\left\{n^{-1}\sum _i\mathbb{E}\left[\sum _t\sum _{j:Y_{j,t}\in {\mathcal{R}}_{i,t}}\frac{\partial U_{i,j,t}({\beta }^{\ast })}{\partial {\beta }^{\ast T}}{\mid }_{\beta }\right]\right\}}^{-1}\end{array}$$

which can be verified to be semipositive definite. Under the null hypothesis H₀, the variance estimator of β̂ used by Christakis and Fowler (2007, 2008) is valid in case (i) of the result, since then

$$1(Y_{s,t}\in {\mathcal{R}}_{i,t})1(Y_{i,t}\in {\mathcal{R}}_{s,t})=0\text{of}\text{all}t,\text{and}(s,i),s\ne i$$

and thus the bias term is equal to 0. However, in case (ii), with mutual/reciprocal ties, this is not the case and thus their variance estimator may be anti-conservative in large samples.