Image Segmentation with Cascaded Hierarchical Models and Logistic Disjunctive Normal Networks

Abstract

Contextual information plays an important role in solving vision problems such as image segmentation. However, extracting contextual information and using it in an effective way remains a difficult problem. To address this challenge, we propose a multi-resolution contextual framework, called cascaded hierarchical model (CHM), which learns contextual information in a hierarchical framework for image segmentation. At each level of the hierarchy, a classifier is trained based on downsampled input images and outputs of previous levels. Our model then incorporates the resulting multi-resolution contextual information into a classifier to segment the input image at original resolution. We repeat this procedure by cascading the hierarchical framework to improve the segmentation accuracy. Multiple classifiers are learned in the CHM; therefore, a fast and accurate classifier is required to make the training tractable. The classifier also needs to be robust against overfitting due to the large number of parameters learned during training. We introduce a novel classification scheme, called logistic disjunctive normal networks (LDNN), which consists of one adaptive layer of feature detectors implemented by logistic sigmoid functions followed by two fixed layers of logical units that compute conjunctions and disjunctions, respectively. We demonstrate that LDNN outperforms state-of-theart classifiers and can be used in the CHM to improve object segmentation performance.

1. Introduction

Contextual information has been widely used for solving high-level vision problems in computer vision [28, 27, 14, 22]. Contextual information can refer to either inter-object configuration, e.g. a segmented horse's body may suggest the position of its legs [28], or intra-object dependencies, e.g. the existence of a keyboard in an image implies that there is very likely a mouse near it [27]. From the Bayesian point of view, contextual information can be interpreted as the probability image map of an object, which caries prior information in the maximum aposteriori (MAP) pixel classification problem.

There have been many methods that use contextual information for image segmentation and scene understanding. He et al. [13] used the conditional random fields (CRF) to capture contextual information at multiple scales for image segmentation. Torralba et al. [27] proposed boosted random field (BRF), which uses boosting to learn the graph structure of CRFs, for object detection. Desai et al. [8] proposed a discriminative model for multiclass object recognition that can lean intra-class relationships between different categories. The cascaded classification model [14] combines scene categorization, object detection, and multiclass image segmentation for scene understanding. Choi et al. [6] also proposed a scene understanding framework, which uses a tree-based graphical architecture to model object dependencies, local features, and local detectors. In a more related work, Tu and Bai [28] introduced the auto-context algorithm, which integrates both image features and contextual information to learn a series of classifiers, for image segmentation. A filter bank is used to extract the image features and the output of each classifier is used as the contextual information for the next classifier in the series.

We also introduce a segmentation framework that takes advantage of both input image features and contextual information. Similar to the auto-context algorithm, we use a filter bank to extract input image features. But we use a hierarchical architecture to capture contextual information at different resolutions. Moreover, this multi-resolution contextual information is learned in a supervised framework, which makes it more discriminative compared to the abovementioned methods. To our knowledge, supervised multi-resolution contextual information has not previously been used in a segmentation framework. We use a cascade of hierarchical models to improve the segmentation accuracy gradually in the series architecture.

Our proposed model learns several classifiers with many free parameters, which can make it slow to train and prone to overfitting. To address these problems, we propose a new probabilistic classifier, logistic disjunctive normal networks (LDNN), that can be trained efficiently. Unlike traditional neural networks, it has only one adaptive layer, which makes it easier and faster to train. In addition, it allows a simple and intuitive initialization of the network weights which avoids the herd-effect [10].

2. Cascaded Hierarchical Model

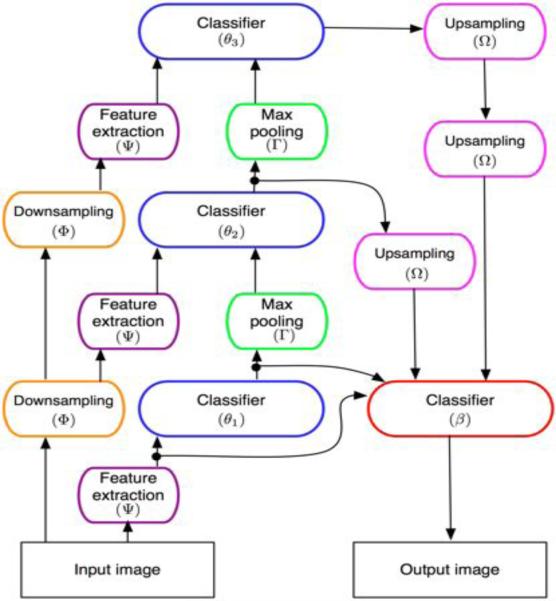
The hierarchical model is illustrated in Figure 1. First, a multi-resolution representation of the input image is obtained by applying downsampling sequentially (orange ovals in Figure 1). Next, a series of classifiers are trained at different resolutions from the finest resolution to the coarsest resolution. At each resolution, the classifier is trained based on the output of the previous classifier in the hierarchy and the input image at that resolution. Finally, the outputs of these classifiers are used to train a new classifier at original resolution. This classifier exploits the rich contextual information from multiple resolutions. The cascaded hierarchical model (CHM) is obtained by repeating the same procedure consecutively. We describe different steps of the model separately in the following subsections.

Figure 1.

Illustration of the hierarchical model. The blue classifiers are learned during the bottom-up step and the red classifier is learned during the top-down step. The height of the hierarchy, L, is three in this model but it can be extended to any arbitrary number. In the cascaded hierarchical model, the red classifier is used as the first classifier of the bottom-up step of next stage.

2.1. Bottom-up step

Let X = (x(m, n)) be the 2D input image with a corresponding ground truth Y = (y(m, n)) where y(m, n) ∈ {0, 1} is the class label for pixel (m, n). For notational simplicity, we use 1D vectors X = (x₁, x₂, . . . , x_n) and Y = (y₁, y₂, . . . , y_n) to denote the input image and corresponding ground truth, respectively. The training dataset then contains K input images, X = {X₁, X₂, . . . , X_K}, and corresponding ground truth images, Y = {Y₁, y₂, . . . , Y_K}. We also define the Φ(·, l) operator which performs down-sampling l times by averaging the pixels in each 2 × 2 window, the Ψ(·) operator that extracts features, and the Γ(·, l) operator which performs max-pooling l times by finding the maximum pixel value in each 2 × 2 window. Each classifier in the hierarchy has some internal parameters θ_l, which are learned during training

$${\widehat{\theta }}_1=\underset{{\theta }_1}{\arg \max }P(\Gamma (\mathbf{Y},l-1)\mid \Psi \left(\Phi (\mathbf{X},l-1)\right),\Gamma ({\widehat{\mathbf{Y}}}_{\mathrm{l}-1},1);{\theta }_1)$$ (1)

where Ŷ_l−1 is the output of classifier at the lower level of hierarchy. The classifier output of each level is obtained using inference

$${\widehat{Y}}_l=\underset{Y}{\arg \max }P(Y\mid \Psi \left(\Phi (X,l-1)\right),\Gamma ({\widehat{Y}}_{l-1},1);{\widehat{\theta }}_1).$$ (2)

The classifier output of the l'th level,Ŷ_l, creates context, i.e., prior information, for the l+1'st level classifier. For l = 1 no prior information is used and the classifier parameters, θ₁, are learned only based on the input image features. It is worth mentioning that while our feature extraction operator, Ψ, is fixed for all the levels, it captures information from larger areas as we go up through the hierarchy because it operates on downsampled images.

In practice, we use a cumulative version of the hierarchical model. In the cumulative framework, each classifier in the l'th level of the hierarchy takes outputs of all lower level classifiers, i.e.,Ŷ₁, . . . ,Ŷ_l−1. The cumulative frame-work provides multi-resolution contextual information for each classifier in the hierarchy and thus can improve the performance.

2.2. Top-down step

Unlike the bottom-up step where multiple classifiers are learned, only one classifier is trained in the top-down step. Once all the classifiers are learned in the bottom-up step, a top-down path is used to feed coarser resolution contextual information into a classifier, which is trained at the finest resolution. We define Ω(·, l) operator that performs upsampling l times by duplicating each pixel. For a hierarchical model with L levels, the classifier is trained based on the input image features and the outputs of stages 1 to L obtained in the bottom-up step. The internal parameters of the classifier, β, are learned using the following

$$\widehat{\beta }=\underset{\beta }{\arg \max }P(\mathbf{Y}\mid \Psi \left(\mathbf{X}\right),{\widehat{\mathbf{Y}}}_1,\Omega ({\widehat{\mathbf{Y}}}_2,1),\dots ,\Omega ({\widehat{\mathbf{Y}}}_{\mathbf{L}},L-1);\beta ).$$ (3)

The output of this classifier can be obtained using the following for inference

$$\widehat{Z}=\underset{Y}{\arg \max }P(Y\mid \Psi \left(X\right),{\widehat{Y}}_1,\Omega ({\widehat{Y}}_2,1),\dots ,\Omega ({\widehat{Y}}_L,L-1);\widehat{\beta }).$$ (4)

The top-down classifier takes advantage of prior information from multiple resolutions. This multi-resolution prior is an efficient mixture of both local and global information since it is drawn from different scales. In a related work, Seyedhosseini et al. [24] proposed multi-scale contextual model that exploits contextual information from multiple scales. The advantage of our model is that the context images are learned at different scales in a supervised framework while the multi-scale contextual model uses simple filtering to create context images at different scales.

2.3. Cascaded model

Our model is built by cascading multiple stages of bottom-up and top-down steps, consecutively. Each stage is composed of one bottom-up and one top-down step. The top-down classifier of each stage is used as the first classifier in the bottom-up step of the next stage. For the first stage, a previous top-down step is not available, the first classifier of the bottom-up step is learned only based on the input image features. We use ${\widehat{\theta }}_{\mathrm{sl}}$ and Ŷ_S1 to denote the parameters and outputs of the l'th classifier in the bottom-up step of stage s. We also use ${\widehat{\beta }}_{\mathrm{s}}$ and Ẑ_s to denote the parameters and outputs of the classifier in the top-down step of stage s. The overall learning algorithm for the cascaded hierarchical model is described in Algorithm 1. During inference, the goal is to infer the final output given the input image. Using the learned parameters for the classifiers, we consecutively infer the bottom-up and top-down classifiers. The inference algorithm is given in Algorithm 2.

Algorithm 1.

Learning algorithm for the CHM.

Input: A set of training images together with their binary groundtruth images, T = {(Xi,Yi),i =1,..., K} and the height of hierarchy, L.

Output: Θs1βa ,Nstage.

• Learn the first classifier, 6, using equation (1) without any prior information and only based on the input image features.

•Compute the output of first classifier, υ̂11,using equation (2).

•s ← 1.

repeat

for l = 2 to L do

• Learn the 1'th classifier, 6a, using equation (1).

• Compute output of the 1'th classifier, υ̂s1, using equation (2).

end for

• Learn the top-down classifier, β̂s, using equation 3.

• Compute output of the top-down classifier, ζ̂s, using equation 4.

• s ← s + 1, ${\widehat{\theta }}_{s1}\leftarrow {\widehat{\beta }}_{s-1}$, Ŷs1 ← Ẑs-1.

• Nstage ← S.

until convergence

Algorithm 2.

Inference algorithm for the CHM.

Input: An input image X, Θs1, βS, Nstage, L.

Output: υ̂.

• Compute the output of first classifier, υ̂11, using equation (2).

for S =1 to Nstage do

for l = 2 to L do

• Compute output of the 1'th bottom-up classifier, υ̂sl, using equation (2).

end for

• Compute output of the top-down classifier, ζ̂sl, using equation (4).

• υ̂(s+1)1→ζ̂s.

end for

• υ̂ → ζ̂s.

Even though our problem formulation is general and not restricted to any specific type of classifier, in practice we need a fast and accurate classifier that is robust against overfitting. Among off-the-shelf classifiers, we consider artificial neural networks (ANN), support vector machines (SVM), and random forests (RF). ANNs are slow at training time due to the computational cost of backpropagation. SVMs offer good generalization performance, but choosing the kernel function and the kernel parameters can be time consuming since they need to be adopted for each classifier in the CHM. Furthermore, SVMs are not intrinsically probabilistic and thus are not completely suitable for our CHM model. Random forests provide an unbiased estimate of testing error, but they are prone to overfitting in the presence of noise. In section 4.4 we show that overfitting can disrupt learning in the CHM model. We introduce a fast and yet powerful probabilistic classifier that can be employed in the CHM model.

3. Logistic Disjunctive Normal Networks

Any Boolean function b : Bⁿ → B where B = {0, 1} can be written as a disjunction of conjunctions which is also known as the disjunctive normal form [12]. Now consider the binary classification problem f : Rⁿ → B. Let X₊ = {X ∈ Rⁿ : f(X) = 1 and X₋ = {X ∈ Rⁿ : f(X) = 0}. One possibility for expressing f in disjunctive normal form is to approximate X₊ as the union of axis aligned hypercubes in R^k. We first define the box function

$$h_{L,U}\left(x\right)=\{\begin{array}{cc}1,\hfill & L\le x\le U\hfill \\ 0,\hfill & otherwise\hfill \end{array}\phantom{\}}$$ (5)

where L ∈ R, U ∈ R and L ≤ U. Then the disjunctive normal form can be rewritten as

$$\tilde{f}\left(X\right)=\underset{i}{\vee }\left(\underset{j=1}{\overset{n}{\wedge }}{h}_{L_{ij}},U_{ij}\left(x_j\right)\right)$$ (6)

where x_j denotes the j'th element of the vector X. This formulation is also known as a fuzzy min-max neural network [26]. The most important drawback of this model is its limitation to axis aligned decision boundaries which can significantly increase the number of conjunctions necessary for a good approximation. We propose to construct a significantly more efficient approximation in disjunctive normal form by approximating X₊ as the union of convex sets which are defined as the intersection of arbitrary half-spaces in Rⁿ. By using hyperplanes to define the half-spaces, we get the approximation

$$\tilde{f}\left(X\right)=\underset{i}{\vee }\underset{q_i\left(X\right)}{\underbrace{\left(\underset{j}{\wedge }{h}_{ij}\left(X\right)\right)}}$$ (7)

where the half-spaces are defined as

$$h_{ij}\left(X\right)=\{\begin{array}{cc}1,\hfill & \sum _{k=1}^n{w}_{ijk}{x}_k+b_{ij}\ge 0\hfill \\ 0,\hfill & otherwise\hfill \end{array}\phantom{\}}$$ (8)

Our next step is to replace equation (7) with a differentiable approximation. First, a conjunction of binary variables Λ_j hij(X) can be replaced by their product Π_j hij(X). Then, using De Morgan's laws we can replace the disjunction of binary variables Λ_i qi(X) with ¬ Λ_i ¬qi(X) which in turn can be replaced by the expression 1 Π_i(1 q_i(X)). Finally, we can approximate the half-spaces h_ij(X) with the logistic sigmoid function

$${\sigma }_{ij}\left(X\right)=\frac{1}{1+e^{-{\sum }_{k=1}^n{w}_{ijk}{x}_k+b_{ij}}}.$$ (9)

This gives in the differentiable disjunctive normal form approximation to f

$$\tilde{f}\left(X\right)=1-\prod _i(1-\underset{g_i\left(X\right)}{\underbrace{\prod _j{\sigma }_{ij}\left(X\right)}}).$$ (10)

This formulation can be interpreted as a 3-layer network. The input vector, i.e. X, is mapped to the first layer by sigmoid functions in equation (9). The first layer consists of N groups of nodes with M nodes each. The nodes in each group are connected to a single node in the second layer. Each node in the second layer implements the logical negations of the conjunctions g_i(X) in equation (10). The output layer is a single node which implements the disjunction using De Morgan's law. We will refer to such a network as a N × M LDNN. Notice that the only parameters of the network are the weights, w_ijk, and biases, b_ij, of the connections between the inputs and the first layer of sigmoid functions. This is an advantage of using parameterless functions, i.e. the products, for representing the conjunctions.

Given a set of training examples T of pairs (X, y) where y denotes the desired binary class corresponding to X and a classifier f(X), the quadratic error over the training set is

$$E(f,\mathbf{T})=\sum _{(X,y)\in \mathbf{T}}{(y-f\left(X\right))}^2.$$ (11)

The gradient of the error function with respect to the parameter w_ijk in the LDNN architecture, evaluated for the training pair (X, y), is

$$\frac{\partial E}{\partial w_{ijk}}=-2(y-f\left(X\right))\prod _{r\ne i}(1-g_r\left(X\right))g_i\left(X\right)(1-{\sigma }_{ij}\left(X\right))x_k.$$ (12)

Similarly the gradient of the error function with respect to the bias term b_ij is

$$\frac{\partial E}{\partial b_{ij}}=-2(y-f\left(X\right))\prod _{r\ne i}(1-g_r\left(X\right))g_i\left(X\right)(1-{\sigma }_{ij}\left(X\right)).$$ (13)

The parameters of the LDNN can be learned by minimizing equation (11) using the gradient descent algorithm and equations (12), (13).

Finally, the disjunctive normal form used in the the LDNN permits a very simple and intuitive initialization of the model parameters. Since each conjunction is a convex set in Rⁿ and X₊ is approximated as the union of N such conjunctions, we can view the convex sets generated by the conjunctions as sub-clusters of X₊. To initialize a model with N conjunctions and M sigmoids per conjunction, we:

• Use the k-means algorithm to partition X₊ and X_– into N and M clusters, respectively. Let C_+,i and C_–,i be the centroid of the i'th clusters in each partition.

• Initialize the weight vectors W_ij as the unit length vectors from the j′th negative to the i′th positive centroid.

• Initialize the bias terms b_ij such that the sigmoid functions σ_ij(X) take the value 0.5 at the midpoints of the lines connecting the positive and negative cluster centroids.

It is noteworthy that our LDNN is fundamentally different from disjunctive fuzzy nets [20]. The LDDN is a differentiable model and hence enables us to minimize an objective function while disjunctive fuzzy nets are based on prototypes and an adhoc training procedure.

4. Experimental Results

We perform experimental studies to evaluate the performance of both LDNN and CHM. The LDNN was tested on three binary and two multi-class datasets. We also tested the CHM model on the Weizmann horse dataset [4], two Electron Microscopy datasets, and the Corel dataset [13].

4.1. LDNN (Binary datasets)

We compared LDNN to random forests, artificial neural networks (ANN), and SVM on three binary datasets: IJCNN [5], Wisconsin breast cancer, and PIMA diabetes [11]. For all the datasets 2/3 of the samples were used for training. The testing error rates are given in Table 1. All classifiers were optimized for accuracy by trying various model settings. LDNN training times were couple of orders of magnitudes faster than ANNs and generally between random forests and SVMs.

Table 1.

Error rates for three binary datasets from UCI repository.

Method	IJCNN	Wis. breast cancer	PIMA
Random Forest	2.00%	1.79%	20.81%
SVM	1.41%	1.59%	21.57%
ANN	2.34%	2.28%	22.11%
LDNN	1.28%	0.8%	17.97%

4.2. LDNN (MNIST dataset)

The MNIST dataset [19] contains 60000 training and 1000 testing images of handwritten digits. There are 10 classes in this dataset corresponding to digits 0 to 9. The size of each image is 28 × 28. We used pixel intensities without any preprocessing as input features. We trained ten 9 × 9 LDNN in the one-vs-all architecture. For comparison, we also trained a random forest classifier with 500 trees, 40000 samples per tree, and 26 features per node. The error rates are given in Table 2. The random forest classifier has more overfitting compared to the LDNN. We tried to decrease the random forest overfitting by tweaking the parameters as much as possible. It is worth mentioning, while the achieved error rate is not state-of-the-art, our simple classifier outperforms SVM [19] (1.4%), neural networks [15] (1.6%), and many other methods for which the error rates can be found in [19]. Moreover, the LDNN results can be improved by applying preprocessing techniques [19] such as deskewing, width normalization, etc.

Table 2.

Error rates for the MNIST and Landsat datasets.

	MNIST		Landsat
Method	Training Error	Testing Error	Training Error	Testing Error
Random Forest	0.005%	2.96%	0.22%	9.15%
SVM	-	1.40%	1.98%	8.15%
LDNN	0.02%	1.23%	2.66%	7.98%

4.3. LDNN (Landsat dataset)

The Landsat dataset [11] contains 4435 training and 2000 testing samples. Each sample is the multi-spectral values of pixels in the 3 × 3 neighborhood of the target pixel in a satellite image. There are 6 classes in this dataset associated with the type of soil. We employed one-vs-all architecture and trained six 9 × 9 LDNN classifiers. We also trained a random forest classifier with 200 trees and a SVM classifier [5] with RBF kernel. The parameters of the kernel were found using the search code available in the LIBSVM library [5]. The error rates are reported in Table 2. LDNN outperforms both random forest and SVM.

4.4. CHM (Weizmann horse dataset)

The Weizmann dataset [4] contains 328 gray scale horse images with corresponding foreground/background truth maps. Similar to Tu et al. [28], we used half of the images for training and the remaining images were used for testing. The task is to segment horses in each image. The features that we extract from input images include Haar features [29], histograms of oriented gradients (HOG) features [7] and SIFT flow features [23]. In addition, we apply a set of Gabor filters and Canny edge detector to obtain more features. We used a patch of size 21 × 21 to extract the image features. Similar to Jurrus et al. [16], we used a 15 × 15 sparse stencil to sample context images, i.e. outputs of classifiers. Note that, only direct samples of context images are used in CHM and no extra features are extracted from context images.

We used a 24 × 24 LDNN as the classifier in a CHM with three stages and 5 levels per stage. To improve the generalization performance, we adopted the dropout idea from the field of neural networks. Hinton et al. [15] showed that removing 50% of the hidden nodes in a neural network during the training can improve the performance on the test data. Using the same idea, we randomly removed half of the nodes in the second layer and half of the nodes per group in the first layer at each iteration during the training. At test time, we used the LDNN that contains all of the nodes with their outputs square rooted to compensate for the fact that half of them were active during the training time.

For comparison, we trained a CHM with random forest as the classifier. To avoid overfitting, only $\frac{1}{20}$ of samples were used to train 100 trees in the random forest. We also trained a multi-scale series of artificial neural networks (MSANN) as in [24]. Three metrics were used to evaluate the segmentation accuracy: Pixel accuracy, $\text{F-value}=\frac{2\times precision\times recall}{precision+recall}$, and $\text{G-mean}=\sqrt{recall\times TNR}$ where $TNR=\frac{truenegative}{truenegative+falsepositive}$. Unlike F-value, G-mean is symmetric with respect to positive and negative classes.

In Table 3 we compare the performance of CHM with some state-of-the-art methods. These results place CHM in the context of state-of-the-art methods. It is worth noting that CHM does not make use of fragments and it is based purely on discriminative classifiers that use neighborhood information. Hence it is applicable to a variety of problems such as boundary detection and object segmentation.

Table 3.

Testing performance of different methods for the Weiz- mann horse dataset.

Method	F-value	G-mean	Pixel accuracy
KSSVM [3]	-	-	94.60%
TWM [17]	-	-	94.70%
Auto-context [28]	84%	-	-
Levin & Weiss [21]	-	-	95.2%
MSANN [24]	87.58%	92.76%	94.34%
CHM-RF	83.15%	90.20%	92.33%
CHM-LDNN	89.89%	94.39%	95.37%

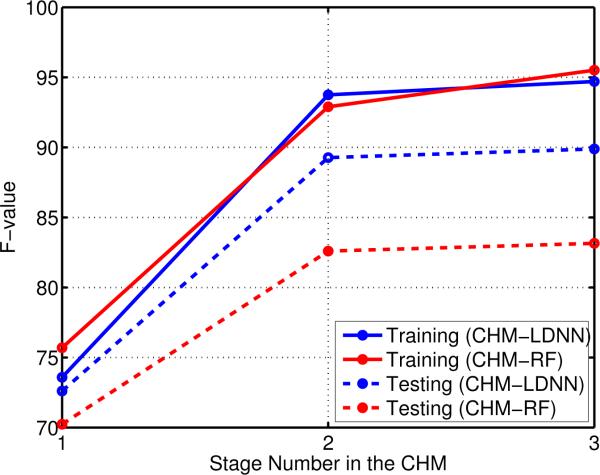
The CHM-LDNN outperforms the state-of-the-art methods while the CHM-RF performs worse than the other methods. The training and testing F-value at different stages of the CHM for both LDNN and random forest are shown in Figure 2. It shows how overfitting propagates through the stages of the CHM when the random forest is used as the classifier. The overfitting disrupts the learning process because there are too few mistakes in the training set compared to the testing set as we go through the stages. For example, the overfitting in the first stage does not permit the second stage to learn the typical mistakes from the first stage that will be encountered at testing time. We tried random forest with different parameters to overcome this problem but were unsuccessful. Figure 3 shows four examples of our test images and their segmentation results using different methods. The CHM-LDNN outperforms the other methods in filling the body of horses.

Figure 2.

F-value at different stages of the CHM with LDNN and random forest. The overfitting in the random forest makes it useless in the CHM architecture.

Figure 3.

Test results of theWeizmann horse dataset. (a) Input image, (b) MSANN [24], (c) CHM-RF, (d) CHM-LDNN, (e) ground truth images. The CHM-LDNN is more successful in completing the body of horses.

4.5. CHM (mouse neuropil dataset)

This dataset is a stack of 70 images from the mouse neuropil acquired using serial block face scanning electron microscopy (SBFSEM). It has a resolution of 10 × 10 × 50 nm/pixel and each 2D image is 700 by 700 pixels. An expert anatomist annotated membranes, i.e. cell boundaries, in these images. From those 70 images, 14 images were randomly selected and used for training and the 56 remaining images were used for testing. The task is to detect membranes in each 2D section. We used the same set of features as we used in the horse experiment. Additionally, we included Radon-like features (RLF) [18], which proved to be informative for membrane detection.

We used a 24 × 24 LDNN with three stages and 5 levels per stage. Since the task is detecting the boundary of cells, we compared our method with two general boundary detection methods, gPb-OWT-UCM (global probability of boundary followed by the oriented watershed transform and ultrametric contour maps) [1] and boosted edge learning (BEL) [9]. The testing results for different methods are given in Table 4. The CHM-LDNN outperforms the other methods with a notably large margin.

Table 4.

Testing performance of different methods for the mouse neuropil and Drosophila VNC datasets.

	Mouse neuropil		Drosophila VNC
Method	F-value	G-mean	F-value	G-mean
gPb-OWT -UCM [1]	45.68%	64.75%	49.90%	69.57%
BEL [9]	71.68%	84.46%	70.21%	84.20%
MSANN [24]	81.99%	90.48%	78.89%	88.74%
CHM-RF	79.28%	88.42%	77.56%	87.82%
CHM-LDNN	86.00%	92.48%	80.72%	90.02%

One example of the test images and corresponding membrane detection results using different methods are shown in Figure 4. As shown in our results, the CHM-LDNN outperforms CHM-RF and MSANN in removing undesired parts from the background and closing some gaps.

Figure 4.

Test results of the mouse neuropil dataset (first row) and the Drosophila VNC dataset (second row). (a) Input image, (b) gPb-OWT-UCM [1], (c) BEL [9], (d) MSANN [24], (e) CHM-RF, (f) CHM-LDNN, (g) ground truth images. The CHM-LDNN is more successful in removing undesired parts and closing small gaps. Some of the improvements are marked with red rectangles. For gPb-OWT-UCM method, the best threshold was picked and the edges were dilated to the true membrane thickness.

4.6. CHM (Drosophila VNC dataset)

This dataset was released for the ISBI 2012 EM challenge [2] and contains 30 images from Drosophila first instar larva ventral nerve cord (VNC) acquired using serialsection transmission electron microscopy (ssTEM). Each image is 512 by 512 pixels and the resolution is 4 × 4 × 50 nm/pixel. The membranes are marked by a human expert in each image. We used 15 images for training and 15 images for testing. The task is to find the membranes in each image. We used the same set of features and CHM parameters as the previous experiment and the testing performance for different methods are reported in Table 4. It can be seen that the CHM-LDNN outperforms the other methods. One test sample and membrane detection results for different methods are shown in Figure 4. We also trained the same model on the whole 30 images and submitted the results for the testing volume to the challenge server [2]. The achieved pixel error was 6.33% which is better than the human error, i.e., how much a second human labeling differed from the first one.

Finally, the training time of different methods in different experiments are reported in Table 5. We used the same resources for all methods. The training times show that CHMLDNN is slower than BEL while it is faster than CHM-RF and MSANN. Note that, gPb-OWT-UCM is unsupervised and thus there is no training time for it.

Table 5.

Training time for different datasets and different methods.

	Mouse neuropil	Drosophila VNC	Weizmann horse
BEL [9]	6 hours	4 hours	-
MSANN [24]	25 days	15 days	30 days
CHM-RF	57 hours	27 hours	66 hours
CHM-LDNN	24 hours	15 hours	35 hours

4.7. CHM (Corel dataset)

We also tested the CHM on the Corel dataset [13]. It contains 100 images which are manually labeled into 7 classes. We used 60 of the images for training and the rest of them were used for testing. We trained 7 CHMs for each of the classes separately. At test time, each pixel was labeled into the class with highest probability among all the trained CHMs. We achieved 79.37% pixel accuracy which outperforms textonboost [25] with 74.6% accuracy.

5. Conclusion

We introduced a discriminative learning scheme for image segmentation, called CHM, which uses contextual information at multiple resolutions. CHM trains several classifiers at multiple resolutions and leverages the obtained results for learning a classifier at the original resolution. The same process is repeated in consecutive stages until the improvement becomes negligible.

We also showed that off-the-shelf classifiers are not suitable for CHM. They are either slow in training such as ANN or prone to overfitting such as random forests. To address these problems, we proposed a novel classifier, called LDNN, which consists of one adaptive layer of feature detectors implemented by logistic sigmoid functions followed by two fixed layers of logical units that compute conjunctions and disjunctions, respectively. We showed LDNN outperforms RF and SVM in general learning tasks as well as image segmentation and it also speeds up the learning process in the CHM architecture.