Capture of Fluorescence Decay Times by Flow Cytometry

Abstract

In flow cytometry, the fluorescence decay time of an excitable species has been largely underutilized and is not likely found as a standard parameter on any imaging cytometer, sorting, or analyzing system. Most cytometers lack fluorescence lifetime hardware mainly owing to two central issues. Foremost, research and development with lifetime techniques has lacked proper exploitation of modern laser systems, data acquisition boards, and signal processing techniques. Secondly, a lack of enthusiasm for fluorescence lifetime applications in cells and with bead-based assays has persisted among the greater cytometry community. In this unit, we describe new approaches that address these issues and demonstrate the simplicity of digitally acquiring fluorescence relaxation rates in flow. The unit is divided into protocol and commentary sections in order to provide a most comprehensive discourse on acquiring the fluorescence lifetime with frequency-domain methods. The unit covers (i) standard fluorescence lifetime acquisition (protocol-based) with frequency-modulated laser excitation, (ii) digital frequency-domain cytometry analyses, and (iii) interfacing fluorescence lifetime measurements onto sorting systems. Within the unit is also a discussion on how digital methods are used for aliasing in order to harness higher frequency ranges. Also, a final discussion is provided on heterodyning and processing of waveforms for multi-exponential decay extraction.

INTRODUCTION

In addition to overall fluorescence emission, the total time for an excited fluorophore to relax is a measurable quantity that indicates a variety of intracellular phenomena. For example, molecular interactions, protein expression, pH changes, protein sequestration, cell cycle discrimination, and presence of bulky quenchers all can be measured using fluorescence decay time (Sailer et al., 1998, 1998, 1997, 1996 Deka et al, 1996, Steinkamp and Crissman, 1993, Lakowicz, 2006). Time-dependent measurements provide a means for discriminating spectrally overlapping fluorophores (Houston et al., 2008, Keij and Steinkamp, 1998) as well as revealing unusual intermediates that exist within an excited molecule. In general, the fluorescence decay time provides quantifiable evidence of decay-dependant events independent of fluorophore concentration (see Lakowicz, 2006 for a thorough review). Because fluorescence decay does not rely on the number of excited molecules, it is also independent of the relative brightness of emitted light.

Fluorescence decay is approximated by the fluorescence lifetime (τ) or the average time a fluorophore spends in its excited energy level prior to decaying back to a ground state. The lifetime is a unique characteristic of an excitable molecule and for common organic fluorophores used in the fields of microscopy, imaging, and cytometry, the lifetime is generally between 1 and 30 nanoseconds. In particular, the ability to measure the nanosecond timescale of a molecule’s decay can be quite powerful for flow cytometry. In cytometers, the fluorescently labeled cell (or particle) traverses an optical excitation source at a constant velocity, limiting the amount of time fluorescence can be measured. The rapid laser transit prevents cells from being carefully and repeatedly scanned rendering lifetime gradients across the cell impossible. Although multiple lifetime methods are challenged by the cytometry throughput, the average fluorescence lifetime can still be accurately sampled and indicates an overall decay rate for the sum of fluorescence species within or on the surface of the cell. Since the nominal transit times of cells in standard cytometers ranges between 1 and 15 microseconds, the nanosecond-scale lifetime can be measured hundreds to thousands of times before the cell leaves the detector pathway.

Time-domain laser pulsing and frequency-domain laser modulation are two primary approaches to measure fluorescence lifetime in flow cytometry. Both approaches have been demonstrated in cytometry with various cell and bead-based applications (Cui et al., 2003, Steinkamp and Keij, 1999, Steinkamp et al., 1993, Deka and Steinkamp, 1996, Jin et al. 2007 and 2009, and Steinkamp 2001). With time-domain approaches, the fluorescence decay is observed over time with single photon counting detectors, then measured and fit using decay functions. The measurement is practiced by pulsing the excitation laser source and with precise timing, collecting the emission photons after laser pulsation. The decaying emission is collected by gating a detector, which involves, literally, activating photosensitivity upon laser pulsation and then deactivating the device after sufficient fluorescence decay has occurred. This method when integrated with flow cytometry hardware requires precise timing for laser pulsation over a flowing cell.

Overall, it is challenging to obtain a single lifetime parameter in real time because the digitized intensity decay needs to be regressed with the decay function to obtain the average fluorescence lifetime. Alternatively, intensity modulation approaches, or frequency-domain methods, have been widely explored because the approach readily works with a flowing cell sample. The laser excitation intensity is simply modulated and photomultiplier tubes (PMTs) are used to detect the modulated emission light. The frequency domain technique is mathematically described by transforming the familiar time-dependent fluorescence decay function (presented later) to the frequency domain, generally using a Fourier transform. Equation 1 demonstrates this result providing the modulated emission intensity, E(t), as a function of time, t, where E_o is the maximum emission intensity, ω is the angular modulation frequency of the intensity-modulated emission signal, φ, is the phase shift relative to the excitation modulation, and m_em is the depth of modulation of the emission signal.

$$E(t)=E_o[1+m_{em}sin(\omega t-\phi )]$$ [Equation 1]

When emission light is collected, the intensity of fluorescence is also modulated at the same frequency. However, the overall phase is shifted and the amplitude of the modulated signal is attenuated relative to the excitation light. The amplitude demodulation, m_em/m_ex, as well as the phase-shift, φ, of the fluorescence signal are directly proportional to the fluorescence lifetime, τ, as shown by equations 2 and 3. Based on the transit of cells through the laser source, the Gaussian-like cytometry pulse is retained during modulation; however, a high frequency component is superimposed on the total signal. Figure 1 illustrates the excitation and emission waveforms resulting from the frequency-domain technique. For simplicity, equation 1 does not include the Gaussian function.

Figure 1.

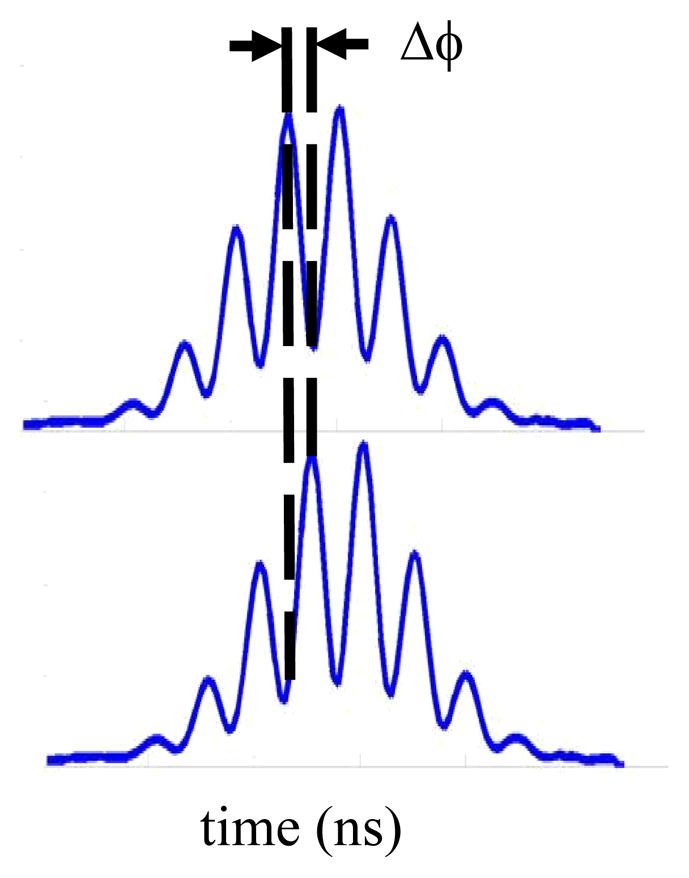
Illustration of a modulated fluorescent pulse (top) detected when acquiring phase-sensitive measurements. The phase shift, ΔΦ, between the modulated fluorescence and side scatter pulse (bottom) is captured in phase-sensitive flow cytometry to compute the average fluorescence lifetime.

$$\tau =\frac{tan(\phi )}{\omega }$$ [Equation 2]

$$\tau =\frac{\sqrt{\left(\frac{{m_{ex}}^2}{m_{em}}-1\right)}}{\omega }$$ [Equation 3]

The retention of high-throughput cell counting has driven the use of frequency-domain techniques in flow cytometry because the phase shift and amplitude attenuation can be quickly and accurately obtained in real time during the cell transit. Because of the dependence on the phase shift value for lifetime acquisition, the frequency-domain cytometry technique was coined as ‘phase-sensitive flow cytometry’ by Steinkamp and others (Steinkamp et al. 1993, Pinsky et al., 1993). A more extensive description of these methods can be found in a previous overview unit where in-depth theory on time-and frequency-domain methods is provided (see Steinkamp 2001). In general, the time-dependent techniques performed in the past involve time-domain approaches (Deka and Steinkamp 1996, Steinkamp and Parson, 2001, Jin, 2007 and 2009), simulation of frequency-domain heterodyning, multi-frequency measurements (Deka et al., 1995; Steinkamp and Parson, 2001), and digital data acquisition (Houston et al, 2010; Beisker and Klocke, 1997; Parson et al., 1994).

In this unit we provide an overview on the procedural approaches that can be taken to transform any non-scanning cytometer to a lifetime-measuring instrument. This is valuable for any less-experienced user who wishes to duplicate such a system in the laboratory. The steps toward developing lifetime cytometry involve utilizing a basic flow cytometer (fluidics, optics, lasers and a data acquisition and processing system) that is either commercial or custom-built, and modifying the instrument with appropriate hardware and data acquisition. The approaches discussed are mainly a result of our recent advances in frequency-domain flow cytometry and are disseminated to reveal the simplicity in hardware changes (Houston et al, 2010). In the modern era of cytometry more cytometric platforms are beginning to exploit direct digitization of waveforms for real-time processing of more than simple area, width, and peak measurements. Herein we describe how complete digitization is implemented for lifetime analysis and sorting. Moreover, we present methods that leverage digital processing to acquire not only single fluorescence lifetimes but also heterogeneous fluorescence decays. The unit is structured by three basic sections for clarity where the first section is a protocol on the conventional lifetime cytometry approach to preface new advances, as this approach has never been presented in a step-by-step fashion. Then, commentary is provide on a digital homodyne lifetime approach as well as the methods that enable lifetime extraction to be coupled to sorting in cytometry. These commentaries are followed by a final discussion on digital data acquisition systems and processing techniques that might improve lifetime measurements such as digital heterodyning, aliasing, measuring fluorescence lifetime by amplitude demodulation, multi-frequency analysis, and phase filtering.

Basic PROTOCOL1: CONVENTIONAL ANALOG ANALYSIS FOR SINGLE LIFETIME ACQUISITION

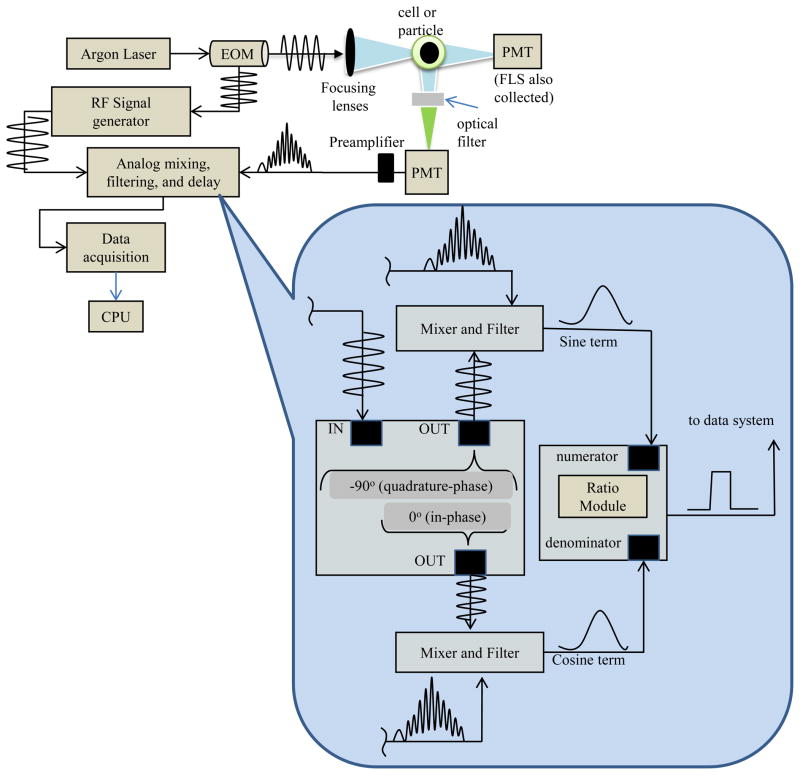
The standard frequency-domain approach for measuring the average fluorescence lifetime with a cytometer is also known as phase-sensitive flow cytometry (PSFC). The theory of PSFC is well described in Steinkamp (2001), which covers not only frequency-domain tactics but also time-domain methods that may be implemented in cytometry in order to measure the average fluorescence lifetime. PSFC adds a single average fluorescence lifetime parameter to compliment the other intensity-based list mode data. The transformation into a traditional PSFC system involves a considerable amount of analog hardware. At the inception of the PSFC technique, analog mixing devices were required, which contributed to a large footprint of several analog, connections, cables, multipliers, and other measurement devices. These components were necessary because data acquisition systems could not handle the digitization rate necessary to retain the high frequency information. Since common fluorophores express nanosecond lifetimes, a phase shift that could reflect this time scale required radio-frequency modulation rates. Therefore, instead of completely digitizing the high frequency signals, other signal processing methods were sought to phase shift and ‘mix-down’ the signals while retaining the phase information. The result of the mixing steps is the generation of three voltage signals that reflect the phase-shifting: (1) the modulated fluorescence signal mixed with a −90° phase-shifted reference sine wave; (2) the modulated fluorescence signal mixed with a 0° phase-shifted reference sine wave; and (3) the analog-space ratio of (1) and (2). Steinkamp (2001) describes mathematically the resulting signals (1) and (2) are dependent on the sine of φ and the cosine of φ, respectively, where φ is the phase shift between the excitation signal and the emission signal. The ratio of sin φ and cos φ is equivalent to tan φ, and assuming single exponential decay kinetics, the lifetime, τ, is related to tan φ as shown by equation 2 where ω is the angular modulation frequency. The hardware and system assembly required for an analog implementation of fluorescence lifetime measurement are illustrated in Figure 2.

Figure 2.

Illustration of frequency-domain flow cytometry hardware modification. This depiction assumes the particles are flowing into the page. Modulated fluorescence emission signals resulting from a modulated laser source during frequency-domain data acquisition are captured by photomultiplier tubes (PMTs). The diagram represents a waveform from a post-amplified signal that is directed to mixing and filtering steps. The bottom callout illustration exemplifies the analog homodyning hardware necessary for only one detector. The fluorescence signal is split, mixed with a reference sine waves that have been phase shifted in time. After mixing, the signals are filtered down and then divided by an analog ratio module. Ultimately, the ratioed signal is digitized into list mode cytometric data.

With the analog fluorescence lifetime approach, an unknown average fluorescence lifetime of a sample is acquired relative to a calibration microsphere with a known fluorescence lifetime (e.g. Flow-Check^™ microspheres with known 7-ns lifetime). By synthesizing a radio-frequency signal with a function generator and driving a modulate-able laser or external modulation unit, fluorescence signals result which carry fluorescence lifetime-dependent phase shifts. The practical approach to an analog homodyne procedure involves first splitting the synthesized radio-frequency signal in half to both drive the laser modulator and mix with a fluorescence signal output from the fluorescence PMT detector when samples are running. Prior to mixing, send this reference sinusoid through two devices. First pass it through a delay line and then to the input channel of a quadrature device. A quadrature device typically has one input and up to three outputs. In this protocol, take only two outputs from the device: (1) the ‘in-phase’ (0° shifted) output, and the (2) ‘quadrature-phase’ (−90° shifted) output. Finally, connect both output signals and mix them independently with the split fluorescence signal. See Figure 2 for reference.

Materials

• External laser modulator (electro-optic modulator device or acousto-optic modulator device, e.g. Conoptics Inc., Model 350-105-1, KD*P Series Electro-Optic Modulator with Model 200 Driver)

• Radio-frequency signal synthesizer to drive modulator and provide a mixing signal (e.g. Tektronix Inc., model AFG 3102 function generator)

• Flow cytometer with at least two photomultiplier tubes with rapid (</=2 nanosecond) rise time specifications

• High speed transimpedance preamplifiers (0 ≥ bandwidth ≥ 10 MHz) for the PMTs used for the modulation detection

• Oscilloscope

• Delay line with nanosecond resolution and manual adjustment (or other device capable of phase-shifting an analog sinusoidal signal)

• High frequency signal multiplier (two required)

• Quadrature hybrid device for creating in-phase carrier wave and ‘phase-quadrature,’ or 90°, out-of-phase carrier wave.

• Low-Pass frequency filter (~100 kHz bandwidth to reduce high frequency)

• Analog ratio module device (capable of dividing two analog pulse waveforms)

1. Turn on the laser and modulator for fluorescence excitation.

   Carefully align the laser excitation source so that it passes through the modulator prior to being focused onto the flow cell. Optimize the modulation depth of the laser to the maximum extent allowable according to the specifications of the modulator and driver device.

2. Set up the cytometry lifetime detection hardware by splitting (three-ways) the output of the fluorescence photomultiplier tube.

   This detector should be the channel used for fluorescence lifetime measurements. Again, Figure 2 provides a graphical representation of the hardware necessary for this step.

3. Mix the first split signal with the ‘in-phase’ reference sinusoid [*Au: please check reference to step after my re-numbering] (from step 7) at the first frequency multiplier.

4. Mix the second split signal with the ‘quadrature-phase’ reference sinusoid at the second frequency multiplier.

5. Send the third component of the split fluorescence signal to a low-pass frequency filter.

   This fluorescence signal will no longer have any radio-frequency component; it will resemble a Gaussian-like cytometry signal to be digitized and represented later in list mode format. It is collected only to provide a standard cytometry pulse from which one can extract standard flow cytometry parameters (peak height, width and area).

6. Filter away the high frequency component in the two mixed (in-phase and quadrature-phase) signals with a low-pass frequency filter.

   These fluorescence-mixed-‘quadrature-phase’ and ‘in-phase’ signals will no longer have any radio-frequency component; they will resemble a Gaussian-like cytometry signal and the amplitude will be proportional to the sine of the phase-shift and cosine of the phase-shift, respectively.

7. Take the ratio of the two mixed and filtered signals from step 3 [*Au: please check step reference after my re-numbering] by directing the ‘quadrature-phase’ (sine-dependant) signal to the numerator of a ratio module and the ‘in-phase’ (cosine-dependant) signal to the denominator of the same ratio module.

   The result is a signal that is proportional to the tangent of the phase shift. Taking the ratio conveniently removes the signal amplitude dependence from the result.

8. Direct the new tangent-dependant ratio signal and signal from step 4 [*Au: please check step reference due to my re-numbering] to the data acquisition system for digitization and to produce list-mode data for histogram development.

9. Run all three bead and/or cell samples (scatter-only microspheres, calibration fluorescence microspheres, and unknown sample) on the cytometer individually to fix the fluorescence PMT voltage. Observe mainly the fluorescence channel to adjust for brightness of all three samples. Adjust the non-fluorescence scatter bead ‘brightness’ by placing a neutral density filter in front of the fluorescence PMT.

   This step is critical in order to adjust the PMT voltage gain during calibration and also during normal fluorescence lifetime acquisition. The voltage must be held constant for all subsequent measurements and therefore should be optimized for the dynamic range of the samples to be used with the help of appropriate optical filters. (See also “Critical Parameters and Troubleshooting)

10. Calibrate the cytometer to read a null lifetime, or zero phase-shift, value by running the scatter-only microspheres.

    Adjust the fluorescence PMT channel by placing only a neutral density filter in front of this detector while the scatter-only microspheres are being measured.

11. Use an oscilloscope to measure the two mixed (sinφ and cosφ) signals from step 2. [*Au: please check step reference after my re-numbering]

    The values acquired (sinφ and cosφ) from the scattering microspheres are representative of an inherent phase-offset that is due to the near-instantaneous phase shift of the Raleigh scattered light, the arbitrary starting phase of the excitation source, as well as the sum of all the delays from the path the signal travels. The overall system phase shift must be ‘zeroed’ for calibration. Thus, the sinφ and cosφ are closely observed to shift down using an analog delay line.

12. Minimize the amplitude of the sinφ-dependent signal and maximize the amplitude of the cosφ-dependant signal by adjusting the delay of the reference sinusoid phase using a delay line (see Materials).

    This process is accomplished by trial and error. Find the correct delay line phase by simply selecting an arbitrary nanosecond delay and observing on the oscilloscope when this delay reduces the sinφ-dependent signal. Keep adjusting the delay until the sinφ signal becomes flat (i.e. no longer a pulse). When sinφ is minimized as close to zero as possible and cosφ is maximized, the tanφ is at approximately zero and thus the lifetime value is nulled.

13. Run the calibration fluorescence lifetime microspheres (e.g. Flow-Check^™) on the cytometer.

    It is critical that you do not adjust any settings made during the scatter-only calibration steps. Observe the histogram resulting from the tanφ value; save the statistics and record the mean.

14. Run the unknown cells or microsphere sample. Observe the histogram resulting from the tanφ value; save the statistics and record the mean.

15. Calculate the unknown cell lifetime by using a proportional relationship between the mean of the known beads, mean of the unknown cells, and the lifetime of the known beads. [*Au: should this be represented as a formula?]

Anticipated Results

In general, the anticipated results from this approach are: the average fluorescence lifetime from any particle or cell; histograms representing two or more subpopulations within a sample; and the revelation of new phenomena related to the excited state decay characteristics of a fluorophore. Additionally, histogram results based on average fluorescence decay times will be useful for sorting, to aid with multiplexing, to corroborate compensation, and simply to separate overlapping signals. The average lifetime could reveal rare events and in general provide a novel parameter for discriminating samples that are independent of the fluorescence intensity.

Time Considerations

The lifetime-dependent protocol will require standard acquisition times (i.e. minutes to hours depending largely on sample preparation time). The actual lifetime measurement is rapid and is no longer than typical flow cytometry analysis and/or sorting. The user should anticipate nominal measurement times that are due to instrument start-up, calibration with unstained controls, instrument adjustment, sample measurement, cleaning, and shut down. In the case of the analog measurement approach there will be some additional set-up time required for nulling out the light scatter signal. Overall, the limiting factor is the time required for upfront hardware and signal processing modifications to the cytometer. Any cytometrist interested in implementing fluorescence lifetime onto an existing system should anticipate several days for procurement of all modulation devices, optical alignment, and routine calibration, testing, and optimization.

COMMENTARY

OVERVIEWOF DIGITAL LIFETIME APPROACHS

While the end result is the same, the digital approach has some advantages when compared to an analog approach. The first advantage is that the physical hardware can be simplified. Both methods require amplifiers, some signal conditioning, and an analog-to-digital converter (ADC) with a data system to capture the results. However, the physical processing components required by the analog approach are replaced with digital signal processing algorithms. This benefit is even more pronounced when using multiple modulation frequencies, a discussion of which is provided in later sections. The main part of measuring lifetime digitally is the capture of a full Gaussian-like pulse that has a high frequency component. Because the entire modulated waveform is needed for processing, the digitization hardware becomes the most critical component in lifetime acquisition. Later, an overview of the data acquisition system we have implemented is provided. In this commentary a general discussion is provided on how to implement digital lifetime in cytometry as well as troubleshoot and optimize for homodyne signal processing.

Optical heterodyne and homodyne detection approaches are methods that enable the extraction of information that is contained in a high-frequency radiative (i.e. optical) signal. The information that is desired from a fluorescence signal is either the amplitude demodulation (total oscillatory AC amplitude divided by the average DC signal level) or the phase of the oscillating signal at a particular frequency. In fluorescence detection systems these measurements (amplitude and phase) provide the total fluorescence intensity output as well as the fluorescence lifetime. Heterodyne and homodyne detection approaches involve mixing the fluorescence signal with a similarly oscillating (same frequency or lower frequency) “reference” signal. The mixed signal(s) carries the desired content, even when filtered down to a reasonable bandwidth (i.e. to a DC level, where no special high-frequency device is needed to capture that high-frequency content). Heterodyne refers to the mixture of the fluorescence signal with a lower frequency reference signal and homodyne is the mixture of the fluorescence signal with a reference signal that is equal (homo=same) in frequency. Because both approaches are reliant on a reference signal, the choice of frequencies of these references becomes critical.

The homodyne approach, which is the basis of the analog phase-sensitive flow cytometry and the digital advances described herein, is limited only by the starting laser modulation frequency. The frequency should be chosen based on Equation 2, which provides the relationship between the modulation frequency and the fluorescence lifetime. In practice, a larger phase shift, Δφ, is easier to resolve than smaller shifts in phase (i.e. a shift of 1° is harder to resolve with homodyne hardware compared to to a shift of 90°). Larger phase perturbations can be accomplished by changing the modulation frequency. For example, to resolve a 2.5-ns fluorescence lifetime, it would be optimum to modulate at a frequency of 100MHz because a 2.5-ns lifetime will result in a phase shift of 90° whereas the same lifetime detected at 10 MHz is equivalent to a phase shift of 9°. Although the modulation frequency in the 100s of MHz range is optimum, this is challenging to implement because each piece of hardware must be able to handle the large bandwidth (DC to 100 MHz, for example). We have shown that a frequency range as low a 1MHz permits reasonable lifetime measurements in the 1 to 20-ns range. Although higher frequencies are more optimal, modulation depth can suffer resulting in higher frequency noise. Below we discuss how to implement digital homodyne lifetime methods and discuss the various frequency bandwidths needed for the frequency hardware. Later in the commentary section, the heterodyne approach is discussed because digital processing approaches may be leveraged to expand the frequency ranges possible.

Digital homodyne methods

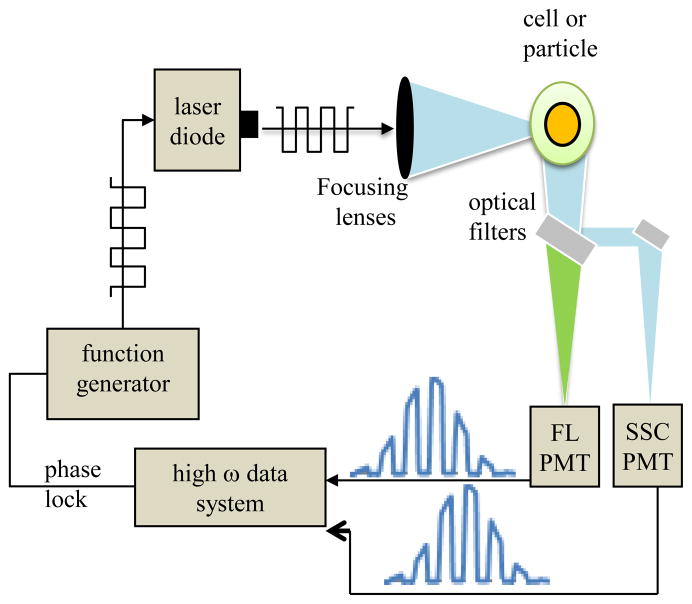
Phase modulation hardware is still necessary on the upstream cytometry components therefore a few items and equipment duplicate the analog approach. That is, a laser that can be either modulated directly (e.g. solid-state laser source that can be driven with a 50% duty cycle signal at a radio frequency) or any continuous-wave laser with an external modulator (e.g. electro-optical modulator) in the excitation path is required. Figure 3 is an illustration of a digital lifetime approach. In addition to the modulated source, a radio-frequency signal synthesizer or function generator (e.g. Tektronix Inc., model AFG 3102 function generator) is necessary to drive the sinusoidal signals. High speed transimpedance preamplifiers (≤ 1-MHz bandwidth) for the PMTs are needed for the modulation detection. The Analog-to-digital converter (ADC) board capable of high-frequency conversion can be procured with the specifications needed (i.e. maximum frequencies, maximum speed, or maximum budget). Considerations for custom lifetime digital data system components are discussed in detail later.

Figure 3.

Depiction of the digital lifetime cytometry system illustrated in a geometry which assumes the particles are flowing into the page. The PMT and properly amplified output signals go directly to a data system for digitization and Fourier analysis that permits on-line and accurate lifetime acquisition.

The procedural steps for digital lifetime acquisition also call for calibration to verify the lifetime value. Thus it is necessary to have a reference suspension of calibration cells or microspheres having a known fluorescence lifetime (e.g. Flow-Check^™ microspheres with known 7 ns lifetime, fluorescein-labeled microspheres, cell nuclei stained with propidium iodide or ethidium bromide, etc.). The lifetime of the reference sample can help dictate the modulation frequency so as to maximize the phase perturbation with equation 2. The frequency is also highly dependent on the sampling rate of the data system as well as the particle transit time. The fluorescence reference sample is measured first, and with the laser modulating (driven by the function generator) the complete waveform is digitized in its entirety. The high-frequency Gaussian-like cytometry signals from the side scatter and fluorescence PMT channels must be collected.

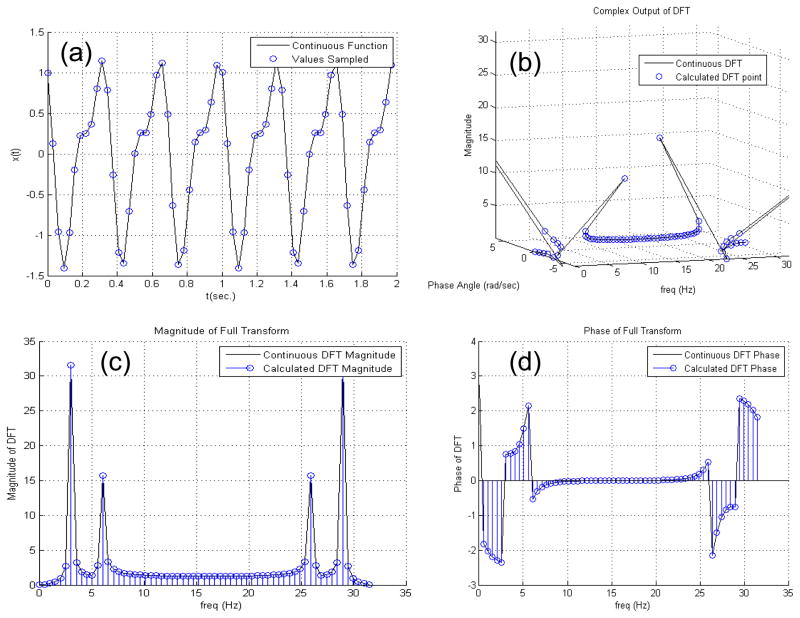
The digital lifetime approach then relies on the measurement of the phase of the modulated signals of both the side scatter and fluorescence waveforms. In order to measure the phase for each event a rapid fitting routine or other processing method is required. In previous work (Houston et al. 2010), we chose to implement a fast Fourier Transform as it can calculate the phase at the fundamental harmonic when written into the digital signal processor. A discrete Fourier Transform (DFT) is preferred for speed and ease of programming. The DFT will give the magnitude and phase of discrete frequencies from DC up to the Nyquist frequency. Assuming the modulation frequency happens to be represented by one of the discrete frequencies in the DFT, it is straightforward to measure the amplitude and phase. Equation 4 defines a discrete Fourier Transform where I(n) is the finite intensity of the waveform measured in time with n equal to the number of samples in the waveform. With the DFT, the intensity, I, is transformed into a frequency domain function from a sequence starting at n=0 to a total of N discrete points where, j is the imaginary unit number. Figure 4 illustrates the discrete Fourier transform by demonstrating the process on normal mixed sinusoidal waves.

Figure 4.

Illustration showing how a DFT acts on a sinusoidal signal. In this example, 2 additive sinusoids of the form x(t)=A₁*cos(2π*f₁+ϕ₁)+A₂*cos(2π*f₂+ϕ₂) are artificially generated having the following variables A₁=1; A₂=0.5; f₁=3 Hz; f₂=6 Hz Φ₁=π/3; and Φ₂=0. (a) x(t) is plotted as a continuous function represented by the solid line. If this signal is digitized, it will be sampled at a consistent sampling rate. In this figure a sample rate of 32 Hz, or 32 Samples per second (SPS) is exemplified by the blue circle markers. (b) The discretized sample is processed with a discrete Fourier transform (DFT) as provided in Equation 4 with N being the number of samples, m being an index of the frequency vector, and j being the complex operator. The output of the DFT is a complex signal. When plotted in the complex plane along the frequency vector, the frequency peaks of the original signal can be seen as dominant influences in the resultant Fourier spectrum. (c) The complex modulus of the signal, which is determined by taking the absolute value of the X(m) series in order to gauge the overall influence of each component of the signal. This magnitude of the complex component snaps the signal back into the real plane. (d) The phase angle of the complex output plotted at each frequency.

$$I(m)=\sum _{n=0}^{N-1}I(n)\ast exp\left(-j\ast 2\pi \ast \frac{m}{N}\ast n\right)$$ [Equation 4]

It is important to note that the DFT for each waveform and for each event requires a significant amount of processing power. An FFT, which is a more efficient algorithm for calculating the DFT can be used to speed up the calculation time. However the optimum approach with respect to processing speed is to calculate the DFT at only one frequency, the modulation frequency. This is faster than calculating the entire FFT and eliminates some of the FFT constraints. The Fourier Transform assumes the signal being measured repeats for all time. Because of this, any discontinuities between the first and last samples will inject noise frequencies into the result. This is known as spectral leakage, which can interfere with the phase measurement (Lyons, 2010). Applying a windowing function to the signal before the DFT is calculated can reduce or even eliminate spectral leakage (Bores Signal Processing, 2010). Careful selection of the windowing function is important, as distortions to the signal caused by applying the windowing function chosen can affect the phase measurement. Filtering the signal before the DFT is calculated can improve the phase measurement by removing unwanted noise frequencies that would otherwise spill into the modulation frequency and interfere with the phase measurement.

The FFT result is the phase angle, φ, at the fundamental frequency, and this calculation is made by taking the phase angle of the complex output of the DFT at the modulation frequency. Equation 5 represents this calculation for both the fluorescence (F) and side scatter (S) signals. Here the inverse tangent is found for the imaginary component divided by the real component of I(f_mod ), the output at the single frequency bin.

$$[{\phi }_F,{\phi }_S]=arctan\frac{\mathit{IMAG}\left[I{(f_{mod})}_{F,S}\right]}{\mathit{REAL}\left[I{(f_{mod})}_{F,S}\right]}$$ [Equation 5]

Prior to calculating the phase and in fact, upon designing the hardware to capture the signals, it is critical that the clocks for all of the ADCs be phase-locked. Any constant phase delays will be cancelled out during calibration, but phase drift will cause errors in the measurement. Phase-locking the ADC clocks is easiest if there is one clock which is used for all ADCs, but if physically separate modules are being used, then there must be some way to synchronize all of the ADC clocks. It is common for commercial equipment to have both clock inputs and outputs which can be used for this purpose. In all approaches, the phase shift of the fluorescence signal is measured relative to some other reference signal. The reference signal is typically either derived from the signal that is used to drive the modulator, or it is the measured signal from a light scatter detector. The digital approach must capture this reference signal along with the fluorescence signal in order to measure the phase shift between them. If the digital data system can be synchronized (phase-locked) to the modulation signal, then it is possible for the digital data system to generate the reference signal digitally instead of capturing it. This not only eliminates the need for an ADC, but it also eliminates any errors or noise in the capture of the reference signal.

Once the phase for each waveform is calculated, then the phase shift between the two channels can be found by simply taking the difference in the independently measured phase shifts. That is, the phase of the scatter signal is subtracted from the phase of the fluorescence signal to calculate the total phase shift. Equation 6 illustrates this step.

$${\phi }_T={\phi }_F-{\phi }_S$$ [Equation 6]

It might be anticipated that the resulting phase-shift (radians or degrees) is proportional to the lifetime of the fluorescent sample when equation 2 is used with the resulting total phase shift (φ_T). However, the total measured phase shift (φ_T) contains an inherent phase offset of the system. Factors such as the arbitrary starting modulation phase and other system delays contribute to this phase offset which must be accounted for when the unknown sample is measured. Ultimately, a fluorophore with a known lifetime is used as a relative calibration value; the unknown sample will reference the known lifetime for final lifetime determination.

Because the lifetime of the fluorescently-labeled calibration sample is known, the phase offset can be found by converting the known lifetime into a phase shift (use equation 2, to result in φ_microspheres) and then subtracting it from the measured phase shift (φ_T). This phase offset (φ_offset = φ_T −φ_microspheres) can then be applied to all phase measurements before calculating the lifetime, which results in absolute (calibrated) lifetime measurements. This correction factor must be calculated and applied in ‘phase-space’ because of the non-linearity of the tangent function (equation 2). Finally, using the phase offset to correct the measured phase shift and equation 2, the absolute (calibrated) lifetime value can be calculated. Figure 5 is an example of fluorescence lifetime histograms when collected from fluorescent microspheres using both the analog PSFC approach as well as the digital lifetime cytometry system.

Figure 5.

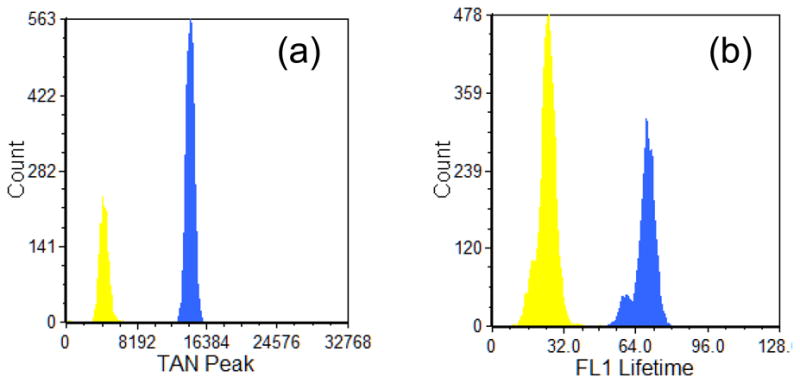
Examples of fluorescence lifetime histograms acquired with the analog phase sensitive flow cytometry approach and the digital fluorescence lifetime method. (a) Histogram results with the analog system where the parameter plotted is the peak of the tangent of the phase shift measurement in arbitrary units labeled as ‘TAN peak’. The tangent value presents a proportionality to the fluorescence lifetime of the sample. Flow-Check^™ (Beckman Coulter, blue histogram) and Yellow-Green (Spherotech, yellow histogram) microspheres resulted in fluorescence lifetime values of 7.0 ns (+/−0.22ns) and 2.1 ns (+/−0.24ns), respectively. (b) The fluorescence lifetime of the Flow-Check^™ (Beckman Coulter, blue histogram) and Yellow-Green (Spherotech, yellow histogram) microspheres using the digital lifetime cytometry approach. The resulting lifetimes were 6.9 ns (+/− 0.44ns) and 2.5 ns (+/−0.38ns), respectively. The x-axis label is the true fluorescence lifetime in units of 0.1 nanoseconds.

When capturing any digital waveform from a PMT, it is important to utilize as much of the dynamic range of the ADC as possible while avoiding clipping the signals. Minimizing signal offsets and maximizing the signal gain are both important for making accurate lifetime measurements. Choosing the ADC sampling rate is also important. This is dependent both on the modulation frequency used and on the particle transit time. It is important to capture the modulation signal with enough resolution to get an accurate phase shift measurement. Even though the Nyquist-Shannon sampling theorem states that two ADC samples per cycle of a sine wave is sufficient to capture it accurately, a more practical number is five samples per cycle in order to compensate for the real world issues of digitization.

The transit time can become a limiting factor for the lowest modulation frequencies. For example, a 5 microsecond transit time will only provide 5 cycles of a 1 MHz modulation frequency and will not be as accurate compared to a transit time of 10 microseconds or a modulation frequency of 2 MHz. At the other extreme - higher modulation frequencies and longer transit times - the amount of data captured for a single waveform could easily overwhelm the data system. For example, a 50 MHz modulation frequency would require an ADC sampling rate of 250 megasamples per second (MSPS) in order to capture 5 samples per cycle. A 20 microsecond transit time would require 5000 samples per waveform. It is possible to capture a smaller part of the entire waveform for each event to keep the amount of data reasonable. A detailed simulation of the effects of various transit times, modulation frequencies, and digital sampling rates is provided in Houston et al., 2010.

Sorting with a fluorescence lifetime parameter

Much like the simple digital lifetime acquisition, digital lifetime sorting techniques are possible and potentially powerful for several reasons. For example, cells are often separated based on protein expression whereby a population of cells are transfected with vectors that result in the expression of fluorescent proteins (XFPs). If sorting in this scenario is performed based on the fluorescence intensity, then an assumption is made about the linear relationship between the brightness and XFP concentration. However, it is known that fluorescence intensity is not related only to the protein concentration, but is also affected by the XFP quantum yield, the quantum efficiency, and the local environment in which the XFP resides. Measuring fluorescence lifetime can help distinguish between these different effectors of total fluorescence intensity, e.g., determining whether increased intensity is due to a higher protein concentration or an altered quantum yield. We are currently investigating the use of fluorescence lifetime to sort different XFP mutants based on intrinsic properties of the XFP as separated from different XFP expression levels. A second common sorting assay is to separate cells based on the presence of a particular surface or internal target molecule. Using fluorescently-labeled antibodies to detect low level antigens is a prime example of the problems associated with this type of sorting, because the emission intensity from the antibody is often low enough to overlap with the background cellular autofluorescence, making unambiguous sorting difficult. Separating the antibody fluorescence from autofluorescence using differences in fluorescence lifetime would be a very useful method for sorting antigen-expressing cells away from untagged cells.

In order to apply fluorescence lifetime to existing fluorescence-activated cell sorters (FACS), three general approaches are suggested: (1) using a fully digital approach where the data system controls sorting as well as processing of the digital lifetime values; (2) using only analog lifetime signals; or (3) using a partial digital approach where the data system only processes digital lifetime values. All options have benefits and considerations which are discussed below.

The first option reduces the level of communication that should be transmitted between a high speed ADC and a commercial system’s own data acquisition board. In fact, in this case one would not use the commercial data system at all. However, if a high-speed data system with digital signal processing is the sole acquisition system, it must completely control all other normal sorting functions, including triggering thresholds, voltage control, sorting decisions, droplet drive and droplet charging control. Complete control by a foreign data system would be highly dependent on the type of sorting hardware present and the depth of knowledge by the user on a specific instrument. This approach would also be ideal for custom-built sorting systems. Although we have developed stand-alone digital data acquisition and control systems that can perform all of these functions, including fluorescence lifetime measurement, application to either commercial or custom sorters goes beyond the scope of this unit and thus is not discussed in more detail.

The second option is closely aligned with general analog phase approaches in which sorting could be implemented with an analog system that produces filtered down waveforms that are dependent on phase shifting. It is possible to simply direct the fluorescence lifetime signals into the FACS system’s own acquisition hardware. Specifically, the fluorescence PMT output is directed through the analog lifetime hardware, then amplified and directed back into the cytometer for normal acquisition and sorting. A time delay may need to be accounted for due to the path a given fluorescence lifetime signal follows throughout the analog hardware. As long as the time interval is known then the sorting delay can be adjusted. In practice, this method might be accomplished by normally detecting and triggering with a scatter signal using the FACS hardware. If the analog hardware introduces an insignificant time delay to produce a signal, then the phase-sensitive and/or lifetime value can be read by the FACS acquisition system and used for sorting like any other parameter. However, if the delay is significant enough to impact the sorting, a delay line could be inserted into the path of the scattering (triggering) signal to effectively correct for the analog hardware delay. Ultimately, no high frequency signals are measured, just the filtered phase-sensitive signals or the ‘ratioed’ signal that represents the lifetime (sinφ/cosφ).

The final sorting option leverages the digital signal processing methods described previously and combines these techniques with a mechanism for communicating fluorescence lifetimes to the FACS, which controls sorting. An example of such a system is illustrated in Figure 6; we have implemented such a system on a commercial FACS instrument (Houston et al., 2010). Two analog output signals are generated by the high speed data system for this sorting communication. The two outputs generate two types of pulses: (1) a constant amplitude trigger pulse to trigger the FACS in time with the events being detected by the data system; and (2) a variable amplitude pulse where the amplitude correlates either to a fluorescence lifetime value or to a sort gate. Calculating a fluorescence lifetime and communicating that to a FACS system takes time, and therefore this approach needs to consider the maximum sort delay of the FACS instrument. If the lifetime calculation/processing is found to be well under the maximum FACS sort delay, then precise timing must be implemented to delay the sort-gate signal to exactly the amount of time needed before droplet break off for that corresponding event. This approach was accomplished previously by combining the analog communication signals with a programmable and precise delay circuit.

Figure 6.

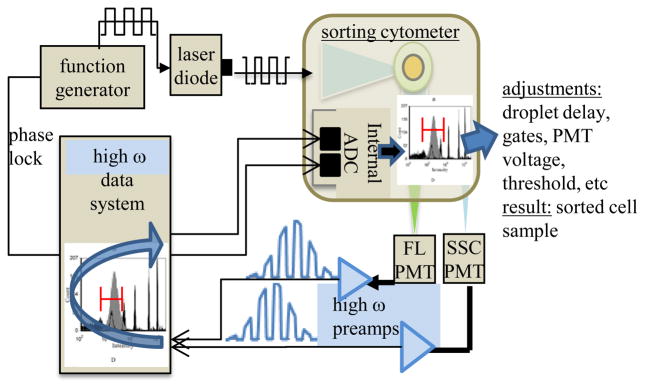
Illustration of a mechanism for implementing fluorescence lifetime measurements on a flow sorter. The figure depicts the direction of signals from the sorting system PMTs to the external data system as well as the analog signals that travel from the data system back to the data acquisition system of the sorter’s PMTs.

Background Information on Additional Approaches to Lifetime Measurement

Acquiring the lifetime parameter digitally, although straightforward, is not without a number of complexities. As revealed in the previous discussion, digital methods will simplify the hardware required for fluorescence lifetime acquisition. However, the process of calculating the lifetime is still quite involved. The lifetime itself when taken outside of any cytometry context, is defined by two decay pathways: radiative and non-radiative decay. The lifetime is the total decay rate and thus inversely proportional to the two rate constants Γ_r [s⁻¹], and Γ_nr [s⁻¹], which represent radiative and nonradiative decay, respectively. The relationship is shown by Equation 7.

$$\tau =\frac{1}{{\mathrm{\Gamma }}_r+{\mathrm{\Gamma }}_{nr}}$$ [Equation 7]

The lifetime as a decay rate contributes to the fluorescence decay function, which is represented by Equation 8. This function is a first order kinetic model of decay where τ is the fluorescence lifetime, I is the fluorescence intensity measured at time, t, and I_o is the initial intensity of fluorescence subsequent to laser pulsation. Equation 8 is the simplest model of fluorescence decay and sufficiently approximates the intensity decay for use in regression or modeling of the fluorescence process.

$$I(t)=I_0{e}^{-t/\tau }$$ [Equation 8]

The simple model of fluorescence decay makes the assumption that a fluorophore population will undergo a single type of exponential decay. That is, only a single lifetime is assumed for the bulk species in the sample. Yet fluorescence decay is stochastic; molecular relaxation happens repeatedly and thus the probability for heterogenous relaxation rates to occur for just one type of fluorophore is high. Moreover, a single cell contains many intrinsic constituents that contribute to the overall lifetime. Every constituent will have a unique single (or multiple) lifetime and contribute to a mixture of fluorescence lifetimes expressed. Thus, it is important to extend the range of frequency-domain flow cytometry techniques to handle multi-frequency modulation and to increase the resolution between multiple lifetimes in a single event. This would lead to an extremely powerful method for rare event sorting and analysis.

Multi-frequency Cytometry

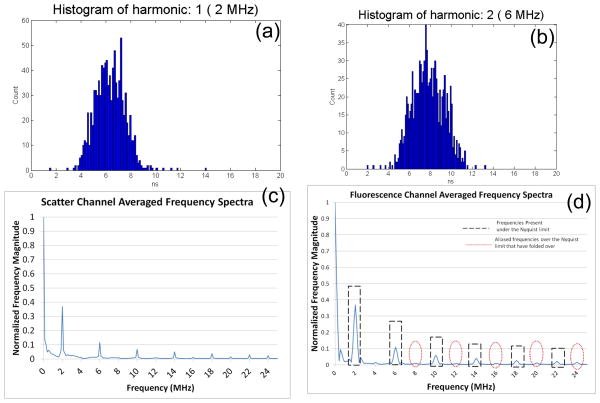
The fluorescence decay model becomes quite complicated when multiple relaxation rates are included. For example, fluorescence can undergo stretched exponential, multi-exponential decay, quenched decay, and other probabilistic models. Each model is important for regression of experimental data, if the intensity decay has been measured as a function of modulation frequency. In cytometry, multiple frequency measurements have not been extensively implemented because multi-frequency modulation is challenging. In order to modulate at multiple frequencies, either multiple lasers are needed for synchronous excitation or a single laser can be modulated at a mix of sinusoidal radio-frequencies. In the later case, multiple lifetimes may be revealed after cumbersome hardware is implemented to separate two or more of the multiple sinusoidal signals from the fluorescence measurements in real time. An alternative to these two techniques is exploiting the multiple harmonics inherent to a square wave. Diode lasers can be directly modulated using a square wave with near-perfect modulation depth (i.e. on-off-on-off). Figure 7 illustrates waveform addition of sine waves to produce a square wave signal. Upon taking the Fourier transform of this type of signal, the multiple frequencies comprising the square wave are revealed and may be exploited for multiple lifetime determination. Thus, this digital approach can extract all frequencies from a square wave modulation by way of a Fourier Transform. With our digital lifetime system, which permits the collection of the full square-wave modulated Gaussian waveform, off-line processing of the waveform for multi-frequency analysis has been performed with fluorescent microspheres. Figure 8 is an example of the results where the phase shift resulting from the fluorescence signal of a single fluorophore is calculated at multiple frequencies post FFT processing.

Figure 7.

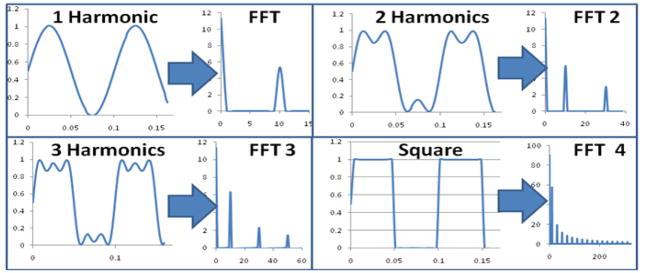
Graphical representation of square wave modulation coupled with Fourier Transform analysis to extract multi-frequency information for heterogeneous fluorescence lifetime measurements. In the four quadrants of the figure, the harmonics (data simulated in MathCAD) are increased steadily to show that multiple frequencies can be extracted for multiple fluorescence decays.

Figure 8.

(a) Fluorescence lifetime histogram generated using an off-line MATLAB (The Mathworks) DFT routine performed on waveforms collected using Flow-Check^™ polystyrene microspheres with a 488-nm laser modulating at a frequency of 2 MHz. The off-line analysis was performed on 1000 waveforms which resulted in a mean fluorescence lifetime of 6.24 (+/−2) ns. (b) Fluorescence lifetime histogram for the same microspheres calculated from the DFT result using the second harmonic frequency of 6 MHz. The average lifetime was 7.76 (+/−2) ns. (c) Normalized and averaged DFT frequency spectra of the same 1000 events measured by the scatter channel. The frequency spectrum is truncated to half of the Fourier spectra at the Nyquist limit. Frequencies present in the initial wave will be odd harmonics of 2 MHz (i.e. 6MHz, 10 MHz, 14 MHz, 18 MHz and 22 MHz). In graph (c) the spectra is cut off at half of the sampling rate, the Nyquist limit which is 25 MHz. (d) Plot of the normalized and averaged DFT frequency spectra of one thousand events from the measured fluorescence channel. The same harmonic frequencies are present up to the Nyquist limit and are represented by the black dashed line. Frequencies over the Nyquist limit are aliased to frequencies below that limit at integer multiples of the sampling frequency. If the primary frequency is chosen carefully with respect to the sampling rate, these foldover frequencies can be detected between the frequency peaks of the lower harmonics, as illustrated by the dotted red lines.

Phase filtering

Another benefit of digitally acquiring fluorescence lifetimes is the real-time ability to relate the relative presence or absence of two near-identical fluorophores. For example, two different fluorophores may have overlapping spectral output as well as overlapping fluorescence intensity. This often restricts the use of multiple fluorophores; another common problem is spectral and intensity overlap of extrinsic fluorophores and the intrinsic cellular autofluorescence. When the unique lifetime of either species is measured, it is then possible to separate and independently measure each fluorophore. Phase-filtering is one such technique that allows the distinction of the two overlapping fluorescence signals in a single cell using fluorescence lifetime. For example, if ethidium bromide (EB) and propidium iodide (PI), which overlap spectrally, are bound to a cell at differing concentrations, then standard fluorescence emission intensity measurements reveals a total fluorescence signal dominated by the fluorophore at a higher concentration. This total fluorescence intensity signal prevents any quantification of the relative concentration between the two dyes because the total intensity is a sum of the dim and bright fluorophore. In order to measure the relative concentrations of the two species, parameter math can be combined with lifetime measurements. First, the fluorescence lifetime for each fluorophore is measured individually (or is known a priori). Second, the fluorescence lifetime of the dual-stained sample is measured, revealing an average fluorescence lifetime centered between the lifetimes of the two dyes. New parameters are then determined by multiplying the mean fluorescence intensity value by a ratio that ‘nulls’ the lifetime of one of the dyes to allow only the fluorescence signal from one fluorophore to emerge. For example, to investigate the amount of PI loading in a cell, the ratio calculation would involve subtracting the lifetime of the EB dye from the mean fluorescence lifetime divided by the difference between the PI and EB lifetime.

This technique can also be done in ‘analog space’ by using external mixers and delay lines. In this scenario, the fluorescence signal is split and both signals are mixed independently with reference sine signals. The sine signals are generated by a function generator and one of the signals is shifted by φ₁−π/2 while the other is shifted by φ₂+π/2 where φ₁ and φ₂ are the phase-shifts resulting from the fluorescence lifetime from the two different fluorophores. The mathematical proof of this phase filtering concept is discussed in previous literature (Steinkamp, 1993). The mixed signals are filtered to only resemble a Gaussian-like pulse that is effectively phase-sensitive. This phase-filtering method results in a measurement of the fluorescence intensity from the fluorophore that was not nulled-out in the mixing step.

Heterodyne methods

Like multi-frequency analysis and phase filtering, frequency heterodyning is an approach that is not fully realized in flow cytometry systems. This technique allows the modulation signal frequency to be shifted to a lower frequency while preserving the phase information. Heterodyning takes advantage of the fact that if the excitation modulation frequency (ω_ex ≫ ADC sample rate) is mixed (multiplied) with a lower frequency (ω_mix < ω_ex), then the resulting signal will contain two frequency components. One component is the sum of the two frequencies, and the other is the difference between the two frequencies. This approach requires the mixed signal to be low-pass filtered to remove the higher component (the sum), leaving just the lower frequency (the difference). The phase information is preserved in this process and is translated to the lower frequency signal. For example, a 10 degree phase shift in a 20 MHz signal (approximately 1.39 ns) which is converted into a 2 MHz signal using this method would result in a 10 degree phase shift (approximately 13.9 ns). The basics of a semi-digital heterodyning approach are illustrated in Figure 9. The heterodyne mixing and frequency filtering is done using analog hardware, and the resulting difference frequency waveforms are digitized for subsequent lifetime computation.

Figure 9.

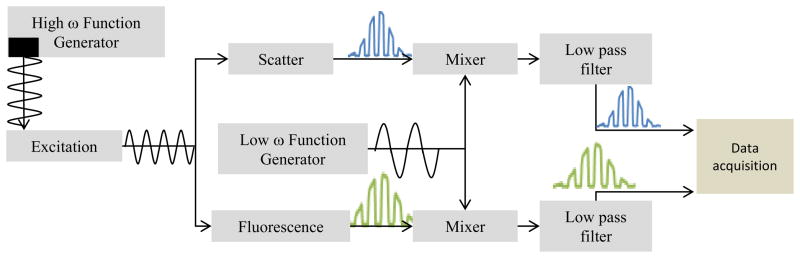
Illustration of the digital frequency-domain heterodyne approach for mixing down high frequency signals for a slower data system.

When implementing heterodyning a frequency multiplier is needed to mix the low and high frequency, and a low-pass frequency filter is also required (both off the shelf components). When practicing the heterodyne approach two independent radio-frequency signals are necessary where the first frequency (the modulation frequency) is chosen to optimize the phase perturbation from the expected lifetimes to be measured. The second frequency (the mixing frequency) is chosen so the difference between the two frequencies is below the Nyquist frequency of the ADC. It is best if the individual frequencies are above the Nyquist frequency, but this is not necessary. For example, if the ADC has a 50 MSPS sampling rate, the Nyquist frequency is 25MHz and the difference between the two frequencies must be less than that. If 30 MHz is chosen as the modulation frequency, and 27 MHz is chosen as the mixing frequency, then the difference between the two values is 3 MHz which is below the Nyquist frequency and can readily be sampled by the ADC. It is worth noting that a mixing frequency of 33 MHz would also result in the same difference frequency of 3 MHz; however, if the mixing frequency is higher than the modulation frequency, the measured phase shift will be negative compared to the actual phase shift.

Digitgization of the heterodyne difference frequency waveforms for fluorescence and side scatter signals allows the phase shift to be calculated by data acquisition software. The preferred approach is to use the DFT of the waveforms, equation 4. The DFTs of the digitized signals are found and used to calculate the phase shift. However, the phase shift is computed using the heterodyned (lower) frequency. The fluorescence lifetime can ultimately be calculated from the phase shift. However, instead of using the heterodyned frequency, the actual laser modulation frequency (higher value) must be used to accurately calculate the lifetime value. As for the homodyne digital approach a known lifetime sample is measured first for a relative lifetime value for the unknown sample.

Digital aliasing methods

Frequency aliasing is much like the digital heterodyne approach; it can be used to reduce the ADC sampling rate required while supporting high modulation frequencies. However, this technique allows the modulation signal frequency to be shifted to a lower frequency while preserving the phase information without the use of external mixers and additional filtering steps. Frequency aliasing has never been fully demonstrated in the literature with a flow cytometer, however the theory is straightforward. Aliasing takes advantage of the fact that when frequencies above the Nyquist frequency are sampled with an ADC, their apparent frequencies are shifted (aliased) into lower frequencies. The aliased frequency will be the difference between the ADC sampling rate and the actual frequency of the signal. While this technique does not require any additional hardware or equipment, it does put additional requirements on the ADC being used. The analog input bandwidth must be high enough to handle the highest frequency modulation signal to be used. Many ADCs and commercial ADC boards only support signals up to the Nyquist frequency of the ADC - and even use input filters to remove frequencies above the Nyquist frequency in order to avoid frequency aliasing. There are ADCs which are designed to allow frequency aliasing, they will not attenuate the higher frequencies and they typically use sample-and-hold circuits in front of the ADC to increase the accuracy when digitizing frequencies above the Nyquist frequency.

The aliasing method, being a simpler approach requires only the standard digital lifetime hardware (i.e. modulated laser, high frequency preamplifier, capable data acquisition system) without any additional analog devices. The modulation frequency of the laser is chosen to be higher than the capability of the data system. Yet like the analog homodyne approach, the frequency is not entirely arbitrary because this technique leverages high frequencies to optimize the phase perturbation that are a result of short lifetimes. The chosen frequency must also be higher than the Nyquist frequency of the ADC. For example, if the ADC has a 50 MSPS sampling rate, the Nyquist frequency is 25MHz and the modulation signal must be chosen higher than 25 MHz. The aliased frequency is simply the difference between the sampling rate of the ADC and the actual frequency. Using an ADC operating at 50 MSPS, a modulation frequency of 45 MHz would be aliased down to 5 MHz. Like heterodyning, phase inversions can occur. In this example, a modulation frequency of 45 MHz or 55 MHz will both be aliased down to 5 MHz, but the 45 MHz frequency will result in a negative measured phase shift compared to the actual phase shift. Figure 8, shown previously, demonstrates the aliasing fact in that several frequency components in the FFT spectrum shown are actually aliased values that originated from higher frequencies.

Again, as for the semi-digital heterodyne approach, a side scatter and fluorescence signal are completely digitized and the phase shift is found by taking the DFT of the digitized signals and calculating the phase shift based on the DFT result. Although the DFT approach is the same, the phase shift is computed at the aliased (lower) frequency instead of the actual modulation frequency. As for heterodyning, the phase information is preserved and shifted to the lower frequency. For example, given a 10 degree phase shift in a 22 MHz signal (1.26 ns) would cause a 10 degree phase shift in a 2 MHz aliased signal (13.9 ns). Finally, the fluorescence lifetime is calculated using Equation 2. However, instead of using the aliased frequency, the actual laser modulation frequency (higher value) must be used to accurately calculate the lifetime value. Also, a lifetime standard is used as the relative lifetime value prior to measuring the unknown lifetime sample.

Critical Parameters and Troubleshooting

General considerations

Overall, the essential parameters for acquiring fluorescence lifetime measurements accurately are choosing the correct modulation frequency, optimizing the bandwidth of all hardware to handle the high frequencies and maximizing the modulation depth and signal output. In fact, the accuracy of phase shift measurement is closely related to the noise level in the measurement. If the overall DC level of the signal is high and the amplitude (AC) measurement over the baseline signal is shallow, then the resulting phase perturbation will be hard to resolve. As modulation frequency goes up, modulation depth decreases. Therefore, it is important to account for the signal levels to be measured and the modulation frequency required to maximize the phase shift without minimizing modulation depth. Again, it is important to emphasize that one cannot make any adjustments to the modulation or acquisition parameters within a single experiment, or else the lifetime measurements will not be accurate across all samples.

With PSFC, high-frequency emission signals travel through a variety of cables, connectors, and splitters. It is critical to implement adequate bandwith and impedance requirements for all cables, devices as well as fittings present within electrical routes taken by the fluorescence and scatter signals. Additionally, more levels of refinement and optimization can be accomplished with other calibrated devices placed in the path of the measured signal. For example, by placing a band pass frequency filter centered at the modulation frequency wavelength at the output of the fluorescence PMT, the signal can be further ‘cleaned’ to eliminate stray frequency noise.

Digital Data Acquisition Systems

If the digital techniques discussed above are to be implemented in real time like standard lifetime analyses, they also require specialty engineering of a capable digital data acquisition system. Because a custom data system may be difficult to compile for the average cytometry user, we culminate the unit by discussing what types of systems can be considered. Since a specific lifetime data system has notbeen available, we describe a range from the most basic data system to the more advanced systems.

The most basic lifetime data acquisition system simply captures correlated waveforms from two detectors and saves these waveforms to a file. These captured waveforms are then processed with a separate data processing application to extract the lifetime information. It is possible to create such a system with minimal software and hardware skills. There are many commercially available hardware systems which can be used for the data system, including oscilloscopes. The data system hardware will consist of one or two data acquisition boards connected to a computer which runs the data capture software. Because of the nature of measuring small phase shifts between high frequency sine waves, there are several precautions and requirements for the data system hardware being used.

No matter what data system hardware is being used, care must be taken in the physical connection of the detectors to the preamplifiers and the data system. Small impedance miss-matches between any parts of the signal path can cause unwanted signal reflections which will interfere with the phase shift measurement. In addition to careful selection of input/output/cable impedances, the use of poor quality cables or connectors can cause impedance miss-matches.

When selecting the data acquisition and processing system hardware to use, it is critical to consider the analog input bandwidth of thesystem. In addition to the ADC itself, this also includes any analog signal conditioning/buffering in the system. Ideally, the data system as a whole must be capable of accurately measuring the modulation frequency as well as the frequency information of the Gaussian pulse itself. Some data acquisition systems have AC coupled inputs, which can heavily distort the Gaussian portion of the signals from the detectors. This can make triggering difficult, and can also interfere with making accurate fluorescence intensity measurements.

The sampling rate of the ADCs in the data system hardware must be at least twice the highest modulation frequency being used, and it is recommended that the sampling rate be at least five times the highest modulation frequency for best results. It is also critical that the clocks for all of the ADCs are phase locked. Phase offsets can easily be removed during calibration, but phase drift will interfere directly with the ability to make accurate phase measurements. Most commercial data acquisition hardware has the ability to synchronize to an external clock, and some systems can generate a clock signal which can be used to synchronize multiple boards. Some hardware systems have multiple analog input channels on a single board, and almost always these systems use one clock for all of the ADCs on the board which eliminates the need for external synchronization.

It is important that the waveforms be captured consistently for all analog input channels. For most systems this is not an issue but it is worth verifying. Similar to phase drift, if the data capture trigger signal has any jitter or drift between channels, this will cause errors in the phase measurement. This type of phase error tends to be pretty obvious, as one cycle of the ADC is typically many nanoseconds long and the accuracy of the phase measurement is less than one nanosecond. As with phase locking of the ADC clocks, data system circuit boards with multiple analog input channels on them have less of an issue with this.

Once the data system hardware is chosen and properly connected to the detectors, it must be set up to acquire the correlated waveforms. The system must be configured to detect (trigger on) pulses from one of the detectors, capture waveforms from both detectors when triggered, and save these correlated waveforms to disk. Most commercial data acquisition hardware comes bundled with software which is capable of this, since it emulates the basic capabilities of an oscilloscope. Upon capture of the correlated waveforms to disk, software must be developed to process the waveforms to extract the lifetime information. Extracting the lifetime is a matter of performing the DFT (or FFT) of the captured waveforms, extracting the magnitude and phase at the modulation frequency, and taking the difference of the measured phase shifts. Software packages such as MATLAB or IDL are ideally suited for such a task since they have flexible data I/O libraries as well as an extensive library of proven data processing routines. The FFT is a common digital signal processing routine, and algorithms can easily be found for most programming languages. The lifetime results can either be shown graphically, or saved out as list mode data for further analysis and visualization. Ideally, the lifetime list mode data would be written to a cytometry standard FCS formatted data file so it can be analyzed with any one of a large number of available 3rd party software packages.

The basic data system just described simply measures the phase shift between two analog signals. This system can measure the lifetime of a single fluorophore with offline processing. Perhaps the easiest way to extend this system is to measure multiple lifetimes simultaneously. This will require adding additional analog signal inputs to the data system hardware (assuming the data capture software supports it).

Writing custom data acquisition software is required if the system needs to display the lifetime results as the sample is being analyzed. This would be done by moving the FFT calculations into the data capture software, and adding the ability to create histograms of the results. Similarly, custom code would be required to write the lifetime results to FCS files directly from the acquisition software. Both of these would make the system easier to use, but would not actually add any additional capability.

Supporting sorting based on lifetime requires the most effort. The data system must be capable of calculating the lifetime in real time. There are commercial data systems with embedded DSP and FPGA hardware which are capable of real time digital signal processing, but selecting these systems can be difficult because of the significant performance required by the FFT algorithm. In addition, the FFT results from all of the detectors must be sent to a central embedded processor in order to calculate the individual lifetimes and to determine the sort decision for each particle in real time. Customization of such a system requires both hardware and software programming language skills as well as the appropriate development tools.