Using an external surrogate for predictor model training in real-time motion management of lung tumors

Abstract

Purpose:

Precise prediction of respiratory motion is a prerequisite for real-time motion compensation techniques such as beam, dynamic couch, or dynamic multileaf collimator tracking. Collection of tumor motion data to train the prediction model is required for most algorithms. To avoid exposure of patients to additional dose from imaging during this procedure, the feasibility of training a linear respiratory motion prediction model with an external surrogate signal is investigated and its performance benchmarked against training the model with tumor positions directly.

Methods:

The authors implement a lung tumor motion prediction algorithm based on linear ridge regression that is suitable to overcome system latencies up to about 300 ms. Its performance is investigated on a data set of 91 patient breathing trajectories recorded from fiducial marker tracking during radiotherapy delivery to the lung of ten patients. The expected 3D geometric error is quantified as a function of predictor lookahead time, signal sampling frequency and history vector length. Additionally, adaptive model retraining is evaluated, i.e., repeatedly updating the prediction model after initial training. Training length for this is gradually increased with incoming (internal) data availability. To assess practical feasibility model calculation times as well as various minimum data lengths for retraining are evaluated. Relative performance of model training with external surrogate motion data versus tumor motion data is evaluated. However, an internal–external motion correlation model is not utilized, i.e., prediction is solely driven by internal motion in both cases.

Results:

Similar prediction performance was achieved for training the model with external surrogate data versus internal (tumor motion) data. Adaptive model retraining can substantially boost performance in the case of external surrogate training while it has little impact for training with internal motion data. A minimum adaptive retraining data length of 8 s and history vector length of 3 s achieve maximal performance. Sampling frequency appears to have little impact on performance confirming previously published work. By using the linear predictor, a relative geometric 3D error reduction of about 50% was achieved (using adaptive retraining, a history vector length of 3 s and with results averaged over all investigated lookahead times and signal sampling frequencies). The absolute mean error could be reduced from (2.0 ± 1.6) mm when using no prediction at all to (0.9 ± 0.8) mm and (1.0 ± 0.9) mm when using the predictor trained with internal tumor motion training data and external surrogate motion training data, respectively (for a typical lookahead time of 250 ms and sampling frequency of 15 Hz).

Conclusions:

A linear prediction model can reduce latency induced tracking errors by an average of about 50% in real-time image guided radiotherapy systems with system latencies of up to 300 ms. Training a linear model for lung tumor motion prediction with an external surrogate signal alone is feasible and results in similar performance as training with (internal) tumor motion. Particularly for scenarios where motion data are extracted from fluoroscopic imaging with ionizing radiation, this may alleviate the need for additional imaging dose during the collection of model training data.

1. INTRODUCTION

Respiration can induce substantial tumor motion particularly for lung tumors or other sites in the thorax and upper abdomen. An enlarged tissue volume is usually irradiated to achieve appropriate dose coverage.¹ However, even with enlarged treatment margins underdosage may occur if the tumor moves outside of the radiation beam during treatment delivery. To reduce both, the risk of underdosage as well as the impact of enlarged treatment margins, it has been proposed to estimate the tumor motion in real-time and to use this information to either adjust the beam aperture location [dynamic multileaf collimator (DMLC) tracking], the position of the patient (couch tracking), or the radiation beam itself (Cyberknife and Vero).

For any of these approaches, it is necessary to have accurate real-time tumor position information. However, there is an inherent system specific time delay between tumor motion and hardware adjustment.^2–6 To overcome this latency and minimize the geometric tracking error it causes, respiratory motion prediction algorithms can be employed.

Various publications have discussed the matter of respiratory motion prediction. Sharp et al.⁷ compared two linear methods, two neural network based methods, and a Kalman filter for lookahead times of (33 ms ≤ τ ≤ 1000 ms). For evaluation, they used a training window of 15 s and found all algorithms to perform similarly for very small lookahead times (τ = 33 ms) and linear regression to work best for longer lookahead times (τ = 200 ms). Also, they report that imaging frame rates (>10 Hz) provide an advantage for all investigated algorithms when compared to lower frame rates. Krauss et al.⁸ have summarized and compared algorithms geared toward the application of DMLC or dynamic couch tracking with lookahead times of 200 ms ≤ τ ≤ 600 ms. Their study includes linear ridge regression, a neural network, kernel density estimation, and support vector regression. They find their in-house developed neural network approach to have the best performance. However, they point out that linear (ridge) regression has the advantage of only using one free parameter which they show can be chosen independent of patients. Their results also indicate that (in agreement with Sharp et al.⁷) for smaller lookahead times (around τ = 200 ms), the performance of linear ridge regression is similar to more complex approaches. Most recently, Ernst et al.⁹ have compared algorithms tailored for the three commercial systems Vero, Cyberknife, and TomoTherapy. They investigated a lookahead time range of 77 ms ≤ τ ≤ 307 ms using a range of algorithms including normalized least mean square (nLMS), recursive least squares (rLS), and a wavelet-based autoregression (wLMS) as well as a support vector regression algorithm and a Kalman filtering approach. Their nLMS algorithm is used clinically by the Cyberknife. They conclude that for larger lookahead times τ ≈ 300 ms, their support vector machine (SVM) regression implementation yields the best results but that their wLMS is the most practical algorithm for clinical applications since it does not require patient dependent parameter tuning.

All of the best performing models that have been investigated require some initial training period. For any kind of tracking technique relying on imaging with ionizing radiation, the time required for predictor model training will add additional radiation dose to the patient. To avoid this circumstance, we seek a predictor that can be trained ahead of time, with data from an external surrogate. More information on applicable doses for various tracking scenarios and imaging modalities may be found in a report by AAPM’s Task Group 75 (Ref. 10) and references therein.

Note that the results of this study are not confined to a single in-treatment tracking method. No matter which technology is used to find the tumor location (kV imaging, MV imaging) and how the tracking is performed (e.g., DMLC, couch, gimballed head, robotic), a method of prediction is needed for respiratory motion tracking. The general method demonstrated in this paper applies to all of these technologies. It has been demonstrated, in the studies described in the Introduction, that linear ridge regression is a simple and effective predictor for respiratory motion in the lookahead time range of interest. For this reason, we will use it in this paper to demonstrate the accuracy of external surrogate training.

2. MATERIALS AND METHODS

Factors that influence the relative geometric accuracy improvements gained from incorporating a prediction algorithm include general systemic parameters (e.g., the patient’s breathing pattern regularity and the required prediction lookahead time) that may not be adjustable and predictor specific parameters. Most prediction algorithms require training data, i.e., a set of N_train data points {(p(t), p(t + τ))} for which ground truth is known [here p(t) is the tumor position at time t and τ is the lookahead time which, in this paper, we set equal to the system latency as defined in the Introduction]. These data can be generated during a training session for which data are recorded and shifted for the lookahead time. The training period should span several breathing cycles in order to capture the individual breathing pattern, several publications have used intervals of 15–80 s.^7–9,11 However, in clinical operation, this practice may be inconvenient. For instance, when using ionizing radiation to monitor tumor motion the dose associated with collecting the training data may be considered a limiting factor. While it has been shown that external surrogate motion may not be in phase with tumor motion,¹² this may not be of importance for learning the pattern of respiratory tumor motion. We therefore propose in this paper to use external surrogate motion data alone for training a respiratory tumor motion prediction model, i.e., we do not employ an internal–external correlation model but train with external surrogate data and then monitor internal motion during therapy.

Using linear ridge regression allows us to write the forecast function as

$${\displaystyle f_{\mathit{p}}\left({\mathit{x}}_{\mathit{i}}\right)={\alpha }^T{\mathit{x}}_{\mathit{i}}+{\alpha }_0\approx p(t_i+\tau ).}$$ (1)

Here, we have defined the history vector x_i≔(p(t_i−(Np−1)), …, p(t_i)) for the past N_p tumor positions. If the training data are appropriately preprocessed (mean free and standard deviation of unity over each history vector) then we can set α₀ = 0 and calculate the parameter vector α from the training data samples directly as

$${\displaystyle \alpha ={(X^{T}X+\lambda \mathbb{1})}^{-1}{X}^{T}Y.}$$ (2)

Here, X = (x₁, …, x_Ntrain)^T ∈ (ℝ^N_train × ℝ^N_p) is a matrix containing in each row a history vector x_i of training data that is already mean free and with standard deviation of unity. Y = (y₁, …, y_Ntrain)^T is a column vector containing the interpolated target positions at times (t_i + τ) (also corrected for a mean free and unity standard deviation of the corresponding x_i). λ is the Tikhonov regularization parameter, which helps to keep the solution of Eq. (2) numerically stable for the cases of a poorly conditioned X (cf. Krauss et al.⁸ for more detail). We implement for each motion axis one predictor model, i.e., we do not use principal component analysis (PCA) to build one model for all three motion axis as we do not see the need with this rather simple predictor. To verify the validity of this claim, we evaluated the model calculation time.

To demonstrate that our proposed approach of using external surrogate data for training generates similar performance as using internal tumor motion data, we calculate performance data for both scenarios using a data set of 91 breathing trajectories from 10 patients.¹³ The data were recorded during radiotherapy delivery to the lung and include 3D tumor motion along with 1D (vertical) external surrogate motion (recorded simultaneously) sampled at a frequency of 30 Hz. We utilize 25 s as training data, followed by a gap of 2 s and followed by 40 s of testing the prediction performance in all data sets (see also Fig. 1).

FIG. 1.

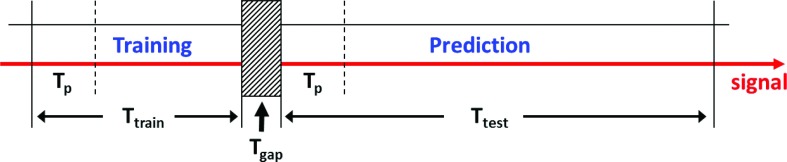
Data usage diagram for predictor training and performance evaluation. T_train denotes the time of the motion trajectory used for predictor training and T_test the one used for its performance evaluation. T_gap in between is used for processing and initialization. Note that during both training and prediction phase first a history vector of length T_p needs to be collected.

While Krauss et al.⁵ did not find notable performance changes from model updates during the prediction phase, we expect to improve prediction accuracy when using this procedure for the external training data case since a 1D signal provides incomplete information for building a 3D motion prediction model. Considering our long training data length (T_train = 25 s) with respect to our test data length (T_test = 40 s) we explore adaptive retraining, i.e., rather than waiting for T_train seconds before updating the model for the first time, we already start retraining after a minimum training time of $T_{\mathrm{train}}^{\left(\min \right)}<T_{\mathrm{train}}$ and then increase training time with each subsequent periodic model update until reaching T_train. We optimize $T_{\mathrm{train}}^{\left(\min \right)}$ by grid search. In this study, we only considered a model update frequency of 1 Hz and for model updates only internal motion data are used.

To generalize our results to a broader range of applications, we looked at various signal sampling frequencies (ν_s) and forecast intervals (τ). Since previous studies have used a range of history vector lengths (T_p = N_p/ν_s), we also studied the influence of this parameter on the prediction performance by performing a grid search over a range of this parameter.

For ease of notion, we summarize the following time intervals in seconds: T_train = N_train/ν_s = 25 s (training data length), T_test = N_test/ν_s = 40 s (test data length), T_p = N_p/ν_s (history vector length). See also Fig. 1 for more details.

As a geometric performance measure we use the root mean square deviation between the original data (shifted by τ) and the predicted data

$${\displaystyle \mathrm{rms}=\sqrt{\frac{1}{N_{\mathrm{test}}}\cdot \sum _{i=1}^{N_{\mathrm{test}}}{\left(\Vert {\hat{p}}_{\mathrm{pred}}\left(t_i\right)-p(t_i+\tau )\Vert \right)}^2}}$$ (3)

and the average deviation with its standard deviation

$${\displaystyle E_{\mathrm{ave}}=\left(\frac{1}{N_{\mathrm{test}}}\cdot \sum _{i=1}^{N_{\mathrm{test}}}\Vert {\hat{p}}_{\mathrm{pred}}\left(t_i\right)-p(t_i+\tau )\Vert \right)\pm \sigma \left(E_{\mathrm{ave}}\right).}$$ (4)

Here, ${\hat{p}}_{\mathrm{pred}}\left(t_i\right)$ denotes the predicted position (from a history vector ending at time t_i), p(t_i + τ) is the artificially shifted tumor position and ‖⋅‖ denotes the Euclidean norm. N_test is the number of sample points in the motion trajectory examined. To measure the relative performance loss (or gain) by using external surrogate training data versus using internal tumor motion for training, we calculate the percent difference or the root mean square deviation of the respective methods.

3. RESULTS

The geometric rms error for the three cases of using (i) no prediction, (ii) linear prediction trained with external surrogate, and (iii) linear prediction trained with tumor motion are depicted side by side in Fig. 2 (top left). We use boxplots to show the results in a comprehensive yet compact fashion. The (bottom left) and (bottom right) show the mean rms (averaged over all trajectories) with standard deviations as a function of history vector length (T_p) and signal sampling frequency (ν_s), respectively. A history vector length of T_p = 3 s appears to be optimal for both performance and the number of columns in X (i.e., calculation time) while the sampling frequency has little effect on the forecast accuracy.

FIG. 2.

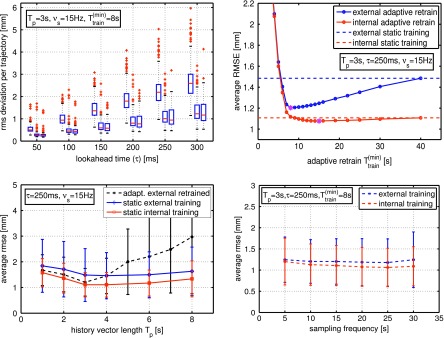
(Top left) Performance comparison between using no prediction (left box), prediction with external surrogate training data (middle box), and prediction with internal (tumor motion) training data (right box) for various lookahead times (τ). Signal sampling frequencies (ν_s), history vector lengths (T_p), and adaptive retraining ($T_{\mathrm{train}}^{\left(\min \right)}$) are kept constant as noted—retraining frequency is 1 Hz. Each boxplot contains 91 breathing trajectories. The training data length was set to T_train = 25 s, and the verification length was T_test = 40 s. (Top right) Average rms deviation versus $T_{\mathrm{train}}^{\left(\min \right)}$—the special marker indicates the optimal $T_{\mathrm{train}}^{\left(\min \right)}$ for this configuration. (Bottom left) Average rms deviation versus history vector length T_p for static internal and external training data as well as adaptive retraining with $T_{\mathrm{train}}^{\left(\min \right)}=8$ s at 1 Hz. (Bottom right) Average rms deviation with variation of the signal sampling frequency ν_s.

In Fig. 2 (top right) average rms error as a function of minimum adaptive retraining time $T_{\mathrm{train}}^{\left(\min \right)}$ is displayed for τ = 250 ms, T_p = 3 s, and ν_s = 15 Hz. In agreement with previously published data, model retraining appears to have only little performance impact when training with 3D internal tumor motion data. However, when using 1D external surrogate motion data for training, substantial performance improvement can be gained from utilizing adaptive retraining. We find optimal performance for a minimum adaptive retraining time of $T_{\mathrm{train}}^{\left(\min \right)}=8$ s and applied this scenario to the other plots in Fig. 2 as well (for the external surrogate training case only). However, the best minimum adaptive retraining time will depend on the history vector length as can be seen in Fig. 2 (left bottom).

External surrogate training yields similar (though slightly less accurate) prediction results compared to the (internal) tumor motion data. However, while prediction with internal motion data training appears to gain performance with increasing sampling frequency, this effect is not observed for training with external surrogate motion data.

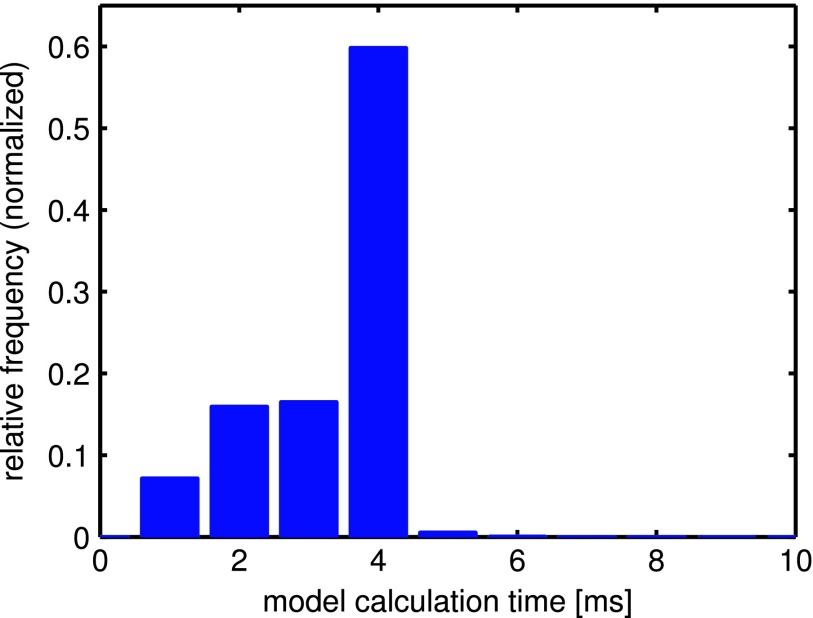
Figure 4 shows a histogram of the model calculation time per motion axis for all evaluated trajectories using the following typical parameters: T_p = 3 s, ν_s = 15 Hz, $T_{\mathrm{train}}^{\left(\min \right)}=8$ s, T_train = 25 s. The calculation time for the full training data (T_train = 25 s) computes to about 4 ms (<15 ms per 3D model). The shorter times correspond to the start of the adaptive retraining phase when less internal motion data are available and therefore the dimensions of the matrix X in Eq. (2) are smaller.

FIG. 4.

Histogram of the calculation time cost per motion axis over all 91 evaluated trajectories for the case of T_p = 3 s, ν_s = 15 Hz, T_train = 25 s. Adaptive retraining with $T_{\mathrm{train}}^{\left(\min \right)}=8$ s is used, which explains the less frequent smaller model calculation times <4 ms.

In Fig. 3 (top), an example trajectory is displayed with all three motion axes (x, y, z top to bottom). Training with 3D internal motion is shown on the (left) and 1D external surrogate training on the (right), respectively. The selected trajectory illustrates the performance on an irregular trajectory. In this particular case, performance can be increased by 18% and 39% for internal training and adaptive external training, respectively. On the (bottom) a histogram shows a comparison of the error distribution for the cases of not using prediction, using prediction with internal training, and prediction with external training plus adaptive retraining. Since this data exhibit extreme changes in motion pattern, adaptive retraining outweighs the disadvantage from initial 1D surrogate motion training when compared to internal training.

FIG. 3.

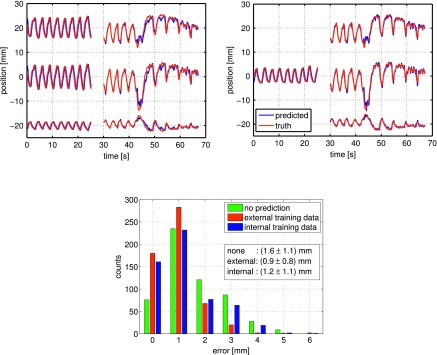
(Top) Tumor trajectory example (x, y, z from top to bottom). (Top left) Trained with 3D internal motion data, (top right) trained with 1D external motion data and adaptively retrained with $T_{\mathrm{train}}^{\left(\min \right)}$ at 1 Hz. (Bottom) Histogram of 3D error for the shown trajectory. In this rather irregular case, the rms error was reduced by 39% for the case of external surrogate training and 18% for tumor motion data training. The used data and prediction model parameters were ν_s = 15 Hz, T_train = 25 s, $T_{\mathrm{train}}^{\left(\min \right)}=8\mathrm{s}$ (for external case only), T_test = 40 s, T_p = 3 s, λ = 0.025, respectively.

Averaged over all investigated lookahead times and signal sampling frequencies using the linear ridge regression prediction model achieved a relative geometric error reduction of about 53% for internal initial training and 48% for external training, respectively (T_p = 3 s, T_train = 25 s, $T_{\mathrm{train}}^{\left(\min \right)}=8$ s, T_test = 40 s). The average performance difference between using external surrogate and tumor motion training data was about 5%.

Since absolute performance depends on the lookahead time, we only explicitly calculate this quantity for a typical lookahead time of τ = 250 ms and a typical sampling rate of ν_s = 15 Hz (see also Fig. 2 top left). Averaged over all trajectories, we yield an absolute mean error of (2.0 ± 1.6)  mm when using no prediction at all, (0.9 ± 0.8)  mm when using the predictor trained with internal tumor motion training data, and (1.0 ± 0.9)  mm when trained with external surrogate motion training data.

4. DISCUSSION

The feasibility of employing only external surrogate data for the initial training of linear respiratory motion prediction models has been tested. Our patient data provide simultaneous trajectories for both internal tumor motion and external surrogate motion at ν_s = 30 Hz sampling rate. Other studies have used Cyberknife log files⁹ which do not allow for direct comparison between tumor and external surrogate motion. Comparing the prediction performance between using internal and external training data shows clearly a slight performance loss of about 5% on average (cf. Fig. 2). This is not surprising as a 3D motion pattern is inferred from a 1D signal. However, this performance loss is small compared to not using any predictor at all. Further performance limitations are connected to breathing pattern changes over time, a problem inherent to any training data based approach for respiratory motion prediction.

It is well known that phase shifts between internal tumor motion and external surrogate motion can occur. We restricted therefore the use of the external surrogate data to learning the respiratory motion pattern and did not try to infer tumor motion directly from surrogate motion as it is common in internal–external correlation models. Not using an internal–external correlation model eliminates poor correlation between tumor and surrogate position as a source of error. However, using an external surrogate as a backup signal may be beneficial and easy to implement in cases where internal tumor location information may be temporarily unobtainable due to image quality problems or target occlusions.

We used a training data period of 25 s driven by the assumption that breathing pattern changes are less likely to occur in such a short time span as compared to training times used by other publications (Ernst et al.⁹ used 80 s and Krauss et al.⁸ used 40 s). We would expect prediction performance to drop as breathing patterns change over time. However, we were not able to illustrate this effect with our data set since the trajectories were not long enough for this undertaking.

Adaptive retraining schemes, i.e., updating the prediction model periodically enable to compensate for missing information in the initial training data as in the case of using 1D external surrogate data. This option also mitigates prediction performance degradation from changing breathing patterns over time. Since model calculation takes only <15 ms (per 3D model for X ∈ ℝ^N_train × ℝ^N_p) in the current matlab implementation (cf. Fig. 4) even an update frequency as high as 1 Hz is feasible. A previously published study⁸ [cf. Fig. 2 (top right)] also found that adaptive retraining does not substantially boost performance when initial training is done with internal motion data.

Various history vector lengths have been used in the literature (3–7.7 s),^7–9 yet to our knowledge no systematic study of the impact of this parameters on prediction performance has been reported. We performed a grid search for this parameter and found optimal prediction performance for T_p = 3 s. This number corresponds approximately to the average breathing cycle time in the entire data set we used, T = (3.3 ± 0.5) s. Under the assumption that all breathing cycles are independent from another this result appears reasonable.

5. CONCLUSIONS

We have shown in this study that using external surrogate training data to train (and adaptively retrain) a linear respiratory motion prediction model yields similar performance as using tumor motion data directly for this purpose. Particularly for scenarios where motion data are extracted from fluoroscopic imaging with ionizing radiation, this may help to avoid additional imaging dose during collection of model training data.