Reducing acquisition times in multidimensional NMR with a time-optimized Fourier encoding algorithm

Abstract

Speeding up the acquisition of multidimensional nuclear magnetic resonance (NMR) spectra is an important topic in contemporary NMR, with central roles in high-throughput investigations and analyses of marginally stable samples. A variety of fast NMR techniques have been developed, including methods based on non-uniform sampling and Hadamard encoding, that overcome the long sampling times inherent to schemes based on fast-Fourier-transform (FFT) methods. Here, we explore the potential of an alternative fast acquisition method that leverages a priori knowledge, to tailor polychromatic pulses and customized time delays for an efficient Fourier encoding of the indirect domain of an NMR experiment. By porting the encoding of the indirect-domain to the excitation process, this strategy avoids potential artifacts associated with non-uniform sampling schemes and uses a minimum number of scans equal to the number of resonances present in the indirect dimension. An added convenience is afforded by the fact that a usual 2D FFT can be used to process the generated data. Acquisitions of 2D heteronuclear correlation NMR spectra on quinine and on the anti-inflammatory drug isobutyl propionic phenolic acid illustrate the new method's performance. This method can be readily automated to deal with complex samples such as those occurring in metabolomics, in in-cell as well as in in vivo NMR applications, where speed and temporal stability are often primary concerns.

INTRODUCTION

Multidimensional nuclear magnetic resonance (NMR) spectroscopy is a powerful tool for the elucidation of molecular structure and dynamics. NMR's versatility arises from the wide variety of parameters that it makes accessible to experimentalists, including relaxation,^1–5 chemical shift,^6,7 and diffusivity,^8,9 all of which can report on key molecular properties at atomic resolution. However valuable this information may be, an important prerequisite is its unambiguous determination at an assignable site-resolved level. An essential aid in both facilitating the measurement of these parameters in complex systems and in assigning their origins within a molecular structure is furnished by multidimensional NMR.¹⁰ In their time-domain acquisition format,^11,12 multidimensional NMR methods allocate a nested acquisition loop to each of the time dimensions to be sampled. Even in the least demanding case of 2D NMR, this need to devote multiple scans N₁ with a stepwise incrementation Δt₁ for sampling the indirect-domain time axis t_1, may be overtly taxing. Indeed, Nyquist criteria¹³ dictate that the spectral bandwidth SW₁ and resolution Δf₁ of the indirectly detected dimension(s) be related to one another as SW₁/Δf₁ = N₁. This in turn means that decreasing the number of scans acquired, necessitates a trade-off in spectral width and/or resolution. Such a constraint can be particularly onerous when examining complex samples at high magnetic fields, where the demand of keeping Δf₁ small clashes with the demand for large SW₁ bandwidths imposed by an increased chemical shift dispersion. This commonly encountered scenario makes it necessary to acquire a large number of scans – often ≥ 1000 – just to achieve minimal resolution and cover a faithful bandwidth. These demands for large N₁ arrays may make the acquisition of NMR experiments unfeasible, particularly in applications where changing sample composition is a principal consideration, such as in-cell and in vitro biomolecular NMR. High-throughput investigations such as those involved in metabolomics may also become discouragingly lengthy.

A number of methods have been developed to address these multidimensional NMR acquisition efficiency limitations, to maintain high resolution while covering a large bandwidth in the indirectly detected dimensions.^14–27 Most widely used among these are schemes that employ non-uniform sampling of the indirect domain time evolution, in combination with specialized processing techniques for spectral reconstruction.^17,18 Unfortunately, non-uniform sampling may result in artificial increases in the apparent noise, unless suitable precautions are taken.^28–35 Alternatively, prior knowledge obtained from 1D measurements can be used to speed up higher-dimensional acquisitions. For instance, the folding-over of peaks observed in the indirect dimension when SW₁ is decreased beyond Nyquist demands, can be corrected by post-processing;^21,36–40 this may yield high resolution spectra in a significantly reduced acquisition time. Another method that relies on information retrieved from previous measurements is Hadamard spectroscopy,^22,23 which utilizes selective excitations while preserving a multiplex advantage, whereby the signal-to-noise ratio increases with the square root of the number of scans. While a remarkably efficient approach for reducing acquisition time, Hadamard multidimensional NMR spectroscopy may still face limitations due to its use of modulating matrices involving minimal discretized sizes; it may also demand unfeasibly high selectivity from excitation pulses to separate resonances in crowded regions of the spectrum. Motivated by these concerns, this study presents a fast Fourier Transform (FFT) based strategy that uses polychromatic (PC) selective excitations and time delays, for speeding up 2D NMR experiments endowed with a priori F₁ knowledge. This new Time-Optimized FouriEr Encoding (TOFEE) approach extends previous work, which utilized an encoding scheme based on PC pulses to separate spectral bands and a double-FFT to unravel their information.^24,41,42 Here it is shown this kind of data could be more conveniently decoded with a single, conventional FFT, where pulse shapes and time delays have been optimally combined to enable this procedure along F₁. The resulting method can be used to produce quality, phase-sensitive spectra that have excellent peak lineshapes and the full bandwidth/resolution targeted along F₁, in a minimal number of scans. The performance of the new method is illustrated with 2D ¹³C-¹H HSQC and 2D ¹³C-¹H HSQC-TOCSY experiments performed on the nonsteroidal anti-inflammatory drug isobutyl propionic phenolic acid (ibuprofen), and on quinine. Detailed descriptions of the experimental setup macros and of the data processing procedures are provided; both of these are available upon request.

METHODS

The ultimate goal of the TOFEE strategy is to impart phase modulations given by an N × N Fourier matrix on a set of {f_n}_{n= 1,…,N} resonance lines of a priori known positions, enabling their separation with an FFT in the minimum number of scans M = N. Because the discrete FT matrix associated with the FFT does not introduce extra noise into the spectrum, such a strategy would be ideally robust against common random errors. Moreover, the strategy could provide the shortest route to discern the correlations associated to indirect-domain F₁ resonances.

Conventional sampling methods take advantage of the robustness of the discrete FT matrix $\mathbf{W}={\left\{e^{-i2\pi \left(m-1\right)\left(n-1\right)/N}/\sqrt{N}\right\}}_{n=1,...,N,m=1,...,M}$ against noise, and couple onto this the computational efficiency of the FFT algorithm to calculate the spectrum being sought. In a general case, however, utilization of the FT matrix requires a considerable investment of experimental time, since it necessitates the acquisition of M equally spaced samples in the time domain; this number is often significantly larger than the minimally required N samples, equal to the number of peaks in the indirect-domain spectrum. Non-uniform sampling schemes have the advantage of reducing the number of signals (FIDs) that need to be acquired; however, they are associated with a transformation matrix, which, unlike the FT matrix W, may increase the apparent noise in the resulting spectrum. In the TOFEE experiment, the phases of the resonances are modulated in a manner ideally suited to their separation using a minimal number of indirect-domain increments. This involves imparting an artificial e^{i2π(m − 1)(n − 1)/N} phase factor onto the nth resonance during the mth scan. Accordingly, an encoding matrix E = {e^{i2π(m − 1)(n − 1)/N}}_{m = 1, …, M, n = 1, …, N} is applied onto N indirect-domain resonances whose positions are a priori known. This matrix is stably invertible, as indicated by its minimal condition number, and upon inversion yields an optimal decoding transformation matrix W for retrieving the desired resonances. When implemented as the indirect-domain encoding module of a 2D NMR acquisition, the spectrum that will result from the application of an FFT, is one where all the indirect-domain peaks appear at equally spaced intervals in an optimal process that does not add noise.^43,44

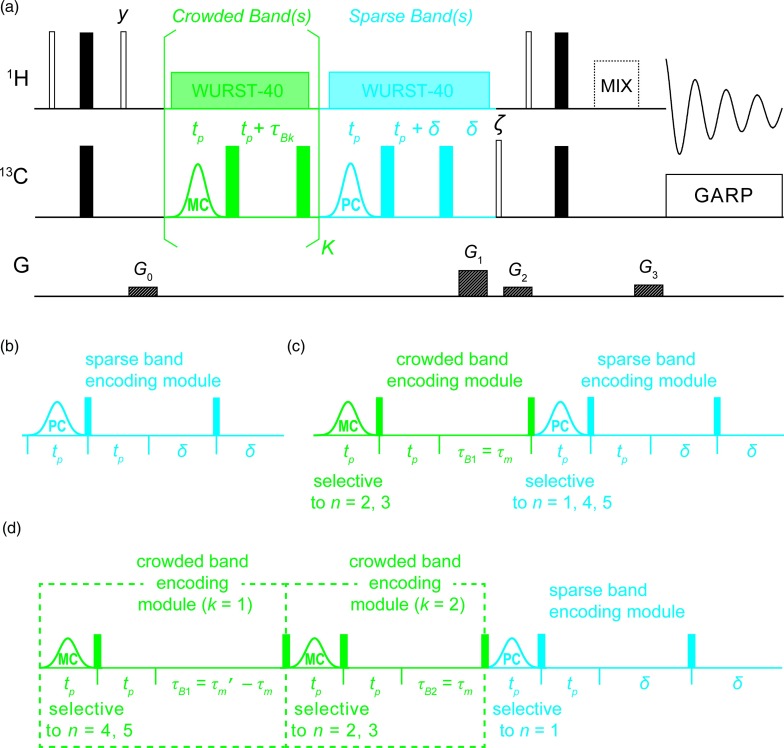
The (known) features of the indirect dimension spectrum will impact the tactics that are best suited to achieving these desired phase modulations. Henceforth, we assume for concreteness that the species whose signals will be phase modulated by E during the indirect domain encoding, is a ¹³C heteronucleus. Three distinct scenarios, associated with the spectra that are shown in the left panels of Figs. 1(a)–1(c), are then envisioned. Figure 1(a) shows a scenario where the F₁ spectrum is sufficiently sparse to have all peaks amenable to be addressed by selective pulses, as their excitation bandwidths do not overlap given the pulse time t_p allotted for excitation. Since such a spectrum is made up of N pulse-addressable bands containing only one peak each we refer to it as a “sparse bands” scenario. In this case, out of the blue and green indirect domain encoding modules shown in the TOFEE pulse sequence diagram in Fig. 2(a), only the blue segment of the pulse sequence diagram, which is referred to as a “sparse band encoding module,” is required for encoding the indirect domain. Peaks in this case can be best untangled by the use of phase-modulated PC pulses, leading to a discrete FT encoding matrix E as shown in the right panel of Fig. 1(a). The sparse band encoding module needed to impart such an indirect-domain encoding matrix is as shown in Fig. 2(b), which for simplicity, only shows the pulse sequence diagram associated to F₁. At the beginning of this indirect-domain encoding, a PC pulse is applied which is the sum of N selective excitation pulses, where N is the number of resonance bands addressed in the ¹³C spectrum. The offset of the nth selective pulse component of the PC pulse is centered on the nth resonance (the dashed lines in Fig. 1), and each of these selective pulse components $P_{RF}^n\left(t\right)$ can be described compactly as a vector of complex numbers specifying the time variation of the phases and amplitudes of the radiofrequency (RF) field. These monochromatic (MC) selective pulse components are synthesized as a discrete histogram of pulse elements clocked out at fixed increments Δt = t_i+1 − t_i, with the phase of the ith $P_{RF}^n$ element applied at a time t_i given by $\arg \left(\gamma B_1^n\left(t_i\right)\right)=2\pi f_n{t}_i$ and its amplitude given by $|\gamma B_1^n\left(t_i\right)|$. Furthermore, we define the overall phase of a selective pulse component by the rotating frame phase of the RF field at the beginning of the pulse.

FIG. 1.

Features of the (known) indirect dimension (F₁) spectrum that influence the design of the TOFEE encoding strategy. Resonances are labeled with their respective n = 1, …, 5 indices underneath the spectra. Scenarios include an F₁ spectrum comprised of (a) sparse spectral bands, (b) sparse spectral bands and a single crowded spectral band, and (c) a sparse band and multiple crowded spectral bands. The frequency of the nth resonance is denoted f_n. These resonances are excited by polychromatic (PC) pulses if bands are well separated (sparse, a), and by a combination of PC pulses and scan-specific time delays τ_m (or τ_m^′, where in general τ_m ≠ τ_m^′) plus monochromatic (MC) selective pulses if bands containing multiple proximate peaks are involved (b) and (c). Excitations that are associated with sparsely (densely) populated spectral bands are shown in blue (green) in the F₁ spectra. Selective excitation offsets are indicated with dashed lines in the spectra. The phase of the MC or PC pulse by which the nth resonance is excited during the mth scan of the experiment is indicated with φ_m,n. The general forms of the encoding matrices E which would be effectively encoding the F₁ peaks in (a), (b), and (c) are shown to the right of the spectra. The critical point to note is that in all cases the encoding matrix simplifies to E = {e^{i2π(m − 1)(n − 1)/N}}_{m = 1…M, n = 1…N}.

FIG. 2.

(a) Scheme employed for the fast acquisition of 2D ¹³C-¹H heteronuclear correlation spectra (¹³C-¹H HSQC TOFEE and ¹H-¹³C 2D HSQC-TOCSY TOFEE spectra). Empty (filled) rectangles are 90° (180°) non-selective pulses, which were applied with x-phase except where otherwise noted. Rectangles shown in the bottom line are gradient pulses. A DIPSI-2 sequence⁴⁵ was used for 2D HSQC-TOCSY TOFEE experiments (depicted as a dashed mixing period, which included a delay and 180° pulse to accommodate G₃). The shaped pulses shown in the ¹³C channel in blue and green are PC and MC selective pulses, respectively, synthesized as described in the main text. The green (blue) encoding module is used to separate resonances in crowded (sparse) regions of the F₁ spectrum; WURST-40 decoupling was applied throughout these encoding modules to suppress ¹³C-¹H J-couplings. G₀ and G₂ are purging gradients; G₁ and G₃ gradients are used to select the anti-echo data set (p = –1) for detection. A two-step phase cycle is employed with ζ = (x, –x) and the receiver phase set to φ_rec = (x, –x). (b)–(d) Strategies appropriate for encoding the illustrative F₁ spectra shown in Figs. 1(a)–1(c), respectively. Detailed descriptions of the encoding modules’ operation are provided in the main text.

To impart the desired modulation specified by the E in Fig. 1(a), a PC pulse is thus synthesized during the mth scan as a superposition of these $P_{RF}^n$ selective pulses, according to

$$P{C}_m=\sum _{n=1}^N{P}_{RF}^n\exp \left[i2\pi \left(m-1\right)\left(n-1\right)/N\right].$$ (1)

Thus, after M = N scans are acquired, a unique fictitious “frequency” 2π(n − 1) / N can be associated to the nth resonance, and an FFT with respect to the scan index, m, resolves the N resonances observed in the F₁ dimension according to the phase modulations imposed upon them by the M = N PC pulses. Notice that in the scheme in Fig. 2(b), chemical shift evolutions occurring during the PC pulses are compensated for by a nonselective 180° pulse and a delay equal to the pulse width t_p; δ delays and a nonselective 180° pulse which follow are used to accommodate coherence selection gradients, and, as shown in Fig. 2, decoupling is applied on the ¹H channel during the sparse band encoding module to suppress ¹³C-¹H J-coupling. Notice as well that because refocusing pulses invert the phases encoded by the PC pulse, the fact that two 180° pulses are applied ensures phases are correctly encoded.

By contrast to this “sparse bands scenario,” Figs. 1(b) and 1(c) show F₁ spectra where the selectivity of the excitation pulses is not sufficient to encode every resonance individually. This could naturally be resolved by extending the length – and hence the selectivity – of the pulses {PC_m}_{m = 1, …, M}, yet at the expense of T₂-like losses that may be too onerous. In such cases, which we refer to as “crowded band” scenarios, including in a single excitation band multiple closely-spaced peaks – for instance resonances 2 and 3 in Fig. 1(b) – might be convenient: this choice avoids subjecting all bands in the spectrum to unnecessarily long excitation pulses. Then, to deal with such cases, we construct E as shown in the right panels Figs. 1(b) and 1(c): for every scan, we precede the PC pulse encoding individual peaks by MC pulse(s) as shown in Figs. 2(c) and 2(d). The phase(s) of these MC pulse(s) are then varied during the M scans of the TOFEE experiment to impart a phase modulation onto crowded band F₁ peaks (if there are multiple crowded bands, multiple MC selective pulses are necessary to encode each individual band). Thereafter, each peak within a band excited by such MC pulse(s) is further encoded by a well-defined delay (or series of delays) specific to the mth scan. The scan-specific delays τ_m and MC pulse phases are chosen to eventually lead to the Fourier matrices depicted in Figs. 1(b) and 1(c). Notice that, for resonances within these crowded bands, the sparse band encoding module which follows behaves merely as a series of spin echoes and ultimately does not affect the phase(s) imparted upon them by the crowded band encoding module(s).

It follows from this that whereas PC pulses will encode peaks in sparse bands as required by Eq. (1), resonances in crowded band(s) will be excited by MC selective excitation pulse(s) centered at their average resonance frequencies, and will be thus imparted a common phase. To further distinguish the peaks within the crowded band(s), additional free evolution delay(s) τ_m are then added. Consider for simplicity a case where there is only one such crowded band containing two peaks, indexed with n₁ and n₂ (Fig. 1(b), with n₁ = 2 and n₂ = 3). Following a selective excitation of the n₁ and n₂ resonances’ common band in a given scan 1 ≤ m ≤ M, a delay of τ_m is then used to phase-label these different peaks. As according to the general scheme in Eq. (1) the phase modulations that one wishes to impart on the n₁ and n₂ resonances are 2π(m − 1)(n₁ − 1) / N and 2π(m − 1)(n₂ − 1) / N, respectively, it follows that the difference in the phases of the n₁ and n₂ resonances of the crowded band should be 2π(m − 1)(n₁ − n₂) / N. Given the addition of a free evolution encoding delay τ_m, this difference in the phases accrued by the resonances can be achieved by setting

$${\tau }_m=\frac{\left(m-1\right)\left(n_1-n_2\right)}{N\left(f_{n_1}-f_{n_2}\right)}.$$ (2)

Notice the appearance of m in the above expression implies that every scan 1 ≤ m ≤ M is associated with its own unique corresponding delay of τ_m. It follows that to achieve the desired phase modulation of the two resonances, the phase of the pulse used to selectively excite them must be set for every scan m as

$$\begin{array}{ccc}\hfill {\phi }_{m,n_1}={\phi }_{m,n_2}& =& \frac{2\pi \left(m-1\right)}{N}\left[\frac{\left(n_1-1\right)+\left(n_2-1\right)}{2}\right]\hfill \\ & & -2\pi f_p{\tau }_m,\hfill \end{array}$$ (3)

where $f_p=\left(f_{n_1}+f_{n_2}\right)/2$ is the pulse's offset. As was the case for sparse-band encoding, 180° pulses and delays (t_p and δ, Fig. 2(c)) are introduced, to refocus chemical shift evolution occurring during the MC pulse and to accommodate coherence selection gradients.

If more than two peaks are present in a single crowded band, it is not possible in general to find a delay τ_m, to be applied during the mth scan of the experiment, which would allow one to reconstruct the 2D spectrum by FT of M = N scans. Only in the particular case where there are NC peaks in a crowded band equally spaced in intervals Δf – in other words, NC peaks resonating at frequencies of $f_{n_1}$, $f_{n_1}+\Delta f$, …, $f_{n_1}+\left(NC-1\right)\Delta f$ – it is possible to find a common τ_m that allows for such an efficient reconstruction. In such cases it can be shown using similar arguments as presented above that by setting the mth scan's delay to

$${\tau }_m=\frac{\left(m-1\right)}{N\Delta f},$$ (4)

setting f_p to the average frequency of the resonances in the crowded band, and setting the phase of the pulse used to excite all of the resonances in crowded band to

$${\phi }_{m,n_i}=\frac{2\pi \left(m-1\right)}{N}\left[\frac{1}{NC}\sum _{i=1}^{NC}\left(n_i-1\right)\right]-2\pi f_p{\tau }_m,$$ (5)

a maximally efficient encoding according to E will be achieved. In the more common scenario where the resonances in a crowded band are not positioned at equally spaced frequencies, it is still possible to distinguish them in one of two forms. One is by choosing a set of {τ_m}_{m = 1…M} delays that will still generate the encoding matrix $\mathbf{E}={\left\{e^{i{\phi }_{m,n}}\right\}}_{m=1...M,n=1...N}$ with a low condition number, even if not invertible by an ideal FFT procedure. Another option is to remain committed to the FFT processing, at the expense of increasing the number of scans acquired so as to include “virtual frequencies,” where it is known that no peaks arise. In this case, it is necessary to find a frequency comb that has all the resonances of the crowded band positioned at one of its “teeth;” the “teeth” of the frequency comb where no peaks are located, will then be associated with empty lines in the reconstructed spectrum. In practice, the number of extra scans required by such an FT-based procedure is usually small, and the convenience of scanner-supplied FFT routines is worth preserving.

When more than one crowded band is present in the indirect domain, different time delays will be necessary to encode the peaks in the different bands. Nevertheless, the underlying strategy employed to separate peaks within each crowded band remains the same, and the phases of the selective pulses used to excite peaks within each of these bands remain determined by Eqs. (3) or (5), as appropriate. In order to show how time delays can be customized to separate peaks in different crowded bands, consider the situation depicted in Fig. 1(c). This involves two crowded bands, each containing two peaks, with |f₂ − f₃| > |f₄ − f₅|. This implies that the time delay required during the mth scan to separate resonances 2 and 3, τ_m, is smaller than the time delay required to separate resonances 4 and 5, τ_m^′. Because there are two crowded bands in the F₁ spectrum two encoding modules are needed, which can be accommodated as shown in Fig. 2(d). The first MC selective pulse ($M{C}_m^{k=1}$) excites only the resonances that require the longest time delay for the encoding (4 and 5). After a non-selective 180° pulse and a t_p delay refocusing the chemical shift evolution that occurred during the selective pulse, a τ_B1 = τ^′_m − τ_m delay follows. Resonances 4 and 5 are unaffected by the following shaped pulse, which is selective to only resonances 2 and 3. The next non-selective 180° pulses and t_p delays then refocus the chemical shift evolution experienced by resonances 4 and 5 during the $M{C}_m^{k=2}$ pulse; resonances 4 and 5 then evolve according to their chemical shifts during the next τ_B2 = τ_m delay. Thus, in total, these resonances experience chemical shift evolution for a period τ_m^′, as desired.

The encoding approach just described (Fig. 2(d)) can be extended to a more general scenario, with multiple crowded bands. Selective pulses for each of the K crowded band encoding modules are synthesized according to Eqs. (3) or (5), and the time delays required to separate peaks in the kth crowded band during the mth scan, ${\tau }_m^k$, are calculated according to Eqs. (2) or (4) as appropriate. Pulses are then arranged in descending order in k, so that ${\tau }_m^1>{\tau }_m^2>...>{\tau }_m^K$; the time delay utilized in the kth crowded band encoding module is thus set to ${\tau }_{Bk}={\tau }_m^k-{\tau }_m^{k+1}$ and τ_BK, the final delay time, is set to ${\tau }_m^K$.

EXPERIMENTAL

A generic heteronuclear 2D correlation sequence based on the arguments above is illustrated in Fig. 2(a), with the indirect encoding modules appropriate for the spectral cases in Figs. 1(a)–1(c) are shown in Figs. 2(b)–2(d), respectively. For this specific study, TOFEE-based 2D ¹³C-¹H HSQC and ¹³C-¹H HSQC-TOCSY experiments were carried out on an 11.7-T magnet equipped with an Agilent VNMRS^® console (Santa Clara, CA) running VNMRJ 3.2 and an indirect detection probe incorporating a z-gradient. Two samples, isobutyl propionic phenolic acid (ibuprofen) in d₆-DMSO and quinine in a 1:2 mixture of CD₃OD:CDCl₃, were tested. Custom-written Matlab^® scripts (The Mathworks Inc.) were employed to generate text files containing the full amplitude- and phase-waveforms of the required pulses and to set the required delays in the experiments. Gaussian pulses with a truncation level of 1% were used for selective PC/MC excitations; all that calculating such pulses required was providing the pulse width (in μs) of a non-selective 90° excitation pulse for a given attenuation (in db) of the transmitting channel. A recycle delay of 5 s was used for all experiments. The G₁ and G₃ gradients shown in Fig. 2(a) were used to select the anti-echo data set (p = –1) for detection; with these gradients, crosstalk between the decoded and separated 1D TOFEE traces remained minimal. These ¹³C -¹H HSQC TOFEE and ¹³C-¹H 2D HSQC-TOCSY TOFEE tests were compared to conventional ¹H-¹³C HSQC and ¹H-¹³C 2D HSQC-TOCSY experiments. To obtain these conventional heteronuclear correlation spectra and avoid phase-twisted lineshapes, both echo and anti-echo datasets had to be acquired. A two-step phase cycle was employed in all cases. For the TOCSY portion of the experiments, an 80 ms mixing time was used. VNMRJ macros and Matlab scripts were also employed to calibrate and set up all experimental parameters conveniently and on-the-fly. Further details of these – including step-by-step instructions on how to set up and run these scripts from a VNMRJ environment – are provided in the supplementary material.⁴⁶ All aforementioned scripts and macros are available upon request.

RESULTS

Figure 3 illustrates the results of applying the protocol outlined here to the acquisition of heteronuclear correlation spectra. Targeted in this test was a concentrated (≈2 M) solution of natural abundance isobutyl propionic phenolic acid in d₆-DMSO, whose 1D {¹H}¹³C trace is shown in Fig. 3(a). A 2D spectrum of this compound acquired conventionally in 1 h 33 min using 256 t₁ increments, is shown in Fig. 3(b). This kind of acquisition time is representative of what it would take to characterize a compound of moderate complexity, which spans over 100 ppm along the indirect ¹³C domain, yet has two very proximate peaks at ≈45 ppm in the ¹³C dimension that are emphasized in the figure. The inset of Fig. 3(b) depicts the detail of this spectral region, whose peaks are separated by 14 Hz along the ¹³C dimension. This uneven clustering of peaks spreading over a sizable range makes this a proper scenario for demonstrating the capabilities of the TOFEE method. Figure 3(c) shows a Fourier decoded stacked plot of 1D traces containing the same information as the 2D spectrum shown in Fig. 3(b), but acquired in only 1 min 18 s. Figure 3(d) shows another rendering of these TOFEE data, whereby an artificial 2D spectrum was constructed by convolving the 1D traces in Fig. 3(c) with a Lorentzian function and placing each trace along its a priori known ¹³C chemical shift offset in the F₁ dimension. This display format facilitates comparison between the new method and traditional HSQC methods. Notice the clean separation of the peaks (inset, Fig. 3(d)) achieved by using a crowded band-encoding module. Notice as well the minimal crosstalk observed between the various traces in Figs. 3(c) and 3(d), comparable to what might be expected to result from t₁-noise in a conventionally acquired 2D NMR spectrum.

FIG. 3.

TOFEE ¹³C-¹H HSQC acquisition exemplified on isobutyl propionic phenolic acid (molecular structure shown in top inset). Shaped pulse widths were 10 ms. 1D traces encoded using parametric time evolution period(s) are shown in green. (a) Single-scan 1D ¹³C spectrum of the compound collected in ∼1 s; chemical shifts (in ppm) are enumerated above the spectrum (corresponding n-indices are shown in parentheses). A residual DMSO solvent peak is observed at ≈39 ppm. (b) Conventional HSQC spectrum acquired in 1 h 33 min and using 256 t₁ increments, two scans per increment (inset, proximate peaks at ≈45 ppm in F₁). (c) Fourier processed stacked plot of 1D spectra arising from the TOFEE strategy illustrated in Fig. 2(c). This 2D trace was acquired in 1 min 18 s using 7 encoding steps; these involved cycling the phases of the six bands that were encoded, while simultaneously incrementing the delay τ_m separating peaks 4 and 5 by 9.5 ms increments from 0 to 57.1 ms. A 5 s recycle delay and two phase cycled scans per encoding were used. (d) Artificial 2D HSQC spectrum reconstructed by subjecting traces in (b) to a Lorentzian convolution procedure, and centering them in their central carrier offset frequency (in ppm) along F₁ (inset, proximate peaks at ≈45 ppm in F₁ separated using parametric time delays).

Figure 4 presents another example of this encoding strategy, this time with a ¹³C-¹H 2D HSQC-TOCSY experiment associating ¹³C-¹H pairs to nearby ¹H nuclei via their through-bond connectivities. The same τ_m delays were used for this TOFEE experiment as were used to acquire the HSQC spectra shown in Figs. 3(c) and 3(d). Figure 4(c) presents a conventional 2D HSQC-TOCSY performed on this compound. This spectrum was acquired in 1 h 35 min using 256 t₁ increments. The detail of the ≈45 ppm region of the ¹³C-¹H HSQC-TOCSY spectrum, shown in the inset of Fig. 4(c), evidences correlations between the ¹³C-¹H pairs seen in Fig. 3(b) and nearby ¹H nuclei. These correlations are faithfully reproduced in the stacked plot of 1D spectra shown in Fig. 4(a), which may obtained using the TOFEE method. Figure 4(b) shows a 2D spectrum constructed from the TOFEE data using a Lorentzian convolution and correct band placing along the F₁ dimension.

FIG. 4.

2D ¹³C-¹H HSQC-TOCSY spectra of isobutyl propionic phenolic acid, collected using TOFEE (a) and (b) and conventional (c) experiments. (a) FFT-decoded stacked plot of the HSQC-TOCSY spectrum, acquired in 1 min 18 s (14 scans) using the same encoding strategy as described in Fig. 3. (b) 2D HSQC-TOCSY spectrum constructed from the traces in (a), using a Lorentzian convolution procedure and band repositioning. (c) Conventional 2D HSQC-TOCSY spectrum acquired in 1 h 35 min, using 256 t₁ increments. The insets show detail of the ≈45 ppm ¹³C spectral regions.

As mentioned, peaks in crowded regions of the spectrum can in principle be encoded by lengthening peak-specific PC pulses, or by addressing bands as a unit and concatenating a series of variable free evolution delays. This flexibility of the TOFEE approach is illustrated in Fig. 5, which compares results of ¹³C-¹H HSQC experiments on isobutyl propionic phenolic acid acquired using either one (c) or two (d) crowded band encoding modules. Figures 5(a) and 5(b) indicate which peaks were included in each band and label these peaks with their n-indices; this includes both real peaks and “virtual” peaks, which were absent in the F₁ spectrum but were nevertheless encoded in the TOFEE scheme. Besides varying the number of crowded band encoding modules employed, the number of indirect domain increments utilized (11 in (a); 7 in (b)) and the shaped pulses’ durations (t_p = 10 ms in (a), t_p = 6 ms in (b)) were also varied. Nevertheless, it is evident that both spectra obtained are high quality. As was also the case earlier, the peaks in the 1D traces evidence absorptive mode lineshapes, and minimal crosstalk among bands.

FIG. 5.

¹³C-¹H HSQC TOFEE spectra of isobutyl propionic phenolic acid. (a) and (c) Acquisition using only one crowded-band encoding module (K = 1), 11 increments (22 phase-cycled scans), and t_p = 10 ms shaped pulses. (b) and (d) Acquisition using two crowded-band encoding modules (K = 2), 7 increments (14 phase-cycled scans), and 6 ms shaped pulses. (a) and (b) show the positions of the spectral bands used in each case (ovals with dashed outline), along with the real and “virtual” peak indices employed in the TOFEE scheme (for details, see main text). For the “crowded band” in (c), peaks were separated by incrementing τ_m from 0 to 63.1 ms in eleven 6.31 ms steps; for (d) two seven element arrays were used with $\Delta {\tau }_m^{k=1}=9.5\mathrm{ms}$ and $\Delta {\tau }_m^{k=2}=0.3\mathrm{ms}$. One-dimensional traces encoded using crowded band modules are shown in green. The specific crowded band encoding modules used in (d) (k = 1 and k = 2) are also indicated. The spectra shown in (c) and (d) were acquired in 2 min 4 s and 1 min 20 s, respectively. All spectra are displayed in phase-sensitive mode.

Exciting a large number frequencies simultaneously with a PC encoding pulse, as may be needed by the TOFEE schemes, is well within the capabilities of modern NMR spectrometers. This fact is demonstrated with the fast acquisition of quinine's ¹³C-¹H 2D HSQC spectrum (Fig. 6). Given the relatively well-resolved nature of the 1D ¹³C spectrum (Fig. 6(a)), every one of the 21 possible signal bearing regions in the ¹³C dimension can be (and was) simultaneously and selectively excited. Suitably phase-modulated 20 ms-long PC pulses, requiring a $\gamma B_1^{\max }$ of only ≈0.34 kHz, could thus effectively encode all resonances expected in the indirect domain (Fig. 6(b)). Notice that since certain peaks within the ¹³C spectrum (Fig. 6(a)) originate from ¹³C nuclei with no attached protons (e.g., those at 147.22 and 144.73 ppm), their rows evidence no ¹³C-¹H correlations in the 2D spectrum. Since, in general, however, it is not known which peaks in a ¹³C spectrum will lack directly-bonded ¹³C-¹H pairs prior to acquiring the HSQC, all ¹³C resonances need to be addressed. This was the procedure adopted in these experiments on quinine. Figure 6(c) shows an artificial 2D spectrum constructed by convolving the 1D traces shown in Fig. 6(b) with a Lorentzian function in the F₁ dimension, and arranging them according to their a priori known frequencies. This is compared with a conventional ¹³C-¹H HSQC spectrum (Fig. 6(d)); notice the close resemblance between this 2D spectrum collected using 512 t₁ increments in 3 h 21 min, and the TOFEE information shown in Figs. 6(b) and 6(c), accessible after collecting only 42 phase-cycled scans in 3 min 54 s. Notice as well that also, despite the large number of ¹³C resonances that had to be excited, the fast acquisition method proved particularly effective sensitivity-wise, boasting a factor of 3.2 improvement in signal-to-noise per scan over the traditional method.

FIG. 6.

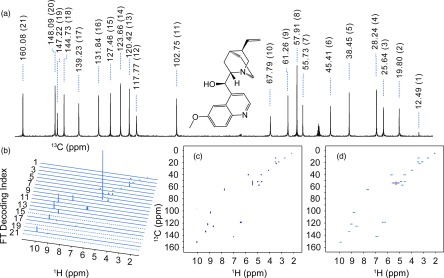
Testing TOFEE's performance in a ¹³C-¹H HSQC experiment on quinine dissolved in 1:2 CD₃OD:CDCl₃. (a) 1D ¹³C spectrum of quinine, enumerating the chemical shifts (in ppm) above the spectrum (n-indices in parentheses). Residual CD₃OD and CDCl₃ solvent peaks are observed at ∼50 ppm and ∼75 ppm, respectively. All non-solvent ¹³C peaks were encoded with single PC pulses, according to the recipe in Fig. 2(b). (b) Stacked plot of 1D HSQC traces arising upon FT of the ensuing data set, acquired in 3 min 54 s using two phase-cycled scans with a 5 s recycling delay, for each indirect domain increment. Dashed lines show empty traces corresponding to ¹³C offsets excited by the PC pulse not associated with ¹³C nuclei bonded to ¹H nuclei. (c) Artificial 2D HSQC spectrum constructed from the traces in (b), using a Lorentzian convolution and proper relocation procedure. (d) 2D HSQC spectrum acquired in 3 h 21 min and 512 scans using the traditional method. TOFEE spectra are shown in phase-sensitive mode.

DISCUSSION

Besides the encoding novelty involved in the TOFEE approach, an interesting point to notice from the experiments, is the quality lineshape that all the resolved traces in Figs. 3–6 show. Along the ¹H dimension peaks display absorptive line shapes and very little cross-talk between the F₁ bands. Moreover, on a per-scan basis, the sensitivity of the new TOFEE encoding method is higher than that observed in the conventionally acquired spectra by factors ranging from of ≈1.45–3. This is due, in part, to the decreased transverse decay (or if present by chemical exchange or homonuclear couplings) felt by the resonances in sparse bands during TOFEE's constant-time RF encoding, vis-à-vis that experienced during a conventional t₁-encoding. Indeed, whereas in conventional 2D experiments the highest resolution demand dictates the evolution time t₁^max that every peak in the spectrum will have to undergo for its indirect-domain encoding, the effective evolution times in TOFEE experiments are tailored according to the resolution demand of each peak. Isolated bands containing single or spread-out peaks will thus undergo shorter indirect-domain evolutions than in conventional experiments, hence attenuating the signal losses. This band-optimized transverse evolution of the F₁ peaks, as opposed to an evolution given by the maximal resolution needed after FFT versus t₁, helps explain the relatively higher signal-to-noise ratios observed for the peaks – even in the crowded bands.

Another aspect of the TOFEE approach to remark relates to the flexibility exemplified in Fig. 5. This shows that the number of “crowded bands” to be assumed is a priori somewhat of a free parameter; this flexibility can be used to relax the selectivity constraints on the PC and MC shaped pulses. Notice that the results also verify the robustness of the approach outlined for encoding peaks multiple crowded bands. Moreover, traces 4–9 in the spectrum shown in Fig. 5(c) – which are encoded with a single crowded band-encoding module – can be viewed as a conventionally acquired “subspectrum” contained within the larger stack of PC-encoded traces. This in turn means that, in cases where only incomplete knowledge of the exact position of the resonances within an indirect-domain crowded band is available, the Fourier encoding approach can be used to precisely measure chemical shifts by acquiring such a region of interest using a small Δf. Note that, in general, increasing the resolution of a particular subspectrum does not necessarily involve superfluously increasing acquisition time to improve the resolution of other bands in F₁; in this important respect TOFEE differs from our previous proposal,²⁴ where indirect spectral domains were also selectively divided into bands, but all of these were examined with identical spectral resolutions. TOFEE-resolved subspectra can therefore also be used in real-time NMR applications, where monitoring chemical shift changes in interesting and/or dynamic spectral regions is necessary.

Notwithstanding the versatility and benefits afforded by the TOFEE encoding technique, there are scenarios that may challenge its effectiveness. One of these is when dealing with uniformly labeled compounds or other abundant-spin networks, where homonuclear J-coupling evolution during the PC/MC selective pulses and delays may present a significant obstacle. In certain situations it may be possible to sufficiently reduce homonuclear J-couplings’ interference by simply shortening the shaped pulses’ durations. In such cases, it may be necessary to increase the number of crowded band encoding modules to accommodate the decreased selectivity of the PC/MC shaped pulses. In other situations, like when using TOFEE to investigate uniformly ¹³C labeled proteins, it might be possible to suppress homonuclear J-couplings by customizing the PC pulses and delays so that couplings between aliphatic and carbonyl ¹³C nuclei would be refocused. The machinery already developed to deal with homonuclear J-evolution in conventional multidimensional NMR experiments may, in either of these scenarios, be put to full use. Another natural limitation stems from the method's need for a priori, low-dimensional information. This may be challenging to obtain in certain sensitivity-limited cases. Instances may arise, however, where this information is readily available; for instance when aiming to analyze many similar samples as is often the case in metabolomic analyses, or when attempting to acquire several complementary multidimensional experiments (e.g., HSQC, HSQC-TOCSY, and HSQC-NOESY) having redundant information along one –and often many– dimensions. Such redundant information can be obtained conventionally once and then incorporated into TOFEE experiments to speed up the acquisition of the remaining experiments.

CONCLUSION

The encoding method outlined here shows promise for accelerating the collection of 2D NMR spectra where a priori information is available. Demonstrations of the technique on organic compounds suggest that it may prove especially valuable in metabolomics or pharmaceutical applications. Further research is needed to fully elucidate its usefulness in biomolecular investigations – particularly if crowding of the 1D projections is excessive. Still, preliminary results show that the technique may be applied when incomplete prior knowledge is available or spectral overlap is excessive, based on band-separation concepts.⁴⁷ In a more general sense, the Fourier encoding approach relieves the experimenter of the requirement to uniformly increase spectral resolution in order to measure chemical shifts precisely in any particular region of the spectrum. We believe that it will be in such instances that the method will prove particularly powerful. It is likely that these overlap-derived difficulties can be overcome when treating higher dimensional NMR experiments; forthcoming investigations will extend the applicability of this method to the acquisition of spectra with more than one indirectly detected dimension. Another aspect worth pointing out is the method's sensitivity enhancing characteristics. When coupled to its absence of reconstruction-related noises or artifacts, this further enhances the prospects of this kind of approach for challenging, time-limited acquisitions.