Trunk orientation causes asymmetries in leg function in small bird terrestrial locomotion

Abstract

In contrast to the upright trunk in humans, trunk orientation in most birds is almost horizontal (pronograde). It is conceivable that the orientation of the heavy trunk strongly influences the dynamics of bipedal terrestrial locomotion. Here, we analyse for the first time the effects of a pronograde trunk orientation on leg function and stability during bipedal locomotion. For this, we first inferred the leg function and trunk control strategy applied by a generalized small bird during terrestrial locomotion by analysing synchronously recorded kinematic (three-dimensional X-ray videography) and kinetic (three-dimensional force measurement) quail locomotion data. Then, by simulating quail gaits using a simplistic bioinspired numerical model which made use of parameters obtained in in vivo experiments with real quail, we show that the observed asymmetric leg function (left-skewed ground reaction force and longer leg at touchdown than at lift-off) is necessary for pronograde steady-state locomotion. In addition, steady-state locomotion becomes stable for specific morphological parameters. For quail-like parameters, the most common stable solution is grounded running, a gait preferred by quail and most of the other small birds. We hypothesize that stability of bipedal locomotion is a functional demand that, depending on trunk orientation and centre of mass location, constrains basic hind limb morphology and function, such as leg length, leg stiffness and leg damping.

1. Introduction

Our understanding of small avian bipedalism has advanced in recent years. Typically, small birds walk at low speeds and run at high speeds with strongly bent legs and without encompassing aerial phases [1–9]. Compliant gaits such as these are energetically not only costly [10], but also offer advantages in return. Long stride lengths and contact times [10–12] permit high-speed locomotion with relatively low peak loading forces, which exceed body weight only slightly [8,10,13]. It has been shown recently that quail fix the angle between their legs before touchdown [8]. By combining experimental data with simulations carried out using the bipedal spring-loaded inverted pendulum (SLIP) [14,15] model, Andrada et al. [8] showed that this leg alignment diminishes local instability and increases tolerance of changes in ground level. However, although our understanding of avian bipedal locomotion has improved in recent years, some features, such as the dynamic role of the trunk and its interaction with the legs, remain largely unexplored [16].

The global dynamics of avian bipedalism can be approximated using the SLIP model [9,17]. However, in contrast to the symmetric ground reaction force (GRF) produced in SLIP simulations of bouncing gaits, the GRF exerted by birds appears to be left-skewed [9,17–20] and was found to be more vertically oriented [9] than the virtual leg, assumed to act between the centre of mass (CoM) and the centre of pressure (CoP). The SLIP model can address neither the question of how such forces may evolve in the bouncing gaits of birds nor how the problem of balancing the trunk is solved.

By replacing the point mass of the SLIP model with a trunk, Maus et al. [21] showed that humans stabilize their trunk when walking by directing the GRF above the CoM. In human walking and chicken running, the GRF roughly intersects at a point above the CoM [21], a finding consistent with more vertically aligned GRF in quail, which may also have benefits in reducing energy consumption during running [22]. Maus et al. [21] termed this intersection point the virtual pivot point (VPP). By setting the GRF to intersect the VPP, they were able to calculate hip torques in their simulations of human walking and found that these hip torques led to stabilization of the upright trunk.

However, in contrast to the upright trunk found in humans, the trunk orientation of most birds is almost pronograde, leading to their CoM being located not above the pelvis but further cranially. This imposes constraints on the effective leg (between hip and CoP) function during locomotion, which are likely to be independent of the variations in segmental hindlimb morphology observed in relation to differences in ecology and biomechanical demands. For example, a CoM that is shifted cranially requires increased hip extension torques to balance the trunk against gravity. It has been shown in small and medium-sized birds that hip extension torques occur throughout stance [9,17,23]. In combination with spring-like leg operation along the leg axis, these hip extension torques introduce a tangential force at the tip of the leg, which results in forward acceleration of the CoM (figure 1b). To achieve locomotion at a steady speed, two effective leg strategies can be exploited. The first is a kinematic asymmetry with respect to the hip, which achieves symmetry of foot contact with respect to the CoM (i.e. longer effective legs at touchdown and shorter effective legs at lift-off; figure 1c). The second is a kinetic asymmetry effected by the exertion of higher forces in the early stance phase and lower forces in the remaining stance phase. This results in a GRF pattern that is skewed to the left (figure 1d). At the same time, the angular momentum about the CoM produced during each stride must be zero to achieve trunk balance. On the basis of these considerations, our main hypothesis is that asymmetric leg behaviour during avian bipedalism, as reflected in the skewed GRF profile and touchdown–lift-off asymmetry, is a result of the pronograde trunk posture and the factor that permits steady-state locomotion.

Figure 1.

Trunk posture, virtual pivot point (VPP) control and leg function. VPP control orients the ground reaction forces (GRFs) to a point above the centre of mass (COM) in order to balance the trunk. The hip torque generates a tangential force (F_t) which in combination with the axial force (F_a) redirects the GRF to the VPP. The arrow marks the direction of movement in all examples. (a) If the VPP point and the CoM are located vertically above the pelvis, symmetric axial effective leg function (e.g. spring-like) can produce steady-state locomotion because braking and accelerating forces (GRF_x) cancel each other out. (b) When the trunk is pitched forwards, symmetric axial effective leg function produces acceleration. (c,d) Asymmetric effective leg behaviour may permit steady-state locomotion with a pronograde trunk. (c) Pure kinematic asymmetry: forces are symmetric with respect to the CoM and accelerative and braking forces compensate each other. (d) Pure kinetic asymmetry: large forces in the short early stance phase are compensated by smaller forces in the remainder of stance phase. (Online version in colour.)

Our goal was to highlight the dynamic effects of a pronograde trunk on leg function and stability during locomotion. In order to do so, we first verified the existence of a VPP in quail terrestrial locomotion by analysing synchronously recorded kinematic and kinetic quail locomotion data. We then analysed numerically the interrelatedness of trunk pitch and leg function during locomotion using parameters obtained during experiments in forward simulations of a minimalistic pronograde VPP (PVPP; figure 2b) quail model. This allowed us to elucidate whether asymmetric leg behaviour in small bird locomotion is a corollary of pronograde trunk orientation.

Figure 2.

Quail and model. (a) Lateral X-ray projection of a quail traversing the two force plates custom-built to obtain single limb kinetic data. Schematic drawing superimposed onto X-ray still image depicting VPP, GRFs, effective legs at touchdown (segments hip–CoP1, hip–CoP2), aperture angle at touchdown ϕ₀, trunk angle θ and angle between effective leg and GRF β. (b) Minimalistic quail model using a VPP for postural control, and asymmetric leg behaviour modelled as parallel spring and damper. τ, hip torque; ψ₀, angle between trunk and VPP; α, angle between ground and effective leg; k, leg stiffness; c, leg damping; l₀, rest length at touchdown; r_h, distance hip–CoM; r_VPP, distance CoM–VPP.

2. Material and methods

(a). Experimental data

For the purposes of this study, we re-analysed the dataset used by Andrada et al. [9], focusing, however, on different aspects. The materials and methods used to obtain kinematic data, the position of the CoM, GRFs and %congruity were documented in detail in the original paper and are only summarized here briefly.

Eight adult common quails (Phasianidae: Coturnix coturnix, Bonnaterre 1791) weighing between 180 and 247 g moved across a walking-track 3 m long at their preferred speeds. Kinematics and GRFs were recorded simultaneously. For the kinematic analysis, synchronized, biplanar X-ray videography (Neurostar, Siemens, Erlangen, Germany) data were used. X-ray recordings were taken from the lateral and ventral projections. The X-ray machine operated at 40 kV and 53 mA, with a sampling frequency of 1 kHz. We measured three-dimensional GRFs and CoP using two custom-built (8 × 9 cm) force plates integrated into the walking-track. GRFs were collected at 1 kHz and force, and X-ray data synchronized electronically (post-trigger; see the electronic supplementary material for further information).

As described in references [7,9], we calculated the instantaneous position of the body's CoM from kinematic and cadaveric data. For the purposes of this study, trials were categorized into walking, grounded running or running. We used the percentage of congruity [24] between the CoM's potential and kinetic energy to discriminate bouncing gaits (grounded running and running) from vaulting gaits (walking). Grounded running deviates from running in featuring double contact phases and no aerial phases.

To determine the VPP, the vertical and horizontal distances between CoM and CoP were measured, and the scaled GRF from 0.1 to 0.9 of stance then drawn into a CoM-fixed coordinate system (figure 3d). VPP height is defined as the vertical distance from the CoM at which the horizontal spread between the GRFs is minimal. To determine axial leg function, the sagittal plane GRF of each leg was projected onto the effective leg axis connecting the hip and the respective CoP. Because of the asymmetric leg behaviour we observed in the results, we modelled axial leg function as parallel spring and damper elements,

2.1

F_a is the axial leg force, l₀ is the rest length of the spring, l is the instantaneous effective leg length, i is the rate of change in the effective leg length, k is the effective leg stiffness and c is the effective leg damping. We obtained k and c with a nonlinear fit by minimizing for each trial the sum of squared distances between measured forces and the forces calculated with equation (2.1) (using effective leg length data from experiments). We obtained a measure for the quality of the fit by dividing the sum of the residuals by the number of data points and the maximal leg force.

Figure 3.

Variation of model-relevant parameters during locomotion of the quail. (a) Effective leg length, axial force in the effective leg and axial leg function (axial force over leg length) in walking (red), grounded running (green) and running (blue), respectively. Curves are mean values (table 1). (b) Mean and standard deviation of trunk angle during walking, grounded running and running. The asterisk highlights the significant difference between walking and running (p = 0.006). (c) Examples of axial leg function in the quail during walking, grounded running and running (coloured asterisks), and results of the nonlinear fit using a parallel spring-damper model (solid lines). (d) GRF traces in the sagittal plane. An estimated virtual pivot point (VPP) relative to the CoM is displayed during walking (VPP height = 0.029 m), grounded running (VPP height = 0.038 m) and running (VPP height = 0.037 m). (Online version in colour.)

We defined the angle ϕ₀ between legs at touchdown as the angle between CoP1–hip–CoP2 (figure 2a), and mean trunk orientation θ_mean as the mean angle between the vertical and the vector hip–CoM measured clockwise (figure 2a) over one step.

We were able to obtain for final data analysis a total of 86 steady-state strides (32 walking, 46 grounded running and 8 running) captured using biplanar X-ray recording and synchronous, single limb GRF traces. We used the t-test in SPSS 18 (IBM, Armonk, NY) to determine whether template-related parameters are gait-related (significance level p < 0.05).

(b). Simulations

The sagittal plane PVPP model consists of a rigid body of mass m with a moment of inertia J connected at the hip to two massless legs modelled as parallel spring-damper elements (figure 2b). The trunk can pivot freely about the hip axis. The CoM of the model is located at a distance r_h from the hip at an inclination θ from the vertical (figure 2b). The location of the VPP is given by the distance r_VPP from the CoM and the inclination ψ₀ from the body axis (figure 2b). The equations of motion are , 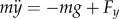and , where F_x and F_y are the sum of the horizontal and vertical components of the GRF of the legs, g is gravitational acceleration, and , and are, respectively, the CoM horizontal, CoM vertical and trunk angular accelerations. The following constant model parameters were taken from literature (r_h = 0.035 m [9]) and our experimental results: l₀ = 0.12 m, m = 0.2 kg; J = 1330 × 10⁻⁷ kg m² (trunk, neck and head modelled as a cylinder). We formed two gait categories of initial parameters based on the parameters obtained from quail walking and bouncing gaits: (i) walking-like, with k = 75 N m⁻¹, ϕ₀ = 45° and horizontal initial speed v_x0 = 0.4 m s⁻¹, and (ii) bouncing-like, with k = 100 N m⁻¹, ϕ₀ = 50° and v_x0 = 0.6 m s⁻¹. We based this classification on the significant differences observed for these parameters between grounded running and walking (table 1). Just as in experiments, we relied on %congruity to discriminate walking from bouncing, and then distinguished running from grounded running by checking for flight phases. A rigorous analysis of stability was not the aim of this paper. In accordance with literature [25], we defined stability as the ability to cope with even undetected perturbations (see the electronic supplementary material for further explanations about the model and stability). To exemplarily show robustness, we applied a step-down step-up perturbation of 0.3 l₀ and a step-down perturbation of 0.1 l₀ after 100 steps and let the simulation continue for another 100 complete steps.

Table 1.

Gait-related effective leg parameters and VPP height obtained from experimental data. k, leg stiffness from fit; c, leg damping from fit; l₀, leg length at touchdown; ϕ₀, aperture angle between legs; r_VPP, distance VPP–CoM (mean ± 1 s.d.); p, significance t-test < 0.05. w, walking; gr, grounded running; r, running.

parameter	walking	n	grounded running	n	running	n	p w versus gr	p wversus r	p gr versus r
k (N m−1)	76.4 ± 40.9	28	106.2 ± 43.8	44	102.8 ± 22	8	0.016	0.05	n.s.
c (Ns m−1)	6.4 ± 3.7	28	6.0 ± 2.1	44	3.8 ± 1.1	8	n.s.	0.002	<0.01
l0 (m)	0.125 ± 0.01	24	0.122 ± 0.03	36	0.114 ± 0.01	8	n.s.	n.s.	0.04
ϕ0 (°)	43.5 ± 4.3	18	48 ± 4.7	21	not defined		<0.001	—	—
rVPP (m)	0.043 ± 0.024	28	0.054 ± 0.024	32	0.051 ± 0.025	8	0.041	n.s.	n.s.

3. Results

(a). Experimental data

Quail walked at speeds ranging from 0.15 to 0.51 m s^–1 (mean 0.34 m s^–1), used grounded running at speeds between 0.42 and 0.79 m s^–1 (mean 0.58 m s^–1) and ran with an occurrence of an aerial phase at speeds ranging from 0.75 to 1.56 m s^–1 (mean 1.06 m s^–1).

The birds exhibited a VPP in all gaits (figure 3d), and its position relative to the CoM varied significantly only between walking and grounded running (mean of VPP height r_VPP: walking 0.043 m, grounded running 0.056 m, running 0.051 m; table 1). The mean trunk angle θ_mean decreased from walking through grounded running to running (figure 3b), and differed significantly between walking and running.

The angle between legs at touchdown (TD; figure 2a) differed significantly between walking (mean ϕ₀ = 43.5°) and grounded running (mean ϕ₀ = 48°; table 1). Effective leg length at TD varied significantly only between grounded running and running (table 1). Effective leg length displayed strong asymmetry during the contact phase (longer legs at TD and shorter legs at toe-off; figure 3a).

The parallel spring-damper system fitted walking data less well than grounded running and running data (figure 3c). The average deviation of model force from measured force was 0.14 (walking), 0.08 (grounded running) and 0.04 (running) of the maximal force. Mean effective leg stiffness was similar during grounded running and running, and in both cases higher than during walking (table 1). The mean value of the effective leg-damping constant c was highest during walking, decreased slightly during grounded running and was significantly lower during running (table 1).

(b). Simulations

We simulated quail locomotion using a minimalistic PVVP model (see Material and methods). Without damping, speed constantly increased during simulations as a result of the mechanism explained in figure 1b. In all gaits, stable locomotion (i.e. after perturbations, even undetected, the model converged asymptotically to a periodic gait) was found only for trunk orientations exceeding 107°, a value similar to the trunk inclinations observed in experiments (figure 3b). GRFs in stable simulations were left-skewed (e.g. grounded running, figure 4a, left). Hip torques in simulations were similar to those observed in experiments (e.g. grounded running, figure 4a, right). Without parameter optimization, PVPP locomotion was robust in response to perturbations in ground level up to 0.3 l₀ (figure 4c,d). The results presented below are stable simulations, with damping values and trunk inclinations based on experimental data obtained from live quail.

Figure 4.

Ground reaction forces (GRFs), hip torque, speed regulation and robustness of the pronograde VPP model (PVPP). (a) Experimental versus model GRF and hip torque during grounded running. Note that the GRFs obtained using the PVPP model are left-skewed owing to the action of the damper (experimental and SLIP curve data taken from Andrada et al.). (b) Speed regulation in the PVPP model: starting from a speed of 0.6 m s⁻¹, model speed can be regulated in the stable regions just by changing damping constant (I_c = 5.8, II_c = 5.5, III_c = 5.2, IV_c = 5.0, V_c = 4.2 Ns m⁻¹). (c,d) Robustness of the PVPP model to perturbations in ground level. (c) CoM traces before, during and after a step-down step-up perturbation of 30% of leg length. Note that the model returns to the same trajectory after a few steps. (d) CoM traces before, during and after a step-down perturbation of 10% of leg length. After the perturbation, the model stabilizes in a different periodic motion. Model parameters for all subplots are k = 100 N m⁻¹, c = 4.2 Ns m⁻¹, ϕ₀ = 50°, r_VPP = 0.04 m, ψ₀ = 131.8°. (Online version in colour.)

(c). Simulations using walking-like parameters

Using parameters obtained from walking quail (effective leg stiffness and damping, average speed of locomotion; see Material and methods and table 1), simulations yielded walking speeds ranging from 0.17 to 0.65 m s⁻¹ and grounded running speeds ranging from 0.2 to 1.2 m s⁻¹. Intriguingly, the majority of the self-stable solutions found were grounded runs (78%; figure 5a), followed by walking (22%; figure 5a).

Figure 5.

Fields of stable locomotion for (a) walking-like and (b) bouncing-like parameters (see Material and methods). The majority of the stable solutions obtained correspond to grounded running (gr). Note that running (r) exists at smaller trunk angles (less inclined from the vertical) and lower damping values than grounded running and walking (w) (right). Higher stiffness and lower damping values facilitate aerial phases and more symmetric locomotion. The opposite applies to walking. (Online version in colour.)

The walking domain is tetrahedral in shape and located in the upper parameter range. Trunk angles become steeper almost linearly as VPP height and damping decrease. No stable walking solutions were found for VPP height less than 0.04 m or damping lower than 4 Ns m⁻¹. Grounded running solutions surround the walking domain, exist at all investigated VPP heights and start at trunk angles close to 120°.

(d). Simulations using bouncing-like parameters

Using parameters obtained from bouncing-like quail gaits (see Material and methods and table 1), simulated walking speeds ranged from 0.36 to 0.54 m s⁻¹, grounded running speeds ranged from 0.2 to 1.7 m s⁻¹, and aerial phase running speeds ranged from 0.52 to 1.85 m s⁻¹. Again, most of the stable solutions were grounded running (80%, figure 5b, green). Walking (figure 5b, red) and aerial phase running (figure 5b, blue) made up the remaining 20% in equal measure.

Grounded running existed in two separate volumes: a small one located at damping values exceeding 5.5 Ns m⁻¹ with relatively shallow trunk angles between 107° and 119° and VPP heights between 0.01 and 0.04 m, and a large one located at VPP heights higher than 0.01 m and mean trunk angles exceeding 120°. For VPP heights higher than 0.06 m, damping greater than 5 Ns m⁻¹ and mean trunk angles exceeding 130°, simulations indicated stable walking. The two grounded running domains were connected by a long, thin, inclined volume of running solutions that stretched from mean trunk angles of 110° at relatively high damping values (6.2 Ns m⁻¹) to mean trunk angles close to 135° at damping values close to 3.2 Ns m⁻¹, and comprised almost the whole range of VPP heights.

4. Discussion

The aim of this study was to analyse the dynamic consequences for leg function during locomotion while balancing a pronograde trunk. We postulated that asymmetric (with respect to the hip) leg function is a prerequisite for the pronograde trunk orientation observed during avian steady-state locomotion. Quail use a combination of the predicted asymmetries (figure 1c,d). By simulating quail gaits using the minimalistic PVPP model in conjunction with parameters obtained through experiments with live quail, we were able to show that asymmetric leg function facilitates steady-state locomotion. Surprisingly, we found not only pronograde walking, but aerial phase running and large ranges of grounded running to be both stable and robust, which could provide a strong biomechanical rationale for why the latter gait seems to be so significant in quail, and perhaps birds in general.

On the basis of a VPP reported in running chicken and walking humans [21], we presumed that the more vertical GRF vector observed by Andrada et al. [9] during quail locomotion could indicate movement strategies resulting in a VPP. This indeed turned out to be the case, and we found that quail display a VPP in all investigated gaits.

Our parameter fit revealed lower effective stiffness in walking than in grounded running and running (table 1). In contrast, damping was highest during walking (table 1), leading to more asymmetric kinematic leg function (figure 3a), and therefore to earlier foot lift-off. This observation ties in with previously published results on leg retraction during stance, according to which amplitude is lower when birds move more slowly [1,2,6,26–28]. On the other hand, the swing phase, characterized by the swing time and the angle of attack is largely independent of speed in the species of bird investigated [1,6,7,26]. This suggests that birds regulate speed during stance, increasing stride length by reducing leg damping, which leads to more symmetrical, spring-like leg motion, and simultaneously decreasing contact times [1,6,8,28] by increasing leg stiffness (figure 3a and table 1).

How can such effective leg behaviour be achieved physiologically? Investigations in human subjects demonstrate that, in the case of ankle extensors, increasing the speed of contraction reduces force development [29]. Switching to running causes the same muscles to operate closer to isometric action, whereas the displacement is covered by the elasticity of the tendons. This same mechanism has been observed in running turkeys [30] and might also apply to quail switching from walking or grounded running to aerial phase running, where the leg undergoes a more pronounced stretch–shortening cycle than in running (figure 3a). This shift from a behaviour dominated by muscle properties to a behaviour increasingly dominated by elastic tissues, as documented in humans and turkeys [29,30], may explain the shift we observed in the viscoelastic properties of the quail leg.

Simple mechanical models (referred to by Full & Koditschek [31] as templates) have been very useful in helping us to understand basic features of locomotion. On the other hand, they are limited in their capacity to explain more detailed field observations because of a lack of parameter space. The nonlinear axial leg function and left-skewed GRF profiles obtained in recent studies [9,32], for example, have highlighted the need for a stepwise refinement of the SLIP template. This study features an expansion of the bipedal SLIP model. Despite its relative simplicity, our PVPP model incorporates three key features of bird locomotion: (i) the pronograde trunk, (ii) asymmetric compliant leg behaviour along the leg axis (modelled as a parallel spring-damper system), and (iii) a fixed aperture angle as a leg alignment strategy. All three features were inferred from in vivo experiments involving quail.

In PVPP simulations, the VPP will always tend to be above the CoM. This is because if the VPP position deviates from vertical above the CoM, restoring hip torques increase. This mechanism allows the mean orientation of the trunk to be set by positioning the VPP relative to it. The more cranial the VPP, the less inclined the mean orientation of the trunk. The more dorsal the VPP, the more inclined the mean orientation of the trunk. In the special case where the orientation of the trunk is vertical (hip, CoM and VPP aligned), symmetric effective leg behaviour along the leg axis (spring-like) generates via VPP the torque pattern necessary to stabilize locomotion [21]. However, as the trunk is pitched, the CoM and VPP are translated cranially with respect to the hip. Although trunk stability might be achieved, the model will increase speed constantly when spring-like legs are involved as the accelerative forces become larger than the braking forces (figure 1). Non-accelerative pronograde locomotion, then, requires asymmetric leg function, in our case modelled by a parallel damper element.

Our findings offer an explanation for the characteristic GRF profile observed in bird locomotion, whose skew to the left highlights an adjustment in leg function to the needs of trunk posture: the leg has to dissipate energy in order to avoid the acceleration of the CoM (figures 1 and 3a,c). In our model, the damper left-skews the GRF profile by increasing leg forces after touchdown. During leg extension, the damper decreases leg forces and leads to early lift-off, inducing at the same time a kinematic asymmetry. Effective leg behaviour such as this may be produced in birds by the damping properties of muscles [33,34].

At the limb joint level, quail seem to employ a division of work principle. While the most proximal joints retract and protract the limb actively, the intertarsal joint acts as a spring, and the tarsometatarso-phalangeal joint, which engages in negative work loops, may function as a damper [9]. This division of work is represented in the PVPP model by the hip torques that introduce energy, the axial spring and the axial damper. Earlier studies in running guinea fowl have also found that more distal joints are likely to act as springs, whereas more proximal ones (hip, knee) contribute to propulsion in both level running and unexpected drops [17,23]. The same division of work seems to apply to small mammals, too [35–37]. The crouched leg posture of smaller animals in general leads to more intrinsic muscle-related damping, greater relative muscle mass and less effective biological springs [38].

One of the most important findings of the present work is that stable pronograde locomotion exists for quail mass dimensions only at the mean trunk inclinations observed in experiments involving actual quail locomotion (greater than 107°). Note that all relevant model parameters (leg length at touchdown, inertia, stiffness, damping, aperture angle, hip–CoM distance and VPP height) were obtained from experimental data pertaining to living quails. Intriguingly, the majority of stable solutions are grounded runs. Recent studies have argued that limb morphology, especially in small-to-medium-sized avian species, maximizes the potential advantages of grounded running [6–13,30,39,40]. Our simulations, which reveal stability for this gait, add a functional argument for the occurrence of grounded running. In addition, our results suggest that, given the general morphology of birds (i.e. crouched hind limbs, nearly pronograde trunk orientation), specific geometric relationships between effective leg length at touchdown, the position of the CoM with respect to the hip and VPP height are mandatory in order to achieve stable locomotion.

Despite different leg lengths in small birds, they apply a similar angle of attack [1,6,9]. Hence, based on our results, we predict that birds with longer legs will display a more symmetric leg function, because more time is available for decelerating horizontal forces to achieve steady-state locomotion (figure 6). Similarly, a caudal shift of the CoM is expected to lead to a similar effect. Species of bird whose CoM is more cranial with respect to the hip would be expected, for example, to increase the inclination of their trunk so as to reduce the horizontal hip–CoM distance, and/or to display increased effective leg length, either through relatively long phalanges or the use of larger angles. Digit lengths in avian feet have been shown not to correlate clearly with either ecology or phylogenetic position [41]. Our results suggest that the relative position of the CoM imposes a functional constraint on the length of the phalanges and may thus help to explain the surprising result obtained by Stoessel et al. [41].

Figure 6.

Two ways of reducing asymmetric leg function. (a) A caudal shift of the CoM. (b) Longer legs, and hence more protracting strides. Assuming constant horizontal velocity, both alternatives lead to more available time to develop decelerating horizontal forces necessary to achieve steady-state locomotion. As a result, the GRF rise can be less steep. In our model, this would require less damping, which would reduce kinetic and kinematic asymmetry at the same time. (Online version in colour.)

Trunk orientation and leg function are coupled. In humans, the placement of the hip below the CoM allows a more elastic operation of the leg (figure 1a), leading to less expected kinetic and kinematic asymmetry, and to hip extension and flexion torques. Still, both asymmetries are present, but their source is different from quail. In human, the leg is about 5% longer at take-off compared with touchdown [42,43], whereas in quail the leg is 25% shorter at take-off (figure 3a). In humans, this kinematic asymmetry seemingly results from elastic ankle function [44]. The kinetic asymmetry observed in human running is mostly explained by the impact forces at TD [45,46]. In contrast, in quail, the impact is much lower owing to the absence of flight phases, the low mass of the highly compliant avian foot and the aperture angle [8,9]. Our results indicate that an inclined trunk necessitates damping in the leg, which is the source of the kinetic and the kinematic asymmetry.

Stability during locomotion has mostly been analysed for tractability using templates such as the SLIP model [14,15] for running and the bipedal SLIP model for walking [47]. Both conservative models can exhibit periodic motion that is only partially asymptotically stable (i.e. it cannot stabilize changes in system energy). However, animals are not energy conserving, so recent investigations have centred on modified spring-mass models capable of energy management [48,49]. Commonly, leg properties such as effective leg stiffness or effective leg length are adapted during stance. A different approach is to add hip torque [50], resulting in a non-physical SLIP model. Most of these approaches are based on the way humans [42,51–53] and birds [17,54,55] seem to adapt stiffness, leg retraction and leg length in advance of or in response to a perturbation. However, even without optimizing parameters, our model is able to cope with ground-level perturbations of up to 30% of leg length without requiring either parameter changes or feedback control (figure 4c). Moreover, the model is also extremely insensitive to errors in parameters such as aperture angle, effective leg stiffness and damping. This surprising robustness may explain the evolutionarily conservative pronograde orientation of the trunk in combination with the widespread occurrence of grounded running in birds. The model may even yield new insights into the relationship between trunk posture and leg function in theropod dinosaur locomotion. Taking into account, for instance, that the theropod trunk was almost pronograde but that the CoM was more caudal [28,56] than in birds, it is likely that theropod leg function was much more symmetric than in modern quail.

Ethics statement

The Committee for Animal Research of the State of Thuringia, Germany, approved the animal care and all experimental procedures (registry number: 02-47/10).

Funding statement

This research was supported by DFG (German Research Council) grant nos. Bl 236/22-1/3 and Fi 410/15-1/3.