Single-Heartbeat Electromechanical Wave Imaging with Optimal Strain Estimation Using Temporally-Unequispaced Acquisition Sequences

Abstract

Electromechanical Wave Imaging (EWI) is a non-invasive, ultrasound-based imaging method capable of mapping the electromechanical wave (EW) in vivo, i.e., the transient deformations occurring in response to the electrical activation of the heart. Achieving the optimal imaging frame rates, in terms of the elastographic signal-to-noise ratio, to capture the EW in a full-view of the heart poses a technical challenge due to the limitations of conventional imaging sequences, in which the frame rate is low and tied to the imaging parameters. To achieve higher frame rates, EWI is typically performed in multiple small regions of interest acquired over separate heartbeats, which are then combined into a single view. However, the reliance on multiple heartbeats has previously precluded the method from its application in non-periodic arrhythmias such as fibrillation. Moreover, the frame rates achieved remain sub-optimal, because they are determined by the imaging parameters rather than being optimized to image the EW. In this paper, we develop a temporally-unequispaced acquisition sequence (TUAS) for which a wide range of frame rates are achievable independently of the imaging parameters, while maintaining a full view of the heart at high beam density. TUAS is first used to determine the optimal frame rate for EWI in a paced canine heart in vivo. The feasibility of performing single-heartbeat EWI during ventricular fibrillation is then demonstrated. These results indicate that EWI can be performed optimally, within a single heartbeat, during free breathing, and implemented in real time for periodic and non-periodic cardiac events.

1. Introduction

Conduction abnormalities in the myocardium have been linked to stroke(Wolf et al., 1991), heart failure(Carson et al., 2005) and sudden cardiac death(Zheng et al., 2001), three major causes of death and disability worldwide. However, no non-invasive imaging method is currently available to the physician at the point of care to characterize the regional electrical activity of the heart for a more accurate diagnosis and longitudinal evaluations of treatment. Electromechanical Wave Imaging (Provost et al., 2010, 2011a, 2011b; Konofagou et al., 2010; Pernot et al., 2007) (EWI) is a non-invasive, ultrasound-based imaging method that can map the transient deformations of the myocardium resulting from local electrical activation, i.e., the electromechanical wave (EW). The EW and electrical activation maps have been shown to be closely correlated (Provost et al., 2011a, 2011b, 2011c), therefore indicating that EWI could become a low-cost, non-invasive, and real-time modality for the characterization of arrhythmias.

To accurately map the EW, it is necessary to achieve high frame rates and a high beam density in a large field of view covering the entire heart. However, in conventional imaging sequences, increasing one of these parameters comes at the cost of reducing others. To date, the approach used in EWI to circumvent this issue relied on dividing the full view of the heart into multiple sectors acquired at different heartbeats and then reconstructing it using either ECG-gating (Pernot et al., 2007) or motion-matching (Provost et al., 2010) and assuming perfect periodicity of the heart motion. However, non-periodic arrhythmias, e.g., atrial fibrillation or ectopic beats, are of great interest clinically but cannot be studied using EWI in its current form. The objective of this study is thus to design a new sequencing approach for EWI that can provide high frame rates and a high beam density in a full view of the heart within a single heartbeat.

EWI maps the transient strains occurring in the vicinity of the electrical activation of the heart. More specifically, at the tissue level, the depolarization of myocardial regions triggers the electromechanical activation, i.e., the onset of the muscle's transition from a relaxation state to a contraction state. Spatially, this electromechanical activation forms the EW front that follows the propagation pattern of the electrical activation sequence. To estimate those strains, inter-frame motion (or displacement) is first estimated axially via cross-correlation of consecutive radio-frequency RF frames. From the displacements, one can then obtain the inter-frame strains (or strains) depicting the EW by applying gradient operators on the displacement field. However, the heart is an organ that undergoes significant three-dimensional motion and large deformations, which both lead to the decorrelation of the RF signals and thus to the degradation of the motion and deformation estimation accuracy. Consequently, the time lapse between the two frames used to estimate motion becomes a critical optimization parameter (Luo et al., 2007; Lee, 2010; Chen et al., 2009). If the interval becomes too long (at lower frame rates), decorrelation will corrupt the motion estimates. Conversely, if this interval becomes too short (at higher frame rates), the resulting smaller motion may lie below the sensitivity of the motion estimator.

While low frame rates can be easily achieved experimentally, imaging at high frame rates over a large field of view and at high resolution constitutes a technical challenge. A number of different approaches have been proposed to increase the frame rate, with different tradeoffs. Standard echocardiography is based on focused insonification and the frame rate is therefore determined by the number of beams acquired per frame. Reducing the number of beams to increase the frame rate consequently results either in a narrower field of view (Konofagou et al., 2002; D'hooge et al., 2002) or in sparse-sector scans (Kanai et al., 1993). By acquiring over multiple heartbeats, composite imaging techniques can achieve very high effective frame rates in a full field of view with high beam density (Wang et al., 2008), but, as indicated previously, are difficult to use on arrhythmic cases or in patients who are unable to hold their breath. Unfocused approaches have also been suggested and show high promise (Provost et al., 2011c), but are still in the early stages of development, require additional hardware and therefore cannot be implemented in conventional scanners (Provost et al., 2011c; Honjo et al., 2010; Cheng and Lu, 2006). Modulated-Excitation and synthetic-aperture methods have also been developed (Misaridis and Jensen, 2005).

Another strategy consists of repeatedly acquiring the same beam before moving to the next, or applying similar interleaving methods to image sectors. Current technologies using this approach include Doppler-effect-based motion and strain imaging techniques such as conventional pulsed Doppler imaging (Jensen, 1996), color flow imaging (Ferrara and DeAngelis, 1997), Strain-Rate Imaging (SRI) (Heimdal et al., 1998), etc. In such techniques, the pulse repetition frequency is linked to the accuracy of the motion-estimation (motion-estimation rate), and the ‘frame rate’ indicates the time lapse between motion maps (motion-sampling rate). We therefore define here the terms ‘motion-estimation rate’ and ‘motion-sampling rate’ for EWI to avoid confusion. This is because ‘frame rate’ is typically used to describe the motion-estimation rate in RF- or B-mode motion estimation techniques, while in Doppler-based techniques it corresponds to the motion-sampling rate. Due to the large number of pulses (usually 8 to 10) necessary to estimate motion using Doppler-based methods, the motion-sampling rates achieved are too low when maintaining a full-view image of the heart to map the EW propagation. When using RF cross-correlation, only two consecutive pulses are necessary to provide a high accuracy estimate of motion, leading to a four- to five-fold increase in the motion-sampling rate, field of view or beam density. Such an approach has been described as ‘sector-based sequencing’ and recently used for steady-state periodic excitations (Baghani et al., 2010; Azar et al., 2010).

For the purpose of this study, we have developed a temporally-unequispaced acquisition sequence (TUAS), which is a sector-based sequence (Baghani et al., 2010) adapted to optimally estimate the EW in terms of the elastographic signal-to-noise ratio (SNRe). TUAS was implemented on a conventional clinical ultrasound scanner as it does not require any additional hardware. In TUAS, it is possible to simultaneously achieve a wide range of frame rates for motion estimation, high beam density (high resolution), and a large field of view in a single heartbeat, with little dependence on depth and beam density. Consequently, for a given set of imaging parameters, motion can be estimated at rates varying from a few Hz to kHz. The tradeoff, in this case, is a reduction of the sampling rate of the motion estimation, which is shown, in this study, to have a minor effect on the accuracy of EW maps as long as it is maintained above a certain threshold.

In TUAS, a wide range of frame rates can be achieved, including very high frame rates, independently of other imaging parameters. Therefore, by maintaining a set of imaging parameters (e.g., field of view, imaging depth), and varying the frame rate, it is possible to identify an optimal frame rate by studying the link between the elastographic signal-to-noise ratio and the EW. In the first part of this paper, we introduce a new probabilistic framework based on experimental estimates acquired in a paced canine in vivo to establish this optimal frame rate. In the second part of this paper, single-heartbeat EWI was used to map the electromechanical activity of fibrillation, a non-periodic arrhythmia, for the first time.

2. Methods

2.1 Experimental Setup

In this study, approved by the Institutional Animal Care and Use Committee of Columbia University, a male mongrel dog, 18 kg in weight, was anesthetized with an intravenous injection of Diazepam 0.5-1.0mg/kg as premedication, and Methohexital 4-11mg/kg as induction anesthetic. The animal was mechanically ventilated with a rate- and volume-regulated ventilator on a mixture of oxygen and titrated isoflurane (0.5%–5.0%). Morphine (0.15 mg/kg, epidural) was administered before surgery, and lidocaine (50 micrograms/kg/h, intravenous) was used during the entire procedure.

To maintain blood volume, 0.9% saline solution was administered intravenously at 5 mL/kg/h. Standard limb leads were placed for surface electrocardiogram (ECG) monitoring. Oxygen saturation of the blood and peripheral blood pressure were monitored throughout the experiment. The chest was opened by lateral thoracotomy using electrocautery. Three pacing electrodes were sutured at the basal region of the lateral wall, at the left ventricular apex and at the right ventricular apex. Only one pacing electrode, located at the basal region of the lateral wall, was used to pace the heart in this study. RF ablation of the left bundle branch was performed under fluoroscopy, and a basket catheter (Boston Scientific, Natick, MA) was introduced in the left ventricle for the purpose of another study.

2.2 Temporally-Unequispaced Sequence

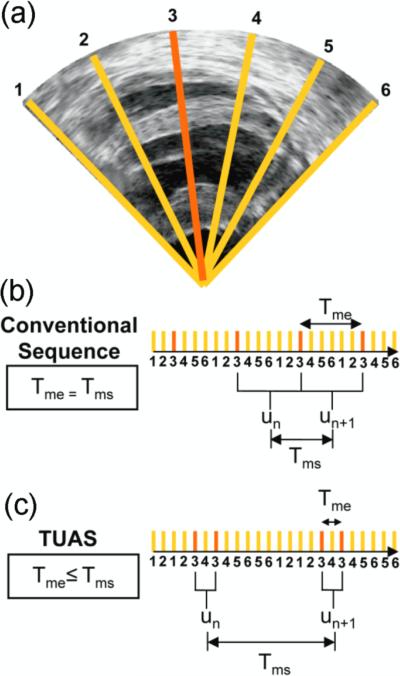
Conventional ultrasound imaging using a phased array consists of acquiring a number of beams, typically 64 or 128, over a 90° field of view (figure 1a). These beams are acquired sequentially, and the process is repeated for each frame. For example, a given beam, e.g., beam k (figure 1(a)), will be acquired at a fixed rate (figure 1(b)). TUAS is thus characterized similarly by two distinct rates, the motion-estimation rate and the motion-sampling rate, defined as follows (figure 1(b),(c)): The motion-estimation rate r_me is defined as the inverse of the time lapsing between the two RF frames used to estimate motion, i.e., T_me. The motion-sampling rate r_ms is defined as the inverse of the time lapsing between two consecutive displacement maps, i.e., T_ms. In conventional imaging sequences, these two rates are equal, because a given frame is typically used for two motion estimations (u_n and u_n+1 in figure 1(b)). In TUAS, the operator can adjust the motion-estimation rate. As shown in figure 1(c), a frame in the TUAS case is used only once for motion estimation (figure 1(c)), thus halving the motion-sampling rate relative to the conventional method.

Figure 1.

Acquisition Sequences. (a) Typical B-mode image containing N=6 lines. Acquisition times of a given line, e.g., line k, (b) in a conventional imaging sequence and (c) in a temporally unequispaced sequence. A displacement estimation is done between two RF lines separated by T_me. Displacement estimations are done every T_ms.

For example, an acquisition performed at an 11-cm-depth with 32 beams with a conventional sequence will correspond to a frame rate of 219 Hz. However, while 219 Hz satisfies the Nyquist sampling criterion of cardiac motion, it is, as we show in this paper, insufficient for accurate motion tracking using RF cross-correlation. Therefore, to reach a higher frame rate of, e.g., 500 Hz, as typically used for EWI, the conventional sequence requires halving the number of beams, and thus reducing either the beam density or the field of view or both. At the same depth and beam density, TUAS provides a motion-sampling rate of 109 Hz and a motion-estimation rate that can be varied, as shown in the following section, within the following group: {7000, 3500, 1750, 875, 438, 219} Hz. Both the lateral resolution and the field of view can be maintained while estimating the cardiac motion with an optimal frame rate, i.e., the motion-estimation rate that results in larger SNRe. The tradeoff in this case is the halving of the motion-sampling rate; however, the motion-sampling rate has only a minor effect on the motion estimation accuracy. Theoretically, if this rate remains above the Nyquist rate of the estimated cardiac motion, it will have no effect. As shown in this paper, a motion-sampling rate above 120 Hz is sufficient to accurately depict the EW. Indeed, the motion measured over time at a given pixel has a bandwidth of approximately 50 Hz at -20dB, corresponding to a minimum sampling rate of 100 Hz. Other studies where the electromechanics of the heart were imaged also used similar or lower motion-sampling rates using other imaging methodologies (Prinzen et al., 1992; Wyman et al., 1999; Faris et al., 2003).

2.3 TUAS Implementation

In a conventional imaging sequence, two consecutive frames with N beams per frame are acquired beam by beam in the order indicated in Table 1. This results in a time between two frames equal to 2dN/c, where d is the imaging depth, N is the number of beams in the image, and c is the speed of sound. Motion is then estimated between the two consecutive acquisitions of beams at the same location. For example, motion is estimated through the cross-correlation of beam 1 acquired first and beam 1 acquired N+1 beams later. Therefore, identical motion estimation and motion-sampling rates are obtained, equal to c(2dN)⁻¹.

Table 1.

TUAS for different sector sizes

k = 1		k = 4		Arbitrary k
Time (2d/c)	Line Number	Time (2d/c)	Line Number	Time (2d/c)	Line Number
1	1	1	1	1	1
2	1	2	2		...
3	2	3	3	k	k
4	2	4	4	k+1	1
5	3	5	1	...	...
6	3	6	2	2k	k
7	4	7	3	2k+1	k+1
8	4	8	4	...	...
...	...	9	5	3k	2k
2N-1	N	10	6	3k+1	k+1
N	N	11	7	...	...
		12	8	4k	2k
		13	5	4k+1	2k+1
		14	6	...	...
		15	7	2N-k	N
		16	8	2N-k+1	N-k+1
		...	...	...	...
		2N-7	N-3	2N	N
		2N-6	N-2
		2N-5	N-1
		2N-4	N
		2N-3	N-3
		2N-2	N-2
		2N-1	N-1
		2N	N

TUAS was implemented in an open-architecture Ultrasonix MDP system (Ultrasonix Corp, Burnaby, BC, Canada) using the Texo Software Development Kit. In TUAS, the beams constituting two frames are acquired in a different order. Beams are acquired consecutively within sectors containing k beams, and then repeated. Table 1 describes different sequences for different values of k, e.g., for k = 1, k =4 and in the general case.

Axial motion is estimated between two beams acquired consecutively at the same location, which results in a motion-estimation rate of c(2dk)⁻¹. Since k needs to be a divisor of N, i.e., div(N), the group of available motion-estimation rates for a given number of beams is given by c(2d)⁻¹{(div(N))⁻¹}. The highest motion-estimation rate occurs at k = 1, i.e., c(2d)⁻¹, and the lowest motion-estimation rate occurs at k = N, and is equal to that of a conventional imaging sequence, i.e., c(2dN)⁻¹. If motion is only estimated between the two closest acquisitions of the same beam in time, the motion-sampling rate is c(4dN)⁻¹. Note that in addition to motion being estimated between beams separated by T_me, lower motion-estimation rates can also be achieved by estimating motion between beams separated by T_ms-T_me (figure 1), corresponding to a motion-estimation rate of c(2d(N-k))⁻¹, in which case the motion-sampling rate would be c(2dN)⁻¹.

A 3.3-MHz phased array was used to image the canine myocardium in vivo. To minimize motion artifacts, the probe was attached to a stabilizer (Medtronic Corp., Minneapolis, MN). Axial displacements were estimated using a 1D cross-correlation algorithm (Luo and Konofagou, 2010) using RF signals sampled at 20 MHz. The window size used was 4.60 mm and the overlap was 90%. The heart was segmented using an automated contour tracking technique (Luo and Konofagou, 2008). The incremental axial strains were estimated with a least-squares method (Kallel and Ophir, 1997) and a kernel size of 10.7 mm. More specifically, the Savitzky-Golay digital differentiator based on a least-square linear fitting was applied onto the axial displacement maps to reduce the noise amplification (Luo et al., 2004). Neither averaging nor median filters was used for the SNR_e analysis. However, a moving average of axial size 19.6mm over three lines was applied for the EWI frames only (Figs. 6 & 7). Images were acquired using separate acquisitions at different motion-estimation rates, i.e., {41, 82, 163, 350, 452, 855, 1100, 1283, 1540} Hz and their corresponding motion-sampling rates {163, 163, 163, 163, 211, 132, 128, 119, 119} at a 10-cm depth.

Figure 6.

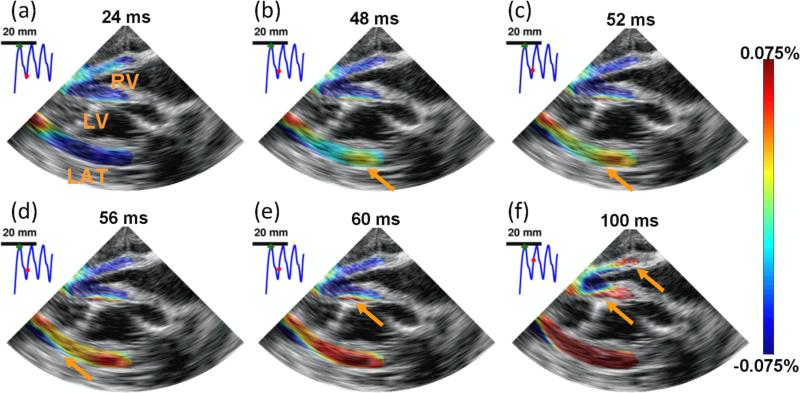
EWI during pacing in the four chamber apical view. RV, LV, and LAT, respectively, denote right ventricle, left ventricle and lateral wall. Arrows depict the propagation of the EW. The EW was initiated in the right part of the lateral wall (b) and propagated toward the apex, followed by the septum (b-e) and right-ventricular wall (f). 0 ms corresponds to the pacing time. Motion-estimation rate : 1100 fps. Motion-sampling rate : 128 fps.

Figure 7.

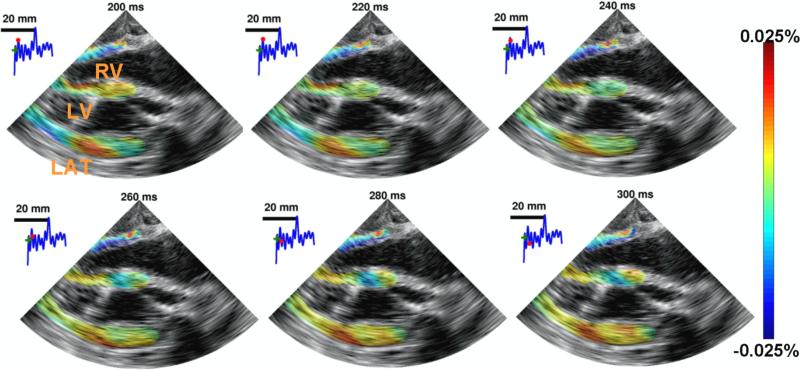
EWI during fibrillation in the four chamber apical view over 100 ms. RV, LV, and LAT, respectively, denote right ventricle, left ventricle and lateral wall. No organized contraction can be observed. EWI was performed with a 2000 Hz motion-estimation rate and a 120 Hz motion-sampling rate.

2.4 Elastographic Signal-to-Noise Ratio (SNR_e)

To assess the accuracy of a strain measurement, we used the SNR_e, defined as:

$$SN{R}_e=\frac{\mu }{\sigma },$$ (1)

where μ is the local average of strains at a given time, and σ the corresponding standard deviation. Measuring the SNR_e in the heart is a challenging task since the strains change rapidly both in time and space. To palliate this issue, the SNR_e at different motion-estimation rates was computed by averaging and calculating the standard deviation of the incremental strains within overlapping small axial windows (4.85 mm) over multiple frames, corresponding to up to five heart cycles, after segmenting the heart. This approach provides the SNR_e as a function of space and time, SNR_e(x,y,t), where x and y are the lateral and axial directions, respectively, and t is the time. Hundreds of thousands of SNR_e values for each motion-estimation rate were measured (the exact number depends on the motion-sampling rate). Previous literature (Varghese and Ophir, 1997) on the strain filter indicates that the SNR_e will depend mostly on the magnitude of the strains measured, when the imaging parameters are fixed. This theoretical framework allows the construction of an upper limit on the SNR_e as a function of the strain amplitude (a.k.a., the strain-filter) using a correlation model (Meunier and Bertrand, 1995). The strain filter corresponds, in this case, to the Ziv-Zakai Lower Bound (ZZLB) on the variance. The ZZLB is a combination of the Cramér-Rao Lower Bound (CRLB) and the Barankin bound (BB). The ZZLB transitions from the CRLB to the BB when decorrelation becomes important to the point that only the envelope of the signal contains information on the motion (Weinstein and Weiss, 1984). The strain filter was adapted to the imaging parameters used in this study as a reference. For that purpose, an SNR of 1500 (60 dB) was assumed for the RF data, similar to what was previously considered in prior literature (Lee et al., 2007). Such a high value is justified since acquisition was performed in an open-chest setting.

The motion-estimation rate is directly linked to the strain distribution in the heart. Consider the cumulative strain function at a given point (x_o, y₀), e(x₀,y₀,t) = e(t). Then, the strain at a time t₀ can be defined as

$$\epsilon \left(t_0\right)=e(t_0+T_{me})-e\left(t_0\right)$$ (2)

When expanding e(t) in Taylor series around t₀, we obtain

$$\begin{array}{cc}\hfill & \epsilon \left(t_0\right)=e\left(t_0\right)+e^{\prime }\left(t_0\right)(T_{me}+t_0-t_0)-[e\left(t_0\right)+e^{\prime }\left(t_0\right)(t_0-t_0)]+O\left(T_{me}^2\right)\hfill \\ \hfill & =e^{\prime }\left(t_0\right)\left(T_{me}\right)+O\left(T_{me}^2\right)\hfill \\ \hfill & \approx \frac{e^{\prime }\left(t_0\right)}{r_{me}},\hfill \end{array}$$ (3)

where e’(t₀) is the first temporal derivative of cumulative strains, or strain rate, and is independent of the motion-estimation rate r_me. Let us consider the same heart with two strain distributions within ε₁±Δε₁ and ε₂±Δε₂ acquired at a rate r_me1 and r_me2, respectively. Then, we have

$${\epsilon }_2\pm \Delta {\epsilon }_2\approx \frac{r_{me1}}{r_{me2}}({\epsilon }_1\pm \Delta {\epsilon }_1)=(\frac{r_{me1}}{r_{me2}}{\epsilon }_1\pm \frac{r_{me1}}{r_{me2}}\Delta {\epsilon }_1)$$ (4)

Therefore, if r_me2 = 2r_me1, ε₂±Δε₂ = ε₁/2±Δε₁/2. In other words, when doubling the motion-estimation rate, both the center and width of the strain distribution are halved. Finding the optimal motion-estimation rate is thus equivalent to finding the optimal strain distribution.

To perform this optimization, we determine the probability of obtaining an SNR_e value within a given interval, e.g., [s₁,s₂], for a given strain ε₀, i.e., in a probabilistic framework, P(s₁ <SNR_e < s₂ | ε = ε₀). Since we simultaneously measure SNR_e and ε, their two-dimensional histogram can be constructed and used to determine their joint probability density function (pdf), i.e., f(SNR_e, ε). The individual pdf of SNRe and ε can also be obtained from 1-D histograms. Finally, the conditional pdf f(SNR_e | ε) can be obtained through the following relationship:

$$f(SN{R}_e\mid \epsilon )=\frac{f(SN{R}_e,\epsilon )}{f\left(\epsilon \right)},$$ (5)

Note that f(SNR_e), f(SNR_e, ε) and f(SNR_e | ε) also depend on the motion-estimation rate, r_me, and on the temporal portion of the heart cycle of interest, Δt_c, i.e.,

$$f(SN{R}_e\mid \epsilon ;r_{me},\Delta t_c)=\frac{f(SN{R}_e,\epsilon ;r_{me},\Delta t_c)}{f(\epsilon ;r_{me},\Delta t_c)}$$ (6)

For simplification, we will use the two following assumptions:

1. f(SNR_e | ε ; r_ME, Δt_c ) = f(SNR_e | ε ; r_ME), i.e., the relationship linking SNR_e and ε does not explicitly depend on the cardiac phase. For example, a 1% strain occurring during systole will lead to the same SNR_e distribution as a 1% strain occurring during diastole.

2. f(SNR_e | ε ; r_ME) = f(SNR_e | ε), i.e., the relationship linking SNR_e and ε does not explicitly depend on the motion-estimation rate. For example, a 1% strain measured with a motion-estimation rate of 1500 Hz will lead to the same SNR_e distribution as a 1% strain measured at 400 Hz. This assumption is stronger than a). Effectively, theoretical models of the correlation coefficient (Meunier and Bertrand, 1995) typically rely, for fixed imaging parameters, only on the strain value, which would support assumption b). However, in the heart, the decorrelation effect due to out-of-beam motion might be important. In such a case, a high motion-estimation rate would reduce decorrelation caused by out-of-beam motion in comparison with a lower motion-estimation rate and thus modify the relationship between SNR_e and ε.

Finally, the expected value of the SNRe was obtained as follows:

$$E\{SN{R}_e;r_{me},\Delta t_c\}={\int }_0^{+\infty }E\{SN{R}_e\mid \epsilon ;r_{me}\}f(\epsilon ;r_{me},\Delta t_c)d\epsilon ,$$ (7)

where the conditional expected value is given by

$$E\{SN{R}_e\mid \epsilon ;r_{me}\}={\int }_0^{+\infty }SN{R}_{e}f(SN{R}_e\mid \epsilon ;r_{me})dSN{R}_e,$$ (8)

under assumption a).

This implies that the expected value of SNRe will vary during the cardiac cycle, i.e. as a function of Δt_c, as indicated in eq. (7). Therefore, two strain distributions were constructed: f(ε; r_ME , Δt_t) and f(ε; r_ME , Δt_a) where Δt_t and Δt_a correspond to five cardiac cycles (approx. 3000 ms) and the 20 frames following the R-wave (approx. 100-170 ms), respectively. f(ε; r_ME , Δt_t) was used to construct a robust conditional pdf, i.e., f(SNR_e| ε; r_ME ), based on a large enough number of samples (approx. 300,000) under assumption a). By averaging f(SNR_e| ε; r_ME ) over all the motion-estimation rates, f(SNR_e | ε) was obtained under assumption b).

3. Results

3.1 Strain estimator optimization

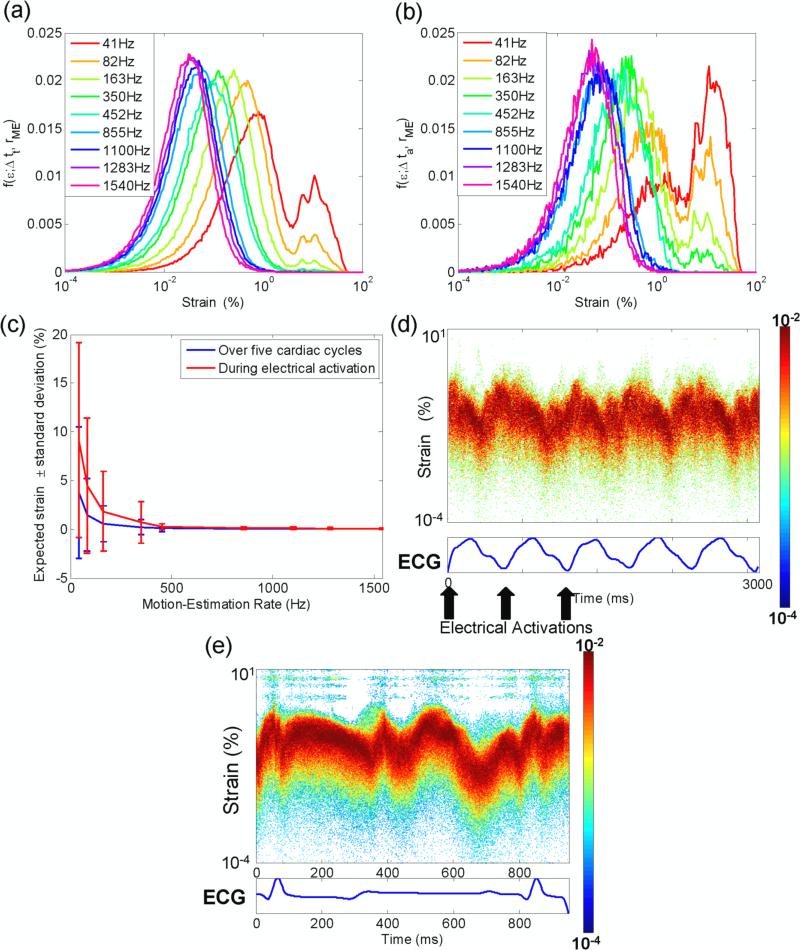
The strain distribution varied both during the cardiac cycle and at different motion-estimation rates. Figure 2 shows the variation of the strain distribution as a function of the motion-estimation rate when acquired over five cardiac cycles (figure 2(a)) and during activation only (figure 2(b)). At high motion-estimation rates, a bimodal distribution is obtained. A local minimum consistently occurs at an approximately 4% strain. This is in contradiction with eq. 4, which predicts a shift of that minimum. However, as the motion-estimation rate increases, the distribution translates towards lower strain values, narrows and becomes unimodal. This phenomenon is clearly depicted in figure 2(c): As predicted by eq. 3, the center and width of the strain distribution decreases in (r_me)⁻¹. Finally, figure 2 (d) and (e) show the highly variable strain distribution as a function of time, during the cardiac cycle both during pacing and during sinus rhythm (for the sinus rhythm case only, data was acquired in a different canine using the automatic composite technique (Provost et al., 2010)). For example, in figure 2(e), high strain values are observed during the electrical activation (0-100 ms) and following repolarization (350-450 ms). During diastole, strain amplitudes vary greatly, i.e., from very high values (500-600 ms) to very low values (600-700 ms).

Figure 2.

Strain distribution during (a) 5 cardiac cycles and (b) during activation only. (c) Center of the strains distribution for varying motion-estimation rates. (d) Strains distribution in a paced heart, motion-estimation rate: 855 Hz. (e) Strains distribution during sinus rhythm, motion-estimation rate: 520 Hz.

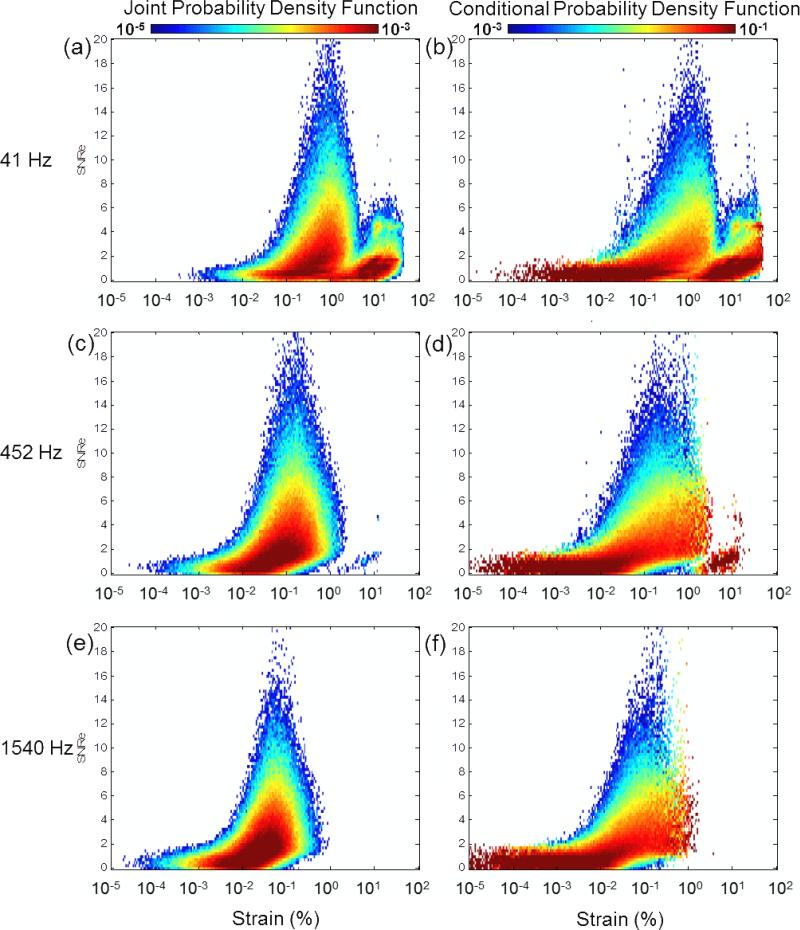
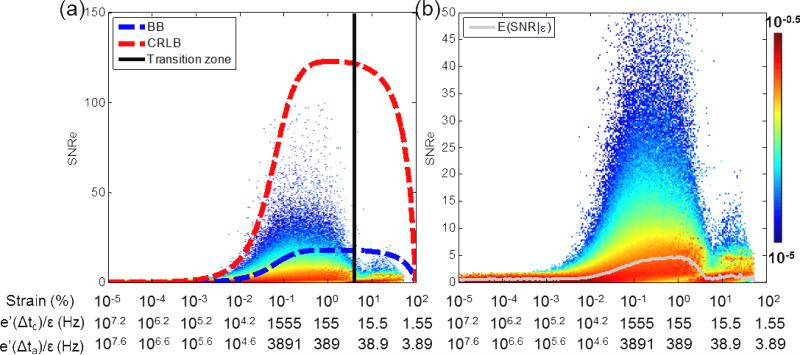
The probability of measuring a SNR_e value simultaneously with a given strain value (i.e., the joint pdf) is shown in figure 3 (a),(c),(e). For low motion-estimation rates (41 Hz) (figure 3(a)), the joint pdf spreads towards larger strain values and is associated with low values of SNR_e. At 452 Hz (figure 3(c)), the probability of higher SNR_e values is higher, and located between 0.01% and 1% strains. At large motion-estimation rates (1540 Hz) (figure 3(e)), the pdf is concentrated in lower strain values and lower SNR_e values are more probable. These joint pdf's are, however, difficult to interpret as they directly depend on the probability of measuring strain; therefore, if, for a given motion-estimation rate, the probability of measuring a given strain was low, the probability of measuring the SNR_e associated with that strain value was also low. To normalize this effect, we used the conditional pdf instead, shown in figure 3 (b),(d),(f). In that case, the probability is normalized for each individual strain value (eq. 6). However, it remains that, if a strain value was not measured in the experiment, it was impossible to obtain the conditional pdf for that strain value and thus it did not appear on these graphs. The different conditional pdfs obtained for different motion-estimation rates are very similar in overlapping domains at different motion-estimation rates; therefore indicating that assumption b) can be used: To obtain a complete representation of the conditional pdf, it was averaged over nine different motion-estimation rates (Fig 4(a)). The theoretical CRLB and BB are also shown. The SNR_e achieved remained below the CRLB (red curve), with the conditional expected SNR_e value being approximately one order of magnitude lower. An experimental transition zone corresponding to the minimum observed in fig. 2(a)-(b) at 4% strain was also added and corresponded to a sharp transition in the conditional pdf. For strains higher than 4%, the conditional pdf remained limited by the BB (blue curve). The motion-estimation rates corresponding to the center of the strain distribution over 5 cardiac cycles and during activation only are also shown, by computing e’(t₀) in eq. (3). The average value of e’(t₀) over five cardiac cycles, i.e., e’(Δt_c), and during activation only, i.e., e’(Δt_a), was 155.5 s⁻¹ and 389.1 s⁻¹, respectively. Figure 4(b) shows the same conditional pdf with the conditional expected value of the SNRe. The peak conditional expected value of the SNR_e is located between approximately 0.1% and 1% strain, which corresponds to 1555 and 155 Hz over 5 cardiac cycles, and to 3891 and 389 Hz during activation only, respectively.

Figure 3.

Joint and conditional pdf for a motion-estimation rate of (a-b) 41 Hz, (c-d) 452 Hz and (e-f) 1540 Hz, respectively.

Figure 4.

Conditional pdf constructed using acquisitions at different motion-estimation rates. (a) The BB, the CRLB and the experimental transition zone corresponding to the minimum observed in the strain distribution (fig. 2(a)-(b)), and (b) the conditional expectation value of SNRe are also displayed. The motion-estimation rates corresponding to the strains amplitude are also indicated when averaging over five cardiac cycles and during activation only. Δt_t and Δt_a correspond to five cardiac cycle and the 20 frames following the R-wave, respectively

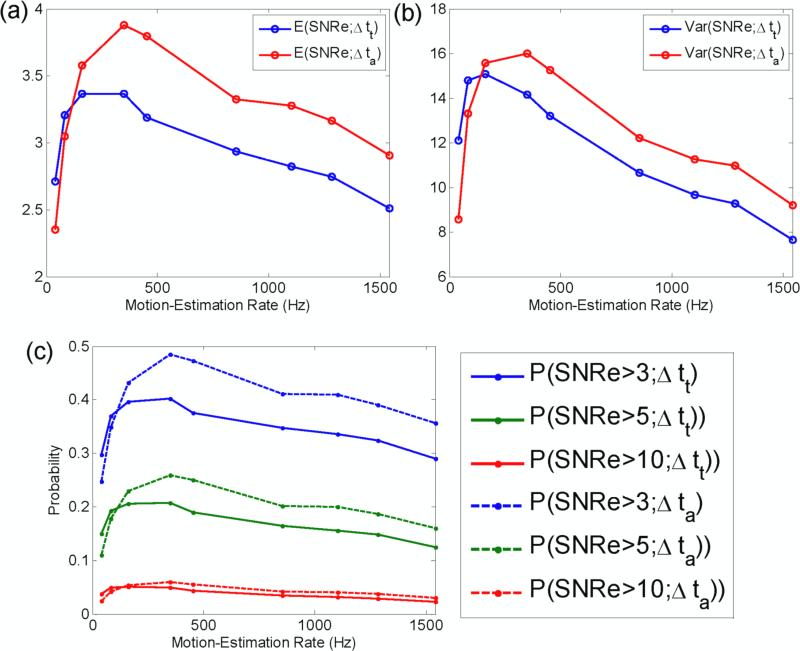
The expected value of the SNR_e as a function of the motion-estimation rate was then obtained following eq. (7) for five cardiac cycles and during activation only (figure 5(a)). Note that unlike the conditional expected value shown in figure 4, the expected value encompasses an entire strain distribution. A sharp increase in the expected value of the SNR_e is observed as the motion-estimation rate transitions from low values up to a maximum at 163 Hz and 350 Hz over five cardiac cycles and during activation only, respectively. The expected value of the SNR_e then slowly decays with the motion-estimation rate. A similar behavior is observed in the variance of the SNR_e (figure 5(b)): a maximum is achieved at 350 Hz that decays at higher motion-estimation rates. Finally, the probability of obtaining a SNR_e value higher than 3, 5 and 10 was also studied (figure 5(c)). A maximum value also occurred at 350 Hz. For example, it is approximately twice as likely to obtain a SNR_e higher than 3 at 350 Hz than at 41 Hz during activation.

Figure 5.

(a) Expectation value and (b) variance of SNRe as a function of the motion-estimation rate. (c) Probability of measuring SNRe for different thresholds. Δt_t and Δt_a correspond to five cardiac cycle and the 20 frames following the R-wave, respectively.

3.2 Imaging the Electromechanics in a Single Heartbeat

The EW was imaged during a single heartbeat using TUAS in a full four-chamber view of a heart in an open-chest canine in vivo. For example, figure 6 shows the axial incremental strains during the EW imaged with an 1100-Hz motion-estimation rate and a 137-Hz motion-sampling rate. These images show features of the EW that are expected during pacing from the basal region of the lateral wall (Provost et al., 2011b). In the parasternal four-chamber view, electrical activation results mostly in thickening (red) of the myocardium; therefore, activation appears as a transition from thinning (blue) to thickening (red). The EW first appears in the basal region of the lateral wall (figure 6 (a),(b)), approximately 30 ms after pacing. The EW was initiated at the epicardium and traveled toward the endocardium of the lateral wall. The EW then propagated to the septum (figure 6 (b)-(f)) and then to the right ventricle (figure 6 (f)).

Previously, the EW had been observed at high resolution in a full view of the heart only during periodic, repeatable heartbeats. Using TUAS, it was possible to image cardiac abnormalities that are non-periodic, such as fibrillation. Figure 7 shows such an example. After prolonged pacing, the heart underwent ventricular fibrillation. EWI was performed with a motion-estimation rate of 2000 Hz. The acquisition was performed during 8 seconds. No or limited wall motion could be observed on the B-mode. However, the incremental strains mapped depicted small, local and oscillating deformations. While pacing from the basal region of the lateral wall was maintained during fibrillation, no clear propagation was observed from the pacing origin.

4. Discussion

In this study, a TUAS-based imaging sequence was developed and implemented in vivo. TUAS provides additional flexibility in terms of the motion-estimation rate. Indeed, TUAS does increase the motion-estimation rate at the cost of a lower motion-sampling rate, thus allowing motion estimation at very high frame rates while maintaining a high lateral resolution and a full view of the heart. The second objective of this study was therefore to find an optimal range of motion-estimation rate to use, i.e., a motion-estimation rate that would result in higher signal-to-noise ratio during the EW. To find this optimal rate, a novel statistical framework of the elastographic signal-to-noise ratio (SNRe) was then developed. Using this technique, we finally showed the feasibility of imaging non-periodic arrhythmias in a full field of view at a high motion-estimation rate.

The strain magnitudes vary greatly throughout the cardiac cycle (figure 2(d),(e)). Since the quality (i.e., the SNR_e) of the strain estimation depends mostly on the strain magnitude and that the motion-estimation rate can be used as a means to translate and narrow the strain distribution (figure 2), the motion-estimation rates used should be adapted to the cardiac phase of interest, e.g., the electrical activation of the ventricles. To find the optimal motion-estimation rate for EWI, the SNR_e distribution was estimated in a paced canine in vivo, with a wide range of motion-estimation rates available with TUAS both during the electrical activation of the ventricles and over five cardiac cycles. By constructing first the joint pdf of the SNR_e and the strain, the conditional pdf was obtained for every motion-estimation rate (figure 3). By averaging these conditional pdfs, a combined conditional pdf spanning a large range of strain values was obtained (figure 4). From this distribution, one can then compute a number of measurements (figure 5) to characterize the distribution.

The combined pdf was in agreement with the strain-filter theory, which provides a higher bound on the SNR_e (figure 4). Electronic noise at very low strain values and decorrelation at very high strain magnitudes prevented high SNR_e values in these ranges. The ZZLB predicts a sharp transition between the CRLB and the BB when decorrelation becomes important to the point that the phase of the signal does not contain information about motion. Our findings suggest that this transition occurs in the vicinity of 4% strains (figures 2(a), (b), 4). Figure 4 confirms that the combined conditional pdf is comprised within the CRLB up to approximately 4% before it becomes comprised within the BB. A sharp decrease in the expected value of the SNR_e is also observed at 4% strain and above, underlining the importance of using the phase information of the RF signal for accurate strain measurements. It was also observed that the strain distribution lacked values around this transition. A distortion in the strain distribution may indicate that while a high SNR_e can be maintained, the accuracy of the strain estimator is strongly impaired at low motion-estimation rates, i.e., less than 452 Hz in this case (figure 2(b)).

To accurately map the EW, it is crucial to measure with high accuracy the strains occurring during the electrical activation. During the electrical activation, the strains mapped will vary from very small to very large values (figure 2(b)): very small, i.e., close to zero, strains occur when the heart transitions from a relaxing to a contracting state and large strains also occur when the heart undergoes rapid changes in cumulative strains, i.e., large incremental strains (see eq. (3)). To achieve this goal, the strain distribution should be maintained below the transition zone, i.e., at motion-estimation rates equal to or above 452 Hz. Note that the common measure to establish the quality of strain estimation, i.e., the expected value of the SNR_e, fails at depicting this fact: both the expected value of the SNR_e and the probability of obtaining a SNR_e value larger than 3, 5 and 10 point to an optimal motion-estimation rate of 350 Hz (figure 5). This is due to the fact that these measures do not reflect the distribution of strains, e.g., the expected SNR_e cannot distinguish a case where all strains result in a similar SNR_e from a case where half the strain values results in a high SNR_e while the other half results in a very low SNR_e. This effect is also illustrated by the fact that the highest expected SNR_e also corresponds to the highest SNR_e variance (figure 5(b)).

In summary, these results indicate that the accuracy of the strain estimator may decrease when the strain distribution crosses a transition zone while a high expected SNRe is maintained. Therefore, a motion-estimation rate sufficiently high to avoid this transition zone should be used, even if it leads to a lower expected SNR_e. In the case considered here, this would suggest the use of a motion-estimation rate above 452 Hz, e.g., 1100 Hz (figure 6). Similarly, since the strain distribution was unknown in the case of fibrillation and because of the technical challenges linked to the imaging of ventricular fibrillation (figure 7), this case was only imaged at 2000 Hz. The analysis performed here can be used to a priori determine which motion-estimation rate to use in a given experiment. Reusing the example provided in section 2, where the possible motion-estimation rates were {7000, 3500, 1750, 875, 438, 219}Hz, we find that the optimal motion-estimation rate is 875 Hz, since 438 and 219 Hz risk crossing the transition zone and motion-estimation rates equal to and above 1750 Hz, on the other hand, will be limited by the sensitivity of the strain estimator. We can then conclude that the optimal motion-estimation rate is 875 Hz in that case.

These results are, however, tied to the context of this study. This validation was performed in an open-chest setting, which provides very good image quality with the ultrasound system used. In a more clinically-relevant transthoracic imaging, the signal-to-noise ratio of the RF signals themselves is expected to be lower, shifting the ZZLB towards higher strain values and thus modifying the optimal motion-estimation rate value. Conversely, in a context of higher RF signal-to-noise ratio such as in trans-esophageal or intra-cardiac echocardiography, the ZZLB may be expanded towards lower strains, thus improving the SNR_e associated with higher motion-estimation rates. Because of the wide motion-estimation range available when using TUAS, an optimization process similar to the one developed here could be adjusted on an individual basis. The RF cross-correlation algorithm used in this study is a standard 1-D motion estimator for which improvements have been proposed in the literature such as principal component analysis (Mauldin et al., 2009; Gallippi et al., 2003) or splines(Viola and Walker, 2005). With the relatively large window size (~10 wavelengths) used in this study, these methods are not expected to improve the SNRe. However, they could be used to maintain the SNR_e when reducing the window size and thus increase the strain spatial resolution at no or little cost to the estimation quality. Moreover, regional disparities in SNR_e that could be caused by decorrelation due to lateral or elevational motion or strain, fiber orientation, or attenuation were not accounted for, since it was assumed that the same motion-estimation rate would be used for the entire image. Further studies on regional effects such as variations in out-of-plane and lateral strains, depth and fiber orientation could be estimated with other methods to further adapt the motion-estimation rate. Finally, estimating 2-D displacements could improve the axial displacements estimation quality and lead ultimately to higher SNR_e's (Lee et al., 2007).

We also investigated the effect of reducing the motion-sampling rate. At motion-sampling rates of 120 Hz, it was found possible to depict the EW. This indicates that the motion-sampling rate can be reduced at very little cost in terms of motion estimation performance. The location of the activation was detected because of the high precision achieved for the motion estimation. This shows that the trade-off in TUAS, i.e., halving the sampling rate compared to a conventional sequence with the same beam density, does not jeopardize the EW depiction. Decoupling the two frame rates may thus be a solution to improving the precision of the axial estimation without sacrificing the lateral resolution.

Finally, we showed that TUAS is capable of accurately depicting non-periodic events at high temporal resolution in a single heartbeat. EWI displacements and strains in a fibrillating canine heart were imaged in a full-view at high beam density and in a single heartbeat for the first time. Disorganized contraction, which wasexpected during such a phenomenon, was depicted in absence of large-scale motion of the heart. Regions of the myocardium were oscillating rapidly from thinning to thickening and thickening to thinning over time. Studying and mapping the frequencies of these oscillations could be useful in understanding the mechanisms of fibrillation (Chen et al., 2000). For example, complex fractionated electrograms measured using electrical mapping are often quantified using the dominant frequency (DF). The DF is defined as the highest frequency within the physiologic range of electrical activation during fibrillation, i.e., 2 to 10 Hz (Sanders et al., 2005). The DF mapped using Fourier-transformed EWI strains during fibrillation (figure 7) were found to be contained within that range.

5. Conclusion

In this study, we developed a novel, temporally unequispaced acquisition sequence to perform single-heartbeat EWI at an optimal motion-estimation rate. In an open-chest setting, EWI in a paced canine heart was found to maximize the expected value of the SNR_e when performed at 350 Hz. However, distortions in the strain distribution at frame rates below 350 Hz indicate that higher frame rates, e.g., between 500 Hz and 1000 Hz, should be used to maintain the accuracy of the EWI strain measurements. TUAS was shown suitable for depicting the EW within a single heartbeat, both during pacing and ventricular fibrillation, at high spatial resolution, for the first time. These results indicate the feasibility of real-time, single-heartbeat EWI in the clinic for the depiction of both periodic and non-periodic cardiac events.