Abstract
Protein function is intimately linked to protein structure and dynamics yet experimentally determined structures frequently omit regions within a protein due to indeterminate data, which is often due protein dynamics. We propose that atomistic molecular dynamics simulations provide a diverse sampling of biologically relevant structures for these missing segments (and beyond) to improve structural modeling and structure prediction. Here we make use of the Dynameomics data warehouse, which contains simulations of representatives of essentially all known protein folds. We developed novel computational methods to efficiently identify, rank and retrieve small peptide structures, or fragments, from this database. We also created a novel data model to analyze and compare large repositories of structural data, such as contained within the Protein Data Bank and the Dynameomics data warehouse. Our evaluation compares these structural repositories for improving loop predictions and analyzes the utility of our methods and models. Using a standard set of loop structures, containing 510 loops, 30 for each loop length from 4 to 20 residues, we find that the inclusion of Dynameomics structures in fragment-based methods improves the quality of the loop predictions without being dependent on sequence homology. Depending on loop length, ∼25–75% of the best predictions came from the Dynameomics set, resulting in lower main chain root-mean-square deviations for all fragment lengths using the combined fragment library. We also provide specific cases where Dynameomics fragments provide better predictions for NMR loop structures than fragments from crystal structures. Online access to these fragment libraries is available at http://www.dynameomics.org/fragments.
Keywords: dynamic fragments, structure prediction, loop prediction, model building, backbone dynamics, loop ensemble
Introduction
Proteins play a critical role in nearly every cellular process. Protein structure and dynamics are critical to biological function. Loops connecting secondary structure segments are frequently essential to mediating biological function by forming the active sites and epitope binding sites of proteins. Specifically, the conformation and dynamics of loops are crucial in molecular recognition, protein–protein interaction, and ligand binding mechanisms.1–3
The intrinsic flexibility and mobility of loops makes these structures difficult to determine experimentally because they often adopt a multitude of conformations. Crystal structures commonly omit loop regions and, even though these structures are considered the gold standard,4 they can contain indeterminate experimental data5 and artifacts introduced from the crystallization process.6 NMR spectroscopy can provide structural ensembles of loops in some cases, but this is generally only performed on smaller protein targets due to the method’s size limitations. Additional structural information is needed to accurately model loops as they exist in their natural, solvated environments.
We propose that atomistic molecular dynamics (MD) simulations provide a diverse sampling of biologically relevant protein structures that can improve the quality of structural modeling in general and loop predictions in particular. To this end, we have developed novel computational methods to efficiently identify, rank and retrieve peptide fragments from structural databases using internal coordinates (IC). We also created novel data models to analyze and compare large repositories of structural data, namely the Protein Data Bank (PDB)7 and the Dynameomics data warehouse.8 Our evaluation analyzes and compares these structural repositories, identifies our contributions to improving loop predictions, and shows the utility of our methods and models.
Computational methods are an established mechanism for supplementing missing or poorly modeled loop regions in experimental data. In particular, database-driven methods are commonly used to predict loop regions in proteins using small peptide backbones, or fragments.9 These methods, considered fragment-based methods, produce excellent results10–12 but are often dependent on sequence homology, which underperforms when similar sequences are not available, or cluster representatives, which potentially eliminates specific loop conformations. Furthermore, most methods rely on relevant related structures being present in the PDB. However, PDB structures may be biased due to experimental methods13,14 or be missing fragment conformations altogether. Fragment-based methods that use sequence similarity to bolster their performance also depend on matching sequences in the PDB, but matches are unlikely for longer loop regions. Many of these methods operate on relatively small repositories of structural data, such as subsets of the PDB, artificially limiting conformational diversity.
MD simulations can provide a plethora of structures to supplement information collected from the PDB.15,16 Structure variability in MD arises from dynamic motion instead of sequence variability. The Dynameomics project17 in particular is well suited to structure prediction as it is a repository of MD simulations that includes representative structures from nearly all known protein fold families18,19 and contains 105 times as many protein structures than the entire PDB. Current fragment-based methods are unable to scale to this amount of data, nor are they able to access the diverse metadata in the Dynameomics data warehouse.
Here we present a variety of results demonstrating how the Dynameomics fragments supplement the structural coverage of the PDB fragments. We highlight where there are improvements in predicting loop structures using the Dynameomics fragments and present several instances where Dynameomics fragments provide better loop predictions than fragments sourced from crystal structures. We present the general architecture of our fragment data model, called a library, and describe the associated search method to operate on large protein structure repositories. This search method integrates into the distributed data warehouse architecture of the Dynameomics project8,20 to efficiently retrieve relevant fragment structures and is central to our data model. We also elucidate a computationally efficient method to compare the structural coverage of the individual fragment libraries. Dynameomics fragments improve conventional loop predictions that use fragments from crystal structures without being dependent on sequence homology. While Dynameomics fragments provide similar predictions of crystal loop targets as crystal fragments, overall predictions are improved when both types of fragments are employed in a combined set. We also show that Dynameomics fragments can provide better predictions for dynamic, solvated loop structures. Online access to these fragment data, the models, the fragment libraries, and a web-based tool to build segments missing from PDB files is available at http://www.dynameomics.org/fragments.
Results
We assessed the utility of the Dynameomics fragment libraries in providing structures for improved loop prediction directly from the Dynameomics data warehouse by evaluating numerous fragment libraries generated using our methods and data models (see Table 1). First, we provide a comparison of the structural coverage of each of the fragment libraries. Second, we show how pooling the PDB and Dynameomics fragment libraries into a combined set of fragments can inform prediction algorithms to improve the overall results for predictions of loops in crystal structures compared with the PDB alone. Finally, we present examples where fragments from the Dynameomics library better predict loops in NMR structures than fragments from crystal structures.
Table 1.
Descriptions and abbreviations for the six fragment libraries generated for our analysis.
| Fragment libraries | ||||
|---|---|---|---|---|
| Abbreviation | Number of unique chains | Number of structures | Number of fragments | Description |
| DYN298 | 807 | 42,068 | 105,112,513 | Dynameomics simulations run at 298K. Structures sampled at 1ns intervals for entire duration of each simulation. |
| DYN498 | 807 | 240,814 | 603,915,700 | Dynameomics simulations run at 498K. Structures sampled at 100ps intervals for last 15ns of each simulation. |
| DYNall | 807 | 282,882 | 709,028,213 | This is a virtual library comprised of the DYN298 and DYN498 libraries. |
| DYNstart | 807 | 807 | 1,996,160 | Starting structure of each Dynameomics simulation. Structures are solvated and minimized. |
| PDBxtal | 23,144 | 23,144 | 99,193,499 | Crystal structures from the PDB. Structures were chosen using a PISCES query as described in the text. |
| PDBnmr | 5,412 | 100,973 | 180,437,054 | NMR spectroscopy structures from the PDB. Structures were chosen using parameters described in the text. |
Our results are based on an IC method we developed for efficiently searching, ranking and comparing fragment structures. When comparing fragment structures against one another or a gap, the peptides were aligned using only the end, or anchor, residues of the fragment or gap.
Comparison of fragment libraries
The Dynameomics project contains native MD simulations of 807 fold representatives which, as determined during the development of our consensus domain dictionary,18 represent 97% of all known autonomous protein folds. In addition, we have multiple thermal unfolding simulations for each of the 807 proteins. By capturing the dynamics of these proteins using simulations, fragments generated from the relatively small number of 807 proteins can represent nearly all fragment structures in the PDB. To confirm, we first compared the library of Dynameomics starting structures (DYNstart, which is comprised of 576 crystal structures and 231 NMR structures) to the library generated from a broad subset of crystal structures in the PDB (PDBxtal), detailed in Table 1. We represented each of the fragment libraries as a histogram and calculated statistics for the intersections and unions of the overlapping histograms (Fig. 1).
Figure 1.
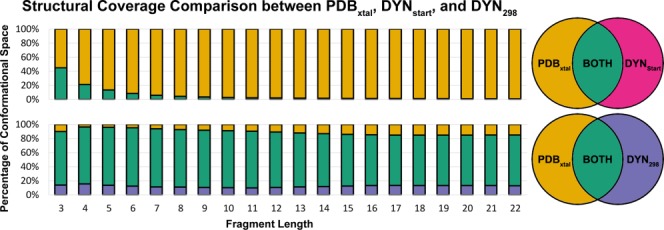
Comparison of structural coverage between fragments generated from crystal structures and native state Dynameomics structures. The colors in the chart correspond to the Venn diagrams on the right. (a) This chart shows the percentage of conformational space shared between the DYNstart fragment library and the PDBxtal fragment library. The DYNstart library only contains a significant number of representatives at short fragment lengths. (b) This chart shows the percentage of conformational space shared between the DYN298 fragment library and PDBxtal fragment library. For all fragment lengths, roughly 80% of the conformational space is shared by the two fragment libraries.
The fragments generated from the 807 static starting structures cover a small portion of the overall fragment conformational space of the 23,144 proteins in the PDBxtal fragment library (Fig. 1). Aside from very short peptides comprised of a few residues, the DYNstart set captured little of the structural diversity of fragments in the PDBxtal library. The DYN298 set contains the structures for the 807 proteins simulated over time at 298 K. The coverage of the DYN298 fragment library was much more comprehensive due to the incorporation of native state dynamics. Figure 1 shows that the coverage for the DYN298 and PDBxtal libraries was very similar. This confirms that the simulations of Dynameomics domain representatives provided excellent coverage of PDB structures despite using only 1/30th of the number of unique experimental structures.
We next compared fragment structural coverage between the PDBxtal, PDBnmr, and DYNall fragment libraries. The DYNall library contains the DYN298 set as well as structures from high temperature (498 K) unfolding simulations of the 807 proteins, referred to as the DYN498 set. Most of the conformational space was shared between the three libraries for all residue lengths (see Fig. 2). From the breakdown of the libraries, the majority was comprised of the unique DYNall conformations and conformations shared between the PDBnmr and the DYNall fragment libraries. On average, 13% of the known conformational space was represented only in the DYNall and PDBnmr fragment libraries, meaning these experimentally derived conformations are modeled by Dynameomics but are not contained within the crystal structures in the PDB.
Figure 2.
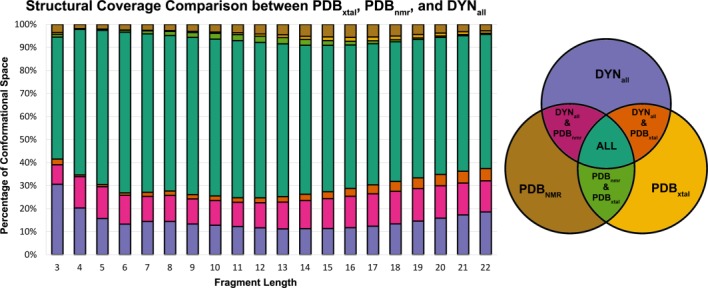
Comparison of structural coverage between fragments generated from crystal structures, NMR structures, and Dynameomics structures. We show the DYNall library here because fragments from both native-state and unfolding simulations provide informative conformations for loop predictions. The colors in the chart correspond to the Venn diagram on the right. The magenta area corresponds to the percentage of histogram bins that are shared between the PDBnmr and DYNall fragment libraries, but do not contain representatives from the PDBxtal fragment library.
Evaluation of MD fragments for improving prediction
To compare the quality of loop structure predictions between different fragment sources, we made structure predictions using each of the PDBxtal, DYN298, and DYN498 libraries. We used a standard benchmark loop test set compiled by Choi and Deane that consists of 510 target loop regions.11 These loop regions are located between two secondary structure regions and range in length from 4 to 20 residues. There are 30 unique loop samples for each loop length. The predictions of the 510 loops were generated and then scored and ranked by the IC scoring metric, as outlined in the Methods section. Loops with steric clashes with the protein were discarded. The ranked predictions were then compared with the known structures by heavy-atom (N, O, C, Cα) root-mean-square deviation (RMSD) and predictions using homologous structures were removed using a sequence similarity metric, as described in the Methods Section. Supporting Information Table SI shows the average main-chain heavy-atom RMSD and standard deviation over the best predictions for each loop length. The best prediction is the fragment with the lowest heavy-atom RMSD in the search result set generated for each target and the average is over the best prediction for each of the 30 loops for each fragment length.
We performed this test individually on the PDBxtal, DYN298, and DYN498 fragment libraries, as well as a pooled, combined set containing all three fragment libraries. The PDBxtal fragment library on average had the lowest RMSD scores for the best prediction metrics. However, this average was not representative of each individual predicted loop structure. A substantial number of the 510 loop structures were best predicted with one of the two Dynameomics-based fragment libraries. Figure 3 shows how many of the 30 best-performing predictions originated from each repository. Over the entire set of 510 loop structures, 47% originated from Dynameomics fragment libraries and 53% originated from the PDBxtal fragment library. The average improvement in RMSD upon inclusion of the Dynameomics fragment libraries is listed in the bottom-right of Figure 3. Loops with a length of 20 residues had the highest proportion of best predictions originating from Dynameomics, with 73% originating from Dynameomics fragment libraries (27% from DYN298 and 47% from DYN498) and 27% originating from the PDBxtal fragment library. Predictions for 20 residue loops had an average improved RMSD of 2.53Å over their counterparts originating from the PDBxtal library. Overall given that ∼25–75% of the best solutions came from the Dynameomics set, the average RMSD is lower for all fragment lengths using the combined fragment library.
Figure 3.
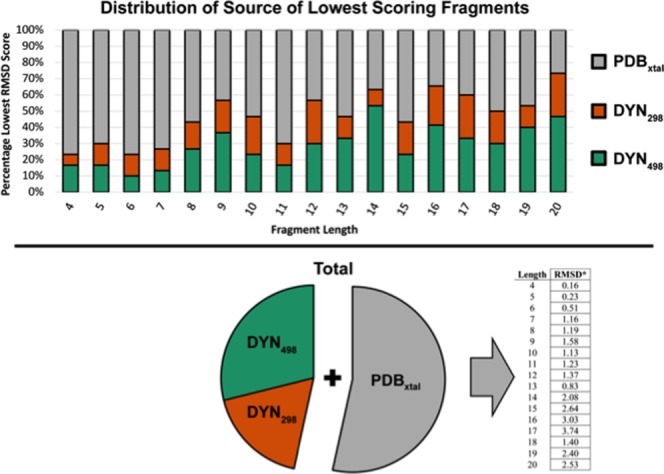
Distributions of the best scoring fragment predictions for all target loops in the 510 standard set. The top histogram shows the percentage of best predictions that are sourced from the PDBxtal, DYN298 and DYN498 fragment libraries for each loop length. The total distribution for all 510 targets is shown in the pie chart. The improvement in the average main chain heavy-atom RMSD by inclusion of the Dynameomics data set is provided on the bottom right per fragment length, in Å. Given that ∼25–75% of the best solutions came from the Dynameomics set, the average RMSD is lower for all fragment lengths using the combined fragment library.
Searching across all three repositories simultaneously results in a combined set or both static structures from the PDB and the snapshots at room and elevated temperature from MD. The PDBxtal, DYN298, and DYN498 repositories first provide a result set for each target loop using the IC method, then these result sets are combined to provide a best overall prediction. The average heavy-atom RMSD and standard deviation is shown in the last two columns of Supporting Information Table SI. Due to the contributions of the DYN298, and DYN498 libraries, the combined set outperforms all other libraries for every loop length. This improvement is quantified in Figure 3. Also note that no refinement of the predicted loops was performed. Further improvement would be expected through energy minimization, MD or other established methods, but here our focus is on description of the methods and libraries and the effect of the improved sampling on generation of starting main chain structures of loops.
Case studies of improved prediction
To investigate the quality of our prediction methods for solvated structures, we identified loops in NMR ensembles with a large number of experimental Nuclear Overhauser Effect (NOE) crosspeaks so we could quantitatively evaluate our predictions. Here we present two examples of prediction of loops within NMR structures that were best modeled by fragments in the DYN298 fragment library. These loop structures and the associated predictions are shown in Figure 4. The NMR structure is in grey, the fragment sourced from the PDBxtal library is in red, and the fragment sourced from the DYN298 library is in blue. A loop structure of 12 residues is shown in Figure 4(a). Here the PDBxtal fragment had an RMSD of 3.4 Å and NOE fulfillment of 61% while the DYN298 fragment had an RMSD of 1.9 Å and NOE fulfillment of 79%. Similarly, in Figure 4(b) depicting a loop structure of 15 residues, the PDBxtal fragment had an RMSD of 4.5 Å and NOE fulfillment of 66% while the DYN298 fragment had an RMSD of 1.3 Å and NOE fulfillment of 91%. The DYN298 predicted fragment satisfies the same percentage of NOEs as the NMR derived structure. Notably, for NOEs that were not satisfied, the PDBxtal structures have much larger average violations. In both cases, the DYN298 prediction outperforms the PDBxtal prediction in both heavy-atom RMSD and NOE satisfaction. Also, in both cases the best prediction is also the top-ranked, structure-blind prediction using the IC scoring metric (see the distributions of the RMSDs for the predicted fragments in Fig. 4). It’s notable that for the longer fragment in Figure 4(b) that the bulk of the PDB predictions are ≥ 9 Å, while the bulk of the Dynameomics library derived predictions are below 9 Å, with many below 3 Å. In particular, for the 12 residue 1NWD loop, the Dynameomics set contributes 9 fragments with main chain RMSD of ≤ 3.5 Å while the PDB set contributes only 2. In the case of the 15 residue 1PS2 loop, Dynameomics contributed 24 predictions within 3.5 Å of the target while the PDB set did not contribute any.
Figure 4.
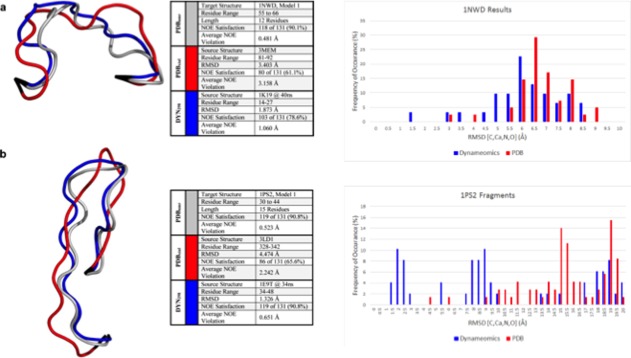
Predictions of loops in NMR structures. The NMR structures are depicted in grey, the crystal predictions in red, the Dynameomics predictions in blue, and anchor residues in black. RMSD and NOE results do not include anchor residues in the calculations. The best prediction in each case is displayed and information regarding the source and statistics are given in the table. In addition, histograms showing the distributions of the predictions with respect to how well they model the experimental loop conformation are provided for both proteins and the best predictions come from the Dynameomics dataset. (a) A 12 residue structure in 1NWD, not including anchor residues. (b) A 15 residue loop structure in 1PS2, not including anchor residues.
Discussion
There is a long history of utilizing fragment libraries in full protein structure prediction, loop prediction, and building NMR structures.21–30 Here we build on previous work and evaluated the utility of Dynameomics structural fragments in predicting loop regions of proteins. Our primary goal was to develop methods and data models to efficiently access and analyze the large numbers of fragments in both the MD and experimental structure repositories. We desired to identify the underlying differences in fragment conformations between the Dynameomics and PDB repositories and in what contexts the Dynameomics fragments are applicable to loop prediction.
From Figure 1 it follows that the collection of native state Dynameomics structures contains fragments with conformational coverage similar to that of the crystal-derived fragments from the PDB. The fragments generated only from the Dynameomics starting structures have extremely poor coverage as compared to the PDBxtal fragment library. Although these structures are representative of most of the known protein folds, it is only through MD that the resulting fragments exhibit a wide range of relevant conformations. Since the sequence variability in Dynameomics fragments is low relative to the PDBxtal fragments, sequence similarity is not needed in order to make accurate structure predictions with Dynameomics fragments.
Dynameomics contains fragment conformations that are also found in solvated NMR structures, but are not commonly identified through X-ray crystallography methods. This is apparent from the overlapping PDBnmr and DYNall regions colored in magenta in Figure 2, representing multidimensional histogram bin overlaps as described in the Methods Section. After investigating the locality of these regions in conformational space, we found that they occur in the outer layers and extended tail of the multidimensional histograms. These bins may contain more transient and flexible conformations, which is characteristic of solvated loops. This implies that Dynameomics structures capture flexible conformations, as in NMR structures, that X-ray crystallography methods do not account for adequately.
Predictions from the combined set of PDBxtal and Dynameomics fragment libraries are better than predictions from either individual library, as shown in Figure 3 and Supporting Information Table SI. Dynameomics fragments can therefore provide additional structural information for fragment-based methods and improve loop structure predictions. Notably all results have overall high standard deviations. This is due to the spread between good predictions and bad predictions; predictions are either extremely similar to the actual loop or fall into a broad distribution of high-scoring predictions, causing the high deviation from the average RMSD.
Finally, we show that Dynameomics outperforms predictions from the PDBxtal for both NMR structures in Figure 4. The DYN298 predictions deliver lower RMSD scores and higher NOE satisfaction rates as compared to the PDBxtal predictions. Furthermore, the average violation for unsatisfied NOEs is much higher for the PDBxtal predictions. That the Dynameomics-derived fragments can improve both the NMR predictions and loop predictions in general is interesting in light of Levy and co-workers work.31 They concluded that the coverage of short fragments from the PDB was sufficient to account for novel folds. Our results are in line with this, in general, but show that the inclusion of Dynameomics fragments improves the accuracy of longer loops and situations lacking sequence homology.
The methods and data models we developed work for either MD or experimental structure repositories. There are several advantages to these methods and models that make them advantageous for big data architectures. First, ICs, unlike Cartesian coordinates, do not require alignment calculations as they are already intrinsically aligned. The necessary computational power for large-scale comparisons is therefore vastly reduced. Second, ICs naturally work with Structured Query Language (SQL) filters to obtain small, relevant result sets quickly and efficiently instead of performing the all-by-all matrix used in conventional methods. Third, the data model does not require explicit storage of Cartesian coordinates, but only the pre-calculated distances between atoms required for the IC method. This lends itself well to distributed architectures such as Dynameomics and is easily applied to repositories such as the PDB. Due to the flexibility of these approaches, fragment libraries can be created from any structure repository and searches can be run on one or many of the libraries simultaneously.
The Dynameomics fragment library is explicitly linked to the Dynameomics data warehouse. As such, a variety of analyses described in detail by van Der Kamp et al.8 are also easily accessible. Of particular interest may be the solvent accessible surface area analysis, which provides additional context-specific information for generation of protein surface loop ensembles.32 Flexibility analysis33 may prove beneficial for predicting highly flexible protein structures such as intrinsically disordered regions. Side-chain conformations for fragment backbones can be predicted using the linked Dynameomics rotamer libraries34 (and S. Rysavy, C. Towse, V. Daggett, unpublished data). Furthermore, additional high-resolution dynamic structures in the Dynameomics data warehouse are readily accessible to the fragment data model, providing an expedient method for fine-tuning of fragment structures.
We have developed a web-based tool for users to build loops in PDB structures from our fragment libraries. These structures can subsequently be refined with energy-based methods using our in lucem molecular mechanics package,35 or other existing refinement methods. For the latter, we have developed web services so that our libraries can be programmatically accessed and implemented within independent software programs. The libraries, web tool, web services, and example code can be found at http://www.dynameomics.org/fragments.
Methods and Materials
Protein structure collections and fragment libraries
We created six libraries of fragment structures for analysis. These libraries originated from two distinct sources of protein structures: experimentally derived structures and MD derived structures. Two of the libraries were generated from the largest repository of experimentally derived structures, the PDB. The remaining four libraries, representing MD structures, were generated from the Dynameomics data warehouse. Descriptions and statistics for each of the resulting fragment libraries are shown in Table 1. Fragments of length 3 to 22 residues were generated for each library to support structure predictions of 1–20 residues in length.
The first library of experimental fragments, abbreviated PDBxtal, was extracted from the majority of crystal PDB structures using a PISCES36 query to filter out low-quality structures. The query specified a sequence identity of 95% or less, a resolution better than 2.7Å, and an R-factor of 0.3 or less, resulting in approximately 23.1 × 103 protein structures. The second set, abbreviated PDBnmr, was extracted from the majority of NMR spectroscopy-derived PDB structures using similar constraints of sequence identity of 95% or less, a minimum length of 40 residues, and deposits had to include experimental data. All models for each NMR structure were included. This query resulted in approximately 100.9 × 103 NMR structures.
The Dynameomics project, which was created to represent the dynamic ensembles of a vast diversity of structural folds in proteins,19 was used as the source repository of MD structures.20,37 For this specific analysis we used the Dynameomics v2009 Release Set18 which contains structural representatives of 95% of the known autonomous protein folds. This set contains 807 distinct protein targets (http://www.dynameomics.org). These proteins were simulated using ilmm (in lucem molecular mechanics),35 which employs the Levitt et al. force field38 and uses explicit F3C water molecules39,40 in the simulation. All Dynameomics target structures were simulated a minimum of one time at 298 K and twice at 498 K, with each simulation running for at least 51 ns. The atomic coordinates of these structures were recorded at 1 ps granularity and stored in the Dynameomics data warehouse.8 More details regarding the simulation protocols can be found elsewhere.17,26
We generated four fragment libraries from Dynameomics. The DYN298 library contains fragments from the native state simulations run at 298 K and is used as a direct comparison to the PDBxtal library. The DYN498 library contains fragments from the unfolding simulations run at 498 K and is used to capture more conformational variety. The DYNstart library contains fragments from the minimized starting structures of the 807 Dynameomics targets. Finally, the DYNall is the combination of both the DYN298 and DYN498 libraries.
Since Dynameomics structures within a simulation are time-dependent, we did not generate fragments from every structure. Sampling fragments at every time point is largely redundant for the applications presented in this manuscript since little structural variation occurs within a fragment for short sampling intervals. For the native state simulations, we generated fragments from structures at 1 ns intervals to optimize conformational variability while minimizing computer resources. For the unfolding simulations, we sampled at a higher rate of 100 ps due to the increased motion of the proteins in high-temperature simulations, and the structures were retrieved from the last 15 ns of the unfolding simulations.
Internal coordinate scoring
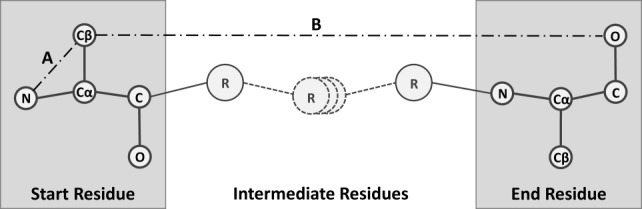
To scale fragment search, retrieval, and matching to a large, distributed structural repository, it is advantageous to pre-process the coordinate data of protein structures and represent the fragment conformations with minimal information loss. We characterized the structure of protein backbone fragments and gaps using ICs. This method is derived from a Cartesian coordinate representation instead of the commonly used torsion angle representation, as suggested by Holmes and Tsai.41 Using an IC representation that we previously briefly introduced,8 the inter-residue and intra-residue distances between the five heavy atoms of each terminal residue of the fragment or gap represent a unique structural identifier. More explicitly, this identifier is comprised of 45 distances between each residue’s N, O, C, Cα, and Cβ atoms as shown in Figure 5. Specific distances are referred to using the convention Xs-to-Xe, where Xs represents the starting residue’s X atom and Xe represents the ending residue’s X atom. Starting and ending residues are determined using a backbone’s N-Terminus to C-Terminus directionality.
Figure 5.
Abstract depiction of fragment. Ten heavy atoms are involved in the end-to-end distance definitions. There are 20 intra-residue distances (a) and 25 inter-residue distances (b). One or more amino acids can exist as intermediate residues in the peptide structure.
A single-valued IC score was used to evaluate the similarity between two fragments or the fit of a fragment to a gap in a protein structure. This IC score was calculated using a RMSD calculation
| (1) |
where xi and yi are equivalent IC atom-atom distance pairs from the fragment and gap being compared and D is the number of distance in each fragment or gap. Since the distances are relative to the end residues, no alignment is necessary before calculating the IC score between fragments or gaps.
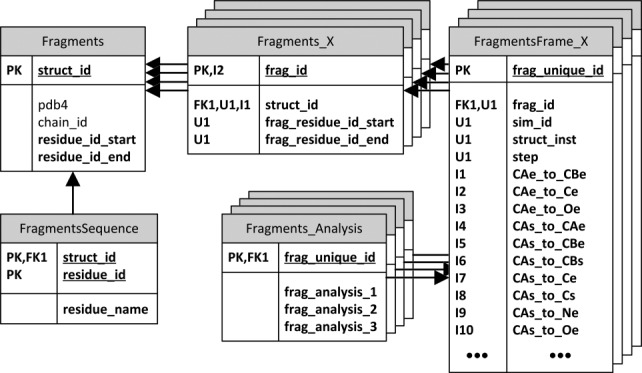
Fragment database schema
The fragment database schema integrates into the Dynameomics data warehouse architecture while supporting efficient fragment searching and filtering using the IC distances and the IC score. A simplified schema for a Dynameomics-based fragment collection is shown in Figure 6. The Fragments table stores metadata about the source protein structure for retrieval of the original PDB file or Dynameomics simulation. The fragments themselves are defined with a combination of two table types, Fragments_X and FragmentsFrame_X, where X denotes the length of fragments contained in the respective table combination. The Fragments_X table defines a unique fragment per individual protein structure. The FragmentsFrame_X table defines a unique instance of each structural fragment (i.e. individual conformations of an individual fragment’s dynamic motion) along with each fragment instances’ IC distances. The fragment frame unique identifier is unique among all fragment lengths within a fragment repository. Additional, fragment-specific analysis can be easily added through the generic, extensible Fragments_Analysis table definition.
Figure 6.
Schema of generic fragment library database. Tables are represented as boxes and foreign key (FK) to primary key (PK) relationships are represented as arrows. Unique identifiers (Ux) and indexes (Ix) are also listed. The X term denotes fragment length.
Fragments can be filtered on any combination of or all individual IC distances. This filtering is implemented by including a range of desired distance thresholds in the SQL query WHERE clause per individual IC distances. The IC score is calculated per result row using an inline SQL function. Every IC distance is indexed within each FragmentsFrame_X table to accelerate the filtering process.
Fragment identification and retrieval
Our fragment libraries were designed to provide structurally relevant fragments based on their IC profile. Anchor residues are first identified in the protein structure of interest and the corresponding IC profile of those anchor residues is calculated. A query is then generated for a fragment repository, calculating the RMSDIC for all fragments of a specified length that also contain IC distances within the specified distance threshold. The default threshold is 1.5 Å to accommodate common bond variance, but the threshold can be specified at query time. The number of results retrieved is adjustable; we specified the top 200 fragments for all results presented in this article. This query runs several orders of magnitude faster than the naïve approach, as is shown in Supporting Information Figure S2.
The query provides a collection of fragments enumerated by unique fragment identifications as defined in the fragment repository schema. For Dynameomics fragments, this unique identifier corresponds to a unique tuple consisting of a simulation identifier, structure identifier, structure instance, time step, starting residue and length. In the case of a PDB fragment, the unique tuple consists of a PDB code, chain identifier, model number, starting residue and length. In both cases, this information is sufficient to retrieve a unique fragment structure from either the Dynameomics data warehouse or PDB, respectively.
The fragment retrieval operation returns the coordinates of the heavy atoms (N, O, C, Cα, and Cβ) in a polyalanine peptide representation generated from the backbone of the source structure. Alanines are used to retain the Cβ coordinate information and first chi dihedral angle for improved side-chain attachment. In the case of Glycine residues, the Cβ coordinates are estimated using the chiral-appropriate hydrogen atom attached to the Cα.
Fragment insertion
Two related but distinct methods can be used for the insertion of fragment structures into the protein structure of interest as shown in Figure 7. The first method is intended to fill a gap in an existing structure with a relevant fragment or collection of relevant fragments. The second method was developed to extend the termini of existing protein structures. Both methods take advantage of the IC profile to search existing fragment structures in the fragment repositories.
Figure 7.
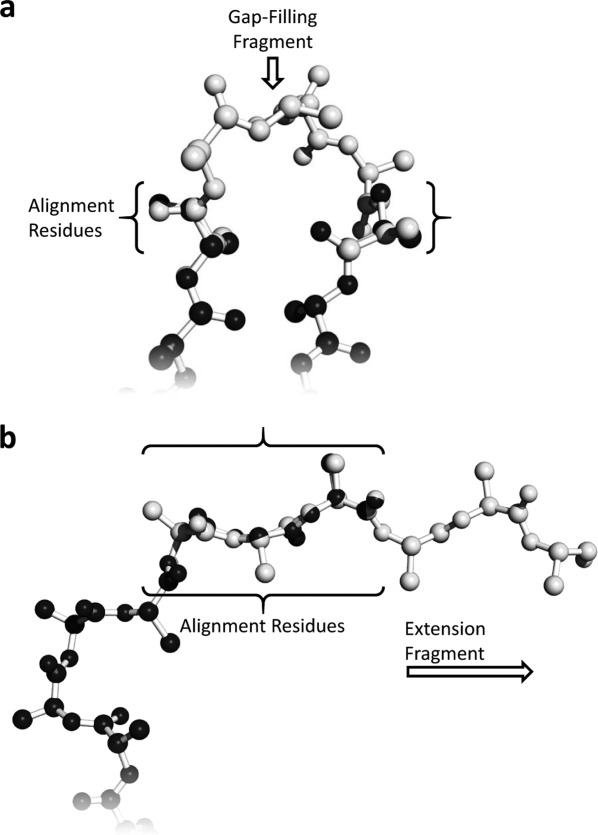
Depictions of anchor residue alignments for fragment attachment. (a) Two anchor residues are used for gap-filling fragment insertions. (b) Three anchor residues are used for extension fragments.
Gap-filling fragment queries use the IC profile of the gap anchor residues. Fragment results are aligned by matching the fragment anchor residues with the gap anchor residues using a heavy atom alignment of the five heavy atoms in each end-residue (N, O, C, Cα, and Cβ). Extension fragment queries use the IC profile of the terminal three residue fragment of the N- or C-terminus. Fragments retrieved for extending a C- or N-terminus were aligned using the three end residues of the protein structure of interest and the corresponding side-chain conformations can optionally be included using the Dynameomics rotamer libraries.23
Fragment evaluation
Loop predictions represent fragments retrieved from the Dynameomics libraries that have been ranked and scored using the IC metric. To evaluate the predictions of the 510 loop set of Choi and Deane11 homologous proteins were excluded, as described below, and the predicted loops were then compared with the known structures by calculating the RMSD over all backbone heavy atoms (N, Cα, C, O,) of the internal residues of the fragment. The anchor residues were not included in these metrics. All backbone heavy atoms were checked for steric clashes with the destination structure atoms. Side-chain conformations were not incorporated in the evaluations in this manuscript as we were focused solely on backbone conformations. In all instances, predictions are never made using fragments sourced from the same structure as the target structure or any MD-generated derivative structure of the target structure.
All fragments sourced from structures with high sequence similarity to the target structure were eliminated from consideration for predictions. This was done to prevent biased results due to fragments being sourced from homologous or identical proteins. Note that Choi and Deane11 did not remove homologous proteins in evaluating their predictions, which improves the predictions, but we wanted an unbiased comparison to assess the ability of the Dynameomics library to aid in the prediction of structures when homologous proteins are not available. In order to allow the search algorithm to perform as intended and identify similar fragments from non-homologous sources, we assessed sequence similarity at the protein chain level. Structures containing 50% or greater sequence similarity to the target loop’s originating structure were eliminated from the search results for that target loop. This evaluation was done on a per-target basis. We integrated the .NET Bio software package to perform the alignments using the Needleman-Wunsch algorithm and calculate the sequence similarity metric using the PAM250 substitution matrix.42,43 The sequence identities in the predictions from the three libraries for the 510 loop set including and omitting homologous proteins are provided in Supporting Information Figure S3.
Evaluations of loop structure predictions were also performed against NMR ensembles using NOE data. In these instances, we only considered NOEs containing at least one atom within the backbone of the target range. NOEs between side-chain atoms in this range and atoms outside of the target range were not considered. NOEs between atom-pairs altogether outside of the target range were also not considered as these would evaluate identically between candidates.
Representing structural diversity in fragment libraries
In order to analyze the structural distribution of the fragment populations in each library, we needed a method to programmatically represent the conformational space. To do this, we used multidimensional histograms as a computationally efficient method of clustering. These also lend themselves well to comparison due to the common bin definitions between different histograms. Fragments were binned using a subset of the end-to-end distances, which were selected to maximize the overall fragment structure representation while keeping correlation between the selected distances to a minimum. These distances were identified using principal component analysis (PCA) as described in the Supporting Information. The resulting histogram bins contain clusters of similarly structured fragments.
The specific distances we used in our histograms were Cβs-to-Cβe, Os-to-Ne, and CBs-to-CAe. These distances most often had the highest correlation with the first three principal components and the percentage of variance captured was 84.4–99.4% so no additional distances were needed (see Supporting Information, Table SII). This finding was consistent across the majority of fragment lengths in each repository. We used a histogram bin size of 0.1 Å as these results in computationally manageable histogram sizes while maintaining a valid representation of the structural diversity in the fragments.
Comparison of fragment libraries
We compared the histogram data for pairs or triplets of fragment repositories to evaluate the coverage of fragment structures in each repository. Since each histogram bin represents a cluster of similarly structured fragments, we were able to simplify each histogram bin representative to a binary value. A bin containing two or more fragments was considered to be filled while a bin containing one or fewer representative fragments was considered empty.
The sets of binary histogram bins from different repositories were aligned to complete the comparison. Bins with the same distance thresholds were considered to be in alignment between datasets. Four outcomes were possible for each bin when comparing two repositories: both repositories contain a representative fragment, only the first repository contains a representative fragment, only the second repository contains a representative fragment, or neither repository contains a representative fragment. When comparing three repositories, eight outcomes are possible for each bin. In this way we can quickly ascertain which fragment structures exist in each of the fragment collections. This technique was used for the repository comparisons in the results section.
Acknowledgments
We are grateful for financial support provided by Microsoft through the External Research Program at Microsoft Research (http://www.microsoft.com/science) (to V.D.), by the National Institutes of Health (GM50789 to V.D.), and by the National Library of Medicine (5T15LM007442 to S.J.R.). Dynameomics simulations were performed using computer time through the DOE Office of Biological Research as provided by the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-05CH11231.
Supporting Information
Additional Supporting Information may be found in the online version of this article.
References
- Wu S-J, Dean DH. Functional significance of loops in the receptor binding domain of Bacillus thuringiensis CryIIIA δ-endotoxin. J Mol Biol. 1996;255:628–640. doi: 10.1006/jmbi.1996.0052. [DOI] [PubMed] [Google Scholar]
- Fetrow JS. Omega loops: nonregular secondary structures significant in protein function and stability. FASEB J. 1995;9:708–717. [PubMed] [Google Scholar]
- Leszczynski JF, Rose GD. Loops in globular proteins: a novel category of secondary structure. Science. 1986;234:849–855. doi: 10.1126/science.3775366. [DOI] [PubMed] [Google Scholar]
- Spronk CAEM, Nabuurs SB, Krieger E, Vriend G, Vuister GW. Validation of protein structures derived by NMR spectroscopy. Prog Nucl Magnet Reson Spectro. 2004;45:315–337. [Google Scholar]
- Eicken C, Sharma V, Klabunde T, Lawrenz MB, Hardham JM, Norris SJ, Sacchettini JC. Crystal structure of Lyme disease variable surface antigen VlsE of Borrelia burgdorferi. J Biol Chem. 2002;277:21691–21696. doi: 10.1074/jbc.M201547200. [DOI] [PubMed] [Google Scholar]
- Wagner G, Hyberts SG, Havel TF. NMR structure determination in solution: a critique and comparison with X-ray crystallography. Ann Rev Biophys Biomol Struct. 1992;21:167–198. doi: 10.1146/annurev.bb.21.060192.001123. [DOI] [PubMed] [Google Scholar]
- Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucl Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Kamp MW, Schaeffer RD, Jonsson AL, Scouras AD, Simms AM, Toofanny RD, Benson NC, Anderson PC, Merkley ED, Rysavy S, Bromley D, Beck DAC, Daggett V. Dynameomics: a comprehensive database of protein dynamics. Structure. 2010;18:423–435. doi: 10.1016/j.str.2010.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verschueren E, Vanhee P, van der Sloot AM, Serrano L, Rousseau F, Schymkowitz J. Protein design with fragment databases. Curr Opin Struct Biol. 2011;21:452–459. doi: 10.1016/j.sbi.2011.05.002. [DOI] [PubMed] [Google Scholar]
- Baeten L, Reumers J, Tur V, Stricher F, Lenaerts T, Serrano L, Rousseau F, Schymkowitz J. Reconstruction of protein backbones from the BriX collection of canonical protein fragments. PLoS Comput Biol. 2008;4:e1000083. doi: 10.1371/journal.pcbi.1000083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi Y, Deane CM. FREAD revisited: accurate loop structure prediction using a database search algorithm. Proteins. 2010;78:1431–1440. doi: 10.1002/prot.22658. [DOI] [PubMed] [Google Scholar]
- Vanhee P, Verschueren E, Baeten L, Stricher F, Serrano L, Rousseau F, Schymkowitz J. BriX: a database of protein building blocks for structural analysis, modeling and design. Nucl Acids Res. 2011;39:D435–D442. doi: 10.1093/nar/gkq972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Søndergaard CR, Garrett AE, Carstensen T, Pollastri G, Nielsen JE. Structural artifacts in protein−ligand X-ray structures: implications for the development of docking scoring functions. J Med Chem. 2009;52:5673–5684. doi: 10.1021/jm8016464. [DOI] [PubMed] [Google Scholar]
- Jacobson MP, Friesner RA, Xiang Z, Honig B. On the role of the crystal environment in determining protein side-chain conformations. J Mol Biol. 2002;320:597–608. doi: 10.1016/s0022-2836(02)00470-9. [DOI] [PubMed] [Google Scholar]
- Cino EA, Choy W-Y, Karttunen M. Comparison of secondary structure formation using 10 different force fields in microsecond molecular dynamics simulations. J Chem Theory Comput. 2012;8:2725–2740. doi: 10.1021/ct300323g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beauchamp KA, Lin Y-S, Das R, Pande VS. Are protein force fields getting better? A systematic benchmark on 524 diverse NMR measurements. J Chem Theory Comput. 2012;8:1409–1414. doi: 10.1021/ct2007814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck DAC, Jonsson AL, Schaeffer RD, Scott KA, Day R, Toofanny RD, Alonso DOV, Daggett V. Dynameomics: mass annotation of protein dynamics and unfolding in water by high-throughput atomistic molecular dynamics simulations. Protein Engin Des Sel. 2008;21:353–368. doi: 10.1093/protein/gzn011. [DOI] [PubMed] [Google Scholar]
- Schaeffer RD, Jonsson AL, Simms AM, Daggett V. Generation of a consensus protein domain dictionary. Bioinformatics. 2011;27:46–54. doi: 10.1093/bioinformatics/btq625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day R, Beck DAC, Armen RS, Daggett V. A consensus view of fold space: combining SCOP, CATH, and the Dali Domain Dictionary. Protein Sci. 2003;12:2150–2160. doi: 10.1110/ps.0306803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simms AM, Toofanny RD, Kehl C, Benson NC, Daggett V. Dynameomics: design of a computational lab workflow and scientific data repository for protein simulations. Protein Engin Des Sel. 2008;21:369–377. doi: 10.1093/protein/gzn012. [DOI] [PubMed] [Google Scholar]
- Reid LS, Thornton JM. Rebuilding flavodoxin from C alpha coordinates: a test study. Proteins. 1989;5:170–182. doi: 10.1002/prot.340050212. [DOI] [PubMed] [Google Scholar]
- Jones TA, Thirup S. Using known substructures in protein model building and crystallography. EMBO J. 1986;5:819–822. doi: 10.1002/j.1460-2075.1986.tb04287.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Summers NL, Karplus M. Modeling of globular proteins. A distance-based data search procedure for the construction of insertion/deletion regions and Pro–non-Pro mutations. J Mol Biol. 1990;216:991–1016. doi: 10.1016/S0022-2836(99)80016-3. [DOI] [PubMed] [Google Scholar]
- Holm L, Sander C. Database algorithm for generating protein backbone and side-chain co-ordinates from a C alpha trace application to model building and detection of co-ordinate errors. J Mol Biol. 1991;218:183–194. doi: 10.1016/0022-2836(91)90883-8. [DOI] [PubMed] [Google Scholar]
- Levitt M. Accurate modelling of protein conformation by automatic segment matching. J Mol Biol. 1992;226:507–533. doi: 10.1016/0022-2836(92)90964-l. [DOI] [PubMed] [Google Scholar]
- Simons K, Kooperberg C, Huang E, Baker D. Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J Mol Biol. 1997;268:209–225. doi: 10.1006/jmbi.1997.0959. [DOI] [PubMed] [Google Scholar]
- van Vlijmen HWT, Karplus M. PDB-based protein loop prediction: parameters for selection and methods for optimization. J Mol Biol. 1997;267:975–1001. doi: 10.1006/jmbi.1996.0857. [DOI] [PubMed] [Google Scholar]
- Kolodny R, Koehl P, Guibas L, Levitt M. Small libraries of protein fragments model native protein structures accurately. J Mol Biol. 2005;323:297–307. doi: 10.1016/s0022-2836(02)00942-7. [DOI] [PubMed] [Google Scholar]
- Bujnicki J. Protein structure prediction by recombination of fragments. ChemBioChem. 2006;7:19–27. doi: 10.1002/cbic.200500235. [DOI] [PubMed] [Google Scholar]
- Andrec M, Du P, Levy RM. Protein backbone structure determination using only residual dipolar couplings from one ordering medium. J Biomol NMR. 2001;21:335–347. doi: 10.1023/a:1013334513610. [DOI] [PubMed] [Google Scholar]
- Du P, Andrec M, Levy R. Have we seen all structures corresponding to short protein fragments in the Protein Data Bank? An update. Prot Engin. 2003;16:407–414. doi: 10.1093/protein/gzg052. [DOI] [PubMed] [Google Scholar]
- Shehu A, Kavraki LE. Modeling structures and motions of loops in protein molecules. Entropy. 2012;14:252–290. [Google Scholar]
- Benson NC, Daggett V. Dynameomics: large-scale assessment of native protein flexibility. Protein Sci. 2008;17:2038–2050. doi: 10.1110/ps.037473.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scouras AD, Daggett V. The dynameomics rotamer library: amino acid side chain conformations and dynamics from comprehensive molecular dynamics simulations in water. Protein Sci. 2011;20:341–352. doi: 10.1002/pro.565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G, Dunbrack RL., Jr PISCES: a protein sequence culling server. Bioinformatics. 2003;19:1589–1591. doi: 10.1093/bioinformatics/btg224. [DOI] [PubMed] [Google Scholar]
- Simms AM, Daggett V. Protein simulation data in the relational model. J Supercomput. 2012;62:150–173. doi: 10.1007/s11227-011-0692-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck DA, Daggett V. Methods for molecular dynamics simulations of protein folding/unfolding in solution. Methods. 2004;34:112–120. doi: 10.1016/j.ymeth.2004.03.008. [DOI] [PubMed] [Google Scholar]
- Levitt M, Hirshberg M, Sharon R, Daggett V. Potential energy function and parameters for simulations of the molecular dynamics of proteins and nucleic acids in solution. Comp Phys Comm. 1995;91:215–231. [Google Scholar]
- Levitt M, Hirshberg M, Sharon R, Laidig KE, Daggett V. Calibration and testing of a water model for simulation of the molecular dynamics of proteins and nucleic acids in solution. J Phys Chem B. 1997;101:5051–5061. [Google Scholar]
- Beck DA, Alonso DOV, Daggett V. A microscopic view of peptide and protein solvation. Biophys Chem. 2003;100:221–237. doi: 10.1016/s0301-4622(02)00283-1. [DOI] [PubMed] [Google Scholar]
- Holmes JB, Tsai J. Some fundamental aspects of building protein structures from fragment libraries. Protein Sci. 2004;13:1636–1650. doi: 10.1110/ps.03494504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Outercurve Foundation. NET Bio Framework. 2013. Available from: http://bio.codeplex.com/
- Needleman SB, Wunsch CDJ. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J Mol Biol. 1970;48:443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


