A hierarchy of intrinsic timescales across primate cortex

Abstract

Specialization and hierarchy are organizing principles for primate cortex, yet there is little direct evidence for how cortical areas are specialized in the temporal domain. We measured timescales of intrinsic fluctuations in spiking activity across areas, and found a hierarchical ordering, with sensory and prefrontal areas exhibiting shorter and longer timescales, respectively. Based on our findings, we suggest that intrinsic timescales reflect areal specialization for task-relevant computations over multiple temporal ranges.

Hierarchy provides a parsimonious description of various functional differences across cortical areas. For instance, spatial receptive field sizes increase along the visual hierarchy¹, and a posterior-anterior hierarchy exists for cognitive abstraction within prefrontal cortex². In the temporal domain, higher areas can activate selectively for stimuli that are coherent over longer periods of time^3,4. It remains an open question whether temporal specialization arises from a cortical area's intrinsic dynamical properties, that is, related to dynamics that exist even in the absence of direct stimulus processing. We hypothesized that differential dynamics would be manifested in the timescales of fluctuations in single-neuron spiking activity.

Variable neuronal activity is ubiquitous across the cortex^5,6, yet it has been unclear what the timescales underlying this variability are, or whether these timescales differ across areas. Neuronal activity fluctuates over a wide range of timescales with potential contributions from distinct underlying mechanisms. For example, the timescales of correlated fluctuations of activity within a local microcircuit are likely longer than the timescales timescales of single-neuron burstiness and refractoriness⁷ but shorter than the timescales of drifts in arousal. In typical electrophysiological recordings from behaving animals, spike trains from a single neuron are recorded over many trials of a task. Using single-neuron spike trains, we sought to characterize these underlying fluctuations in activity that are not locked to trial onset. To measure the timescales of these fluctuations, we used the spike-count autocorrelation for pairs of time bins separated by a time lag. The spike-count autocorrelation is calculated as the correlation coefficient between the number of spikes in each time bin across all trials (Online Methods). As the time lag increases, the autocorrelation decays according to the fluctuation timescales⁸ (Supplementary Mathematical Note).

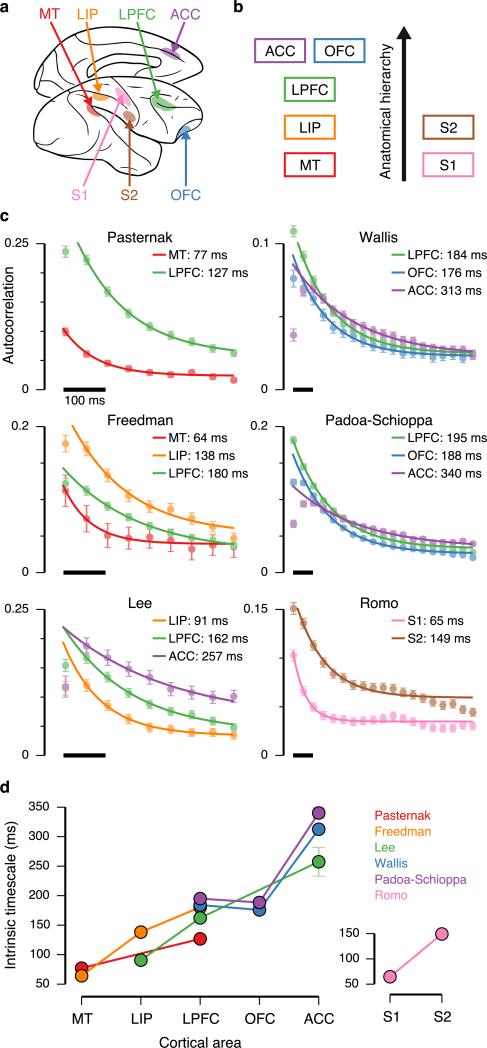
We measured intrinsic timescales using single-neuron spike trains in datasets from six research groups, recorded in a total of 26 monkeys, that include seven cortical areas (Fig. 1a). Five cortical areas are constituents of the visual–prefrontal hierarchy, including sensory, parietal association, and prefrontal cortex: medial-temporal area (MT) in visual cortex; lateral intraparietal area (LIP) in parietal association cortex; lateral prefrontal cortex (LPFC); orbitofrontal cortex (OFC); and anterior cingulate cortex (ACC). To test for generality of results outside of the visual system, we also examined two somatosensory areas: primary somatosensory cortex (S1) and secondary somatosensory cortex (S2). These areas span multiple levels of the anatomical hierarchy defined by the laminar patterns of long-range projections among cortical areas^9,10 (Fig. 1b). For each dataset, monkeys were engaged in cognitive tasks. We restricted our analysis to one epoch of the task, the foreperiod that begins each trial. During the foreperiod, the monkey was in a controlled, attentive state awaiting stimulus onset (fixation of eye position for visual tasks, lever hold for the somatosensory task). This restriction minimizes stimulus-related confounds and allows application of the same analyses across areas and datasets. This definition of intrinsic timescale does not refer to single-neuron physiology or imply that the timescale does not change with stimulus conditions.

Figure 1.

Spike-count autocorrelation reveals a hierarchical ordering of intrinsic timescales. (a) Datasets span seven cortical areas in the macaque monkey: MT, LIP, LPFC, OFC, ACC, S1, and S2. (b) Anatomical hierarchy of the areas, based on long-range projection patterns^9,10. (c) Spike-count autocorrelation was computed for neuronal spiking activity during the foreperiod of cognitive tasks. Each panel shows the dataset for one of six research groups. The decay of autocorrelation was fit by an exponential decay with an offset. Some areas in datasets show refractory adaptation at short time lags, which were excluded from the fit (Online Methods). Solid lines show the exponential fit. Intrinsic timescale extracted from the fit is shown for each area. Autocorrelation was computed with 50-ms time bins. (d) Intrinsic timescales across the visual–prefrontal hierarchy in five datasets (left), and the somatosensory hierarchy (right). Error bars mark s.e.

The decay of autocorrelation with increasing time lag could be well fit by an exponential decay with an offset (Fig. 1c). This fit was obtained at the population level, rather than single neuron level (Online Methods, and Supplementary Figs. 1 & 2), enabling us to extract an intrinsic timescale as a population-level statistic for each area in a dataset. Within each dataset, the intrinsic timescales differed across areas, in the range of 50–350 ms. Over all datasets, we found a consistent ordering of the intrinsic timescales across cortical areas (P < 10⁻⁵, r_s = 0.89, Spearman's rank correlation) (Fig. 1d). Sensory cortex showed shorter timescales, parietal association cortex showed intermediate timescales, and prefrontal cortex showed longer timescales, with medial prefrontal area ACC consistently showing the longest timescale in our datasets. Hierarchical ordering was present in both visual and somatosensory systems. Differences in intrinsic timescales could not be explained by differences in mean firing rates across areas (Supplementary Fig. 3). Interestingly, this hierarchy of intrinsic timescales aligns with the anatomical hierarchy defined by long-range projections among cortical areas^9,10, although our physiologically-defined hierarchy differs from the anatomical hierarchy for OFC (P = 0.002, r_s = 0.97, Spearman's rank correlation). The correspondence between physiological, anatomical, and functional hierarchies suggests functional importance of these timescales in large-scale cortical coordination.

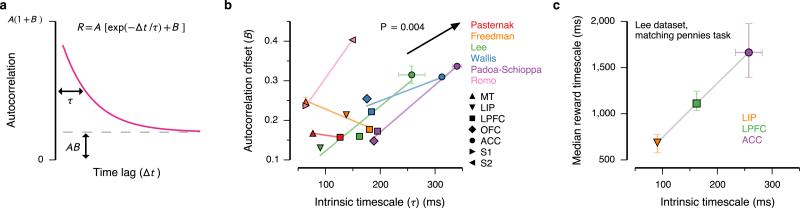
What is the potential relevance of intrinsic timescales to functions which may operate over longer timescales? We examined whether the intrinsic timescale (in the range of 50–350 ms) may be correlated with the capacity for neurons in an area to sustain signals over long behavioral timescales (e.g., 5–10 s). Neuronal fluctuations include contributions that operate over a wide range of timescales. Long timescales contribute an effective offset to the autocorrelation (Fig. 2a and Supplementary Mathematical Note). The offset can therefore reflect the strength of fluctuations at long timescales that cannot be resolved with a limited duration of the foreperiod. We found that the autocorrelation offset positively correlates with the intrinsic timescale (P = 0.004, t(9) = 3.4, t-test) (Fig. 2b). We also found that the offset reflects the strength of trial-to-trial correlations (P = 0.002, t(9) = 3.9, t-test), indicating that a portion of long-timescale variability persists across trials (Supplementary Fig. 4). These results imply that hierarchy may exist across multiple temporal ranges.

Figure 2.

Links between intrinsic timescale and longer functional timescales. (a) Autocorrelation offset (B) reflects the strength of contributions with long timescales, which do not decay substantially within the fixation epoch. (b) Autocorrelation offset increases with intrinsic timescale. Colored lines show trends for individual datasets. The arrow shows the slope of dependence from a regression analysis (slope m = 0.8 ± 0.2 kHz). (c) In the Lee dataset, we previously measured timescales characterizing the decay of modulation of single-neuron firing rates by reward events, while monkeys performed a competitive decision-making task¹¹. The ordering of areas by reward timescale aligns with the ordering by intrinsic timescale. Error bars mark s.e.

Of relevance to function, fluctuations at long timescales can include contributions from long-lasting memory traces of stimuli or task variables such as reward. In the Lee dataset, which includes areas LIP, LPFC, and ACC, we previously measured the temporal modulation of neuronal activity by reward events during a decision-making task, at the single-neuron level¹¹ (Supplementary Fig. 5). We refer to the time constant characterizing the decay of a neuron's modulation by reward as its reward timescale. Consistent with this link between intrinsic timescale and long functional timescales, the order of areas according to median reward timescale aligns with the order according to intrinsic timescale (Fig. 2c). It is noteworthy that the median reward timescale is an order of magnitude longer than the intrinsic timescale. These results support the interpretation that intrinsic timescales may reflect areal specialization for task-relevant computations over long timescales.

In summary, our physiological analyses show that cortical areas follow a hierarchical ordering in their timescales of intrinsic fluctuations. One interpretation of their functional relevance is that these timescales set the duration over which a neural circuit integrates its inputs¹². In this interpretation, shorter timescales in sensory areas enable them to rapidly detect or faithfully track dynamic stimuli^13,14. By contrast, prefrontal areas can utilize longer timescales to integrate information and improve the signal-to-noise ratio in short-term memory or decision-making computations^{12, 15}. There is known hierarchical specialization across areas at the functional level, in sensory processing and cognitive tasks^1–3.

The present study leaves as an open question what underlying mechanisms contribute to this hierarchy of intrinsic timescales. Computational models of recurrent neural circuits have demonstrated multiple potential mechanisms¹². A longer intrinsic timescale in the circuit could reflect timescales of cellular or synaptic dynamics. Consistent with this mechanism, there are interareal differences in the dynamical properties of recurrent excitatory synapses, including differential composition of glutamate receptors¹⁶, expression of short-term synaptic plasticity¹⁷, and level of neuromodulation¹⁸. Interareal differences in cellular physiology can also be driven by factors such as neuronal morphology ¹⁹. A longer timescale in the circuit could also arise from stronger synaptic connections mediating recurrent excitation, which slows intrinsic dynamics by partially canceling leak¹². There are increases across the cortical hierarchy in the number and density of excitatory synapses onto pyramidal cells²⁰, which may reflect increased recurrent strength across areas. Modeling studies have further shown that strong recurrent connections can endow a cortical circuit with the capability to exhibit persistent activity in working memory and slow accumulation of information in decision making¹⁵. A hierarchy of intrinsic timescales may link neurophysiological properties to functional specialization.

Online Methods

Datasets

All experimental methods were approved by the relevant institutional animal care and use committees. Experimental details for the datasets have been reported previously. We used single-neuron spike train data, recorded in macaque monkeys, from the foreperiod of various cognitive tasks. For the Romo dataset, the foreperiod entailed holding a lever by the free hand; for all other datasets, the foreperiod entailed fixation of eye position to a central target. Datasets were selected as they comprised multiple cortical areas, and the task foreperiod had durations of at least 500 ms with minimal task-related stimulus during the foreperiod (for visual tasks, only a fixation point on the screen). Only completed trials were analyzed. Cells and trials were filtered for further analysis by two criteria. To allow computation of spike-count autocorrelation, we required that each time bin have a non-zero mean firing rate²¹. To minimize spurious autocorrelation due to very slow drift of firing rates across the recording session, we selected the longest block of trials in which the total foreperiod spike count was statistically stationary across trials²².

The Pasternak dataset consists of neurons recorded in MT and LPFC^23–27. Monkeys compared two motion stimuli separated by a brief delay. The foreperiod duration was either 500 ms or 1,000 ms. For single neurons recorded over multiple tasks, each task-neuron pair was treated as a separate single neuron to control for task-dependent changes in foreperiod firing. Single-neuron counts were 485 from MT (2 monkeys) and 427 from LPFC (4 monkeys). The Freedman dataset contains neurons from MT, LIP, and LPFC^28,29. Monkeys performed a motion delayed match-to-category task. The foreperiod duration was 500 ms. Single-neuron counts were 59 from MT (2 monkeys), 222 from LIP (4 monkeys), and 458 from LPFC (2 monkeys). The Lee dataset consists of neurons recorded in LIP, LPFC, and ACC^30–32. Monkeys performed a competitive decision-making task called matching pennies. The foreperiod duration was 500 ms. Single-neuron counts were 192 from LIP (3 monkeys), 293 from LPFC (5 monkeys), and 146 from ACC (2 monkeys). The Wallis dataset contains neurons from LPFC, OFC, and ACC^33–35. Monkeys performed tasks involving value-based choice. The foreperiod duration was 1,000 ms. Single-neuron counts were 946 from LPFC (6 monkeys), 481 from OFC (7 monkeys), and 841 from ACC (6 monkeys). The Padoa-Schioppa dataset contains neurons from LPFC, OFC, and ACC^36–39. Monkeys performed tasks involving value-based choice. The foreperiod duration was 1,500 ms. Single-neuron counts were 1,024 from LPFC (2 monkeys), 1,768 from OFC (2 monkeys), and 987 from ACC (2 monkeys). The Romo dataset contains cells from S1 and S2⁴⁰. Two monkeys performed a vibrotactile delayed discrimination task. The foreperiod duration was variable, with a minimum of 1,400 ms. Single-neuron counts were 711 from S1 (2 monkeys) and 928 from S2 (2 monkeys).

Analysis

Our primary analysis was the temporal autocorrelation of spike counts, which we computed in the following way for single neurons. We divided the foreperiod into separate, successive time bins of duration Δ. We set Δ = 50 ms; results were similar for changes of ±20%. For two time bins, indexed by their onset times iΔ and jΔ, we computed the across-trial correlation between spike counts N in those time bins using the Pearson's correlation coefficient R:

$$\begin{array}{cc}\hfill R=& \frac{\mathrm{Cov}(N\left(i\Delta \right),N\left(j\Delta \right))}{\sqrt{\mathrm{Var}\left(N\left(i\Delta \right)\right)\times \mathrm{Var}\left(N\left(i\Delta \right)\right)}}\hfill \\ \hfill =& \frac{\langle (N\left(i\Delta \right)-\stackrel{‒}{N}\left(i\Delta \right))(N\left(j\Delta \right)-\stackrel{‒}{N}\left(j\Delta \right))\rangle }{\sqrt{\mathrm{Var}\left(N\left(i\Delta \right)\right)\times \mathrm{Var}\left(N\left(j\Delta \right)\right)}}\hfill \end{array}$$ (1)

where covariance (Cov) and variance (Var) are computed across trials for those time bins, and is the mean spike count for a particular bin. Importantly, spike-count autocorrelation corrects for nonstationarity in the mean firing rate during the foreperiod (e.g., ramping), because covariance and varience subtract the mean spike count for each time bin.

Based on our theoretical calculations for doubly stochastic processes (Supplementary Mathematical Note), the decay of autocorrelation was fit to the population of neurons within an area by an exponential decay with an offset as a function of the time lag kΔ between time bins (k = |i − j|):

$$R\left(k\Delta \right)=A\left[\exp \left(-\frac{k\Delta }{\tau }\right)+B\right]$$ (2)

where τ is the intrinsic timescale and B is the offset that reflects the contribution of timescales much longer than our observation window. Some areas in the datasets showed sign of refractoriness or negative adaptation at short time lags (Fig. 1c), which would not be captured by Equation (2). To accommodate this feature of the autocorrelation data, fitting started at the time lag with maximum decrease of the mean autocorrelation. We fit Equation 3 to the full autocorrelation data for all neurons and times; fits were therefore performed at the population level rather than single-neuron level, yielding a set of fit parameters for an area in a dataset. For the visual presentation in Fig. 1c, autocorrelation was averaged across neurons and times. Autocorrelation averaged across neurons but not time is presented in Supplementary Fig. 1, and autocorrelation averaged across time but not neurons is presented in Supplementary Fig. 2.

Equation 2 was fit to the autocorrelation data using nonlinear least-squares fitting via the Levenberg-Marquardt algorithm (through the SciPy function optimize.curve fit). The parameter covariance matrix generated by the Levenberg-Marquardt fitting procedure describes the dependence between parameters in fitting an individual area in a dataset. A positive (negative) off-diagonal term for two parameters indicates that increasing one parameter will increase (decrease) the other to optimize the fit. For most areas (11 of 16), this term had negative sign, indicating that the positive correlation in between τ and B shown in Fig. 2b was not a consequence of the fitting procedure. Standard error for fit parameters was computed by the delete-one jackknife procedure.

To test for hypothesized relationships between two measures we used a linear regression model:

$$y_d=mx+\sum _{k\in \left\{\text{datasets}\right\}}{b}_k{\delta }_{d,k}$$

where δ_d,k is a dummy variable, which is 1 for a particular dataset k and 0 otherwise. This model assumes that all datasets have a linear dependence of y on x across all datasets (m), and allows datasets to have different constant terms (b_k). The statistical significance of a regressor, in particular the dependence term m, was assessed by a t-test. This regression analysis was applied to test three dependences: (1) x is intrinsic timescale, y is autocorrelation offset (Fig. 2b); (2) x is mean firing rate, y is intrinsic timescale (Supplementary Fig. 3); and (3) x is trial-to-trial correlation, y is autocorrelation offset (Supplementary Fig. 4). We assessed normality of residuals for the regression analyses; in all cases, the magnitude of skew was < 0.4. Statistical significance (defined by P < 0.05), or lack thereof, for each test was preserved if a single constant term b_k = b was used for all datasets.

To test for correlation between the timescale hierarchy and anatomical hierarchy, we calculated the Spearman rank correlation between the ordering of areas by mean timescale and the discrete anatomical ordering shown in Fig. 1b. The rank correlation coefficient was the same for the visual–prefrontal system (MT, LIP, LPFC, OFC, ACC) and for the somatosensory–prefrontal hierarchy (S1, S2, LPFC, OFC, ACC). Unless otherwise stated, reported p-values are one-sided, as we tested a priori hypotheses of positive correlations between variables. Custom Python code was used for all analyses; analysis code is available from the authors upon request.