Abstract
Right ventricular (RV) failure in response to pulmonary hypertension (PH) is a severe disease that remains poorly understood. PH-induced pressure overload leads to changes in the RV free wall (RVFW) that eventually results in RV failure. While the development of computational models can benefit our understanding of the onset and progression of PH-induced pressure overload, detailed knowledge of the underlying structural and biomechanical events remains limited. The goal of the present study was to elucidate the structural and biomechanical adaptations of RV myocardium subjected to sustained pressure overload in a rat model. Hemodynamically confirmed severe chronic RV pressure overload was induced in Sprague-Dawley rats via pulmonary artery banding. Extensive tissue-level biaxial mechanical and histomorphological analyses were conducted to assess the remodeling response in the RV free wall. Simultaneous myofiber hypertrophy and longitudinal re-orientation of myo- and collagen fibers was observed, with both fiber types becoming more highly aligned. Transmural myo- and collagen fiber orientations were co-aligned in both the normal and diseased state. The overall tissue stiffness increased, with larger increases in longitudinal versus circumferential stiffness. Interestingly, estimated myofiber stiffness increased while the collagen fiber stiffness remained unchanged. The latter was attributed to longitudinal fiber re-orientation, which increased the degree of anisotropy. Increased mechanical coupling between the two axes was attributed to the increased fiber alignment. The increased myofiber stiffness was consistent with clinical results showing titin-associated increased sarcomeric stiffening observed in PH patients. These results further our understanding of the underlying adaptive and maladaptive remodeling mechanisms and may lead to improved techniques for prognosis, diagnosis, and treatment for PH.
Key Terms: hypertrophy, tissue-level biomechanics, pulmonary hypertension, myofiber orientation, collagen fiber orientation
1. Introduction
Right ventricular (RV) failure is a major cause of mortality for patients of pulmonary hypertension (PH), with a mortality rate of 37.2% at 3 years post-diagnosis (1,2). RV function is the most critical determinant of patient longevity in PH (57). Mechanistically, the RV is the end organ, in that PH leads to RV failure, which is the cause of a majority of deaths (directly or indirectly) from PH (16,25,54). While several therapies have been developed which address the pressure and flow in the pulmonary vascular bed (2,25), little is known regarding their effect on RV function. Moreover, no curative treatments have been made available except lung transplantation (4). Following transplantation, dramatic improvements in mean pulmonary artery pressure, pulmonary vascular resistance, and RV ejections fractions have been observed (27), although the exact mechanisms by which the RV can revert back to normal function (reversibility) are yet to be defined.
Predicting RV failure resulting from PH is difficult since some patients survive years, while others rapidly develop RV failure. Current clinical techniques are successfully used to diagnose and predict RV function, such as right heart catheterization (30) and echocardiography-derived tricuspid annular plane systolic excursion, or TAPSE (21), respectively. Clinical predictors of mortality include stroke volume index, pulmonary artery capacitance, and estimated globular filtration rate (7). Several parameters, including the size and mass of the RV (10), the right atrial pressure, (10) and conditions such as hypnoatremia (22), reflect the functional status of the RV and are correlated with advanced RV failure and survival. However, some techniques recommended for screening for PH are frequently inaccurate. For example, Doppler echocardiography gives inaccurate estimates of pulmonary artery systolic pressure in 48% of cases, according to a recent study of 65 PH patients (20).
At the organ level PH imposes a pressure overload on the RV leading to ventricular enlargement (6). This overload affects the RV free wall (RVFW), resulting in increased transmural wall stress and wall weakening, ultimately resulting in ventricular failure (4). Hypertrophy of the associated myofibers occurs via an addition of sarcomeres, with evidence of fibrosis and changes to the extracellular matrix (ECM) both in humans and in rat models (4). However, the specific tissue-level compensatory adaptations of the main structural constituents of the myocardium (myofibers and collagen fibers) to pressure overload remain unknown (57). Although the effects of myocardial stress on cardiac remodeling have been studied for decades (28), the precise mechanisms by which cardiomyocytes sense the force imposed by ventricular pressure and volume overload and respond with sarcomerogenesis remains unknown (29). Knowledge of the underlying adaptive mechanisms is essential for developing multi-scale models of pressure-induced growth and remodeling (G&R). Such modeling efforts may ultimately be used to improve diagnosis and prognosis, as well as provide a framework to develop therapies specifically targeting improving RV response to disease.
Our long-term goal is to quantify and model the cellular- and tissue- level G&R of the RV myocardium in PH. While the development of such models can benefit our understanding of the onset and progression of PH-induced pressure overload, detailed biomechanical data of the underlying events remains limited. Thus, the objective of the present study was to elucidate the hypertrophic and micro-architectural remodeling events that occur in response to organ-level chronic pressure overload in an animal model of PH. A pulmonary artery (PA) banding model was utilized to create a pulmonary hypertensive condition in a rat. In vivo hemodynamic measurements were made to evaluate cardiac performance. Microstructural analysis was performed to quantify micro-architectural remodeling, and the tissue-level biomechanical response of the myocardium was assessed using a novel experimental approach in which the isolated tissue maintains viability (56).
2. Materials and Methods
A total of 55 male Sprague-Dawley rats, 8 weeks old at the start of the experiment, were used in this study. Note that 8 of the rats were used for the 1-week study as described in the Dc iscussion. The experimental protocol was approved by the University of Pittsburgh IACUC (Protocol #13021226) and conformed to the Guide for the Care and Use of Laboratory Animals. There were several factors that entered into this choice of animal model, which have been discussed previously (56). Briefly, the RVFW thickness is appropriate for our biomechanical studies, being sufficiently thin to maintain viability after dissection (56). In addition, the mass is sufficiently large for analyzing tissue constituents, as well as allowing for the quantification of myocardial remodeling due to pressure overload. In the following, the number of rats from the total is provided for each section.
2.1. Pulmonary artery banding procedure and in vivo hemodynamic analysis
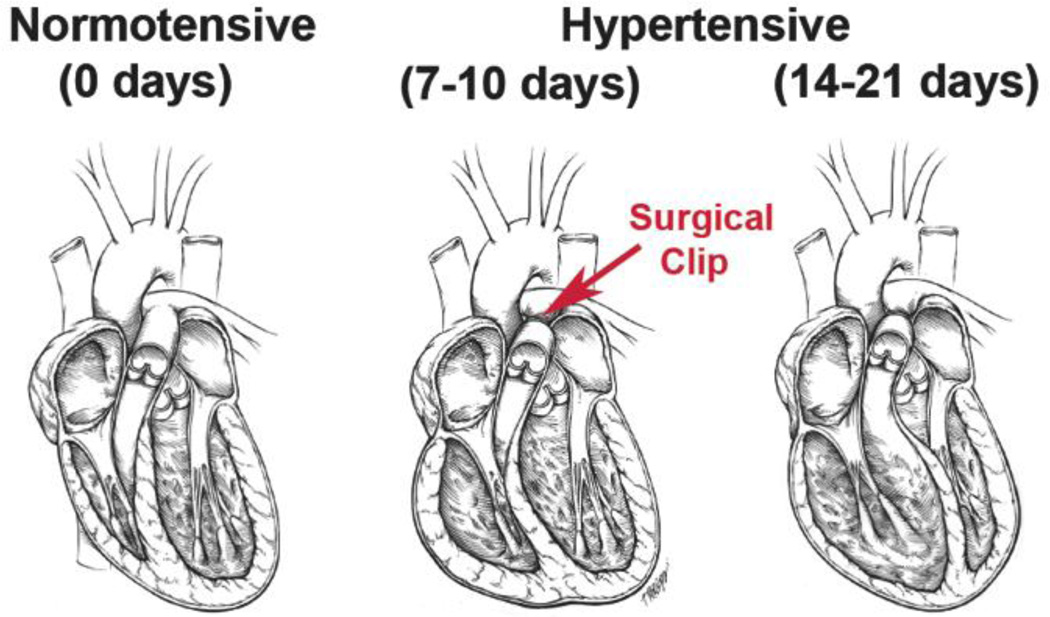
Of the 55 total rats, RV pressure overload was induced surgically by restriction of the pulmonary artery (Figure 1) on 20 animals. Animals were anesthetized with 5% isoflurane and placed on a heated table to maintain a core temperature of 37°C, measured by a rectal probe. The chest was entered via a lateral incision to expose the mid-thoracic aorta. A surgical clip was placed around the PA with a radius such that a uniform right ventricular pressure of 45–50 mmHg was generated. Alternatively, a suture was placed around the PA and brought taught around a 27-gauge needle, which was removed after tying the suture. The chest was closed and sutured, and the animal was extubated and observed continuously for 2 hours post-procedure and daily afterwards for the first week.
Figure 1.
Pulmonary hypertension is induced via banding the pulmonary artery with a surgical clip. Before surgery, the RV is a thin shell like wall sitting on the LV chamber, whereas after 2–3 weeks, the RV has enlarged both its wall and thickened compared to the LV.
Terminal invasive hemodynamics was performed on the normotensive (n=10) and hypertensive (n=10; noting that the same hypertensive rats were used in tissue-level biomechanical studies) rats to generate pressure-volume loops, from which relevant hemodynamic parameters were derived using methods described previously (38), (18). Ees was obtained by standard methods utilizing vena cava occlusion, e.g., (10,18,50). Volume calibration was performed in 2 steps (relative and then absolute). First, a saline volume calibration was performed in which the catheter rests in saline for at least 30 minutes followed a 2-point calibration to obtain a relative volume unit using the MPVS-400 transducer box (Millar Instruments, Houston, TX). Next, absolute volume calibration was performed using volume calibration cuvettes (ADInstruments, Colorado Springs, CO). At 3 weeks post-surgery, control (normotensive) and PA banded (hypertensive) rats (weighing 310 ± 9.15g) were euthanized via inhalation of isoflurane, and the heart was removed along with proximal sections of the great vessels and arrested by placing in cardioplegic solution (40). The RVFW was dissected from each heart and analyzed with the following techniques.
2.2. Tissue level measurements
Myofibers and collagen fibers in the extracellular matrix (ECM) were assumed to be the dominant mechanical constituents comprising the myocardium. RVFW constituent content was quantified by using a lyophilization and decellularization technique on normotensive (n=5) and hypertensive (n=3) specimens. To determine the changes in constituent content between specimens, density was computed as mass of each constituent divided by total specimen volume. Mass fractions Φm and Φc were computed as myo- or collagen fiber density divided by dry tissue density, respectively, for normo- and hypertensive specimens.
2.3. Histomorphology
Comprehensive transmural orientation angle and orientation index (OI) data were determined by analyzing histologically-stained sections from normotensive (n=2) and hypertensive (n=5) specimens using the techniques described below. A total of 10 sections were taken of each normotensive specimen, and 15–20 sections were taken of the hypertensive specimens. Entire RVFWs were dissected and fixed in 10% buffered neutral formalin. Specimens were embedded in paraffin and 5 µm thick sections were obtained with a microtome en face from epi- to endocardium at 50 µm intervals, and histological staining was performed with Gomori One-Step Trichrome. This stain was chosen so that the myofibers and collagen fibers were easily discernable, with the former appearing pink and the latter gray. The sections were imaged with a Nikon Super Coolscan 900 ED slide scanner running Nikon Scan 4.0 software, with resolution of 6.35 µm/pixel. Length ratios were computed as the length of the specimen along the longitudinal direction (Ll) divided by the length along the circumferential direction (Lc). Measurements were taken from each histological section image and averaged.
The orientations of myo- and collagen fibers were quantified from each histologically stained section, using gradient methods similar to those used previously in our lab (15) (Figure 3a,b). A custom program written in MATLAB was used to quantify fiber orientation from the scanned images of size n×m pixels. First, pixels (given by location i,j) representing myofibers (pink) and collagen (grey) were separated into 8-bit grey scale images by manual selection of appropriate ranges of RGB values in the color images. Second, for each image, gradients in the x and y directions, and and , were determined by convolving masks over each pixel in the color-separated grey scale images, by following previous methods (15) and setting s = 3 and σ = 2.5. At each pixel, the magnitude of the gradient and the orientation angle were computed by
| (1) |
and
| (2) |
respectively. We follow our previous convention by assigning 0° aligned to the outflow tract (OT), with positive increasing angles denoting counter-clockwise (right-handed) rotation from the perspective of an observer looking from outside the heart (epicardium) (Figure 3a). From the orientation distribution function, a standard 2nd order structural tensor H (e.g., see (23,26,43)), was computed by
| (3) |
. The eigenvalues, ν1 and ν2, (ν1≥ν2), and eigenvectors, e1 and e2, of H were determined using standard methods, following the normalization of the structure tensor by its determinant. We subsequently defined preferred direction angle θk, for each individual histological k, as defined as the direction of the principal eigenvector ν1 (Figure 3b). Circular statistics were used to compare the mean orientation angles between the two groups, since standard statistics are not applicable for angular data (41). Finally, the mean orientation angle for each specimen was computed, by taking an average over the total number, p, of transmural images of each set of sections per specimen, using
| (4) |
, where , and angular SEM for each specimen was computed from the angular variance, , as
| (5) |
, where is the length of the mean vector. Note that the mean orientation angle and angular SEM were analogous to the standard mean and SEM in standard summary statistics (see Section 2.7). The degree of alignment, along the direction of the principal eigenvector, was computed using OI = 100 (%)*(1 – ν2/ν1). Thus, an OI of 100% indicated perfect alignment, and an OI of 0% represented random fiber distribution. The transmural location of each section was expressed as a normalized thickness as a percentage of total thickness, with 0% representing the endocardium and 100% the epicardium. Mean orientation angle was plotted against normalized thickness. For comparison, interpolation was performed on the hypertensive specimens to determine values on the same evenly spaced grid, at 10% thickness intervals, as the normotensive specimens.
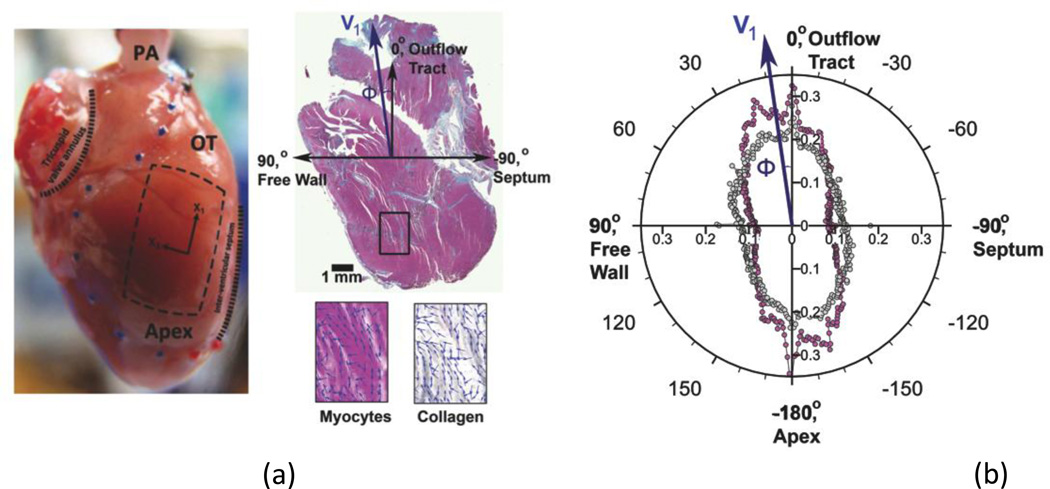
Figure 3.
Methodology and results of fiber orientation angle and orientation index quantification for Gomori-stained histological sections. (a) Image of the rat heart, showing outline of RVFW (blue and red dots) and square slab for biaxial testing (dotted lines). Histological section shown is taken from the midwall at 53% thickness of a hypertensive rat RVFW specimen, stained with Gomori One-Step Trichrome for myofibers (pink) and collagen (gray). Overall measured myofiber and collagen fiber orientation angles in the illustrative image were both ϕ = 7.7°, indicated by the blue arrow (V1). Insets illustrate the local fiber orientation angles with vectors (blue arrows) in the separate myofiber and collagen images. (b) Polar plot depicting the variation in gradient magnitude with angle for myofibers (pink circle) and collagen (gray circles) in a single histological section. Orientation angle is along the direction of the principal eigenvector (V1).
2.4. Tissue-level biomechanical studies
Biaxial mechanical studies was performed on isolated myocardium using protocols described previously. (56) Briefly, square specimens of RVFW myocardium from normotensive (n=10) and hypertensive (n=12, with 10 of these from in vivo hemodynamic analysis) rats were dissected and mounted trampoline-fashion in a biaxial testing device (CellScale Biomaterials Testing BioTester 5000, Waterloo, Ontario, Canada), in modified Kreb’s solution with BDM and oxygen. Multi-protocol displacement-controlled testing was performed by varying the ratio of maximum displacements in each axial direction. The Green-Lagrange strain tensor (E) and the 2nd Piola-Kirchhoff stress tensor (S) were computed for each test protocol using standard methods (31,45), with longitudinal and circumferential components given respectively by ELL, SLL, and ECC, SCC. While shear stresses SCL were measured, their magnitudes were very small and were neglected.
To statistically compare the degree of anisotropy between the normo- and hypertensive states, the differences between maximum values of SLL and SCC were computed from the interpolated equi-biaxial response, in which ELL = ECC (19,46). A larger difference would indicate a higher degree of anisotropy, i.e., the stress-strain responses along the longitudinal and circumferential directions would follow distinctly different paths. Since the mechanical tests were performed under displacement control, the equi-biaxial stress-strain response was interpolated from the multi-protocol experimental dataset with a custom MATHEMATICA program (Wolfram Research Corp.) (19).
2.5. Biomechanical Modeling
As a first step in determining the intrinsic fiber-level changes, the effective fiber ensemble stress-strain responses were determined from the interpolated equi-biaxial strain. We note that this response represents the effective mechanical behavior of the intrinsic combined myofiber-collagen fiber structural unit, i.e., the effective fiber ensemble, defined as a set of fibers with a common orientation that undergoes an equi-biaxial strain (Eens = ELL = ECC, ELC = 0) for a given fiber ensemble direction. The ensemble stress was computed by adding the stress components, Sens = SLL + SCC, as shown previously (46). With this method, it was possible to obtain the stress-strain relationship (Sens–Eens) for the effective myo- and collagen fiber ensemble, from which characteristics of the individual constituents may be derived, as described in the following.
In the present work, we took a quasi-structural approach to characterize the tissue mechanical responses. We assumed the myofibers to be solely responsible for low stress response, followed by increasing contributions of the collagen fibers due to their gradual recruitment with strain. Recruitment models have been utilized to represent the behavior of myo- and collagen fibers in myocardium (33), in which collagen is gradually recruited at higher strains to bear load. Justification for the assumption that collagen is initially crimped and is gradually uncrimped to bear load with increasing tissue strain arises from SEM analysis of fixed myocardium, in which collagen fibers appeared wavy in diastole and taut in systole (9). From the interpolated equi-biaxial (Sens–Eens) data set, the myofiber-dominated response was determined from the tangent modulus of the low-strain region, while the collagen-dominated response was determined from the tangent modus of the high-strain region, both obtained via linear regression.
Applying a basic rule-of-mixtures approach (34), the total second Piola-Kirchhoff stress was given as
| (6) |
where Φm is the mass fraction of myofibers. Although we do not model recruitment directly, we took the following phenomenological approach to estimate recruitment characteristics. We observed that low-stress portion of the Sens-Eens curve (Figure 7) exhibited a linear relation. We thus assumed that no collagen fibers were recruited in this region, and that it was entirely due to the response of the myofibers with an associated tangent modulus TMm. The intrinsic myofiber stiffness ηm can be determined using ηm = TMm / Φm . Next, the strain at which collagen fiber recruitment initiated was defined as the lower transition from the initial linear to the nonlinear portions of the curve. The “upper bound” strain at which collagen fibers were assumed to be fully recruited was defined as the upper transition from the nonlinear to the linear portion of the curve. We assumed all collagen fibers were recruited beyond this upper bound, characterized by a post-transition tangent modulus PTTM (Fig. 7). Assuming that the collagen fibers are linear elastic, we note that
| (7) |
where η̅c is the effective collagen fiber modulus. Since the collagen fiber recruitment was not explicitly modeled η̅c ≤ η̅c, where ηc is the true collagen fiber elastic modulus. The transitions strains that encompass the fiber recruitment Elb and Eub, were determined directly from tangent modulus-Eens curves, as in Fata et al. (19). We note that these transitions were always marked and identifiable.
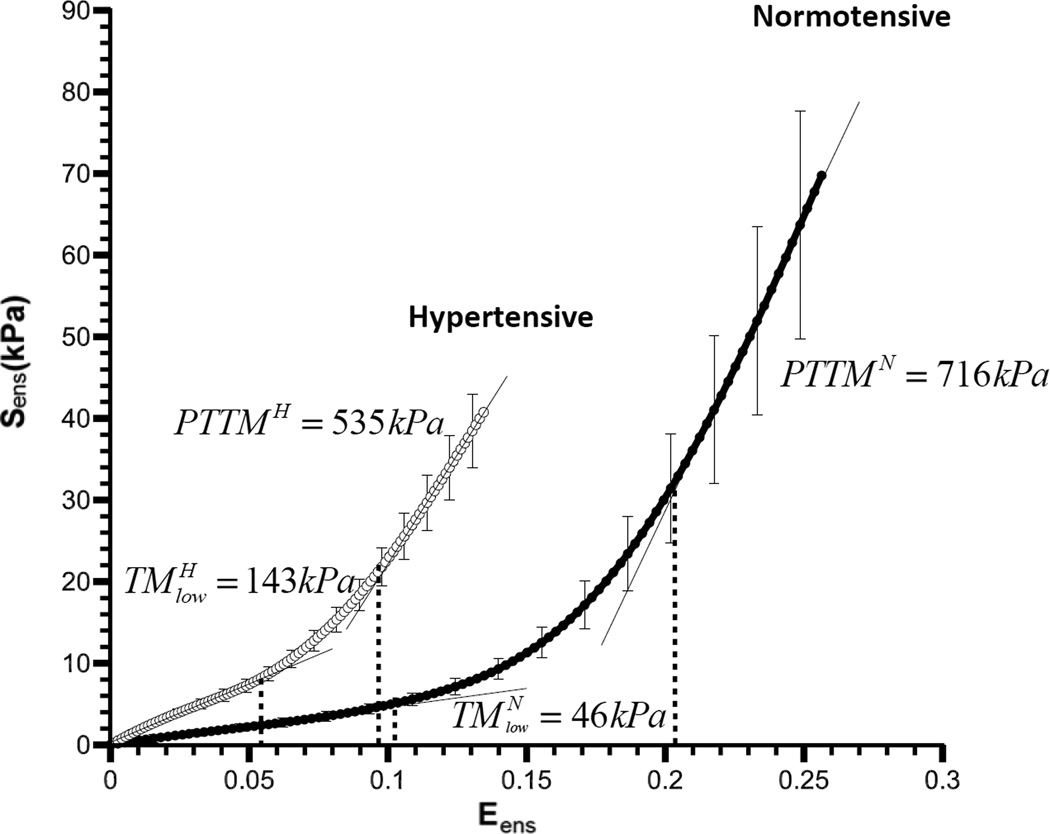
Figure 7.
Changes in the mechanical (stress-strain) response of the intrinsic combined myofiber-collagen EFE response from the normo- to the hypertensive state (bars = SEM). From left to right, dotted lines indicate the strain at which fiber recruitment initiates and the maximum strain for the normotensive state, and , and for the hypertensive state, and , respectively. Straight lines represent linear fit to the upper and lower portions of the curves, with effective tangent moduli defined as the slopes of these lines. Low strain tangent modulus was significantly higher (p = 0.003) in hyper- versus normotensive specimens.
Next, to explore the responses of the entire measured stress-strain response, the biomechanical response of the myocardium specimens was represented by the following in-plane Kirchhoff stress-strain relations (12), which have been derived through a two-dimensional strain energy function (see (47) for details).
| (8) |
Equations (8) were simultaneously fit to the experimental data to determine the material parameters using a nonlinear regression algorithm in MATLAB (The MathWorks, Inc.). Goodness of fit was determined by computing the standard r2 value. This model form was chosen over others, e.g., Fung-type exponential (24), because it allows explicit decoupling of the response extensional and coupling responses, reducing the parameter covariance. Specifically, the first term on the right hand side of equation (8) for SCC is independent of ELL. The second term in equations (8) represents the degree of mechanical coupling between the tissue axes. We also note that Fung-type constitutive models can have convexity issues unless certain restrictions are imposed (see, e.g., (32,52)), and therefore are not as desirable. Moreover, in the present study our purpose for using eqn. 8 was to provide insight into the effects of tissue remodeling from mechanical behavior over the entire strain range. We note that future work will involve using full structural models (e.g., (19)) to directly account for the myo-and collagen fiber architecture.
2.6. Tissue Viability Studies
While we have shown viability and confirmed stable active contraction for healthy rat RVFW tissue for at least 3 hours after harvesting, (56) we evaluated viability for the PH specimens, since they had undergone adaptive remodeling to the sustained pressure overload, e.g., they became thicker. To ensure we were testing living, viable myocardium, tissue viability was assessed. Mitochondrial function was determined for the time course of biaxial mechanical evaluation, approximately one hour. Since mitochondrial respiratory control is the best general measure of function in isolated mitochondria, we used a Clark-type oxygen electrode (5), a technique that has been used for over 50 years (11), to measure respiratory control ratios (RCRs) on n=3 specimens at baseline and at 1.5 hours post dissection.
2.7. Statistical analysis
All data, excluding histomorphology, were reported as sample mean ± sample standard error of the mean (SEM. Statistical comparisons were made using a two-sample Student’s t-test in MATLAB (ttest2.m) with α = 0.05. For histomorphological data, circular statistics (41) were used to compute mean and SEM, analogous to standard summary statistics, for the angular data, and comparisons were made using a circular analysis of variance (aov.circular) in the ‘circular’ package (35) in R software (R Project for Statistical Computing, http://www.rproject.org).
3. Results
3.1. In vivo hemodynamic analysis
Changes in hemodynamics and tissue properties (Table 1) were evident. The P-V loops shifted to the right and doubled in size (Figure 2), indicating RV enlargement during pressure overload. Pressure-derived measurements were available for n=10 specimens, while volume measures were only obtained from n=5 specimens due to difficulties in volume measurement. Changes in hemodynamics reflected significant alterations to the RV in the hypertensive specimens (Table 2). Pressure and volume were higher, while a small increase in SV and large increase in SW were observed. Maximal dP/dt and Ees, measures of contractility, significantly increased. Diastolic function worsened as evidenced by the increase in tau. Ea, a measure of vascular load, increased, and the ratio Ees/Ea increased, indicating a de-coupling of the RV function from the vascular load.
Table 1.
Summary of multi-scale changes to the right ventricle under pressure overload
| Scale | Change from Normo-to Hypertensive |
|---|---|
| Organ-level | Hemodynamic changes Chamber dilation Sphericalization of RV chamber shape |
| Tissue-level | Increased overall RVFW mass and volume Increased myo-and collagen fiber mass Increased myofiber mass density Decreased ECM mass density Longitudinal re-orientation of myo-and collagen fibers Increased myo-and collagen fiber degree of alignment Highly increased longitudinal stiffness Increased circumferential stiffness Increased mechanical coupling between axes Increased combined effective fiber ensemble (EFE) stiffness |
| Cellular/Fiber-level | Increased myofiber EFE stiffness Slightly decreased collagen-dominated EFE stiffness Little changes in relative recruitment strain |
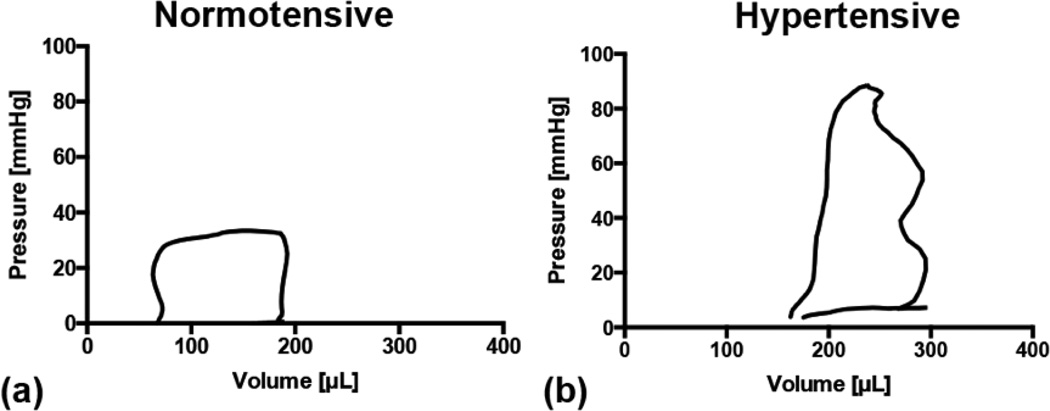
Figure 2.
Right-ventricular pressure-volume (P-V) loops for (a) the control, normotensive state and for (b) the pressure-overloaded, hypertensive state. The P-V loops shifted to the right and doubled in area, indicating the RV enlargement during PH
Table 2.
Derived hemodynamic parameters and bulk tissue properties. Significant differences indicated between normotensive and hypertensive states.
| Measure | Normotensive | Hypertensive |
|---|---|---|
| Hemodynamic Parameter | ||
| RVESP (mmHg) | 28.0 ± 1.2i | 93.8 ± 5.6i |
| RVEDV (µL) | 124.8 ± 18.1ii | 223.1 ± 45.2ii |
| SV (µL) | 131.4 ± 12.7ii | 190.0 ± 22.2ii |
| SW (µL*mmHg) | 2,671.8 ± 217.3iii | 9,354.6 ± 1,986.6iii |
| Maximum dP/dt (mmHg/s) | 2,297.8 ± 124.5iv | 4,547.2 ± 420.3iv |
| Tau, 1/e (msec) | 3.8 ± 0.4iv | 7.0 ± 0.3iv |
| Ees (mmHg/µL) | 0.216 ± 0.046iii | 0.808 ± 0.117iii |
| Ea (mmHg/µL) | 0.242 ± 0.085iii | 0.440 ± 0.033iii |
| Ees/Ea | 0.82 ± 0.28v | 1.98 ± 0.66v |
| Bulk RVFW myocardium tissue property | ||
| Specimen Thickness (µm) | 754 ± 10vi | 1,223 ± 48vi |
| Specimen volume (µL w.v.) | 29.7 ± 1.8 | 73.2 ± 6.0 |
| Specimen mass (mg w.w.) | 61 ± 3vii | 123 ± 7vii |
| Longitudinal length, Ll (mm) | 11.53 ± 0.47 | 12.41 ± 0.36 |
| Circumferential length, Lc (mm) | 7.24 ± 0.14viii | 10.13 ± 0.28viii |
| Ll / Lc Length ratio | 1.58 ± 0.04ix | 1.22 ± 0.02ix |
| Tissue wet density (mg/mL w.w./w.v.) | 2,173 ± 126 | 1,922 ± 47 |
| Tissue dry density (mg/mL d.w./w.v.) | 434 ± 16 | 424 ± 9 |
| Myofiber mass (mg d.w.) | 6.3 ± 1.1 | 14.0 ± 1.4 |
| ECM mass (mg d.w.) | 6.1 ± 0.9 | 8.7 ± 2.2 |
| Myofiber density (mg/mL d.w./w.v.) | 191 ± 24 | 265 ± 33 |
| Collagen fiber density (mg/mL d.w./w.v.) | 243 ± 26 | 159 ± 24 |
p < 10−9,
p = .03,
p < .001,
p < 10−4,
p = .009,
p < 10−7,
p < 10−8,
p < 10−5,
p < 10−11
key: w.w. = wet weight, w.v. = wet volume, d.w. = dry weight
3.2. Tissue constituents
Changes in bulk RVFW myocardial tissue were observed from the normo- to the hypertensive state (Table 1). Statistically significant increases in both thickness and mass of the RVFW myocardium were observed. Average mass of both myofibers and ECM increased. The mean overall tissue density was found to decrease slightly. The mean density of total myofibers and ECM remained approximately equal, with the mean density of myofibers increasing and ECM density decreasing. Mass fractions of myo- and collagen fibers for normo-and hypertensive specimens were Φm = 44% and 63%, respectively for muscle, and Φc = 56% and 37%, respectively for collagen.
3.3. Histomorphology
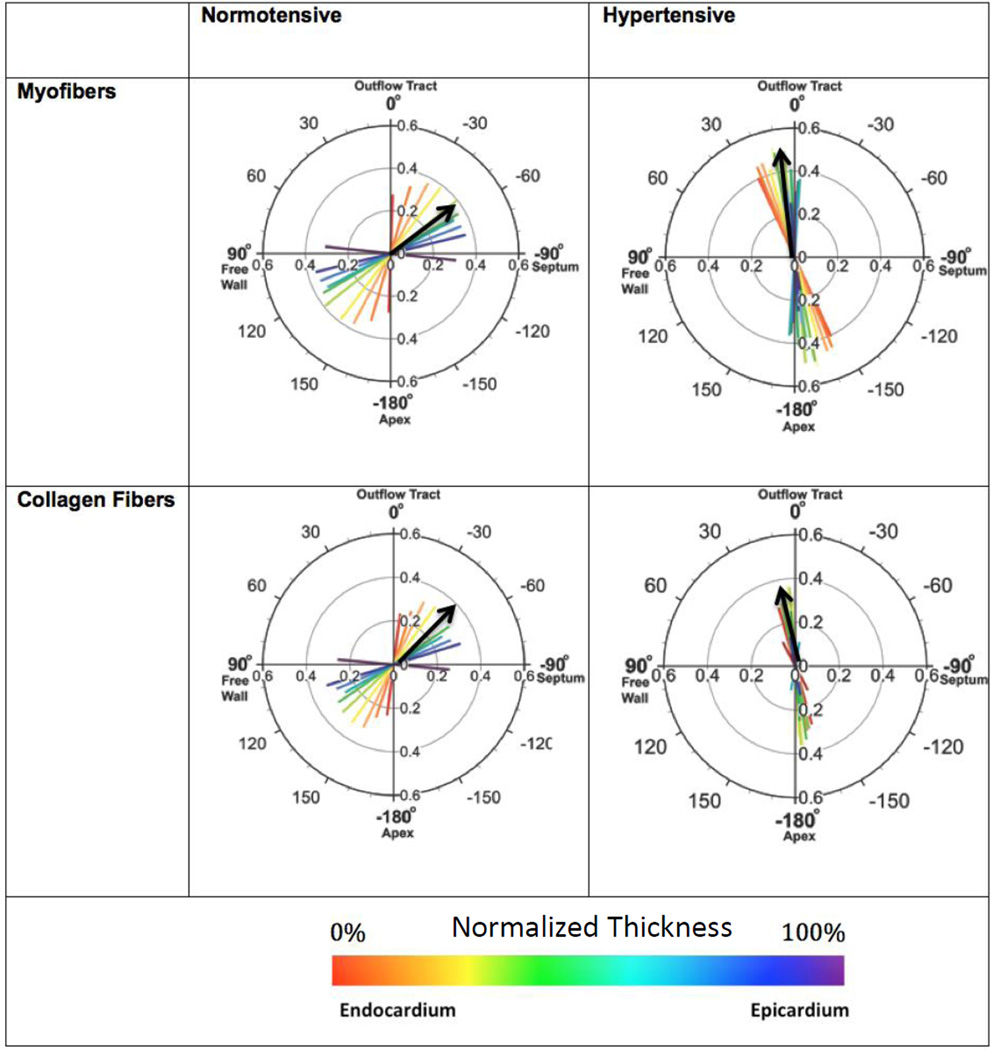
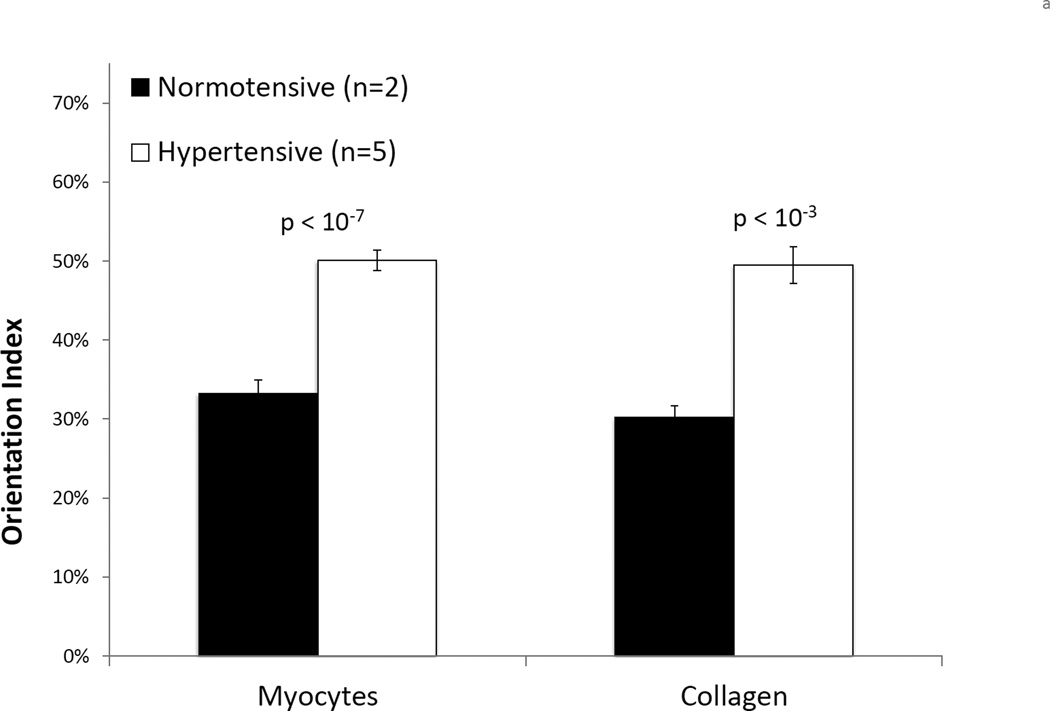
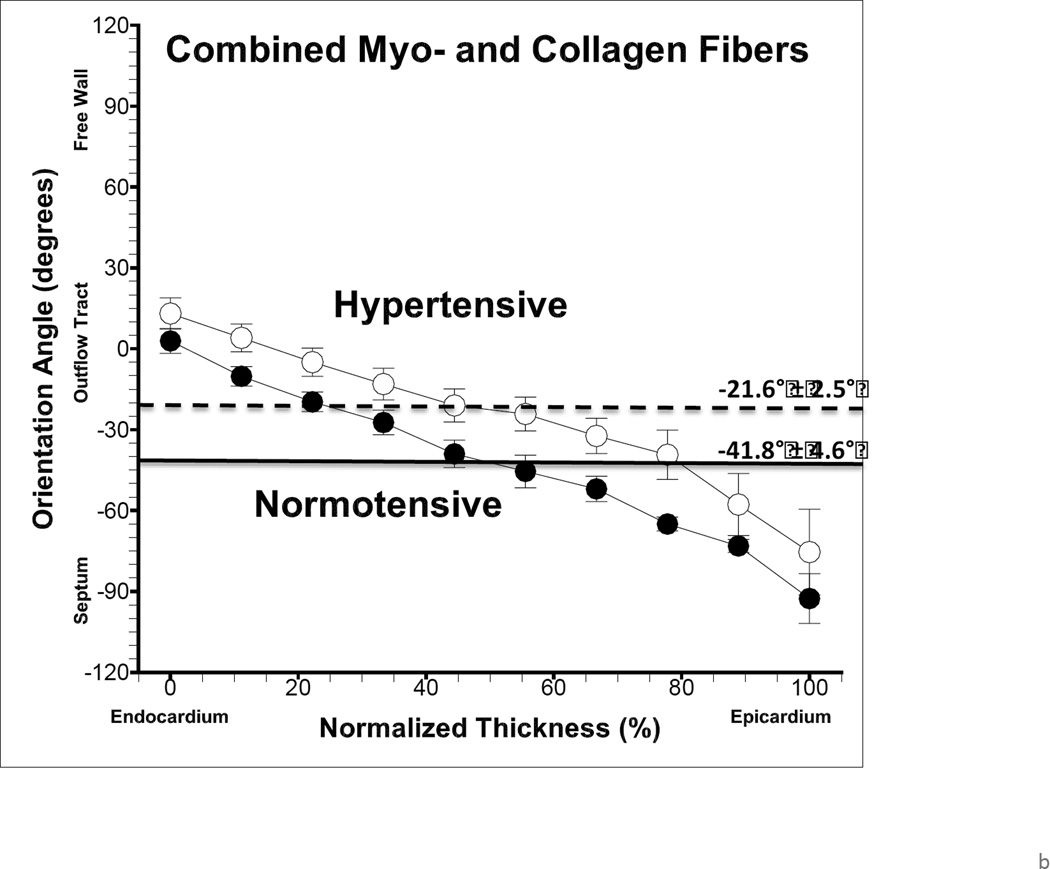
Histological staining revealed increases in bulk tissue in the hypertensive state (Figure 3a). Longitudinal length (Ll) increased, though not significantly, and circumferential length (Lc) significantly increased (Table 2), indicating an overall increase in cross-sectional area. The ratio Ll/Lc decreased significantly under pressure overload, suggesting a change in ellipticity of RV shape from highly ellipsoidal, with the long axis oriented longitudinally, towards more spherical. Within each histological section, myo- and collagen fibers were oriented along similar directions in both states (Figures 3b and 4). In the normotensive state, there was a transmural (through-thickness) variation in the fiber orientation. Moving outward, the preferred orientation direction followed a helical clockwise (left-handed) rotation, from longitudinally in the endocardium to circumferentially in the epicardium. We observed a trend in the hypertensive specimens where the transmural fiber orientation clearly lost its helical through-wall variation, and dramatically re-oriented towards the longitudinal direction (Figure 4). For all specimens, the mean degree of alignment, or orientation index (OI), increased significantly for both myo- and collagen fibers (Figures 4 and 5a), and the mean fiber angle was −41.8° ± 4.6° in the normo-and −21.6° ± 2.5° in the hypertensive state (Figure 5b).
Figure 4.
Transmural variation in orientation angle, depicted in the polar plots, and orientation index (OI), shown in the bar graphs, for myofibers and collagen fibers in illustrative normotensive and hypertensive specimens. Color represents position along thickness of the RVFW. Orientation angle is indicated by the direction of the vectors in the polar plots. The length of these vectors represents OI and matches the ordinate values of the bar graph. An OI of 0% indicates randomly oriented fibers, with 100% being perfectly aligned. Black arrows depict mean fiber angle.
Figure 5.
(a) Mean orientation index, or OI, for myofibers and collagen in normotensive and hypertensive specimens. Statistically significant differences indicated on plot (bars = SEM). (b) Variation of mean orientation angle with normalized thickness
3.4. Tissue-level biomechanical behavior
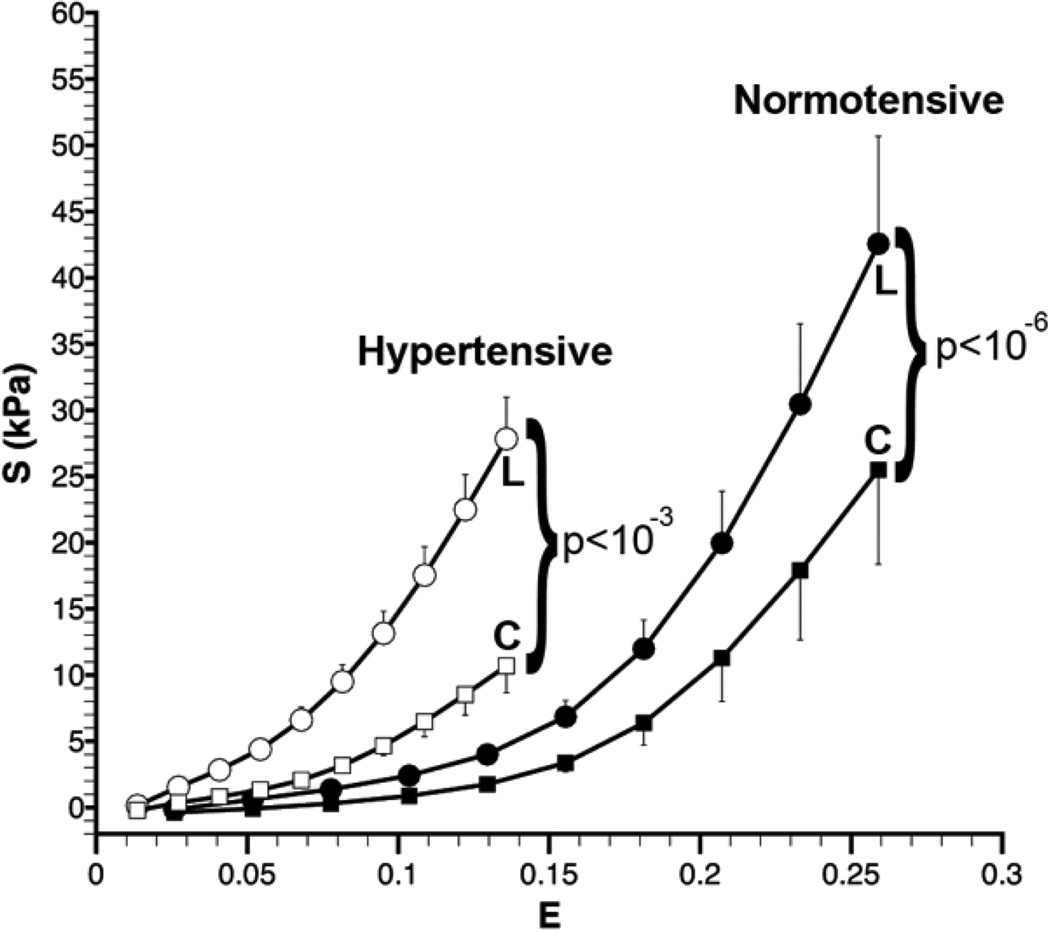
Biaxial mechanical evaluation of the isolated RVFW myocardium was very reproducible, giving qualitatively comparable responses to previous studies (56). Stability in the response was confirmed by the reproducibility of the 1:1 displacement-controlled testing performed at the beginning and at the conclusion of specimen testing, where we observed a similar stress-strain behavior between the two responses (results not shown). The degree of anisotropy increased in the pressure-overloaded state, illustrated by the increase in difference between the longitudinal and circumferential mechanical response curves and by the increased separation of the maximum values for SLL and SCC in the hypertensive state (Figure 6). Furthermore, the tissue stiffness was higher in the longitudinal direction than in the circumferential direction.
Figure 6.
Mechanical response of right ventricle free wall (RVFW) myocardium: mean interpolated longitudinal (L) and circumferential (C) stress (S) versus mean interpolated equibiaxial strain (E) response, determined from biquintic finite element interpolation, of normotensive (n=10) and hypertensive (n=12) specimens of isolated rat RVFW myocardium. Statistically significant differences indicated on plot (bars = SEM).
3.5. Biomechanical Modeling
There was a change in the mechanical response of the intrinsic fiber ensemble. Fiber recruitment initiated at lower strain levels in the hypertensive specimens (Figure 7). Relative recruitment increased slightly from 50.2% and 54.6%. The low strain tangent modulus ( TMm) was significantly greater in hyper- versus normotensive specimens (p=0.003), with no statistical differences in PPTM. The intrinsic myofiber stiffness modulus increased from ηm = 105 kPa in the normotensive to 228 kPa in the hypertensive state. The intrinsic collagen fiber stiffness modulus decreased slightly from η̅c =1,240 kPa to 1,190 kPa, from normo- to hypertensive.
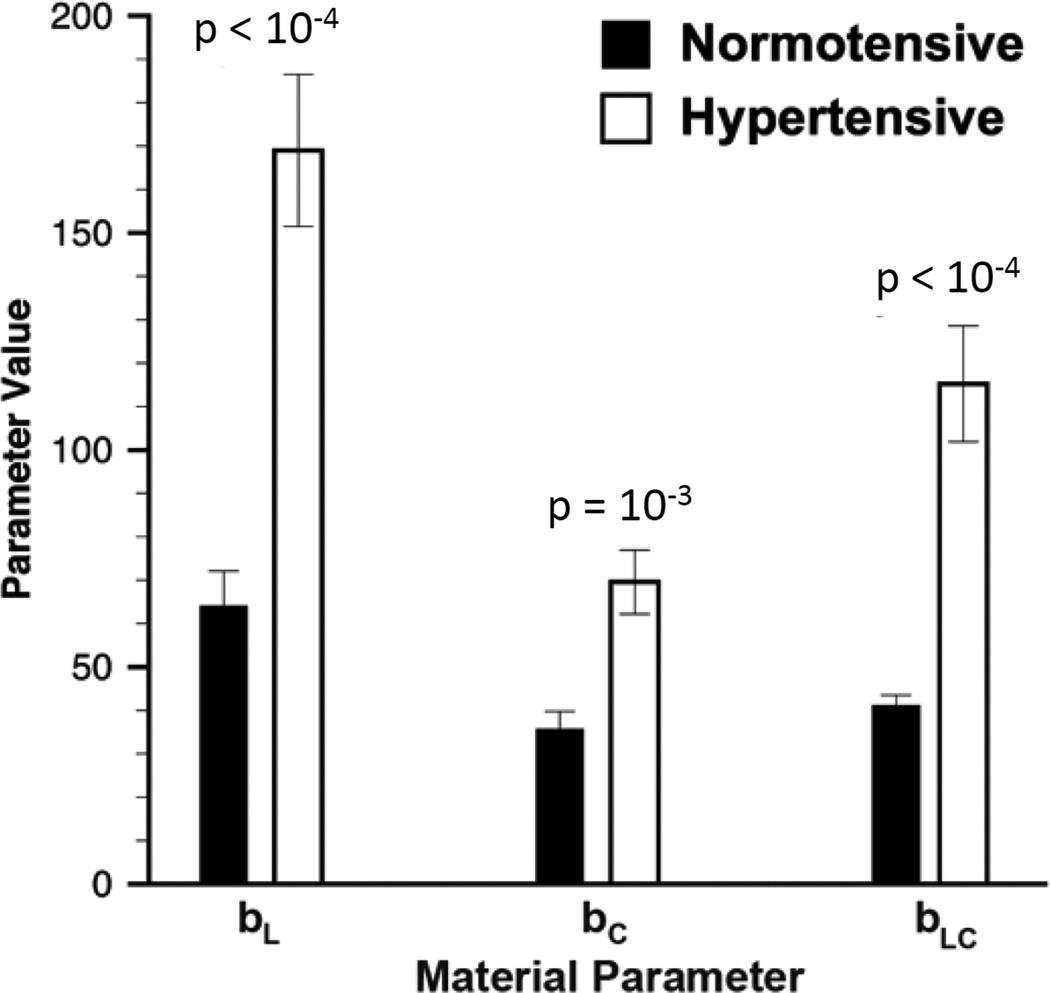
The constitutive model fit the mechanical data generally well for both states; mean R2 values were 0.9446 ± 0.0078 for normotensive and 0.8856 ± 0.0141 for hypertensive. The scaling parameter b0 increased from 0.16 ± 0.02kPa to 0.23 ± 0.08kPa, though the difference was not significant. Very large and significant increases were observed in other mean parameter values by approximately 163% for bL, from 64.1 ± 8.0 to 169.0 ± 17.5; 95% for bC, from 35.7 ± 4.0 to 69.6 ± 7.3; and 180% for bLC, from 41.2 ± 2.3 to 115.2 ± 13.3 (Figure 8), indicating an increased stiffness in the longitudinal versus circumferential direction and an increase in coupling. These results reflect the substantial remodeling of the tissue mechanical behavior with PH.
Figure 8.
Mean values for material parameters given in equations (11)–(13) for normotensive (n=10) and hypertensive (n=12) specimens. Statistically significant differences indicated on plot (bars = SEM).
3.6. Tissue Viability
Respiratory control ratios (RCR) at baseline were 4.64 ± 0.41 and at 1.5 hours were 2.22 ± 0.07. Values above 2 are considered viable; thus, mitochondria were respiring, intact, and functional, indicating living tissue throughout the time course required for biomechanical testing (5).
4. Discussion
The objective of the current study was to elucidate the hypertrophic and architectural remodeling events that occur in response to organ-level chronic pressure overload in a rat model of PH. Interestingly, we observed changes at all length scales (Table 2). This results suggests that that myocardium’s response to PH is complex and multi-scale. Interpretation of specific results is given in the following by scale level.
4.1. RV Response to Pressure Overload
In vivo hemodynamic studies confirmed RV pressure overload in the PA-banded group (Figure 2,Table 2). End-diastolic pressure increased significantly, as previously seen in PAB rat models (18) and as expected in the hypertensive condition. Clinically, hypertrophy has been described as the initial adaptive response to PH, in order to increase contractility (57). Here, higher dP/dt and Ees were indicative of an increase in RV contraction to maintain flow against the increased pressure afterload. In response to an increase in end-systolic pressure, we saw an increase in end-diastolic volume (124.8 ± 18 to 223.1 ± 45.2 uL) as expected. End-systolic volume also increased (from 75 ± 52 to 160 ± 119 uL, p=0.07) but the increase in ESV was not as great as the increase in EDV, therefore the resultant stroke volume increased. The ejection fraction and cardiac output did not significantly change (EF: 85 ± 22% to 79 ± 23%, p=0.58; CO: 53 ± 16 to 70 ± 23 mL/min, p=0.12), and stroke work increased as expected. Bogaard et al. found similar results (as discussed above) in the PA banding model, in which they reported no change in cardiac output. This is consistent with the observations of Maughan et al. (42), in which an increase in afterload is associated with greater volumes, including stroke volume.
There was a significant increase in both tissue thickness and mass, indicative of hypertrophy, i.e, more bulk myocardium was being created to increase contractility. We found the density of combined myofibers and extracellular matrix (ECM) remained relatively constant from the normo- to the hypertensive state, and the relative density of myofibers increased (Table 2). So hypertrophy, as opposed to ECM expansion (fibrosis), likely dominated the remodeling process. This hypertrophic response likely underlies the increase in contractility seen in pressure overload prior to overt ventricular failure.
According to the Laplace relationship (4), T = Pr/h, where T is wall stress, P is intraluminal pressure, r is chamber internal radius, and h is chamber wall thickness. In the hypertensive state, chamber pressure, P, must be increased to pump against increased afterload. The RV likely responded to increase this pressure through hypertrophy, which simultaneously achieved a bulk increases in thickness, h, and an increase in pressure, P (Table 2), via increased contractility.
Clinically, hypertrophy is followed by progressive contractile dysfunction (57), along with chamber dilation to maintain cardiac output in spite of reduced contractility (18,57). Here, an increase in end diastolic volume was indicative of RV chamber dilation. As the condition progresses with sustained pressure overload, contractility increases are insufficient to maintain cardiac output (i.e, decoupling of ventricular function to its vascular load), resulting in progressive chamber dilation, i.e., increase in chamber internal radius, r, to increase ejection volumes through increased pressure. Ees/Ea increased, indicative of ventricular-vascular decoupling, as seen clinically in PH (39,48,53,55), suggesting that the increased contractility was not sufficient to maintain cardiac output against the increased afterload. Moreover, sphericalization, as shown here with the change in ratio of longitudinal to circumferential length towards unity, has been associated with the onset of heart failure (see Janicki et al. (36) and references therein). Eventually, RV failure occurs and is characterized by increased filling pressures, diastolic dysfunction, and decreased cardiac output (57). Tau significantly increased with PA banding from 3.8 ± 0.4 to 7.0 ± 0.3 msec, p<10−4, suggesting that diastolic dysfunction is occurring here in the PA banding model, and that the rats are at the onset of RV failure. Thus, we conclude that these PA-banded rats were in a stage of advanced right ventricular dysfunction, prior to overt failure.
4.2. Structural and Mechanical Adaptations to Pressure Overload
We found the intrinsic mechanical properties and microstructure of the myocardium were altered from the normo- to the hypertensive state, in addition to bulk tissue accumulation. First, the overall tissue stiffness increased (Figure 6), demonstrated quantitatively by increases in both material parameters bL and bC (Figure 8), which we attributed to stiffening of the combined myofiber-collagen fiber ensemble structural unit (Figure 7). The increased fiber ensemble stiffness was likely due to intrinsic stiffening of the myofibers alone, since a greater than two-fold increase in intrinsic myofiber stiffness was observed and a slight decrease in intrinsic stiffness and slight increase in relative recruitment strains was observed for collagen.
Second, a larger increase in bL compared to bC (Figure 8) suggested a greater increase in longitudinal stiffness compared to circumferential (Figure 6), which we attributed to longitudinal re-orientation of fibers (Figures 4 and 5b). This angle exhibits a clockwise transmural variation through the myocardial thickness similar to previous measurements in the normotensive canine RVFW (13), with spiral variations also observed in canine left ventricle free wall (49) and in mice septum (37). While this variation has been measured previously and used in biomechanical models of myocardium (17), we believe this to be the first report of a stress-induced loss of spiral variation.
Third, the increase in the bLC parameter (Figure 8) suggested that the coupling between the longitudinal and circumferential axes increased, indicating a more highly anisotropic material behavior in the hypertensive state. We have shown in previous studies of valve tissues (3) that as fiber alignment becomes more clustered about a given direction, coupling between this preferred direction and orthogonal directions increases, suggesting a more highly anisotropic behavior. For example, given a fiber distribution about a single direction, if the fiber splay is randomly distributed (e.g., an OI of 0%), the response along each axis will be similar. Separation in the axial response (e.g., the longitudinal and circumferential) occurs as the fibers become more highly aligned (e.g., as the OI increases from 0 to 100%). Here, the average OI increased for the both myo- and collagen fibers (Figures 4 and 5b), so we conjectured that increased myofiber alignment was the predominant microstructural change underlying increased coupling.
4.3. Further insight into time rate changes
The results we presented here demonstrated dramatic changes between normotensive rats and hypertensive rats subjected to 3 weeks of chronic pressure overload from banding. Future endeavors should be taken to elucidate the time-evolving G&R response of the RVFW. In pilot studies, we banded n=8 rats for 1-week, isolated the RVFW, and performed biomechanical analysis on the tissue slabs as described above. The low stress tangent modulus was significantly greater in 1-week hyper- (TMm = 104kPa) versus normotensive specimens (Figure 7; p=0.003), but less than the 3-week hypertensive, though not significantly. No significant differences were observed between the post transition tangent moduli of the 1-week hypertensive (PTTM = 524 kPa) and the normo- and 3-week hypertensive specimens (Figure 7). Therefore, we provided evidence that intrinsic collagen properties are not altered in response to pressure overload, but myofiber stiffness is increased over time, likely to increase contractility.
4.4. Implications
We demonstrated an increase in myofiber stiffness in response to pressure overload, with little change in collagen biomechanical properties. The increase in myofiber stiffness was beyond that expected by simple addition of mass (increase in mass fraction). Therefore, not only was myofiber mass increased, the intrinsic stiffness of the myofibers also increased. Increased cardiomyocyte cross-sectional area and increased intrinsic stiffness has been reported in pulmonary artery hypertension (PAH) patients by Rain et al. (44), so our findings may suggest a pressure-driven remodeling process that occurs clinically. Tau significantly increased with PA banding from 3.8 ± 0.4 to 7.0 ± 0.3 msec, p<10−4. Therefore, diastolic dysfunction is occurring in the PA banding model. Also, we’d like to distinguish between the organ-level stiffness, which we represent by the time-constant tau, and the intrinsic stiffness of the myofibers, given in our manuscript by ηm. The latter is a measure of the changes in intrinsic stiffness of the myofibers, irrespective of the mass accretion. In this study, we found that both myofiber mass and intrinsic stiffness increased. Similarly, and highly exciting to us, our findings of myocyte hypertrophy are consistent with the clinical findings of Rain et al.
Myocardial insults often result in decreased myofiber numbers, with remaining myofibers becoming elongated or hypertrophied to maintain stroke volume to compensate for their absence. Stretch-induced myofiber remodeling may lead to new contractile protein synthesis and new sarcomere assembly (14). In pressure-overload hypertrophy associated with hypertension, ventricular thickening is associated with parallel deposition to sarcomeres, to increase myofiber cross sectional area relative to cell length (see Sugden and Clerk (51) and references therein), and clinically, it has been shown that titin phosphorylation was reduced in PH patients with sarcomeric stiffening (44). However, the mechanotransduction mechanisms by which wall stress is sensed by cardiomyocytes to activate G&R pathways remains unknown (29). While we have demonstrated quantitatively here the manifestation of these changes to the tissue level mechanical properties of the cardiomyocytes, future studies into these sub-cellular myofiber changes, molecular pathways, and their effects on the cellular mechanical and contractile properties are warranted.
Clinically, longitudinal shortening of the myocardium has been shown to be a greater contributor to RV stroke volume than circumferential shortening during normal contraction (8). Regional myocardial shortening during contraction has been correlated with local transmural myocardial fiber orientations (13). Here, we hypothesize that the tissue responds to pressure overload by re-orienting myo- and collagen fibers to increase longitudinal shortening, a possible mechanism of contractile reserve, beyond hypertrophy, chamber dilation, and increases in fiber stiffness. Moreover, low tricuspid annular plane systolic excursion (TAPSE) values are strongly correlated with RV dysfunction (21). We further hypothesize that towards the final stages of RV failure, a loss of contractility in the longitudinally re-oriented myofibers reduces longitudinal shortening and underscores the decrease in excursion measured with TAPSE.
4.5. Limitations
There were limitations to the methodology and approach used in this study. First, regarding methodology, when quantifying tissue constituent density, we assumed that our decellularization technique completely isolated the ECM from the tissue by removing myofibers, and when performing histomorphology, we assumed that the Gomori stain targeted only myofibers and collagen fibers. Although no technique is perfect, inspection of the Gomori-stained decelluarized tissue revealed all gray with no remaining pink color, i.e., the myofibers were removed with this process, with only ECM remaining. Therefore, we are confident these limitations did not affect the accuracy of our results. Moreover, both normo- and hypertensive specimens were subjected to the same processing steps, so direct comparisons could be made between the two groups.
Second, regarding our approach, a higher degree of variation in results was observed in the hyper- versus normotensive rats. Although specimens were taken at the same time point, the pathological response differed among rats. Some rats may have been in a more advanced stage of RV compensation or dysfunction than others, depending on their individual responses to the pressure overload. This variation may explain the higher standard error observed in the hyper- versus normotensive specimens. Here, we applied a phenomenological approach to model the biomechanical response of the myocardium, noting that fully structural models, e.g., as in (19), will be employed in future studies to fully represent the growth and remodeling response and to identify the specific tissue- and cellular level adaptations within the RVFW.
4.6. Conclusions
The RVFW myocardium responded to a sustained pressure increase via an increase in bulk tissue amount, stiffness, and proportion of myofiber density to ECM. The initial response to pressure overload was hypertrophic. However, hypertrophy alone was insufficient to maintain cardiac output, so the RV chamber dilated to increase output. Overall tissue stiffness increased, which we attributed to increased effective structural fiber unit stiffness due to myofiber hypertrophy. Longitudinal stiffness increased proportionately more than circumferential, and we attributed this increased stiffening to longitudinal re-orientation of the myofibers and collagen fibers. The intrinsic mechanical stiffness of the myofibers increased, independent of mass fraction increases, with little changes to collagen recruitment or intrinsic stiffness. The biomechanical and microstructural changes measured in this study will be used in future computational models of the pressure-induced growth and remodeling of the RVFW myocardium, which may eventually be used to predict the response to altered hemodynamic states.
Acknowledgements
This work was supported by the U.S. National Institutes of Health [1F32 HL117535 to M.R.H., P01 HL103455 and U01 HL108642-01 to H.C.C.]; the American Heart Association [13POST14720047 to M.R.H., 11POST6950004 to D.V-J., 10BGIA3790022 to M.A.S.]; and The Pittsburgh Foundation [M2010-0052 to M.A.S. and M.S.S.]. We’d like to thank Sunaina Rustagi, Andrea Sebastiani, and Samantha Carter at the University of Pittsburgh (Pitt) for performing the biomechanical testing; Jeffrey J. Baust at Pitt for performing pulmonary artery banding procedures; Sruti Shiva at Pitt for performing the tissue viability study; Simone Siegel, Michelle Atkins, and John Lesicko at the University of Texas at Austin (UT-Austin) for performing the histomorphological analysis.
Nomenclature
Anatomy
- RV
Right ventricle
- RVFW
RV free wall
- PA
Pulmonary artery
Hemodynamic Parameters
- RVESP
RV end-systolic pressure
- RVEDV
RV end-diastolic volume
- SV
Stroke Volume
- SW
Stroke Work
- Maximum dP/dt
Maximal first time-derivative of pressure (a measure of systolic function)
- tau
RV diastolic time constant (a measure of diastolic function)
- Ees
RV elastance (a measure of contractility)
- Ea
PA elastance (a measure of afterload)
- Ees/Ea
RV-PA coupling
Constitutive model measures and parameters
- ELL
Green’s strain in longitudinal direction
- ECC
Green’s strain in circumferential direction
- SLL
2nd Piola-Kirchhoff (PK) stress in longitudinal direction
- SCC
2nd Piola-Kirchhoff stress in circumferential direction
- b0
Model scaling parameter
- bL
Model parameter, representing longitudinal stiffness
- bC
Model parameter, representing circumferential stiffness
- bLC
Model parameter, representing coupling, between longitudinal and circumferential response
- Sens
Combined myofiber-collagen effective fiber ensemble stress
- Eens
Combined myofiber-collagen effective fiber ensemble strain
- Φm
Mass fraction of myofibers
- Φc
Mass fraction of collagen fibers
- ηm
Intrinsic myofiber modulus
- η̅c
Intrinsic collagen fiber modulus, that accounts for the effects of gradual fiber recruitment
- Elb
Lower bound on recruitment strain for the collagen fiber ensemble
- Eub
Upper bound on recruitment strain for the collagen fiber ensemble
- PTTM
Post-transition tangent modulus
The following orientation convention was used (Figure 3a):
0° is along the +xL direction (oriented longitudinally towards the outflow tract)
180° is along the -xL direction (oriented longitudinally towards the apex)
90 is along the +xC direction (oriented circumferentially towards the free wall)
−90° is along the -xC direction (oriented circumferentially towards the septum)
Footnotes
Conflict of Interest
No benefits in any form have been or will be received from a commercial party related directly or indirectly to the subject of this manuscript.
References
- 1.Badui E, Robles E, Hernandez C, Garcia Rubi D, Mintz G. [Cardiovascular manifestations in progressive systemic sclerosis. Arch Inst Cardiol Mex. 1985;55(3):263–268. [PubMed] [Google Scholar]
- 2.Benza RL, Park MH, Keogh A, Girgis RE. Management of pulmonary arterial hypertension with a focus on combination therapies. J Heart Lung Transplant. 2007;26(5):437–446. doi: 10.1016/j.healun.2007.01.035. [DOI] [PubMed] [Google Scholar]
- 3.Billiar KL, Sacks MS. Biaxial mechanical properties of the native and glutaraldehyde-treated aortic valve cusp: Part II--A structural constitutive model. J Biomech Eng. 2000;122(4):327–335. doi: 10.1115/1.1287158. [DOI] [PubMed] [Google Scholar]
- 4.Bogaard HJ, Abe K, Vonk Noordegraaf A, Voelkel NF. The right ventricle under pressure: cellular and molecular mechanisms of right-heart failure in pulmonary hypertension. Chest. 2009;135(3):794–804. doi: 10.1378/chest.08-0492. [DOI] [PubMed] [Google Scholar]
- 5.Brand MD, Nicholls DG. Assessing mitochondrial dysfunction in cells. Biochem J. 2011;435(2):297–312. doi: 10.1042/BJ20110162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bristow MR, Zisman LS, Lowes BD, Abraham WT, Badesch DB, Groves BM, Voelkel NF, Lynch DM, Quaife RA. The pressure-overloaded right ventricle in pulmonary hypertension. Chest. 1998;114(1 Suppl):101S–106S. doi: 10.1378/chest.114.1_supplement.101s. [DOI] [PubMed] [Google Scholar]
- 7.Campo A, Mathai SC, Le Pavec J, Zaiman AL, Hummers LK, Boyce D, Housten T, Champion HC, Lechtzin N, Wigley FM, Girgis RE, Hassoun PM. Hemodynamic predictors of survival in scleroderma-related pulmonary arterial hypertension. Am J Respir Crit Care Med. 2010;182(2):252–260. doi: 10.1164/rccm.200912-1820OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Carlsson M, Ugander M, Heiberg E, Arheden H. The quantitative relationship between longitudinal and radial function in left, right, and total heart pumping in humans. Am J Physiol Heart Circ Physiol. 2007;293(1):H636–H644. doi: 10.1152/ajpheart.01376.2006. [DOI] [PubMed] [Google Scholar]
- 9.Caulfield JB, Borg TK. The collagen network of the heart. Lab Invest. 1979;40(3):364–372. [PubMed] [Google Scholar]
- 10.Champion HC, Michelakis ED, Hassoun PM. Comprehensive invasive and noninvasive approach to the right ventricle-pulmonary circulation unit: state of the art and clinical and research implications. Circulation. 2009;120(11):992–1007. doi: 10.1161/CIRCULATIONAHA.106.674028. [DOI] [PubMed] [Google Scholar]
- 11.Chance B, Williams GR. Respiratory enzymes in oxidative phosphorylation. I. Kinetics of oxygen utilization. J Biol Chem. 1955;217(1):383–393. [PubMed] [Google Scholar]
- 12.Choi HS, Vito RP. Two-dimensional stress-strain relationship for canine pericardium. J Biomech Eng. 1990;112(2):153–159. doi: 10.1115/1.2891166. [DOI] [PubMed] [Google Scholar]
- 13.Chuong CJ, Sacks MS, Templeton G, Schwiep F, Johnson RL., Jr Regional deformation and contractile function in canine right ventricular free wall. Am J Physiol. 1991;260(4 Pt 2):H1224–H1235. doi: 10.1152/ajpheart.1991.260.4.H1224. [DOI] [PubMed] [Google Scholar]
- 14.Cohn JN, Ferrari R, Sharpe N. Cardiac remodeling--concepts and clinical implications: a consensus paper from an international forum on cardiac remodeling. Behalf of an International Forum on Cardiac Remodeling. J Am Coll Cardiol. 2000;35(3):569–582. doi: 10.1016/s0735-1097(99)00630-0. [DOI] [PubMed] [Google Scholar]
- 15.Courtney T, Sacks MS, Stankus J, Guan J, Wagner WR. Design and analysis of tissue engineering scaffolds that mimic soft tissue mechanical anisotropy. Biomaterials. 2006;27(19):3631–3638. doi: 10.1016/j.biomaterials.2006.02.024. [DOI] [PubMed] [Google Scholar]
- 16.D'Alonzo GE, Barst RJ, Ayres SM, Bergofsky EH, Brundage BH, Detre KM, Fishman AP, Goldring RM, Groves BM, Kernis JT, PS L, Pietra GG, Reid LM, Reeves JT, Rich S, Vreim CE, Williams GW, Wu M. Survival in patients with primary pulmonary hypertension. Results from a national prospective registry. Ann Intern Med. 1991;115(5):343–349. doi: 10.7326/0003-4819-115-5-343. [DOI] [PubMed] [Google Scholar]
- 17.Eriksson TS, Prassl AJ, Plank G, Holzapfel GA. Modeling the dispersion in electromechanically coupled myocardium. Int j numer method biomed eng. 2013;29(11):1267–1284. doi: 10.1002/cnm.2575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Faber MJ, Dalinghaus M, Lankhuizen IM, Steendijk P, Hop WC, Schoemaker RG, Duncker DJ, Lamers JM, Helbing WA. Right and left ventricular function after chronic pulmonary artery banding in rats assessed with biventricular pressure-volume loops. Am J Physiol Heart Circ Physiol. 2006;291(4):H1580–H1586. doi: 10.1152/ajpheart.00286.2006. [DOI] [PubMed] [Google Scholar]
- 19.Fata B, Zhang W, Amini R, Sacks M. Insights into Regional Adaptations in the Growing Pulmonary Artery Using a Meso-Scale Structural Model: Effects of Ascending Aorta Impingement. J Biomech Eng. 2014 doi: 10.1115/1.4026457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fisher MR, Forfia PR, Chamera E, Housten-Harris T, Champion HC, Girgis RE, Corretti MC, Hassoun PM. Accuracy of Doppler echocardiography in the hemodynamic assessment of pulmonary hypertension. Am J Respir Crit Care Med. 2009;179(7):615–621. doi: 10.1164/rccm.200811-1691OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Forfia PR, Fisher MR, Mathai SC, Housten-Harris T, Hemnes AR, Borlaug BA, Chamera E, Corretti MC, Champion HC, Abraham TP, Girgis RE, Hassoun PM. Tricuspid annular displacement predicts survival in pulmonary hypertension. Am J Respir Crit Care Med. 2006;174(9):1034–1041. doi: 10.1164/rccm.200604-547OC. [DOI] [PubMed] [Google Scholar]
- 22.Forfia PR, Mathai SC, Fisher MR, Housten-Harris T, Hemnes AR, Champion HC, Girgis RE, Hassoun PM. Hyponatremia predicts right heart failure and poor survival in pulmonary arterial hypertension. Am J Respir Crit Care Med. 2008;177(12):1364–1369. doi: 10.1164/rccm.200712-1876OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Freed AD, Einstein DR, Vesely I. Invariant formulation for dispersed transverse isotropy in aortic heart valves: an efficient means for modeling fiber splay. Biomech Model Mechanobiol. 2005;4(2–3):100–117. doi: 10.1007/s10237-005-0069-8. [DOI] [PubMed] [Google Scholar]
- 24.Fung YC. Biomechanics: Mechanical Properties of Living Tissues. New York: Springer Verlag; 1993. [Google Scholar]
- 25.Galie N, Hoeper MM, Humbert M, Torbicki A, Vachiery JL, Barbera JA, Beghetti M, Corris P, Gaine S, Gibbs JS, Gomez-Sanchez MA, Jondeau G, Klepetko W, Opitz C, Peacock A, Rubin L, Zellweger M, Simonneau G. Guidelines for the diagnosis and treatment of pulmonary hypertension: the Task Force for the Diagnosis and Treatment of Pulmonary Hypertension of the European Society of Cardiology (ESC) and the European Respiratory Society (ERS), endorsed by the International Society of Heart and Lung Transplantation (ISHLT) Eur Heart J. 2009;30(20):2493–2537. doi: 10.1093/eurheartj/ehp297. [DOI] [PubMed] [Google Scholar]
- 26.Gasser TC, Ogden RW, Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J R Soc Interface. 2006;3(6):15–35. doi: 10.1098/rsif.2005.0073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.George MP, Champion HC, Pilewski JM. Lung transplantation for pulmonary hypertension. Pulm Circ. 2011;1(2):182–191. doi: 10.4103/2045-8932.83455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Grossman W, Jones D, McLaurin LP. Wall stress and patterns of hypertrophy in the human left ventricle. J Clin Invest. 1975;56(1):56–64. doi: 10.1172/JCI108079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Grossman W, Paulus WJ. Myocardial stress and hypertrophy: a complex interface between biophysics and cardiac remodeling. J Clin Invest. 2013;123(9):3701–3703. doi: 10.1172/JCI69830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hemnes AR, Champion HC. Right heart function and haemodynamics in pulmonary hypertension. International Journal of Clinical Practice. 2008;62:11–19. doi: 10.1111/j.1742-1241.2008.01812.x. [DOI] [PubMed] [Google Scholar]
- 31.Holzapfel GA. Nonlinear solid mechanics : a continuum approach for engineering. Chichester; New York: Wiley; 2000. [Google Scholar]
- 32.Holzapfel GA, Gasser TC. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity. 2000;61:1–48. [Google Scholar]
- 33.Horowitz A, Lanir Y, Yin FC, Perl M, Sheinman I, Strumpf RK. Structural three-dimensional constitutive law for the passive myocardium. J Biomech Eng. 1988;110(3):200–207. doi: 10.1115/1.3108431. [DOI] [PubMed] [Google Scholar]
- 34.Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Mathematical models and methods in applied sciences. 2002;12(3):407–430. [Google Scholar]
- 35.Jammalamadaka SR, Sengupta A. Topics in circular statistics. River Edge, N.J.: World Scientific; 2001. [Google Scholar]
- 36.Janicki JS, Brower GL, Gardner JD, Forman MF, Stewart JA, Jr, Murray DB, Chancey AL. Cardiac mast cell regulation of matrix metalloproteinase-related ventricular remodeling in chronic pressure or volume overload. Cardiovasc Res. 2006;69(3):657–665. doi: 10.1016/j.cardiores.2005.10.020. [DOI] [PubMed] [Google Scholar]
- 37.Karlon WJ, Covell JW, McCulloch AD, Hunter JJ, Omens JH. Automated measurement of myofiber disarray in transgenic mice with ventricular expression of ras. Anat Rec. 1998;252(4):612–625. doi: 10.1002/(SICI)1097-0185(199812)252:4<612::AID-AR12>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 38.Kass DJ, Rattigan E, Kahloon R, Loh K, Yu L, Savir A, Markowski M, Saqi A, Rajkumar R, Ahmad F, Champion HC. Early treatment with fumagillin, an inhibitor of methionine aminopeptidase-2, prevents Pulmonary Hypertension in monocrotaline-injured rats. PLoS One. 2012;7(4):e35388. doi: 10.1371/journal.pone.0035388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kuehne T, Yilmaz S, Steendijk P, Moore P, Groenink M, Saaed M, Weber O, Higgins CB, Ewert P, Fleck E, Nagel E, Schulze-Neick I, Lange P. Magnetic resonance imaging analysis of right ventricular pressure-volume loops: in vivo validation and clinical application in patients with pulmonary hypertension. Circulation. 2004;110(14):2010–2016. doi: 10.1161/01.CIR.0000143138.02493.DD. [DOI] [PubMed] [Google Scholar]
- 40.Lin DH, Yin FC. A multiaxial constitutive law for mammalian left ventricular myocardium in steady-state barium contracture or tetanus. J Biomech Eng. 1998;120(4):504–517. doi: 10.1115/1.2798021. [DOI] [PubMed] [Google Scholar]
- 41.Mahan RP. Special Report 16. Alexandria, Virginia: United States Army Research Institute for the Behavioral and Social Sciences; 1991. Circular Statistical Methods: Applications in Spatial and Temporal Performance Analysis. [Google Scholar]
- 42.Maughan WL, Shoukas AA, Sagawa K, Weisfeldt ML. Instantaneous pressure-volume relationship of the canine right ventricle. Circ Res. 1979;44(3):309–315. doi: 10.1161/01.res.44.3.309. [DOI] [PubMed] [Google Scholar]
- 43.Onat ET, Leckie FA. Representation of Mechanical-Behavior in the Presence of Changing Internal Structure. Journal of Applied Mechanics- Transactions of the Asme. 1988;55(1):1–10. [Google Scholar]
- 44.Rain S, Handoko ML, Trip P, Gan CT, Westerhof N, Stienen GJ, Paulus WJ, Ottenheijm CA, Marcus JT, Dorfmuller P, Guignabert C, Humbert M, Macdonald P, Dos Remedios C, Postmus PE, Saripalli C, Hidalgo CG, Granzier HL, Vonk- Noordegraaf A, van der Velden J, de Man FS. Right ventricular diastolic impairment in patients with pulmonary arterial hypertension. Circulation. 2013;128(18):2016–2025. 1–10. doi: 10.1161/CIRCULATIONAHA.113.001873. [DOI] [PubMed] [Google Scholar]
- 45.Sacks M. Biaxial mechanical evaluation of planar biological materials. Journal of Elasticity. 2000;61:199–246. [Google Scholar]
- 46.Sacks MS. Incorporation of experimentally-derived fiber orientation into a structural constitutive model for planar collagenous tissues. J Biomech Eng. 2003;125(2):280–287. doi: 10.1115/1.1544508. [DOI] [PubMed] [Google Scholar]
- 47.Sacks MS, Chuong CJ. Orthotropic mechanical properties of chemically treated bovine pericardium. Ann Biomed Eng. 1998;26(5):892–902. doi: 10.1114/1.135. [DOI] [PubMed] [Google Scholar]
- 48.Sanz J, Garcia-Alvarez A, Fernandez-Friera L, Nair A, Mirelis JG, Sawit ST, Pinney S, Fuster V. Right ventriculo-arterial coupling in pulmonary hypertension: a magnetic resonance study. Heart. 2012;98(3):238–243. doi: 10.1136/heartjnl-2011-300462. [DOI] [PubMed] [Google Scholar]
- 49.Streeter DD, Jr, Spotnitz HM, Patel DP, Ross J, Jr, Sonnenblick EH. Fiber orientation in the canine left ventricle during diastole and systole. Circ Res. 1969;24(3):339–347. doi: 10.1161/01.res.24.3.339. [DOI] [PubMed] [Google Scholar]
- 50.Suga K, Sagawa H. Instantaneous pressure-volume relationships and their ratio in the excised, supported canine left ventricle. Circ Res. 1974;35(1):117–126. doi: 10.1161/01.res.35.1.117. [DOI] [PubMed] [Google Scholar]
- 51.Sugden PH, Clerk A. Cellular mechanisms of cardiac hypertrophy. J Mol Med (Berl) 1998;76(11):725–746. doi: 10.1007/s001090050275. [DOI] [PubMed] [Google Scholar]
- 52.Sun W, Sacks MS, Sellaro TL, Slaughter WS, Scott MJ. Biaxial mechanical response of bioprosthetic heart valve biomaterials to high in-plane shear. Journal Biomechanical Engineering. 2003;125:372–380. doi: 10.1115/1.1572518. [DOI] [PubMed] [Google Scholar]
- 53.Tedford RJ, Mudd JO, Girgis RE, Mathai SC, Zaiman AL, Housten-Harris T, Boyce D, Kelemen BW, Bacher AC, Shah AA, Hummers LK, Wigley FM, Russell SD, Saggar R, Saggar R, Maughan WL, Hassoun PM, Kass DA. Right ventricular dysfunction in systemic sclerosis-associated pulmonary arterial hypertension. Circ Heart Fail. 2013;6(5):953–963. doi: 10.1161/CIRCHEARTFAILURE.112.000008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tonelli AR, Arelli V, Minai OA, Newman J, Bair N, Heresi GA, Dweik RA. Causes and circumstances of death in pulmonary arterial hypertension. Am J Respir Crit Care Med. 2013;188(3):365–369. doi: 10.1164/rccm.201209-1640OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Trip P, Nossent EJ, de Man FS, van den Berk IA, Boonstra A, Groepenhoff H, Leter EM, Westerhof N, Grunberg K, Bogaard HJ, Vonk Noordegraaf A. Severely reduced diffusion capacity in idiopathic pulmonary arterial hypertension - patient characteristics and treatment responses. Eur Respir J. 2013 doi: 10.1183/09031936.00184412. [DOI] [PubMed] [Google Scholar]
- 56.Valdez-Jasso D, Simon MA, Champion HC, Sacks MS. A murine experimental model for the mechanical behaviour of viable right-ventricular myocardium. The Journal of Physiology. 2012;590(18):4571–4584. doi: 10.1113/jphysiol.2012.233015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Voelkel NF, Natarajan R, Drake JI, Bogaard HJ. Right ventricle in pulmonary hypertension. Compr Physiol. 2011;1(1):525–540. doi: 10.1002/cphy.c090008. [DOI] [PubMed] [Google Scholar]