Unintentional movements produced by back-coupling between the actual and referent body configurations: Violations of equifinality in multi-joint positional tasks

Abstract

We tested several predictions of a recent theory that combines the ideas of control with referent configurations, hierarchical control, and the uncontrolled manifold (UCM) hypothesis. In particular, we tested a hypothesis that unintentional changes in hand coordinate can happen following a long-lasting transient perturbation. The subjects grasped a handle with the right hand, occupied an initial position against a bias force produced by the Hapticmaster robot, and then tried not to react to changes in the robot-produced force. Changes in the force were smooth and transient; they always ended with the same force as the bias force. The force-change amplitude and the time the force was kept at the new level (dwell time) varied across conditions. After the transient force change was over, the handle rested in a position that differed significantly from the initial position. The amplitude of this unintentional movement increased with the amplitude of transient force change and with the dwell time. In the new position, the across-trials joint configuration variance was mostly confined to a sub-space compatible with the average handle coordinate and orientation (the UCMs for these variables). We view these results as the first experimental support for the hypothesis on back-coupling between the referent and actual body configurations during multi-joint actions. The results suggest that, even under the instruction “not to react to transient force changes”, the subjects may be unable to prevent unintentional drift of the referent configuration. The structure of joint configuration variance after such movements was similar to that in earlier reports on joint configuration variance after intentional movements. We conclude that the intentional and unintentional movements are products of a single neural system that can lead to intentional and unintentional shifts of the referent body configuration.

Introduction

Natural human movements involve redundant sets of elements at any level of analysis (Bernstein 1967). This means that the number of variables produced by the elements (elemental variables) is larger than the number of constraints associated with typical tasks. The problem of coordinating such apparently redundant sets of elemental variables has recently been reformulated within the principle of motor abundance (Latash 2012). According to this view, the central nervous system is not searching for unique (maybe optimal) solutions for such problems but uses all the elemental variables to ensure stability of important performance variables and also a possibility to perform other tasks with the same set of elemental variables (reviewed in Latash et al. 2007). As a result, families of solutions are observed across repetitive attempts at the same task.

Several recent studies have attempted to combine the principle of abundance with the idea of control with referent body configuration (RCs) and hierarchical organization of the neural control of movements (Latash et al. 2007; Martin et al. 2009; Latash 2010). These schemes accept that the neural control of movement can be adequately described as setting referent values for salient variables at the highest (task) level (Latash et al. 2009; Feldman 2010). The difference between the RC and actual body configuration drives muscle activations in a way that moves the actual configuration towards the RC. A sequence of few-to-many transformations leads to inputs into alpha-motoneuronal pools controlling the involved muscles according to the ideas of the equilibrium-point hypothesis (Feldman 1966, 1986).

The scheme introduced by Martin, Scholz, and Schöner (2009) involves two types of relations between RC and actual body configuration. First, as mentioned above, RC attracts the actual configuration (direct coupling). Second, this scheme postulates the existence of back-coupling, that is, shifts of RC produced by the difference between the actual configuration and RC. The back-coupling was assumed to update the trajectory of the referent joint configuration within the null-space of end-effector motion, such that joint configuration yielded in directions that did not affect the end-effector path (a similar idea was suggested in Latash et al. 2005). Until recently, the idea of back-coupling has been purely theoretical.

A recent study has provided the first evidence for the hypothesized back-coupling and suggested that its effects were not limited to the null-space of end-effector motion (Ambike et al. in press). In that study, the subjects held a handle using a prismatic grasp (the thumb opposing the four fingers). The width of the handle changed slowly (over 1 cm at 1.8 mm/s), first it expanded and then contracted to the initial width. The subjects were instructed not to react to possible digit force changes induced by the handle motion. After the transient change in the handle width, the grip force dropped by about 25% without the subjects being aware of these effects. The grip force drop was interpreted as a reflection of the back-coupling between the referent and actual digit tip coordinates.

The main purpose of this study has been to test the hypotheses that back-coupling leads to shifts in RC (Hypothesis 1), these shifts increase with time during which the actual body configuration is kept far away from the RC (Hypothesis 2), and these shifts increase with the magnitude of the difference between RC and actual body configuration (Hypothesis 3). We used a HapticMaster robot to introduce smooth, transient changes in the external force applied to the handle gripped by the subjects. Across all conditions, the subjects were instructed not to interfere with possible motion of the handle (“allow the robot to move your arm”). The force change by the HapticMaster was quick and smooth (over about 0.5 s), followed by varying dwell time, after which the force returned to the bias level; the force change could lead to a large or small handle deviation. In all conditions, the final force was always the same as the initial force. Given the smoothness of the force changes, the handle was expected to come to the same coordinate after the perturbation (cf. equifinality, Bizzi et al. 1976; Kelso and Holt 1980; Schmidt and McGown 1980; Latash and Gottlieb 1990). This expectation was violated.

We assumed that any consistent changes in the final steady-state of the arm compared to the initial steady-state were due to unintentional changes in the hand RC interpreted as a consequence of the back-coupling between RC and actual configuration (test of Hypothesis 1). We explored the dependence of the difference between the initial and final steady-states on the duration of the time interval over which the perturbing force was applied (dwell time, T_DWELL) and on the actual maximal deviations of the hand caused by the force application. These analyses tested Hypotheses 2 and 3. We also performed analysis of the structure of inter-trial joint configuration variance within the framework of the uncontrolled manifold (UCM) hypothesis (reviewed in Latash et al. 2002, 2007). This analysis explored the structure of variance during the unintentional movements.

Methods

Participants

Four male subjects (all self-reported right-handed) and four female subjects (one left-handed) with the mean age 28.8 ± 0.8 years (mean ± standard error), mean height 1.69 ± 0.04 m, and mean mass 65.5 ± 4.2 kg took part in this study. All subjects were healthy and had no history of hand injury. All subjects provided informed consent in accordance with the procedures approved by the Office for Research Protection of the Pennsylvania State University.

Apparatus and Procedure

Experimental setup

The HapticMaster (Moog, The Netherlands) is an admittance-controlled robot with an arm that possesses three degrees of freedom (DOFs). A handle with three kinematic DOFs - pitch, roll and yaw - was attached to the end of the robot arm. The robot arm was used to generate both baseline force (F_BASE) and perturbation force (F_PERT) (details in Procedures). A laser pointer was used to align the height of the robot arm with the shoulder height of the subject sitting in a chair. Visual feedback was presented with a 20-inch monitor placed 0.8 m from the subject.

Each subject sat upright in the chair and held the handle attached to the robot arm with the right hand. One reflective marker was placed on the suprasternal notch (SN) and another marker was placed 2 cm below the acromion process (AP). Three-dimensional coordinates of the suprasternal notch (SN) marker were used as the origin of the XYZ global coordinate system {G}. The X-axis was a horizontal axis in a sagittal plane pointing in the anterior direction, the Y-axis was a horizontal axis in a frontal plane pointing to right side of the subject, and the Z-axis pointed vertically upward. The height of the robot arm and the position of the chair were adjusted so that the laser beam pointed at the marker 2 cm below AP. The robot arm was aligned such that the subject’s hand moved primarily in a parasagittal plane. Deviations of the arm motion from the parasagittal plane were relatively small (see Results). Note that all the kinematic analyses were performed in the 3D space and having the arm motion confined to a parasagittal plane was not critical.

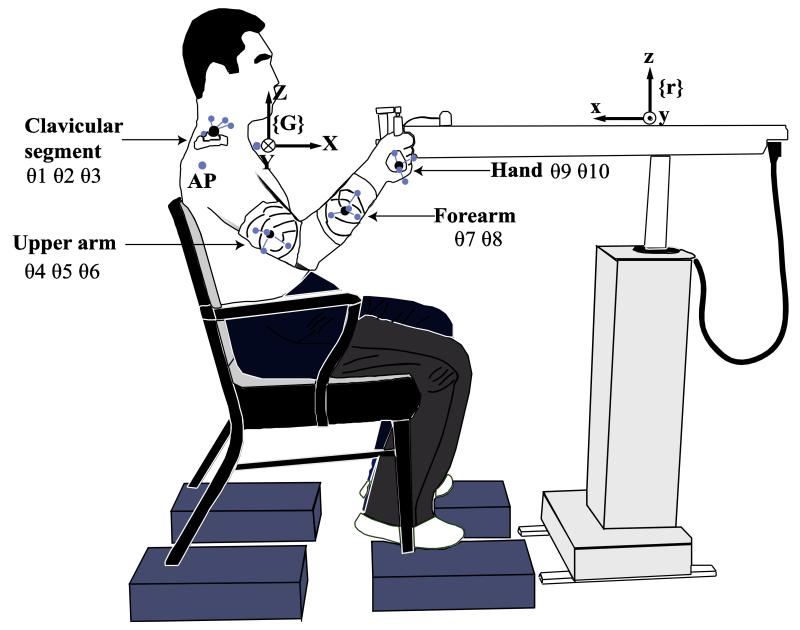
The subject selected a comfortable hand position, from which the hand could move 20 cm freely along positive (X+) direction in the global coordinate system. The 3D position of the handle of the robot arm was set as the initial position by the robot control program. The initial position was also set as the origin of the robot coordinate system. The axes of the robot coordinate system {r} (x^r y^r z^r) were parallel to the axes of the global coordinate system {G} (X Y Z). The directions of x^r and y^r were opposite to the directions of X and Y, while the direction of z^r coincided with that of Z. The global and robot coordinate systems, as well as the initial joint configuration of the subject, are illustrated in Figure 1.

Figure 1.

An illustration of the initial posture. The subject sits in a chair, using the right arm to hold the handle in an initial position. The robot arm is aligned such that the subject’s hand moves primarily in a parasagittal plane. The marker clusters and additional markers that are used to determine the joint locations and segment lengths are shown. {G} and {r} show the Global and the Robot Coordinate Systems respectively.

Kinematic data collection

A Qualisys Motion Capture System (Qualisys AB, Sweden), consisting of five ProReflex MCU240 infrared light emitting cameras, was used to record three-dimensional (3D) kinematic data at 120 Hz. The five cameras were mounted on tripods positioned around the experimental space. A 30-cm wand was used for the calibration of camera system. Calibration was considered to be successful if the standard deviation of the wand length was less than 1 mm.

Marker clusters, molded to fit body segments, (four markers per cluster, see Mattos et al. 2011) were used to track positions and orientations of right arm segments. These clusters were placed at the following positions: (1) the upper torso, at two-thirds of the distance between the neck and the acromion process; (2) the upper arm, at the half-distance of the lateral midline; (3) the dorsal surface of the forearm, at two-thirds of the length; and (4) the dorsal surface of the hand. Self-adherent wrap (Coban™ LF, 3M) and surgical tape (Transpore™, 3M) was used to fasten the clusters.

Additional four markers were attached to the subject’s body to calibrate the kinematical model; these markers were removed before the main experiment. The markers were attached at: 1) medial and 2) lateral epicondyles of humerus; 3) ulnar and 4) radial styloid processes. These markers were used to calculate limb segment lengths and joint centers. For this procedure, subjects maintained a steady anatomical calibration posture with the right arm parallel to the floor in a parasagittal plane, elbow joint fully extended, and wrist in a neutral position. The zero angle of each joint was defined using this posture. Each limb segment had its own local xyz coordinate system whose origin was at the proximal joint center and the axes were aligned with XYZ.

Experimental procedure

Each trial started with the subject in the initial configuration: Sitting in the chair and holding the handle with the right arm. The robot generated a constant baseline force (F_BASE+) along positive X+ axis. For males, F_BASE+ was 10 N while it was 5 N for females. These values were selected rather arbitrarily to make sure that the subject’s hand acted against a well-defined external force in the initial configuration and the force did not produce fatigue. The subject was instructed to resist the baseline force and maintain the initial joint configuration and position.

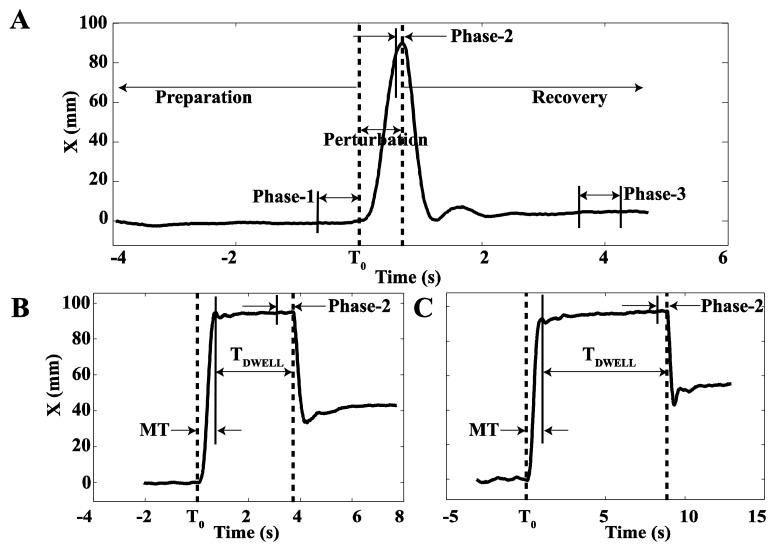
Each trial consisted of three phases. The first phase, Preparation, was a steady state until perturbation onset (T₀, Figure 2). During the second phase, Perturbation, the force produced by the robot increased; the final phase was Recovery, in which the robot force returned to F_BASE.

Figure 2.

A: A typical hand trajectory along X direction in the global coordinate system with zero dwell time (T_DWELL = TS). The time before T₀ is Preparation (shown by the left arrow), in which the subject holds a position against F_BASE. The time between T₀ and the time when the force returns to F_BASE is Perturbation (shown by the double-arrow line). The two dashed lines show the start and the end of the perturbation force (F_PERT). The directions of both F_BASE and F_PERT are along positive X (X+). The right arrow on the right of the second dashed line shows Recovery, when the force is back to F_BASE. Three phases for analysis were: Phase-1, the 0.5 s time interval prior to T₀; Phase-2, the 0.1 s time interval prior to the initiation of F_PERT drop, and Phase-3, the 0.5 s time interval that ended 0.5 s before the end of the trial. B: A typical hand trajectory along X direction in the global coordinate system with T_DWELL = 3 s (TM). Phase-2 is the 0.5 s time interval prior to the initiation of F_PERT drop. Perturbation time (PT) is the sum of movement time (MT) and T_DWELL. C: A typical hand trajectory with T_DWELL = 8 s (TL). Phase-2 is the 0.5 s time interval prior to the initiation of F_PERT drop.

During Preparation, the subject was required to hold the handle against F_BASE. This part lasted for 2 – 4 s. During the next two phases, the subject was instructed not to interfere voluntarily (“allow the robot to move your arm, do not relax and do not resist”) (Feldman 1966; Latash 1994). After T₀, the robot force increased in the same direction as F_BASE and the subject’s hand was pulled away from the subject. During the perturbation, peak velocity (V_PEAK) of the handle was computed on-line. The perturbation force increased to a new level over 500 ms in a ramp fashion and was kept at that level until the handle velocity dropped under 10% V_PEAK, which was used as the criterion for the pause in the movement. Movement time was defined as time elapsed from the initiation of the perturbation to the time when the movement paused. The perturbation distance depended on the new force level set in the robot control program. Before experiment, the subject was given a few trials for practice. During those practice trials, appropriate magnitudes of F_PERT were defined, which moved the handle over about 10 cm (small perturbation) and 15 cm (large perturbation) away from its initial position by the time the robot paused. During small perturbations, the magnitude of F_PERT was, on average, 18.8 ± 1.3 N for males and 11.2 ± 1.3 N for females while for the large perturbation the magnitude of F_PERT was 30.0 ± 2.0 N for males and 19.8 ± 3.5 N for females. The update rate of the robot was 60 Hz. Given the magnitudes of F_PERT, the rate of force change was relatively small; it varied from about 22 N/s to about 40 N/s. As a result, the handle excursion was approximately matched across subjects while F_PERT magnitude varied from subject to subject.

After the handle velocity dropped under 10% V_PEAK, the program started to count dwell time (T_DWELL). T_DWELL could be 0 s, 3 s or 8 s. If T_DWELL was 0 s, F_PERT was immediately removed over 0.5 s after the handle velocity dropped to 10% V_PEAK. For larger T_DWELL, the robot paused for 3 s or 8 s. Perturbation time was defined as the sum of movement time and dwell time. After the robot force changes were over, the subject kept the final position for 2 – 3 s and then released the handle; the handle returned to the initial position, and the system was ready for the next trial.

Given different combinations of perturbation distance (D_PERT) and T_DWELL, there were six conditions: Two D_PERT (short and long) × three T_DWELL (short, medium, and long). Subjects performed each condition 20 times (120 trials in total). Trials were blocked, while conditions were randomized. Short rest intervals were offered between trials within a condition (about 5 s), while 1-min rest was given between conditions.

Data Processing

The data were analyzed with a customized Matlab program (Mathworks Inc, MA, USA). Marker coordinates were low-pass filtered at 5 Hz with a zero-lag 4^th-order Butterworth filter. Joint angles between two adjacent segments were calculated in the following steps; first, the relationship between the orientation of each segment and its orientation in the anatomical calibration posture was derived from marker coordinates to represent the rotation matrices; next, rotation matrices were obtained for the relative orientation of distal segments with regard to proximate segments. Next, matrices of relative orientation were parsed into angles between adjacent segments using Euler’s Zx’y’’ sequence. The second rotation was performed around the local x-axis, which was rotated previously around the global Z-axis. The third rotation was around the local y-axis, which was rotated previously around the global Z-axis and then around the x-axis. Finally, ten angles were computed for further analyses (Figure 1): three angles for the clavicular rotation relative to the trunk (θ1—about z-axis, θ2—about x-axis, and θ3—about y-axis), three angles for the relative rotation of the upper arm (θ4—about z-axis, θ5—about x-axis, and θ6—about y-axis), two angles for the relative rotation of the forearm (θ7—about estimated x-axis oblique to the local coordinate system and θ8—about y-axis), and two angles for the relative rotation of the hand (θ9—about z-axis, θ10—about x-axis). The ten angles formed the joint configuration vector, $\overrightarrow{\theta }$.

The trials were aligned in time according to perturbation onset (T₀). At each frame, joint angles were averaged across trials for each condition separately to obtain the average joint configuration vector ($\overline{\overrightarrow{\theta }}$). Elemental variables ($\overrightarrow{\theta }$) and two performance variables -- hand position (X-, Y- and Z- coordinates) and hand orientation (α, β and γ—orientation angles of the hand, the first rotation α about Z, the second rotation β about x’, the third rotation γ about y’’) -- were linked together with a forward kinematic model (Scholz et al. 2000). A Jacobian matrix, $\mathbf{J}\left(\overline{\overrightarrow{\theta }}\right)$, was deduced from the forward kinematic model for each time step to determine the relationship between infinitesimal deviations of joint angles from the average configuration vector and the change of selected performance variables. Subsequently, singular value decomposition (SVD) was used to compute the null-space of $\mathbf{J}\left(\overline{\overrightarrow{\theta }}\right)$. This null-space was taken as a linear approximation of the uncontrolled manifold (UCM).

Variance per DOF within the UCM and orthogonal sub-space was:

$$V_{UCM}=\frac{\sum {\mid {\overrightarrow{\theta }}_{UCM}-\overline{{\overrightarrow{\theta }}_{UCM}}\mid }^2}{(\mathrm{n}-\mathrm{d})\cdot {\mathrm{N}}_{\text{trial}}}$$ (1)

$$V_{ORT}=\frac{\sum {\mid {\overrightarrow{\theta }}_{ORT}-\overline{{\overrightarrow{\theta }}_{ORT}}\mid }^2}{\mathrm{d}\cdot {\mathrm{N}}_{\text{trial}}}$$ (2)

Where ${\overrightarrow{\theta }}_{UCM}$ and ${\overrightarrow{\theta }}_{ORT}$ are projections of joint configuration onto the UCM and its orthogonal complement; $\overline{{\overrightarrow{\theta }}_{UCM}}$ and $\overline{{\overrightarrow{\theta }}_{ORT}}$ are the corresponding averaged joint configuration projections across trials. n = 10 is the dimensionality of joint angles, $\overrightarrow{\theta }$. N_trial is the number of trials used in the analysis. The dimensionality of each performance variable, position and orientation, is d = 3.

The total variance V_TOT was computed as

$$V_{TOT}=\frac{\sum {\mid \overrightarrow{\theta }-\overline{\overrightarrow{\theta }}\mid }^2}{n\cdot {\mathrm{N}}_{\text{trial}}}$$ (3)

All variance indices in (1) - (3) are computed per DOF. Further, an index of synergy (ΔV) was computed:

$$\Delta V=\frac{V_{UCM}-V_{ORT}}{V_{TOT}}$$ (4)

For statistical analysis, modified Fisher’s z-transform was applied to ΔV (Solnik et al. 2013):

$$\Delta V_Z=\frac{1}{2}\cdot \log \left(\frac{\mid \Delta V_{lower}\mid +\Delta V}{\Delta V_{upper}-\Delta V}\right)-\frac{1}{2}\cdot \log \left(\frac{\mid \Delta V_{lower}\mid }{\Delta V_{upper}}\right)$$ (5)

Here ΔV_upper and ΔV_lower are the upper limit and the lower limit of ΔV, respectively. The log transformation here was used to ensure normality of the outcome variable, which could be violated due to the limits of ΔV inherent to its calculation. V_UCM > V_ORT (ΔV > 0) was interpreted as a synergy in the joint configuration space stabilizing the performance variable (cf. Latash et al. 2007).

Overall, six dependent variables were calculated: V_UCM-P, V_ORT-P, and ΔV_Z-P with respect to hand position and V_UCM-O, V_ORT-O, and ΔV_Z-O with respect to hand orientation.

Three time intervals were extracted from the three phases of each trial for further analysis. During Preparation, the 0.5 s time interval prior to T₀ was defined as Phase-1. During Perturbation, for T_DWELL = 0 s, Phase-2 was defined as the 0.1 s time interval prior to the initiation of F_PERT drop; for T_DWELL = 3 s and T_DWELL = 8 s, Phase-2 was defined as the final 0.5 s of the perturbation time. During Recovery, Phase-3 was defined as the 0.5 s time interval that ended 0.5 s before the end of the trial (see Figure 2). The variance indices were averaged over each of the three phases for further processing.

The coordinates of the suprasternal notch (SN) marker were subtracted from the coordinates of all markers. To obtain the hand coordinates, one marker of the hand marker cluster was selected to represent the hand. The hand coordinates were averaged over each of the three phases in each trial and the Euclidean distance of the hand was calculated between 1) Phase-1 and Phase-2 (D12), and 2) Phase-1 and Phase-3 (D13). The mean hand Euler angles relative to global coordinate system were also calculated for the three phases. The absolute differences in the angles between Phase-1 and Phase-2 and between Phase-1 and Phase-3 were computed similarly to the computation for the hand coordinates.

Statistics

All descriptive statistics are reported in the text and figures as means and standard errors unless stated otherwise. Three-way repeated-measures ANOVAs were used to test effect of D_PERT (short and long), T_DWELL [short (0 s), medium (3 s), and long (8 s)] and Phase (Perturbation and Recovery) on the hand position and the hand orientation across trials. Four-way repeated-measures ANOVAs were used to test effect of D_PERT, T_DWELL, Phase and Variable (two levels: position and orientation) on the variance indices computed within the UCM-based analysis, V_UCM, V_ORT, and ΔV_Z. To fulfill the assumption of normality, dependent variables were log-transformed when needed. Pairwise comparisons with Bonferroni corrections were used to explore significant effects, while post-hoc ANOVAs were performed to explore interaction effects in the three-way analysis. The statistical tests were performed with SPSS 20.0 (IBM Corporation, USA) and Matlab (Mathworks Inc, MA, USA).

Results

Hand excursion

Changes in the baseline force (F_BASE) produced by the perturbation force (F_PERT) resulted in hand motion to a new position and orientation. Deviations of the subject’s hand from a parasagittal plane were small. Before the movement, the initial angle deviations from the X-Z plane were 0.063 ± 0.025 rad for the hand, 0.41 ± 0.018 rad for the forearm and −0.486 ± 0.014 rad for the upper arm. During the movement, the average orientation change was −0.018 ± 0.005 rad for the hand, −0.036 ± 0.003 rad for the forearm and 0.064 ± 0.003 rad for the upper arm. When F_PERT was removed and the robot force returned to F_BASE, the hand moved back towards the initial position and orientation. The amount by which a subject undershot the initial position changed in a consistent way with both F_PERT magnitude and dwell time (T_DWELL). With T_DWELL = 0, little difference was observed between the hand position in Phase-1 and in Phase-3. However, with larger T_DWELL, the subject’s final hand position was farther from the initial position; in general, the longer this time, the larger the difference between the final and initial positions.

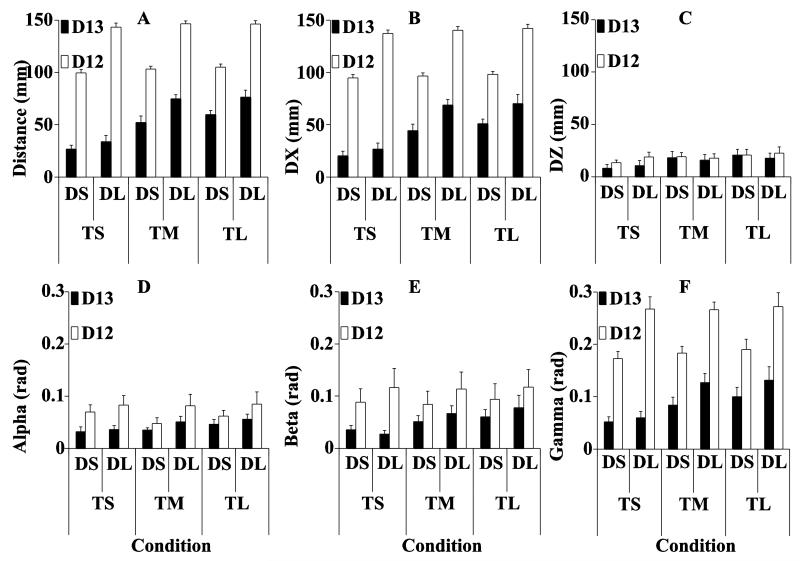
The changes in the hand coordinates and orientation angles between Phase-2 and Phase-1 (D12) and between Phase-3 and Phase-1 (D13) are illustrated in Figure 3. F_PERT was effective in inducing handle motion over different distances (D12) that were close to 10 cm and 15 cm for the short and long D_PERT conditions respectively (panel A). Following the removal of F_PERT, the handle moved towards the initial location, but stopped short of the initial position by a distance (D13) that scaled with both D_PERT (larger values for the long distance, compare the white and black bars) and T_DWELL (larger values for longer T_DWELL).

Figure 3.

The top left panel (A) shows the Euclidean distance for D12 and D13. The top middle (B) and right (C) panels show the distance for D12 and D13 along the X and Z directions separately. The bottom panels (D - F) show the absolute angle difference for D12 and for D13. Note that D12 > D13 in all conditions and for all variables. DS and DL indicate short and long perturbation distance, respectively. TS, TM and TL indicate short, medium and long dwell time, respectively. Averages across subjects are presented with standard error bars.

The changes in the D13 distance were mostly due to the handle displacement along the X-axis, DX (the direction of force vector change). These data are shown in panel B; note the similarity of the values in panels A and B. There was a consistent change in the vertical handle coordinate downwards (DZ, panel C), but the magnitude of this motion was small compared to DX, and it showed only minor effects of D_PERT and T_DWELL. The handle deviations along the Y-axis were very small and are not illustrated. Based of these observations, further we analyzed only the overall handle deviation dominated by DX.

D12 (123.60 ± 3.45 mm) was significantly larger than D13 (53.52 ± 3.37 mm) confirmed by the main effect of Phase in a three-way repeated-measures ANOVA [F_{(1, 7)} = 142.197; p < 0.01]. D13 for the large perturbation, DL (60.8 ± 5.13 mm) was significantly higher than for the small perturbation, DS (46.2 ± 4.00 mm) confirmed by the main effect of D_PERT in a two-way repeated-measures ANOVA [F_{(1, 7)} = 18.798; p < 0.01]. D13 for the short T_DWELL, TS (30.25 ± 3.48 mm) was significantly shorter than for the medium, TM (63.54 ± 4.61 mm) and long, TL (66.77 ± 4.38 mm) T_DWELL confirmed by the main effect of T_DWELL [F_{(2, 14)} = 32.887; p < 0.01]. No significant interactions were observed.

The relatively small angular handle deviations, illustrated in the lower three panels in Fig. 3, were also larger for D12 (white bars) compared to D13 (black bars), 0.071 ± 0.007 vs. 0.042 ± 0.003 rad for α [F_{(1, 7)} = 5.221, p = 0.056], 0.102 ± 0.012 vs. 0.053 ± 0.006 rad for β [F_{(1, 7)} = 88.973, p < 0.01], and 0.225 ± 0.009 vs. 0.092 ± 0.007 rad for γ [F_{(1, 7)} = 325.265, p < 0.01].

For D13, angular handle deviations for TS were always smaller than for TM and TL. For α, the deviations were 0.034 ± 0.006 vs. 0.043 ± 0.006 and 0.051 ± 0.006 rad [F_{(2, 14)} = 4.725, p < 0.05]; for β, they were 0.031 ± 0.005 vs. 0.059 ± 0.009 and 0.069 ± 0.013 rad [F_{(2, 14)} = 14.588, p < 0.01]; and for γ, they were 0.056 ± 0.007 vs. 0.106 ± 0.012 and 0.116 ± 0.015 rad [F_{(2, 14)} = 7.848, p < 0.01]; Besides, γ deviations were smaller for DS (0.079 ± 0.009 rad) compared to DL (0.106 ± 0.012 rad), confirmed by the main effect of D_PERT [F_{(1, 7)} = 23.798; p < 0.01]. No significant interactions were observed.

For D12, angular handle deviations for DS were always smaller than for DL: 0.060 ± 0.007 vs. 0.083 ± 0.012 rad for α [F_{(1, 7)} = 6.173, p < 0.05]; 0.086 ± 0.014 vs. 0.116 ± 0.019 rad for β [F_{(1, 7)} = 10.502, p < 0.05]; and 0.182 ± 0.002 vs. 0.269 ± 0.012 rad for γ [F_{(1, 7)} = 98.920, p < 0.01]. No significant effect of T_DWELL and no interactions were observed.

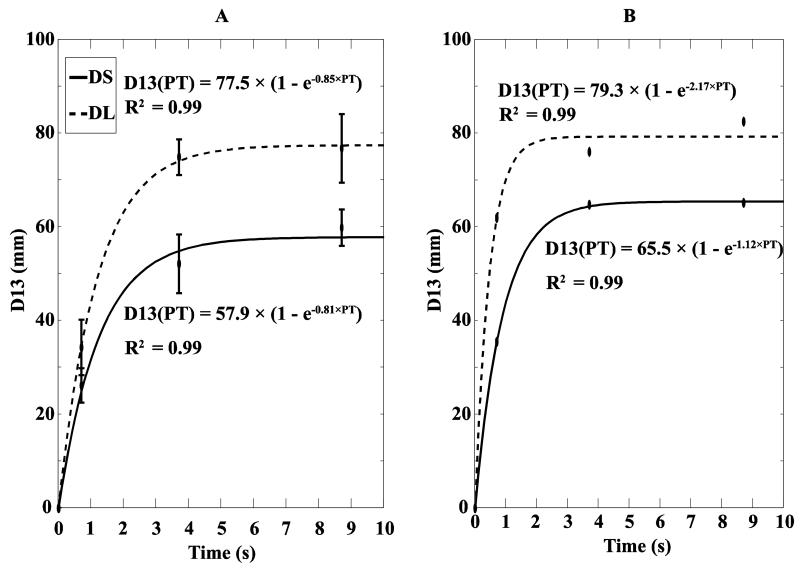
We further explored the dependence of D13 on perturbation time (PT, the sum of force-change time and T_DWELL, see Methods) using regression analysis. Figure 4 illustrates averaged across subjects data for different combination of perturbation time and perturbation distance. We assumed D13 = 0 when no perturbation was applied (based on no visible drift in the handle position during the initial steady state). An exponential function D13(PT) = a × (1 − e^{−b × PT}) was used to fit the data. For DS, the best fit was D13(PT) = 57.9 × (1 − e^{−0.81 × PT}); while for DL, it was D13(PT) = 77.5 × (1 − e^{−0.85 × PT}). Similar regression analyses were run on the data for individual subjects (a typical example is shown in Figure 4B). Paired t-tests confirmed a significant difference in the coefficient a between the small and large D_PERT (60.7 ± 4.1 vs. 82.7 ± 6.6, t₇ = 4.35, p < 0.01), while there was no significant difference in the exponent coefficient b (on average, 0.80 ± 0.15 vs. 1.06 ± 0.29).

Figure 4.

A: D13 averaged across all subjects with standard error bars. The data points correspond to the three perturbation times (the sum of movement time and T_DWELL) for the two different perturbation distances. For zero perturbation time we assume D13 = 0. Given the four points, an exponential regression D13 (PT) = a × (1 − e^{−b × PT}) was performed. The corresponding R² are provided. The solid line is for the short perturbation distance (DS); the dashed line is for the long perturbation distance (DL). B: The same data for a typical subject.

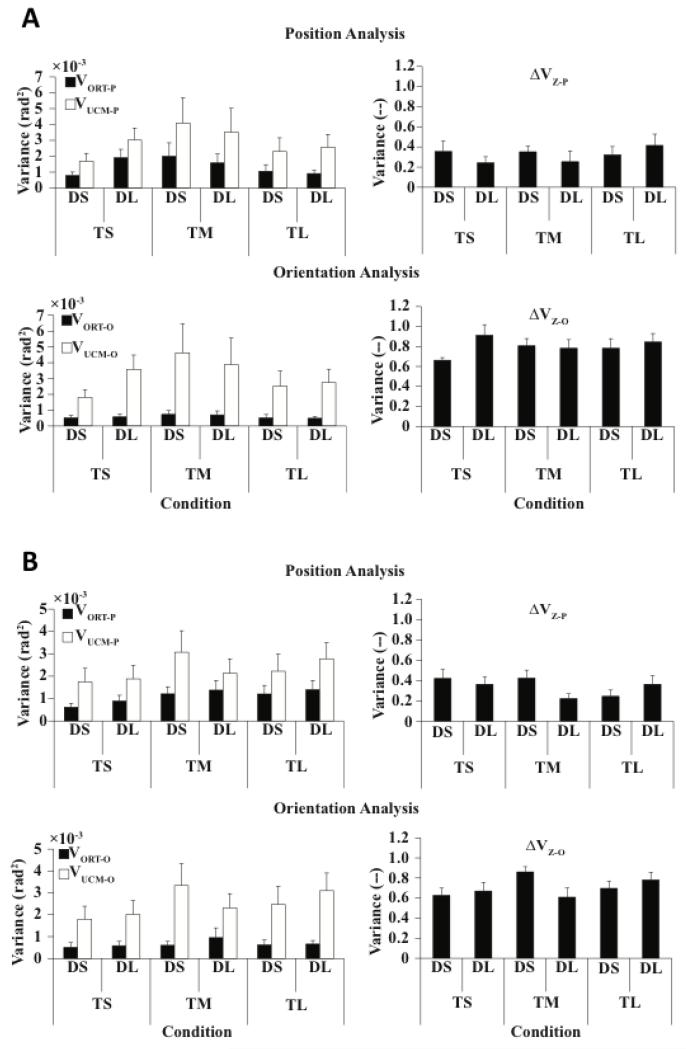
Joint configuration variance

Two components of the across-trials variance in the joint configuration space were calculated, V_UCM compatible with no changes in a selected performance variable (hand position or orientation) and V_ORT leading to changes in that variable (for details see Methods). This analysis was run for hand position and orientation separately based on the data in Phase-2 and Phase-3 (see Fig. 2).

Figure 5 illustrates the indices of joint configuration variance for D12 (Fig. 5A) and D13 (Fig. 5B). Across all six combinations of D_PERT and T_DWELL, most joint configuration variance was consistently confined within the UCM (V_UCM > V_ORT). This was true for both the position-related and orientation-related analyses as illustrated in the left panels on Fig. 5A and Fig. 5B (white columns are consistently larger than black columns). These results are also reflected in the consistently positive ΔV indices (the right panels of Fig. 5A and Fig. 5B). For the position analysis, V_UCM-P larger than V [was 2.68 ± 0.26 rad² _ORT-P vs. 1.02 ± 0.12 rad², F_{(1, 7)} = 387.383, p < 0.01]. For the orientation analysis, V_UCM-O was larger than V _{2 ORT-O} [2.85 ± 0.28 rad vs. 0.62 ± 0.05 rad², F_{(1, 7)} = 55.245, p < 0.01]. No significant effects of D_PERT, T_DWELL and Phase were found.

Figure 5.

A: Indices of joint configuration variance for D12. Left panels: Variance within the UCM for position- and orientation-related analyses (V_UCMP and V_UCMO) and variance orthogonal to the UCM for position- and orientation-related analyses (V_ORTP and V_ORTO). Right panels: Z-transformed synergy indices for position- and orientation-related analyses (ΔV_ZP and ΔV_ZO). Averages across subjects with standard error bars are presented. Note that V_UCM > V_ORT (ΔV > 0) across all conditions and variables. B: Indices of joint configuration variance for D13.

While V_UCM > V_ORT across conditions and analyses, the difference between the two indices was larger for the orientation-related analysis. This was reflected in significantly smaller z-transformed synergy indices for position-related analysis (ΔV_Z-P = 0.33 ± 0.02) as compared to the orientation-related analysis (ΔV_Z-O = 0.75 ± 0.02) [F_{(1, 7)} = 54.172, p < 0.01]. No significant differences between D12 and D13 were found.

Discussion

The experiments have demonstrated that a transient force application leads to violations of equifinality in support of our Hypothesis-1. These violations scaled with the perturbation magnitude and amount of time the external force was kept at the new level before dropping back to the baseline value in support of Hypotheses-2 and -3. Note that the magnitude of the deviation of the final handle position from the initial position could be very large, over 50% of the total handle deviation at the peak of the external force (see Figure 3).

Violations of equifinality have been reported earlier in experiments with relatively fast voluntary movements performed in the presence of a destabilizing force field (DiZio and Lackner 1995; Hinder and Milner 2003; Lackner and DiZio 1994). In our case, violations of equifinality happened under the action of a slowly changing external force in the same direction as the baseline force despite the fact that the subjects were specifically instructed not to intervene with handle motion produced by the changing external force. Based on the ideas of equilibrium-point control (Feldman 1986), when the external force returns to the initial level, the handle has to return to the initial position. Indeed, equifinality in such experiments has been demonstrated several times (Bizzi et al. 1976; Kelso and Holt 1980; Latash and Gottlieb 1990; Schmidt and McGown 1980).

A major feature of our experiment that makes it different from similar earlier studies is the relatively long time, during which the handle was kept at a new position (T_DWELL). We believe that this feature led to the observed violations of equifinality. We interpret this result as a consequence of back-coupling between the actual and referent handle positions (cf. Martin et al. 2009) leading to a relatively slow drift of the referent position towards the actual one. Clearly, in experiments with fast movements or fast, transient force changes, effects of this slow process could not be observed. Obviously, for geometrical reasons, non-equifinality of the hand was associated with non-equifinality at the joint configuration level. Our analysis of the structure of variance in the joint configuration space addressed this issue in more detail and showed that joint configuration variance was mostly compatible with unchanged hand position at the final state (confined to the UCM).

Intentional and unintentional movements

Movements can be produced by two main factors. One of them is a change in the external force field; such movements may be called passive, although they are typically associated with changes in muscle activation patterns due to reflex effects from peripheral receptors. The other factor is a neural process leading to a shift of the body referent configuration. In this case, the movement can be called voluntary. Our results suggest that, within this definition, voluntary movements may be intentional or unintentional. The latter may result from a drift of the body referent configuration produced by a transient change in the external forces, even if the person is trying not to interfere with the force-produced body motion.

There are several potential sources of effects that could lead to violations of a net displacement of the body configuration (including the end-effector position) after a transient force perturbation. First, muscle forces are known to depend on the history of contraction (reviewed in Zatsiorsky and Prilutsky 2013). In particular, muscle shortening can lead to force depression (De Ruiter et al. 1998; Lee and Herzog 2009) while muscle stretch can lead to residual force enhancement (Oskouei and Herzog 2005; Pinninger and Cresswell 2007) compared to force values at the same muscle length in isometric conditions. These effects, however, are relatively large following quick changes in muscle length, while in our experiment these changes were relatively slow and modest in amplitude (hand motion over 10-15 cm in 0.5 s). Muscle reflexes are also known to show history effects (reviewed in Partridge and Partridge 1993). There are no reliable estimates of these effects for the kind of experiment we performed.

It is possible that perceptual effects contributed to the observed shift of the hand. For example, a blindfolded subject reports position shifts over time when holding an arm at a particular position; this phenomenon is known as proprioceptive drift (Tsay et al. 2014). In addition, there may be some kind of a “dead-zone” when the difference between proprioceptive signals is small and not perceived by the subject as a sign of a change in the position. Note, however, that our subjects were not instructed to move to a specific position after the perturbation. Actually, they were asked to ignore possible changes in the arm position (“allow the robot to move your arm”). They also did not know that the perturbation ended up with the same robot force as F_BIAS. The subjects were very much aware of the fact that their hand stopped short of the initial posture; so, perceptually, they were not within a dead-zone. Besides, the idea of dead-zone predicts highly variable behavior distributed within the dead-zone; in contrast, for a given dwell time, we observed consistent undershoot values. To our knowledge, neither of the mentioned factors is expected to lead to stronger effects following a longer dwell time in the middle of a transient force change. Given the large magnitude of the observed effects and their significant dependence on the dwell time, we favor a neural explanation based on unintentional changes in the body RC.

We view the unintentional changes in the body configuration in our experiment as consequences of an unintentional drift of the body RC. While this drift happened without subject’s intention, it likely involved some of the same neurophysiological pathways as purposeful RC shift used to produce intentional movement. One argument in favor of this conclusion is the similar structure of variance in the joint configuration space observed during unintentional movements in our experiment compared to earlier studies of multi-joint intentional movements (Domkin et al. 2002, 2005; Gera et al. 2010; Mattos et al. 2011). Indeed, in all those studies, the amount of variance within the UCM computed for the end-effector position and orientation was significantly larger than the amount of variance orthogonal to the UCM.

Our observations are not the first to report unintentional movements that were likely consequences of RC shifts. It has been known for many years that when a person produces constant force against a stop, turning visual feedback off leads to a rather quick decline in the force (Slifkin et al. 2000; Vaillancourt and Russell 2002; Shapkova et al. 2008; Wilhelm et al. 2013). This force drop could be rather large without the subjects noticing that the task was not performed adequately. Another example is the reported drop in grip force during a transient changes in the grip aperture (Ambike et al. in press). Note that in the last study, the time of handle aperture change was about 5 s, comparable to the dwell times in our experiment.

Direct and back-coupling between referent and actual configurations

The current schemes on the control of redundant motor systems with shifts in referent body configurations share a few important common features (Martin et al. 2009; Feldman 2010; Latash 2010). The process begins with specifying a relatively low-dimensional set of referent values for salient, task-specific variables – the highest RC. Further, a sequence of few-to-many transformations leads to RCs at lower levels of the assumed hierarchy. At each step, feedback loops (e.g., as in Latash et al. 2005) ensure that variance in the RCs at a lower level is mostly compatible with a desired RC at the higher level (in other words, this variance is mostly within the corresponding UCM). RC attracts the actual body configuration via feedback mechanisms including the tonic stretch reflex.

A number of studies reported changes in RC prior to changes in actual body configuration (Latash and Gottlieb 1991; Feldman et al. 1995; Latash et al. 1996; Adamovich et al. 1997). These changes reflect coupling between RC shifts and actual movement trajectories – direct coupling. When a redundant motor system performs a task, RCs can be analyzed at two levels, the task-specific level and the level of elemental variables. For example, during multi-finger accurate total force production in isometric conditions, RC at the highest level defines time profile of the total force, while RCs at the lower level define individual finger force changes (Latash et al. 2009). The concept of back-coupling between the actual and referent body configurations was developed in a model by Martin, Scholz and Schöner (2009) as a mechanism ensuring stability of the task-related common output of the elemental variables. In their model, estimates of the real configuration in the space of elemental variables are assumed to couple onto the subspace of task-irrelevant combinations of the elemental variables. This mechanism updates the RCs at the level of elemental variables making sure that their changes do not affect the task-related output (e.g., total force). A particular neuronal model for such back-coupling had been proposed earlier based on feedback loops similar to those provided by Renshaw cells (Latash et al. 2005). Characteristic times of this mechanism are expected to be low, possibly under 100 ms (cf. Shim et al. 2003; Latash et al. 2004).

In the current study, we present evidence for a different kind of back-coupling. It leads to changes in RC at the task-specific highest level of the assumed hierarchy and may be viewed as a mechanism for updating the movement plan. Its characteristic time delays are unknown at the moment, but our regression analysis suggests that this mechanism leads to effective RC shifts at times on the order of 1 s (Fig. 4). If RC may be metaphorically viewed as a carrot attracting the head of a donkey, the back-coupling suggests that the hungry donkey possesses telekinetic powers to induce carrot motion towards its head if the carrot is kept away for a long time.

What could be the functional importance of this, different kind of back-coupling? First, this mechanism may be involved in reducing overall muscle activation levels and saving energy as long as this does not lead to task failure. If external conditions prevent motion to a target (RC), keeping pushing against this wall is pointless. Second, as any feedback loop helping the system to achieve equilibrium, it may be viewed as a contributor to stability of motor behavior. Briefly, the system reaches maximal stability when its referent and actual configurations are identical. Typically, as in the current versions of the RC hypothesis, actual configuration drifts towards the referent one if allowed by external forces. A drift of the referent configuration towards the actual one is another, hypothesized, mechanism that reduces the difference between the two configurations and thus contributes to stability of the whole system. There may be other reasons from purely motor to perceptual and even to cognitive, but we are not ready to discuss them based on the available limited data set.

While we offer an interpretation of the results based on the RC hypothesis, this is not the only framework in the field of motor control. An alternative approach assumes computational processes within the central nervous system imitating the interactions within the body and between the body and the environment (internal models, reviewed in Wolpert et al. 1995; Kawato 1999). This approach can certainly account for all the experimental observations assuming appropriate changes in internal models. Since we see the main goal of our research as understanding the physics and physiology of motor control, we prefer not to assume computational processes within the central nervous system.

Emerging questions

Our study leads to a few questions that have to be explored experimentally in future.

Do intentional and unintentional RC shift lead to similar structure of variance within redundant systems? Our UCM analysis of joint configuration variance (Figure 5) suggests that this is the case. However, a direct comparison between the joint configuration structure during similar intentional and unintentional movements performed by the same subjects in the same conditions is needed to answer this question conclusively. In particular, it is possible that unintentional movements lead to more stereotypical actions reflected in smaller synergy indices.

Our regression analysis of the dependence of the final deviation on the handle on dwell time and perturbation magnitude (Figure 4) has to be viewed as pilot. Indeed, the regression curves were computed based on only three actual observations and one assumed one (zero point). The outcome of the regression analysis is, however, raising a few important questions. First, the asymptotic character of the data with increasing T_DWELL suggests that RC is drawn not to the actual configuration but to a point about half-way between the initial coordinate and the largest deviation from it (D13). It is not clear why this is the case and what is special about that mid-point. The analysis also suggests that the RC drift is faster for the larger initial deviations to the actual coordinate. While this may seem expected, the effects on perturbation distance on only one of the two coefficients is not obvious.

Another approach to explore the hypothesized RC shift would be to use a double-perturbation paradigm, in particular to use the robot to actively move the hand back to the original position. If the RC has shifted, the subjects should move away from the original posture. All these issues require a detailed further exploration.

There are a few drawbacks within the study that limit its generality. In particular, we trained the subjects to ignore the arm motion induced by the perturbation, but there was no objective measure of “non-interference”. In pilot trials, we recorded electromyographic signals (EMGs) from a subset of arm muscles and found only minor modulation of EMGs corresponding to relatively small and not very fast changes in the muscle length. No obvious EMG bursts were seen that would suggest a volitional correction. An earlier study compared behaviors under the “intervene” and “do not intervene” instructions and showed more consistent behavior in subjects under the latter instruction (Latash 1994).

Another drawback of this experiment is the rather arbitrary setting of the bias force. The purpose of the bias force was to make sure that the subject’s hand acted against a well-defined external force in the initial configuration and that the force did not lead to fatigue. To keep the experimental procedure short, we decided against scaling the bias force using percentage of maximal force production by individual subjects. We view this as a relatively minor methodological factor unlikely to affect the results qualitatively.