Hierarchical Organization in Liquid Crystal-in-Liquid Crystal Emulsions

Abstract

We report the formation and characterization of hierarchical ordering in systems comprised of micrometer-sized droplets of thermotropic nematic liquid crystals (LCs) dispersed in continuous nematic phases of a lyotropic chromonic LC (disodium cromoglycate (DSCG)). Significantly, we find the orientations of the two LC phases to be coupled, with nematic droplets of 4′-pentyl-4-cyanobiphenyl (5CB) exhibiting a bipolar configuration with an axis of symmetry aligned orthogonal to the far-field director of the DSCG phase. We determine that this coupling of orientations does not result from either anisometric LC droplet shape or interfacial ionic phenomena but rather is consistent with the influence of van der Waals interactions that arise from the anisotropic polarizabilities of nematic 5CB (Δn = + 0.18) and DSCG (Δn = − 0.02) phases. We also find that it is possible to rotate and uniformly align the nematic droplets by using a weak magnetic field (B ∼ 0.3 T). An analysis of the dynamics of relaxation of the orientations of the 5CB droplets following removal of the magnetic field reveals the DSCG and 5CB droplets to be coupled by energies of ∼10⁴kT, consistent with a simple theoretical estimate of the influence of anisotropic van der Waals interactions. We also observed the nematic 5CB droplets to form dimers and larger assemblies mediated by the elasticity of the nematic DSCG. Overall, these results reveal that LC-in-LC emulsions define a new class of hierarchically ordered soft matter in which both thermotropic and lyotropic LCs are coupled in their ordering.

Introduction

Over the past several decades, liquid crystals (LCs) confined within either direct or inverted emulsions have been widely explored as a new class of anisotropic soft matter.^1–7 In direct emulsions, the LCs are confined within micrometer-sized droplets dispersed within a continuous isotropic phase. The ordering of thermotropic LCs within droplets of direct emulsions has been shown to be influenced by the anisotropic elasticity of the LCs, the presence of topological defects, and interfacial interactions that can arise from hydrogen bonding, van der Waals forces, and electrical double layers.^1,4,7–9 More recently, lyotropic chromonic LCs (LCLCs), which form nematic or hexagonal columnar phases through face-to-face stacking of plank-like, polyaromatic molecules into columnar aggregates in aqueous solutions,^10,11 have also been characterized within emulsion droplets dispersed in immiscible isotropic oils.^12–15 These emulsions are, in some cases, distinguished from their thermotropic droplet-based counterparts by the formation of faceted LC droplets.¹⁵ Alternatively, in the case of inverted LC emulsions, droplets of an isotropic phase (e.g., oil or aqueous solution) have been dispersed within a continuous LC phase.^3,5,16–19 In these studies, the elasticity and topological defects of LCs have been shown to generate interdroplet forces that drive the isotropic droplets into complex structures including linear chains and hexagonal arrays.^5,16,18,19 While initial studies largely focused on characterization of isotropic droplets in thermotropic LCs, recently it has been demonstrated that LCLC elasticity-mediated forces also induce self-assembly of micrometer-sized colloids²⁰ and living bacteria²¹.

In this paper, we move beyond these past studies involving a single LC phase (dispersed or continuous) to investigate dispersions comprised of two immiscible LC phases. Specifically, we focus on droplets of nematic thermotropic LCs dispersed in an immiscible nematic LCLC (15 wt% disodium cromoglycate – DSCG) phase. Our investigation of these “LC-in-LC emulsions” was motivated by a number of fundamental questions, particularly the question of whether the ordering of the LCs in the two phases would be coupled through interactions mediated by, for example, anisotropic droplet shapes, or alternatively interfacial interactions (surface anchoring). In addition, we sought to explore how nematic LC droplets would interact and self-assemble when dispersed within the LCLC.

Experimental

Materials

4′-pentyl-4-cyanobiphenyl (5CB) was obtained from EM Sciences (New York, NY). N-(4-methoxybenzylidene)-4-butylaniline (MBBA), disodium cromoglycate (DSCG), glycerol, and phosphate-buffered saline (PBS) (0.01 M phosphate, 0.138 M NaCl, 0.0027 M KCl, pH 7.4) were purchased from Sigma-Aldrich (St. Louis, MO). Polyimide was obtained from HD Microsystems (Parlin, NJ). 1-methyl-2-pyrrolidinone, silicone oil, Fisher's Finest Premium Grade glass slides and cover glass were purchased from Fisher Scientific (Pittsburgh, PA). Deionization of a distilled water source was performed with a Milli-Q system (Millipore, Bedford, MA) to give water with a resistivity of 18.2 MΩ cm.

Lyotropic LC preparation

Lyotropic LCs containing DSCG were prepared by mixing 15 wt% of DSCG with 85 wt% of PBS. The mixture was shaken for at least 12h to ensure complete solubility and homogeneity. Prior to the preparation of emulsions, the DSCG solution was heated at 65°C for 10 min as described elsewhere.^22,23 At this concentration, DSCG forms a nematic LC phase below ∼32°C and an isotropic phase above ∼40°C.Two-phase coexistence is observed within the range of intermediate temperatures.

Preparation of LC-in-LC emulsions

LC-in-LC emulsions were formed by sequential sonication and vortexing of mixtures of ∼1 μL of 5CB (or MBBA) and ∼100 μL of 15 wt% DSCG (in PBS). Five cycles consisting of 10s of vortexing followed by 10s of sonication in a bath held at 55°C were performed. Emulsions containing isotropic silicone oil droplets were prepared in the same manner. Emulsions were analyzed within 4h of their preparation.

Assembly of experimental imaging chambers

To create imaging chambers that induced a uniform azimuthal alignment of the nematic DSCG, we first rubbed a polyimide-coated glass slide and glass cover slip unidirectionally 30 times with a velvet cloth. A small volume (∼4.5 μL) of LC-in-LC emulsion was then drawn between the two polyimide-coated glass substrates in a cavity created using two sheets of Mylar film (∼60 μm in thickness). The two polyimide-coated glass substrates were oriented such that the rubbing directions of the two substrates were antiparallel. Following assembly, the chamber was immediately sealed with epoxy to prevent water evaporation. The imaging chamber was then heated into the isotropic phase of DSCG for 30s. Approximately 10 – 20 min after cooling the sample back to room temperature, the nematic DSCG film exhibited a planar orientation with largely uniform azimuthal alignment in the direction of rubbing of the polyimide-coated substrates.

Optical characterization of LC-in-LC emulsions

The configurations adopted by dispersed thermotropic LC droplets within continuous nematic lyotropic LCs were investigated using an Olympus IX71 inverted microscope (Center Valley, PA) equipped with a 100× oil-immersion objective and crossed polarizers. Bright field and polarized light micrographs of the LC-in-LC emulsions were collected with a Hamamatsu 1394 ORCAER CCD camera (Bridgewater, NJ) connected to a computer and controlled through SimplePCI imaging software (Compix, Inc., Cranberry Twp., NJ). Slow translational diffusion of LC droplets within the viscous nematic DSCG solution (μ ∼ 0.7 Pa s)²¹ enabled us to easily capture both bright field and crossed polars micrographs of individual droplets. Only droplets that were freely translating within the nematic DSCG and not adsorbed to one of the polyimide-coated glass substrates were imaged and analyzed, as contact with surfaces has been previously demonstrated to influence the configurations adopted by LC droplets.²⁴

Results and Discussion

As detailed in the Experimental section, we prepared emulsions comprised of droplets of nematic thermotropic LCs in continuous phases of aqueous nematic DSCG phase (15 wt%) by the sequential vortexing and sonication of mixtures of these two LCs. Subsequently, we confined a thin film (∼60 μm in thickness) of the emulsion between rubbed polyimide surfaces that caused a planar orientation and uniform azimuthal alignment of the continuous nematic DSCG (Fig. S1^†). Our initial experiments were performed using 4′-pentyl-4-cyanobiphenyl (5CB) as the thermotropic LC (at room temperature). After emulsification, we optically characterized the orientations assumed by both the continuous (DSCG) and dispersed (5CB) LCs within the thin films of the emulsions. The emulsions were polydisperse, and our observations below are made with reference to the size of the emulsion droplets within the dispersion.

In general, we observed that nematic 5CB droplets with diameters greater than ∼6 μm exhibited bipolar configurations and thus planar anchoring at the interface of the droplet with the continuous nematic DSCG phase. Our observations of the optical textures of the 5CB droplets between crossed polars (Fig. 1A-C) as well as the positions of the boojums of the droplets evident in bright field images (Fig. 1D-F) confirmed the bipolar configuration. Both boojums of bipolar 5CB droplets were observed in some bright field images (Fig. S2). For droplets with diameters smaller than ∼6 μm, we found it difficult to determine the configuration of the LC within the droplets due to the birefringence of the encompassing nematic DSCG (Fig. S3; see ESI for details). All of the 5CB droplets characterized in our experiments (diameters ranging from 6 μm to 35 μm) exhibited very slow translational and rotational diffusion within the nematic DSCG. For example, we measured a 5CB droplet with diameter ∼20 μm to move at less than 0.5 μm/min and to rotate at less than 1°/min in the absence of convective flows within the DSCG phase (Fig. S4). This observation is consistent with our theoretical estimates of the root mean square displacement and root mean square angular deviation of a 20 μm -diameter spherical particle with in nematic 15 wt% DSCG (see ESI).

Fig. 1.

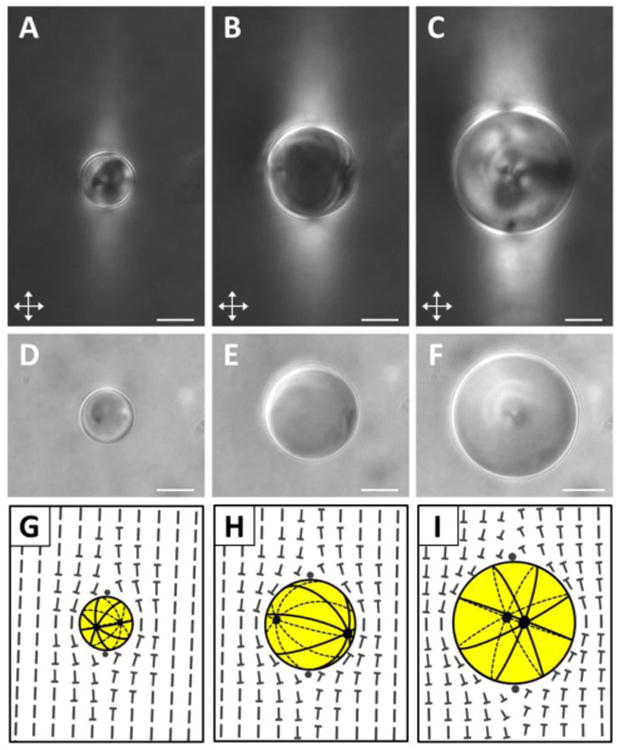
Orientations of nematic 5CB emulsion droplets in aligned nematic 15 wt% DSCG. (A-C) Crossed polars and (D-F) bright field micrographs of 5CB droplets with diameters of (A, D) 14.0 μm, (B, E) 24.4 μm, and (C, F) 33.2 μm. (G-I) Corresponding schematics illustrating the director profiles within the 5CB droplets as well as in the encompassing nematic DSCG. The handedness of the twist at the poles of all droplets is arbitrarily depicted to be the same (see text for details). Scale bars = 10 μm.

Within the continuous DSCG phase, distortion of the nematic director around the 5CB droplets generated brightly birefringent “tails” that extended away from the surface of the 5CB droplets parallel to the far-field DSCG director (Fig. 1A-C).In addition, we observed four small bright lobes near the surface of the droplets when viewed between crossed polars. Nych et al. recently observed similar optical patterns around isotropic water droplets and synthetic microparticles (planar anchoring) dispersed within nematic 15 wt% DSCG and demonstrated that they are a signature of a twisted DSCG director configuration near the boojum defects located at the poles of the colloids.²⁰ The twisted director profile is a consequence of the small twist elastic constant (K₂) of this chromonic LC,²⁰ as K₂(∼1 pN) is approximately an order of magnitude smaller than the elastic constants for splay (K1) or bend (K₃) (∼10 pN).²⁵ Our observations lead us to conclude that nematic DSCG also forms twisted director configurations around both nematic 5CB droplets (Fig. 1G-I) and isotropic silicone oil droplets (Fig. S5). This result also leads us to conclude that nematic DSCG exhibits a planar orientation at the interfaces of the 5CB droplets. Similar to the observations of Nych et al., we found (i) the brightness and the length of the birefringent tails in the DSCG to increase with increasing LC droplet size, and (ii) there to be no optical signature indicative of a twisted director configuration around droplets with diameters smaller than ∼6 μm (Fig. S3).²⁰ Finally, we note that while our schematic illustrations in Fig. 1 all arbitrarily depict the handedness of the twist deformations to be the same at the poles of each LC droplet, the actual twist directions were observed to vary.²⁰ While the absolute handedness of the twist influences interactions between pairs of 5CB droplets (see below), it does not significantly impact the conclusions that we draw in the remainder of this paper regarding isolated 5CB droplets.

Next, we characterized the orientations of the bipolar 5CB droplets with diameters between 6 and 35 μm within the nematic DSCG phase in order to determine if the droplets aligned in a preferred direction relative to the far-field DSCG director (n_DSCG). By measuring the positions of the boojums of a droplet apparent in bright field micrographs (Fig. 1D-F), we were able to determine the orientation of the axis of symmetry of the bipolar configuration, as depicted schematically in Fig. 1G-I. Significantly, by quantifying the angle (θ) formed between the symmetry axis of the bipolar 5CB droplets relative to n_DSCG (see ESI for details), we found that the nematic 5CB droplets were oriented in directions that were largely orthogonal to n_DSCG (θ ∼ 80-90°) (Fig. 2A). We note that the bipolar 5CB droplets, while maintaining that orthogonal orientation, were observed to slowly rotate about an axis defined by the far-field orientation of the DSCG phase in our experiments (See arrows in Fig. 2A;Fig. S4).

Fig. 2.

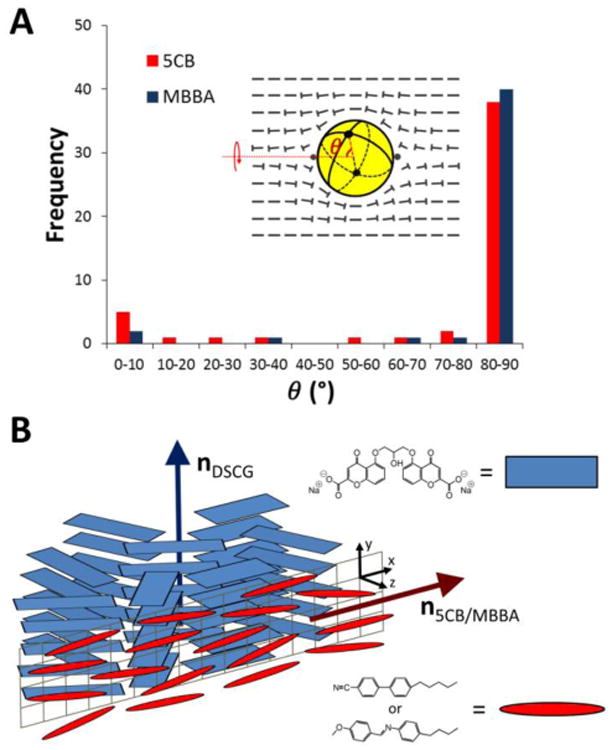
(A) Quantification of the angle formed between the symmetry axis of bipolar 5CB (N = 50) and MBBA (N = 45) droplets relative to the far-field director of nematic DSCG. (B) Schematic illustrating the preferred orthogonal orientations of the local directors at the interface of nematic thermotropic LCs and nematic DSCG.

We explored several hypotheses regarding the possible origin of this preferential relative orientation of the bipolar 5CB droplets and nematic DSCG phase. First, we considered the possibility that a slight elongation in the shape of the 5CB droplets might impact their orientation in the nematic DSCG. Elongation of the LC droplets is predicted when the elastic energy within the 5CB droplet and encompassing nematic DSCG (both which scale as ∼KR) is similar to or greater in magnitude than the interfacial energy of the droplets (which scales as ∼γR²). For 5CB droplets of R ∼ 10 μm, with K ∼ 10^-11 N for DSCG²⁵ and 5CB²⁶ and γ of 10^-3 – 10^-2 N/m (measured for interfaces between 5CB and either pure water²⁷ or an aqueous polymer solution²⁸ (see ESI)), however, the surface energy (∼10^-13 J) is much greater than the bulk elastic energies (∼10^-16 J). Consistent with this prediction, we did not find the 5CB droplets observed in our experiments to measurably depart from a spherical shape. Finally, we note also that ellipsoidal droplets (5CB tactoids) with planar anchoring would be predicted to align with their major axis parallel to the far-field DSCG director in order to minimize the elastic energy of the DSCG.¹² Because our measurements show that the preferred orientation of the symmetry axis of the bipolar 5CB droplets is orthogonal rather than parallel to n_DSCG (see Fig. 2), we conclude that the orientations of the nematic 5CB droplets and DSCG are not coupled through the elasticity of the nematic DSCG and the anisometric shape of the 5CB droplets.

Second, we considered the possibility that the coupling between the nematic directors of the 5CB and 15 wt% DSCG phases arises from the presence of interfacial electric fields associated with electrical double layers.^29,30 Here we note that electric fields within double layers can generate torques on LCs due to the anisotropic dielectric properties (Δε) of the LC phases.^31,32 In particular, past studies have demonstrated that, due to the positive Δε of 5CB (Δε = +13)²⁶, formation of an electrical double layer at an interface of 5CB can cause the anchoring of 5CB to change from planar to homeotropic.^31,32 We tested the possible role of electrical double layers in the observed coupling of the orientations of the 5CB droplets and DSCG by creating dispersions of nematic N-(4-methoxybenzylidene)-4-butylaniline (MBBA) droplets within nematic DSCG. Since MBBA possesses a negative Δε (Δε = − 0.7)²⁶, if interfacial electric fields played a key role in the coupling of the orientation of thermotropic LC droplets to the nematic DSCG phase, we would expect the orientation of the MBBA droplets to differ from 5CB. Our measurements of the orientations adopted by bipolar MBBA droplets within aligned DSCG phases (Fig. S6), however, revealed that the MBBA droplets also oriented with the axis of symmetry of the bipolar configuration orthogonal to n_DSCG (Fig. 2A). The result of this experiment leads us to conclude that interfacial ionic phenomena (and the electric fields associated with interfacial adsorption of ions) do not play a dominant role in coupling the orientations of bipolar thermotropic LC droplets and continuous nematic phases of DSCG.

Third, we hypothesized that van der Waals interactions (which arise from anisotropic polarizabilities or refractive indices) between 5CB and nematic DSCG phases may couple their orientations. Past studies have established that van der Waals forces play a central role in determining the orientations adopted by LCs near interfaces, including 5CB near alignment layers such as rubbed polymer films^33,34 and self-assembled alkanethiol monolayers.^35,36 In addition, theoretical studies suggest that anisotropic van der Waals interactions can act over long distances, for example causing the orientation of LCs to be influenced by an anisotropic substrate even when separated from the substrate by a thin (1 – 100 nm) isotropic film.^37-39 In our experiments, on the basis of observations of the LC droplets through crossed polars, we concluded above that both nematic 5CB and DSCG are oriented tangential (or close to tangential) to the nematic-nematic interface. However, since individual DSCG molecules stack face-to-face into columnar aggregates to form the nematic phase, the polyaromatic cores of the molecules are on average orthogonal to n_DSCG and nematic DSCG exhibits negative optical birefringence (Δn = − 0.02).^10,11,40 Thus, as illustrated in the schematic in Fig. 2B, although the local director of the DSCG phase (n_DSCG) is oriented in a direction tangential to the 5CB/DSCG interface (along the y axis in Fig. 2B), the orientations of the optical axis with the highest refractive index lie within the plane normal to n_DSCG. In contrast, the optical birefringence of nematic 5CB is positive (Δn = +0.18)²⁶ and the optical axis with the highest refractive index is tangential to the 5CB/DSCG interface, coinciding with the local director n_5CB. Consequently, when n_5CB adopts an in-plane orientation orthogonal to n_DSCG (i.e. n_5CB oriented along the x axis in Fig. 2B), the optical axes of the two phases with the highest refractive indices are aligned, a mutual orientation that generates the strongest van der Waals coupling between the phases.

At the interface of a LC droplet in a LC-in-LC emulsion, the mutual orientations of the two directors of the LC phases will vary with position across the droplet surface. However, when the symmetry axis of a bipolar 5CB droplet is orthogonal to the far-field director of the nematic DSCG phase, over a significant fraction of the droplet surface, the local directors of the nematic 5CB and DSCG phases are orthogonal (or nearly orthogonal) to one another. In contrast, when the symmetry axis of a bipolar LC droplet is aligned parallel to the far-field director of the DSCG phase, the directors of the two LC phases are largely parallel at the droplet surface. Our observation that the symmetry axis of both bipolar 5CB and MBBA (Δn = +0.21)²⁶ droplets aligns orthogonal to the far-field director of nematic DSCG is thus consistent with the hypothesis that the orientations of the nematic thermotropic and lyotropic LCs are coupled to one another through anisotropic van der Waals interactions in our experiments. We comment also that the twisted DSCG director field²⁰ around a 5CB droplet will also influence the relative orientations of the nematic phases at the droplet interface and thus the strength of coupling of the two LC phases.

To obtain an estimate of the strength of the orientational coupling between the 5CB droplets and nematic DSCG continuum, we applied a magnetic field parallel to the orientation of the far-field director of the DSCG phase (Fig. 3A-C). We found that a magnetic field strength of ∼0.3 T was sufficient to rotate the axis of the bipolar 5CB droplets towards the direction of the applied magnetic field (Fig. 3D-F), a result that is consistent with the positive diamagnetic anisotropy of 5CB (Δχ = +1.7 × 10^-7 (cgs))²⁶. Upon removal of the magnetic field, we observed the 5CB droplets to relax back towards their initial orientation over the course of minutes (Fig. 3D-P; see Fig. S7 for additional examples).We did not observe the nematic DSCG to realign during the application of the magnetic field in our experiments (a result consistent with a small magnitude of the diamagnetic anisotropy of DSCG), nor did we observe 5CB droplets dispersed in an isotropic phase to relax to a preferred orientation following removal of an applied magnetic field (Fig. S8; see ESI for details). The driving force for the relaxation of the orientation of the 5CB droplet following the removal of the magnetic field in the experiment described above, according to our hypothesis, is a torque due to anisotropic dispersion forces (Γ_vdw) acting across the 5CB-DSCG interface. During the relaxation process, Γ_vdw is balanced by a torque that arises from rotational drag on the 5CB droplet of radius R, which can be evaluated as Γ_drag = 8πηR³ω, where is ω is the rotational velocity of the droplet. We estimate ω ∼ 0.36°/s (0.006 rad/s) from the slope of the approximately linear portion of the plot in Fig. 3P (between 0 and 60s) as the droplet relaxes from θ₁ ∼ 52° to θ₂ ∼ 74°. Using η ∼ 0.7 Pa s for the viscosity of the nematic DSCG phase²¹, we calculate Γ_drag∼ 2 × 10-¹⁶ J/rad for the droplet in Fig. 3 (the diameter of the droplet was ∼24 μm). The energy dissipated during the rotation of the droplet is estimated as E_rotation = Γ_drag(θ₁−θ₂), which we calculate to be ∼8 × 10^-17 J (∼ 2 × 10⁴kT). We conclude, therefore, that the orientations of the nematic 5CB droplets and DSCG are coupled through an energy of ∼8 × 10^-17 J.

Fig. 3.

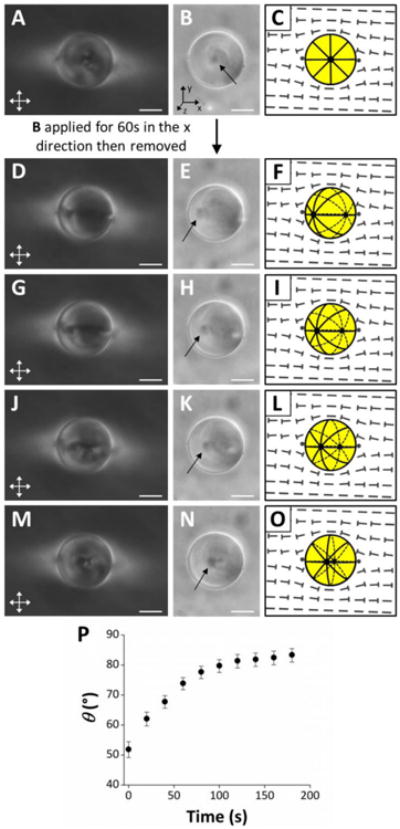
Rotation of 5CB droplets following application and removal of a magnetic field. (A, D, G, J, M) Crossed polars, (B, E, H, K, N) bright field (with arrows indicating the locations of boojums), and (C, F, I, L, O) schematic illustrations of a bipolar 5CB droplet in an aligned region of nematic DSCG. (A-C) Initial configuration of the droplet. (D-O) Configuration of the droplet after application of a magnetic field (B ∼ 0.3 T) in the x direction (see coordinate system in B) and removal at t = 0s. (D-F) Configuration of droplet at t = 0s, (G-I) t = 20s, (J-L) t = 40s, and (M-O) t = 120s. (P) Plot of the angle formed between the symmetry axis of the 5CB droplet depicted in D-O relative to the far-field director of nematic DSCG (θ) as a function of time following removal of the applied magnetic field. Error bars represent uncertainty in the calculation of θ associated with estimating the positions of the 5CB droplet center and one of the boojums of the droplet. Scale bars = 10 μm.

To determine whether the above-described estimate of the energy that couples the orientations of the 5CB and DSCG phases is consistent with the presence of anisotropic van der Waals interactions, we performed a simple theoretical estimate of the orientation-dependent van der Waals interaction between two semi-infinite planar slabs of uniformly aligned nematic 5CB and nematic DSCG using the expression⁴¹:

$${\mathrm{E}}_{\text{aniso}}=\frac{-\mathrm{\text{kT}}}{64\mathrm{\pi }{\mathrm{d}}^2}{\mathrm{\gamma }}_{5\mathrm{\text{CB}}}{\mathrm{\gamma }}_{\text{DSCG}}{cos}^2\theta .$$

In this expression, γ_i is evaluated as ${\mathrm{\gamma }}_{\mathrm{i}}=\frac{\sqrt{{\varepsilon }_{\perp }^{\mathrm{i}}{\varepsilon }_{\parallel }^{\mathrm{i}}}({\varepsilon }_{\perp }^{\mathrm{i}}-{\varepsilon }_{\parallel }^{\mathrm{i}})}{2{\varepsilon }_{\parallel }^{\mathrm{i}}(\sqrt{{\varepsilon }_{\perp }^{\mathrm{i}}{\varepsilon }_{\parallel }^{\mathrm{i}}}+{\varepsilon }_{\mathrm{m}})}$, where ${\varepsilon }_{\parallel }^{\mathrm{i}}$ And ${\varepsilon }_{\perp }^{\mathrm{i}}$ are the dielectric response functions parallel and perpendicular to each LC director, respectively, and ε_m is the dielectric response of an isotropic medium that separates the two LC slabs at a distance d. When the relative orientations of the nematic directors of 5CB and DSCG (with surface area equal to the interfacial area of the droplet in the experiment described above) changes from θ ∼ 52° to θ ∼ 74°, we estimate that the free energy of the system is lowered by ∼ 1 × 10^-16 J (see ESI for details). Although this value is obtained using a geometry that is simplified relative to our experiment, its close agreement to the estimate obtained from our experiment (∼ 8 × 10^-17 J) provides support for our hypothesis that a torque due to anisotropic dispersion forces couples the orientations of the 5CB and DSCG phases.

We note that the magnitude of the energy arising from anisotropic van der Waals interactions that couples the orientations of the nematic 5CB and nematic DSCG phases is large compared to kT and thus it leads us to predict that 5CB droplets, if at equilibrium, should not be observed to deviate from an orientation that is orthogonal to n_DSCG. We speculate that our experimental observation of several 5CB and MBBA droplets oriented at θ < 80° (Fig. 2A) may be the result of (i) the slow relaxation of droplets to an equilibrium orientation (Fig. 3P), (ii) proximity of other droplets altering the near-field alignment of DSCG, or (iii) interactions between the droplets and the polyimide alignment layer.

We also performed experiments using an applied external field to demonstrate that it was possible to use the field to select a unique droplet orientation from the family of degenerate orientations defined by rotation of the symmetry axis of the bipolar 5CB droplet about the axis defined by n_DSCG in the nematic DSCG (Fig. 4). By applying a magnetic field in a direction orthogonal to both n_DSCG and the initial axis of symmetry of a 5CB droplet (Fig. 4A-C), we found that we could orient the symmetry axis of the bipolar 5CB droplet parallel to the direction of the applied field. Due to slow rotational diffusion in DSCG (< 1°/min, see above), the droplet retained this orientation for the duration of our observations (5 min) following removal of the field (Fig. 4D-I). By repeating this sequence but with the magnetic field rotated to the initial orientation of the LC droplet, the droplet returned to its initial orientation (Fig. 4J-O). In this manner, we were able to rotate bipolar 5CB droplets between energetically degenerate orientations orthogonal to n_DSCG. These results demonstrate the ability to direct the orientations of 5CB droplets in aligned nematic DSCG through the transient application of an external field.

Fig. 4.

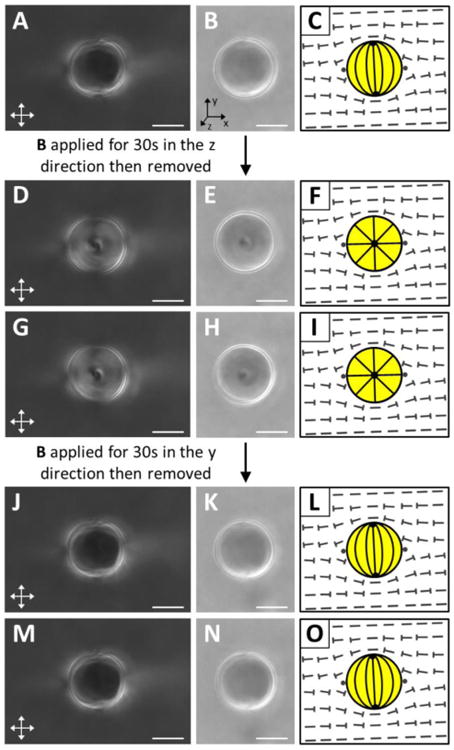
Selection of unique orientations of a 5CB droplet dispersed in nematic DSCG using a transient magnetic field. (A, D, G, J, M) Crossed polars, (B, E, H, K, N) bright field, and (C, F, I, L, O) schematic illustrations of a 5CB droplet in an aligned region of nematic DSCG. (A-C) Initial configuration of the droplet. (D-I) Configuration of the droplet after the application and removal of a magnetic field (B ∼ 0.3 T) in the z direction (see coordinate system in B). (D-F) Configuration of the droplet 30s and (G-I) 300s after the field was removed. (J-O) Configuration of the droplet after the application and removal of a magnetic field (B ∼ 0.3 T) in the y direction. (J-L) Configuration of the droplet 30s and (M-O) 300s after the field was removed. Scale bars = 10 μm.

We end our paper by making some observations regarding interactions between the 5CB droplets that are mediated by the DSCG phase. Similar to the inverted LC emulsions studied previously (i.e., isotropic water droplets dispersed in nematic 5CB^3,16,17), we observed pairs of nematic 5CB droplets dispersed in nematic DSCG to exhibit attractive interactions. In particular, we found that droplets adhered upon approaching one another (Fig. 5), consistent with the effects of the elasticity of the nematic DSCG phase on inter-droplet interactions.^3,16,17,20 We occasionally observed adhered nematic droplets to coalesce (Fig. S9), but more often we found that droplets remained adhered to one another for long times. Although the elasticity of nematic droplets has been reported to create a barrier that inhibits coalescence of nematic droplets in an isotropic continuous phase,⁴² we also found that isotropic silicone oil droplets dispersed in DSCG adhered to one another without coalescing (Fig. S10). This leads us to conclude that the barrier to coalescence arises from either elastic forces mediated by the DSCG or potentially other colloidal forces such as electrical double layer forces arising from charging of the interface of the 5CB in the DSCG.³²

Fig. 5.

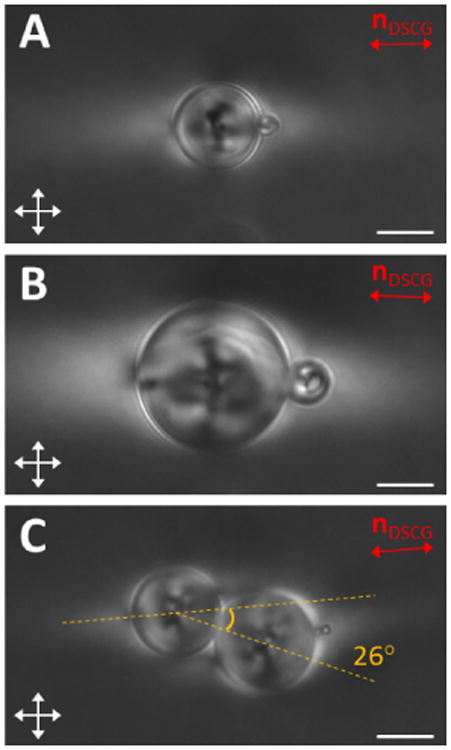
Organization of pairs of 5CB droplets in nematic DSCG. Micrographs of adhered 5CB droplets (crossed polars) (A) with diameters of 15.3 μm and 3.7 μm, (B) 26.9 μm and 7.9 μm, and (C) 18.5 μm and 16.0 μm within aligned regions of nematic DSCG. The far-field orientation of the nematic DSCG is indicated by a double headed red arrow. Scale bars = 10 μm.

We found that the alignment of pairs of 5CB droplets relative to the far field director of the DSCG phase depended upon the diameters (d₁ and d₂) of the two interacting 5CB droplets. When the difference in size was large (d₁ > 3d₂), we found that the droplets aligned parallel to n_DSCG, with the smaller droplet positioned at the site of one of the boojums in the nematic DSCG near the large droplet. We observed this arrangement when the smaller droplet (d₂ < 3 μm) did not noticeably deform the DSCG (Fig. 5A) and when it was large enough (d₂ > 6 μm) to induce observable twist in the DSCG (Fig. 5B and Fig. S11). However, when d₁ < 3d₂, we found the 5CB droplets instead to align at a small angle from n_DSCG, with the angle approaching a maximum value of ∼30° for the case of d₁ ∼ d₂ (Fig. 5C), consistent with recent observations of isotropic droplets in nematic DSCG²⁰ as well as spherical colloids that induced strain with a quadrupolar symmetry in LCs¹⁶. We note that whenever both d₁ and d₂ were > 6 μm, attraction between the droplets only occurred when the chirality of the twisted distortions in adjacent “tails” was the same, while repulsion was observed in cases when the chirality was opposite.²⁰

Conclusions

In conclusion, this paper reports the formation and characterization of hierarchical ordering present in LC-in-LC emulsions, specifically with nematic thermotropic LC droplets dispersed within a nematic LCLC Most interestingly, we demonstrate that the orientations of the LCs in the dispersed and continuous phases are coupled, and report a series of experiments that support our hypothesis that the coupling reflects anisotropic van der Waals interactions (and not, for example, anisometric LC droplet shapes).This coupling of the local directors of the LC phases leads to a hierarchy of organization in the system. For example, the coupling induces the symmetry axis of micrometer-sized bipolar nematic thermotropic LC droplets to align orthogonal to the far-field director of the nematic LCLC phase, which itself is aligned by the rubbed polyimide substrates in our experiments. In addition, we show that the LCLC phase can mediate interactions that lead to clustering of the aligned, thermotropic LC droplets. By analyzing the dynamics of the response of the orientations of the LC droplets to an applied magnetic field, we conclude that the orientations of the 5CB and DSCG phases are coupled through interaction energies of order ∼10⁴kT for 5CB droplets with R ∼ 10 μm. These results and others reported in this paper involving assemblies of multiple droplets suggest that the hierarchical organization of LC-in-LC emulsions and their responsiveness to weak external perturbations (e.g., magnetic fields) makes them fertile territory for fundamental soft matter research as well as technologically promising (e.g., for the creation of novel photonic devices that can be driven by weak fields).We envision that these studies could be extended to include investigations of the coupling of LC orientations within LC-in-LC emulsions in which the dispersed LC phase is confined within droplets having higher geometrical complexity, such as handlebody-shaped thermotropic LC droplets of non-zero genus (e.g., toroids) within a nematic LCLC^43-45 or faceted columnar phase LCLC droplets¹⁵ dispersed in a thermotropic LC. The results also suggest that interfaces defined by thermotropic LC materials may offer the basis of a general and facile approach to control of the surface anchoring of chromonic LC phases.